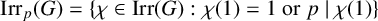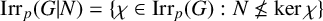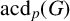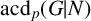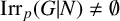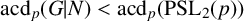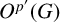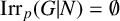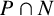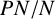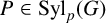1 Introduction
In this paper, G is a finite group and p is a prime divisor of
![]() $|G|$
. Let
$|G|$
. Let
![]() $\mathrm{Irr}(G)$
denote the set of (complex) irreducible characters of G. For a normal subgroup N of G and
$\mathrm{Irr}(G)$
denote the set of (complex) irreducible characters of G. For a normal subgroup N of G and
![]() $\theta \in \mathrm{Irr}(N)$
, let
$\theta \in \mathrm{Irr}(N)$
, let
![]() $\mathrm{Irr}(G|N) = \{\chi \in \mathrm{Irr}(G) : N \not \leq \mathrm{ker}\,\chi \}$
and
$\mathrm{Irr}(G|N) = \{\chi \in \mathrm{Irr}(G) : N \not \leq \mathrm{ker}\,\chi \}$
and
![]() $\mathrm{Irr}(\theta ^G)$
denote the set of the irreducible constituents of the induced character
$\mathrm{Irr}(\theta ^G)$
denote the set of the irreducible constituents of the induced character
![]() $\theta ^G$
. The average character degree of G is denoted by
$\theta ^G$
. The average character degree of G is denoted by
![]() $\mathrm{acd}(G)$
(see [Reference Moretó and Nguyen5, Reference Qian8]) and it is defined by
$\mathrm{acd}(G)$
(see [Reference Moretó and Nguyen5, Reference Qian8]) and it is defined by
 $$ \begin{align*}\mathrm{acd}(G) =\frac{ \Sigma_{\chi \in \mathrm{Irr}(G)}\chi(1)}{|\mathrm{Irr}(G)|}.\end{align*} $$
$$ \begin{align*}\mathrm{acd}(G) =\frac{ \Sigma_{\chi \in \mathrm{Irr}(G)}\chi(1)}{|\mathrm{Irr}(G)|}.\end{align*} $$
By
![]() $\mathrm{acd}(G|N)$
, we mean the average character degree of the irreducible characters in
$\mathrm{acd}(G|N)$
, we mean the average character degree of the irreducible characters in
![]() $\mathrm{Irr}(G|N)$
(see [Reference Akhlaghi3]). In [Reference Ahanjideh1], it has been shown that if
$\mathrm{Irr}(G|N)$
(see [Reference Akhlaghi3]). In [Reference Ahanjideh1], it has been shown that if
![]() $\mathrm{acd}(G|N) < \mathrm{\max }(\mathrm{acd}(\mathrm{PSL}_2(p)),16/5)$
, then G is p-solvable.
$\mathrm{acd}(G|N) < \mathrm{\max }(\mathrm{acd}(\mathrm{PSL}_2(p)),16/5)$
, then G is p-solvable.
We write
 $$ \begin{align*} \mathrm{Irr}_p(G)&=\{\chi \in \mathrm{Irr}(G): \chi(1)=1 ~\mathrm{or}~ p \mid \chi(1) \}\\ \mathrm{Irr}_p(G|N)&= \mathrm{Irr}_p(G) \cap \mathrm{Irr}(G|N) \\ \mathrm{Irr}_p(\theta^G)&=\mathrm{Irr}_p(G) \cap \mathrm{Irr}(\theta^G) \quad \mbox{for every } \theta \in \mathrm{Irr}(N). \end{align*} $$
$$ \begin{align*} \mathrm{Irr}_p(G)&=\{\chi \in \mathrm{Irr}(G): \chi(1)=1 ~\mathrm{or}~ p \mid \chi(1) \}\\ \mathrm{Irr}_p(G|N)&= \mathrm{Irr}_p(G) \cap \mathrm{Irr}(G|N) \\ \mathrm{Irr}_p(\theta^G)&=\mathrm{Irr}_p(G) \cap \mathrm{Irr}(\theta^G) \quad \mbox{for every } \theta \in \mathrm{Irr}(N). \end{align*} $$
Let
![]() $\mathrm{acd}_p(G)$
,
$\mathrm{acd}_p(G)$
,
![]() $\mathrm{acd}_p(G|N)$
and
$\mathrm{acd}_p(G|N)$
and
![]() $\mathrm{acd}_p(\theta ^G)$
be the average degree of irreducible characters belonging to
$\mathrm{acd}_p(\theta ^G)$
be the average degree of irreducible characters belonging to
![]() $\mathrm{Irr}_p(G)$
,
$\mathrm{Irr}_p(G)$
,
![]() $\mathrm{Irr}_p(G|N)$
and
$\mathrm{Irr}_p(G|N)$
and
![]() $\mathrm{Irr}_p(\theta ^G)$
, respectively. For
$\mathrm{Irr}_p(\theta ^G)$
, respectively. For
![]() $\Delta \subseteq \mathrm{Irr}(G)$
,
$\Delta \subseteq \mathrm{Irr}(G)$
,
 $$ \begin{align*} \mathrm{acd}_p(\Delta)=\frac{\Sigma_{ \chi \in \Delta \cap \mathrm{Irr}_p(G)}\chi(1)}{|\Delta \cap \mathrm{Irr}_p(G)|}. \end{align*} $$
$$ \begin{align*} \mathrm{acd}_p(\Delta)=\frac{\Sigma_{ \chi \in \Delta \cap \mathrm{Irr}_p(G)}\chi(1)}{|\Delta \cap \mathrm{Irr}_p(G)|}. \end{align*} $$
Nguyen and Tiep [Reference Nguyen and Tiep7] have shown that if either
![]() $p \geq 5$
and
$p \geq 5$
and
![]() $\mathrm{acd}_p(G) <\mathrm{acd}_p(\mathrm{PSL}_2(p))$
or
$\mathrm{acd}_p(G) <\mathrm{acd}_p(\mathrm{PSL}_2(p))$
or
![]() $p \in \{2,3\}$
and
$p \in \{2,3\}$
and
![]() $\mathrm{acd}_p(G) <\mathrm{acd}_p(\mathrm{PSL}_2(5))$
, then G is p-solvable and
$\mathrm{acd}_p(G) <\mathrm{acd}_p(\mathrm{PSL}_2(5))$
, then G is p-solvable and
![]() $O^{p'}(G)$
is solvable, where
$O^{p'}(G)$
is solvable, where
![]() $O^{p'}(G)$
is the minimal normal subgroup of G whose quotient is a
$O^{p'}(G)$
is the minimal normal subgroup of G whose quotient is a
![]() $p'$
-group. Akhlaghi [Reference Akhlaghi2] proved that if N is a nontrivial normal subgroup of G with
$p'$
-group. Akhlaghi [Reference Akhlaghi2] proved that if N is a nontrivial normal subgroup of G with
![]() $\mathrm{Irr}_2(G|N) \neq \emptyset $
and
$\mathrm{Irr}_2(G|N) \neq \emptyset $
and
![]() $\mathrm{acd}_2(G|N) <5/2$
, then G is solvable.
$\mathrm{acd}_2(G|N) <5/2$
, then G is solvable.
We continue this investigation and show that considering the appropriate bound for
![]() $\mathrm{acd}_p(G|N)$
instead of
$\mathrm{acd}_p(G|N)$
instead of
![]() $\mathrm{acd}_p(G)$
leads us to the p-solvability of G.
$\mathrm{acd}_p(G)$
leads us to the p-solvability of G.
Let
![]() $f(p)=\mathrm{acd}_p(\mathrm{PSL}_2(p))$
if
$f(p)=\mathrm{acd}_p(\mathrm{PSL}_2(p))$
if
![]() $p \geq 5$
and otherwise, let
$p \geq 5$
and otherwise, let
![]() $f(p)=\mathrm{acd}_p(\mathrm{PSL}_2(5))$
. So,
$f(p)=\mathrm{acd}_p(\mathrm{PSL}_2(5))$
. So,
 $$ \begin{align*} f(p)=\left\{\begin{array}{ll} (p+1)/2 & \text{if } p \geq 5,\\ 7/3 & \text{if } p=3,\\ 5/2 & \text{if } p=2. \end{array} \right. \end{align*} $$
$$ \begin{align*} f(p)=\left\{\begin{array}{ll} (p+1)/2 & \text{if } p \geq 5,\\ 7/3 & \text{if } p=3,\\ 5/2 & \text{if } p=2. \end{array} \right. \end{align*} $$
Theorem 1.1. Let
![]() $ 1 \neq N \unlhd G $
and
$ 1 \neq N \unlhd G $
and
![]() $p $
be an odd prime divisor of
$p $
be an odd prime divisor of
![]() $|G|$
. If
$|G|$
. If
![]() $G/N$
is not p-solvable, then
$G/N$
is not p-solvable, then
![]() $\mathrm{acd}_p(\lambda ^G) \geq f(p)$
for every
$\mathrm{acd}_p(\lambda ^G) \geq f(p)$
for every
![]() $\lambda \in \mathrm{Irr}(N)$
with
$\lambda \in \mathrm{Irr}(N)$
with
![]() $\mathrm{Irr}_p(\lambda ^G) \neq \emptyset $
.
$\mathrm{Irr}_p(\lambda ^G) \neq \emptyset $
.
Theorem 1.2. Let p be an odd prime and
![]() $1 \neq N \unlhd G$
with
$1 \neq N \unlhd G$
with
![]() $\mathrm{acd}_p(G | N)<f(p)$
. Then:
$\mathrm{acd}_p(G | N)<f(p)$
. Then:
-
(i) either G is p-solvable and
 $O^{p'}(G)$
is solvable;
$O^{p'}(G)$
is solvable; -
(ii) or
 $\mathrm{Irr}_p(G|N)=\emptyset $
, N is p-solvable and for every
$\mathrm{Irr}_p(G|N)=\emptyset $
, N is p-solvable and for every
 $P \in \mathrm{Syl}_p(G)$
,
$P \in \mathrm{Syl}_p(G)$
,
 $P \cap N$
and
$P \cap N$
and
 $PN/N$
are abelian.
$PN/N$
are abelian.
Example 1.3. Let N be a cyclic group of order
![]() $2$
,
$2$
,
![]() $p $
be an odd prime and let
$p $
be an odd prime and let
![]() $G=\mathrm{PSL}_2(p) \times N$
. If
$G=\mathrm{PSL}_2(p) \times N$
. If
![]() $p \geq 5$
, then
$p \geq 5$
, then
![]() $\mathrm{acd}_p(G|N)=\mathrm{acd}_p(\mathrm{PSL}_2(p))$
. Also, if
$\mathrm{acd}_p(G|N)=\mathrm{acd}_p(\mathrm{PSL}_2(p))$
. Also, if
![]() $p=5$
, then
$p=5$
, then
![]() $\mathrm{acd}_3(G|N)=\mathrm{acd}_3(\mathrm{PSL}_2(5))$
. This example shows that the bound given in Theorem 1.2 is the best possible.
$\mathrm{acd}_3(G|N)=\mathrm{acd}_3(\mathrm{PSL}_2(5))$
. This example shows that the bound given in Theorem 1.2 is the best possible.
Let
![]() $\mathrm{Irr}_p(G^{\sharp }) = \mathrm{Irr}_p(G)-\{1_G \}$
and
$\mathrm{Irr}_p(G^{\sharp }) = \mathrm{Irr}_p(G)-\{1_G \}$
and
![]() $\mathrm{acd}(G^{\sharp }) ={\Sigma _{\chi \in \mathrm{Irr}_p(G^{\sharp })} \chi (1) }/{|\mathrm{Irr}_p(G^{\sharp })|}$
. By setting
$\mathrm{acd}(G^{\sharp }) ={\Sigma _{\chi \in \mathrm{Irr}_p(G^{\sharp })} \chi (1) }/{|\mathrm{Irr}_p(G^{\sharp })|}$
. By setting
![]() $G=N$
in Theorem 1.2, we arrive at the following corollary.
$G=N$
in Theorem 1.2, we arrive at the following corollary.
Corollary 1.4. If
![]() $\mathrm{acd}_p(G^{\sharp })<f(p) $
, then G is p-solvable and
$\mathrm{acd}_p(G^{\sharp })<f(p) $
, then G is p-solvable and
![]() $O^{p'}(G)$
is solvable.
$O^{p'}(G)$
is solvable.
We can see that
![]() $\mathrm{acd}_3(\mathrm{Alt}_4^{\sharp })=5/3<7/3 $
and the Sylow
$\mathrm{acd}_3(\mathrm{Alt}_4^{\sharp })=5/3<7/3 $
and the Sylow
![]() $3$
-subgroup of
$3$
-subgroup of
![]() $\mathrm{Alt}_4$
is not normal in
$\mathrm{Alt}_4$
is not normal in
![]() $\mathrm{Alt}_4$
. This shows that the assumption
$\mathrm{Alt}_4$
. This shows that the assumption
![]() $\mathrm{acd}_p(G^{\sharp })<f(p) $
does not guarantee normality of the Sylow p-subgroup of G.
$\mathrm{acd}_p(G^{\sharp })<f(p) $
does not guarantee normality of the Sylow p-subgroup of G.
2 The main results
We first state some lemmas that will be used in the proof of Theorems 1.1 and 1.2. For a nonempty finite subset of real numbers X, by
![]() $\mathrm{ave}(X)$
, we mean the average of X.
$\mathrm{ave}(X)$
, we mean the average of X.
Lemma 2.1 [Reference Ahanjideh1, Lemma 3].
Let X be a nonempty finite subset of real numbers and
![]() $\{A_1,\ldots ,A_t\}$
be a partition of X. If d is a real number such that
$\{A_1,\ldots ,A_t\}$
be a partition of X. If d is a real number such that
![]() $\mathrm{ave}( A_i) \geq d$
(respectively
$\mathrm{ave}( A_i) \geq d$
(respectively
![]() $<d$
) for
$<d$
) for
![]() $1 \leq i \leq t$
, then
$1 \leq i \leq t$
, then
![]() $\mathrm{ave}( X) \geq d$
(respectively
$\mathrm{ave}( X) \geq d$
(respectively
![]() $<d$
).
$<d$
).
Lemma 2.2 [Reference Nguyen and Tiep7, Theorem B].
Let p be a prime divisor of
![]() $|G|$
. If
$|G|$
. If
![]() $\mathrm{acd}_p(G) < f(p)$
, then G is p-solvable and
$\mathrm{acd}_p(G) < f(p)$
, then G is p-solvable and
![]() $O^{p'}(G)$
is solvable.
$O^{p'}(G)$
is solvable.
Lemma 2.3 [Reference Navarro and Tiep6, Theorem A].
Let Z be a normal subgroup of a finite group G,
![]() $ \lambda \in \mathrm{Irr}(Z)$
and let
$ \lambda \in \mathrm{Irr}(Z)$
and let
![]() $P/Z \in \mathrm{Syl}_p(G/Z)$
. If
$P/Z \in \mathrm{Syl}_p(G/Z)$
. If
![]() $ \chi (1)/\lambda (1)$
is coprime to p for every
$ \chi (1)/\lambda (1)$
is coprime to p for every
![]() $ \chi \in \mathrm{Irr}(G)$
lying over
$ \chi \in \mathrm{Irr}(G)$
lying over
![]() $\lambda $
, then
$\lambda $
, then
![]() $P/Z$
is abelian.
$P/Z$
is abelian.
We are ready to prove Theorems 1.1 and 1.2.
Proof of Theorem 1.1.
We complete the proof by induction on
![]() $|G|+|N|$
. Take
$|G|+|N|$
. Take
![]() $\lambda \in \mathrm{Irr}(N)$
with
$\lambda \in \mathrm{Irr}(N)$
with
![]() $\mathrm{Irr}_p(\lambda ^G) \neq \emptyset $
. Let E be a maximal normal subgroup of G such that
$\mathrm{Irr}_p(\lambda ^G) \neq \emptyset $
. Let E be a maximal normal subgroup of G such that
![]() $N \leq E$
and
$N \leq E$
and
![]() $G/E$
is not p-solvable. Then,
$G/E$
is not p-solvable. Then,
![]() $G/E$
admits the unique minimal normal subgroup
$G/E$
admits the unique minimal normal subgroup
![]() $M/E$
and it is easy to check that
$M/E$
and it is easy to check that
![]() $M/E$
is not p-solvable. Assume that
$M/E$
is not p-solvable. Assume that
![]() $\{\mu _1, \ldots , \mu _t\} \subseteq \mathrm{Irr}(\lambda ^E)$
such that every element of
$\{\mu _1, \ldots , \mu _t\} \subseteq \mathrm{Irr}(\lambda ^E)$
such that every element of
![]() $\mathrm{Irr}(\lambda ^E)$
is conjugate to exactly one of the elements in
$\mathrm{Irr}(\lambda ^E)$
is conjugate to exactly one of the elements in
![]() $\{\mu _1, \ldots , \mu _t\}$
. If
$\{\mu _1, \ldots , \mu _t\}$
. If
![]() $N \neq E$
, then from the hypothesis,
$N \neq E$
, then from the hypothesis,
![]() $\mathrm{Irr}_p(\mu _i^G)=\emptyset $
or
$\mathrm{Irr}_p(\mu _i^G)=\emptyset $
or
![]() $\mathrm{acd}_p(\mu _i^G) \geq f(p)$
, for
$\mathrm{acd}_p(\mu _i^G) \geq f(p)$
, for
![]() $1 \leq i \leq t$
. As
$1 \leq i \leq t$
. As
![]() $\mathrm{Irr}(\lambda ^G) =\dot {\cup }_{i=1}^t \mathrm{Irr}(\mu _i^G)$
and
$\mathrm{Irr}(\lambda ^G) =\dot {\cup }_{i=1}^t \mathrm{Irr}(\mu _i^G)$
and
![]() $\mathrm{Irr}_p(\lambda ^G) \neq \emptyset $
, we conclude that
$\mathrm{Irr}_p(\lambda ^G) \neq \emptyset $
, we conclude that
![]() $\mathrm{Irr}_p(\mu _j^G) \neq \emptyset $
for some j with
$\mathrm{Irr}_p(\mu _j^G) \neq \emptyset $
for some j with
![]() $1 \leq j \leq t$
. So, it follows from Lemma 2.1 that
$1 \leq j \leq t$
. So, it follows from Lemma 2.1 that
![]() $\mathrm{acd}_p(\lambda ^G) \geq f(p) $
, as desired. Next, suppose that
$\mathrm{acd}_p(\lambda ^G) \geq f(p) $
, as desired. Next, suppose that
![]() $N=E$
. If
$N=E$
. If
![]() $\lambda $
is extendible to
$\lambda $
is extendible to
![]() $\chi \in \mathrm{Irr}(G)$
, then Gallagher’s theorem [Reference Isaacs4, Corollary 6.17] implies that
$\chi \in \mathrm{Irr}(G)$
, then Gallagher’s theorem [Reference Isaacs4, Corollary 6.17] implies that
![]() $\mathrm{Irr}(\lambda ^G)=\{\chi \mu : \mu \in \mathrm{Irr}(G/N)\}$
and for every
$\mathrm{Irr}(\lambda ^G)=\{\chi \mu : \mu \in \mathrm{Irr}(G/N)\}$
and for every
![]() $\mu _1,\mu _2 \in \mathrm{Irr}(G/N)$
with
$\mu _1,\mu _2 \in \mathrm{Irr}(G/N)$
with
![]() $\mu _1 \neq \mu _2$
, we have
$\mu _1 \neq \mu _2$
, we have
![]() $\chi \mu _1 \neq \chi \mu _2$
. Thus, either
$\chi \mu _1 \neq \chi \mu _2$
. Thus, either
![]() $p \mid \chi (1)$
and
$p \mid \chi (1)$
and
![]() $\mathrm{acd}_p(\lambda ^G)=\chi (1) \mathrm{acd}(G/N)$
or
$\mathrm{acd}_p(\lambda ^G)=\chi (1) \mathrm{acd}(G/N)$
or
![]() $p \nmid \chi (1)$
and
$p \nmid \chi (1)$
and
![]() $\mathrm{acd}_p(\lambda ^G)=\chi (1) \mathrm{acd}_p(G/N)$
. Obviously,
$\mathrm{acd}_p(\lambda ^G)=\chi (1) \mathrm{acd}_p(G/N)$
. Obviously,
![]() $\mathrm{acd}(G/N) \geq 1$
. So, in the former case,
$\mathrm{acd}(G/N) \geq 1$
. So, in the former case,
![]() $\mathrm{acd}_p(\lambda ^G) \geq p> f(p)$
, as needed. Since
$\mathrm{acd}_p(\lambda ^G) \geq p> f(p)$
, as needed. Since
![]() $G/N$
is not p-solvable, Lemma 2.2 yields
$G/N$
is not p-solvable, Lemma 2.2 yields
![]() $\mathrm{acd}_p(G/N) \geq f(p)$
. Hence, if
$\mathrm{acd}_p(G/N) \geq f(p)$
. Hence, if
![]() $p \nmid \chi (1)$
, then
$p \nmid \chi (1)$
, then
![]() $\mathrm{acd}_p(\lambda ^G)=\chi (1) \mathrm{acd}_p(G/N) \geq f(p)$
, as desired. Finally, suppose that
$\mathrm{acd}_p(\lambda ^G)=\chi (1) \mathrm{acd}_p(G/N) \geq f(p)$
, as desired. Finally, suppose that
![]() $\lambda $
is not extendible to G. Then, for every
$\lambda $
is not extendible to G. Then, for every
![]() $\chi \in \mathrm{Irr}(\lambda ^G)$
,
$\chi \in \mathrm{Irr}(\lambda ^G)$
,
![]() $\chi (1)> \lambda (1) \geq 1$
. This means that
$\chi (1)> \lambda (1) \geq 1$
. This means that
![]() $p \mid \chi (1) $
for every
$p \mid \chi (1) $
for every
![]() $\chi \in \mathrm{Irr}_p(\lambda ^G)$
. Therefore,
$\chi \in \mathrm{Irr}_p(\lambda ^G)$
. Therefore,
![]() $\mathrm{acd}_p(\lambda ^G) \geq p> f(p)$
. Now, the proof is complete.
$\mathrm{acd}_p(\lambda ^G) \geq p> f(p)$
. Now, the proof is complete.
Proof of Theorem 1.2.
First, assume that
![]() $\mathrm{Irr}_p(G|N) \neq \emptyset $
. As
$\mathrm{Irr}_p(G|N) \neq \emptyset $
. As
![]() $\mathrm{acd}_p(G|N) < f(p) < p $
, we see that
$\mathrm{acd}_p(G|N) < f(p) < p $
, we see that
![]() $\mathrm{Irr}_p(G|N)$
contains a linear character
$\mathrm{Irr}_p(G|N)$
contains a linear character
![]() $\chi $
. Then,
$\chi $
. Then,
![]() $\chi _N \neq 1_N $
and as
$\chi _N \neq 1_N $
and as
![]() $\chi (1)=1$
, we have
$\chi (1)=1$
, we have
![]() $\chi _N \in \mathrm{Irr}(N)$
. This implies that N admits some linear characters which are extendible to G and they are nonprincipal. Assume that
$\chi _N \in \mathrm{Irr}(N)$
. This implies that N admits some linear characters which are extendible to G and they are nonprincipal. Assume that
![]() $\{\mu _1,\ldots , \mu _t\}$
is the set of all linear characters of N which are extendible to G and are nonprincipal. Since the
$\{\mu _1,\ldots , \mu _t\}$
is the set of all linear characters of N which are extendible to G and are nonprincipal. Since the
![]() $\mu_i$
s are extendible to G, none of them are G-conjugate. If
$\mu_i$
s are extendible to G, none of them are G-conjugate. If
![]() $1 \leq i \neq j \leq t$
and there exists
$1 \leq i \neq j \leq t$
and there exists
![]() $\chi \in \mathrm{Irr}(\mu _i^G) \cap \mathrm{Irr}(\mu _j^G)$
, then
$\chi \in \mathrm{Irr}(\mu _i^G) \cap \mathrm{Irr}(\mu _j^G)$
, then
![]() $\mu _i$
and
$\mu _i$
and
![]() $\mu _j$
are irreducible constituents of
$\mu _j$
are irreducible constituents of
![]() $\chi _N$
. It follows from Clifford’s correspondence that
$\chi _N$
. It follows from Clifford’s correspondence that
![]() $\mu _i$
and
$\mu _i$
and
![]() $\mu _j$
are G-conjugate, which is a contradiction with our former assumption on the
$\mu _j$
are G-conjugate, which is a contradiction with our former assumption on the
![]() $\mu _i$
s. This shows that
$\mu _i$
s. This shows that
Let
![]() $1 \leq i \leq t$
. Our assumption on the
$1 \leq i \leq t$
. Our assumption on the
![]() $\mu _i$
guarantees the existence of a linear character
$\mu _i$
guarantees the existence of a linear character
![]() $\chi _i \in \mathrm{Irr}(G) $
such that
$\chi _i \in \mathrm{Irr}(G) $
such that
![]() $(\chi _i)_N=\mu _i$
. By Gallagher’s theorem [Reference Isaacs4, Corollary 6.17],
$(\chi _i)_N=\mu _i$
. By Gallagher’s theorem [Reference Isaacs4, Corollary 6.17],
![]() $\mathrm{Irr}(\mu _i^G)=\{\chi _i \varphi : \varphi \in \mathrm{Irr}(G/N)\}$
and for distinct characters
$\mathrm{Irr}(\mu _i^G)=\{\chi _i \varphi : \varphi \in \mathrm{Irr}(G/N)\}$
and for distinct characters
![]() $\varphi _1,\varphi _2 \in \mathrm{Irr}(G/N)$
,
$\varphi _1,\varphi _2 \in \mathrm{Irr}(G/N)$
,
![]() $\chi _i\varphi _1 \neq \chi _i \varphi _2$
. Since
$\chi _i\varphi _1 \neq \chi _i \varphi _2$
. Since
![]() $\chi _i(1)=1$
,
$\chi _i(1)=1$
,
As
![]() $\mu _i \neq 1_N$
,
$\mu _i \neq 1_N$
,
![]() $\chi _i \in \mathrm{Irr}(G|N)$
. Therefore,
$\chi _i \in \mathrm{Irr}(G|N)$
. Therefore,
In view of (2.1),
![]() $\bigcup _{i=1}^t\mathrm{Irr}(\mu _i^G)$
is disjoint. Take
$\bigcup _{i=1}^t\mathrm{Irr}(\mu _i^G)$
is disjoint. Take
If
![]() $\chi \in \mathrm{Irr}(G|N)$
is linear, then
$\chi \in \mathrm{Irr}(G|N)$
is linear, then
![]() $\chi _N \neq 1_N$
and
$\chi _N \neq 1_N$
and
![]() $\chi _N(1)=\chi (1)=1$
. Thus,
$\chi _N(1)=\chi (1)=1$
. Thus,
![]() $\chi _N \in \mathrm{Irr}(N)$
is nonprincipal. It follows from our assumption on the
$\chi _N \in \mathrm{Irr}(N)$
is nonprincipal. It follows from our assumption on the
![]() $\mu _i$
that
$\mu _i$
that
![]() $\chi _N \in \{\mu _1,\ldots , \mu _t\}$
. Therefore,
$\chi _N \in \{\mu _1,\ldots , \mu _t\}$
. Therefore,
![]() $\chi \in \mathrm{Irr}(\mu _j^G)$
for some
$\chi \in \mathrm{Irr}(\mu _j^G)$
for some
![]() $1 \leq j \leq t$
. This implies that
$1 \leq j \leq t$
. This implies that
![]() $\chi (1) \geq p$
for every
$\chi (1) \geq p$
for every
![]() $\chi \in \mathfrak {A}$
. Therefore,
$\chi \in \mathfrak {A}$
. Therefore,
By (2.1) and (2.2),
![]() $|\dot {\cup }_{i=1}^t \mathrm{Irr}_p(\mu _i^G)|=t|\mathrm{Irr}_p(G/N)|$
and
$|\dot {\cup }_{i=1}^t \mathrm{Irr}_p(\mu _i^G)|=t|\mathrm{Irr}_p(G/N)|$
and
 $$ \begin{align*} \mathrm{acd}_p(\dot{\cup}_{i=1}^t \mathrm{Irr}(\mu_i^G))&= \frac{\Sigma_{i=1}^t \Sigma_{\chi \in \mathrm{Irr}_p(\mu_i^G)} \chi(1) }{|\dot{\cup}_{i=1}^t \mathrm{Irr}_p(\mu_i^G)|}\\ &= \frac{\Sigma_{i=1}^t \Sigma_{\varphi \in \mathrm{Irr}_p(G/N)} (\chi_i \varphi)(1)}{t|\mathrm{Irr}_p(G/N)|}\\\nonumber &= \frac{t \Sigma_{\varphi \in \mathrm{Irr}_p(G/N)} \varphi(1)}{t|\mathrm{Irr}_p(G/N)|}=\mathrm{acd}_p(G/N). \end{align*} $$
$$ \begin{align*} \mathrm{acd}_p(\dot{\cup}_{i=1}^t \mathrm{Irr}(\mu_i^G))&= \frac{\Sigma_{i=1}^t \Sigma_{\chi \in \mathrm{Irr}_p(\mu_i^G)} \chi(1) }{|\dot{\cup}_{i=1}^t \mathrm{Irr}_p(\mu_i^G)|}\\ &= \frac{\Sigma_{i=1}^t \Sigma_{\varphi \in \mathrm{Irr}_p(G/N)} (\chi_i \varphi)(1)}{t|\mathrm{Irr}_p(G/N)|}\\\nonumber &= \frac{t \Sigma_{\varphi \in \mathrm{Irr}_p(G/N)} \varphi(1)}{t|\mathrm{Irr}_p(G/N)|}=\mathrm{acd}_p(G/N). \end{align*} $$
If
![]() $\mathrm{acd}_p(G/N) \geq f(p)$
, then
$\mathrm{acd}_p(G/N) \geq f(p)$
, then
Note that
![]() $\mathrm{Irr}_p(G|N) = (\dot {\cup }_{i=1}^t\mathrm{Irr}_p(\mu _i^G)) \dot {\cup } \mathfrak {A}$
. It follows from (2.3), (2.4) and Lemma 2.1 that
$\mathrm{Irr}_p(G|N) = (\dot {\cup }_{i=1}^t\mathrm{Irr}_p(\mu _i^G)) \dot {\cup } \mathfrak {A}$
. It follows from (2.3), (2.4) and Lemma 2.1 that
![]() $\mathrm{acd}_p(G|N) \geq f(p)$
, which is a contradiction. This implies that
$\mathrm{acd}_p(G|N) \geq f(p)$
, which is a contradiction. This implies that
![]() $\mathrm{acd}_p(G/N) <f(p)$
. As
$\mathrm{acd}_p(G/N) <f(p)$
. As
![]() $\mathrm{acd}_p(G|N) < f(p)$
and
$\mathrm{acd}_p(G|N) < f(p)$
and
![]() $\mathrm{Irr}_p(G) =\mathrm{Irr}_p(G|N) \dot {\cup } \mathrm{Irr}_p(G/N)$
, we deduce from Lemma 2.1 that
$\mathrm{Irr}_p(G) =\mathrm{Irr}_p(G|N) \dot {\cup } \mathrm{Irr}_p(G/N)$
, we deduce from Lemma 2.1 that
![]() $\mathrm{acd}_p(G) < f(p)$
. Hence, Lemma 2.2 implies that G is p-solvable and
$\mathrm{acd}_p(G) < f(p)$
. Hence, Lemma 2.2 implies that G is p-solvable and
![]() $O^{p'}(G)$
is solvable, as desired.
$O^{p'}(G)$
is solvable, as desired.
Now, assume that
![]() $\mathrm{Irr}_p(G|N)=\emptyset $
. Working towards a contradiction, suppose that there exists
$\mathrm{Irr}_p(G|N)=\emptyset $
. Working towards a contradiction, suppose that there exists
![]() $\theta \in \mathrm{Irr}(N) $
such that
$\theta \in \mathrm{Irr}(N) $
such that
![]() $p \mid \theta (1)$
. We have
$p \mid \theta (1)$
. We have
![]() $\theta (1) \mid \chi (1)$
for every
$\theta (1) \mid \chi (1)$
for every
![]() $\chi \in \mathrm{Irr}(\theta ^G)$
. Thus,
$\chi \in \mathrm{Irr}(\theta ^G)$
. Thus,
![]() $p \mid \chi (1)$
for every
$p \mid \chi (1)$
for every
![]() $\chi \in \mathrm{Irr}(\theta ^G)$
. Clearly,
$\chi \in \mathrm{Irr}(\theta ^G)$
. Clearly,
![]() $\theta \neq 1_N$
. So,
$\theta \neq 1_N$
. So,
![]() $\chi \in \mathrm{Irr}_p(\theta ^G) \subseteq \mathrm{Irr}_p(G|N) $
. This means that
$\chi \in \mathrm{Irr}_p(\theta ^G) \subseteq \mathrm{Irr}_p(G|N) $
. This means that
![]() $\mathrm{Irr}_p(G|N) \neq \emptyset $
, which is a contradiction. This implies that
$\mathrm{Irr}_p(G|N) \neq \emptyset $
, which is a contradiction. This implies that
![]() $p \nmid \theta (1)$
for every
$p \nmid \theta (1)$
for every
![]() $\theta \in \mathrm{Irr}(N)$
. It follows from the Ito–Michler theorem [Reference Isaacs4, Corollary 12.34] that N has a normal and abelian Sylow p-subgroup. Thus, N is p-solvable. Now, assume that
$\theta \in \mathrm{Irr}(N)$
. It follows from the Ito–Michler theorem [Reference Isaacs4, Corollary 12.34] that N has a normal and abelian Sylow p-subgroup. Thus, N is p-solvable. Now, assume that
![]() $1_N \neq \theta \in \mathrm{Irr}(N)$
and
$1_N \neq \theta \in \mathrm{Irr}(N)$
and
![]() $\chi \in \mathrm{Irr}(\theta ^G)$
. Hence,
$\chi \in \mathrm{Irr}(\theta ^G)$
. Hence,
![]() $\chi \in \mathrm{Irr}(G|N) $
. As
$\chi \in \mathrm{Irr}(G|N) $
. As
![]() $\mathrm{Irr}_p(G|N) = \emptyset $
, we deduce that
$\mathrm{Irr}_p(G|N) = \emptyset $
, we deduce that
![]() $p \nmid \chi (1)$
. Thus,
$p \nmid \chi (1)$
. Thus,
![]() $p \nmid \chi (1)/\theta (1)$
. It follows from Lemma 2.3 that
$p \nmid \chi (1)/\theta (1)$
. It follows from Lemma 2.3 that
![]() $G/N$
has an abelian Sylow p-subgroup. This completes the proof.
$G/N$
has an abelian Sylow p-subgroup. This completes the proof.