Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-06T10:52:51.255Z Has data issue: false hasContentIssue false
  • English
  • Français

ON PERMUTATION BINOMIALS OVER FINITE FIELDS

Part of: Finite fields and commutative rings (number-theoretic aspects) General field theory

Published online by Cambridge University Press:  28 March 2013

MOHAMED AYAD ,
KACEM BELGHABA  and
OMAR KIHEL
MOHAMED AYAD
Affiliation:
Laboratoire de Mathématiques Pures et Appliquées, Université du Littoral, F-62228 Calais, France email ayad@lmpa.univ-littoral.fr
KACEM BELGHABA
Affiliation:
Laboratoire de Mathématiques et ses Applications, Université d’Oran, BP 15 24, Algeria email belghaba.kacem@univ-oran.dz
OMAR KIHEL*
Affiliation:
Department of Mathematics, Brock University, Ontario, Canada L2S 3A1 email okihel@brocku.ca
*
✉okihel@brocku.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

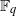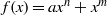Let ${ \mathbb{F} }_{q} $ be the finite field of characteristic $p$ containing $q= {p}^{r} $ elements and $f(x)= a{x}^{n} + {x}^{m} $, a binomial with coefficients in this field. If some conditions on the greatest common divisor of 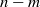$n- m$ and 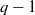$q- 1$ are satisfied then this polynomial does not permute the elements of the field. 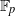We prove in particular that if $f(x)= a{x}^{n} + {x}^{m} $ permutes ${ \mathbb{F} }_{p} $, where $n\gt m\gt 0$ and $a\in { \mathbb{F} }_{p}^{\ast } $, then 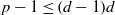$p- 1\leq (d- 1)d$, where 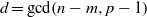$d= \gcd (n- m, p- 1)$, and that this bound of $p$, in terms of 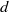$d$ only, is sharp. We show as well how to obtain in certain cases a permutation binomial over a subfield of 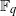${ \mathbb{F} }_{q} $ from a permutation binomial over ${ \mathbb{F} }_{q} $.

Keywords

finite fieldspermutation polynomialsHermite–Dickson theorem

MSC classification

Secondary: 11T06: Polynomials 12E20: Finite fields (field-theoretic aspects)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 1 , February 2014 , pp. 112 - 124
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Dickson, L. E., ‘The analytic representation of substitutions on a power of a prime number of letters with a discussion of the linear group’, Ann. of Math. 11 (16) (1896/97), 161–183.Google Scholar
Fried, M., Guralnick, R. and Saxl, J., ‘Schur covers and Carlitz’s conjecture’, Israel J. Math. 82 (1993), 157–225.CrossRefGoogle Scholar
Hermite, C., ‘Sur les fonctions de sept lettres’, C. R. Acad. Sci. Paris 57 (1863)750–757.Google Scholar
Lidl, R. and Niedereiter, H., Finite Fields, Encyclopedia of Mathematics and its Applications (Cambridge University Press, Cambridge, 2008).Google Scholar
Masuda, A. and Zieve, M., ‘Permutation binomials over finite fields’, Trans. Amer. Math. Soc. 361 (2009), 4169–4180.CrossRefGoogle Scholar
Niederreiter, H. and Robinson, K. H., ‘Complete mappings of finite fields’, J. Aust. Math. Soc. (Ser. A) 33 (1982), 197–212.Google Scholar
Small, C., Arithmetic of Finite Fields (Marcel Dekker, New York, 1991).Google Scholar
Small, C., ‘Permutation binomials’, Internat. J. Math. Math. Sci. 13 (1990), 337–342.CrossRefGoogle Scholar
Turnwald, G., Permutation polynomials of binomial type, Contributions to General Algebra 6 (Holder-Pichler-Tempsky, Vienna, 1988), pp. 281–286.Google Scholar
Wan, D. Q., ‘Permutation polynomials over finite fields’, Acta Math. Sinica (N. S.) 3 (1987), 1–5.Google Scholar
Weil, A., ‘Sur les courbes algébriques et les variétés qui s’en déduisent’, Actualités Sci. Ind., 1041 (Hermann, Paris, 1948).Google Scholar