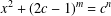Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-10T13:23:41.240Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE DIOPHANTINE EQUATION $x^{2}+(2c-1)^{m}=c^{n}$

Part of: Diophantine equations

Published online by Cambridge University Press:  12 July 2018

MOU-JIE DENG Open the ORCID record for MOU-JIE DENG [Opens in a new window] ,
JIN GUO  and
AI-JUAN XU
MOU-JIE DENG*
Affiliation:
Department of Applied Mathematics, Hainan University, Haikou, Hainan 570228, PR China email moujie_deng@163.com
JIN GUO
Affiliation:
Department of Applied Mathematics, Hainan University, Haikou, Hainan 570228, PR China email guojinecho@163.com
AI-JUAN XU
Affiliation:
Department of Applied Mathematics, Hainan University, Haikou, Hainan 570228, PR China email xaj1650404852@163.com
*
✉moujie_deng@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 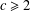$c\geq 2$ be a positive integer. Terai [‘A note on the Diophantine equation 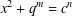$x^{2}+q^{m}=c^{n}$’, Bull. Aust. Math. Soc.90 (2014), 20–27] conjectured that the exponential Diophantine equation 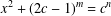$x^{2}+(2c-1)^{m}=c^{n}$ has only the positive integer solution 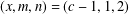$(x,m,n)=(c-1,1,2)$. He proved his conjecture under various conditions on $c$ and $2c-1$. In this paper, we prove Terai’s conjecture under a wider range of conditions on $c$ and 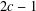$2c-1$. In particular, we show that the conjecture is true if 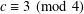$c\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}4)$ and 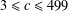$3\leq c\leq 499$.

Keywords

exponential Diophantine equation

MSC classification

Primary: 11D61: Exponential equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 2 , October 2018 , pp. 188 - 195
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

This research was supported by the National Natural Science Foundation of China (grant no. 11601108) and the Natural Science Foundation of Hainan Province (grant no. 20161002).

References

Arif, S. A. and Abu Muriefah, F. S., ‘On the Diophantine equation x 2 + q 2k+1 = y n ’, J. Number Theory 95 (2002), 95–100.Google Scholar
Bennett, M. A. and Skinner, C. M., ‘Ternary Diophantine equations via Galois representations and modular forms’, Canad. J. Math. 56 (2004), 23–54.Google Scholar
Carmichael, R. D., ‘On the numerical factor of the arithmetic forms 𝛼 n ±𝛽 n ’, Ann. Math. 15 (1913), 30–70.Google Scholar
Deng, M.-J., ‘A note on the Diophantine equation x 2 + q m = c 2n ’, Proc. Japan Acad. 91 (2015), 15–18.Google Scholar
Ljunggren, W., ‘Some theorems on indeterminate equations of the form (x n - 1/x - 1) = y q ’, Norsk Mat. Tidsskr. 25 (1943), 17–20; (in Norwegian).Google Scholar
Terai, N., ‘A note on the Diophantine equation x 2 + q m = c n ’, Bull. Aust. Math. Soc. 90 (2014), 20–27.Google Scholar
Zhu, H. L., ‘A note on the Diophantine equation x 2 + q m = y 3 ’, Acta Arith. 146 (2011), 195–202.Google Scholar