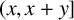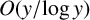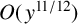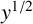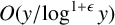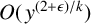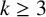1 Introduction and main result
A number n is squarefull if its prime factorisation
![]() $n = p_1^{a_1} p_2^{a_2} \cdots p_r^{a_r}$
satisfies
$n = p_1^{a_1} p_2^{a_2} \cdots p_r^{a_r}$
satisfies
![]() $a_i \ge 2$
for all
$a_i \ge 2$
for all
![]() $1 \le i \le r$
. Similarly, a number n is k-full if
$1 \le i \le r$
. Similarly, a number n is k-full if
![]() $a_i \ge k$
for
$a_i \ge k$
for
![]() $1 \le i \le r$
. For example,
$1 \le i \le r$
. For example,
![]() $72 = 2^3 \cdot 3^2$
is squarefull and
$72 = 2^3 \cdot 3^2$
is squarefull and
![]() $243 = 3^5$
is
$243 = 3^5$
is
![]() $5$
-full. Let
$5$
-full. Let
![]() $Q_k(x)$
denote the number of k-full numbers which are less than or equal to x. It is known that
$Q_k(x)$
denote the number of k-full numbers which are less than or equal to x. It is known that
 $$ \begin{align} Q_k(x) = \prod_{p} \bigg(1 + \sum_{m = k+1}^{2k - 1} \frac{1}{p^{m/h}} \bigg) \kern1pt x^{1/k} + O(x^{1/(k+1)}), \end{align} $$
$$ \begin{align} Q_k(x) = \prod_{p} \bigg(1 + \sum_{m = k+1}^{2k - 1} \frac{1}{p^{m/h}} \bigg) \kern1pt x^{1/k} + O(x^{1/(k+1)}), \end{align} $$
where the product is over all primes (see, for example, [Reference Bateman and Grosswald1, Reference Erdős and Szekeres4]). There are also estimates for the number of k-full numbers in short intervals
![]() $(x, x+y]$
with
$(x, x+y]$
with
![]() $y = o(x)$
. For moderate size y, there are some asymptotic results. For example, Trifonov [Reference Trifonov8] and Liu [Reference Liu6] respectively obtained
$y = o(x)$
. For moderate size y, there are some asymptotic results. For example, Trifonov [Reference Trifonov8] and Liu [Reference Liu6] respectively obtained
 $$ \begin{align*} Q_2 (x + x^{1/2 + \theta} ) - Q_2(x) \sim \frac{\zeta(3/2)}{2 \zeta(3)} x^\theta \quad\text{for } \frac{19}{154} = 0.12337\ldots < \theta < \frac{1}{2}, \end{align*} $$
$$ \begin{align*} Q_2 (x + x^{1/2 + \theta} ) - Q_2(x) \sim \frac{\zeta(3/2)}{2 \zeta(3)} x^\theta \quad\text{for } \frac{19}{154} = 0.12337\ldots < \theta < \frac{1}{2}, \end{align*} $$
and
 $$ \begin{align*} Q_3 (x + x^{2/3 + \theta} ) - Q_3(x) \sim \frac{\zeta(4/3)}{3 \zeta(4)} x^\theta \quad\text{for } \frac{5}{42} = 0.11904\ldots < \theta < \frac{1}{3}. \end{align*} $$
$$ \begin{align*} Q_3 (x + x^{2/3 + \theta} ) - Q_3(x) \sim \frac{\zeta(4/3)}{3 \zeta(4)} x^\theta \quad\text{for } \frac{5}{42} = 0.11904\ldots < \theta < \frac{1}{3}. \end{align*} $$
What happens when y is very small, say
![]() $y \ll x^{1/2}$
or even
$y \ll x^{1/2}$
or even
![]() $y \ll \log x$
? For such short intervals, one can only expect suitable upper bounds rather than asymptotic formulae. Thus, in this note, we are interested in finding uniform upper bounds for
$y \ll \log x$
? For such short intervals, one can only expect suitable upper bounds rather than asymptotic formulae. Thus, in this note, we are interested in finding uniform upper bounds for
![]() $Q_k(x + y) - Q_k(x)$
with
$Q_k(x + y) - Q_k(x)$
with
![]() $1 \le y \le x$
that are independent of x. By comparing k-full numbers with perfect kth powers, we suspect the following conjecture to be true.
$1 \le y \le x$
that are independent of x. By comparing k-full numbers with perfect kth powers, we suspect the following conjecture to be true.
Conjecture 1.1. Given an integer
![]() $k \ge 2$
and a real number
$k \ge 2$
and a real number
![]() $x \ge 1$
, there exists some constant
$x \ge 1$
, there exists some constant
![]() $C_k \ge 1$
such that
$C_k \ge 1$
such that
uniformly over
![]() $1 \le y \le x$
.
$1 \le y \le x$
.
We are far from proving this at the moment. The current best upper bound,
 $$ \begin{align} Q_k(x + y) - Q_k(x) \ll \frac{y \log \log (\kern1.3pt y + 2)}{\log (\kern1.3pt y + 2)}, \end{align} $$
$$ \begin{align} Q_k(x + y) - Q_k(x) \ll \frac{y \log \log (\kern1.3pt y + 2)}{\log (\kern1.3pt y + 2)}, \end{align} $$
was obtained by De Koninck et al. [Reference De Koninck, Luca and Shparlinski3]. We improve (1.2) slightly.
Theorem 1.2. Given an integer
![]() $k \ge 2$
and a real number
$k \ge 2$
and a real number
![]() $x \ge 1$
, we have
$x \ge 1$
, we have
uniformly over
![]() $1 \le y \le x$
.
$1 \le y \le x$
.
In fact, we shall prove the following more general result concerning squarefull numbers in arithmetic progression over short intervals which gives Theorem 1.2 immediately, as k-full numbers are included in squarefull numbers.
Theorem 1.3. Given real numbers
![]() $x \ge 1$
and
$x \ge 1$
and
![]() $0 < \alpha < 1$
and integers
$0 < \alpha < 1$
and integers
![]() $q> 0$
and r with
$q> 0$
and r with
![]() $\gcd (r, q) = 1$
, we have
$\gcd (r, q) = 1$
, we have
 $$ \begin{align*} \sum_{\substack{x < n \le x + y\\ n\ {\mathrm{squarefull}}\\ n \equiv r \!\pmod{q}}} 1 \ll_\alpha \frac{y}{\phi(q) \log (\kern1.3pt y + 1)} \end{align*} $$
$$ \begin{align*} \sum_{\substack{x < n \le x + y\\ n\ {\mathrm{squarefull}}\\ n \equiv r \!\pmod{q}}} 1 \ll_\alpha \frac{y}{\phi(q) \log (\kern1.3pt y + 1)} \end{align*} $$
uniformly over
![]() $1 \le y \le x$
and
$1 \le y \le x$
and
![]() $1 \le q \le y^{1 - \alpha }$
.
$1 \le q \le y^{1 - \alpha }$
.
Using a similar technique, we can obtain some power savings over (1.3) for smooth k-full numbers in short intervals.
Theorem 1.4. Given an integer
![]() $k \ge 2$
and a real number
$k \ge 2$
and a real number
![]() $x \ge 1$
, we have
$x \ge 1$
, we have
 $$ \begin{align} \sum_{\substack{x < n \le x + y\\ n\ k\mbox{-}\mathrm{full}\\ p^{+}(n) \le y^{1/2}}} 1 \le \sum_{\substack{x < n \le x + y\\ n\ {\mathrm{squarefull}}\\ p^{+}(n) \le y^{1/2}}} 1 \ll y^{11/12} \end{align} $$
$$ \begin{align} \sum_{\substack{x < n \le x + y\\ n\ k\mbox{-}\mathrm{full}\\ p^{+}(n) \le y^{1/2}}} 1 \le \sum_{\substack{x < n \le x + y\\ n\ {\mathrm{squarefull}}\\ p^{+}(n) \le y^{1/2}}} 1 \ll y^{11/12} \end{align} $$
uniformly over
![]() $1 \le y \le x$
. Here
$1 \le y \le x$
. Here
![]() $p^{+}(n)$
stands for the largest prime factor of n.
$p^{+}(n)$
stands for the largest prime factor of n.
One may increase the exponent
![]() $1/2$
up to
$1/2$
up to
![]() $1$
and obtain a similar power saving upper bound.
$1$
and obtain a similar power saving upper bound.
The bound (1.4) lends evidence towards Conjecture 1.1 and shows that the difficulty lies with nonsmooth k-full numbers. Another piece of evidence comes from the famous
![]() $abc$
-conjecture. It was proved in [Reference De Koninck, Luca and Shparlinski3] that, given any
$abc$
-conjecture. It was proved in [Reference De Koninck, Luca and Shparlinski3] that, given any
![]() $\delta> 0$
, the interval
$\delta> 0$
, the interval
contains at most one k-full number for sufficiently large x under the
![]() $abc$
-conjecture. From this, one has the following result.
$abc$
-conjecture. From this, one has the following result.
Theorem 1.5. Assume the
![]() $abc$
-conjecture. Given an integer
$abc$
-conjecture. Given an integer
![]() $k \ge 2$
and real numbers
$k \ge 2$
and real numbers
![]() $\delta> 0$
and
$\delta> 0$
and
![]() $x \ge 1$
, we have
$x \ge 1$
, we have
uniformly over
![]() $1 \le y \le x$
.
$1 \le y \le x$
.
We shall modify the proof in [Reference De Koninck, Luca and Shparlinski3] concerning (1.5) slightly to correct an inaccuracy (since the a, b, c in the application of the
![]() $abc$
-conjecture might not be relatively prime). Then we apply it to obtain Theorem 1.5. Observe that (1.5) or (1.6) give us nothing nontrivial when
$abc$
-conjecture might not be relatively prime). Then we apply it to obtain Theorem 1.5. Observe that (1.5) or (1.6) give us nothing nontrivial when
![]() $k = 2$
. To remedy this, we shall prove the following conditional result which improves (1.3) slightly by a small power of a logarithm.
$k = 2$
. To remedy this, we shall prove the following conditional result which improves (1.3) slightly by a small power of a logarithm.
Theorem 1.6. The
![]() $abc$
-conjecture implies that for some absolute constant
$abc$
-conjecture implies that for some absolute constant
![]() $c> 0$
,
$c> 0$
,
uniformly over
![]() $1 \le y \le x$
.
$1 \le y \le x$
.
The proof relies on the following recent breakthrough result of Bloom and Sisask on the density of integer sequences without three-term arithmetic progressions.
Theorem 1.7 (Bloom–Sisask, [Reference Bloom and Sisask2])
Let
![]() $N \ge 2$
and
$N \ge 2$
and
![]() $A \subset \{1, 2, \ldots , N \}$
be a set with no nontrivial three-term arithmetic progressions, that is, solutions to
$A \subset \{1, 2, \ldots , N \}$
be a set with no nontrivial three-term arithmetic progressions, that is, solutions to
![]() $x + y = 2z$
with
$x + y = 2z$
with
![]() $x \,{\neq}\, y$
. Then
$x \,{\neq}\, y$
. Then
 $$ \begin{align*} |A| \ll \frac{N}{(\log N)^{1+c}}, \end{align*} $$
$$ \begin{align*} |A| \ll \frac{N}{(\log N)^{1+c}}, \end{align*} $$
where
![]() $c> 0$
is an absolute constant.
$c> 0$
is an absolute constant.
This paper is organised as follows. First, we will prove Theorems 1.3 and 1.4 using the Brun–Titchmarsh inequality and ideas from Shiu’s generalisation [Reference Shiu7]. Then we will prove Theorem 1.5 using the
![]() $abc$
-conjecture. Finally, we will prove Theorem 1.6 by establishing the nonexistence of three-term arithmetic progressions for squarefull numbers in short intervals.
$abc$
-conjecture. Finally, we will prove Theorem 1.6 by establishing the nonexistence of three-term arithmetic progressions for squarefull numbers in short intervals.
Notation. We use
![]() $| A |$
to denote the number of elements in a finite set A and
$| A |$
to denote the number of elements in a finite set A and
![]() $\lfloor x \rfloor $
to denote the greatest integer less than or equal to x. We let
$\lfloor x \rfloor $
to denote the greatest integer less than or equal to x. We let
![]() $p_{-}(n)$
and
$p_{-}(n)$
and
![]() $p^{+}(n)$
be the smallest and the largest prime factor of n, respectively. The symbols
$p^{+}(n)$
be the smallest and the largest prime factor of n, respectively. The symbols
![]() $f(x) = O(g(x))$
and
$f(x) = O(g(x))$
and
![]() $f(x) \ll g(x)$
are equivalent to
$f(x) \ll g(x)$
are equivalent to
![]() $|f(x)| \leq C g(x)$
for some constant
$|f(x)| \leq C g(x)$
for some constant
![]() $C> 0$
. Also,
$C> 0$
. Also,
![]() $f(x) = O_{\lambda _1, \ldots , \lambda _r} (g(x))$
and
$f(x) = O_{\lambda _1, \ldots , \lambda _r} (g(x))$
and
![]() $f(x) \ll _{\lambda _1, \ldots , \lambda _r} g(x)$
mean that the implicit constant may depend on
$f(x) \ll _{\lambda _1, \ldots , \lambda _r} g(x)$
mean that the implicit constant may depend on
![]() $\lambda _1, \ldots , \lambda _r$
. Furthermore,
$\lambda _1, \ldots , \lambda _r$
. Furthermore,
![]() $f(x) = o(g(x))$
means
$f(x) = o(g(x))$
means
![]() $\lim _{x \rightarrow \infty } f(x)/g(x) = 0$
and
$\lim _{x \rightarrow \infty } f(x)/g(x) = 0$
and
![]() $f(x) \sim g(x)$
means
$f(x) \sim g(x)$
means
![]() $\lim _{x \rightarrow \infty } f(x)/g(x) = 1$
. Finally, the summation symbol
$\lim _{x \rightarrow \infty } f(x)/g(x) = 1$
. Finally, the summation symbol
![]() $\mathop {\sum \nolimits '}$
signifies that a sum is over squarefull numbers only.
$\mathop {\sum \nolimits '}$
signifies that a sum is over squarefull numbers only.
2 Some preparations
Lemma 2.1. For any
![]() $X \ge 1$
,
$X \ge 1$
,
 $$ \begin{align*} \mathop{\sum\nolimits'}_{X < n \le X^2} \frac{1}{n} \ll X^{-1/2}. \end{align*} $$
$$ \begin{align*} \mathop{\sum\nolimits'}_{X < n \le X^2} \frac{1}{n} \ll X^{-1/2}. \end{align*} $$
Proof. From (1.1),
![]() $Q_2(X) \ll X^{1/2}$
. By partial summation, the above sum is
$Q_2(X) \ll X^{1/2}$
. By partial summation, the above sum is
 $$ \begin{align*} \hspace{-22pt}\int_{X}^{X^2} \!\frac{1}{u} \,d Q(u) = \frac{Q(X^2)}{X^2} - \frac{Q(X)}{X} + \!\int_{X}^{X^2} \frac{Q(u)}{u^2} \,du \ll \frac{1}{X^{1/2}} + \!\int_{X}^{X^2} \frac{1}{u^{3/2}} \,du \ll \frac{1}{X^{1/2}}.\\[-42pt] \end{align*} $$
$$ \begin{align*} \hspace{-22pt}\int_{X}^{X^2} \!\frac{1}{u} \,d Q(u) = \frac{Q(X^2)}{X^2} - \frac{Q(X)}{X} + \!\int_{X}^{X^2} \frac{Q(u)}{u^2} \,du \ll \frac{1}{X^{1/2}} + \!\int_{X}^{X^2} \frac{1}{u^{3/2}} \,du \ll \frac{1}{X^{1/2}}.\\[-42pt] \end{align*} $$
Lemma 2.2 (Brun–Titchmarsh inequality)
Let
![]() $q \ge 1$
and r be integers satisfying
$q \ge 1$
and r be integers satisfying
![]() $\gcd (r, q) = 1$
. Suppose
$\gcd (r, q) = 1$
. Suppose
![]() $q < y \le x$
and
$q < y \le x$
and
![]() $z \ge 2$
. Then,
$z \ge 2$
. Then,
 $$ \begin{align*} \sum_{\substack{x < n \le x + y\\ n \equiv r \!\pmod{q}\\ p_{-}(n)> z}} 1 \ll \frac{y}{\phi(q) \log z} + z^2. \end{align*} $$
$$ \begin{align*} \sum_{\substack{x < n \le x + y\\ n \equiv r \!\pmod{q}\\ p_{-}(n)> z}} 1 \ll \frac{y}{\phi(q) \log z} + z^2. \end{align*} $$
The above bound is still true when
![]() $y \le q$
or
$y \le q$
or
![]() $y < 1$
since there is at most one term in the sum. The estimate follows from the Selberg upper bound sieve method (see, for example, [Reference Halberstam and Richert5, page 104]).
$y < 1$
since there is at most one term in the sum. The estimate follows from the Selberg upper bound sieve method (see, for example, [Reference Halberstam and Richert5, page 104]).
Finally, let us recall the
![]() $abc$
-conjecture. For any nonzero integer m, the kernel of m is
$abc$
-conjecture. For any nonzero integer m, the kernel of m is
 $$ \begin{align*} \kappa(m) := \prod_{p | m} p. \end{align*} $$
$$ \begin{align*} \kappa(m) := \prod_{p | m} p. \end{align*} $$
Conjecture 2.3 (
 $abc$
-conjecture)
$abc$
-conjecture)
For any
![]() $\epsilon> 0$
, there exists a constant
$\epsilon> 0$
, there exists a constant
![]() $C_\epsilon> 0$
such that, for any integers
$C_\epsilon> 0$
such that, for any integers
![]() $a, b, c$
with
$a, b, c$
with
![]() $a + b = c$
and
$a + b = c$
and
![]() $\gcd (a,b) = 1$
, we have
$\gcd (a,b) = 1$
, we have
3 Proof of Theorem 1.3
Our proof is inspired by Shiu [Reference Shiu7] on the Brun–Titchmarsh theorem for multiplicative functions. We may assume that
![]() $y \ge 2^{2/\alpha }$
for the theorem is clearly true when
$y \ge 2^{2/\alpha }$
for the theorem is clearly true when
![]() $1 \le y < 2^{2/\alpha }$
by choosing a large enough implicit constant. Recall that
$1 \le y < 2^{2/\alpha }$
by choosing a large enough implicit constant. Recall that
![]() $1 \le q \le y^{1 - \alpha }$
for some
$1 \le q \le y^{1 - \alpha }$
for some
![]() $\alpha> 0$
. Let
$\alpha> 0$
. Let
![]() $z = y^{\alpha / 2} \ge 2$
. Any squarefull number n in
$z = y^{\alpha / 2} \ge 2$
. Any squarefull number n in
![]() $[x, x + y]$
can be factored as
$[x, x + y]$
can be factored as
 $$ \begin{align*} n = \underbrace{p_1^{a_1} \cdots p_j^{a_j}}_{b_n} \underbrace{p_{j+1}^{a_{j+1}} \cdots p_s^{a_s}}_{d_n}\quad \text{with } p_1 < p_2 < \cdots < p_s, \end{align*} $$
$$ \begin{align*} n = \underbrace{p_1^{a_1} \cdots p_j^{a_j}}_{b_n} \underbrace{p_{j+1}^{a_{j+1}} \cdots p_s^{a_s}}_{d_n}\quad \text{with } p_1 < p_2 < \cdots < p_s, \end{align*} $$
where j is the greatest index such that
![]() $ p_1^{a_1} \cdots p_j^{a_j} \le z$
. Hence,
$ p_1^{a_1} \cdots p_j^{a_j} \le z$
. Hence,
![]() $b_n \le z < b_n p_{j+1}^{a_{j+1}}$
. Note that j may be
$b_n \le z < b_n p_{j+1}^{a_{j+1}}$
. Note that j may be
![]() $0$
(the product is an empty product) if
$0$
(the product is an empty product) if
![]() $p_1^{a_1}> z$
. In this case,
$p_1^{a_1}> z$
. In this case,
![]() $b_n = 1$
and
$b_n = 1$
and
![]() $d_n = n$
. Also, since
$d_n = n$
. Also, since
![]() $n \equiv r \pmod {q}$
with
$n \equiv r \pmod {q}$
with
![]() $\text {gcd}(r,q) = 1$
, we must have
$\text {gcd}(r,q) = 1$
, we must have
![]() $\text {gcd}(b_n, q) = 1 = \text {gcd}(d_n, q)$
.
$\text {gcd}(b_n, q) = 1 = \text {gcd}(d_n, q)$
.
Case 1:
![]() $b_n> z^{1/2}$
. As
$b_n> z^{1/2}$
. As
![]() $q \le y^{1 - \alpha }$
and
$q \le y^{1 - \alpha }$
and
![]() $z = y^{\alpha /2}$
, the number of such squarefull numbers is bounded by
$z = y^{\alpha /2}$
, the number of such squarefull numbers is bounded by
 $$ \begin{align} \mathop{\sum\nolimits'}_{\substack{z^{1/2} < b \le z\\ \gcd(b, q) = 1}} \sum_{\substack{x < n \le x + y\\ b \mid n\\ n \equiv r \!\pmod{q}}} 1 \le \mathop{\sum\nolimits'}_{z^{1/2} < b \le z} \bigg( \frac{y/b}{q} + 1 \bigg) \ll \frac{y}{q z^{1/4}} + z^{1/2} \ll_\alpha \frac{y}{\phi(q) \log y} \end{align} $$
$$ \begin{align} \mathop{\sum\nolimits'}_{\substack{z^{1/2} < b \le z\\ \gcd(b, q) = 1}} \sum_{\substack{x < n \le x + y\\ b \mid n\\ n \equiv r \!\pmod{q}}} 1 \le \mathop{\sum\nolimits'}_{z^{1/2} < b \le z} \bigg( \frac{y/b}{q} + 1 \bigg) \ll \frac{y}{q z^{1/4}} + z^{1/2} \ll_\alpha \frac{y}{\phi(q) \log y} \end{align} $$
Case 2:
![]() $b_n \le z^{1/2}$
and
$b_n \le z^{1/2}$
and
![]() $p_{-}(d_n) \le z^{1/2}$
. Then
$p_{-}(d_n) \le z^{1/2}$
. Then
![]() $p_{j+1} \le z^{1/2}$
and
$p_{j+1} \le z^{1/2}$
and
![]() $p_{j+1}^{a_{j+1}}> z^{1/2}$
which implies
$p_{j+1}^{a_{j+1}}> z^{1/2}$
which implies
![]() $p_{j+1}^{-a_{j+1}} \le \min (z^{-1/2}, p_{j+1}^{-2})$
as
$p_{j+1}^{-a_{j+1}} \le \min (z^{-1/2}, p_{j+1}^{-2})$
as
![]() $a_{j+1} \ge 2$
. Hence, the sum
$a_{j+1} \ge 2$
. Hence, the sum
 $$ \begin{align*} \sum_{p_{j+1} \le z^{1/2}} \frac{1}{p_{j+1}^{a_{j+1}}} \le \sum_{p_{j+1} \le z^{1/4}} z^{-1/2} + \sum_{z^{1/4} < p_{j+1} \le z^{1/2}} \frac{1}{p_{j+1}^2} \ll \frac{1}{z^{1/4}}. \end{align*} $$
$$ \begin{align*} \sum_{p_{j+1} \le z^{1/2}} \frac{1}{p_{j+1}^{a_{j+1}}} \le \sum_{p_{j+1} \le z^{1/4}} z^{-1/2} + \sum_{z^{1/4} < p_{j+1} \le z^{1/2}} \frac{1}{p_{j+1}^2} \ll \frac{1}{z^{1/4}}. \end{align*} $$
Therefore, by replacing
![]() $p_{j+1}^{a_{j+1}}$
with a generic
$p_{j+1}^{a_{j+1}}$
with a generic
![]() $p^a$
, the number of squarefull numbers in this case is bounded by
$p^a$
, the number of squarefull numbers in this case is bounded by
 $$ \begin{align} \sum_{\substack{p \le z^{1/2}\\ \gcd(p,q) = 1}} \sum_{\substack{x < n \le x + y\\ p^a \mid n\\ n \equiv r \!\pmod{q}}} 1 \le \sum_{p \le z^{1/2}} \bigg(\frac{y / p^a}{q} + 1 \bigg) \ll \frac{y}{q z^{1/4}} + z^{1/2} \ll_\alpha \frac{y}{\phi(q) \log y}, \end{align} $$
$$ \begin{align} \sum_{\substack{p \le z^{1/2}\\ \gcd(p,q) = 1}} \sum_{\substack{x < n \le x + y\\ p^a \mid n\\ n \equiv r \!\pmod{q}}} 1 \le \sum_{p \le z^{1/2}} \bigg(\frac{y / p^a}{q} + 1 \bigg) \ll \frac{y}{q z^{1/4}} + z^{1/2} \ll_\alpha \frac{y}{\phi(q) \log y}, \end{align} $$
since
![]() $q \le y^{1 - \alpha }$
and
$q \le y^{1 - \alpha }$
and
![]() $z = y^{\alpha /2}$
.
$z = y^{\alpha /2}$
.
Case 3:
![]() $b_n \le z^{1/2}$
and
$b_n \le z^{1/2}$
and
![]() $p_{-}(d_n)> z^{1/2}$
. As
$p_{-}(d_n)> z^{1/2}$
. As
![]() $q \le y^{1 - \alpha }$
and
$q \le y^{1 - \alpha }$
and
![]() $z = y^{\alpha /2}$
, the number of such squarefull numbers is bounded by
$z = y^{\alpha /2}$
, the number of such squarefull numbers is bounded by
 $$ \begin{align} \mathop{\sum\nolimits'}_{\substack{b \le z^{1/2}\\ \gcd(b,q) = 1}} \sum_{\substack{x/b < n/b \le (x + y)/b\\ p_{-}(n / b)> z^{1/2}\\ (n/b) \equiv r \overline{b} \!\pmod q}} 1 \ll \mathop{\sum\nolimits'}_{b \le z} \bigg( \frac{y / b}{\phi(q) \log z} + z \bigg) \ll \frac{y}{\phi(q) \log z} + z^{3/2} \ll_\alpha \frac{y}{\phi(q) \log y} \end{align} $$
$$ \begin{align} \mathop{\sum\nolimits'}_{\substack{b \le z^{1/2}\\ \gcd(b,q) = 1}} \sum_{\substack{x/b < n/b \le (x + y)/b\\ p_{-}(n / b)> z^{1/2}\\ (n/b) \equiv r \overline{b} \!\pmod q}} 1 \ll \mathop{\sum\nolimits'}_{b \le z} \bigg( \frac{y / b}{\phi(q) \log z} + z \bigg) \ll \frac{y}{\phi(q) \log z} + z^{3/2} \ll_\alpha \frac{y}{\phi(q) \log y} \end{align} $$
by (1.1), Lemma 2.2 and the convergence of the sum of reciprocals of squarefull numbers (which follows from Lemma 2.1 for instance). Here
![]() $\overline {b}$
denotes the multiplicative inverse of
$\overline {b}$
denotes the multiplicative inverse of
![]() $b \;(\bmod {q})$
, that is,
$b \;(\bmod {q})$
, that is,
![]() $b \overline {b} \equiv 1 \pmod {q}$
.
$b \overline {b} \equiv 1 \pmod {q}$
.
4 Proof of Theorem 1.4
This is very similar to the proof of Theorem 1.3, so we just highlight the necessary adjustments. We set
![]() $q = 1$
and
$q = 1$
and
![]() $z = y^{1/3}$
. The arguments for Case 1 and Case 2 are exactly the same as (3.1) and (3.2), and we get the bound
$z = y^{1/3}$
. The arguments for Case 1 and Case 2 are exactly the same as (3.1) and (3.2), and we get the bound
It remains to deal with Case 3, where
![]() $b_n \le z^{1/2}$
and
$b_n \le z^{1/2}$
and
![]() $z^{1/2} < p_{-}(d_n) \le y^{1/2}$
as the squarefull numbers are assumed to be
$z^{1/2} < p_{-}(d_n) \le y^{1/2}$
as the squarefull numbers are assumed to be
![]() $y^{1/2}$
-smooth. Thus, with
$y^{1/2}$
-smooth. Thus, with
![]() $p := p_{-}(d_n)$
and
$p := p_{-}(d_n)$
and
![]() $d_n := p^2 d$
, the number of squarefull numbers in this case is bounded by
$d_n := p^2 d$
, the number of squarefull numbers in this case is bounded by
 $$ \begin{align*} \mathop{\sum\nolimits'}_{b \le z^{1/2}} \sum_{z^{1/2} < p \le y^{1/2}} & \sum_{\substack{x/b < p^2 d \le (x + y)/b\\ p_{-}(d)> z^{1/2}}} 1 = \mathop{\sum\nolimits'}_{b \le z^{1/2}} \sum_{z^{1/2} < p \le y^{1/2}} \sum_{\substack{{x}/{b p^2} < d \le {(x + y)}/{b p^2}\\ p_{-}(d)> z^{1/2}}} 1 \\ \ll& \mathop{\sum\nolimits'}_{b \le z^{1/2}} \sum_{z^{1/2} < p \le y^{1/2}} \bigg( \frac{y/ (b p^2)}{\log z} + z \bigg) \ll \frac{y}{z^{1/2} \log z} + \frac{z^{5/4} y^{1/2}}{\log y} \ll y^{11/12} \end{align*} $$
$$ \begin{align*} \mathop{\sum\nolimits'}_{b \le z^{1/2}} \sum_{z^{1/2} < p \le y^{1/2}} & \sum_{\substack{x/b < p^2 d \le (x + y)/b\\ p_{-}(d)> z^{1/2}}} 1 = \mathop{\sum\nolimits'}_{b \le z^{1/2}} \sum_{z^{1/2} < p \le y^{1/2}} \sum_{\substack{{x}/{b p^2} < d \le {(x + y)}/{b p^2}\\ p_{-}(d)> z^{1/2}}} 1 \\ \ll& \mathop{\sum\nolimits'}_{b \le z^{1/2}} \sum_{z^{1/2} < p \le y^{1/2}} \bigg( \frac{y/ (b p^2)}{\log z} + z \bigg) \ll \frac{y}{z^{1/2} \log z} + \frac{z^{5/4} y^{1/2}}{\log y} \ll y^{11/12} \end{align*} $$
by (1.1), Lemma 2.2 and the convergence of the sum of reciprocals of squarefull numbers. The above bounds together yield Theorem 1.4.
5 Proof of (1.5) and Theorem 1.5
Given an integer
![]() $k \ge 2$
and a small real number
$k \ge 2$
and a small real number
![]() $\delta> 0$
, we claim that the interval from (1.5), namely
$\delta> 0$
, we claim that the interval from (1.5), namely
contains at most one k-full number for all sufficiently large
![]() $x> C$
(in terms of
$x> C$
(in terms of
![]() $\delta $
and k) under the
$\delta $
and k) under the
![]() $abc$
-conjecture.
$abc$
-conjecture.
Following De Koninck et al. [Reference De Koninck, Luca and Shparlinski3], we suppose that the interval
![]() $(x, x + x^{1 - (2 + \delta )/k}]$
contains two k-full numbers,
$(x, x + x^{1 - (2 + \delta )/k}]$
contains two k-full numbers,
![]() $b < c$
. Then
$b < c$
. Then
![]() $c = a + b$
for some integer a with
$c = a + b$
for some integer a with
![]() $0 < a \le x^{1 - (2 + \delta )/k}$
. With
$0 < a \le x^{1 - (2 + \delta )/k}$
. With
![]() $d = \text {gcd}(a, b)$
, the integers
$d = \text {gcd}(a, b)$
, the integers
![]() $a/d$
,
$a/d$
,
![]() $b/d$
and
$b/d$
and
![]() $c/d$
are pairwise relatively prime. Note that
$c/d$
are pairwise relatively prime. Note that
![]() $\kappa (n) \le n^{1/k}$
for any k-full number. Applying the
$\kappa (n) \le n^{1/k}$
for any k-full number. Applying the
![]() $abc$
-conjecture with
$abc$
-conjecture with
![]() $\epsilon = \delta / k$
to the equation
$\epsilon = \delta / k$
to the equation
![]() $a/d + b/d = c/d$
, we get
$a/d + b/d = c/d$
, we get
 $$ \begin{align*} \frac{x}{d} < \frac{c}{d} &\le C_{\delta/k} \bigg( \kappa \bigg(\frac{a}{d} \bigg) \kappa \bigg( \frac{b}{d} \bigg) \kappa \bigg( \frac{c}{d} \bigg) \bigg)^{1 + \delta/k} \le C_{\delta / k} \bigg( \frac{a}{d} \cdot \kappa(b) \kappa(c) \bigg)^{1 + \delta/k} \\ &\le C_{\delta/k} \bigg( \frac{x^{1 - (2 + \delta)/k}}{d} (2x)^{2/k} \bigg)^{1 + \delta/k} = 2^{({2}/{k}) (1 + {\delta}/{k})} C_{\delta/k} \frac{x^{1- \delta^2 / k^2}}{d^{1 + \delta /k}} \\ &\le 2^{({2}/{k} )(1 + {\delta}/{k})} C_{\delta/k} \frac{x^{1- \delta^2 / k^2}}{d}. \end{align*} $$
$$ \begin{align*} \frac{x}{d} < \frac{c}{d} &\le C_{\delta/k} \bigg( \kappa \bigg(\frac{a}{d} \bigg) \kappa \bigg( \frac{b}{d} \bigg) \kappa \bigg( \frac{c}{d} \bigg) \bigg)^{1 + \delta/k} \le C_{\delta / k} \bigg( \frac{a}{d} \cdot \kappa(b) \kappa(c) \bigg)^{1 + \delta/k} \\ &\le C_{\delta/k} \bigg( \frac{x^{1 - (2 + \delta)/k}}{d} (2x)^{2/k} \bigg)^{1 + \delta/k} = 2^{({2}/{k}) (1 + {\delta}/{k})} C_{\delta/k} \frac{x^{1- \delta^2 / k^2}}{d^{1 + \delta /k}} \\ &\le 2^{({2}/{k} )(1 + {\delta}/{k})} C_{\delta/k} \frac{x^{1- \delta^2 / k^2}}{d}. \end{align*} $$
This implies
and the claim follows.
Clearly, Theorem 1.5 is true for
![]() $1 \le y \le C$
by picking the implicit constant to be C. Now, for
$1 \le y \le C$
by picking the implicit constant to be C. Now, for
![]() $C < y \le x$
, the above claim implies that the interval
$C < y \le x$
, the above claim implies that the interval
contains at most one k-full number. By dividing the interval
![]() $(x, x+y]$
into subintervals of length
$(x, x+y]$
into subintervals of length
![]() $y^{1 - (2 + \delta )/k}$
, we obtain
$y^{1 - (2 + \delta )/k}$
, we obtain
which gives Theorem 1.5.
6 Proof of Theorem 1.6
First, we suppose
![]() $y \le x^{0.2}$
. We claim that there is no nontrivial three-term arithmetic progression among the squarefull numbers in the interval
$y \le x^{0.2}$
. We claim that there is no nontrivial three-term arithmetic progression among the squarefull numbers in the interval
![]() $(x, x + y]$
under the
$(x, x + y]$
under the
![]() $abc$
-conjecture. Suppose the contrary. Then we have three squarefull numbers
$abc$
-conjecture. Suppose the contrary. Then we have three squarefull numbers
![]() $x < a_1^2 b_1^3 < a_2^2 b_2^3 < a_3^2 b_3^3 \le x + y$
such that
$x < a_1^2 b_1^3 < a_2^2 b_2^3 < a_3^2 b_3^3 \le x + y$
such that
for some positive integer d with
![]() $2 d \le y$
. Multiplying the above two equations, we get
$2 d \le y$
. Multiplying the above two equations, we get
Say
![]() $D^2 = \text {gcd}(a_2^4 b_2^6, d^2)$
as the numbers are perfect squares. Then, the three integers
$D^2 = \text {gcd}(a_2^4 b_2^6, d^2)$
as the numbers are perfect squares. Then, the three integers
 $$ \begin{align*} \frac{a_1^2 a_3^2 b_1^3 b_3^3}{D^2}, \; \; \frac{d^2}{D^2}, \; \; \frac{a_2^4 b_2^6}{D^2} \end{align*} $$
$$ \begin{align*} \frac{a_1^2 a_3^2 b_1^3 b_3^3}{D^2}, \; \; \frac{d^2}{D^2}, \; \; \frac{a_2^4 b_2^6}{D^2} \end{align*} $$
are pairwise relatively prime and we have the equation
 $$ \begin{align*} \frac{a_1^2 a_3^2 b_1^3 b_3^3}{D^2} + \frac{d^2}{D^2} = \frac{a_2^4 b_2^6}{D^2}. \end{align*} $$
$$ \begin{align*} \frac{a_1^2 a_3^2 b_1^3 b_3^3}{D^2} + \frac{d^2}{D^2} = \frac{a_2^4 b_2^6}{D^2}. \end{align*} $$
Now, by the
![]() $abc$
-conjecture,
$abc$
-conjecture,
 $$ \begin{align*} \frac{x^2}{D^2} \le \frac{a_2^4 b_2^6}{D^2} &\ll_\epsilon \kappa \bigg(\frac{a_1^2 a_3^2 b_1^3 b_3^3}{D^2} \frac{d^2}{D^2} \frac{a_2^4 b_2^6}{D^2} \bigg)^{1+\epsilon} \\ &\ll_\epsilon \kappa ( a_1^2 a_3^2 b_1^3 b_3^3 )^{1 + \epsilon} \kappa \bigg(\frac{d^2}{D^2} \bigg)^{1 + \epsilon} \kappa (a_2^4 b_2^6 )^{1 + \epsilon} \\ &\ll_\epsilon (a_1 b_1 a_2 b_2 a_3 b_3)^{1 + \epsilon} \bigg(\frac{d}{D}\bigg)^{1 + \epsilon} \ll_\epsilon x^{3/2 + 3\epsilon/2} \frac{y^{1 + \epsilon}}{D^{1 + \epsilon}}. \end{align*} $$
$$ \begin{align*} \frac{x^2}{D^2} \le \frac{a_2^4 b_2^6}{D^2} &\ll_\epsilon \kappa \bigg(\frac{a_1^2 a_3^2 b_1^3 b_3^3}{D^2} \frac{d^2}{D^2} \frac{a_2^4 b_2^6}{D^2} \bigg)^{1+\epsilon} \\ &\ll_\epsilon \kappa ( a_1^2 a_3^2 b_1^3 b_3^3 )^{1 + \epsilon} \kappa \bigg(\frac{d^2}{D^2} \bigg)^{1 + \epsilon} \kappa (a_2^4 b_2^6 )^{1 + \epsilon} \\ &\ll_\epsilon (a_1 b_1 a_2 b_2 a_3 b_3)^{1 + \epsilon} \bigg(\frac{d}{D}\bigg)^{1 + \epsilon} \ll_\epsilon x^{3/2 + 3\epsilon/2} \frac{y^{1 + \epsilon}}{D^{1 + \epsilon}}. \end{align*} $$
Since
![]() $1 \le D \le d \le y$
, this implies
$1 \le D \le d \le y$
, this implies
![]() $x^{1/2 - 3\epsilon /2} \ll _\epsilon D^{1 - \epsilon } y^{1+\epsilon } \ll y^2 \le x^{0.4}$
, which is a contradiction for small enough
$x^{1/2 - 3\epsilon /2} \ll _\epsilon D^{1 - \epsilon } y^{1+\epsilon } \ll y^2 \le x^{0.4}$
, which is a contradiction for small enough
![]() $\epsilon $
, say
$\epsilon $
, say
![]() $\epsilon = 0.01$
, and sufficiently large
$\epsilon = 0.01$
, and sufficiently large
![]() $x> C$
(in terms of the implicit constant).
$x> C$
(in terms of the implicit constant).
Clearly, the theorem is true for
![]() $1 \le y \le C$
by picking an appropriate implicit constant. So, we may assume
$1 \le y \le C$
by picking an appropriate implicit constant. So, we may assume
![]() $y> C$
. Since arithmetic progressions are invariant under translation, we may shift the interval
$y> C$
. Since arithmetic progressions are invariant under translation, we may shift the interval
![]() $(x, x+y]$
to
$(x, x+y]$
to
![]() $(0, y]$
. Therefore, by Theorem 1.7, we have
$(0, y]$
. Therefore, by Theorem 1.7, we have
which gives the theorem.
Now, if
![]() $y> x^{0.2}$
, one can simply divide the interval
$y> x^{0.2}$
, one can simply divide the interval
![]() $(x, x + y]$
into subintervals of length
$(x, x + y]$
into subintervals of length
![]() $x^{0.2}$
:
$x^{0.2}$
:
Then, over each interval
![]() $(x + i x^{0.2}, x + (i+1) x^{0.2}]$
, we have the bound
$(x + i x^{0.2}, x + (i+1) x^{0.2}]$
, we have the bound
 $$ \begin{align*} Q_2(x + (i+1) x^{0.2}) - Q_2(x + i x^{0.2}) \ll \frac{x^{0.2}}{\log^{1+c} x}. \end{align*} $$
$$ \begin{align*} Q_2(x + (i+1) x^{0.2}) - Q_2(x + i x^{0.2}) \ll \frac{x^{0.2}}{\log^{1+c} x}. \end{align*} $$
Summing over
![]() $\lfloor \,{y}/{x^{0.2}} \rfloor + 1$
of these intervals, we have
$\lfloor \,{y}/{x^{0.2}} \rfloor + 1$
of these intervals, we have
 $$ \begin{align*} Q_2(x + y) - Q_2(x) \ll \frac{y}{x^{0.2}} \cdot \frac{x^{0.2}}{\log^{1+c} x} \ll \frac{y}{\log^{1+c} y}, \end{align*} $$
$$ \begin{align*} Q_2(x + y) - Q_2(x) \ll \frac{y}{x^{0.2}} \cdot \frac{x^{0.2}}{\log^{1+c} x} \ll \frac{y}{\log^{1+c} y}, \end{align*} $$
which gives the theorem as well.