Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-09T13:56:02.021Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON CYCLIC AMENABILITY OF THE LAU PRODUCT OF BANACH ALGEBRAS DEFINED BY A BANACH ALGEBRA MORPHISM

Part of: Topological algebras, normed rings and algebras, Banach algebras

Published online by Cambridge University Press:  16 June 2015

F. ABTAHI  and
A. GHAFARPANAH
F. ABTAHI*
Affiliation:
Department of Mathematics, University of Isfahan, PO Box 81746-73441, Isfahan, Iran email abtahi.fatemeh@yahoo.com, f.abtahi@sci.ui.ac.ir
A. GHAFARPANAH
Affiliation:
Department of Mathematics, University of Isfahan, PO Box 81746-73441, Isfahan, Iran email ghafarpanah@sci.ui.ac.ir, ghafarpanah2002@gmail.com
*
✉abtahi.fatemeh@yahoo.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $T$ be a Banach algebra homomorphism from a Banach algebra ${\mathcal{B}}$ to a Banach algebra 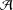${\mathcal{A}}$ with 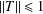$\Vert T\Vert \leq 1$. Recently, Bhatt and Dabhi [‘Arens regularity and amenability of Lau product of Banach algebras defined by a Banach algebra morphism’, Bull. Aust. Math. Soc.87 (2013), 195–206] showed that cyclic amenability of 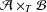${\mathcal{A}}\times _{T}{\mathcal{B}}$ is stable with respect to $T$, for the case where ${\mathcal{A}}$ is commutative. In this note, we address a gap in the proof of this stability result and extend it to an arbitrary Banach algebra ${\mathcal{A}}$.

Keywords

cyclic amenabilityT-Lau product

MSC classification

Primary: 46H05: General theory of topological algebras
Secondary: 46H99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 2 , October 2015 , pp. 282 - 289
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Abtahi, F., Ghafarpanah, A. and Rejali, A., ‘Biprojectivity and biflatness of Lau product of Banach algebras defined by a Banach algebra morphism’, Bull. Aust. Math. Soc. 91 (2015), 134–144.CrossRefGoogle Scholar
Bhatt, S. J. and Dabhi, P. A., ‘Arens regularity and amenability of Lau product of Banach algebras defined by a Banach algebra morphism’, Bull. Aust. Math. Soc. 87 (2013), 195–206.CrossRefGoogle Scholar
Gronbaek, N., ‘Weak and cyclic amenability for non-commutative Banach algebras’, Proc. Edinb. Math. Soc. (2) 35 (1992), 315–328.CrossRefGoogle Scholar
Javanshiri, H. and Nemati, M., ‘On a certain product of Banach algebras and some of its properties’, Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 15(3) (2014), 219–227.Google Scholar
Khoddami, A. R. and Ebrahimi Vishki, H. R., ‘Biflatness and biprojectivity of Lau product of Banach algebras’, Bull. Iranian Math. Soc. 39(3) (2013), 559–568.Google Scholar