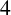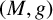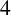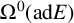1 Introduction
Let
$(M,g)$
be a closed Riemannian manifold of real dimension
$4$
and let E be a vector bundle over M with structure group G, where G is a compact Lie group. The Yang–Mills functional, defined on the space of connections of E, is given by
$$ \begin{align*} \mathcal{YM}(\nabla)=\frac{1}{2}\int_M|F_{\nabla}|^2\,d\mathrm{vol}_g, \end{align*} $$
where
$\nabla $
is a metric compatible connection,
$F_{\nabla }$
denotes the curvature, and the pointwise norm
$|\cdot |$
is given by g and the Killing form of
$\mathrm {Lie}(G)$
. The connection
$\nabla $
is called a Yang–Mills connection of E if it satisfies the Yang–Mills equation:
$$ \begin{align*} D^*_{\nabla}F_{\nabla}=0. \end{align*} $$
A solution of the Yang–Mills flow is given by a family of connections
$\nabla _t:=\nabla (x,t)$
such that
$$ \begin{align*} \frac{\partial \nabla_t}{\partial t}=-D^*_{\nabla_t}F_{\nabla_t}\quad \mbox{in } M\times [0,T). \end{align*} $$
The Yang–Mills flow was initially studied by Atiyah–Bott [Reference Atiyah and Bott2] to understand the topology of the space of connections by infinite dimensional Morse theory.
We consider the Yang–Mills–Higgs k-functional (or Yang–Mills–Higgs k-energy):
$$ \begin{align} \mathcal{YMH}_k(\nabla,u)=\frac{1}{2}\int_M[|\nabla^{(k)}F_{\nabla}|^2+|\nabla^{(k+1)}u|^2]\,d\mathrm{vol}_g, \end{align} $$
where
$k\in \mathbb {N}\cup \{0\}$
,
$\nabla $
is a connection on E and u is a section of
$\Omega ^0(\text {ad}E)$
. In [Reference Zhang13], we considered the case when u is a section of
$\Omega ^0(E)$
. When
$k=0$
, (1.1) is the Yang–Mills–Higgs functional studied in [Reference Hassell4, Reference Hong and Tian5]. In [Reference Hassell4], Hassell proved the global existence of the Yang–Mills–Higgs flow in 3-dimensional Euclidean space. In [Reference Hong and Tian5], Hong–Tian studied the global existence of the Yang–Mills–Higgs flow in 3-dimensional hyperbolic space. Their results yield non-self-dual Yang–Mills connections on
$S^4$
. The Yang–Mills–Higgs flow has aroused much attention. For example, Li–Zhang [Reference Li and Zhang8] and Song–Wang [Reference Song and Wang10] studied the asymptotic behaviour at time infinity of some Yang–Mills–Higgs flows.
The Yang–Mills–Higgs k-system, that is, the corresponding Euler–Lagrange equations of (1.1), is
$$ \begin{align*} \begin{cases} \displaystyle(-1)^kD^*_{\nabla}\Delta_{\nabla}^{(k)}F_{\nabla}+\sum_{v=0}^{2k-1}P_1^{(v)}[F_{\nabla}]+P_2^{(2k-1)}[F_{\nabla}] +\sum_{i=0}^k\nabla^{*(i)}(\nabla^{(k+1)}u\ast \nabla^{(k-i)}u)=0,\\ \nabla^{*(k+1)}\nabla^{(k+1)}u=0, \end{cases} \end{align*} $$
where
$\Delta _{\nabla }^{(k)}$
denotes k iterations of the Bochner Laplacian
$-\nabla ^*\nabla $
and the notation P is defined in (2.1). A solution of the Yang–Mills–Higgs k-flow is given by a family of pairs
$(\nabla (x,t),u(x,t)):=(\nabla _t,u_t)$
such that
$$ \begin{align} \begin{cases} \displaystyle\dfrac{\partial \nabla_t}{\partial t}&\hspace{-9pt}\displaystyle=(-1)^{(k+1)}D^*_{\nabla_t}\Delta_{\nabla_t}^{(k)}F_{\nabla_t}+\sum\limits_{v=0}^{2k-1}P_1^{(v)}[F_{\nabla_t}] \\ &\displaystyle +\ P_2^{(2k-1)}[F_{\nabla_t}]+\sum\limits_{i=0}^k\nabla_t^{*(i)}(\nabla_t^{(k+1)}u_t\ast \nabla_t^{(k-i)}u_t), \\ \dfrac{\partial u_t}{\partial t}&\hspace{-9pt}=-\ \nabla^{*(k+1)}_t\nabla_t^{(k+1)}u_t, \quad \mbox{in } M\times [0,T). \end{cases} \end{align} $$
When
$k=0$
, the flow (1.2) is a Yang–Mills–Higgs flow [Reference Hong and Tian5].
From an analytic point of view, the Yang–Mills–Higgs k-flow (1.2) admits similar properties to the case in which the Higgs field takes values in
$\Omega ^0(E)$
. In fact, by the approach in [Reference Zhang13], we can prove the following theorem.
Theorem 1.1. Let E be a vector bundle over a closed Riemannian
$4$
-manifold
$(M,g)$
and k be an integer with
$k> 1$
. For every smooth initial data
$(\nabla _0,u_0)$
, there exists a unique smooth solution
$(\nabla _t,u_t)$
to the Yang–Mills–Higgs k-flow (1.2) in
$M\times [0,+\infty )$
.
Our motivation for considering such flows comes from recent work of Waldron who proved long-time existence for the Yang–Mills flow [Reference Waldron12], thereby settling a long standing conjecture. In the context of the Yang–Mills–Higgs flow, it is still unknown whether the flow exists for all times on a Riemannian 4-manifold. The above theorem shows that provided
$k> 1$
, the Yang–Mills–Higgs k flow does obey long time existence on a 4-manifold. A question that arises at this point is to understand what is the optimum value for k. By assuming our bundle E is a line bundle, we are able to make progress on this question and show that long-time existence holds for all positive k.
Theorem 1.2. Let E be a line bundle over a closed Riemannian
$4$
-manifold
$(M,g)$
and k be an integer with
$k>0$
. For every smooth initial data
$(\nabla _0,u_0)$
, there exists a unique smooth solution
$(\nabla _t,u_t)$
to the Yang–Mills–Higgs k-flow (1.2) in
$M\times [0,+\infty )$
.
At present, we do not know if this theorem is optimal, meaning that we cannot rule out long-time existence occurring for
$k=0$
.
The proof of Theorem 1.1 involves local
$L^2$
derivative estimates, energy estimates and blow-up analysis. An interesting aspect of this work is that by using a different blow-up procedure, we are able to obtain a proof of Theorem 1.2, which may be of independent interest. Another interesting aspect is that the proof of long-time existence obstruction (see Theorem 3.7) relies on properties of the Green function, which is very different from the previous techniques in [Reference Kelleher6, Reference Saratchandran9, Reference Zhang13].
2 Preliminaries
In this section, we introduce the basic setup and notation that will be used throughout the paper. We follow the notation of [Reference Kelleher6, Reference Saratchandran9, Reference Zhang13].
Let E be a vector bundle over a smooth closed manifold
$(M,g)$
of real dimension n. The set of all smooth unitary connections on E will be denoted by
$\mathcal {A}_E$
. A given connection
$\nabla \in \mathcal {A}_E$
can be extended to other tensor bundles by coupling with the corresponding Levi–Civita connection
$\nabla _M$
on
$(M,g)$
.
Let
$D_{\nabla }$
be the exterior derivative, or skew symmetrisation of
$\nabla $
. The curvature tensor of E is denoted by
$$ \begin{align*}F_{\nabla}=D_{\nabla}\circ D_{\nabla}.\end{align*} $$
We set
$\nabla ^{*},D_{\nabla }^{*}$
to be the formal
$L^2$
-adjoints of
$\nabla ,D_{\nabla }$
, respectively. The Bochner and Hodge Laplacians are given respectively by
$$ \begin{align*}\Delta_{\nabla}=-\nabla^{*}\nabla, \quad \Delta_{D_{\nabla}}=D_{\nabla}D^*_{\nabla}+D^*_{\nabla}D_{\nabla}.\end{align*} $$
Let
$\xi ,\eta $
be p-forms valued in E or
$\mathrm {End}(E)$
. Let
$\xi \ast \eta $
denote any multilinear form obtained from a tensor product
$\xi \otimes \eta $
in a universal way. That is to say,
$\xi \ast \eta $
is obtained by starting with
$\xi \otimes \eta $
, taking any linear combination of this tensor, taking any number of metric contractions and switching any number of factors in the product. We then have
$$ \begin{align*}|\xi\ast\eta|\leq C|\xi||\eta|.\end{align*} $$
Denote
$$ \begin{align*}\nabla^{(i)}=\underbrace{\nabla\cdots\nabla}_{i\ \mathrm{times}}.\end{align*} $$
We will also use the P notation, as introduced in [Reference Kuwert and Schätzle7]. Given a tensor
$\xi $
, we denote
$$ \begin{align} P_v^{(k)}[\xi]:=\sum_{w_1+\cdots+w_v=k}(\nabla^{(w_1)}\xi)\ast\cdots\ast(\nabla^{(w_v)}\xi)\ast T, \end{align} $$
where
$k,v\in \mathbb {N}$
and T is a generic background tensor dependent only on g.
3 Long-time existence obstruction
We can use De Turck’s trick to establish the local existence of the Yang–Mills–Higgs k-flow. We refer to [Reference Kelleher6, Reference Saratchandran9, Reference Zhang13] for more details. As the proof is standard, we will omit the details.
Theorem 3.1 (Local existence)
Let E be a vector bundle over a closed Riemannian manifold
$(M,g)$
. There exists a unique smooth solution
$(\nabla _t,u_t)$
to the Yang–Mills–Higgs k-flow (1.2) in
$M\times [0,\epsilon )$
with smooth initial value
$(\nabla _0,u_0)$
.
Following [Reference Kelleher6, Reference Saratchandran9], we can derive estimates of Bernstein–Bando–Shi type, similar to [Reference Zhang13, Proposition 4.10].
Proposition 3.2. Let
$q\in \mathbb {N}$
,
$\gamma \in C^{\infty }_c(M)\ (0\leq \gamma \leq 1)$
and
$(\nabla _t,u_t)$
be a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$M\times I$
. Suppose
$Q=\max \{1,\sup _{t\in I} |F_{\nabla _t}|\}$
,
$K=\max \{1,\sup _{t\in I}|u_t|\}$
and
$s\geq (k+1)(q+1)$
. For
$t\in [0,T)\subset I$
with
$T<{1}/{(QK)^{4}}$
, there exists a positive constant
$C_q:=C_q(\mathrm {dim} (M),\mathrm {rk} (E),G,q,k,s,g,\gamma )\in \mathbb {R}_{>0}$
such that
$$ \begin{align*} \|\gamma^{s}\nabla_t^{(q)}F_{\nabla_t}\|_{L^2}^2+\|\gamma^{s}\nabla_t^{(q)}u_t\|_{L^2}^2 \leq C_qt^{-{q}/{(k+1)}}\sup_{t\in[0,T)}(\|F_{\nabla_t}\|^2_{L^2}+\|u_t\|^2_{L^2}). \end{align*} $$
The following corollary is a direct consequence of the above proposition and will be used in the blow-up analysis. The proof relies on the Sobolev embedding,
$W^{p,2}\subset C^0$
provided
$p>{n}{/2}$
, and Kato’s inequality
$|d|u_t||\leq |\nabla _tu_t|$
. More details can be found in Kelleher’s paper [Reference Kelleher6, Corollary 3.14].
Corollary 3.3. Suppose
$(\nabla _t,u_t)$
solves the Yang–Mills–Higgs k-flow (1.2) defined on
$M\times [0,\tau ]$
. Set
$\bar {\tau }:=\min \{\tau ,1\}$
. Suppose
$Q=\max \{1,\sup _{t\in [0,\bar {\tau }]} |F_{\nabla _t}|\}$
,
$K\,{=}\,\max \{1,\sup _{t\in [0,\bar {\tau }]}|u_t|\}$
. Assume
$\gamma \in C^{\infty }_c(M)\ (0\leq \gamma \leq 1)$
. For
$s,l\in \mathbb {N}$
with
$s\geq (k+1)(l+1)$
, there exists
$C_l:=C_l(\dim (M),\mathrm {rk}(E),K,Q,G,s,k,l,\tau ,g,\gamma )\in \mathbb {R}_{>0}$
such that
$$ \begin{align*} \sup_M(|\gamma^{s}\nabla_{\bar{\tau}}^{(l)}F_{\nabla_{\bar{\tau}}}|^2+|\gamma^{s}\nabla_{\bar{\tau}}^{(l)}u_{\bar{\tau}}|^2) \leq C_l\sup_{M\times [0,{\bar{\tau}})}(\|F_{\nabla_t}\|^2_{L^2}+\|u_t\|^2_{L^2}). \end{align*} $$
From Corollary 3.3, we deduce the following corollary, which can be used for finding obstructions to long-time existence.
Corollary 3.4. Suppose
$(\nabla _t,u_t)$
solves the Yang–Mills–Higgs k-flow (1.2) defined on
$M\times [0,T)$
for
$T\in [0,+\infty )$
. Suppose
$$ \begin{align*}Q=\max\{1,\sup\limits_{t\in [0,T)} |F_{\nabla_t}|,\sup\limits_{t\in [0,T)} \|F_{\nabla_t}\|_{L^2}\}\end{align*} $$
and
$$ \begin{align*} K=\max\{1,\sup\limits_{t\in [0,T)}|u_t|,\sup\limits_{t\in [0,T)}\|u_t\|_{L^2}\}\end{align*} $$
are finite. Assume
$\gamma \in C^{\infty }_c(M)\ (0\leq \gamma \leq 1)$
. Then, for
$t\in [0,T)$
and
$s,l\in \mathbb {N}$
with
${s\geq (k+1)(l+1)}$
, there exists
$C_l:=C_l(\nabla _0,u_0,\dim (M),\mathrm {rk}(E),K,Q,G,s,k,l,g,\gamma )\in \mathbb {R}_{>0}$
such that
$$ \begin{align*} \sup_{M\times[0,T)}(|\gamma^{s}\nabla_t^{(l)}F_{\nabla_{t}}|^2+|\gamma^{s}\nabla_t^{(l)}u_t|^2)\leq C_l. \end{align*} $$
We will use Corollary 3.4 to show that the only obstruction to long-time existence of the Yang–Mills–Higgs k-flow (1.2) is a lack of a supremal bound on
$|F_{\nabla _t}|+|\nabla _tu_t|$
. Before doing so, we need the following proposition, which is similar to [Reference Zhang13, Proposition 4.15].
Proposition 3.5. Suppose
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$M\times [0,T)$
for
$T\in [0,+\infty )$
. Suppose that for all
$l\in \mathbb {N}\cup \{0\}$
, there exists
$C_l\in \mathbb {R}_{>0}$
such that
$$ \begin{align*}\max\bigg\{\sup_{M\times[0,T)}\bigg|\nabla_t^{(l)}\bigg[\frac{\partial \nabla_t}{\partial t}\bigg]\bigg|, \sup_{M\times[0,T)}\bigg|\nabla_t^{(l)}\bigg[\frac{\partial u_t}{\partial t}\bigg]\bigg|\bigg\}\leq C_l.\end{align*} $$
Then
$\lim _{t\rightarrow T}(\nabla _t,u_t)=(\nabla _T,u_T)$
exists and is smooth.
The following proposition is straightforward.
Proposition 3.6. Suppose
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$M\times [0,T)$
. We have
$$ \begin{align*} \sup_{t\in[0,T)}\|u_t\|_{L^2}<+\infty. \end{align*} $$
Using Propositions 3.5 and 3.6, we are ready to prove the main result in this section.
Theorem 3.7. Assume E is a line bundle. Suppose
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) for some maximal
$T<+\infty $
. Then,
$$ \begin{align*}\sup_{M\times[0,T)}(|F_{\nabla_t}|+|\nabla_t u_t|)=+\infty.\end{align*} $$
Proof. Suppose to the contrary that
$$ \begin{align*}\sup_{M\times[0,T)}(|F_{\nabla_t}|+| \nabla_t u_t|)<+\infty,\end{align*} $$
which means that
$$ \begin{align*}\sup_{M\times[0,T)}|F_{\nabla_t}|<+\infty, \quad \sup_{M\times[0,T)}| \nabla_t u_t|<+\infty.\end{align*} $$
Denote by
$G_t(x,y)$
the Green function associated to the operator
$\Delta _{\nabla _t}$
. Then for any fixed
$x\in M$
,
$\|\nabla _0 G_t(x,\cdot )\|_{L^{\infty }(M)}\leq C_G$
for a constant
$C_G$
from [Reference Alesker and Shelukhin1, Appendix A]. Note that
$\nabla _tG_t-\nabla _0 G_t=[\nabla _t-\nabla _0,G_t]=0$
. We conclude that
$\|\nabla _t G_t\|_{L^{\infty }(M)}$
is also uniformly bounded. Therefore, using the properties of the Green function in [Reference Alesker and Shelukhin1, Appendix A],
$$ \begin{align*} \begin{split} \bigg|u_t(x)-\frac{1}{\text{Vol}(M)}\int_M u_t(y)\,{d}y\bigg|&=\bigg|\int_M \Delta_{\nabla_t} G_t(x,y) u_t(y)\,{d}y\bigg|\\ &=\bigg|\int_M \nabla_t G_t(x,y)\nabla_tu_t(y)\,{d}y\bigg|\\ &< +\infty, \end{split} \end{align*} $$
which together with Proposition 3.6 implies
$$ \begin{align*}\sup_{M\times[0,T)}|u_t|<+\infty.\end{align*} $$
For all
$t\in [0,T)$
and
$l\in \mathbb {N}\cup \{0\}$
, by Corollary 3.4,
$\sup _{M}(|\nabla _t^{(l)}F_{\nabla _{t}}|^2+|\nabla _t^{(l)}u_t|^2)$
is uniformly bounded and so by Proposition 3.5,
$\lim _{t\rightarrow T}(\nabla _t,u_t)=(\nabla _T,u_T)$
exists and is smooth. However, by local existence (Theorem 3.1), there exists
$\epsilon>0$
such that
$(\nabla _t,u_t)$
exists over the extended domain
$[0,T+\epsilon )$
, which contradicts the assumption that T is maximal. Thus, we prove the theorem.
4 Blow-up analysis
In this section, we will address the possibility that the Yang–Mills–Higgs k-flow admits a singularity given no bound on
$|F_{\nabla _t}|+|\nabla _tu_t|$
. To begin with, we first establish some preliminary scaling laws for the Yang–Mills–Higgs k-flow.
Proposition 4.1. Suppose
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$M\times [0,T)$
. Define the 1-parameter family
$\nabla _t^{\rho }$
with local coefficient matrices given by
$$ \begin{align*}\Gamma_t^{\rho}(x):=\rho \Gamma_{\rho^{2(k+1)}t}(\,\rho x),\end{align*} $$
where
$\Gamma _t(x)$
is the local coefficient matrix of
$\nabla _t$
. Define the
$\rho $
-scaled Higgs field
$u_t^{\rho }$
by
$$ \begin{align*}u_t^{\rho}(x):=\rho u_{\rho^{2(k+1)}t}(\,\rho x).\end{align*} $$
Then
$(\nabla _t^{\rho },u_t^{\rho })$
is also a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$[0,{T}/{\rho ^{2(k+1)}})$
.
Next we will show that if the curvature coupled with a Higgs field is blowing up as one approaches the maximal time, then one can extract a blow-up limit. The proof will closely follow the arguments in [Reference Kelleher6, Proposition 3.25] and [Reference Zhang13, Theorem 5.2].
Theorem 4.2. Assume E is a line bundle. Suppose
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on some maximal time interval
$[0,T)$
with
$T< +\infty $
. Then there exists a blow-up sequence
$(\nabla ^i_t,u^i_t)$
which converges pointwise to a smooth solution
$(\nabla ^{\infty }_t,u^{\infty }_t)$
to the Yang–Mills–Higgs k-flow (1.2) defined on the domain
$\mathbb {R}^n\times \mathbb {R}_{<0}$
.
Proof. From Theorem 3.7,
$$ \begin{align*}\lim_{t\rightarrow T}\sup_M(|F_{\nabla_t}|+|\nabla_t u_t|)=+\infty.\end{align*} $$
Therefore, we can choose a sequence of times
$t_i\nearrow T$
within
$[0,T)$
and a sequence of points
$x_i$
, such that
$$ \begin{align*}|F_{\nabla_{t_i}}(x_i)|+|\nabla_{t_i} u_{t_i}(x_i)| =\sup_{M\times [0,t_i]}(|F_{\nabla_t}|+|\nabla_t u_t|).\end{align*} $$
Let
$\{\rho _i\}\subset \mathbb {R}_{>0}$
be constants to be determined. Define
$\nabla _t^i(x)$
by
$$ \begin{align*}\Gamma_t^i(x)=\rho_i^{{1}/{2(k+1)}}\Gamma_{\rho_i t+t_i}(\,\rho_i^{{1}/{2(k+1)}} x+x_i)\end{align*} $$
and
$$ \begin{align*}u_t^i(x)=\rho_i^{{1}/{2(k+1)}}u_{\rho_i t+t_i}(\,\rho_i^{{1}/{2(k+1)}} x+x_i).\end{align*} $$
By Proposition 4.1,
$(\nabla ^i_t,u^i_t)$
are also solutions to the Yang–Mills–Higgs k-flow (1.2) and the domain for each
$(\nabla ^i_t,u^i_t)$
is
$B_0(\,\rho _i^{-{1}/{2(k+1)}})\times [-{t_i}/{\rho _i},{(T-t_i)}/{\rho _i})$
. We observe that
$$ \begin{align*}F_t^i(x):=F_{\nabla_t^i}(x)=\rho_i^{{1}/{(k+1)}}F_{\nabla_{\rho_i t+t_i}}(\,\rho_i^{{1}/{2(k+1)}}x+x_i),\end{align*} $$
which means that
$$ \begin{align*} \begin{split} &\sup_{t\in[-{t_i}/{\rho_i},{T-t_i}/{\rho_i})} (|F_t^i(x)|+|\nabla_{t}^iu_t^i(x)|)\\ &\qquad =\rho_i^{{1}/{(k+1)}}\sup_{t\in[-{t_i}/{\rho_i},{T-t_i}/{\rho_i})}(|F_{\nabla_{\rho_i t+t_i}}(\,\rho_i^{{1}/{2(k+1)}} x+x_i)|+|\nabla_{\rho_i t+t_i} u_{\rho_i t+t_i}(\,\rho_i^{{1}/{2(k+1)}} x+x_i)|)\\ &\qquad =\rho_i^{{1}/{(k+1)}}\sup_{t\in[0,t_i]}(|F_{\nabla_t}(x)|+|\nabla_tu_t(x)|)\\ &\qquad =\rho_i^{{1}/{(k+1)}}(|F_{\nabla_{t_i}}(x_i)|+|\nabla_{t_i}u_{t_i}(x_i)|). \end{split} \end{align*} $$
Therefore, setting
$$ \begin{align*}\rho_i=(|F_{\nabla_{t_i}}(x_i)|+|\nabla_{t_i}u_{t_i}(x_i)|)^{-(k+1)}\end{align*} $$
gives
$$ \begin{align} 1=|F^i_0(0)|+|\nabla_0^i u_0^i(0)|=\sup_{t\in[-{t_i}/{\rho_i},0]}(|F_t^i(x)|+|\nabla_t^i u_t^i(x)|). \end{align} $$
Now, we are ready to construct smoothing estimates for the sequence
$(\nabla ^i_t,u^i_t)$
. Let
$y\in \mathbb {R}^n$
,
$\tau \in \mathbb {R}_{\leq 0}$
. For any
$s\in \mathbb {N}$
,
$$ \begin{align*}\sup_{t\in [\tau-1,\tau]}(|\gamma^s_y F^i_t(x)|+|\gamma^s_y \nabla_t^i u^i_t(x)|)\leq 1.\end{align*} $$
Note that E is a line bundle and, similar to the proof of Theorem 3.7, it suffices to use Corollary 3.3. Then for all
$q\in \mathbb {N}$
, one may choose
$s\geq (k+1)(q+1)$
so that there exists a positive constant
$C_q$
such that
$$ \begin{align*} \begin{split} &\sup_{x\in B_y({1}/{2})}(|(\nabla^i_{\tau})^{(q)} F^i_{\tau}(x)|+|(\nabla^i_{\tau})^{(q)} u^i_{\tau}(x)|)\\ &\quad \leq\sup_{x\in B_y(1)}(|\gamma^s_y(\nabla^i_{\tau})^{(q)} F^i_{\tau}(x)|+|\gamma^s_y(\nabla^i_{\tau})^{(q)} u^i_{\tau}(x)|) \leq C_q. \end{split} \end{align*} $$
Then by the Coulomb gauge theorem of Uhlenbeck [Reference Uhlenbeck11, Theorem 1.3] (see also [Reference Hong and Tian5]) and the gauge patching theorem [Reference Donaldson and Kronheimer3, Corollary 4.4.8], passing to a subsequence (without changing notation) and in an appropriate gauge,
$(\nabla ^i_t,u^i_t)\rightarrow (\nabla ^{\infty }_t,u^{\infty }_t)$
in
$C^{\infty }$
.
5 Proof of Theorem 1.2
The following energy estimates are similar to the ones in [Reference Zhang13, Section 6].
Proposition 5.1. Suppose
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$M\times [0,T)$
. Then the Yang–Mills–Higgs k-energy (1.1) is decreasing along the flow (1.2).
Proposition 5.2. Suppose
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$M^4\times [0,T)$
with
$T< +\infty $
. Then the Yang–Mills–Higgs energy
$$ \begin{align*} \mathcal{YMH}(\nabla_t,u_t)=\frac{1}{2}\int_M[|F_{\nabla_t}|^2+|\nabla_t u_t|^2]\,d\mathrm{vol}_g \end{align*} $$
is bounded along the flow (1.2).
Next, we will complete the proof of Theorem 1.2. To accomplish this, we first show that the
$L^p$
-norm controls the
$L^{\infty }$
-norm by blow-up analysis.
Proposition 5.3. Assume E is a line bundle. Suppose
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$M^4\times [0,T)$
and
$$ \begin{align*}\sup_{t\in[0,T)}(\|F_{\nabla_t}\|_{L^p}+\|\nabla_t u_t\|_{L^p})<+\infty.\end{align*} $$
If
$p>2$
, then
$$ \begin{align*}\sup_{t\in[0,T)}(\|F_{\nabla_t}\|_{L^{\infty}}+\|\nabla_t u_t\|_{L^{\infty}})<+\infty.\end{align*} $$
Proof. To obtain a contradiction, assume
$$ \begin{align*}\sup_{t\in[0,T)}(\|F_{\nabla_t}\|_{L^{\infty}}+\|\nabla_t u_t\|_{L^{\infty}})=+\infty.\end{align*} $$
As we did in Theorem 4.2, we can construct a blow-up sequence
$(\nabla ^i_t,u^i_t)$
, with blow-up limit
$(\nabla ^{\infty }_t,u^{\infty }_t)$
. Noting (4.1), by Fatou’s lemma and the natural scaling law,
$$ \begin{align*} \begin{split} \|F_{\nabla^{\infty}_t}\|^p_{L^p}+\|\nabla_t^{\infty} u^{\infty}_t \|^p_{L^p} &\leq \lim_{i\rightarrow +\infty}\inf(\|F_{\nabla^{i}_t}\|^p_{L^p}+\|\nabla_t^i u^{i}_t \|^p_{L^p})\\ &\leq \lim_{i\rightarrow +\infty}\rho_i^{{(2p-4)}/{(2k+2)}}(\|F_{\nabla_t}\|^p_{L^p}+\|\nabla_t u_t\|^p_{L^p}). \end{split} \end{align*} $$
Since
$\lim _{i\rightarrow +\infty }\rho _i^{{(2p-4)}/{(2k+2)}}=0$
when
$p>2$
, the right-hand side of the above inequality tends to zero, which is a contradiction since the blow-up limit has nonvanishing curvature.
Now we are ready to give the proof of Theorem 1.2.
Proof of Theorem 1.2
By the Sobolev embedding theorem, we can solve for p such that
$W^{k,2}\subset L^{p}$
, when
$k>0$
. Using the interpolation inequalities [Reference Kuwert and Schätzle7, Corollary 5.5]:
$$ \begin{align*} \begin{split} \|F_{\nabla_t}\|_{L^{p}}+\|\nabla_t u_t\|_{L^{p}} & \leq CS_{k,p}\sum_{j=0}^k(\|\nabla_t^{(j)}F_{\nabla_t}\|^2_{L^2}+\|\nabla_t^{(j)}u_t\|^2_{L^2}+1)\\ & \leq CS_{k,p}(\|\nabla_t^{(k)}F_{\nabla_t}\|^2_{L^2}+\|F_{\nabla_t}\|^2_{L^2}+\|\nabla_t^{(k+1)}u_t\|^2_{L^2}+\|u_t\|^2_{L^2}+1)\\ & \leq CS_{k,p}(\mathcal{YMH}_k(\nabla_t,u_t)+\mathcal{YMH}(\nabla_t,u_t)+\|u_t\|^2_{L^2}+1), \end{split} \end{align*} $$
then using Propositions 5.1, 3.6 and 5.2, we conclude that the flow exists smoothly for all time.
