Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-11T10:12:54.474Z Has data issue: false hasContentIssue false
  • English
  • Français

INTERSECTIONS OF SUBGROUPS IN VIRTUALLY FREE GROUPS AND VIRTUALLY FREE PRODUCTS

Part of: Graph theory Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  18 July 2019

ANTON A. KLYACHKO  and
ANASTASIA N. PONFILENKO
ANTON A. KLYACHKO*
Affiliation:
Faculty of Mechanics and Mathematics, Moscow State University, Leninskie gory, Moscow 119991, Russia email klyachko@mech.math.msu.su
ANASTASIA N. PONFILENKO
Affiliation:
Faculty of Mechanics and Mathematics, Moscow State University, Leninskie gory, Moscow 119991, Russia email stponfilenko@gmail.com
*
✉klyachko@mech.math.msu.su
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This note contains a (short) proof of the following generalisation of the Friedman–Mineyev theorem (earlier known as the Hanna Neumann conjecture): if 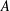$A$ and 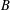$B$ are nontrivial free subgroups of a virtually free group containing a free subgroup of index $n$, then 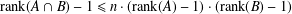$\text{rank}(A\cap B)-1\leq n\cdot (\text{rank}(A)-1)\cdot (\text{rank}(B)-1)$. In addition, we obtain a virtually-free-product analogue of this result.

Keywords

virtually free groupvirtually free productHanna Neumann conjecture

MSC classification

Primary: 20E05: Free nonabelian groups
Secondary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.) 20E06: Free products, free products with amalgamation, Higman-Neumann-Neumann extensions, and generalizations 20E08: Groups acting on trees 20E15: Chains and lattices of subgroups, subnormal subgroups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 2 , April 2020 , pp. 266 - 271
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Footnotes

The work of the first author was supported by the Russian Foundation for Basic Research, project no. 19-01-00591.

References

Antolin, Y., Martino, A. and Schwabrow, I., ‘Kurosh rank of intersections of subgroups of free products of right-orderable groups’, Math. Res. Lett. 21(4) (2014), 649–661.Google Scholar
Araújo, V., Silva, P. V. and Sykiotis, M., ‘Finiteness results for subgroups of finite extensions’, J. Algebra 423 (2015), 592–614.Google Scholar
Dicks, W. and Šunić, Z., ‘Orders on trees and free products of left-ordered groups’, Canad. Math. Bull. (to appear).Google Scholar
Friedman, J., Sheaves on Graphs, Their Homological Invariants, and a Proof of the Hanna Neumann Conjecture. With an Appendix by Warren Dicks, Memoirs of the American Mathematical Society, 233 (American Mathematical Society, Providence, RI, 2014).Google Scholar
Ivanov, S. V., ‘Intersecting free subgroups in free products of left ordered groups’, J. Group Theory 20(4) (2017), 807–821.Google Scholar
Mineyev, I., ‘Groups, graphs, and the Hanna Neumann conjecture’, J. Topol. Anal. 4(1) (2012), 1–12.Google Scholar
Mineyev, I., ‘Submultiplicativity and the Hanna Neumann conjecture’, Ann. Math. 175 (2012), 393–414.Google Scholar
Vinogradov, A. A., ‘On the free product of ordered groups’, Mat. Sb. (N.S.) 25(67(1)) (1949), 163–168.Google Scholar
Zakharov, A., ‘On the rank of the intersection of free subgroups in virtually free groups’, J. Algebra 418 (2014), 29–43.Google Scholar