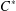Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-11T22:50:07.308Z Has data issue: false hasContentIssue false
  • English
  • Français

HAAGERUP PROPERTY FOR $C^{\ast }$ -CROSSED PRODUCTS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  19 October 2016

QING MENG
QING MENG*
Affiliation:
Chern Institute of Mathematics, Nankai University, Tianjin 300071, PR China email mengqing80@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 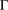$\unicode[STIX]{x1D6E4}$ be a countable discrete group that acts on a unital 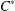$C^{\ast }$ -algebra 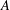$A$ through an action $\unicode[STIX]{x1D6FC}$ . If 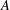$A$ has a faithful $\unicode[STIX]{x1D6FC}$ -invariant tracial state $\unicode[STIX]{x1D70F}$ , then 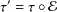$\unicode[STIX]{x1D70F}^{\prime }=\unicode[STIX]{x1D70F}\circ {\mathcal{E}}$ is a faithful tracial state of 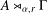$A\rtimes _{\unicode[STIX]{x1D6FC},r}\unicode[STIX]{x1D6E4}$ where 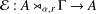${\mathcal{E}}:A\rtimes _{\unicode[STIX]{x1D6FC},r}\unicode[STIX]{x1D6E4}\rightarrow A$ is the canonical faithful conditional expectation. We show that 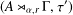$(A\rtimes _{\unicode[STIX]{x1D6FC},r}\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D70F}^{\prime })$ has the Haagerup property if and only if both 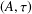$(A,\unicode[STIX]{x1D70F})$ and 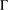$\unicode[STIX]{x1D6E4}$ have the Haagerup property. As a consequence, suppose that 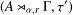$(A\rtimes _{\unicode[STIX]{x1D6FC},r}\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D70F}^{\prime })$ has the Haagerup property where 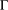$\unicode[STIX]{x1D6E4}$ has property 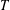$T$ and 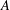$A$ has strong property 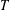$T$ . Then 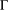$\unicode[STIX]{x1D6E4}$ is finite and 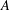$A$ is residually finite-dimensional.

Keywords

C ∗ -algebraHaagerup propertytracial statecrossed product

MSC classification

Primary: 46L55: Noncommutative dynamical systems
Secondary: 46L05: General theory of $C^*$-algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 1 , February 2017 , pp. 144 - 148
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Brown, N. P. and Ozawa, N., C ∗ -Algebras and Finite-Dimensional Approximations, Graduate Studies in Mathematics, 88 (American Mathematical Society, Providence, RI, 2008).CrossRefGoogle Scholar
Choda, M., ‘Group factors of the Haagerup type’, Proc. Japan Acad. Ser. A Math. Sci. 59(5) (1983), 174–177.CrossRefGoogle Scholar
Dong, Z., ‘Haagerup property for C ∗ -algebras’, J. Math. Anal. Appl. 377 (2011), 631–644.CrossRefGoogle Scholar
Haagerup, U., ‘An example of a nonnuclear C ∗ -algebra which has the metric approximation property’, Invent. Math. 50(3) (1979), 279–293.CrossRefGoogle Scholar
Leung, C. W. and Ng, C. K., ‘Property (T) and strong property (T) for unital C ∗ -algebras’, J. Funct. Anal. 256 (2009), 3055–3070.CrossRefGoogle Scholar
Suzuki, Y., ‘Haagerup property for C ∗ -algebras and rigidity of C ∗ -algebras with property (T)’, J. Funct. Anal. 265 (2013), 1778–1799.CrossRefGoogle Scholar
You, C., ‘Group action preserving the Haagerup property of C ∗ -algebras’, Bull. Aust. Math. Soc. 93 (2016), 295–300.CrossRefGoogle Scholar