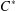Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-06T12:30:26.139Z Has data issue: false hasContentIssue false
  • English
  • Français

GROUP ACTION PRESERVING THE HAAGERUP PROPERTY OF $C^{\ast }$-ALGEBRAS

Part of: Normed linear spaces and Banach spaces; Banach lattices Selfadjoint operator algebras

Published online by Cambridge University Press:  11 August 2015

CHAO YOU
CHAO YOU*
Affiliation:
Center for Mathematics and Interdisciplinary Sciences, Academy of Fundamental and Interdisciplinary Sciences, Harbin Institute of Technology, Harbin 150001, Heilongjiang, PR China Research Center for Operator Algebras, Department of Mathematics, East China Normal University, Shanghai 200062, PR China email youchao@hit.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

From the viewpoint of $C^{\ast }$-dynamical systems, we define a weak version of the Haagerup property for the group action on a 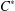$C^{\ast }$-algebra. We prove that this group action preserves the Haagerup property of 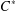$C^{\ast }$-algebras in the sense of Dong [‘Haagerup property for $C^{\ast }$-algebras’, J. Math. Anal. Appl.377 (2011), 631–644], that is, the reduced crossed product 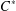$C^{\ast }$-algebra 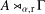$A\rtimes _{{\it\alpha},\text{r}}{\rm\Gamma}$ has the Haagerup property with respect to the induced faithful tracial state $\widetilde{{\it\tau}}$ if $A$ has the Haagerup property with respect to ${\it\tau}$.

Keywords

group actionC∗ -algebracrossed productHaagerup property

MSC classification

Primary: 46L55: Noncommutative dynamical systems
Secondary: 46C05: Hilbert and pre-Hilbert spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 2 , April 2016 , pp. 295 - 300
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Brown, N. P. and Ozawa, N., C ∗ -algebras and finite-dimensional approximations, Graduate Studies in Mathematics, 88 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Dong, Z., ‘Haagerup property for C ∗ -algebras’, J. Math. Anal. Appl. 377 (2011), 631–644.CrossRefGoogle Scholar
Dong, Z. and Ruan, Z.-J., ‘A Hilbert module approach to the Haagerup property’, Integral Equations and Operator Theory 73 (2012), 431–454.Google Scholar
Gromov, M., ‘Geometric group theory, Asymptotic invariants of infinite groups’, Proc. Symp. Sussex Univ., Brighton, July 14–19, 1991, Vol. 2, London Mathematical Society Lecture Notes, 182 (eds. Niblo, A. and Roller, M. A.) (Cambridge University Press, Cambridge, 1993).Google Scholar
Haagerup, U., ‘An example of nonnuclear C ∗ -algebra which has the metric approximation property’, Invent. Math. 50 (1979), 279–293.Google Scholar
Jolissaint, P., ‘Haagerup approximation property for finite von Neumann algebras’, J. Operator Theory 48 (2002), 549–571.Google Scholar
Lance, E. C., ‘On nuclear C ∗ -algebras’, J. Funct. Anal. 12 (1973), 157–176.Google Scholar
Suzuki, Y., ‘Haagerup property for C ∗ -algebras and rigidity of C ∗ -algebras with property (T)’, J. Funct. Anal. 265 (2013), 1778–1799.Google Scholar