Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T13:21:17.279Z Has data issue: false hasContentIssue false
  • English
  • Français

A GENERALISATION OF FINITE PT-GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  07 March 2018

BIN HU ,
JIANHONG HUANG Open the ORCID record for JIANHONG HUANG [Opens in a new window]  and
ALEXANDER N. SKIBA
BIN HU
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou 221116, PR China email hubin118@126.com
JIANHONG HUANG*
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou 221116, PR China email jhh320@126.com
ALEXANDER N. SKIBA
Affiliation:
Department of Mathematics and Technologies of Programming, Francisk Skorina Gomel State University, Gomel 246019, Belarus email alexander.skiba49@gmail.com
*
✉jhh320@126.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 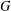$G$ be a group and $\unicode[STIX]{x1D70E}=\{\unicode[STIX]{x1D70E}_{i}\mid i\in I\}$ some partition of the set of all primes. A subgroup 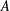$A$ of $G$ is 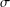$\unicode[STIX]{x1D70E}$-subnormal in 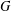$G$ if there is a subgroup chain 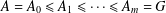$A=A_{0}\leq A_{1}\leq \cdots \leq A_{m}=G$ such that either 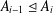$A_{i-1}\unlhd A_{i}$ or 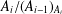$A_{i}/(A_{i-1})_{A_{i}}$ is a finite $\unicode[STIX]{x1D70E}_{j}$-group for some $j=j(i)$ for 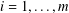$i=1,\ldots ,m$, and it is modular in $G$ if 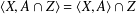$\langle X,A\cap Z\rangle =\langle X,A\rangle \cap Z$ when 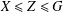$X\leq Z\leq G$ and $\langle A,Y\cap Z\rangle =\langle A,Y\rangle \cap Z$ when $Y\leq G$ and 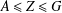$A\leq Z\leq G$. The group 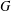$G$ is called $\unicode[STIX]{x1D70E}$-soluble if every chief factor $H/K$ of 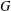$G$ is a finite $\unicode[STIX]{x1D70E}_{i}$-group for some 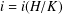$i=i(H/K)$. In this paper, we describe finite $\unicode[STIX]{x1D70E}$-soluble groups in which every $\unicode[STIX]{x1D70E}$-subnormal subgroup is modular.

Keywords

finite group𝜎-subnormal subgroupmodular subgroupquasinormal subgroupM-group

MSC classification

Primary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Secondary: 20D15: Nilpotent groups, $p$-groups 20D30: Series and lattices of subgroups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 3 , June 2018 , pp. 396 - 405
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

This research is supported by the NNSF of China (grant no. 11401264) and TAPP of Jiangsu Higher Education Institutions (PPZY 2015A013).

References

Ballester-Bolinches, A., Esteban-Romero, R. and Asaad, M., Products of Finite Groups (Walter de Gruyter, Berlin, 2010).Google Scholar
Ballester-Bolinches, A. and Ezquerro, L. M., Classes of Finite Groups (Springer, Dordrecht, 2006).Google Scholar
Doerk, K. and Hawkes, T., Finite Soluble Groups (Walter de Gruyter, Berlin, 1992).Google Scholar
Guo, W. and Skiba, A. N., ‘Finite groups with permutable complete Wielandt sets of subgroups’, J. Group Theory 18 (2015), 191–200.Google Scholar
Guo, W. and Skiba, A. N., ‘Finite groups whose $n$ -maximal subgroups are $\unicode[STIX]{x1D70E}$ -subnormal’, Preprint, 2016, arXiv:1608.03353 [math.GR].Google Scholar
Kegel, O. H., ‘Untergruppenverbände endlicher Gruppen, die den Subnormalteilerverband echt enthalten’, Arch. Math. 30(3) (1978), 225–228.CrossRefGoogle Scholar
Ore, O., ‘Contributions in the theory of groups of finite order’, Duke Math. J. 5 (1939), 431–460.CrossRefGoogle Scholar
Robinson, D. J. S., ‘The structure of finite groups in which permutability is a transitive relation’, J. Aust. Math. Soc. 70 (2001), 143–159.CrossRefGoogle Scholar
Schmidt, R., ‘Modulare Untergruppen endlicher Gruppen’, Illinois J. Math. 13 (1969), 358–377.Google Scholar
Schmidt, R., Subgroup Lattices of Groups (Walter de Gruyter, Berlin, 1994).Google Scholar
Shemetkov, L. A., Formations of finite groups (Nauka, Main Editorial Board for Physical and Mathematical Literature, Moscow, 1978).Google Scholar
Skiba, A. N., ‘A generalization of a Hall theorem’, J. Algebra Appl. 15(4) (2015), 21–36.Google Scholar
Skiba, A. N., ‘On 𝜎-subnormal and 𝜎-permutable subgroups of finite groups’, J. Algebra 436 (2015), 1–16.CrossRefGoogle Scholar
Skiba, A. N., ‘Characterizations of some classes of finite 𝜎-soluble P𝜎T-groups’, J. Algebra, to appear.Google Scholar
Zacher, G., ‘I gruppi risolubili finiti in cui i sottogruppi di composizione coincidono con i sottogruppi quasi-normali’, Atti Accad, Naz. Lincei Rend. cl. Sci. Fis. Mat. Natur. 37(8) (1964), 150–154.Google Scholar