Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-11T07:25:40.483Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FLOOR OF THE ARITHMETIC MEAN OF THE CUBE ROOTS OF THE FIRST $n$ INTEGERS

Part of: Convergence and divergence of infinite limiting processes Inequalities

Published online by Cambridge University Press:  08 January 2020

BOONYONG SRIPONPAEW Open the ORCID record for BOONYONG SRIPONPAEW [Opens in a new window]  and
SOMKID INTEP Open the ORCID record for SOMKID INTEP [Opens in a new window]
BOONYONG SRIPONPAEW
Affiliation:
Department of Mathematics, Faculty of Science, Burapha University, Thailand email boonyong@buu.ac.th
SOMKID INTEP*
Affiliation:
Department of Mathematics, Faculty of Science, Burapha University, Thailand Center of Excellence in Mathematics, CHE, Bangkok10400, Thailand email intep@buu.ac.th
*
✉intep@buu.ac.th
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Zacharias [‘Proof of a conjecture of Merca on an average of square roots’, College Math. J.49 (2018), 342–345] proved Merca’s conjecture that the arithmetic means 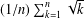$(1/n)\sum _{k=1}^{n}\sqrt{k}$ of the square roots of the first $n$ integers have the same floor values as a simple approximating sequence. We prove a similar result for the arithmetic means 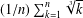$(1/n)\sum _{k=1}^{n}\sqrt[3]{k}$ of the cube roots of the first $n$ integers.

Keywords

floorarithmetic meancube roots

MSC classification

Primary: 26D15: Inequalities for sums, series and integrals
Secondary: 40A25: Approximation to limiting values (summation of series, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 2 , October 2020 , pp. 261 - 267
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Footnotes

The authors were supported by the Faculty of Science, Burapha University, Thailand.

References

Gould, H. W., ‘Evaluation of sums of convolved powers using Stirling and Eulerian numbers’, Fibonacci Quart. 16 (1978), 488–497.Google Scholar
Merca, M., ‘On the arithmetic mean of the square roots of the first n positive integers’, College Math. J. 48 (2017), 129–133.CrossRefGoogle Scholar
Ramanujan, S., ‘On the sum of the square roots of the first n natural numbers’, J. Indian Math. Soc. 7 (1915), 173–175.Google Scholar
Shekatkar, S., ‘The sum of the $r$th roots of the first $n$ natural numbers and new formula for factorial’, Preprint, 2013, arXiv:1204.0877.Google Scholar
Wihler, T. P., ‘Rounding the arithmetic mean value of the square roots of the first $n$ integers’, Preprint, 2018, arXiv:1803.00362.Google Scholar
Zacharias, J., ‘Proof of a conjecture of Merca on an average of square roots’, College Math. J. 49 (2018), 342–345.CrossRefGoogle Scholar