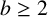1 Introduction
Let
![]() $\mathbb {N}$
denote the set of positive integers and let
$\mathbb {N}$
denote the set of positive integers and let
![]() $b\geq 2$
be an integer. For all
$b\geq 2$
be an integer. For all
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $0\leq i\leq \lfloor \log _bn\rfloor $
, let
$0\leq i\leq \lfloor \log _bn\rfloor $
, let
![]() $\nu _b(n,i)$
be nonnegative integers such that
$\nu _b(n,i)$
be nonnegative integers such that
![]() $\nu _b(n,i)\leq b-1$
and
$\nu _b(n,i)\leq b-1$
and
![]() $n=\sum _{i=0}^{\lfloor \log _bn\rfloor }\nu _b(n,i)b^i$
. In other words,
$n=\sum _{i=0}^{\lfloor \log _bn\rfloor }\nu _b(n,i)b^i$
. In other words,
![]() $\nu _b(n,i)$
is the
$\nu _b(n,i)$
is the
![]() $(i+1)$
st digit from the right in the base-b representation of n. Furthermore, define
$(i+1)$
st digit from the right in the base-b representation of n. Furthermore, define
![]() $s_b:\mathbb {N}\to \mathbb {N}$
by
$s_b:\mathbb {N}\to \mathbb {N}$
by
![]() $s_b(n)=\sum _{i=0}^{\lfloor \log _bn\rfloor }\nu _b(n,i)$
. A positive integer n is b-Niven if
$s_b(n)=\sum _{i=0}^{\lfloor \log _bn\rfloor }\nu _b(n,i)$
. A positive integer n is b-Niven if
![]() $s_b(n)\mid n$
.
$s_b(n)\mid n$
.
It was shown in 1993 by Cooper and Kennedy [Reference Cooper and Kennedy1] that there are no 21 consecutive
![]() $10$
-Niven numbers. Their result was generalised in 1994 by Grundman [Reference Grundman4], who showed that there are no
$10$
-Niven numbers. Their result was generalised in 1994 by Grundman [Reference Grundman4], who showed that there are no
![]() $2b+1$
consecutive b-Niven numbers. In 1994, Wilson [Reference Wilson6] proved that for each b, there are infinitely many occurrences of
$2b+1$
consecutive b-Niven numbers. In 1994, Wilson [Reference Wilson6] proved that for each b, there are infinitely many occurrences of
![]() $2b$
consecutive b-Niven numbers. These results were recently extended by Grundman et al. [Reference Grundman, Harrington and Wong5], who investigated the maximum lengths of arithmetic progressions of b-Niven numbers. Furthermore, an asymptotic estimate for the number of b-Niven numbers not exceeding x was found in 2003 by De Koninck et al. [Reference De Koninck, Doyon and Kátai2] and in 2008, they [Reference De Koninck, Doyon and Kátai3] showed that given any
$2b$
consecutive b-Niven numbers. These results were recently extended by Grundman et al. [Reference Grundman, Harrington and Wong5], who investigated the maximum lengths of arithmetic progressions of b-Niven numbers. Furthermore, an asymptotic estimate for the number of b-Niven numbers not exceeding x was found in 2003 by De Koninck et al. [Reference De Koninck, Doyon and Kátai2] and in 2008, they [Reference De Koninck, Doyon and Kátai3] showed that given any
![]() $r\in \{2,3,\ldots ,2b\}$
, there exists a constant
$r\in \{2,3,\ldots ,2b\}$
, there exists a constant
![]() $c=c(b,r)$
such that the number of r-tuples of consecutive b-Niven numbers not exceeding x is asymptotic to
$c=c(b,r)$
such that the number of r-tuples of consecutive b-Niven numbers not exceeding x is asymptotic to
![]() $cx/(\log x)^r$
as x tends to infinity.
$cx/(\log x)^r$
as x tends to infinity.
In this article, we prove that every arithmetic progression contains infinitely many b-Niven numbers.
2 Main results
The following lemma is sometimes referred to as the ‘postage stamp theorem’, the ‘chicken McNugget theorem’ or the ‘Frobenius coin theorem’.
Lemma 2.1. Let u and v be integers with
![]() $uv\geq 0$
and
$uv\geq 0$
and
![]() $\gcd (u,v)=1$
. Then every integer w such that w shares the same sign with u and v and satisfies
$\gcd (u,v)=1$
. Then every integer w such that w shares the same sign with u and v and satisfies
![]() $|w|\geq (|u|-1)(|v|-1)$
can be written in the form
$|w|\geq (|u|-1)(|v|-1)$
can be written in the form
![]() $w=gu+hv$
for some nonnegative integers g and h.
$w=gu+hv$
for some nonnegative integers g and h.
The following two lemmas, which will be useful in our proof, are easy exercises in elementary number theory.
Lemma 2.2. If
![]() $d\mid b-1$
, then for all
$d\mid b-1$
, then for all
![]() $u\in \mathbb {N}$
, we have
$u\in \mathbb {N}$
, we have
![]() $d\mid u$
if and only if
$d\mid u$
if and only if
![]() $d\mid s_b(u)$
.
$d\mid s_b(u)$
.
Lemma 2.3. For all integers n and
![]() $n'$
with
$n'$
with
![]() $2\leq n'\leq n$
,
$2\leq n'\leq n$
,
![]() $s_b(n')\leq (b-1)\lceil \log _b(n)\rceil $
.
$s_b(n')\leq (b-1)\lceil \log _b(n)\rceil $
.
For positive integers m and r, let
Proposition 2.4. Let
![]() $d=\gcd (s_b(m),s_b(r),b-1)$
. If
$d=\gcd (s_b(m),s_b(r),b-1)$
. If
![]() $\gcd (s_b(m),s_b(r))=d$
, then
$\gcd (s_b(m),s_b(r))=d$
, then
![]() $\mathcal {S}_{m,r}$
contains at least one b-Niven number.
$\mathcal {S}_{m,r}$
contains at least one b-Niven number.
Proof. Let
![]() $k_0(b,m,r)\in \mathbb {N}$
be such that for all integers
$k_0(b,m,r)\in \mathbb {N}$
be such that for all integers
![]() $k\geq k_0$
,
$k\geq k_0$
,
Note that
![]() $k_0$
is well defined since
$k_0$
is well defined since
![]() $b,m,r$
are constants and the right-hand side of (2.1) is of order
$b,m,r$
are constants and the right-hand side of (2.1) is of order
![]() $O(\log k)$
. Using Dirichlet’s theorem on primes in arithmetic progressions, let
$O(\log k)$
. Using Dirichlet’s theorem on primes in arithmetic progressions, let
![]() $k\in \mathbb {N}$
be such that
$k\in \mathbb {N}$
be such that
![]() $k\geq \max \{k_0,b,m\}$
and
$k\geq \max \{k_0,b,m\}$
and
is a prime. Since
![]() $p>k\geq \max \{b,m\}$
, we have
$p>k\geq \max \{b,m\}$
, we have
![]() $p\nmid bm$
. Furthermore, let
$p\nmid bm$
. Furthermore, let
![]() $\tilde {x}$
be the smallest positive integer such that
$\tilde {x}$
be the smallest positive integer such that
![]() $\tilde {x}\equiv -m^{-1}r\text { (mod }p\text {)}$
. From Lemma 2.3 and (2.1),
$\tilde {x}\equiv -m^{-1}r\text { (mod }p\text {)}$
. From Lemma 2.3 and (2.1),
By Lemma 2.1, there exist nonnegative integers g and h such that
Let
![]() $\omega {\kern-1.3pt}\in{\kern-1.3pt} \mathbb {N}$
be a multiple of
$\omega {\kern-1.3pt}\in{\kern-1.3pt} \mathbb {N}$
be a multiple of
![]() $p{\kern-1.3pt}-{\kern-1.3pt}1$
such that
$p{\kern-1.3pt}-{\kern-1.3pt}1$
such that
![]() $b^\omega{\kern-1.3pt}>{\kern-1.3pt}\max \{m,r\}$
. Note that
$b^\omega{\kern-1.3pt}>{\kern-1.3pt}\max \{m,r\}$
. Note that
![]() $b^\omega {\kern-1.3pt}\equiv{\kern-1.3pt} 1\text { (mod }p\text {)}$
by Fermat’s little theorem since
$b^\omega {\kern-1.3pt}\equiv{\kern-1.3pt} 1\text { (mod }p\text {)}$
by Fermat’s little theorem since
![]() $p\nmid b$
. We now define a function
$p\nmid b$
. We now define a function
![]() $\tau _b:\mathbb {N}\to \mathbb {N}$
as follows. For each fixed
$\tau _b:\mathbb {N}\to \mathbb {N}$
as follows. For each fixed
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $\sigma _{-1}=0$
and
$\sigma _{-1}=0$
and
![]() $\sigma _i=\sum _{j=0}^i\nu _b(n,j)$
for
$\sigma _i=\sum _{j=0}^i\nu _b(n,j)$
for
![]() $0\leq i\leq \lfloor \log _bn\rfloor $
. Then,
$0\leq i\leq \lfloor \log _bn\rfloor $
. Then,
 $$ \begin{align*}\tau_b(n)=\sum_{j=1}^{\sigma_{\lfloor\log_bn\rfloor}}b^{j\omega+\ell_j},\end{align*} $$
$$ \begin{align*}\tau_b(n)=\sum_{j=1}^{\sigma_{\lfloor\log_bn\rfloor}}b^{j\omega+\ell_j},\end{align*} $$
where
![]() $\ell _j=i$
for the unique
$\ell _j=i$
for the unique
![]() $i\in \{0,1,2,\dotsc ,\lfloor \log _bn\rfloor \}$
satisfying
$i\in \{0,1,2,\dotsc ,\lfloor \log _bn\rfloor \}$
satisfying
![]() $\sigma _{i-1}<j\leq \sigma _i$
. It is important to notice that the construction of
$\sigma _{i-1}<j\leq \sigma _i$
. It is important to notice that the construction of
![]() $\tau _b(n)$
guarantees
$\tau _b(n)$
guarantees
![]() $s_b(\tau _b(n))=\sigma _{\lfloor \log _bn\rfloor }=s_b(n)$
and
$s_b(\tau _b(n))=\sigma _{\lfloor \log _bn\rfloor }=s_b(n)$
and
![]() $\tau _b(n)\equiv \sum _{j=1}^{\sigma _{\lfloor \log _bn\rfloor }}b^{\ell _j}\equiv \sum _{i=0}^{\lfloor \log _bn\rfloor }\nu _b(n,i)b^i\equiv n\text { (mod }p\text {)}$
.
$\tau _b(n)\equiv \sum _{j=1}^{\sigma _{\lfloor \log _bn\rfloor }}b^{\ell _j}\equiv \sum _{i=0}^{\lfloor \log _bn\rfloor }\nu _b(n,i)b^i\equiv n\text { (mod }p\text {)}$
.
Let
![]() $x_0=\tau _b(\tilde {x})$
and, for each positive integer
$x_0=\tau _b(\tilde {x})$
and, for each positive integer
![]() $t\leq g$
, let
$t\leq g$
, let
 $$ \begin{align*}x_t=x_{t-1}-b^{\lfloor\log_bx_{t-1}\rfloor}+\sum_{\iota=1}^bb^{\iota\omega+\lfloor\log_bx_{t-1}\rfloor-1}.\end{align*} $$
$$ \begin{align*}x_t=x_{t-1}-b^{\lfloor\log_bx_{t-1}\rfloor}+\sum_{\iota=1}^bb^{\iota\omega+\lfloor\log_bx_{t-1}\rfloor-1}.\end{align*} $$
From this construction,
![]() $s_b(x_t)=s_b(x_{t-1})+b-1$
and
$s_b(x_t)=s_b(x_{t-1})+b-1$
and
for all
![]() $t\leq g$
. It follows that
$t\leq g$
. It follows that
![]() $s_b(x_g)=s_b(x_0)+g(b-1)=s_b(\tilde {x})+g(b-1)$
and
$s_b(x_g)=s_b(x_0)+g(b-1)=s_b(\tilde {x})+g(b-1)$
and
![]() ${x_g\equiv x_0\equiv \tilde {x}\text { (mod }p\text {)}}$
. Lastly, let
${x_g\equiv x_0\equiv \tilde {x}\text { (mod }p\text {)}}$
. Lastly, let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be integers such that
$\beta $
be integers such that
![]() $b^{\alpha \omega }>x_g$
and
$b^{\alpha \omega }>x_g$
and
![]() $b^{\beta \omega }>\tau _b(p)$
. We define
$b^{\beta \omega }>\tau _b(p)$
. We define
 $$ \begin{align*}x=x_g+\sum_{\iota=0}^{h-1}\tau_b(p)\cdot b^{(\iota\beta+\alpha)\omega}.\end{align*} $$
$$ \begin{align*}x=x_g+\sum_{\iota=0}^{h-1}\tau_b(p)\cdot b^{(\iota\beta+\alpha)\omega}.\end{align*} $$
Now,
![]() $s_b(x)=s_b(x_g)+h\cdot s_b(\tau _b(p))=k$
,
$s_b(x)=s_b(x_g)+h\cdot s_b(\tau _b(p))=k$
,
![]() $x\equiv x_g+\sum _{\iota =0}^{h-1}p\cdot b^{(\iota \beta +\alpha )\omega }\equiv -m^{-1}r\text { (mod }p\text {)}$
and since every summand of x is a distinct power of b where the powers differ by at least
$x\equiv x_g+\sum _{\iota =0}^{h-1}p\cdot b^{(\iota \beta +\alpha )\omega }\equiv -m^{-1}r\text { (mod }p\text {)}$
and since every summand of x is a distinct power of b where the powers differ by at least
![]() $\omega $
, we have
$\omega $
, we have
![]() $s_b(mx+r)=s_b(m)\cdot s_b(x)+s_b(r)=s_b(m)\cdot k+s_b(r)=dp$
. Therefore,
$s_b(mx+r)=s_b(m)\cdot s_b(x)+s_b(r)=s_b(m)\cdot k+s_b(r)=dp$
. Therefore,
![]() $mx+r$
is a b-Niven number based on the following observations:
$mx+r$
is a b-Niven number based on the following observations:
-
•
 $mx+r\equiv m(-m^{-1}r)+r\equiv 0\text { (mod }p\text {)}$
;
$mx+r\equiv m(-m^{-1}r)+r\equiv 0\text { (mod }p\text {)}$
; -
•
 $d\mid (mx+r)$
since
$d\mid (mx+r)$
since
 $d\mid m$
and
$d\mid m$
and
 $d\mid r$
by Lemma 2.2;
$d\mid r$
by Lemma 2.2; -
•
 $\gcd (p,d)=1$
since
$\gcd (p,d)=1$
since
 $p>b$
and
$p>b$
and
 $d\mid b-1$
.
$d\mid b-1$
.
Lemma 2.5. Let n be a nonnegative integer. For all nonnegative integers y,
![]() $s_b(yn)=ys_b(n)+z(b-1)$
for some integer z.
$s_b(yn)=ys_b(n)+z(b-1)$
for some integer z.
Proof. Note that for all nonnegative integers n, if
![]() $n=\sum _{i=0}^{\lfloor \log _bn\rfloor }\nu _b(n,i)b^i$
, then
$n=\sum _{i=0}^{\lfloor \log _bn\rfloor }\nu _b(n,i)b^i$
, then
![]() $s_b(n)=\sum _{i=0}^{\lfloor \log _bn\rfloor }\nu _b(n,i)\equiv n\text { (mod }b-1\text {)}$
. Hence,
$s_b(n)=\sum _{i=0}^{\lfloor \log _bn\rfloor }\nu _b(n,i)\equiv n\text { (mod }b-1\text {)}$
. Hence,
![]() $s_b(yn)\equiv yn\equiv ys_b(n)\text { (mod }b-1\text {)}$
.
$s_b(yn)\equiv yn\equiv ys_b(n)\text { (mod }b-1\text {)}$
.
Proposition 2.6. Let
![]() $d=\gcd (s_b(m),s_b(r),b-1)$
. Then there exists a positive multiple
$d=\gcd (s_b(m),s_b(r),b-1)$
. Then there exists a positive multiple
![]() $\overline {m}$
of m such that
$\overline {m}$
of m such that
![]() $\gcd (s_b(\overline {m}),s_b(r))=d$
.
$\gcd (s_b(\overline {m}),s_b(r))=d$
.
Proof. Let
![]() $i_0$
be the smallest nonnegative integer such that
$i_0$
be the smallest nonnegative integer such that
![]() $\nu _b(m,i_0)\neq 0$
. Then there exists a nonnegative integer
$\nu _b(m,i_0)\neq 0$
. Then there exists a nonnegative integer
![]() $a\leq b-1$
such that
$a\leq b-1$
such that
![]() $\nu _b(am,i_0)=\nu _b(a\cdot \nu _b(m,i_0),0)\geq {b}/{2}$
. Next, if
$\nu _b(am,i_0)=\nu _b(a\cdot \nu _b(m,i_0),0)\geq {b}/{2}$
. Next, if
![]() $\nu _b(am,i_0+1)\neq b-1$
, then let
$\nu _b(am,i_0+1)\neq b-1$
, then let
![]() $m'=am$
; otherwise, let
$m'=am$
; otherwise, let
![]() $m'=(b+1)am$
so that
$m'=(b+1)am$
so that
![]() $\nu _b(m',i_0)=\nu _b(am,i_0)\geq {b}/{2}$
and
$\nu _b(m',i_0)=\nu _b(am,i_0)\geq {b}/{2}$
and
Furthermore, define
![]() $m"$
to be a multiple of
$m"$
to be a multiple of
![]() $m'$
such that the leading digit of
$m'$
such that the leading digit of
![]() $m"$
in base-b representation is at least
$m"$
in base-b representation is at least
![]() ${b}/{2}$
, that is,
${b}/{2}$
, that is,
![]() $\nu _b(m",\lfloor \log _bm"\rfloor )\geq {b}/{2}$
. Let
$\nu _b(m",\lfloor \log _bm"\rfloor )\geq {b}/{2}$
. Let
![]() $m^*=b^2m"+m'$
. Then
$m^*=b^2m"+m'$
. Then
![]() $m^*$
is a multiple of m such that
$m^*$
is a multiple of m such that
![]() $\nu _b(m^*,i_0)\geq {b}/{2}$
,
$\nu _b(m^*,i_0)\geq {b}/{2}$
,
![]() $\nu _b(m^*,i_0+1)\neq b-1$
and
$\nu _b(m^*,i_0+1)\neq b-1$
and
![]() $\nu _b(m^*,\lfloor \log _bm^*\rfloor )\geq {b}/{2}$
.
$\nu _b(m^*,\lfloor \log _bm^*\rfloor )\geq {b}/{2}$
.
Let
![]() $x,y,z$
be integers such that
$x,y,z$
be integers such that
![]() $xs_b(r)+ys_b(m)+z(b-1)=d$
. Define
$xs_b(r)+ys_b(m)+z(b-1)=d$
. Define
![]() $y^*$
such that
$y^*$
such that
![]() $m^*=y^*m$
and let
$m^*=y^*m$
and let
![]() $z^*$
be an integer such that
$z^*$
be an integer such that
![]() $s_b(m^*)=y^*s_b(m)+z^*(b-1)$
by Lemma 2.5. Letting
$s_b(m^*)=y^*s_b(m)+z^*(b-1)$
by Lemma 2.5. Letting
![]() $m^{**}=(b^{\lfloor \log _bm^*\rfloor -i_0}+1)m^*$
, we see that
$m^{**}=(b^{\lfloor \log _bm^*\rfloor -i_0}+1)m^*$
, we see that
![]() $\nu _b(m^{**}, \lfloor \log _bm^*\rfloor )=\nu _b(m^*,\lfloor \log _bm^*\rfloor )+\nu _b(m^*,i_0)-b$
and
$\nu _b(m^{**}, \lfloor \log _bm^*\rfloor )=\nu _b(m^*,\lfloor \log _bm^*\rfloor )+\nu _b(m^*,i_0)-b$
and
![]() $\nu _b(m^{**},\lfloor \log _bm^*\rfloor +1)=\nu _b(m^*, i_0+1)+1\leq b-1$
. Hence,
$\nu _b(m^{**},\lfloor \log _bm^*\rfloor +1)=\nu _b(m^*, i_0+1)+1\leq b-1$
. Hence,
![]() $s_b(m^{**})=2s_b(m^*)-(b-1)=2y^*s_b(m)+(2z^*-1)(b-1)$
. By Lemma 2.1, there exist nonnegative integers g and h such that
$s_b(m^{**})=2s_b(m^*)-(b-1)=2y^*s_b(m)+(2z^*-1)(b-1)$
. By Lemma 2.1, there exist nonnegative integers g and h such that
![]() $gz^*+h(2z^*-1)\equiv z\text { (mod }s_b(r)\text {)}$
. Let j be a nonnegative integer such that
$gz^*+h(2z^*-1)\equiv z\text { (mod }s_b(r)\text {)}$
. Let j be a nonnegative integer such that
![]() $gy^*+h(2y^*)+j\equiv y\text { (mod }s_b(r)\text {)}$
. Consider
$gy^*+h(2y^*)+j\equiv y\text { (mod }s_b(r)\text {)}$
. Consider
 $$ \begin{align*} \overline{m}=&\sum_{\iota=0}^{g-1}m^*b^{\iota(\lfloor\log_bm^*\rfloor+1)}+\sum_{\iota=0}^{h-1}m^{**}b^{\iota(\lfloor\log_bm^{**}\rfloor+1)+g(\lfloor\log_bm^*\rfloor+1)}\\ &+\sum_{\iota=0}^{j-1}mb^{\iota(\lfloor\log_bm\rfloor+1)+g(\lfloor\log_bm^*\rfloor+1)+h(\lfloor\log_bm^{**}\rfloor+1)}. \end{align*} $$
$$ \begin{align*} \overline{m}=&\sum_{\iota=0}^{g-1}m^*b^{\iota(\lfloor\log_bm^*\rfloor+1)}+\sum_{\iota=0}^{h-1}m^{**}b^{\iota(\lfloor\log_bm^{**}\rfloor+1)+g(\lfloor\log_bm^*\rfloor+1)}\\ &+\sum_{\iota=0}^{j-1}mb^{\iota(\lfloor\log_bm\rfloor+1)+g(\lfloor\log_bm^*\rfloor+1)+h(\lfloor\log_bm^{**}\rfloor+1)}. \end{align*} $$
By construction,
![]() $\overline {m}$
is a multiple of m and
$\overline {m}$
is a multiple of m and
 $$ \begin{align*} s_b(\overline{m})&=gs_b(m^*)+hs_b(m^{**})+js_b(m)\\ &=g(y^*s_b(m)+z^*(b-1))+h(2y^*s_b(m)+(2z^*-1)(b-1))+js_b(m)\\ &=(gy^*+h(2y^*)+j)s_b(m)+(gz^*+h(2z^*-1))(b-1)\\ &\equiv ys_b(m)+z(b-1)\equiv d\text{ (mod }s_b(r)\text{)}. \end{align*} $$
$$ \begin{align*} s_b(\overline{m})&=gs_b(m^*)+hs_b(m^{**})+js_b(m)\\ &=g(y^*s_b(m)+z^*(b-1))+h(2y^*s_b(m)+(2z^*-1)(b-1))+js_b(m)\\ &=(gy^*+h(2y^*)+j)s_b(m)+(gz^*+h(2z^*-1))(b-1)\\ &\equiv ys_b(m)+z(b-1)\equiv d\text{ (mod }s_b(r)\text{)}. \end{align*} $$
Note that
![]() $d\mid s_b(\overline {m})$
since
$d\mid s_b(\overline {m})$
since
![]() $d\mid s_b(m)$
and
$d\mid s_b(m)$
and
![]() $d\mid b-1$
. Therefore,
$d\mid b-1$
. Therefore,
![]() $\gcd (s_b(\overline {m}),s_b(r))=d$
.
$\gcd (s_b(\overline {m}),s_b(r))=d$
.
Combining Propositions 2.4 and 2.6, we obtain the following theorem.
Theorem 2.7. Let m and r be positive integers. The arithmetic progression
![]() $\mathcal {S}_{m,r}$
contains infinitely many b-Niven numbers.
$\mathcal {S}_{m,r}$
contains infinitely many b-Niven numbers.
Proof. By Proposition 2.6, there exists a multiple
![]() $\overline {m}$
of m such that
$\overline {m}$
of m such that
Hence, by Proposition 2.4,
![]() $\mathcal {S}_{\overline {m},r}$
, and thus
$\mathcal {S}_{\overline {m},r}$
, and thus
![]() $\mathcal {S}_{m,r}$
, contains at least one b-Niven number since
$\mathcal {S}_{m,r}$
, contains at least one b-Niven number since
![]() $\mathcal {S}_{\overline {m},r}$
is a subset of
$\mathcal {S}_{\overline {m},r}$
is a subset of
![]() $\mathcal {S}_{m,r}$
. Let this b-Niven number be
$\mathcal {S}_{m,r}$
. Let this b-Niven number be
![]() $\eta m+r$
for some nonnegative integer
$\eta m+r$
for some nonnegative integer
![]() $\eta $
. Applying the same argument on the arithmetic progression,
$\eta $
. Applying the same argument on the arithmetic progression,
![]() $\mathcal {S}_{m,(\eta +1)m+r}$
yields another b-Niven number and our proof is complete by induction.
$\mathcal {S}_{m,(\eta +1)m+r}$
yields another b-Niven number and our proof is complete by induction.