Hostname: page-component-66644f4456-vjjx6 Total loading time: 0 Render date: 2025-02-12T18:37:21.474Z Has data issue: true hasContentIssue false
  • English
  • Français

EMBEDDINGS OF FREE TOPOLOGICAL VECTOR SPACES

Part of: Fairly general properties Special properties Topological linear spaces and related structures

Published online by Cambridge University Press:  20 August 2019

ARKADY LEIDERMAN Open the ORCID record for ARKADY LEIDERMAN [Opens in a new window]  and
SIDNEY A. MORRIS Open the ORCID record for SIDNEY A. MORRIS [Opens in a new window]
ARKADY LEIDERMAN
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, Beer Sheva, P.O.B. 653, Israel email arkady@math.bgu.ac.il
SIDNEY A. MORRIS*
Affiliation:
Centre for Informatics and Applied Optimization, Federation University, Australia, P.O.B. 663, Ballarat, Victoria, 3353, Australia Department of Mathematics and Statistics, La Trobe University, Melbourne, Victoria, 3086, Australia email morris.sidney@gmail.com
*
✉morris.sidney@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is proved that the free topological vector space 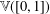$\mathbb{V}([0,1])$ contains an isomorphic copy of the free topological vector space 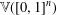$\mathbb{V}([0,1]^{n})$ for every finite-dimensional cube 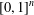$[0,1]^{n}$, thereby answering an open question in the literature. We show that this result cannot be extended from the closed unit interval 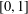$[0,1]$ to general metrisable spaces. Indeed, we prove that the free topological vector space 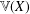$\mathbb{V}(X)$ does not even have a vector subspace isomorphic as a topological vector space to $\mathbb{V}(X\oplus X)$, where 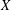$X$ is a Cook continuum, which is a one-dimensional compact metric space. This is also shown to be the case for a rigid Bernstein set, which is a zero-dimensional subspace of the real line.

Keywords

free topological vector spacefree locally convex spacevariety of locally convex spacesembeddingCook continuumrigid Bernstein set

MSC classification

Primary: 46A03: General theory of locally convex spaces
Secondary: 54D50: $k$-spaces 54F15: Continua and generalizations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 2 , April 2020 , pp. 311 - 324
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

References

Arhangel’skii, A. V., Topological Spaces and Continuous Mappings. Remarks on Topological Groups (Moscow University, Moscow, Russia, 1969) (in Russian).Google Scholar
Arkhangel’skii, A. V., Topological Function Spaces (Kluwer Academic Press, Dordrecht–Boston–London, 1992).Google Scholar
Baars, J., ‘Equivalence of certain free topological groups’, Comment. Math. Univ. Carolin. 33 (1992), 125–130.Google Scholar
Brooks, M. S., Morris, S. A. and Saxon, S. A., ‘Generating varieties of topological groups’, Proc. Edinb. Math. Soc. (2) 18 (1973), 191–197.Google Scholar
Cook, H., ‘Continua which admit only the identity mapping onto non-degenerate subcontinua’, Fund. Math. 60 (1967), 241–249.Google Scholar
Diestel, J., Morris, S. A. and Saxon, S. A., ‘Varieties of linear topological spaces’, Trans. Amer. Math. Soc. 172 (1972), 207–230.Google Scholar
Gabriyelyan, S. S. and Morris, S. A., ‘Free topological vector spaces’, Topology Appl. 223 (2017), 30–49.Google Scholar
Gabriyelyan, S. S. and Morris, S. A., ‘Embedding into free topological vector spaces on compact metrizable spaces’, Topology Appl. 233 (2018), 33–43.Google Scholar
Gartside, P. and Feng, Z., ‘Spaces l-dominated by I or R’, Topology Appl. 219 (2017), 1–8.Google Scholar
Hardy, J. P. L., Morris, S. A. and Thompson, H. B., ‘Applications of the Stone–C̆ech compactification to free topological groups’, Proc. Amer. Math. Soc. 55 (1976), 160–164.Google Scholar
Hart, K. P., Nagata, J. and Vaughan, J. E., Encyclopedia of General Topology (Elsevier Science B.V., Amsterdam, 2004).Google Scholar
Joiner, C., ‘Free topological groups and dimension’, Trans. Amer. Math. Soc. 220 (1976), 401–418.Google Scholar
Kawamura, K. and Leiderman, A., ‘Linear continuous surjections of C p(X)-spaces over compacta’, Topology Appl. 227 (2017), 135–145.Google Scholar
Krupski, M. and Marciszewski, W., ‘A metrizable X with C p(X) not homeomorphic to C p(X) × C p(X)’, Israel J. Math. 214 (2016), 245–258.Google Scholar
Krupski, M., Leiderman, A. and Morris, S. A., ‘Embedding of the free abelian topological group A (X⊕X) into A (X)’, Mathematika 65 (2019), 708–718.Google Scholar
Kuratowski, K., Topology, Vol II (Academic Press, New York–London; PWN, Warsaw, 1968).Google Scholar
Leiderman, A., Levin, M. and Pestov, V., ‘On linear continuous open surjections of the spaces C p(X)’, Topology Appl. 81 (1997), 269–279.Google Scholar
Leiderman, A., Morris, S. A. and Pestov, V., ‘The free abelian topological group and the free locally convex space on the unit interval’, J. Lond. Math. Soc. (2) 56 (1997), 529–538.Google Scholar
Levin, M., ‘A property of C p[0, 1]’, Trans. Amer. Math. Soc. 363 (2011), 2295–2304.Google Scholar
Mac Lane, S., Categories for the Working Mathematician (Springer, Berlin, 1971).Google Scholar
van Mill, J., ‘The infinite-dimensional topology of function spaces’, in: Proc. Int. Conf. Categorical Topology, North-Holland Mathematical Library, 64 (Amsterdam, 2001).Google Scholar
Morris, S. A., ‘Varieties of topological groups’, Bull. Aust. Math. Soc. 1 (1969), 145–160.Google Scholar
Morris, S. A., ‘Varieties of topological groups. A survey’, Colloq. Math. 46 (1982), 147–165.10.4064/cm-46-2-147-165Google Scholar
Morris, S. A. and Diestel, J., ‘Remarks on varieties of locally convex linear topological spaces’, J. Lond. Math. Soc. (2) 8 (1974), 271–278.10.1112/jlms/s2-8.2.271Google Scholar
Nickolas, P., ‘Subgroups of the free topological group on [0, 1]’, J. Lond. Math. Soc. (2) 12 (1976), 199–205.10.1112/jlms/s2-12.2.199Google Scholar
Pestov, V., ‘The coincidence of the dimension dim of ℓ-equivalent topological spaces’, Soviet Math. Dokl 28 (1982), 380–383.Google Scholar
Pol, R., ‘On metrizable E with C p(E) ≇ C p(E) × C p(E)’, Mathematika 42 (1995), 49–55.Google Scholar
Sipacheva, O. V., ‘The topology of free topological groups’, J. Math. Sci. 131 (2005), 5765–5838.Google Scholar
Sipacheva, O. V., ‘Free Boolean topological groups’, Axioms 4 (2015), 492–517.Google Scholar