Hostname: page-component-6dbcb7884d-wnk8j Total loading time: 0 Render date: 2025-02-13T15:55:00.927Z Has data issue: false hasContentIssue false
  • English
  • Français

ELEMENTARY PROOFS OF THE DIAMETER BOUNDS FOR POWER GRAPHS

Part of: Graph theory Representation theory of groups

Published online by Cambridge University Press:  11 February 2025

MARCO BARBIERI Open the ORCID record for MARCO BARBIERI [Opens in a new window]  and
KAMILLA REKVÉNYI Open the ORCID record for KAMILLA REKVÉNYI [Opens in a new window]
MARCO BARBIERI
Affiliation:
Dipartimento di Matematica ‘Felice Casorati’, University of Pavia, Via Ferrata 5, 27100 Pavia, Italy e-mail: marco.barbieri07@universitadipavia.it
KAMILLA REKVÉNYI*
Affiliation:
Department of Mathematics, University of Manchester, M13 9PL Manchester, UK and Heilbronn Institute for Mathematical Research, BS8 1UG Bristol, UK
*
e-mail: kamilla.rekvenyi@manchester.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a simplified version of the proofs that, outside of their isolated vertices, the complement of the enhanced power graph and of the power graph are connected and have diameter at most 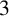$3$.

Keywords

power graphenhanced power graphconnecteddiameter

MSC classification

Primary: 20D60: Arithmetic and combinatorial problems
Secondary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 4
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdollahi, A. and Mohammadi Hassanabadi, A., ‘Noncyclic graph of a group’, Comm. Algebra 35(7) (2007), 2057–2081.CrossRefGoogle Scholar
Cameron, P. J., ‘Graphs defined on groups’, Int. J. Group Theory 11(2) (2022), 53–107.Google Scholar
Chakrabarty, I., Ghosh, S. and Sen, M. K., ‘Undirected power graphs of semigroups’, Semigroup Forum 78(3) (2023), 410–426.CrossRefGoogle Scholar
Freedman, S. D., ‘The non-commuting, non-generating graph of a non-simple group’, Algebr. Comb. 6(5) (2023), 1395–1418.Google Scholar
Grazian, V., Lucchini, A. and Monetta, C., ‘Group nilpotency from a graph point of view’, Int. J. Group Theory 13(4) (2024), 351–367.Google Scholar
Lucchini, A. and Nemmi, D., ‘Semiregularity and connectivity of the non- $\mathfrak{F}$ graph of a finite group’, J. Algebra Appl. 22(9) (2023), Article no. 2350190.CrossRefGoogle Scholar
Ma, X., Doostabadi, A. and Wang, K., ‘Notes on the diameter of the complement of the power graph of a finite group’, Ars Math. Contemp., to appear.Google Scholar
Rekvényi, K., ‘On the orbital diameter of groups of diagonal type’, J. Combin. Theory Ser. A 190 (2022), Article no. 105636.CrossRefGoogle Scholar