Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-11T03:12:16.714Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DUAL STRUCTURE OF CROSSED PRODUCT ${C}^{\ast } $-ALGEBRAS WITH FINITE GROUPS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  18 January 2013

FIRUZ KAMALOV
FIRUZ KAMALOV*
Affiliation:
Mathematics Department, Canadian University of Dubai, Dubai, UAE email firuz@cud.ac.ae
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the space of irreducible representations of a crossed product ${C}^{\ast } $-algebra 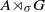${\mathop{A\rtimes }\nolimits}_{\sigma } G$, where 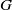$G$ is a finite group. We construct a space $\widetilde {\Gamma } $ which consists of pairs of irreducible representations of 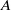$A$ and irreducible projective representations of subgroups of 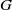$G$. We show that there is a natural action of 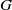$G$ on 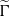$\widetilde {\Gamma } $ and that the orbit space $G\setminus \widetilde {\Gamma } $ corresponds bijectively to the dual of 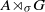${\mathop{A\rtimes }\nolimits}_{\sigma } G$.

Keywords

irreducible representationscrossed product C∗-algebrafinite groupsdual structure

MSC classification

Secondary: 46L55: Noncommutative dynamical systems 46L05: General theory of $C^*$-algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 2 , October 2013 , pp. 243 - 249
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Arias, A. and Latremoliere, F., ‘Irreducible representations of ${C}^{\ast } $-crossed products by finite groups’, J. Ramanujan Math. Soc. 25 (2) (2010), 193–231.Google Scholar
Echterhoff, S. and Williams, D., ‘Inducing primitive ideals’, Trans. Amer. Math. Soc. 360 (11) (2008), 6113–6129.CrossRefGoogle Scholar
Hoegh-Krohn, R., Landstad, M. and Stormer, E., ‘Compact ergodic groups of automorphisms’, Ann. of Math. (2) 114 (1) (1981), 75–86.CrossRefGoogle Scholar
Mackey, G., ‘Unitary representations of group extensions, I’, Acta Math. 99 (1958), 265–311.CrossRefGoogle Scholar
Rieffel, M., ‘Actions of finite groups on ${C}^{\ast } $-algebras’, Math. Scand. 47 (1980), 176–257.CrossRefGoogle Scholar
Takesaki, M., ‘Covariant representations of ${C}^{\ast } $-algebras and their locally compact automorphism groups’, Acta Math. 119 (1967), 273–303.CrossRefGoogle Scholar
Williams, D., ‘The topology on the primitive ideal space of transformation group ${C}^{\ast } $-algebras and CCR transformation group ${C}^{\ast } $-algebras’, Trans. Amer. Math. Soc. 266 (1981), 335–359.Google Scholar