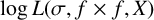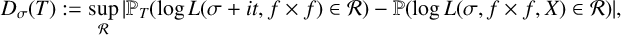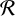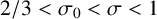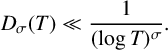1 Introduction
Let
![]() $X(p)$
be independent random variables uniformly distributed on the unit circle, where p runs over the prime numbers. The random Euler product of the Riemann zeta-function is defined by
$X(p)$
be independent random variables uniformly distributed on the unit circle, where p runs over the prime numbers. The random Euler product of the Riemann zeta-function is defined by
![]() $\zeta (\sigma ,X) = \prod _p (1- ({X(p)}/{p^{\sigma }}))^{-1}$
. The behaviour of
$\zeta (\sigma ,X) = \prod _p (1- ({X(p)}/{p^{\sigma }}))^{-1}$
. The behaviour of
![]() $p^{-it}$
is almost like the independent random variables
$p^{-it}$
is almost like the independent random variables
![]() $X(p)$
, which indicates that
$X(p)$
, which indicates that
![]() $\zeta (\sigma , X)$
should be a good model for the Riemann zeta-function.
$\zeta (\sigma , X)$
should be a good model for the Riemann zeta-function.
Bohr and Jessen [Reference Bohr and Jessen1] suggested that
![]() $\log \zeta (\sigma +it)$
converges in distribution to
$\log \zeta (\sigma +it)$
converges in distribution to
![]() $\log \zeta (\sigma , X)$
for
$\log \zeta (\sigma , X)$
for
![]() $\sigma> 1/2$
. In 1994, Harman and Matsumoto [Reference Harman and Matsumoto4] studied the discrepancy between the distribution of the Riemann zeta-function and that of its random model. For fixed
$\sigma> 1/2$
. In 1994, Harman and Matsumoto [Reference Harman and Matsumoto4] studied the discrepancy between the distribution of the Riemann zeta-function and that of its random model. For fixed
![]() $\sigma $
with
$\sigma $
with
![]() $1/2 <\sigma \leq 1$
and any
$1/2 <\sigma \leq 1$
and any
![]() $\varepsilon>0$
, they proved that the discrepancy
$\varepsilon>0$
, they proved that the discrepancy
where the supremum is taken over rectangles
![]() $\mathcal {R}$
with sides parallel to the coordinate axes, satisfies the bound
$\mathcal {R}$
with sides parallel to the coordinate axes, satisfies the bound
![]() $D_{\sigma , \zeta } (T) \ll {1}/{(\log T)^{(4\sigma -2)/(21+8\sigma )-\varepsilon }}$
. Here,
$D_{\sigma , \zeta } (T) \ll {1}/{(\log T)^{(4\sigma -2)/(21+8\sigma )-\varepsilon }}$
. Here,
![]() $\mathbb {P}_T (f(t) \in \mathcal {R}) := T^{-1} \text {meas}\{T \leq t \leq 2T: f(t) \in \mathcal {R}\}$
. Lamzouri et al. [Reference Lamzouri, Lester and Radziwiłł8] improved the result by showing that
$\mathbb {P}_T (f(t) \in \mathcal {R}) := T^{-1} \text {meas}\{T \leq t \leq 2T: f(t) \in \mathcal {R}\}$
. Lamzouri et al. [Reference Lamzouri, Lester and Radziwiłł8] improved the result by showing that
![]() $D_{\sigma , \zeta } (T) \ll {1}/{(\log T)^{\sigma }}$
.
$D_{\sigma , \zeta } (T) \ll {1}/{(\log T)^{\sigma }}$
.
Dong et al. [Reference Dong, Wang and Zhang3] analysed the discrepancy between the distribution of values of Dirichlet L-functions and the distribution of values of random models for Dirichlet L-functions in the q-aspect. Lee [Reference Lee9] investigated the upper bound on the discrepancy between the joint distribution of L-functions on the line
![]() $\sigma = 1/2 + 1/G(T), t \in [T, 2T]$
, and that of their random models, where
$\sigma = 1/2 + 1/G(T), t \in [T, 2T]$
, and that of their random models, where
![]() $\log \log T \leq G(T) \leq (\log T)/(\log \log T)^2$
.
$\log \log T \leq G(T) \leq (\log T)/(\log \log T)^2$
.
Let f be a primitive holomorphic cusp form of weight k for
![]() ${\mathrm {SL}}_2(\mathbb {Z})$
. The normalised Fourier expansion at the cusp
${\mathrm {SL}}_2(\mathbb {Z})$
. The normalised Fourier expansion at the cusp
![]() $\infty $
is
$\infty $
is
![]() $f(z)=\sum _{n \geq 1}\lambda _f(n)n^{{(k-1)}/{2}}e^{2\pi inz}$
, where
$f(z)=\sum _{n \geq 1}\lambda _f(n)n^{{(k-1)}/{2}}e^{2\pi inz}$
, where
![]() $\lambda _f(n) \in \mathbb {R}$
,
$\lambda _f(n) \in \mathbb {R}$
,
![]() $n = 1, 2, \ldots, $
are normalised eigenvalues of Hecke operators
$n = 1, 2, \ldots, $
are normalised eigenvalues of Hecke operators
![]() $T(n)$
with
$T(n)$
with
![]() $\lambda _f(1)=1$
, that is,
$\lambda _f(1)=1$
, that is,
![]() $T(n)f=\lambda _f(n)f$
.
$T(n)f=\lambda _f(n)f$
.
According to Deligne [Reference Deligne2], for all prime numbers p, there are complex numbers
![]() $\alpha _f(p)$
and
$\alpha _f(p)$
and
![]() $\beta _f(p)$
, satisfying
$\beta _f(p)$
, satisfying
 $$ \begin{align} \left\{\! \begin{aligned} & |\alpha_f(p)| = \alpha_f(p)\beta_f(p) = 1, \\ & \lambda_f(p^{\nu}) = \sum_{0\leq j \leq \nu} \alpha_f(p)^{\nu -j} \beta_f(p)^{\,j} \quad (\nu \geq 1). \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{\! \begin{aligned} & |\alpha_f(p)| = \alpha_f(p)\beta_f(p) = 1, \\ & \lambda_f(p^{\nu}) = \sum_{0\leq j \leq \nu} \alpha_f(p)^{\nu -j} \beta_f(p)^{\,j} \quad (\nu \geq 1). \end{aligned} \right. \end{align} $$
The function
![]() $\lambda _f(n)$
is multiplicative. Moreover,
$\lambda _f(n)$
is multiplicative. Moreover,
![]() $\lambda _f(p)$
is real and satisfies Deligne’s inequality
$\lambda _f(p)$
is real and satisfies Deligne’s inequality
![]() $|\lambda _f(n)| \leq d(n)$
for
$|\lambda _f(n)| \leq d(n)$
for
![]() $n \geq 1$
, where
$n \geq 1$
, where
![]() $d(n)$
is the divisor function. In particular,
$d(n)$
is the divisor function. In particular,
![]() $|\lambda _f(p)| \leq 2$
. For
$|\lambda _f(p)| \leq 2$
. For
![]() $\mathrm {Re}\, s>1$
, the L-function attached to f is defined by
$\mathrm {Re}\, s>1$
, the L-function attached to f is defined by
 $$ \begin{align*} L(s, f) = \sum_{n \geq 1} \frac{\lambda_f(n)}{n^s} = \prod_p \bigg(1 - \frac{\alpha_f(p)}{p^s}\bigg)^{-1} \bigg(1 - \frac{\beta_f(p)}{p^s}\bigg)^{-1}. \end{align*} $$
$$ \begin{align*} L(s, f) = \sum_{n \geq 1} \frac{\lambda_f(n)}{n^s} = \prod_p \bigg(1 - \frac{\alpha_f(p)}{p^s}\bigg)^{-1} \bigg(1 - \frac{\beta_f(p)}{p^s}\bigg)^{-1}. \end{align*} $$
For
![]() $\mathrm {Re}\, s>1$
, the Rankin–Selberg L-function associated to f is defined by
$\mathrm {Re}\, s>1$
, the Rankin–Selberg L-function associated to f is defined by
 $$ \begin{align*} L(s, f \times f) := \prod_p \bigg(1 - \frac{\alpha_f(p)^2}{p^s}\bigg)^{-1} \bigg(1 - \frac{\beta_f(p)^2}{p^s}\bigg)^{-1} \bigg(1 - \frac{1}{p^s}\bigg)^{-2} = \zeta(2s) \sum_{n = 1}^{\infty} \frac{\lambda_f(n)^2}{n^s}. \end{align*} $$
$$ \begin{align*} L(s, f \times f) := \prod_p \bigg(1 - \frac{\alpha_f(p)^2}{p^s}\bigg)^{-1} \bigg(1 - \frac{\beta_f(p)^2}{p^s}\bigg)^{-1} \bigg(1 - \frac{1}{p^s}\bigg)^{-2} = \zeta(2s) \sum_{n = 1}^{\infty} \frac{\lambda_f(n)^2}{n^s}. \end{align*} $$
According to [Reference Iwaniec and Kowalski6], for
![]() $\mathrm {Re} s>1$
,
$\mathrm {Re} s>1$
,
 $$ \begin{align*} \log L(s, f \times f) = \sum_{n=2}^{\infty} \frac{\Lambda_{f \times f}(n)}{n^s \log n}, \end{align*} $$
$$ \begin{align*} \log L(s, f \times f) = \sum_{n=2}^{\infty} \frac{\Lambda_{f \times f}(n)}{n^s \log n}, \end{align*} $$
where
 $$ \begin{align*}\Lambda_{f \times f}(n) := \begin{cases} |\alpha_f(p)^{\nu} + \beta_f(p)^{\nu}|^2 \log p & \text{for } n = p^{\nu}, \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*}\Lambda_{f \times f}(n) := \begin{cases} |\alpha_f(p)^{\nu} + \beta_f(p)^{\nu}|^2 \log p & \text{for } n = p^{\nu}, \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
For automorphic L-functions, from [Reference Lü10],
 $$ \begin{align} \sum_{p \leq x} \lambda_f^4(p) \sim C_f \frac{x}{\log x}. \end{align} $$
$$ \begin{align} \sum_{p \leq x} \lambda_f^4(p) \sim C_f \frac{x}{\log x}. \end{align} $$
Recently, Xiao and Zhai [Reference Xiao and Zhai12] studied the discrepancy between the distributions of
![]() $\log L(\sigma +it,f)$
and its corresponding random variable
$\log L(\sigma +it,f)$
and its corresponding random variable
![]() $\log L(\sigma , f, X)$
. In this article, we investigate the discrepancy between the distribution of the random variable
$\log L(\sigma , f, X)$
. In this article, we investigate the discrepancy between the distribution of the random variable
![]() $\log L (\sigma , f \times f, X)$
and that of
$\log L (\sigma , f \times f, X)$
and that of
![]() $\log L(\sigma +it, f \times f)$
. Define the Euler product
$\log L(\sigma +it, f \times f)$
. Define the Euler product
 $$ \begin{align*} L(\sigma, f \times f, X) = \prod_p \bigg(1 - \frac{\alpha_f(p)^2 X(p)}{p^{\sigma}}\bigg)^{-1} \bigg(1 - \frac{\beta_f(p)^2 X(p)}{p^{\sigma}}\bigg)^{-1} \bigg(1 - \frac{X(p)}{p^{\sigma}}\bigg)^{-2}, \end{align*} $$
$$ \begin{align*} L(\sigma, f \times f, X) = \prod_p \bigg(1 - \frac{\alpha_f(p)^2 X(p)}{p^{\sigma}}\bigg)^{-1} \bigg(1 - \frac{\beta_f(p)^2 X(p)}{p^{\sigma}}\bigg)^{-1} \bigg(1 - \frac{X(p)}{p^{\sigma}}\bigg)^{-2}, \end{align*} $$
which converges almost surely for
![]() $\sigma> \tfrac 12$
. Consider
$\sigma> \tfrac 12$
. Consider
where the supremum is taken over rectangles
![]() $\mathcal {R}$
with sides parallel to the coordinate axes. We prove the following theorem.
$\mathcal {R}$
with sides parallel to the coordinate axes. We prove the following theorem.
Theorem 1.1. Let
![]() $T>3$
and
$T>3$
and
![]() $2/3 <\sigma _0 < \sigma < 1$
, where T and
$2/3 <\sigma _0 < \sigma < 1$
, where T and
![]() $\sigma _0$
are fixed. Then,
$\sigma _0$
are fixed. Then,
 $$ \begin{align*} D_{\sigma} (T) \ll \frac{1}{(\log T)^{\sigma}}, \end{align*} $$
$$ \begin{align*} D_{\sigma} (T) \ll \frac{1}{(\log T)^{\sigma}}, \end{align*} $$
where the implied constant depends on f and
![]() $\sigma $
.
$\sigma $
.
The proof follows the method in [Reference Lamzouri, Lester and Radziwiłł8]. The range of
![]() $\sigma $
depends on the zero density theorem of
$\sigma $
depends on the zero density theorem of
![]() $L(s,f\times f)$
and
$L(s,f\times f)$
and
![]() $L(s, \mathrm {sym}^2f)$
by noticing that
$L(s, \mathrm {sym}^2f)$
by noticing that
![]() $L(s, f \times f) = \zeta (s) L(s, \mathrm {sym}^2f)$
. Unfortunately, the zero density of
$L(s, f \times f) = \zeta (s) L(s, \mathrm {sym}^2f)$
. Unfortunately, the zero density of
![]() $L(s, \mathrm {sym}^2f)$
can only be obtained nontrivially when
$L(s, \mathrm {sym}^2f)$
can only be obtained nontrivially when
![]() $2/3 < \sigma \leq 1$
(see [Reference Huang, Zhai and Zhang5]).
$2/3 < \sigma \leq 1$
(see [Reference Huang, Zhai and Zhang5]).
2 Preliminaries
This section gathers several preliminary results. Since several proofs are essentially the same as those in [Reference Lamzouri, Lester and Radziwiłł8], we omit their details. For any prime number p and integer
![]() $\nu>0$
, we define
$\nu>0$
, we define
![]() $b_f(p^{\nu }) = |\alpha _f(p)^{\nu } + \beta _f(p)^{\nu }|^2$
. Thanks to (1.1),
$b_f(p^{\nu }) = |\alpha _f(p)^{\nu } + \beta _f(p)^{\nu }|^2$
. Thanks to (1.1),
From probability theory, if the characteristic functions of two real-valued random variables are close, then the corresponding probability distributions are also close. The key to proving Theorem 1.1 is to demonstrate that the joint distribution characteristic function of
![]() $\mathrm {Re} \log L(\sigma + it)$
and
$\mathrm {Re} \log L(\sigma + it)$
and
![]() $\mathrm {Im} \log L(\sigma + it)$
can be well estimated. For u,
$\mathrm {Im} \log L(\sigma + it)$
can be well estimated. For u,
![]() $v \in \mathbb {R}$
, we define
$v \in \mathbb {R}$
, we define
 $$ \begin{align} \Phi_{\sigma, T}(u,v) := \frac{1}{T} \int_T^{2T} \exp (iu\,\mathrm{Re} \log L(\sigma + it, f \times f) + iv\,\mathrm{Im} \log L(\sigma + it, f \times f))\,dt \end{align} $$
$$ \begin{align} \Phi_{\sigma, T}(u,v) := \frac{1}{T} \int_T^{2T} \exp (iu\,\mathrm{Re} \log L(\sigma + it, f \times f) + iv\,\mathrm{Im} \log L(\sigma + it, f \times f))\,dt \end{align} $$
and
Lemma 2.1 [Reference Lamzouri7, Lemma 4.3].
Let
![]() $y>2$
and
$y>2$
and
![]() $|t|\geq y+3$
be real numbers. Let
$|t|\geq y+3$
be real numbers. Let
![]() $\tfrac 12< \sigma _0 < \sigma \leq 1$
and suppose that the rectangle
$\tfrac 12< \sigma _0 < \sigma \leq 1$
and suppose that the rectangle
![]() $\{s: \sigma _0 < \mathrm {Re} (s) \leq 1, |\mathrm {Im} (s) - t|\leq y+2\}$
does not contain zeros of
$\{s: \sigma _0 < \mathrm {Re} (s) \leq 1, |\mathrm {Im} (s) - t|\leq y+2\}$
does not contain zeros of
![]() $L(s, f \times f)$
. Then,
$L(s, f \times f)$
. Then,
 $$ \begin{align*} \log L(s, f \times f) = \sum_{p^{\nu} \leq y} \frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma+it)}} + O\bigg(\frac{\log |t|}{(\sigma_1 - \sigma_0)^2} y^{\sigma_1 - \sigma}\bigg), \end{align*} $$
$$ \begin{align*} \log L(s, f \times f) = \sum_{p^{\nu} \leq y} \frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma+it)}} + O\bigg(\frac{\log |t|}{(\sigma_1 - \sigma_0)^2} y^{\sigma_1 - \sigma}\bigg), \end{align*} $$
where
![]() $\sigma _1 = \min (\sigma _0 + {1}/{\log y}, {(\sigma + \sigma _0)}/{2})$
.
$\sigma _1 = \min (\sigma _0 + {1}/{\log y}, {(\sigma + \sigma _0)}/{2})$
.
Lemma 2.2. Define
![]() $N(\sigma _0,T)$
as the number of zeros
$N(\sigma _0,T)$
as the number of zeros
![]() $\rho _f = \beta _f + i \gamma _f$
of
$\rho _f = \beta _f + i \gamma _f$
of
![]() $L(s, f \times f)$
with
$L(s, f \times f)$
with
![]() $\sigma _0 \leq \beta _f \leq 1$
and
$\sigma _0 \leq \beta _f \leq 1$
and
![]() $|\gamma _f| \leq T$
. Then,
$|\gamma _f| \leq T$
. Then,
 $$ \begin{align*} N(\sigma_0,T) = \begin{cases} T^{{5(1-\sigma_0)}/{(3-2\sigma_0)}+\epsilon} & \text{for } 1/2 < \sigma_0 < 23/32, \\ T^{{26(1-\sigma_0)}/{(11-4\sigma_0)}+\epsilon} & \text{for } 23/32 \leq \sigma_0 < 3/4, \\ T^{{2(1-\sigma_0)}/{\sigma_0}+\epsilon} & \text{for } 3/4 \leq \sigma_0 < 1. \end{cases} \end{align*} $$
$$ \begin{align*} N(\sigma_0,T) = \begin{cases} T^{{5(1-\sigma_0)}/{(3-2\sigma_0)}+\epsilon} & \text{for } 1/2 < \sigma_0 < 23/32, \\ T^{{26(1-\sigma_0)}/{(11-4\sigma_0)}+\epsilon} & \text{for } 23/32 \leq \sigma_0 < 3/4, \\ T^{{2(1-\sigma_0)}/{\sigma_0}+\epsilon} & \text{for } 3/4 \leq \sigma_0 < 1. \end{cases} \end{align*} $$
Proof. Here,
![]() $L(s, f \times f)$
can be written as
$L(s, f \times f)$
can be written as
![]() $L(s, f \times f) = \zeta (s) L(s, \mathrm {sym}^2f)$
. The result is easily obtained from the zero density of the Riemann zeta-function [Reference Ye and Zhang13] and symmetric square L-functions [Reference Huang, Zhai and Zhang5].
$L(s, f \times f) = \zeta (s) L(s, \mathrm {sym}^2f)$
. The result is easily obtained from the zero density of the Riemann zeta-function [Reference Ye and Zhang13] and symmetric square L-functions [Reference Huang, Zhai and Zhang5].
Lemma 2.3. Let
![]() $2/3 < \sigma <1$
and
$2/3 < \sigma <1$
and
![]() $3 \leq Y \leq T/2$
. Then, for all
$3 \leq Y \leq T/2$
. Then, for all
![]() $t \in [T, 2T]$
,
$t \in [T, 2T]$
,
 $$ \begin{align*} \log L(s, f \times f) = \sum_{p^{\nu} \leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma +it)}} + O_f(Y^{-{(\sigma-2/3)}/{2}}\log^3 T) \end{align*} $$
$$ \begin{align*} \log L(s, f \times f) = \sum_{p^{\nu} \leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma +it)}} + O_f(Y^{-{(\sigma-2/3)}/{2}}\log^3 T) \end{align*} $$
except for a set
![]() $\mathcal {D}(T)$
with
$\mathcal {D}(T)$
with
![]() $\text {meas}(\mathcal {D}(T)) \ll _f T^{{(10/3-5/2\sigma )}/{(7/3-\sigma )}+\epsilon }Y$
.
$\text {meas}(\mathcal {D}(T)) \ll _f T^{{(10/3-5/2\sigma )}/{(7/3-\sigma )}+\epsilon }Y$
.
Proof. Take
![]() $\sigma _0 = \tfrac 12 (\tfrac 23 + \sigma )$
in Lemma 2.1. The result follows easily from Lemma 2.2.
$\sigma _0 = \tfrac 12 (\tfrac 23 + \sigma )$
in Lemma 2.1. The result follows easily from Lemma 2.2.
The details of the next three results can be found in [Reference Xiao and Zhai12].
Lemma 2.4. Let
![]() $2/3 < \sigma <1$
,
$2/3 < \sigma <1$
,
![]() $128 \leq y \leq z$
and
$128 \leq y \leq z$
and
![]() $\{b(p)\}$
be any real sequence with
$\{b(p)\}$
be any real sequence with
![]() $|b(p)| \leq 4$
. For any positive integer
$|b(p)| \leq 4$
. For any positive integer
![]() $k \leq {\log T}/{20 \log z}$
,
$k \leq {\log T}/{20 \log z}$
,
 $$ \begin{align*} \frac{1}{T} \int_{T}^{2T} \bigg| \sum_{y \leq p \leq z} \frac{b(p)}{p^{\sigma +it}} \bigg|^{2k} \,dt \ll k! \bigg(\sum_{y \leq p \leq z} \frac{(b(p))^2}{p^{2 \sigma}}\bigg)^k + T^{-{1}/{3}}. \end{align*} $$
$$ \begin{align*} \frac{1}{T} \int_{T}^{2T} \bigg| \sum_{y \leq p \leq z} \frac{b(p)}{p^{\sigma +it}} \bigg|^{2k} \,dt \ll k! \bigg(\sum_{y \leq p \leq z} \frac{(b(p))^2}{p^{2 \sigma}}\bigg)^k + T^{-{1}/{3}}. \end{align*} $$
Moreover,
 $$ \begin{align*} \mathbb{E}\bigg ( \bigg|\sum_{y \leq p \leq z} \frac{b(p)X(p)}{p^{\sigma}} \bigg|^{2k}\bigg) \ll k! \bigg(\sum_{y \leq p \leq z} \frac{(b(p))^2}{p^{2\sigma}}\bigg)^k. \end{align*} $$
$$ \begin{align*} \mathbb{E}\bigg ( \bigg|\sum_{y \leq p \leq z} \frac{b(p)X(p)}{p^{\sigma}} \bigg|^{2k}\bigg) \ll k! \bigg(\sum_{y \leq p \leq z} \frac{(b(p))^2}{p^{2\sigma}}\bigg)^k. \end{align*} $$
Proposition 2.5. Let
![]() ${2}/{3} < \sigma < 1$
and
${2}/{3} < \sigma < 1$
and
![]() $Y = (\log T)^A$
for a fixed
$Y = (\log T)^A$
for a fixed
![]() $A \geq 1$
. There exist
$A \geq 1$
. There exist
![]() $a_1 = a_1(\sigma , A)>0$
and
$a_1 = a_1(\sigma , A)>0$
and
![]() $a_1' = a_1'(\sigma , A)>0$
such that
$a_1' = a_1'(\sigma , A)>0$
such that
 $$ \begin{align*} \mathbb{P}_T\bigg(\bigg|\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma+it)}}\bigg| \geq \frac{(\log T)^{1-\sigma}}{\log \log T}\bigg) \ll \exp \bigg(-a_1 \frac{\log T}{\log \log T}\bigg) \end{align*} $$
$$ \begin{align*} \mathbb{P}_T\bigg(\bigg|\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma+it)}}\bigg| \geq \frac{(\log T)^{1-\sigma}}{\log \log T}\bigg) \ll \exp \bigg(-a_1 \frac{\log T}{\log \log T}\bigg) \end{align*} $$
and
 $$ \begin{align*} \mathbb{P}\bigg(\bigg|\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}}\bigg| \geq \frac{(\log T)^{1-\sigma}}{\log \log T}\bigg) \ll \exp \bigg(-a_1' \frac{\log T}{\log \log T}\bigg). \end{align*} $$
$$ \begin{align*} \mathbb{P}\bigg(\bigg|\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}}\bigg| \geq \frac{(\log T)^{1-\sigma}}{\log \log T}\bigg) \ll \exp \bigg(-a_1' \frac{\log T}{\log \log T}\bigg). \end{align*} $$
Lemma 2.6. Let Y be a large positive real number and
![]() $|z|\leq Y^{\sigma - 1/2}$
. Then,
$|z|\leq Y^{\sigma - 1/2}$
. Then,
 $$ \begin{align*} \mathbb{E} (|L(\sigma, f \times f, X)|^z) & = \mathbb{E} \bigg( \exp \bigg( z \,\mathrm{Re} \bigg( \sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}} \bigg) \bigg) \bigg)\\ &\quad + O \bigg( \mathbb{E} (|L(\sigma, f \times f, X)|^{\mathrm{Re} (z))}) \frac{|z|}{Y^{\sigma - 1/2}} \bigg). \end{align*} $$
$$ \begin{align*} \mathbb{E} (|L(\sigma, f \times f, X)|^z) & = \mathbb{E} \bigg( \exp \bigg( z \,\mathrm{Re} \bigg( \sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}} \bigg) \bigg) \bigg)\\ &\quad + O \bigg( \mathbb{E} (|L(\sigma, f \times f, X)|^{\mathrm{Re} (z))}) \frac{|z|}{Y^{\sigma - 1/2}} \bigg). \end{align*} $$
Moreover, if u, v are real numbers such that
![]() $|u|+|v| \leq Y^{\sigma - 1/2}$
, then
$|u|+|v| \leq Y^{\sigma - 1/2}$
, then
 $$ \begin{align*} \Phi_{\sigma}^{rand} (u,v) & = \mathbb{E} \bigg( \exp \bigg( iu\,\mathrm{Re} \bigg( \sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}}\bigg) + iv \,\mathrm{Im} \bigg(\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}} \bigg) \bigg) \bigg) \\ &\quad + O\bigg(\frac{|u|+|v|}{Y^{\sigma - 1/2}}\bigg). \end{align*} $$
$$ \begin{align*} \Phi_{\sigma}^{rand} (u,v) & = \mathbb{E} \bigg( \exp \bigg( iu\,\mathrm{Re} \bigg( \sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}}\bigg) + iv \,\mathrm{Im} \bigg(\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}} \bigg) \bigg) \bigg) \\ &\quad + O\bigg(\frac{|u|+|v|}{Y^{\sigma - 1/2}}\bigg). \end{align*} $$
Lemma 2.7. Let
![]() $2/3 < \sigma <1$
and
$2/3 < \sigma <1$
and
![]() $Y = (\log T)^A$
for a fixed
$Y = (\log T)^A$
for a fixed
![]() $A \geq 1$
. For any positive integer
$A \geq 1$
. For any positive integer
![]() $k \leq \log T/(20 A \log \log z)$
, there exist
$k \leq \log T/(20 A \log \log z)$
, there exist
![]() $a_2(\sigma )> 0$
and
$a_2(\sigma )> 0$
and
![]() $a_2'(\sigma )> 0$
such that
$a_2'(\sigma )> 0$
such that
 $$ \begin{align*} \frac{1}{T} \int_{T}^{2T} \bigg| \sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma+it)}} \bigg|^{2k}\,dt \ll \bigg(\frac{a_2(\sigma)k^{1-\sigma}}{(\log k)^{\sigma}}\bigg)^{2k} \end{align*} $$
$$ \begin{align*} \frac{1}{T} \int_{T}^{2T} \bigg| \sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma+it)}} \bigg|^{2k}\,dt \ll \bigg(\frac{a_2(\sigma)k^{1-\sigma}}{(\log k)^{\sigma}}\bigg)^{2k} \end{align*} $$
and
 $$ \begin{align*} \mathbb{E} \bigg(\bigg|\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}}\bigg|^{2k}\bigg) \ll \bigg(\frac{a_2'(\sigma)k^{1-\sigma}}{(\log k)^{\sigma}}\bigg)^{2k}. \end{align*} $$
$$ \begin{align*} \mathbb{E} \bigg(\bigg|\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}}\bigg|^{2k}\bigg) \ll \bigg(\frac{a_2'(\sigma)k^{1-\sigma}}{(\log k)^{\sigma}}\bigg)^{2k}. \end{align*} $$
Here the implied constants are absolute.
Proof. By using Lemma 2.4, the lemma follows easily from the method in [Reference Lamzouri, Lester and Radziwiłł8, Lemma 3.3].
Lemma 2.8 [Reference Tsang11, Lemma 6].
Let
![]() ${2}/{3} < \sigma < 1$
and
${2}/{3} < \sigma < 1$
and
![]() $Y = (\log T)^A$
for a fixed
$Y = (\log T)^A$
for a fixed
![]() $A \geq 1$
. For any positive integers u, v such that
$A \geq 1$
. For any positive integers u, v such that
![]() $u+v \leq \log T/(6A \log \log T)$
,
$u+v \leq \log T/(6A \log \log T)$
,
 $$ \begin{align*} \begin{aligned} \frac{1}{T} & \int_{T}^{2T} \bigg(\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma+it)}}\bigg)^u \bigg(\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma-it)}}\bigg)^v \,dt \\ & = \mathbb{E}\bigg(\bigg(\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}}\bigg)^u \bigg(\sum_{p^{\nu}\leq Y}\frac{\overline{b_f(p^{\nu})X(p)^{\nu}}}{\nu p^{\nu\sigma}}\bigg)^v\bigg) + O\bigg(\frac{Y^{u+v}}{\sqrt{T}}\bigg), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{1}{T} & \int_{T}^{2T} \bigg(\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma+it)}}\bigg)^u \bigg(\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma-it)}}\bigg)^v \,dt \\ & = \mathbb{E}\bigg(\bigg(\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}}\bigg)^u \bigg(\sum_{p^{\nu}\leq Y}\frac{\overline{b_f(p^{\nu})X(p)^{\nu}}}{\nu p^{\nu\sigma}}\bigg)^v\bigg) + O\bigg(\frac{Y^{u+v}}{\sqrt{T}}\bigg), \end{aligned} \end{align*} $$
with an absolute implied constant.
Proposition 2.9. Let
![]() $2/3 < \sigma <1$
and
$2/3 < \sigma <1$
and
![]() $Y = (\log T)^A$
for a fixed
$Y = (\log T)^A$
for a fixed
![]() $A \geq 1$
. For all complex numbers
$A \geq 1$
. For all complex numbers
![]() $z_1$
,
$z_1$
,
![]() $z_2$
, there exist positive constants
$z_2$
, there exist positive constants
![]() $a_3 = a_3(\sigma ,A)>0$
and
$a_3 = a_3(\sigma ,A)>0$
and
![]() $a_4 = a_4(\sigma ,A)>0$
with
$a_4 = a_4(\sigma ,A)>0$
with
![]() $|z_1|$
,
$|z_1|$
,
![]() $|z_2| \leq a_3(\log T)^{\sigma }$
such that
$|z_2| \leq a_3(\log T)^{\sigma }$
such that
 $$ \begin{align*} \begin{aligned} \frac{1}{T} & \int_{\mathcal{A}(T)} \exp \bigg(z_1 \sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma+it)}} + z_2 \sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma-it)}}\bigg)\,dt \\ & = \mathbb{E} \bigg(\exp \bigg(z_1 \sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}} + z_2 \sum_{p^{\nu}\leq Y}\frac{\overline{b_f(p^{\nu})X(p)^{\nu}}}{\nu p^{\nu\sigma}} \bigg) \bigg) + O \bigg(\exp \bigg(-a_4 \frac{\log T}{ \log \log T}\bigg)\bigg), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{1}{T} & \int_{\mathcal{A}(T)} \exp \bigg(z_1 \sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma+it)}} + z_2 \sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma-it)}}\bigg)\,dt \\ & = \mathbb{E} \bigg(\exp \bigg(z_1 \sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu\sigma}} + z_2 \sum_{p^{\nu}\leq Y}\frac{\overline{b_f(p^{\nu})X(p)^{\nu}}}{\nu p^{\nu\sigma}} \bigg) \bigg) + O \bigg(\exp \bigg(-a_4 \frac{\log T}{ \log \log T}\bigg)\bigg), \end{aligned} \end{align*} $$
with an absolute implied constant. Here,
![]() $\mathcal {A}(T)$
is the set of those
$\mathcal {A}(T)$
is the set of those
![]() $t \in [T, 2T]$
such that
$t \in [T, 2T]$
such that
 $$ \begin{align*} \bigg|\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma+it)}}\bigg| \leq \frac{(\log T)^{1-\sigma}}{\log \log T}. \end{align*} $$
$$ \begin{align*} \bigg|\sum_{p^{\nu}\leq Y}\frac{b_f(p^{\nu})}{\nu p^{\nu(\sigma+it)}}\bigg| \leq \frac{(\log T)^{1-\sigma}}{\log \log T}. \end{align*} $$
Proof. The proof is the same as that of [Reference Lamzouri, Lester and Radziwiłł8, Proposition 2.3] by using Lemma 2.7, Proposition 2.5 and Lemma 2.8.
Proposition 2.10. Let
![]() $2/3 < \sigma _0 < \sigma <1$
and
$2/3 < \sigma _0 < \sigma <1$
and
![]() $A \geq 1$
be fixed. There exists a constant
$A \geq 1$
be fixed. There exists a constant
![]() $a_5 = a_5(\sigma , A)$
such that for
$a_5 = a_5(\sigma , A)$
such that for
![]() $|u|$
,
$|u|$
,
![]() $|v| \leq a_5 (\log T)^{\sigma }$
,
$|v| \leq a_5 (\log T)^{\sigma }$
,
 $$ \begin{align*} \Phi_{\sigma, T}(u,v) = \Phi_{\sigma}^{\mathrm{rand}} (u,v) + O\bigg(\frac{1}{(\log T)^A}\bigg), \end{align*} $$
$$ \begin{align*} \Phi_{\sigma, T}(u,v) = \Phi_{\sigma}^{\mathrm{rand}} (u,v) + O\bigg(\frac{1}{(\log T)^A}\bigg), \end{align*} $$
with the implied constant depending on
![]() $\sigma _0$
only.
$\sigma _0$
only.
Proof. Follow the general idea of the proof of [Reference Lamzouri, Lester and Radziwiłł8, Theorem 2.1]. Let
![]() $B=B(A)$
be a large enough constant. Let
$B=B(A)$
be a large enough constant. Let
![]() $ Y = (\log T)^{B/(\sigma - 2/3)}$
. By Lemma 2.3,
$ Y = (\log T)^{B/(\sigma - 2/3)}$
. By Lemma 2.3,
 $$ \begin{align*} \log L(s, f \times f) = \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} + O\bigg(\frac{1}{(\log T)^{B/2-3}}\bigg) \end{align*} $$
$$ \begin{align*} \log L(s, f \times f) = \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} + O\bigg(\frac{1}{(\log T)^{B/2-3}}\bigg) \end{align*} $$
for all
![]() $t \in [T, 2T]$
, except for a set
$t \in [T, 2T]$
, except for a set
![]() $\mathcal {D}(T)$
of measure
$\mathcal {D}(T)$
of measure
![]() $T^{1-d(\sigma )}$
for some constant
$T^{1-d(\sigma )}$
for some constant
![]() $d(\sigma )>0$
. Define
$d(\sigma )>0$
. Define
![]() $\mathcal {C}(T) = \{t \in [T, 2T], t \notin \mathcal {D} (T)\}$
. Then,
$\mathcal {C}(T) = \{t \in [T, 2T], t \notin \mathcal {D} (T)\}$
. Then,
 $$ \begin{align*} & \Phi_{\sigma,T} (u,v) \\& \quad = \frac{1}{T} \int_{\mathcal{C}(T)} \exp ( iu\, \mathrm{Re} \log L(\sigma+it, f \times f) + iv\, \mathrm{Im} \log L(\sigma+it, f \times f) ) \,dt + O (T^{-d(\sigma)} )\\& \quad = \frac{1}{T} \int_{\mathcal{C}(T)} \exp \bigg(iu\, \mathrm{Re} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} + iv\, \mathrm{Im} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} \bigg) \,dt + O \bigg(\frac{1}{(\log T)^{B/2-4}}\bigg)\\& \quad = \frac{1}{T} \int_T^{2T} \exp \bigg(iu\, \mathrm{Re} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} + iv\, \mathrm{Im} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} \bigg) \,dt + O\bigg(\frac{1}{(\log T)^{B/2-4}}\bigg). \end{align*} $$
$$ \begin{align*} & \Phi_{\sigma,T} (u,v) \\& \quad = \frac{1}{T} \int_{\mathcal{C}(T)} \exp ( iu\, \mathrm{Re} \log L(\sigma+it, f \times f) + iv\, \mathrm{Im} \log L(\sigma+it, f \times f) ) \,dt + O (T^{-d(\sigma)} )\\& \quad = \frac{1}{T} \int_{\mathcal{C}(T)} \exp \bigg(iu\, \mathrm{Re} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} + iv\, \mathrm{Im} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} \bigg) \,dt + O \bigg(\frac{1}{(\log T)^{B/2-4}}\bigg)\\& \quad = \frac{1}{T} \int_T^{2T} \exp \bigg(iu\, \mathrm{Re} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} + iv\, \mathrm{Im} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} \bigg) \,dt + O\bigg(\frac{1}{(\log T)^{B/2-4}}\bigg). \end{align*} $$
Let
![]() $\mathcal {A}(T)$
be defined as in Proposition 2.9 and take
$\mathcal {A}(T)$
be defined as in Proposition 2.9 and take
![]() $z_1={i}(u-iv)/2$
and
$z_1={i}(u-iv)/2$
and
![]() $z_2 = i(u+iv)/2$
in Proposition 2.9. From Proposition 2.5 and Lemma 2.6, the integral above is
$z_2 = i(u+iv)/2$
in Proposition 2.9. From Proposition 2.5 and Lemma 2.6, the integral above is
 $$ \begin{align*} & = \frac{1}{T} \int_{\mathcal{A}(T)} \exp \bigg( iu \,\mathrm{Re} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} + iv\, \mathrm{Im} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} \bigg) \,dt + O\bigg(\frac{1}{(\log T)^B}\bigg)\\& = \mathbb{E} \bigg(\exp \bigg(iu\, \mathrm{Re} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu (\sigma+it)}} + iv\, \mathrm{Im} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu (\sigma+it)}}\bigg) \bigg) + O\bigg(\frac{1}{(\log T)^B}\bigg)\\& = \Phi_{\sigma}^{\mathrm{rand}} (u,v) + O\bigg(\frac{1}{(\log T)^{B-1}}\bigg).\\[-39pt] \end{align*} $$
$$ \begin{align*} & = \frac{1}{T} \int_{\mathcal{A}(T)} \exp \bigg( iu \,\mathrm{Re} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} + iv\, \mathrm{Im} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})}{\nu p^{\nu (\sigma+it)}} \bigg) \,dt + O\bigg(\frac{1}{(\log T)^B}\bigg)\\& = \mathbb{E} \bigg(\exp \bigg(iu\, \mathrm{Re} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu (\sigma+it)}} + iv\, \mathrm{Im} \sum_{p^{\nu}\leq Y} \frac{b_f(p^{\nu})X(p)^{\nu}}{\nu p^{\nu (\sigma+it)}}\bigg) \bigg) + O\bigg(\frac{1}{(\log T)^B}\bigg)\\& = \Phi_{\sigma}^{\mathrm{rand}} (u,v) + O\bigg(\frac{1}{(\log T)^{B-1}}\bigg).\\[-39pt] \end{align*} $$
Lemma 2.11 [Reference Lamzouri, Lester and Radziwiłł8, Lemma 7.2].
Let
![]() $\lambda>0$
be a real number. Let
$\lambda>0$
be a real number. Let
![]() $\chi (y)=1$
if
$\chi (y)=1$
if
![]() $y>1$
and
$y>1$
and
![]() ${0}$
otherwise. For any
${0}$
otherwise. For any
![]() $c>0$
,
$c>0$
,
 $$ \begin{align*} \chi(y) \leq \frac{1}{2 \pi i} \int_{(c)} y^s \frac{e^{\lambda s}-1}{\lambda s} \,\frac{ds}{s} \quad\text{for } y>0. \end{align*} $$
$$ \begin{align*} \chi(y) \leq \frac{1}{2 \pi i} \int_{(c)} y^s \frac{e^{\lambda s}-1}{\lambda s} \,\frac{ds}{s} \quad\text{for } y>0. \end{align*} $$
We cite the following smooth approximation [Reference Lamzouri, Lester and Radziwiłł8] for the indicator function.
Lemma 2.12. Let
![]() $\mathcal {R} = \{z=x+iy \in \mathbb {C}: m_1 < x < m_2, n_1 < y < n_2\}$
for real numbers
$\mathcal {R} = \{z=x+iy \in \mathbb {C}: m_1 < x < m_2, n_1 < y < n_2\}$
for real numbers
![]() $m_1, m_2, n_1, n_2$
. Let
$m_1, m_2, n_1, n_2$
. Let
![]() $K>0$
be a real number. For any
$K>0$
be a real number. For any
![]() $z=x+iy \in \mathbb {C}$
, we denote the indicator function of
$z=x+iy \in \mathbb {C}$
, we denote the indicator function of
![]() $\mathcal {R}$
by
$\mathcal {R}$
by
 $$ \begin{align*} \mathbf{1}_{\mathcal{R}} (z) = W_{K, \mathcal{R}} (z) \,{+} \,&O \bigg( \frac{\sin^2 (\pi K(x-m_1))}{(\pi K(x-m_1))^2} + \frac{\sin^2 (\pi K(x-m_2))}{(\pi K(x-m_2))^2} \\ & {+}\, \frac{\sin^2 (\pi K(y-n_1))}{(\pi K(y-n_1))^2} + \frac{\sin^2 (\pi K(y-n_2))}{(\pi K(y-n_2))^2} \bigg), \end{align*} $$
$$ \begin{align*} \mathbf{1}_{\mathcal{R}} (z) = W_{K, \mathcal{R}} (z) \,{+} \,&O \bigg( \frac{\sin^2 (\pi K(x-m_1))}{(\pi K(x-m_1))^2} + \frac{\sin^2 (\pi K(x-m_2))}{(\pi K(x-m_2))^2} \\ & {+}\, \frac{\sin^2 (\pi K(y-n_1))}{(\pi K(y-n_1))^2} + \frac{\sin^2 (\pi K(y-n_2))}{(\pi K(y-n_2))^2} \bigg), \end{align*} $$
where
 $$ \begin{align*} W_{K, \mathcal{R}} (z) = \frac{1}{2} \mathrm{Re} \int_0^K \int_0^K &G \bigg(\frac{u}{K}\bigg) G\bigg(\frac{v}{K}\bigg) (e^{2\pi i (ux-vy)}f_{m_1,m_2}(u) \overline{f_{n_1,n_2}(v)} \\ & {-}\, e^{2\pi i (ux+vy)}f_{m_1,m_2}(u) f_{n_1,n_2}(v)) \,\frac{du}{u} \frac{dv}{v}. \end{align*} $$
$$ \begin{align*} W_{K, \mathcal{R}} (z) = \frac{1}{2} \mathrm{Re} \int_0^K \int_0^K &G \bigg(\frac{u}{K}\bigg) G\bigg(\frac{v}{K}\bigg) (e^{2\pi i (ux-vy)}f_{m_1,m_2}(u) \overline{f_{n_1,n_2}(v)} \\ & {-}\, e^{2\pi i (ux+vy)}f_{m_1,m_2}(u) f_{n_1,n_2}(v)) \,\frac{du}{u} \frac{dv}{v}. \end{align*} $$
Here,
and
Lemma 2.13. Let
![]() $2/3 < \sigma <1$
. Let u be a large positive real number. There exist constants
$2/3 < \sigma <1$
. Let u be a large positive real number. There exist constants
![]() $a_6 = a_6(f, \sigma )$
and
$a_6 = a_6(f, \sigma )$
and
![]() $a_6' = a_6'(f, \sigma )$
such that
$a_6' = a_6'(f, \sigma )$
such that
 $$ \begin{align*} \mathbb{E} (\exp (iu\, \mathrm{Re} \log L(\sigma, f \times f, X))) \ll \exp \bigg(-a_6\frac{u^{2/\sigma -2}}{\log u} \bigg) \end{align*} $$
$$ \begin{align*} \mathbb{E} (\exp (iu\, \mathrm{Re} \log L(\sigma, f \times f, X))) \ll \exp \bigg(-a_6\frac{u^{2/\sigma -2}}{\log u} \bigg) \end{align*} $$
and
 $$ \begin{align*} \mathbb{E} (\exp (iu\, \mathrm{Im} \log L(\sigma, f \times f, X))) \ll \exp \bigg(-a_6'\frac{u^{2/\sigma -2}}{\log u} \bigg). \end{align*} $$
$$ \begin{align*} \mathbb{E} (\exp (iu\, \mathrm{Im} \log L(\sigma, f \times f, X))) \ll \exp \bigg(-a_6'\frac{u^{2/\sigma -2}}{\log u} \bigg). \end{align*} $$
Proof. Follow the general idea of the proof of [Reference Lamzouri, Lester and Radziwiłł8, Lemma 6.3]. We denote the Bessel function of order 0 by
![]() $J_0(s)$
for all
$J_0(s)$
for all
![]() $s \in \mathbb {R}$
. Note that for any prime p,
$s \in \mathbb {R}$
. Note that for any prime p,
![]() $\mathbb {E} (e^{is \mathrm {Re} X(p)}) = \mathbb {E} (e^{is \mathrm {Im} X(p)}) = J_0(s)$
. Since
$\mathbb {E} (e^{is \mathrm {Re} X(p)}) = \mathbb {E} (e^{is \mathrm {Im} X(p)}) = J_0(s)$
. Since
![]() $\log (1+t)=t+O(t^2)$
for
$\log (1+t)=t+O(t^2)$
for
![]() $ |t|<1$
,
$ |t|<1$
,
 $$ \begin{align*} |\mathbb{E} & (\exp (iu\, \mathrm{Re} \log L(\sigma, f \times f, X)))|\\ & = \bigg|\mathbb{E} \bigg(\exp \bigg(iu\, \mathrm{Re} \log \bigg( \prod_p \bigg(1 - \frac{\alpha_f(p)^2 X(p)}{p^{\sigma}}\bigg)^{-1} \bigg(1 - \frac{\beta_f(p)^2 X(p)}{p^{\sigma}}\bigg)^{-1} \bigg(1 - \frac{X(p)}{p^{\sigma}}\bigg)^{-2} \bigg) \bigg)\bigg)\bigg|\\ & \leq \prod_{p>u^{2/\sigma}} \mathbb{E} \bigg(\exp \bigg(\frac{iu \lambda_f^2(p)}{p^{\sigma}} \mathrm{Re} X(p) + O \bigg(\frac{u}{p^{2\sigma}}\bigg) \bigg) \bigg) = \exp (O(u^{2/\sigma -3})) \prod_{p>u^{2/\sigma}} \bigg|J_0 \bigg(\frac{u \lambda_f^2(p)}{p^{\sigma}}\bigg)\bigg|. \end{align*} $$
$$ \begin{align*} |\mathbb{E} & (\exp (iu\, \mathrm{Re} \log L(\sigma, f \times f, X)))|\\ & = \bigg|\mathbb{E} \bigg(\exp \bigg(iu\, \mathrm{Re} \log \bigg( \prod_p \bigg(1 - \frac{\alpha_f(p)^2 X(p)}{p^{\sigma}}\bigg)^{-1} \bigg(1 - \frac{\beta_f(p)^2 X(p)}{p^{\sigma}}\bigg)^{-1} \bigg(1 - \frac{X(p)}{p^{\sigma}}\bigg)^{-2} \bigg) \bigg)\bigg)\bigg|\\ & \leq \prod_{p>u^{2/\sigma}} \mathbb{E} \bigg(\exp \bigg(\frac{iu \lambda_f^2(p)}{p^{\sigma}} \mathrm{Re} X(p) + O \bigg(\frac{u}{p^{2\sigma}}\bigg) \bigg) \bigg) = \exp (O(u^{2/\sigma -3})) \prod_{p>u^{2/\sigma}} \bigg|J_0 \bigg(\frac{u \lambda_f^2(p)}{p^{\sigma}}\bigg)\bigg|. \end{align*} $$
For
![]() $|s|<1$
, we have
$|s|<1$
, we have
![]() $J_0(s) = 1 - ({s}/{2})^2 + O(s^4)$
. By using (1.2), for some constant
$J_0(s) = 1 - ({s}/{2})^2 + O(s^4)$
. By using (1.2), for some constant
![]() $a_6 = a_6(f, \sigma ), c>0 $
, the product above is
$a_6 = a_6(f, \sigma ), c>0 $
, the product above is
 $$ \begin{align*} = \exp \bigg\{ -\frac{u^2}{4} \sum_{p>u^{2/\sigma}} \bigg(\frac{\lambda_f^4(p)}{p^{2\sigma}} + O\bigg(\frac{u^2}{p^{4\sigma}}\bigg) \bigg) \bigg\} \leq \exp \bigg(-a_6\frac{u^{2/\sigma -2}}{\log u} \bigg). \end{align*} $$
$$ \begin{align*} = \exp \bigg\{ -\frac{u^2}{4} \sum_{p>u^{2/\sigma}} \bigg(\frac{\lambda_f^4(p)}{p^{2\sigma}} + O\bigg(\frac{u^2}{p^{4\sigma}}\bigg) \bigg) \bigg\} \leq \exp \bigg(-a_6\frac{u^{2/\sigma -2}}{\log u} \bigg). \end{align*} $$
The second inequality can be derived similarly.
3 Proof of the main theorem
Let
![]() $\mathcal {R}$
be a rectangle with sides parallel to the coordinate axes. Define
$\mathcal {R}$
be a rectangle with sides parallel to the coordinate axes. Define
![]() $\Psi _T(\mathcal {R}) = \mathbb {P}(\log L(\sigma +it, f \times f) \in \mathcal {R}) \text { and } \Psi (\mathcal {R}) = \mathbb {P}(\log L(\sigma , f \times f, X) \in \mathcal {R})$
. Let
$\Psi _T(\mathcal {R}) = \mathbb {P}(\log L(\sigma +it, f \times f) \in \mathcal {R}) \text { and } \Psi (\mathcal {R}) = \mathbb {P}(\log L(\sigma , f \times f, X) \in \mathcal {R})$
. Let
According to Lemma 2.3 and Proposition 2.5, for some constant
![]() $a_7>0$
,
$a_7>0$
,
 $$ \begin{align*} \Psi_T(\mathcal{R}) = \Psi_T(\widetilde{\mathcal{R}}) + O \bigg(\exp \bigg(-a_7\frac{\log T}{\log \log T} \bigg) \bigg). \end{align*} $$
$$ \begin{align*} \Psi_T(\mathcal{R}) = \Psi_T(\widetilde{\mathcal{R}}) + O \bigg(\exp \bigg(-a_7\frac{\log T}{\log \log T} \bigg) \bigg). \end{align*} $$
Similarly to [Reference Xiao and Zhai12], by using Lemmas 2.6 and 2.11, we can obtain the relationship between
![]() $\Psi (\mathcal {R})$
and
$\Psi (\mathcal {R})$
and
![]() $\Psi (\widetilde {\mathcal {R}})$
: for some constant
$\Psi (\widetilde {\mathcal {R}})$
: for some constant
![]() $a_7'>0$
,
$a_7'>0$
,
 $$ \begin{align*} \Psi(\mathcal{R}) = \Psi(\widetilde{\mathcal{R}}) + O \bigg(\exp \bigg(-a_7'\frac{\log T}{\log \log T} \bigg) \bigg). \end{align*} $$
$$ \begin{align*} \Psi(\mathcal{R}) = \Psi(\widetilde{\mathcal{R}}) + O \bigg(\exp \bigg(-a_7'\frac{\log T}{\log \log T} \bigg) \bigg). \end{align*} $$
Let
![]() $\mathcal {S}$
be the set of rectangles
$\mathcal {S}$
be the set of rectangles
![]() $\mathcal {R} \subset [-(\log T)^3, (\log T)^3]\times [-(\log T)^3, (\log T)^3]$
with sides parallel to the coordinate axes. Then,
$\mathcal {R} \subset [-(\log T)^3, (\log T)^3]\times [-(\log T)^3, (\log T)^3]$
with sides parallel to the coordinate axes. Then,
 $$ \begin{align*} D_{\sigma}(T) = \sup_{\mathcal{R} \subset \mathcal{S}} |\Psi_T(\mathcal{R}) - \Psi(\mathcal{R})| + O \bigg(\exp \bigg(-a_7\frac{\log T}{\log \log T} \bigg) \bigg). \end{align*} $$
$$ \begin{align*} D_{\sigma}(T) = \sup_{\mathcal{R} \subset \mathcal{S}} |\Psi_T(\mathcal{R}) - \Psi(\mathcal{R})| + O \bigg(\exp \bigg(-a_7\frac{\log T}{\log \log T} \bigg) \bigg). \end{align*} $$
In light of Lemma 2.12, choose
![]() $K = a_8(\log T)^{\sigma }$
, for some
$K = a_8(\log T)^{\sigma }$
, for some
![]() $a_8> 0$
, and
$a_8> 0$
, and
![]() $|m_1|, |m_2|, |n_1|, |n_2| \leq (\log T)^3$
. Then it follows that
$|m_1|, |m_2|, |n_1|, |n_2| \leq (\log T)^3$
. Then it follows that
 $$ \begin{align} \Psi_T(\mathcal{R})= \frac{1}{T} \int_{T}^{2T} W_{K,\mathcal{R}} (\log L(\sigma+it, f \times f))\,dt + E_1 \end{align} $$
$$ \begin{align} \Psi_T(\mathcal{R})= \frac{1}{T} \int_{T}^{2T} W_{K,\mathcal{R}} (\log L(\sigma+it, f \times f))\,dt + E_1 \end{align} $$
and, in addition,
where
 $$ \begin{align} I_T(K, m) = \frac{1}{T} \int_{T}^{2T} \frac{\sin^2(\pi K(\mathrm{Re} \log L(\sigma+it, f \times f) - m))}{(\pi K (\mathrm{Re} \log L(\sigma+it, f \times f) - m))^2} \,dt \end{align} $$
$$ \begin{align} I_T(K, m) = \frac{1}{T} \int_{T}^{2T} \frac{\sin^2(\pi K(\mathrm{Re} \log L(\sigma+it, f \times f) - m))}{(\pi K (\mathrm{Re} \log L(\sigma+it, f \times f) - m))^2} \,dt \end{align} $$
and
 $$ \begin{align*} J_T(K, n) = \frac{1}{T} \int_{T}^{2T} \frac{\sin^2(\pi K(\mathrm{Im} \log L(\sigma+it, f \times f) - n))}{(\pi K (\mathrm{Im} \log L(\sigma+it, f \times f) - n))^2} \,dt. \end{align*} $$
$$ \begin{align*} J_T(K, n) = \frac{1}{T} \int_{T}^{2T} \frac{\sin^2(\pi K(\mathrm{Im} \log L(\sigma+it, f \times f) - n))}{(\pi K (\mathrm{Im} \log L(\sigma+it, f \times f) - n))^2} \,dt. \end{align*} $$
First, we treat the main term of (3.1):
 $$ \begin{align*} \begin{aligned} \frac{1}{T} & \int_{T}^{2T} W_{K,\mathcal{R}} (\log L(\sigma+it, f \times f))\,dt = \frac{1}{2} \mathrm{Re} \int_0^K \int_0^K G \bigg(\frac{u}{K}\bigg) G \bigg(\frac{v}{K}\bigg)\\ & \times (\Phi_{\sigma,T}(2\pi u, -2\pi v)f_{m_1, m_2}(u) \overline{f_{n_1,n_2}(v)} - \Phi_{\sigma, T}(2\pi u, 2\pi v) f_{m_1, m_2}(u) f_{n_1, n_2}(v) ) \,\frac{du}{u}\, \frac{dv}{v}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{1}{T} & \int_{T}^{2T} W_{K,\mathcal{R}} (\log L(\sigma+it, f \times f))\,dt = \frac{1}{2} \mathrm{Re} \int_0^K \int_0^K G \bigg(\frac{u}{K}\bigg) G \bigg(\frac{v}{K}\bigg)\\ & \times (\Phi_{\sigma,T}(2\pi u, -2\pi v)f_{m_1, m_2}(u) \overline{f_{n_1,n_2}(v)} - \Phi_{\sigma, T}(2\pi u, 2\pi v) f_{m_1, m_2}(u) f_{n_1, n_2}(v) ) \,\frac{du}{u}\, \frac{dv}{v}, \end{aligned} \end{align*} $$
where
![]() $\Phi _{\sigma ,T}$
is defined by (2.1). Since
$\Phi _{\sigma ,T}$
is defined by (2.1). Since
![]() $0 \leq G(u) \leq 2/\pi $
and
$0 \leq G(u) \leq 2/\pi $
and
![]() $|f_{\alpha , \beta }(u)| \leq \pi u |\beta - \alpha |$
, by Proposition 2.10,
$|f_{\alpha , \beta }(u)| \leq \pi u |\beta - \alpha |$
, by Proposition 2.10,
 $$ \begin{align*} \frac{1}{T} \int_{T}^{2T} W_{K,\mathcal{R}} (\log L(\sigma+it, f \times f))\,dt = \mathbb{E} (W_{K,\mathcal{R}} (\log L(\sigma, f \times f, X))) + O \bigg(\frac{1}{(\log T)^2} \bigg). \end{align*} $$
$$ \begin{align*} \frac{1}{T} \int_{T}^{2T} W_{K,\mathcal{R}} (\log L(\sigma+it, f \times f))\,dt = \mathbb{E} (W_{K,\mathcal{R}} (\log L(\sigma, f \times f, X))) + O \bigg(\frac{1}{(\log T)^2} \bigg). \end{align*} $$
Moreover,
Here,
where
 $$ \begin{align*} I_{\mathrm{rand}}(K, m) = \mathbb{E} \bigg( \frac{\sin^2(\pi K(\mathrm{Re} \log L(\sigma, f \times f, X) - m))}{(\pi K (\mathrm{Re} \log L(\sigma, f \times f, X) - m))^2} \bigg), \end{align*} $$
$$ \begin{align*} I_{\mathrm{rand}}(K, m) = \mathbb{E} \bigg( \frac{\sin^2(\pi K(\mathrm{Re} \log L(\sigma, f \times f, X) - m))}{(\pi K (\mathrm{Re} \log L(\sigma, f \times f, X) - m))^2} \bigg), \end{align*} $$
and
 $$ \begin{align*} J_{\mathrm{rand}}(K, n) = \mathbb{E} \bigg( \frac{\sin^2(\pi K(\mathrm{Im} \log L(\sigma, f \times f, X) - n))}{(\pi K (\mathrm{Im} \log L(\sigma, f \times f, X) - n))^2} \bigg). \end{align*} $$
$$ \begin{align*} J_{\mathrm{rand}}(K, n) = \mathbb{E} \bigg( \frac{\sin^2(\pi K(\mathrm{Im} \log L(\sigma, f \times f, X) - n))}{(\pi K (\mathrm{Im} \log L(\sigma, f \times f, X) - n))^2} \bigg). \end{align*} $$
Hence,
where
 $$ \begin{align*} E_3 = E_1 + E_2 + O \bigg(\frac{1}{(\log T)^2} \bigg). \end{align*} $$
$$ \begin{align*} E_3 = E_1 + E_2 + O \bigg(\frac{1}{(\log T)^2} \bigg). \end{align*} $$
Notice that
 $$ \begin{align} \frac{\sin^2 (\pi K x)}{(\pi K x)^2} = \frac{2(1-\cos (2 \pi K x))}{K^2(2\pi x)^2} = \frac{2}{K^2} \int_0^K (K-v) \cos (2\pi xv) \,dv. \end{align} $$
$$ \begin{align} \frac{\sin^2 (\pi K x)}{(\pi K x)^2} = \frac{2(1-\cos (2 \pi K x))}{K^2(2\pi x)^2} = \frac{2}{K^2} \int_0^K (K-v) \cos (2\pi xv) \,dv. \end{align} $$
To bound
![]() $E_1$
, we use (3.4) to rewrite (3.2):
$E_1$
, we use (3.4) to rewrite (3.2):
 $$ \begin{align*} \begin{aligned} I_T (K, m) & = \mathrm{Re} \bigg( \frac{1}{T} \int_T^{2T} \frac{2}{K^2} \int_0^K (K-v) \exp (2\pi i v (\mathrm{Re} \log L (\sigma+it, f \times f) - m) ) \,dv\,dt \bigg)\\ & = \mathrm{Re} \frac{2}{K^2} \int_0^K (K-v) e^{-2\pi ivm} \Phi_{\sigma, T} (2\pi v, 0)\,dv. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} I_T (K, m) & = \mathrm{Re} \bigg( \frac{1}{T} \int_T^{2T} \frac{2}{K^2} \int_0^K (K-v) \exp (2\pi i v (\mathrm{Re} \log L (\sigma+it, f \times f) - m) ) \,dv\,dt \bigg)\\ & = \mathrm{Re} \frac{2}{K^2} \int_0^K (K-v) e^{-2\pi ivm} \Phi_{\sigma, T} (2\pi v, 0)\,dv. \end{aligned} \end{align*} $$
From Proposition 2.10,
 $$ \begin{align*} I_T (K, m) = \mathrm{Re} \frac{2}{K^2} \int_0^K (K-v) e^{-2\pi ivm} \Phi_{\sigma}^{rand} (2\pi v, 0)\,dv + O \bigg(\frac{1}{(\log T)^9} \bigg), \end{align*} $$
$$ \begin{align*} I_T (K, m) = \mathrm{Re} \frac{2}{K^2} \int_0^K (K-v) e^{-2\pi ivm} \Phi_{\sigma}^{rand} (2\pi v, 0)\,dv + O \bigg(\frac{1}{(\log T)^9} \bigg), \end{align*} $$
uniformly for all
![]() $m \in \mathbb {R}$
. Lemma 2.13 implies that
$m \in \mathbb {R}$
. Lemma 2.13 implies that
The bound
![]() $J_T(K, n) \ll {1}/{K}$
can be obtained using the same method. Therefore,
$J_T(K, n) \ll {1}/{K}$
can be obtained using the same method. Therefore,
Then, using (2.2), (3.4) and Lemma 2.13,
 $$ \begin{align*} \begin{aligned} I_{\mathrm{rand}} (K, m) & = \mathbb{E} \bigg(\frac{2}{K^2} \int_0^K (K-v) \cos (2\pi v [ \mathrm{Re} \log L(\sigma, f \times f, X) - m] ) \bigg) \,dv \\ & = \mathrm{Re} \frac{2}{K^2} \int_0^K (K-v) e^{-2\pi ivm} \Phi_{\sigma}^{\mathrm{rand}}(2\pi v, 0) \,dv \ll \frac{1}{K}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} I_{\mathrm{rand}} (K, m) & = \mathbb{E} \bigg(\frac{2}{K^2} \int_0^K (K-v) \cos (2\pi v [ \mathrm{Re} \log L(\sigma, f \times f, X) - m] ) \bigg) \,dv \\ & = \mathrm{Re} \frac{2}{K^2} \int_0^K (K-v) e^{-2\pi ivm} \Phi_{\sigma}^{\mathrm{rand}}(2\pi v, 0) \,dv \ll \frac{1}{K}, \end{aligned} \end{align*} $$
uniformly for all
![]() $m \in \mathbb {R}$
. Similarly, we can obtain
$m \in \mathbb {R}$
. Similarly, we can obtain
![]() $J_{\mathrm {rand}} (K, n) \ll {1}/{K}$
, uniformly for all
$J_{\mathrm {rand}} (K, n) \ll {1}/{K}$
, uniformly for all
![]() $n \in \mathbb {R}$
. Thus,
$n \in \mathbb {R}$
. Thus,
Combining the estimates with (3.3), (3.5) and (3.6),
 $$ \begin{align*} D_{\sigma}(T) \ll \frac{1}{(\log T)^{\sigma}}, \end{align*} $$
$$ \begin{align*} D_{\sigma}(T) \ll \frac{1}{(\log T)^{\sigma}}, \end{align*} $$
which completes the proof.