The aim of this research is to analyse the impact of extreme market movements on future pension plan solvency by applying a regime switching approach. The motivation for undertaking the analysis came from the financial crisis and the collapse of Lehman Brothers in September 2008 and the subsequent policy response in March 2009 of quantitative easing (QE). According to the Pension Protection Fund (PPF), between June 2007 and March 2009, the overall asset values of defined benefit plans fell by nearly 8% (as a combination of a severe fall in equity values but an offsetting rise in bond prices), while the present value of future liabilities rose by almost 40% as Gilt yields fell. Since then, the aggregate funding position has worsened despite a recovery in asset values as further declines in Gilt yields have driven the present value of liabilities even higher.
This situation highlighted two key issues when considering future pension fund solvency. First, traditional ‘one state’ models of asset returns and discount rates assume that the statistical drivers of these factors remain constant through time. As a consequence, these models underestimate the severity, frequency and duration of extreme market movements. Second, it is essential to capture the correlation between pension assets and interest rate processes in different market conditions. As a result, the current piece addresses these issues by applying a ‘multi state’ approach. To do so we employ a multivariate Gaussian Markov regime switching model. These models have been widely applied in the economics and finance literature as they better reflect changing economic circumstances (See for example, Hamilton, Reference Hamilton1989 and Kemp Reference Kemp2011). Moreover, these models have been found to be better than the traditional ‘one state’ model at capturing extreme market movements, the time-varying correlation between different asset returns and the ‘fat-tails’ that have been observed in stock returns.
The impact of extreme market movements and the need to model such events has also been highlighted by the Actuarial Profession's Benchmarking Stochastic Models (BSM) Working Party. A key finding of the 2008 BSM report, which was subsequently published in 2009 (Frankland et al., 2009), was that the frequency of severe falls in equities, which are assigned a 0.5% probability assuming normally distributed stock returns, occur more often in reality than the normal distribution implies. To better model these extreme market movements is therefore useful in understanding the potential impact that such events might have on the value of future pension fund solvency. Moreover, to capture the inter-relation between asset values, interest rates, and the present value of pension liabilities, would provide a powerful decision making tool within both a pension management context and to assist with macro-prudential regulation e.g. the PPF.
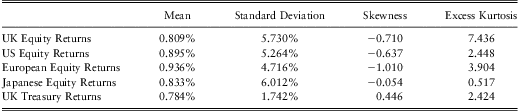
To construct our pension fund assets we set up a 5 asset class portfolio consisting of UK Equities, US Equities, European Equities (excluding the UK), Japanese Equities and 10-Year UK Gilts. To discount the liabilities we use the yield on 10-year UK Treasury bonds. To calculate our returns we compute the log normal returns,
$${{{{R}}}_{nt}}\,{\rm{ = }}\,ln({{I}_{nt}}/{{I}_{nt{\rm{ - }}1}})$$
where Int is the total returns index of asset class n. In the following table we present descriptive statsitics of the monthly returns for each of our asset classes.
For our illustrative portfolio, we assume that it invests similar weights in the different asset classes to the average UK pension portfolio weightings based upon the UBS 2011 Pension Fund Survey. We do however, make an adjustment to remove illiquid investments such as property, but keep the other asset classes in broadly the same relative quantities. We also assume that the portfolio is rebalanced at the end of each month to keep these weights constant. Our portfolio weightings are:
To estimate our future pension liabilities we set up a simple growing annuity and assume that at any point in time the pension fund has a 30 year liability and that these liabilities grow at a fixed rate of inflation i. From the following table C 1 is the first expected liability value which is then inflated forward based upon i. This therefore gives us a projection of future pension liabilities.
In doing so we can estimate the present value of pension liabilities at any point in time based upon the growth annuity formula G(rft, i, 30) where,
$$P{{V}_L}\: = \:{}{{C}_1} {{(1\: + \:i)}^{t - 1}} \,G({{r}_{ft}}, i, 30)$$
Our measure of pension fund solvency is Zt where,
$${{Z}_t}\, = \,\frac{{Asset\,Valu{{e}_t}\,{\rm{ - }}\,PV\,Liabilitie{{s}_t}}}{{PV\,Liabilitie{{s}_t}}}$$
The final factor that we incorporate into our analysis is a stochastic discount rate factor. To do so we model the discount rate using a discrete-time Ornstein-Uhlenbeck (O-U) process, where we estimate for the whole sample,
$${{r}_{ft}}\:{\rm{\, - \, }}\:{{r}_{ft - 1}}\: = \:a\: + \:b{{r}_{ft{\rm{\, - \, }}1}}\: + \:{{{\epsilon}}_t}$$
We then construct xt where,
$${{x}_t}\: = \:{{r}_{ft}}\:{\rm{\, - \, }}\:{\rm{(1}}\: + \:\widehat{b}){{r}_{ft - {\rm{1}}}}\: = \:\widehat{a}\: + \:{{{\epsilon}}_t}$$
In doing so we can then use xt to construct forward the future discount rate,
$${{r}_{ft}}\: = \:{{x}_t}\: + \:{\rm{(1}}\: + \:\widehat{b}){{r}_{ft - {\rm{1}}}}$$
Putting all of these factors together we can therefore estimate 6 different models of future pension fund solvency. Model 1 and 4 are estimated using a fixed discount rate process, models 2 and 5 are estimated using an independent (O-U) discount rate process and Models 3 and 6 incorporate a discount rate process that correlates with asset returns. Following Guidolin & Timmerman (Reference Guidolin and Timmerman2006) we use a 4-state Markov process for Models 4–6 as they show that this is optimal for jointly capturing stock and bond data. Statistical information criteria also reveal that using four states is better than using either two or three states based on our own data. This approach is also sufficiently complex to capture many of the extreme market dynamics that are understated by the traditional 1-state model, while being computationally tractable such that the model remains parsimonious. Models 1–3 use the one-state model for asset returns.
We then project forward future probabilities of insolvency for each of these models using Monte Carlo Simulation for Models 4–6, numerical integration for Models 2–3 and in closed form for Model 1. The results of each model can be seen in figure 1 based on the assumption that the scheme is initially overfunded by 15%.
Figure 1 The probability of pension scheme underfunding at different horizons over the next 30 years.
From figure 1 there are a number of key research conclusions that can be drawn. First, models 1 and 4, which assume a fixed interest rate process, dramatically underestimate the probability of underfunding, compared to all of the other models estimated. Second, for our most sophisticated models, 3 which assumes log normal returns with a stochastic interest rate process that varies with asset returns, and 6, which is a ‘four-state’ Markov model with a stochastic interest rate process that varies with asset returns, the prediction of underfunding is much higher compared to models 1 and 4. Although graphically, the predictions of models 3 and 6 appear to be similar, model 6 predicts around 2.5–4.5% more schemes being underfunded. Put in the context of the aggregate value of UK defined benefit pensions this is a significant amount. As a result, applying more sophisticated modelling of this problem should help with macro-prudential decision making as a better assessment of future insolvency can be estimated. The final conclusion that can be drawn from the current piece is that different choices of model selection and calibration can lead to very different outcomes. From a pensions management perspective this is important as picking one individual model or one particular set of assumptions leads to very specific outcomes. If this were to be the sole focus of decision making then sub-optimal decisions may occur as a wider set of information was not considered. Although this may create a communication issue between actuaries and trustees, if the communication problem can be alleviated, then more informed and potentially better decision making can take place.
