Masked translation priming studies with unbalanced bilinguals have shown that significant L1-L2 noncognate translation priming effects reliably occur in lexical decision tasks (LDTs). That is, L2 targets (e.g., ANGEL) are responded to significantly faster when they are primed by L1 translation equivalents (e.g., 天使, angel) than by unrelated L1 words (e.g., 日記, diary) (Dimitropoulou, Duñabeitia & Carreiras, Reference Dimitropoulou, Duñabeitia and Carreiras2011a; Reference Dimitropoulou, Duñabeitia and Carreiras2011b; Gollan, Forster & Frost, Reference Gollan, Forster and Frost1997; Jiang, Reference Jiang1999; Kim & Davis, Reference Kim and Davis2003; Nakayama, Sears, Hino & Lupker, Reference Nakayama, Sears, Hino and Lupker2013; Voga & Grainger, Reference Voga and Grainger2007). Priming in the reverse direction, however, does not always emerge. That is, a number of previous studies with unbalanced bilinguals have shown no masked L2-L1 noncognate translation priming effects in an LDT (e.g., Dimitropoulou et al., Reference Dimitropoulou, Duñabeitia and Carreiras2011a; Gollan et al., Reference Gollan, Forster and Frost1997; Grainger & Frenck-Mestre, Reference Grainger and Frenck-Mestre1998; Jiang Reference Jiang1999; Jiang & Forster, Reference Jiang and Forster2001; Nakayama et al., Reference Nakayama, Sears, Hino and Lupker2013; Wang & Forster, Reference Wang and Forster2015; Witzel & Forster, Reference Witzel and Forster2012; Xia & Andrews, Reference Xia and Andrews2015), even though significant L2-L1 priming has been found reliably in other tasks, such as semantic categorization (e.g., Wang & Forster, Reference Wang and Forster2010; Xia & Andrews, Reference Xia and Andrews2015) or episodic recognition (e.g., Jiang & Forster, Reference Jiang and Forster2001; Witzel & Forster, Reference Witzel and Forster2012).
The bilinguals tested in the studies cited above typically started learning English as a second language between the ages of 8 and 13 and, thus, would be considered late learners of their L2. The null effects they produced have led to the development of new accounts of L2 word representations. One example is the Episodic L2 hypothesis (Jiang & Forster, Reference Jiang and Forster2001; Witzel & Forster, Reference Witzel and Forster2012), which explains the null L2-L1 priming effects as being due to L2 and L1 words being stored in different memory systems (i.e., the episodic and lexical systems, respectively). Another example is the Sense Model (Finkbeiner, Forster, Nicol & Nakamura, Reference Finkbeiner, Forster, Nicol and Nakamura2004), which explains the null effects as being due to a large gap in the richness of semantic senses for L2 and L1 words (i.e., L1 words have much richer representations, representations that cannot be activated sufficiently by L2 primes). Indeed, the lack of L2-L1 priming effects in an LDT for unbalanced bilinguals was one of the main motivating forces for the development of these two new theoretical accounts.
In contrast, although, as noted above, the relevant literature contains a number of failures to find L2-L1 priming effects in an LDT with unbalanced bilinguals, that literature also contains several reports of such effects, most often involving bilinguals whose two languages have the same or similar written scripts. For example, Duyck and Warlop (Reference Duyck and Warlop2009), using a 64 ms prime duration (and a 64 ms backward mask, e.g., #####, for a 128 ms SOA), reported that Dutch–French bilinguals responded to L1 targets 27 ms faster when the targets were primed by L2 translation primes than by unrelated L2 primes. Similarly, with Dutch–English bilinguals, Schoonbaert, Duyck, Brysbaert and Hartsuiker (Reference Schoonbaert, Duyck, Brysbaert and Hartsuiker2009), using a 50 prime duration (and a 50 ms backward mask, for a 100 ms SOA) found a significant 12 ms L2-L1 priming effect. Dimitropoulou et al. (Reference Dimitropoulou, Duñabeitia and Carreiras2011b), using a 50 ms prime duration/SOA, also reported significant 11–14 ms priming effects with three groups of Greek–English bilinguals (although Greek and English do have different alphabets, and thus Greek–English bilinguals are technically different-script bilinguals, there are many obvious similarities between the corresponding letters in the two scripts).
Further, there is also at least one report of significant L2-L1 noncognate translation priming effects for bilinguals whose languages have completely different scripts. Nakayama, Ida and Lupker (Reference Nakayama and Ida2016), using a 50 ms prime duration/SOA found significant 10–22 ms priming effects for their very proficient (but, nonetheless, unbalanced) Japanese–English bilinguals (the mean TOEIC score of these individuals was higher than 870 and they began learning English at 9–10 years of age).Footnote 1 Nakayama et al. however, did not find significant priming for a group of weaker, but still quite proficient, bilinguals (their mean TOEIC score was 710 and they began learning English at 11 years of age). Although the exact reason why these researchers found L2-L1 priming effects while others did not is not entirely certain, Nakayama et al.’s results suggest that the L2 proficiency of the bilinguals may be a potent determinant in obtaining a significant L2-L1 noncognate translation priming effect in an LDT (although, see also Dimitropoulou et al., Reference Dimitropoulou, Duñabeitia and Carreiras2011b, who, as will be discussed below, reported no significant effects of L2 proficiency on the sizes of L2-L1 noncognate translation priming effects for their Greek–English bilinguals).Footnote 2
Nakayama et al. (Reference Nakayama and Ida2016) interpreted their results as being consistent with the assumptions of Bilingual Interactive Activation plus model (BIA+, Dijkstra & van Heuven, Reference Dijkstra and Van Heuven2002), that the main impact of greater L2 proficiency would be higher resting activation levels for L2 words and thus more efficient processing of L2 primes, which would then increase the chance of those primes producing significant priming effects. The main point to be made, however, is that simply that the existence of significant effects in several different experiments across different language combinations does imply that those effects are not merely empirical anomalies (i.e., L2 words will prime their L1 noncognate translation equivalents in certain situations).
Given that the existence (or nonexistence) of L2-L1 noncognate translation priming effects has important implications for model specifications (as noted, both the Episodic L2 hypothesis and the Sense Model are based on the assumption that these effects do not exist) and, more broadly, for understanding the bilingual mental lexicon, examining the nature of L2-L1 noncognate translation priming effects would seem to be important. The present experiment was conducted in an effort to examine these effects in a situation where such effects are likely to emerge. More specifically, as noted above, in Nakayama et al. (Reference Nakayama and Ida2016, Experiments 1 and 2), significant L2-L1 priming effects were observed for Japanese–English bilinguals whose L2 proficiency was very high. Therefore, in order to maximize the chances of obtaining significant L2-L1 priming, the bilinguals investigated in the present experiment were unbalanced bilinguals who were highly proficient in their L2. To anticipate the necessary result, a 47 ms prime duration with a 23 ms backward mask (hence, a 70 ms SOA) did produce a significant L2-L1 noncognate priming effect with these very proficient Japanese–English bilinguals.
In our attempt to then learn more about the nature of L2-L1 noncognate translation priming, we applied RT distributional analyses to examine how the significant effect manifests itself in the shapes of the RT distributions. Further, we analyzed the observed distributional patterns more closely by focusing on how prime frequency and target frequency affected the size of the priming effect. The information provided by these analyses about the nature of this effect should help us better understand how masked L2 primes are processed by highly proficient bilinguals as well as providing insights that may help uncover at least some of the reasons why priming arises in some situations but not in others. To the best of our knowledge, no previous studies have used these techniques to investigate translation priming effects.
Distributional analyses
In the RT distributional analyses, the shapes of the RT distributions for the translation and unrelated prime conditions were examined using two somewhat different procedures. In the first, observed data were fit by mathematical formulations and then how the experimental manipulations affected the parameters of the distributions was examined. The observed RTs were fit by the ex-Gaussian function (Balota & Yap, Reference Balota and Yap2011; Heathcote, Popiel & Mewhort, Reference Heathcote, Popiel and Mewhort1991), which typically well simulates the shape of a response latency distribution. The fitted distribution produces three parameters: μ, σ, and τ. The μ is the mean of the normal component of the distribution whereas the σ is the standard deviation of that component. Finally, the τ is the mean and standard deviation of the exponential component and it reflects the skew of the distribution. This procedure is carried out for each experimental condition separately.
In the second procedure, the data were simply plotted in order to estimate the distribution's shape empirically for each of the experimental conditions. In this procedure, raw data from each participant per condition are rank ordered and then segments of the ordering are grouped into ordered bins (e.g., first 20%, the next 20% and so forth, i.e., quantiles). Average quantile values (over participants) are then plotted for each experimental condition in order to evaluate how an experimental variable affects RTs at different points in the distribution. Generally, the two procedures show similar results: a shift in only the µ parameter manifests itself in a constant effect across RT bins including the initial bin, and a shift in the τ parameter manifests itself in larger effects in the slower RT bins. These two approaches are recommended for RT experiments in which no explicit computational models/theories making precise predictions about the nature of the distributions are available (see Balota & Yap, Reference Balota and Yap2011; Balota, Yap, Cortese & Watson, Reference Balota, Yap, Cortese and Watson2008, for further discussion).
One main advantage of RT distributional analyses is that they provide information that is not provided by the conventional analyses of RT means (e.g., Heathcote et al., Reference Heathcote, Popiel and Mewhort1991). For instance, a significant priming effect in the mean latency in a conventional analysis of means may reflect a large difference confined to very slow responses or it may reflect a constant effect across the response time distribution (or both). These alternative possibilities would often have different implications for theories of the processes at play.
Because no previous studies have applied RT distributional analysis to translation priming effects, we did not have specific expectations about the nature of the distributional pattern underlying significant L2-L1 priming. Nevertheless, based on the results from some similar experiments, there would appear to be a couple of hypotheses for what those data patterns might look like. One hypothesis derives from previous distributional analysis studies on within-language masked semantic priming effects (Balota et al., Reference Balota, Yap, Cortese and Watson2008, Experiment 7; Gomez, Perea & Ratcliff, Reference Gomez, Perea and Ratcliff2013). Using a masked priming procedure with a 42 ms prime duration, Balota et al. reported that a significant semantic priming effect (for clearly presented targets) was associated only with a shift in the RT distribution: the sizes of the priming effects were constant across the RT distribution. Similarly, Gomez et al. using a 56 ms prime duration found that a masked semantic/associative priming effect was significantly associated with a mean shift according to their RT distributional analysis, although there was no overall priming effect in the standard means analysis (a nonsignificant 12 ms effect). The mechanism associated with the priming in both experiments was presumed to be an activation mechanism, with the prime activating conceptual information that is also relevant to the target, aiding target processing for all targets. That is, equal-sized priming effects across the RT distribution emerged because the facilitation affected all related-target pairs, independently of the absolute speed/difficulty of target processing. Translation priming and (within-language) semantic priming are similar in that both effects likely have a conceptually-based component and thus the two effects may share many underlying operations. As such, then, like the within-language semantic priming effect, the L2-L1 priming effect may also be associated with a distributional shift alone.
On the other hand, it is also possible that we might find the other commonly observed pattern in distributional analyses, a larger priming effect on slower trials (a differential skewing of the distributions for the translation and unrelated conditions). For example, consider the following hypothesis. L2-L1 translation priming clearly is different from within-language (i.e., L1) semantic priming in that L2 primes are likely to be processed less efficiently than L1 primes (especially for unbalanced bilinguals, even highly proficient ones). Therefore, some proportion of L2 primes, especially the lower-frequency primes, may not be able to be processed to the point where they could produce a priming effect prior to when the target is presented. Thus, the priming effect observed would be essentially determined by the difficulty of prime processing. In such a situation it's not clear how (or if) the distributional analysis would be affected. However, if prime processing were to continue after the target is presented, slower target latencies would allow more time for the prime to be processed to a sufficient level to produce priming. If so, whereas there may or may not be a small priming effect on faster trials, one would expect to find a large L2-L1 priming effect on slower trials because more of the primes would be contributing to the priming effect on those slower trials. If the distributional analysis does show a larger priming effect on slower trials, our examination of the priming patterns as a function of prime and target frequency should help clarify its origin.
Method
Participants
Forty proficient bilinguals from Waseda University participated in this experiment in exchange for 1000 yen (about US$ 8.00). ERP data were concurrently recorded from 22 of the participants. Those data are not reported here. All were native speakers of Japanese who started learning English, on average, at 9.3 years of age. Their mean TOEIC score was 878 (range: 800–990, where the maximum test score is 990). This mean test score approximately falls within the top 4% of the score distribution. The participants used English predominantly in an academic setting.
Stimuli
The critical stimuli were 180 English–Japanese noncognate translation equivalents (e.g., doll-人形/ni.n.gyo.o/). The Japanese targets were two-character Kanji compound words (M = 36 occurrences per million (SD = 46.6), according to Amano & Kondo, Reference Amano and Kondo2003). The mean number of strokes in the targets was 18.2 (SD = 5.4). English translation primes were on average 5.0 letters in length (range = 3–6) and their mean word frequency was 141 occurrences per million (SD = 226.3) (Brysbaert & New, Reference Brysbaert and New2009). The translation primes, on average, had 3.9 orthographic neighbors (SD = 4.3). The unrelated primes were a different set of 180 English words that were orthographically, phonologically and conceptually unrelated to their targets. Unrelated primes were matched on a word by word basis on mean word length (M = 5.0, range = 3–6), neighborhood size (N = 3.9, SD = 4.3) and word frequency (M = 142, SD = 242.2) with the translation primes. The translation and unrelated primes were also matched on their mean concreteness ratings (both Ms = 3.6/5.0, SDs = 1.0 and 1.1, respectively, according to Brysbaert, Warriner & Kuperman, Reference Brysbaert, Warriner and Kuperman2014). In one list, half of the targets were primed by their translation equivalents and the other half by unrelated primes, and in the other list, the pairings of translation and unrelated primes were reversed.
For the “no” responses in the lexical decision task, 180 English word primes and Japanese two-character Kanji nonwords were also selected (e.g., song-債糸). The mean number of strokes in the nonword targets was 18.2. The English primes preceding nonword targets were matched to those preceding word targets on mean word length (M = 5.0, range = 3–6), neighborhood size (N = 4.0, SD = 4.6), word frequency (M = 140, SD = 234.1) and concreteness ratings (M = 3.6, SD = 1.0). There was only one presentation list for the nonword targets, as prime type was not manipulated for nonwords.
Procedure
Participants were tested individually. The stimulus presentation software was programmed in MATLAB using the Psychtoolbox package extensions (Brainard, Reference Brainard1997; Pelli, Reference Pelli1997; Kleiner, Brainard & Pelli, Reference Kleiner, Brainard and Pelli2007). The stimuli were presented on a 19 inch CRT monitor. The sequence of each trial was as follows: the fixation point “+” was initially presented for 800 ms and then a forward mask (“######”) was presented for 500 ms. Immediately following the forward mask, the English prime appeared for 47 ms and then was backward masked (“&&&&&”) for 23 ms. This timing sequence was similar to one that was used in Hoshino, Midgley & Holcomb (Reference Hoshino, Midgley, Holcomb and Grainger2010)’s ERP study (note that no L2-L1 priming was observed for Hoshino et al.’s Japanese–English bilinguals in that study). The Japanese target was then presented and remained on the screen until a lexical decision response was made. Participants pressed the “m” key on a keyboard to indicate the target was an existing Japanese word and pressed the “c” key to indicate it was a nonword. Prior to the experiment, participants performed 16 practice trials.
Results
The results of three separate analyses, the mean RT analysis, the ex-Gaussian analysis and the quantile analysis, of the observed data are reported in that order in below. Prior to the analyses, correct response latencies that were further than 3.5 standard deviations from each participant's mean per condition were removed from the data set (1.1% of the data). Throughout the analyses reported below, the significance level used was .05.
Mean RT analysis
The data were analyzed by a repeated measures ANOVA with Prime Type being the only independent variable and mean RTs for each condition being the dependent variable. There was a 20 ms priming effect (525 ms vs. 545 ms for the translation and unrelated prime conditions, respectively) which was significant in both the subject and item analyses [F s(1, 39) = 16.32, MSE = 495.8; Fi(1, 179) = 48.08, MSE = 736.5]. There also was a significant priming effect in the error data (3.5% vs. 4.7% errors for the translation and unrelated prime conditions, respectively), F s (1, 39) = 3.96, MSE = 7.9; F i(1, 179) = 7.10, MSE = 19.8. As the main issues investigated here focus on the RT data, and there was no speed-accuracy trade off in the RT data, the error data were not analyzed further. The mean RT and error rate for nonword targets were 597 ms and 3.5%, respectively.
RT distributions of the L2-L1 priming effect: ex-Gaussian analyses and quantile analyses
RT distributions were fitted with QMPE, ver. 2.18 (Cousineau, Brown & Heathcote, Reference Cousineau, Brown and Heathcote2004; Heathcote, Brown & Mewhort, Reference Heathcote, Brown and Mewhort2002) to obtain estimates of the ex-Gaussian distribution parameters, μ, σ, and τ. In order to best describe the RT distributions, the maximal numbers of quantiles (n – 1, where n is the number of data points per condition) were used to fit the data (Heathcote et al., Reference Heathcote, Brown and Mewhort2002; Rouder, Lu, Speckman, Sun & Jiang, Reference Rouder, Lu, Speckman, Sun and Jiang2005; White & Staub, Reference White and Staub2012). The exit codes indicated that all fits successfully converged. Figure 1 shows the shapes of the estimated RT distributions for L1 targets primed by L2 translation words and unrelated words. For μ, there was a significant 10 ms difference between the translation and unrelated conditions (443 ms vs. 453 ms) [t(39) = −2.78], indicating that the priming effect is associated with a shift in the distribution. For σ, there was a marginal effect with the translation condition tending to be less variable than the unrelated condition (34 ms vs. 38 ms) [t(39) = 1.98, p = .06]. For τ, there was a significant 10 ms difference between the translation and unrelated conditions (83 ms vs. 93 ms) [t(39) = 2.18], indicating that priming effects were larger toward the right tail of the distribution.
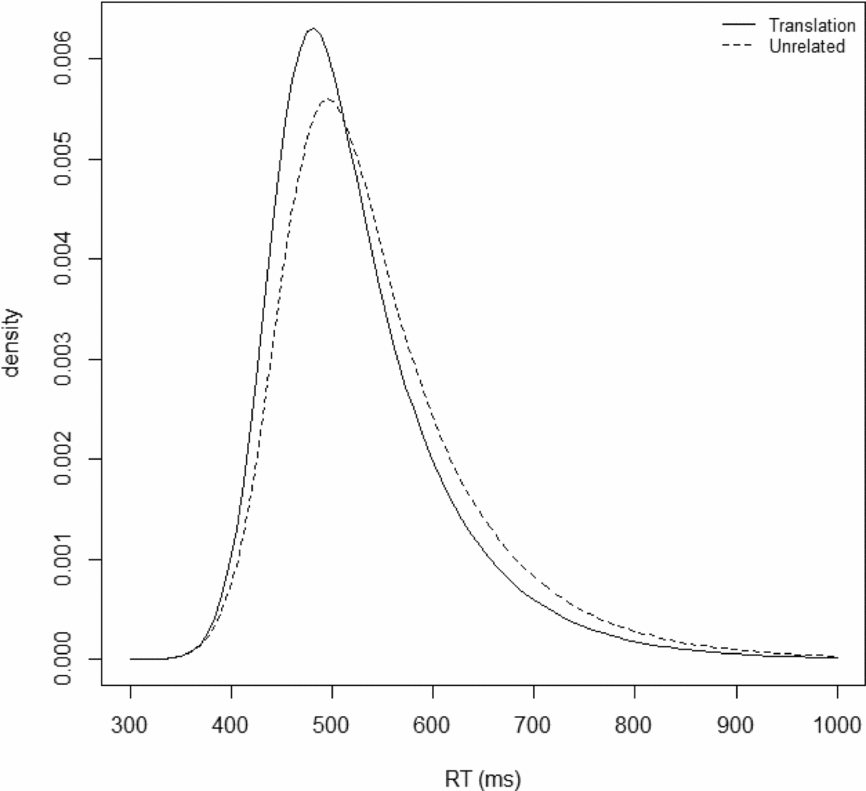
Figure 1. Shapes of the estimated RT distributions for L1 targets primed by L2 translation words and unrelated words.
In the quantile analysis, all RTs in the same condition for each participant were rank ordered and then the RTs were grouped into bins allowing calculation of the .2, .4, .6, and .8 quantiles, opting for as much reliability in the data as possible. The mean quantiles based on the empirical RTs are plotted in Figure 2. The calculated means for each participant in each bin were then analyzed by 2 (Prime Type: Translation vs. Unrelated) x 4 (RT Bin: 1, 2, 3, 4) repeated measures ANOVA. For the Bin factor, the assumption of sphericity was violated and, thus, the Greenhouse-Geisser correction for degrees of freedom was used in interpreting the results associated with that factor. There was a significant main effect of Prime Type [F(1, 39) = 17.07, MSE = 1734.5]. The main effect of Bin was also significant [F(1,143.01) = 201.18, MSE = 3843.4]. More importantly, Prime Type significantly interacted with Bin [F(1.6, 62.6) = 5.29, MSE = 365.9]. The priming effect became larger as responses became slower, which was statistically verified by the significant Prime Type x Bin linear trend interaction [F(1, 39) = 7.59, MSE = 399.3] with there being no additional significant interactions when considering any of the higher order trends [all Fs < 1.2, ns]. Finally, consistent with the distributional shift documented in the overall distributional analysis (i.e., a shift in µ), a significant priming effect was evident in the fastest quantile [a 12 ms effect, t(39) = 4.12, SEM = 2.9]. Thus, it does appear that the two analyses of the latency distributions are telling the same story.Footnote 3
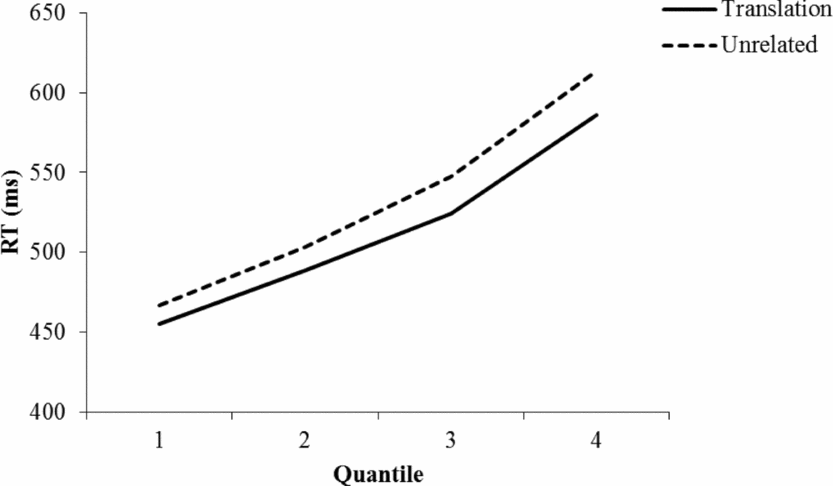
Figure 2. Quantile plot of the significant L2-L1 priming effect for very proficient bilinguals observed in the present experiment.
Discussion
The present results showed a significant 20 ms L2-L1 priming effect, confirming the fact that this effect can be observed reliably with a group of highly proficient bilinguals even if their languages involve different scripts (Nakayama et al., Reference Nakayama and Ida2016). In the distributional analyses, the ex-Gaussian analysis indicated that the priming effect is associated with both a shift in the means and a differential positive skewing of the distributions. The quantile analysis of the empirical RT distributions was consistent with the ex-Gaussian analysis; a significant priming effect was apparent throughout but increased across quantiles. Based on previous theorizing concerning the nature of masked priming effects (e.g., Balota et al., Reference Balota, Yap, Cortese and Watson2008), in the Introduction we discussed two possible patterns that might emerge in the distributional analyses following a significant L2-L1 priming effect, either a shift in the distributions alone or a differential skewing of the distributions (i.e., larger priming effects on slower trials) with the potential for a shift as well. Thus, the observed distributional pattern was inconsistent with the former prediction and generally consistent with the latter. The question, of course, then becomes, what was the nature of processing that produced this pattern?
The existence of priming in the shorter quantiles indicates that at least some L2 primes must have been processed fast enough to produce priming even in the faster trials, although it's also possible that some primes were not. This specific pattern of priming actually fits nicely within the framework of the BIA+ Model (Dijkstra & van Heuven, Reference Dijkstra and Van Heuven2002). That model assumes that L2 words are processed slowly because their resting activation levels are generally low. A priming effect, therefore, would only be expected from those primes that have been processed sufficiently by the time the target was presented. Because resting activation levels of words are tightly related to their frequency, if this explanation is correct then the prime's frequency should be a primary determinant of the size of the priming effects (i.e., there should be a positive relationship between prime frequency and priming). This expectation is examined below.
The existence of larger priming effects in the longer quantiles would also be consistent with the BIA+ position, particularly if one makes the assumption mentioned in the Introduction, that prime processing continues after the target has been presented. That is, when target processing is slower, there is more time for even more slowly processed primes to be processed to a level that would allow them to facilitate target processing as long as the target presentation does not terminate prime processing prematurely. Hence, a second expectation would be that target frequency would be a strong determinant of the size of the priming effects (i.e., there would be a negative relationship between target frequency and priming). This expectation is also examined below.
What should be noted is that if these patterns hold, they would not allow us to distinguish between an activation process account versus a strategic-use process account of the nature of the priming effect. That is, while priming in the BIA+ is based on an activation process, it might also be possible to explain our pattern in terms of strategic use of the prime (e.g., prime information is, in some way, used to a greater degree when responding to difficult items (e.g., Gollan et al., Reference Gollan, Forster and Frost1997)). In fact, Balota et al. (Reference Balota, Yap, Cortese and Watson2008, Experiment 7) found that when targets processing was made difficult by degrading their targets, the distributional pattern of masked semantic priming was associated with both a shift in and a differential skewing of the distributions. This pattern (i.e., larger priming effects on slower trials) was deemed to reflect a greater reliance on masked primes that occurs when target processing is difficult. Note that although our targets were not degraded, the L1 targets used in the present experiment were, in general, relatively low frequency words (M = 36) and included some very low-frequency words (e.g., about 30% of the targets occurred less than 5 times per million). As a result, there would have been a number of difficult-to-process targets in this experiment, potentially making the increased use of prime information on difficult trials an attractive strategy, assuming that participants have the ability to do so. Therefore there may very well be a theoretical parallel between our results and Balota et al.’s results for their degraded targets.Footnote 4
Prime frequency and/or target frequency as explanations for the distributional patterns
To investigate the impact of prime and target frequency, we analyzed L2-L1 priming effects using linear mixed effects (LME) models using lme4 (Bates, Maechler, Bolker & Walker, Reference Bates, Maechler, Bolker and Walker2015) and the lmer Test package (Kuznetsova, Brockhoff & Christensen, Reference Kuznetsova, Brockhoff and Christensen2014). In this analysis, the critical fixed factors were Prime Type (Translation vs. Unrelated), Prime Frequency and Target Frequency, and the random factors were by-subject and by-item intercepts and by-subject and by-item slopes for Prime Type. The values used for Prime Frequency were those of the translation equivalents (not those of the unrelated primes). However, doing so seemed reasonable because translation primes and unrelated primes were selected pair-wise, and thus the two variables were strongly correlated (r = .97). Prior to the analyses, raw RT was transformed by using the transformation -1000/RT to meet the Gaussian assumption required by the LME analysis. Prime Type was contrast coded by 0.5/-0.5, and both frequency factors were log-transformed and centered around their respective means.Footnote 5
As might be expected, our initial analysis showed that Target Frequency was significantly correlated with Prime Frequency (r = .20) [t(178) = 2.66]. One statistical treatment to eliminate the collinearity would be to regress one variable against the other and use the residual term for the regressed predictor as a new predictor (e.g., Kuperman, Bertram & Baayen, Reference Kuperman, Bertram and Baayen2008; Lemhöfer et al., Reference Lemhöfer, Dijkstra, Schriefers, Baayen, Grainger and Zwitserlood2008; Miwa, Dijkstra, Bolger & Baayen, Reference Miwa, Dijkstra, Bolger and Baayen2014). However, the correlation was smaller than the ones that seemed to require using this residualizing procedure in the past (e.g., r 12 > .50 according to Kuperman et al., Reference Kuperman, Bertram and Baayen2008). Therefore, following the recommendation by Wurm and Fisicaro (Reference Wurm and Fisicaro2014), we entered the two variables simultaneously.
The main effect of Prime Type was significant [t = 6.63]. Consistent with the results of the mean RT analysis, there was a significant 19 ms priming effect. The main effect of Target Frequency was also significant [t = −6.78]. Lower frequency targets were associated with significantly longer responses. In addition, the main effect of Prime Frequency was also significant [t = −3.90]. Responses were significantly slower overall when lower-frequency L2 words primed targets. This latter effect indicates that L2 primes, although they are likely not consciously identified, were nevertheless processed at least to the lexical level. Target Frequency and Prime Frequency did not interact [t < 1]. With respect to the central issues, those involving the Prime Type factor, there was a significant two-way interaction between Prime Type and Target Frequency [t = −2.71], indicating that priming effects were larger for lower frequency targets. This result is consistent with the idea that priming effects increase because the prime has a greater impact when target processing is difficult. On the other hand, Prime Type did not interact with Prime Frequency [t < 1]. This result is not consistent with the idea that priming effects would be strongly affected by prime frequency (i.e., that higher-frequency primes would be more likely to produce priming). Importantly, however, there was a significant three-way interaction between Prime Type, Target Frequency and Prime Frequency [t = −2.78]. The three-way interaction indicated that the nature of the Prime Type by Target Frequency interaction differed depending on Prime Frequency.
In an effort to better understand the significant three-way interaction between Prime Type, Prime Frequency and Target Frequency, we looked at the Prime Type by Target Frequency interaction in four different prime frequency ranges (n = 45 in each) from the lowest to the highest (Ms = 14, 42, 98, and 410 occurrences per million, respectively). Treating Prime Frequency in this way (i.e., as a categorical variable) did not eliminate the significant three-way interaction [t = −2.45]. When the Prime Type x Target Frequency interaction was examined in each of the prime frequency ranges, Prime Type did not interact with Target Frequency in any of the lowest three prime frequency ranges [all ts < 1]. Such was also the case when the three lowest prime frequency ranges were combined and analyzed together [t = −1.11, n.s.]. That is, when targets were primed by L2 primes from the lowest three prime frequency ranges (range 3–158, that is, 75% of the primes in the present experiment), priming effects were statistically equivalent across target frequency.
The source of the three-way interaction, therefore, can be found when considering the highest frequency primes. For those primes (frequency range 173–1959), there was a significant interaction between Prime Type and Target Frequency [t = −2.90]. Inspection of this Prime Type by Target Frequency interaction revealed that for targets primed by unrelated L2 words, response latencies became significantly faster as target frequency increased [i.e., a standard target frequency effect, t = −3.68]. On the other hand, for targets primed by L2 translation equivalents, response latencies were statistically equivalent across target frequency [t = −1.30, n.s.] (i.e., the slope was not statistically different from 0, indicating no target frequency effect). The non-significant interaction between Prime Type and Target Frequency for items in the three lowest frequency L2 prime ranges (combined) is shown in the right panel of Figure 3 and the interaction for items in the highest frequency L2 prime range is shown in the left panel of Figure 3.

Figure 3. Priming effects as a function of target frequency by the highest prime frequency range (left panel) and for targets primed by the first three lower prime frequency ranges (right panel).
Our LME analyses were conducted to test two ideas following from our analysis of the BIA+ model's predictions concerning priming effects as a function of prime and target frequency. The first idea was that slow L2 prime processing can reduce or eliminate priming effects. The second idea was that slower L1 target processing leads to increased priming effects. We will discuss our results with regard to these possibilities in some detail in the General Discussion, however, to summarize the results described above, what we found is that the sizes of priming effects were in general equivalent across prime frequency and also across target frequency with one exception. The exception was when very high-frequency L2 words primed L1 targets; in that situation, there was greater priming for lower frequency targets (Figure 3, left panel). Essentially, high frequency L2 translation primes, caused the target frequency effect to disappear. Such was not, of course, the case for targets primed by unrelated L2 words: responses became faster as target frequency increased (i.e., a standard frequency effect). As a result, the priming effect for the highest frequency targets, when preceded by the highest frequency primes, disappeared.
General Discussion
The present research was conducted in order to gain a better understanding of the nature of L2-L1 noncognate translation priming effects. Using very proficient Japanese–English bilinguals, we examined the shape of the RT distributions for the relevant conditions and explored the causes for that pattern by focusing on the effects of prime frequency and target frequency. The means-level analysis showed a significant L2-L1 priming effect, confirming that this effect is a reliable phenomenon, at least for very proficient bilinguals. The ex-Gaussian analysis showed that the significant L2-L1 priming was associated with both a shift in and a differential skewing of the distributions. The quantile analysis showed a similar pattern, that a significant priming effect was apparent across all RT bins with the effect increasing in the slower bins.
In an effort to analyze the observed distributional pattern in a more detailed way, priming effects were also examined as a function of both prime and target frequency using the LME model. One possibility considered for explaining the distributional pattern was the speed of processing L2 (prime) words. The assumption was that priming effects are dependent on whether there is sufficient time for conceptual level activation to arise from L2 translation primes. Specifically, high-frequency primes would be able to produce priming for more targets than lower-frequency primes. This idea would predict a priming advantage for higher-frequency primes. Inconsistent with this idea, the sizes of priming effects were, in general, not affected by prime frequency (the effectiveness of lower-frequency primes can be seen by examining the right panel in Figure 3). In fact, the only primes that were not effective were the high-frequency primes, when paired with high-frequency targets. The implication is that the distributional pattern of larger priming effects for slower trials cannot be explained in terms of inefficient processing of lower-frequency L2 primes.
What is also worth noting, however, is that there was an overall effect of prime frequency. Target responses were slower when the primes (both translation and unrelated) were lower in frequency. This result suggests that even these high proficient bilinguals were not able to process those lower frequency primes without some overall cost. The implications of this effect will be discussed below.
The other idea we examined was that the increase in priming for the slower trials was essentially an effect of target frequency, that is, that more slowly processed low-frequency L1 targets benefitted more from prime processing. As indicated in the Introduction, this type of effect could be due to an automatic activation of target information based on more fully processed primes (assuming that prime processing continues after the target is presented) although one could also propose that it arose from more extensive strategic use of the prime when target processing is difficult. In either case, the basic prediction was that larger priming effects would be expected as target frequency decreased. We found little evidence for this basic idea either. That is, as shown on the right panel of Figure 3, the sizes of priming effects were constant across target frequency for 75% of the primes.
The pattern of larger priming effects for lower-frequency primes did, however, emerge for a subset of items, targets that were primed by our highest frequency primes (see the left panel of Figure 3). As noted, these high-frequency translation primes produced target latencies unaffected by target frequency while, for unrelated primes, a standard target frequency effect was observed. As a result, the rapidly processed high-frequency L1 targets showed no priming following high frequency L2 primes whereas the more slowly processed low-frequency L1 targets showed a large priming effect following high frequency L2 primes. As one might imagine, it was this interaction observed for the high frequency primes that essentially drove the observed distributional patterns in the present experiment. Specifically, the smaller priming effects for the shorter quantiles occurred because trials involving high-frequency L1 targets primed by very high-frequency L2 words (those pairs showing no priming) were most frequently found in the shorter quantiles. Indeed, as shown in the right panel of Figure 3, if we had not included very high frequency primes in this experiment, the RT distribution pattern would have clearly involved a shift only, a result that would be consistent with previous distributional analyses of within-language masked semantic priming effects (Balota et al., Reference Balota, Yap, Cortese and Watson2008, for clear targets; Gomez et al., Reference Gomez, Perea and Ratcliff2013).
Our overall pattern, therefore, appears to suggest the following type of account. For most primes and targets, priming effects are fairly constant showing that very proficient bilinguals are able to process masked L2 primes up to the conceptual level, even quite low-frequency L2 primes. This fact also suggests that the assumption noted at the end of the Introduction, that prime processing continues after the target has been presented, is likely a viable one. That is, it seems unlikely that in the 70 ms between the presentation of the prime and the target (a 47 ms prime presentation plus a 23 ms backward mask), all primes, regardless of their frequency could have been processed to the same level. Instead, at least in the majority of cases, prime processing, at least at the conceptual level, must be continuing after target onset.Footnote 6
This assumption is also supported by the fact that there was an overall Prime Type effect, latencies were longer for lower frequency primes in both the translation and unrelated prime conditions. What this result suggests is that, although all primes were ultimately processed to approximately the same degree regardless of their frequency, prime frequency likely determined the speed of their processing. As a result, there was likely more prime processing ongoing after target onset when the prime was of lower frequency (i.e., prime and target processing went on together longer when the prime was of lower frequency). To the extent that ongoing prime processing robbed capacity from target processing, target latencies would be slowed, producing a Prime Frequency effect of the sort that was observed.
How, exactly, would this process, outlined above, unfold? An argument can be made based on previous masked priming studies that there is some type of processing reset when the visual recognition system detects a sufficient perceptual mismatch (i.e., soon after the target is presented, a reset of prime processing occurs). Critically, this reset appears to affect form level information from the prime, but not necessarily conceptual level information. That is, the idea is that, although form level information from the primes may be reset by target presentation, conceptual level processing can still go on (Forster, Reference Forster2013; Grainger, Lopez, Eddy, Dufau & Holcomb, Reference Grainger, Lopez, Eddy, Dufau and Holcomb2012). Thus, if form-level L2 prime processing has already passed some critical threshold, continuing activation of conceptually-based information will be possible, as it would be unaffected by any reset. Presumably, if prime processing at the form level has not been sufficiently advanced at the point that the target is presented (e.g., when primes are very low frequency words, when SOA/prime duration is short or, most importantly for the present research, when bilinguals are low-proficient ones), the chance of conceptual facilitation would be greatly diminished.
The implication of this reasoning is that the presence/absence of the L2-L1 priming may depend to a substantial degree on how efficiently bilinguals can process the prime's form level information in order to allow activation of conceptual information. Note that this idea would seem to predict that it would be harder to get L2-L1 priming when the two languages are not formally similar because, in those situations, the reader's form processing skills in their L2 would be weak. Hence, this account would explain why, as noted initially by Schoonbaert et al. (Reference Schoonbaert, Duyck, Brysbaert and Hartsuiker2009), many previous reports of null L2-L1 priming effects tended to involve bilinguals whose L2 has a completely different orthography from their L1 (Gollan et al., Reference Gollan, Forster and Frost1997; Jiang Reference Jiang1999; Jiang & Forster, Reference Jiang and Forster2001; Nakayama et al., Reference Nakayama, Sears, Hino and Lupker2013; Wang & Forster, Reference Wang and Forster2015; Witzel & Forster, Reference Witzel and Forster2012; Xia & Andrews, Reference Xia and Andrews2015) and many reports of significant effects tended to involve bilinguals whose L2 has the same or a similar orthography as their L1 (Dimitoropoulou et al., Reference Dimitropoulou, Duñabeitia and Carreiras2011b: Duyck & Warlop, Reference Duyck and Warlop2009; Schoonbaert et al., Reference Schoonbaert, Duyck, Brysbaert and Hartsuiker2009).Footnote 7 Of course, the strength of the connection between the form level representation and the conceptual level representation would also play a role in determining whether prime processing at the form level would have been sufficient to activate conceptual processing. Significant priming would, presumably, be difficult to observe if the form level activation did not easily flow into the conceptual level representations because of weak connections.
The role/importance of form level processing may explain why, as noted in the Introduction, Dimitropoulou et al. (Reference Dimitropoulou, Duñabeitia and Carreiras2011b) did not report that L2 proficiency affected the sizes of L2-L1 translation priming for their Greek–English bilinguals. Certainly, their results could have been due to a weak L2 proficiency manipulation (as discussed in Nakayama et al., Reference Nakayama and Ida2016, Dimitropoulou et al.’s three proficiency groups did not appear to differ to any great degree). However, it may also have been due to L2 proficiency having only a very small effect on the form level processing skills of their bilinguals because the Roman and Greek alphabets are quite similar orthographically. On the other hand, for bilinguals whose two languages have completely different orthographies, as is the case for Japanese and English or Chinese and English, L2 proficiency may play much a greater role in their ability to process form level information in their L2.
The final question, of course, is what explains our results for the very high frequency primes, the set of stimuli that did show a smaller priming effect for high-frequency targets (and, by doing so, produced the overall pattern in the distributional analyses)? As noted, there was an overall prime frequency effect: higher-frequency primes produced shorter overall latencies. Most likely then, processing of these very high-frequency primes would generally have been completed faster than for all the other prime types, which would have caused them to draw very little capacity during target processing as well as to strongly pre-activate their L1 translation equivalents (possibly to the full extent possible). As such, it is, perhaps, unsurprising that the impact of target frequency would substantially diminish when the prime is a translation prime. In contrast, on the unrelated prime trials, because the L1 target would not have been activated by the prime, a standard target frequency effect would emerge. As a result, one would expect that the priming effect would be reasonably large for low-frequency targets and would shrink as target frequency increases (and LDT latency decreases), as shown in the left panel in Figure 3.Footnote 8
Conclusion
In our distributional analysis in the present experiment, we found that significant L2-L1 priming effects in terms of mean latencies were associated with both a shift in and a differential skewing of the latency distributions. A more detailed analysis, however, showed that this pattern was produced essentially entirely by our very high-frequency L2 primes. Otherwise, the sizes of L2-L1 priming effects were generally constant across prime frequency and target frequency, indicating that, in general, L2-L1 priming effects tend to be associated with a shift in the distributions alone. Our data also showed that difficult prime processing delayed response latencies, which appears to be due to the primes continuing to be processed conceptually during target processing. We believe, therefore, that these results do provide new information that helps better understand the nature of the L2-L1 translation priming effect for highly proficient bilinguals.
As noted earlier, many previous experiments found a null L2-L1 cognate translation priming effect in an LDT and researchers have not yet discovered the precise factors that determine when the effect will emerge. Investigations focusing on this specific issue have started (e.g., Nakayama et al., Reference Nakayama and Ida2016; Wang & Forster, Reference Wang and Forster2015), but given the complexity of the phenomenon, further research is clearly going to be needed. Although still speculative, we propose that the presence/absence of L2-L1 noncognate translation priming may be predicted by how efficiently a prime's form level information can be resolved and how strongly form level information is connected to the conceptual level information. In subsequent analyses of factors leading to the absence of an L2-L1 priming effect, distributional analyses will be clearly a useful tool. Specifically, it will be useful to examine the shape of the RT distributions of low-proficient bilinguals, those who typically do not show significant L2-L1 priming when considering mean latency. Further, examining the effects of lexical variables (i.e., prime frequency and target frequency) will also provide important information in understanding L2-L1 priming effects (or the lack of such effects) in less proficient bilinguals.






