The object of our study is
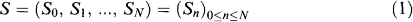
where each Sn is a m-dimensional stochastic (real valued) vector, i.e.
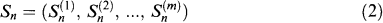
denned on a probability space (Ω, 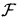 , P) and adapted to a filtration (
, P) and adapted to a filtration (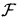 n)0≤n≤N with
n)0≤n≤N with 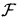 0 being the σ-algebra consisting of all null sets and their complements. In this paper we interpret
0 being the σ-algebra consisting of all null sets and their complements. In this paper we interpret 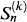 as the value of some financial asset k at time n.
as the value of some financial asset k at time n.
Remark: If the asset generates dividends or coupon payments, think of 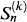 as to include these payments (cum dividend process). Think of dividends as being reinvested immediately at the ex-dividend price.
as to include these payments (cum dividend process). Think of dividends as being reinvested immediately at the ex-dividend price.
Definition 1
(a) A sequence of random vectors
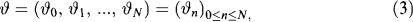
where
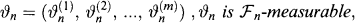
is called a trading strategy. Since our time horizon ends at time N we must always have ϑN ≡ 0.
The interpretation is obvious: 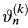 stands for the number of shares of asset k you hold in the time interval [n,n + 1). You must choose ϑn at time n.
stands for the number of shares of asset k you hold in the time interval [n,n + 1). You must choose ϑn at time n.
(b) The sequence of random variables
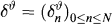
where 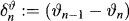 Sn stands for the payment stream generated by ϑ (set ϑ−1 ≡ 0).
Sn stands for the payment stream generated by ϑ (set ϑ−1 ≡ 0).