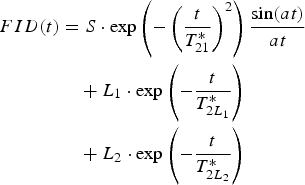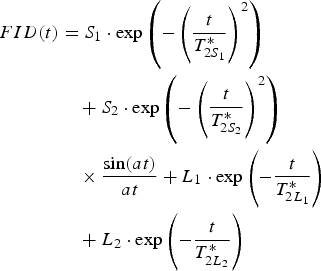Introduction
Among extremophilic Antarctic lichens, Umbilicaria aprina Nyl. belongs to the species surviving under the harshest environmental conditions of low temperature and/or water deficit. Schroeter et al. Reference Schroeter, Green, Kappen and Seppelt1994, measured the CO2 exchange rates of Umbilicaria aprina in its natural habitat (Cape Geology, Antarctica). They detected the net photosynthesis down to -17°C (which is the lowest temperature of photosynthesis recorded in field conditions), whereas the dark respiration significantly decreased at -7°C and ceased at -11°C. Light maximum value of net photosynthesis declined with temperature in two phases: first, rapidly, between -1°C and -9°C to about 10% of the rate at +1°C, second, slower but steadily, to very low rates at -17°C (Schroeter & Scheidegger Reference Schroeter and Scheidegger1995). They suggested that a two step mechanism of net photosynthesis decline with decreased temperature might be the result of increased CO2 diffusion resistance, possibly by the ice nucleation activity (INA) which occurs in water saturated thalli of Umbilicaria aprina at -5.4°C (Schroeter & Scheidegger Reference Schroeter and Scheidegger1995). In fact, numerous lichen species display biological INA in thallus extracts at temperatures much higher than the low temperature limit of their photosynthetic activity (Nash et al. Reference Nash III, Kappen, Loesch, Larson and Matthes-Sears1987, Kieft Reference Kieft1988, Kieft & Ahmadjian Reference Kieft and Ahmadjian1989, Kieft & Ruscetti Reference Kieft and Ruscetti1990, Schroeter & Scheidegger Reference Schroeter and Scheidegger1995). Low-temperature scanning electron microscopy revealed the extracellular ice formation within the thallus, leading to cytorrhysis in the photobiont cells and to cavitation in the mycobiont cells. Both processes are reversible with the re-warming of thalli (Schroeter & Scheidegger Reference Schroeter and Scheidegger1995).
Many other lichen species of genus Umbilicaria share the unusual ability to survive low temperature. Umbilicaria decussata (Vill.) Zahlbr. can resist slow freezing at liquid nitrogen temperature (-196°C), and rapid freezing at -78°C, whereas U. vellea (L.) Hoffm. from Central Europe resists slow and rapid freezing at -196°C and -50°C, respectively (Kappen Reference Kappen1993).
The intracellular space mild dehydration (Harańczyk et al. Reference Harańczyk, Gaździński and Olech2000a, Reference Harańczyk, Gaździński and Olech2000b) accompanied by the stimulated ice nucleation in extracellular spaces (Schroeter & Scheidegger Reference Schroeter and Scheidegger1995, Harańczyk et al. Reference Harańczyk, Grandjean and Olech2003a, Reference Harańczyk, Grandjean, Olech and Michalik2003b) is one of the ways of dealing with freezing. Thus it is very interesting to observe water uptake from the gaseous phase by a lichen.
A good example of the lichen gaseous phase hydration ability is the hydration process occurring from snow cover. Umbilicaria aprina showed net photosynthesis and dark respiration down to -4°C when a lichen thallus was rehydrated only from snow (Schroeter & Scheidegger Reference Schroeter and Scheidegger1995). In Usnea sphacelata R. Br. and in Umbilicaria aprina snowfall can activate photosynthetic CO2 uptake below 0°C (down to -10°C and to -17°C, respectively) (Kappen Reference Kappen1989, Schroeter et al. Reference Schroeter, Green, Kappen and Seppelt1994). Water uptake from snow at freezing temperatures occurs from the gaseous phase via sublimation and requires a water potential gradient between the dehydrated lichen thallus and surrounding snow.
The effectiveness of thallus hydration from the gaseous phase focused our attention on the process of hydration during its initial stages, various water fractions (differentiated by the proximity to the thallus surfaces) and their mobility. We used hydration kinetics, sorption isotherm and high power proton nuclear magnetic resonance relaxometry for our investigations.
As a result of adaptation, the temperature and magnitude of the net photosynthesis maximum change with the average temperatures in lichen habitat. For example the Mediterranean population of U. nylanderiana (Zahlbr.) H. Magn. shows an increase in the temperature of the net photosynthesis maximum to +15°C from +3°C for the Antarctic population (Sancho et al. Reference Sancho, Valladares, Schroeter, Kappen, Davidson, Howard-Williams and Broady2000). As the adaptation to a mild habitat may change the temperature range of lichen physiological activity, we assumed that the molecular mechanisms dealing with extremely low temperature and desiccation shock resistance would be ideally developed in lichens often experiencing the most extreme environmental conditions. Thus, we used thalli of U. aprina collected in continental Antarctic, as representative of individuals from a harsh habitat.
Materials and methods
Umbilicaria aprina Nyl. thalli were collected from a glacial stream in Schirmacher Oasis, Queen Maud Land, East Antarctica, on 2 February 2004, and at an altitude of 107 m above sea level. Air-dry thalli were stored at room temperature with the hydration level Δm/m 0 = 0.096 ± 0.010, where m 0 is the dry mass of the sample, and Δm is mass of water taken up.
Before the hydration experiments thalli were incubated for 164 hours over silica gel (p/p 0 = 0%), dehydrating to the hydration level Δm/m 0 = 0.048 ± 0.004.
The hydration time-courses were performed from the gaseous phase with controlled humidity, at room temperature (t = 22°C), over the surface of H3PO4 (p/p 0 = 9%), over the surface of supersaturated solutions of CaCl2 (p/p 0 = 32%), Na2Cr2O7 (p/p 0 = 52%), Na2S2O3 (76%), K2CrO3 (88%), Na2 SO4 (93%), and over a water surface (p/p 0 = 100%). After completing the hydration courses, the dry mass of the thallus was determined after heating at 70°C for 72 h. Higher temperatures were not used as they could cause the decomposition of some organic constituents of the thallus (Gaff Reference Gaff1977).
Hydration kinetics experiments were performed on one sample per given relative humidity. The air-dry thalli used for the NMR measurements were chopped and placed in NMR tubes, and then the hydration procedure was performed. The NMR measurements were performed on eight samples. Every sample covered a part of the hydration range which overlapped with other parts.
Proton free induction decays (FIDs) were recorded on WNS HB - 65 high power relaxometer (Waterloo NMR Spectrometers, St Agatha, Ontario, Canada). The resonance frequency was 30 MHz (at B 0 = 0.7 T); the transmitter power was 400 W; the pulse length π/2 = 1.4 µs. The high power of the pulse allowed us to observe the total proton signal. FIDs were acquired using a Compuscope 2000 card in an IBM clone computer, controlling the spectrometer, and averaged over 2000 accumulations. Repetition time was 2.003s. The data obtained were analysed using the one-dimensional, FID analysing procedure of the two-dimensional (in time domain) NMR signal-analysing program CracSpin written at the Jagiellonian University, Cracow (Węglarz & Harańczyk Reference Węglarz and Harańczyk2000).
Results
Hydration kinetics
The hydration trials for U. aprina thalli performed from the gaseous phase at the relative humidity, p/p 0, controlled between 9% and 76%, were fitted well by a single exponential function (see Fig. 1)
where Δm/m 0 is the relative mass increase, A 1h is the saturation level for the fast component (solely observed in this relative humidity range), t 1h is the corresponding hydration time constant, and C h is the total hydration level for saturation.

Fig. 1. The rehydration of the lichen Umbilicaria aprina from the gaseous phase at different values of relative humidity p/p 0, recorded as relative mass increase expressed in units of dry mass Δm/m 0. Targets humidity (p/p 0) open circles = 9%, closed circles = 32%, open squares = 52%, closed squares = 76%, open triangles = 88%, closed triangles = 93%, asterisks = 100%. The error bars are within the plot symbols.
At a relative humidity higher than 76% the slow hydration component appeared and the hydration courses were fitted well by the two-exponential function (Fig. 1)
where A 0h = C h − A 1h − A 2h is the saturation level at incubation (p/p 0 = 0%), A 1h and A 2h are the saturation hydration levels for the fast and slow component, t 1h and t 2h are the corresponding hydration time constants.
The value of A 0h, averaged over all hydration courses, equals 0.054 ± 0.011, which is close to that obtained for the other species of Antarctic lichens, e.g. for fruticose Usnea antarctica Du Rietz A 0h = 0.040 ± 0.011, (Harańczyk et al. Reference Harańczyk, Pietrzyk, Leja and Olech2006b).
The amplitude of the tightly bound water fraction A 1h = 0.059 ± 0.038, with the hydration time t 1h= (4.7 ± 2.6) h. The loosely bound water fraction, appearing for hydration traces performed for higher values of relative humidity (p/p 0 > 76%), is characterized by the hydration time t 2h = (31.0 ± 1.9) h and a saturation level A 2h that increases gradually with increased humidity.
Two-exponential functions of hydration kinetics are characteristic for fruticose thalli, whereas for foliose thalli, in milder habitats, e.g. Umbilicaria antarctica Frey & Lamb from maritime Antarctic, single exponential kinetics is observed (Harańczyk Reference Harańczyk2003).
The total saturation hydration level, C h = A 0h + A 1h + A 2h, obtained at a given relative humidity, p/p0, was taken for construction of sorption isotherms.
Sorption isotherm
For U. aprina thalli the adsorption isotherm reveals a sigmoidal form (Fig. 2), which is usually well fitted by the Dent (Dent Reference Dent1977) and/or the BET (Brunauer et al. Reference Brunauer, Emmett and Teller1938) model. Both models distinguish two types of water binding sites on the surfaces of the system investigated, namely, i) ‘primary’ water binding sites (directly to the adsorbent surface); and ii) ‘secondary’, usually weaker, water binding sites (to the primary bound water molecules, or to the previous water layers). The difference is that the BET model takes a fixed value of the ratio of the number of binding sites covered by n water molecules to that covered by n-1 water molecules, b = S n/S n-1|h=1 = 1 (which is to some extent an artificial assumption), whereas in the Dent model this ratio may be varied between 0 and 1 (partially simulating the clustering effect).
The sorption isotherm for both models is described by
where h is relative humidity, p/p 0, expressed in absolute units, ΔM/m 0 is the mass fraction of water saturating primary binding sites. At h = 1 the contribution of empty primary binding sites, S 0, is expressed through the reciprocal of b 1 as S 0/S 1|h=1 = 1/b 1.
To test the relevance of the sorption model the sorption isotherm is usually presented in parabolic form (see Fig. 3). The parabolic form for the Dent isotherm is expressed as
where parameters ΔM/m 0, b, b 1 are connected with A, B, C by the formulas

Fig. 3. Parabolic form of Dent and BET model (open circles = experimental data, solid line = fitted Dent model, dotted line = fitted BET model).
The parabolic form of the BET isotherm is described by
For U. aprina thalli the sorption isotherm is much better described by the Dent model (see Fig. 3). The mass fraction of water saturating primary water binding sites was ΔM/m 0 = 0.054, which is the number slightly lower than for fruticose lichens and for U. antarctica from maritime Antarctic, where ΔM/m 0 = 0.073 (Harańczyk Reference Harańczyk2003). For U. aprina the model parameter b, indicating the applicability of the Dent model, is equal 0.941, a value slightly higher than for other lichens, e.g. for Usnea antarctica b = 0.913. The contribution from empty binding sites at h = 1 is given by 1/b 1 = 0.02% (expressed as a percentage) for U. aprina, which is comparable to that for U. antarctica, for which 1/b 1 = 0.09% (Harańczyk Reference Harańczyk2003). The contribution of empty binding sites at h = 1, S0/N ≈ 10-5, where N is the total number of primary binding sites.
Compared to other investigated lichens, U. aprina shows elevated hydrophilicity of the thallus surfaces (higher b 1 parameter; even higher that of U. antarctica) and a slightly lower density of primary water binding sites.
Proton free induction decays
The free induction decay for protons of U. aprina thallus, at lower hydration levels, is well fitted by the superposition of one Gaussian component, with the amplitude S coming from the solid matrix of thallus and one exponential component with amplitude equal to L 1. For higher hydration levels two exponential components, L 1 and L 2, coming from water tightly and loosely bound on the surfaces of thallus, respectively are observed (Harańczyk et al. Reference Harańczyk, Gaździński and Olech1998, Reference Harańczyk, Gaździński and Olech2000a, Reference Harańczyk, Pietrzyk, Leja and Olech2006b)
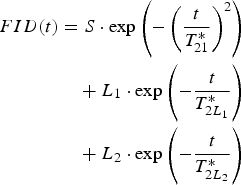
where T *2S is the proton spin-spin relaxation time of solid component taken as the 1/e-value of Gaussian solid signal, and T *2L 1 and T *2L 2 are the relaxation times of proton liquid fractions L 1 and L 2 respectively. A typical FID is shown in Fig. 4.

Fig. 4. a. Proton free induction decay recorded for Umbilicaria aprina thalli at 30 MHz; the pulse length π/2 = 1.4 µs. The relative mass increase was Δm/m 0 = 0.114. Y-axis shows the normalized signal amplitude. The solid line represents a least squares fit of Eq. (6a) to the data with the fitted parameters given in the figure legend (Amp1 = S, Amp2 = L1 and Amp3 = L2). b. The residual function calculated as the difference between the fitted and recorded values of the FID signal, which for any recorded point does not exceed 1.44%.
The solid signal for lichen thalli is usually nearly Gaussian in form (Harańczyk et al. Reference Harańczyk, Gaździński and Olech2000a), and in the present case we obtained satisfactory Gaussian fits. The spin-spin relaxation time for solid component, T *2S, is close to the value obtained for other lichen thalli (e.g. for Usnea antarctica T *2S ≈ 18 µs), and for different solid tissues such as dentine, dental enamel, the shells of molluscs, bark and bast (e.g. Harańczyk et al. Reference Harańczyk, Gaździński and Olech1998, and the references therein), which suggests similar distribution of local magnetic fields (Pintar Reference Pintar1991).
The residuals calculated for the fits of Eq. (6a) to the data show a beat pattern (Fig. 4b), which may be observed if a solid FID signal with oscillations in its tail, is fitted to a superposition of Gaussian and exponential functions. A better model for such a solid FID signal is the product of a Gaussian and a sinc function (called an Abragam function) (Abragam Reference Abragam1961, Derbyshire et al. Reference Derbyshire, Van Den Bosch, Van Dusschoten, Macnaughtan, Farhat, Hemminga and Mitchell2004). We analysed the applicability of an Abragam function to describe the solid signal for U. aprina, testing two models of FID function:
a) the solid signal described solely by Abragam function, plus one or two exponentials (liquid components);
(6b)
b) the solid signal described by superposition of Gaussian and Abragam function, plus two exponentials for liquid components:
(6c)
For hydration levels below Δm/m 0 ≈ 0.09 only model (b) is fitted, because model (a) gives non-physical values for some of the fitted parameters (negative values for the signal fractions), and T *2 values that are either too long or too short to be physically meaningful (compared with the known range of water proton T *2), or at least almost constant in the time range of sampling points. For higher hydration levels several sets of data are successfully fitted using both (a) and (b), but for other datasets only model (b) works. In cases where both models are applied to a particular dataset either T *2L 1 or T *2L 2 is not altered much; the value of T *2S 1 for the Gaussian, for fits involving the Gaussian-Abragam combination of Eq. (6c), is almost the same as for the cases where the solid signal is fitted solely by the Gaussian function. However, even for reasonable values of parameters the contributions of both solid components, S1 and S2, fluctuate randomly over a wide range of values with the increased hydration level. This suggests that the Abragam function contribution does not reflect any hydration-correlated effects. In some cases the FID shape of the solid components has more structure than that of a simple Gaussian so that application of a more complicated function improves the fit somewhat, but does not affect the conclusions reached in this report. Beat pattern in line shape gives the value of parameter a, with the averaged value close to a ≈ 0.12 µs-1 (giving the NMR solid line half-widths (Δω = 2a) ≈ 38 kHz). The sinc function parameter a shows no monotonic, continuous or step-wise changes caused by the hydration process, which suggests that the present experiments cannot discern a clear change with hydration in the solid component of the signal fitted by the Abragam function.
Often the solid signal fitted by Abragam function is a marker of a glassy state in dry amorphous samples (Crowe Reference Crowe2002). However, glass transition temperature, T g, for sugar-water systems decreases very rapidly with water content (Gordon & Taylor Reference Gordon and Taylor1952). The hydration levels for which the Abragam function is successfully fitted to the solid signal component in U. aprina extends to much higher levels than those for lichen sugar(including starch)-water binary systems for which T g occurs at room or at higher temperatures. Preliminary DSC courses performed by us for U. aprina thalli at several hydration levels of thallus did not reveal glass transition for temperatures up to +50°C (M. Marzec, personal communication 2008). This suggests that the modelling of the solid FID signal in U. aprina, with superposition of Gaussian function and Abragam function, yields a reasonable approximation of the solid signal, but it is not a marker of the presence of glassy state.
The observed water fractions are differentiated by their mobility and, thus, by their binding and/or proximity to the thallus surfaces, which means that intracellular water as well as extracellular water fraction usually contributes to both these water fractions. The T *2L 1 ≈ 100 µs of the L 1 component is characteristic of tightly bound water in lichen thalli as well as of many biological systems (e.g. Harańczyk et al. Reference Harańczyk, Gaździński and Olech1998, and the references therein). The L 2 signal with T 2L 2* ≈ 550 µs, shortened by B 0 inhomogeneities, comes from water loosely bound on thallus surface and, for higher hydration levels, from free water fraction (Figs 4 & 5).

Fig. 5. The hydration dependence of proton FID relaxation times for Umbilicaria aprina. Solid Gaussian, S, component – closed circles, tightly bound water, L1, component – open triangles, and loosely bound water, L2, fraction – open squares.
The spin-spin relaxation times measured in FID experiment are shortened by B 0 inhomogeneities according to (Timur Reference Timur1969)
where T 2 is spin-spin relaxation time, γ is gyromagnetic ratio, and Δ B 0 is a change of magnetic field B 0 within the sample. The solid and short exponential components in the FID experiment are detected and not changed by Δ B 0 as compared to those measured by the CPMG echo train, but the measured T *2L 2 may be an average T *2L 2 values of several loosely bound water pools, e.g. extra- and intramolecular loosely bound water pools.
For U. aprina the relaxation time T *2S for the Gaussian component does not vary much with thallus hydration level (Fig. 5), suggesting that the structure of the solid matrix of the thallus is not appreciably modified by the hydration process. Thus we used solid signal amplitude, S, as an unit with which to scale the amplitudes of liquid components.
The hydration dependence of total liquid signal, expressed in the units of solid, (L 1 + L 2)/S, is shown in Fig. 6 and is well fitted by the rational function

Fig. 6. The (L 1 + L 2)/S hydration dependence for Umbilicaria aprina. The solid line was calculated from Eq. (8).
The hydration dependence of the liquid-to-solid signal amplitude ratio is described by the rational function if the water soluble solid fraction is present in the sample (Harańczyk et al. Reference Harańczyk, Strzałka, Jasiński and Mosna-Bojarska1996). If all of the water soluble solid fraction is dissolved, the liquid-to-solid hydration dependence becomes linear (Harańczyk et al. Reference Harańczyk, Węglarz and Sojka1999), which was not observed for initial hydration steps for the thallus of U. aprina.
The detailed analysis of hydration dependencies for both observed liquid signal components shows that tightly bound water fraction saturates with increasing hydration level (open triangles on Fig. 7). It confirms the assignment of the L 1 fraction to water closest in proximity to the lichen thallus (presumably first hydration shell (Harańczyk Reference Harańczyk2003)). The loosely bound water fraction, visualized as L 2/S, is influenced by the water soluble solid fraction (see Fig. 8). The hydration dependence of L 2/S is well fitted by the rational function

Fig. 7. The population of monolayer sorption predicted by the Dent isotherm in thallus of Umbilicaria aprina (solid line), and L 1/S (open triangles) hydration dependence.

Fig. 8. The L 2/S hydration dependence for Umbilicaria aprina. The solid line was calculated from Eq. (9).
Sorption isotherm fitted to NMR data
Total liquid signal hydration dependence may be used to construct the NMR-isotherm, with the same sorption parameters (ΔM/m 0, b, and b 1) obtained from gravimetry. Only the constant water component A, ‘sealed’ in thallus pores, and the proportionality coefficient k, scaling NMR signal in units of water mass, should be fitted. The proportionality coefficient depends on the ratio of proton densities in aqueous medium to that in the solid matrix, and on the ratio of the screening effect on the liquid signal to that on the solid signal caused by paramagnetic ions present in the system. This method allows the combination of the classic sorption isotherm with NMR hydration data.
The normalized amplitude of NMR total liquid signal expressed as a function of h was fitted to the function:
The line in Fig. 9 (showing the data in Fig. 6 re-plotted as a function of h), marked by the small, open triangles, was calculated from Eq. (10) with the best- fit parameters k = 7.14 ± 0.28 and A = 0.

Fig. 9. Sorption isotherm fitted to total FID proton liquid signal for water hydrating thallus of Umbilicaria aprina. Open circles = experimental data, line marked by small open triangles = Dent model with one k-coefficient Eq. (10), line marked by small open circles = Dent model with two different k-coefficients Eq. (11).
If paramagnetic ions, present in the solid matrix, affect the proximal, tightly bound water and more distant, loosely bound water differently, the respective influence being quantified through k 1 and k 2, then a two-k parameter model applies
![\eqalign{{L_1 + L_2 \over S} \lpar h\rpar & = A + {\Delta M \over m_0} {b_1 h \over 1 + \lpar b_1 - b\rpar h} \cr &\quad\times\left[k_1 + k_2 {bh \over 1 - bh}\right]}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160203104204390-0465:S0954102008001363_eqn14.gif?pub-status=live)
The line in Fig. 9, marked by the small, open circles, was calculated from Eq. (11) with the best-fit parameters k 1 = 2.0 ± 1.3; k 2 = 8.0 ± 3.4, and for A = 0. This two-k model clearly yields a significantly better approximation of the total liquid NMR signal (Fig. 9).
The fact that application of each of the two models yields A = 0 means that the fraction of bound water ‘sealed’ in pores of the solid matrix of thallus is not present in the thallus of U. aprina (as it is in lyophilized photosynthetic membranes (Harańczyk et al. Reference Harańczyk, Leja and Strzałka2006a)). Having two different values of k is consistent with paramagnetic ions on the lichen's surface affecting the signal from tightly bound water differently from that from loosely bound water.
The hydration dependence of the tightly bound water fraction is well fitted by the sorption isotherm for water saturating primary binding sites in the Dent model (Dent Reference Dent1977). The function fitted to the NMR hydration data (Fig. 7) was
The solid line in Fig. 7 was calculated from Eq. (12) with best-fit parameters k 1 = 2.6 ± 0.2 and A = 0. These parameter values are consistent with values obtained from NMR sorption isotherm analysis for the total water signal. This suggests that for the U. aprina thalli tightly bound water signal L 1 may be attributed to primary bound water fraction in Dent sorption isotherm, although the criterion for this differentiation is different in both methods (bond strengths in sorption isotherm, and hindered mobility in NMR).
Discussion
During the daylight period in Antarctica, in situ hydration level of Lasallia pustulata (L.) Mérat varies between Δm/m 0 = 0.5 and 4.0, whereas it varies between 1.0 and 5.0 for Umbilicaria spodochroa (Hoffm.) DC. in Lam. & DC. (Kappen et al. Reference Kappen, Schroeter, Hestmark and Winkler1996). For twelve species from the genus Umbilicaria the maximal water content (after 30 min soaking in distilled water) varied from 1.55 for U. cinereorufescens (Schaer.) Frey to 3.10 for U. polyrrhiza (L.) Ach., with the volume of intracellular spaces varying from 0.69 to 0.44, respectively (extracellular spaces were airfilled, waterfilled, or partially occupied by gelatinous substances) (Valladares et al. Reference Valladares, Sancho and Ascaso1998). The upper limits of hydration levels significantly exceed the hydration level obtained by us for U. aprina hydrated from the gaseous phase.
Field measurements have shown that in Ramalina terebrata Hook. f. & Taylor net photosynthesis is lower in thalli hydrated to Δm/m 0 = 1.12 than in thalli hydrated to <0.92 (with the maximum at 0.87) (Kappen et al. Reference Kappen, Bölter and Kühn1986). The maximum of CO2 exchange occurs for Usnea sphacelata R. Br. (=Usnea sulphurea Th. Fr.) and for Usnea aurantiaco-atra (=Usnea fasciata) at Δm/m 0 = 0.70 (Kappen Reference Kappen and Brown1985), for Lasallia pustulata at Δm/m 0 = 1.50 and for U. spodochroa at Δm/m 0 = 0.90 (laboratory conditions, temperature t = +5°C) (Kappen et al. Reference Kappen, Schroeter, Hestmark and Winkler1996). For Umbilicaria decussata the optimal net photosynthesis is recorded at Δm/m 0 = 1.0, for U. aprina at Δm/m 0 = 1.2, whereas for Usnea antarctica and for Usnea sphacelata it is at Δm/m 0 = 0.85 (Kappen & Breuer Reference Kappen and Breuer1991). Interesting information on U. aprina rehydration from the gaseous phase is available from the rehydration courses conducted from snow. At -4°C, the photosynthetic CO2 exchange was monitored, and the functional response of the thallus on hydration was not directly proportional to Δm/m 0. Thus, with hydration level increased up to Δm/m 0 = 0.20 no significant rates of CO2 exchange were found. At Δm/m 0 = 0.30 CO2 release indicated respiratory activity in the thallus, and at 0.40, positive gas exchanges were observed. An equilibrium was reached after 20 h at Δm/m 0 ≈ 0.60 with a photosynthetic rate of +1.1 µM CO2kg-1 (Schroeter & Scheidegger Reference Schroeter and Scheidegger1995).
The above data, for hydration levels at which optimal photosynthesis occurs, compares well with the maximal total saturation hydration level obtained during gaseous phase hydration in our experiment (at p/p 0 = 100% equal of Δm/m 0 = 0.848 ± 0.009, see Fig. 1) and shows the very high effectiveness of U. aprina hydration performed purely from the gaseous phase, allowing this thallus to obtain a hydration level close to that needed for optimal net photosynthesis.
The analysis of the hydration of U. aprina thallus enables us to distinguish three types of bound water, differentiated by the proximity to the thalli surfaces, namely i) very tightly bound water (Δm/m 0 = 0.054 ± 0.011), which is bound with a short hydration time compared to the values recorded using static gravimetry, and detected for higher values of target humidity ii) tightly bound water (Δm/m 0 = 0.051 ± 0.038), which saturates for low hydration levels and has an hydration time t hyd = (4.7 ± 2.6) h, and iii) loosely bound water with its mass increasing with relative humidity of the gaseous environment, and which has an hydration time t hyd = (31.0 ± 1.9) h. Proton relaxation does not distinguish very tightly and tightly bound water by mobility. Sorption isotherm models treat very tightly bound components as water bound to ‘primary’ water binding site. All three water fractions may occur in intracellular spaces as well as in extracellular spaces of thalli.
Sorption isotherm fitted to NMR data showed the absence of a ‘sealed’ water fraction trapped in pores of U. aprina, which is consistent with the model in which partial drying of the thallus is one of the ways to preserve lichens from ice nucleation inside the thallus. The ‘sealed’ water fraction, containing a freezing loosely bound water pool (Harańczyk et al. Reference Harańczyk, Grandjean and Olech2003a, Reference Harańczyk, Grandjean, Olech and Michalik2003b) might initiate the growth of ice crystallites. Different k-coefficients being needed for tightly (L 1) and loosely (L 2) bound water, to properly model the behaviour of total liquid signal with hydration, shows the different effect of paramagnetic species on the NMR signal of these two water phases. The gyromagnetic ratio is c. 2000 higher for electrons than for nuclei and the influence of electron paramagnetic species on the signal is amplified by photosynthetic manganese migration to the outer surfaces of the photosynthetic membranes of the photobiont (Wydrzynski et al. Reference Wydrzyński, Marks, Schmidt, Govindjee and Gutowsky1978, Robinson et al. Reference Robinson, Sharp and Yocum1980, Reference Robinson, Sharp and Yocum1981).
The water soluble solid fraction in horse chestnut bark comes from sucrose (Harańczyk et al. Reference Harańczyk, Węglarz and Sojka1999), which focuses attention on the simple sugars when elucidating the origin of a similar fraction in U. aprina. In fact, the accumulation of large quantities of monosaccharides (glucose, fructose, mannitol, and arabitol) in lichen mycobionts (in Evernia esorediosa (Müll. Arg.) Du Rietz, in Ramalina subbreviuscula Asah., and in Ramalina sublitoralis Asah.) may be an adaptative feature for growing in dry conditions (Hamada et al. Reference Hamada, Okazaki and Shinozaki1994). Thalli of Umbilicaria decussata (hydrated to Δm/m 0 ≈ 2.0) collected from wet habitats of Clark Peninsula, Windmill Islands, East Antarctica, did not differ in total levels of low molecular weight carbohydrates from thalli collected from dry habitats (Δm/m 0 ≈ 0.17). Usually, in the samples from wet habitats the proportion of algal products (ribitol) relative to fungal products (arabitol and mannitol) was greater (Melick & Seppelt Reference Melick and Seppelt1994). However, the NMR experiment could not decide what sugar fraction forms the water soluble solid fraction in U. aprina populating post glacial streams because in the present range of hydration the total amount of this fraction was not dissolved.
Acknowledgements
We would like to thank the reviewers for their comments and suggested improvements.