Introduction
As climate changes alter global temperatures and weather patterns, understanding how these changes affect active layer temperature dynamics in climatically sensitive regions, such as the Western Antarctic Peninsula (WAP), becomes increasingly important. Between 1951 and 2004, mean annual air temperatures (MAAT) along the WAP increased by 2.9°C, compared to the global rise in MAAT of 0.5°C over the same period (van Lipzig et al. Reference van Lipzig, Marshall, Orr and King2008). The regional warming of the WAP is typically attributed to the positive shift in the Southern Hemisphere Annular Mode (SAM) beginning in the 1960s. This shift in atmospheric weather patterns has been amplified by the loss of stratospheric ozone over the Antarctic region during the last 50 years (Marshall et al. Reference Marshall, Orr, van Lipzig and King2006).
Increases in air temperature can significantly alter the environment of temperature-sensitive areas, such as the WAP, through the melting of glaciers, thawing of permafrost and increase in annual degree-days (Gupta & England Reference Gupta and England2006). Thawing of permafrost is often used as an indicator of long-term warming in a region (WMO 1997). Although several studies have examined the atmospheric conditions controlling permafrost depth in the Northern Hemisphere, relatively little is known about atmosphere–soil interactions along the WAP (Turner et al. Reference Turner, Overland and Walsh2007).
The effects of high latitude atmospheric conditions on ground temperatures have long been the focus of many studies in the Northern and Southern Hemispheres. In northern Mongolia, soil temperature fluctuations closely follow those of solar radiation inputs and air temperature variations, while winter snow thickness also plays a role in the control of ground temperature variations (Heggem et al. Reference Heggem, Etzelmuller, Anarmaa, Sharkhuu, Goulden and Nandinsetseg2006). When Alaskan ground temperatures were compared to several climatic factors, air temperature was determined to be the most important factor controlling ground temperature, where a 20% increase in air temperature would increase ground temperatures by nearly 2°C. Snow depth was the second most influential factor with a 28% increase in snow depth increasing ground temperatures by 1.1°C (Zhang & Stamnes Reference Zhang and Stamnes1998). Snow accumulation timing can also be a very influential factor on ground temperatures. In Switzerland, a one month delay in autumn snow accumulation decreased ground temperatures by 0.5°C. The delay in snow cover accumulation increased the time of interaction between atmosphere and ground allowing for colder air temperatures to exchange with the ground (Luetschg et al. Reference Luetschg, Lehning and Haeberli2008). In interior Antarctica, air temperature, solar radiation and snow cover along with wind speed were the most important factors controlling ground temperatures in the soils of eastern Antarctica (R 2 =73%) (Guglielmin et al. Reference Guglielmin, Balks and Paetzold2003, Adlam et al. Reference Adlam, Balks, Seybold and Campbell2010). Along the Antarctic Peninsula, ground temperatures and active layer thicknesses at Rothera Station were proportional to summer air temperatures and inversely related to autumn snow depths (Guglielmin et al. Reference Guglielmin, Worland, Baio and Convey2014).
The objective of this study was to investigate thermal interactions between the atmosphere and ground in soils of Amsler Island along the WAP. While there are several atmospheric conditions that can affect temperatures within an unconsolidated material, we will determine which factors are the most closely correlated with active layer temperatures. We hypothesize that throughout the summer season active layer temperature variations will be closely related to four atmospheric conditions: i) air temperature, ii) solar radiation, iii) precipitation and iv) wind speed. We also suggest that during the winter, active layer temperature fluctuations will be strongly related to both air temperature and snow depths. These five mechanisms account for the largest conductive and convective means of heat transfer through unconsolidated materials.
Site description
The study was conducted on Amsler Island (64.76°S, 64.07°W), a small island (0.90 km north–south and 1.9 km east–west) along the coast of the WAP. Amsler Island is located 1 km south-east of the larger Anvers Island where Palmer Station is located (Fig. 1). Operated by the United States Antarctic Program, Palmer Station provides long-term atmospheric data sets. From 1995–2013 the MAAT of Palmer Station ranged from -2.6°C to -0.7°C. Anvers Island receives 714–1410 mm of water-equivalent precipitation annually. During winter, snow depths can exceed 1 m; however, most seasonal snow cover on deglaciated regions melts in the summer.
Fig. 1 Amsler Island map. Modified from Google Earth’s Digitalglobe 2012 image.
The summit of Amsler Island is on the north shore with an elevation of 68 m a.s.l. The eastern 200 m of the island contains stagnant glaciers and ice fields, and the remainder of the island is ice-free. A 120 m wide east–west, glacially derived valley bisects the island; much of the island’s snowmelt drains into this valley and collects in seasonal ponds on the eastern end. This valley has a gradual (0–13%) slope from NW–SE, while the surrounding bedrock slopes are very steep (60–90%). There are also sporadic tuffs of Antarctic hairgrass (Deschampsia antarctica Desv.) throughout the island. The basin of the central valley is filled with outwash sands 1–2 m thick, which covers glaciolacustrine sediments that are>1 m thick. Along the southern boundary of the central valley there are large solifluction lobes overriding outwash sands. Active layer depths are potentially extremely deep at this location, 7–10 m thick (Wilhelm & Bockheim Reference Wilhelm and Bockheim2016).
Materials and methods
Monitoring station
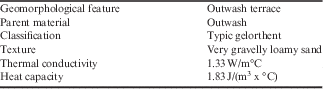
In April 2011, a soil climate and atmospheric monitoring station was installed in the central valley of Amsler Island (Table I). Data were recorded using a Campbell Scientific CR1000 logger powered by a combination of a 12 V, 155 amp hour deep cycle battery and a 90 W, 12 V solar panel (BP590J, BP Solar). Three Campbell Scientific 107-L temperature sensors (error≤±0.01°C) were installed within 1 m of the monitoring station at depths of 0.02, 0.6 and 1.6 m below the ground surface. The temperature sensors were in direct contact with the soil, and mean hourly temperatures were recorded. Data from the temperature sensor nearest the surface (0.02 m) was considered to be analogous to measuring ground surface temperatures. Above ground, the climate station had six instruments recording atmospheric conditions: an air temperature probe (109-L, Campbell Scientific), a relative humidity probe (HMP-45C, Vaisala), a pyranometer (LI200X-L, LI-COR) which recorded solar radiation, an anemometer (05103, R.M. Young) which recorded wind speed and direction, and a tipping bucket rain gauge (TE525WS, Texas Electronics). Data from all devices were sent to the logger every minute but only an hourly mean was recorded. Also attached to the monitoring station was a time-lapse camera; this camera was aimed toward six, 1 m tall snow stakes and took a picture every four hours. Information from these pictures aided in determining snow event timing and snow depths.
Table I Amsler Island monitoring station site description.
Soil collection
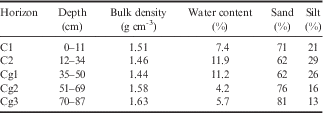
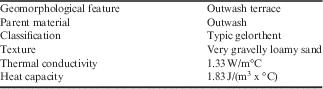
A soil pit was dug at the monitoring station to a depth of 1.6 m and soil descriptions were taken. Maximum annual temperatures at 2 m depths were measured to be>0°C and no ice was found in soil pores; both soils are classified as Entisols. Soil samples from each horizon were collected for laboratory analysis (Table II). Soil particles were separated into sand, silt and clay fractions using a Coulter LS230 laser (Arriaga et al. Reference Arriaga, Lowery and Mays2006). Soil cores were collected using an Uhland coring device (Blake Reference Blake1965). Bulk density was estimated from sand and organic matter contents using the equations of Minasny & Hartemink (Reference Minasny and Hartemink2011).
Table II Monitoring station soil horizon characteristics.
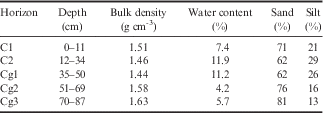
Thermal conductivity and heat capacity of surface soil samples were collected in triplicate from around the climate station for use in the dampening depth prediction equations (Table I). Measurements were taken from the centre of each core using a KD2 Pro probe (Decagon Devices). Thermal conductivity and heat capacity were recorded under both thawed and frozen conditions; for consistency each measurement was repeated three times.
Data analysis
Weather conditions at the nearby Palmer Station have been continuously monitored since the mid-1990s. We use these data in conjunction with our climate station data to better understand a wider range of atmospheric conditions in the area (see Table III and Table S1 found at https://doi.org/10.1017/S0954102016000511). Although the Amsler Island climate station and Palmer Station report data by the hour or minute, for simplicity we combined all data collected between 2011 and 2014 into daily, weekly or monthly averages. Using data sets from both recording locations, we are able to examine a much more diverse set of atmospheric data.
Table III Amsler Island monthly average data.
For atmospheric data, monthly averages from 2011–14.
For ground surface temperature data, monthly averages from October 2011 to February 2014.
± indicates standard deviation from mean value, n=3.
Winter season snow depths were determined through examining daily, mid-afternoon images taken with the time-lapse camera. Depths of the six marked snow stakes in the view-field were averaged for a daily snow depth. Days where the camera was covered by snow or when the camera was not functional were filled-in with readings reported by Palmer Station.
In soils, it can be difficult to accurately predict thermal lags, particularly under natural conditions where precipitation and drainage constantly alter water contents. The most commonly used method to determine thermal lag times is to use the heat transfer equation. However, this equation assumes steady state conditions with no changes in water content (Smerdon et al. Reference Smerdon, Pollack, Enz and Lewis2003). In the present study we were interested in evaluating both the heat transfer method and a second observational method where the 0°C isotherm was tracked and a thermal propagation rate was calculated.
With each variation in ground surface temperatures, there is a delay between that change and the thermal response from within the active layer. This delay time varies based on soil texture, water content, depth and magnitude of temperature change, which makes correlations between atmospheric conditions and active layer temperatures difficult. To work around this thermal lag, soil properties were applied to the heat transfer equation (Hillel Reference Hillel2004):
$$T(z,t)\, {\equals}\, T_{{ave}} A_{0} \left[ {{\rm sin}\left( {\omega t \, {\minus}\, {z \over d}} \right)} \right]e^{{{{{\minus}z} \over d}}} ,$$
where T represents temperature (°C), z is depth below surface (m), t is time (s), A is the air temperature amplitude in given period (°C), ω is the period (s) and d is dampening depth (m). Dampening depth (d) is determined by (Jury & Horton Reference Jury and Horton2004):
$$d\, {\equals}\, \left( {{{2K} \over {C\omega }}} \right)^{{\!\!{1 \over 2}}} ,$$
where K is thermal conductivity (W/m°C) and C is heat capacity (J/(m3 x °C)). While Eq. (1) determines what the predicted temperature should be at a given depth, an important estimate in this study was the length of time it would take for a change at the surface to reach a given depth. Within Eq. (1) the
$${\minus}{z \over d}$$
formula is specific in accounting for the delay between surface temperature changes and changes within the soil. It should be kept in mind that
${\minus}{z \over d}$
is a steady state approach which takes into account only the most prominent factors in thermal propagation; seasonal variations in water content are not taken into account. This equation provides an approximate delay time that allows for a comparison between climatic variations and their effects on below ground active layer thermal dynamics.
Temperature propagation rates within the soil, during thaw, were calculated by first selecting an easy to observe temperature event, which in this study was when temperatures crossed the 0°C isotherm. The start of isotherm transmission was when temperatures at 0.15 m below the surface (a depth where short-term atmospheric effects were minimal) had consistently crossed the 0°C isotherm (going into positive temperatures). When this event was observable at the maximum monitored depth, the number of days between initial surface observation and final maximum depth observation were summed. The maximum monitored depth was then divided by the summed period of time to determine the rate of temperature movement in centimetres per day:
$$\eqalignno{ &{{\rm Temperature}\,{\rm propagation}\, {\equals}\, } \cr &\ {{{{\rm Maximum}\,{\rm monitored}\,{\rm depth -Transmission }\,{\rm start}\,{\rm depth}} \over \displaystyle{\mathop{\sum}{{\rm Days }\,{\rm for }\,{\rm event}\,{\rm to}\,{\rm travel}\,{\rm from }\,0.15\,{\rm m} \,{\rm depth}} \atop \displaystyle{{\rm to}\,{\rm maximum }\,{\rm monitored}\,{\rm depth}} \atop \displaystyle \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \qquad \,(3)}}.$$
Thermal diffusivity was measured at the soil surface (data not shown), but not below ground; since soil conditions change with depth diffusivity rates measured at the surface cannot be assumed to be the same underground.
Statistical comparisons
To determine the influence of summer (defined in this study as months with an mean snow depth<0.1 m) atmospheric conditions on ground temperatures at Amsler Island, mean, minimum and maximum air temperature, wind speed and direction, air pressure, relative humidity, and solar radiation were compared to ground temperatures (surface and at-depth) using the Spearman correlations in the R statistical program (R Core Team 2014). Mean monthly values for 2011–14 were used for each factor in the comparisons (Table III). The Spearman method was selected for these comparisons since it is a nonparametric comparison that is not sensitive to outliers (Hollander et al. Reference Hollander, Wolfe and Chicken1973, Choi Reference Choi1977). The same comparison was made on an annual basis to determine how the presence of a deeper snow cover would change the relationship between atmospheric conditions and ground temperatures.
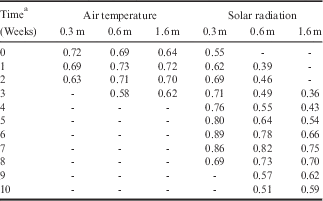
To determine the effects of atmospheric factors on temperature variations below the ground surface, thermal lag times in non-steady state conditions must be taken into account. To accomplish this, ground temperatures at three depths (0.3, 0.6, 1.6 m) were compared to the two climatic conditions with the strongest relation to ground surface temperatures (solar radiation and mean air temperature) for each of the preceding ten weeks, using Spearman correlations. The atmospheric measurements (back-calculated from the ground temperatures) which had the best correlation to ground temperatures can be assumed to be the approximate thermal lag time experienced in the soils (and should be similar to the number of days calculated by the heat transfer method). The strength of the correlation should also indicate which atmospheric factor is most influential on temperatures below the ground surface (Fig. 2)
Fig. 2 Thermal lag correlation (hypothetical). Schematic of how lag times were accounted for between seasonal atmospheric factors (such as peak air temperature and peak solar radiation) and seasonal maximums in ground temperature. The numbers are correlation coefficients calculated between the weekly averages of the two factors. In this example solar radiation peaked in Week 1 while temperatures at a depth of 1.6 m under the ground surface peaked on Week 4 indicating a three week lag period. This image is for methodological purposes and the displayed measurements are hypothetical.
Results
Atmospheric effects on ground surface temperature
January was the warmest month recorded on Amsler Island with a mean monthly temperature of 1.4°C. September was the coldest month with a mean temperature of -5.5°C (Table III). The maximum incoming solar radiation of 214 W m-2 occurred a month earlier (December) than the maximum air temperatures. The highest wind speeds were observed during winter, 10–15 km h-1 from the south-east, while during summer the wind speeds were 6–13 km h-1 from the south-west. Air pressure and relative humidity were relatively consistent throughout the year at 983–994 mb and 75–82%, respectively. During the summer, total liquid precipitation was 27–56 mm per month, while monthly snow depths during winter averaged 0.2 m and had maximum depths of up to 1 m with an estimated water equivalence of 292 mm per month. Monthly mean ground surface temperature trends followed those of air temperatures, with January being the warmest at 4.5°C and August being the coldest at -5.3°C (Table III).
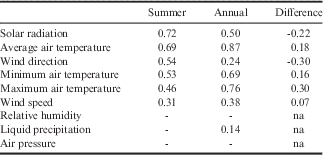
Ground surface temperatures during the summer (typically December to May) were strongly correlated and significantly related to incoming solar radiation and mean air temperature (R 2 =0.72 and 0.69, respectively, P≤0.001) (Table IV). Ground surface temperatures were less strongly correlated but still significantly related to mean wind direction and minimum air temperatures (R 2 =0.54 and 0.53, respectively, P≤0.01). There were weak correlations between ground surface temperature and maximum air temperature and wind speed (R 2 =0.46 and 0.31, respectively, P≤0.05), while there was no significant correlation to relative humidity, liquid precipitation and air pressure (R 2 <0.30, P≥0.05).
Table IV Correlation coefficients between atmospheric factors and ground surface temperatures.
Correlations of monthly averages 2011–14.
Missing values had P>0.01.
Summer included months with an average of<0.1 m of snow cover.
Annual measurements were from April (the start of the winter season) to March.
When months with snow depths>0.1 m were factored into the correlations, ground surface temperatures were more strongly correlated with air temperatures (R 2 =0.87, 0.76, 0.69 for average, maximum and minimum air temperatures, respectively, P≤0.001), while the correlation to solar radiation was weakened (R 2 =0.50; P≤0.001) (Table IV). Liquid precipitation, and wind direction and speed were poorly correlated to ground surface temperature (R 2 =0.14, 0.24, 0.38, respectively, P≤0.01), while there continued to be no significant correlation to relative humidity and air pressure (R 2 <0.30, P≥0.05). The low correlation between precipitation and ground surface temperatures is further emphasized in Fig. 3, where high precipitation events do not consistently have associated temperature spikes.
Fig. 3 Temperature correlation to precipitation. Comparison of daily average temperatures to precipitation for January to March 2013; air temperatures (primary axis, hashed line), ground surface temperatures (primary axis, solid line) and precipitation (secondary axis, solid bars).
Thermal movement calculations
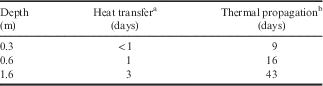
The heat transfer method (Eqs. (1) & (2)) used soil thermal properties to determine heat movement, while the thermal propagation method was established from observations of the 0°C isotherm (Eq. (3), Fig. 4). The heat transfer method determined that it would take three days for an event at the ground surface to transfer through the soil to a depth of 1.6 m (Table V). Thermal propagation observations indicated that the same event would take significantly longer, 43 days, to transmit 1.6 m through the soil. Movement rates of heat through soils are rarely constant; heat near the ground surface moves at a slower rate than heat deeper within the ground. During the early summer thaw in 2011, it took four weeks for the 0°C isotherm to travel from the surface to 0.6 m below the surface; then after four more days the zero isotherm travelled 1 m more to the deepest measured depth (Fig. 4).
Fig. 4 Climate station ground temperature profile of hourly ground temperatures between September 2011 and January 2014 (graphed in Origin). Light grey shading=>0°C, dark grey shading=<0°C.
Table V Thermal lag calculated times.
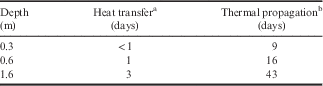
a Calculated from heat transfer equation.
b Observed 0°C isotherm thaw rate.
Atmospheric influences on ground temperature
Comparisons between measured ground temperatures (0.3, 0.6 and 1.6 m) and preceding solar radiation seasonal peaks revealed that correlations became stronger with increasing time differences, up to seven weeks (0.89), at all depths (Table VI). A similar comparison between ground temperatures and mean air temperature demonstrated that a time difference greater than two weeks (0.73) decreased the correlation between the two factors. Not only was there a lag of up to seven weeks between the solar radiation peak and temperature events at 1.6 m below ground surface, but there was a similar lag of up to six weeks between the solar radiation maximum and temperature maximums in the air and on the ground surface (Fig. 5).
Fig. 5 Climate station ground temperatures and solar radiation. Average monthly measurements for 2012 and 2013; incoming solar radiation (primary axis, solid bars), air temperature (secondary axis, solid line) and ground temperature at 0.02 and 1.6 m below surface (secondary axis, dashed lines).
Table VI Correlation between atmospheric factors and ground temperatures with increasing time gaps.
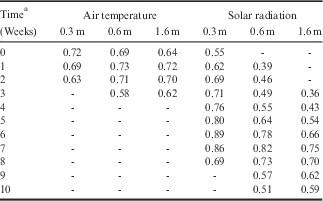
Correlations of monthly averages 2011–14 (P≤0.01).
Missing values had P>0.01.
a Time indicates the estimated number of weeks between mean ground temperature peak and mean atmospheric event peak (event being maximum seasonal air or solar radiation). Increasing the number of weeks increases the delay between atmospheric peak and ground temperature peak (see Fig. 2 for method).
Discussion
Atmospheric effects on ground surface temperature
Several atmospheric events factor into soil temperature variations; however, many are not as influential as others and have minimal effect on active layer temperature dynamics. The strong correlation between both incoming solar radiation and mean air temperature to ground surface temperature suggests that these two factors are highly influential on ground surface temperature variations (Table IV). Maximum solar radiation inputs occurred between November and January, while the highest mean air temperatures occurred between January and March; the highest mean ground surface temperatures occurred between December and February (Table III), suggesting that both factors are equally strong controllers of soil ground surface temperatures. In the absence of snow cover, solar radiation will directly strike the soil surface and since the albedo of soil is very low, energy from this radiation will be absorbed by the soils (Ishikawa Reference Ishikawa2003). The soil surface is also in direct contact with atmospheric air, so any variations in air temperature will directly influence ground surface temperatures as temperature gradients force heat transfers into or out of soil as the two bodies equilibrate (Kane et al. Reference Kane, Hinkel, Goering, Hinzman and Outcalt2001, Ishikawa Reference Ishikawa2003). While the timing of when heating or cooling events occurred within the soil were influenced by air temperature fluctuations, solar radiation inputs controlled atmospheric heating and increased the magnitude of these heating and cooling events on the ground surface.
It is unknown if the relationship between wind direction and ground surface temperature is true or a relic of near-ground wind directions shifting at the same time as solar radiation increases. During the summer, winds shifted from the mainland peninsula to coming from the open ocean where temperatures are moderated by the water. Several other studies examining winds along the Antarctic Peninsula have also found that winds primarily travel from the south and west (van den Broeke Reference van den Broeke2000), although continental winter katabatic winds can alter the winds to come slightly from the south-east (van den Broeke & van Lipzig Reference van den Broeke and van Lipzig2003).
Effects of snow cover
Atmospheric conditions were not the only factor influencing ground surface temperatures. The presence of snow also indirectly controlled the transfer of heat between the atmosphere and soil by acting as a barrier. The presence of a seasonal snow cover significantly strengthened the influence of atmospheric temperatures on ground surface temperatures while reducing the impact of solar radiation and wind direction (Table IV). The correlation changes confirm the lower albedo of snow-reflected solar radiation, decreasing the potential energy that could be absorbed by the soil surface (Zhang et al. Reference Zhang, Barry, Gilichinsky, Bykhovets, Sorokovikov and Ye2001). Snow cover also acted as a physical barrier between the atmosphere and the ground, preventing wind from convectively transferring temperature changes through the soils (Humlum Reference Humlum1997).
Although snow created a physical barrier preventing radiation inputs and air circulation, snow thicknesses were not enough to create a thermal barrier. A strong relationship between ground and air temperatures when months with snow cover were added to the comparison suggests that even the thickest snow depths measured on Amsler Island were not enough to completely insulate the ground surface from air temperature changes (Ishikawa Reference Ishikawa2003). Since snow thickness was not great enough to create a fully insulating body between air and ground temperatures, temperature gradients continued to be conducted through the snow to the ground surface. The minimum snow depth to create this barrier is dependent on snow properties; however, in the Northern Hemisphere, a general snow depth between 0.6 and 0.8 m is accepted as a complete thermal barrier (Keller & Gubler Reference Keller and Gubler1993, Hanson & Hoelzle Reference Hanson and Hoelzle2004). In the Swiss Alps, snow depths<0.6 m do not insulate the ground from atmospheric temperature changes (Luetschg et al. Reference Luetschg, Lehning and Haeberli2008). At Signy Island, ground surface temperatures were slightly cooler (<1°C) on average than air temperatures during the spring and autumn when snow depths were<0.3 m; the difference became greater under thicker (undefined) snow cover (Guglielmin et al. Reference Guglielmin, Worland and Cannone2012). Between 2011 and 2014, Amsler Island experienced only one winter with snow depths exceeding 0.6 m, indicating that snow cover in this region is not typically thick enough to become a thermal barrier, although during years with heavy snowfall it can become a potential insulating body.
Evaluation of thermal movement calculations
The heat transfer method calculated that it would take approximately three days for heat to transfer 1.6 m through the soils, while the thermal propagation method determined it would take significantly longer, 43 days, for heat to transfer to the same depth (Table V). While significantly different, neither method was incorrect, but rather a reflection of the data used in the calculations. The heat transfer method is an equilibrium model which calculated a single heat movement rate for the soil, regardless of changes in season or thermal conditions. Since thermal properties were measured during the summer, this method is only valid during months where temperatures were above freezing, and even then the heat transfer method will have some error due to variations in soil water content throughout the season. The slower rate calculated by the thermal propagation method was calculated by following the thawing front observed within the soil. Since the process of thawing ice takes large amounts of energy (latent heat of fusion=334 kJ kg-1), the transfer of sensible heat changes through thawing soils will be significantly slowed, compared to energy movement through previously thawed soils (Outcalt et al. Reference Outcalt, Nelson and Hinkel1990, Kane et al. Reference Kane, Hinkel, Goering, Hinzman and Outcalt2001).
Atmospheric influences on ground temperature
The influence of air temperature and solar radiation was not restricted to the ground surface; exchanges of heat at the surface are propagated through the soil affecting temperatures deeper in the soil. Comparisons between weekly mean ground temperatures and weekly mean air temperatures during previous weeks indicated that any changes in air temperature were propagated through 1.6 m of soil in one to two weeks, slightly longer than the lag time predicted by the heat transfer method (Tables V & VI). However, the strength of the correlation between solar radiation and ground temperatures demonstrated that there was a much larger lag between solar radiation events and associated ground temperatures, up to seven weeks.
While the large lag time after radiation events may appear similar to the number of days predicted by the thermal propagation method, the long lag time was actually due to a similar delay in the change of sensible atmospheric temperatures after solar radiation events (Fig. 5). During 2013, it was nearly six weeks after the solar radiation maximum when air temperatures reached a maximum. This delayed atmospheric reaction was due to a phenomenon called atmospheric phase lag, where incoming radiation was absorbed by water on the ground and in the air before sensible temperatures could begin to rise (Bintanja et al. Reference Bintanja, Jonsson and Knap1997). At the Faraday Antarctic Peninsula monitoring station, winter temperatures were delayed due to this atmospheric lag (van den Broeke Reference van den Broeke2000), while sea ice melting around the Antarctic Peninsula lagged one to two months behind the seasonal calendar due to thermal lag caused by phase change energy absorption (Hanna & Bamber Reference Hanna and Bamber2001). Once ground surface temperatures began to change, those variations were transferred through the soil with a delay time similar to those related to air temperature delays. Ground surface temperatures experienced thermal delays similar to air temperatures; however, temperature maximums were up to 5°C higher than those reached by air temperature due to the absorption of solar radiation by the soil surface.
Conclusions
With shifts in weather patterns and rising temperatures across the WAP, there becomes a greater need to understand how atmospheric conditions influence active layer thermal dynamics. The purpose of this study was to determine the most influential atmospheric factors on ground temperature dynamics. Thermal lag times were also examined in the study using observations and equations; which were applied to atmosphere–ground temperature comparisons to determine which atmospheric condition was the most influential below the ground surface.
Incoming solar radiation and mean air temperature had the strongest correlation to ground surface temperature when comparing atmospheric factors to ground surface temperatures during the summer months. Surprisingly, wind speed and precipitation, convective drivers of heat movement, had little influence on ground surface temperatures. Winter month snow cover strengthened the influence of air temperature on ground surface temperature, while the influence of solar radiation and wind direction became weaker. This relationship change indicated that accumulations of snow created a physical barrier, reflecting solar radiation and blocking wind circulation; however, the snow was not deep enough to prevent thermal exchange between the atmosphere and the ground.
Heat exchanges between the atmosphere and the ground surface are propagated through the ground; these propagation rates are based on the thermal conductivity and heat capacity of the soils. To determine the amount of time for an event to travel from the ground surface through the soil, two methods were examined: i) heat transfer method and ii) thermal propagation method. Application of the heat transfer method suggests that it would take three days for heat to move 1.6 m through the soil, while the thermal propagation method implies that it would take 43 days. The discrepancy in thermal movement rates is derived from latent heat absorption of energy during phase change which delayed the movement of the 0°C isotherm in the thermal propagation method.
Thermal lag was applied to ground temperatures by comparing weekly below ground temperatures to solar radiation and air temperature peaks from the preceding ten weeks. Solar radiation had the strongest correlation after a seven week delay, while the strongest correlation to air temperature occurred after a delay of two weeks. The discrepancy in lag times was due to a five week delay in atmospheric sensible heat increase after the solar radiation peak. The strong correlation after a two week lag was longer than the three days predicted by the heat transfer method because the calculation did not take variations in soil water content throughout the summer into account, potentially decreasing predicted thermal lag times.
Acknowledgements
The authors wish to thank the National Science Foundation (OPP_0943799) and the United States Antarctic Program for their support throughout this project, in particular John Evans, Cara Ferrier and Alexandra Isern, without whom this study would not have been possible. Thanks also to Adam Beilke, Neal Scheibe, Glenn Grant, Nicholas Haus and Graham Tilbury for helping in the field and maintaining equipment during the winter months. Finally, we would like to thank the crew of the Laurence M. Gould and the staff at Palmer Station for always being available to help with this project, without them this project would have been impossible. Funding for this project was provided by the National Science Foundation.
Author contribution statement
Kelly Wilhelm: site construction and maintenance, data collection and interpretation, manuscript research, writing and editing. James Bockheim: site construction and maintenance, scientific and editorial advice, and review of manuscript.
Supplemental material
A supplemental table will be found at https//doi.org/10.1017/S0954102016000511.
