Minimizing the ruin probability through capital injections

Ciyu Nie; David C. M. Dickson; Shuanming Li

doi:10.1017/S1748499511000054

Minimizing the ruin probability through capital injections

Published online by Cambridge University Press: 31 May 2011

Ciyu Nie ,

David C. M. Dickson and

Shuanming Li

Article contents

Abstract
Introduction
Preliminaries
Premium calculation for the reinsurer
Minimizing the ultimate ruin probability
Examples
Concluding remarks
References

Rights & Permissions

Abstract

We consider an insurer who has a fixed amount of funds allocated as the initial surplus for a risk portfolio, so that the probability of ultimate ruin for this portfolio is at a known level. We consider the question of whether the insurer can reduce this ultimate ruin probability by allocating part of the initial funds to the purchase of a reinsurance contract. This reinsurance contract would restore the insurer's surplus to a positive level k every time the surplus fell between 0 and k. The insurer's objective is to choose the level k that minimizes the ultimate ruin probability. Using different examples of reinsurance premium calculation and claim size distribution we show that this objective can be achieved, often with a substantial reduction in the ultimate ruin probability from the situation when there is no reinsurance. We also show that by purchasing reinsurance the insurer can release funds for other purposes without altering its ultimate ruin probability.

Keywords

Ruin probability Capital injections Lower barrier

Type: Papers
Information: Annals of Actuarial Science , Volume 5 , Issue 2 , September 2011 , pp. 195 - 209

DOI: https://doi.org/10.1017/S1748499511000054 [Opens in a new window]
Copyright: Copyright © Institute and Faculty of Actuaries 2011

1. Introduction

We consider an insurer who has allocated a fixed amount of funds, U, to a portfolio of risks so that the ultimate ruin probability for this portfolio is known. Our aim is to investigate whether the insurer can reduce this ultimate ruin probability by splitting U into two parts. The first of these, u ≤ U, will be the initial surplus held for the portfolio. The second part is a reinsurance premium which we denote by Q(u, k), and which equals U−u. The reinsurance being purchased is not a traditional type of contract. It does not relate to either individual claims or aggregate claims. Rather, it relates to the amount by which the surplus process falls below a fixed level k ≤ u. Each time that the insurer's surplus falls to a level k−y such that 0 < y < k the reinsurer makes an immediate payment of y to the insurer, restoring the insurer's surplus to k. If any claim causes the insurer's surplus to fall from a level above k to a level below 0, the reinsurer does not make a payment and ruin for the portfolio occurs at the time of this claim.

This paper is written in terms of a direct insurer and a reinsurer. However, as we are considering a portfolio of risks, it may be possible to secure ‘reinsurance’ within the insurance company by passing the risk onto a different line of business within the company. It is important to appreciate that the type of reinsurance risk associated with this study is quite different to traditional reinsurance arrangements. In many such arrangements, for example excess of loss reinsurance, the insurer is seeking to limit the amount paid out on any individual claim. By contrast, under the reinsurance arrangement in this study, it is the reinsurer's payments that are bounded above by k, and, depending on the method of calculating the reinsurance premium, the value of k can be quite low relative to the mean individual claim amount for the insurer, although it can also be quite high. Following our numerical examples, we discuss the level of reinsurance.

Capital injections have been discussed by authors such as Pafumi (Reference Pafumi1998), Dickson & Waters (Reference Dickson and Waters2004) and Eisenberg & Schmidli (Reference Eisenberg and Schmidli2010). A major difference in this study is that capital injections occur before the surplus falls below zero, and the capital injections in this study do not eliminate the possibility of ruin for the insurer.

2. Preliminaries

Consider first the classical risk model. Let {U(t)}_t _{≥ 0} be the surplus process of an insurer, where u ≥ 0 is the insurer's surplus at time t = 0, and let c be the insurer's rate of premium income per unit time, which we assume to be received continuously. Let {N(t)}_t _{≥ 0} be the counting process for the number of claims, so that for a fixed value t > 0, the random variable N(t) denotes the number of claims that occur in the time interval [0, t]. We assume that {N(t)}_t _{≥ 0} is a Poisson process with parameter λ. Individual claim amounts are modelled as a sequence of independent and identically distributed (i.i.d.) random variables $)(--><$> \{ {{X}_i}\} _{{i = 1}}^{\infty } <$><!--$ , so that X_i denotes the amount of the ith claim. We assume that X ₁ has probability density function (p.d.f.) p and distribution function (c.d.f.) P. The surplus at time t is then

$--><$$>U(t) = u + ct{\rm{\, - \,}}\mathop{\sum}\limits_{i = 1}^{N(t)} {{X}_i}.\eqno<$$><!--$

We assume that c > λm ₁, where m ₁ is the mean individual claim amount, so that the premium income exceeds the expected aggregate claim amount per unit of time. We write c = (1 + θ ₁)λm ₁, where θ ₁ > 0 is the insurer's premium loading factor.

Let T_u denote the time of ruin so that

$--><$$> {{T}_u} = \inf \{ t\,|\,U(t) \lt 0\} \eqno<$$><!--$

with T_u = ∞ if U(t) ≥ 0 for all t > 0. Then the ultimate ruin probability is

$--><$$>\psi (u) = {\rm{Pr}}({{T}_u} \lt \infty ).\eqno<$$><!--$

Define

$--><$$> G(u,y) = {\rm{Pr}}\,({{T}_u} \lt \infty \:\;{\rm{and}}\;\:|U({{T}_u})|\leq y) \eqno<$$><!--$

to be the probability that ruin occurs with a deficit at ruin of no more than y, with $)(--><$> g(u,y) = \frac{d}{{dy}}G(u,y) <$><!--$ . Further, let w(u, y, t) denote the defective joint p.d.f. of the time of ruin (t) and deficit at ruin (y), and let w(u, t) denote the p.d.f. of T_u.

We now introduce a modified process which includes a lower barrier k, where 0 ≤ k ≤ u. The modification to the classical risk model is that each time the surplus drops below k but not below 0, an injection of funds will immediately restore the surplus level back to k, so that the surplus process continues from level k after payment of the claim that had taken the surplus below k. We discuss below how this injection of funds is provided. A realisation of this modified process is shown in Figure 1.

Figure 1 Surplus process with lower barrier k

Now define ψ_k(u) to be the ultimate ruin probability for the modified surplus process with the lower barrier at k. We can obtain a formula for ψ_k(u), starting with the case u = k. By conditioning on the amount of the first drop below level k, we have

$--><$$> {{\psi }_k}(k) = {\int}_{\!\!\!\!0}^{k} g(0,y)\,{{\psi }_k}(k)\,dy + {\int}_{\!\!\!\!k}^{\infty } g(0,y)\,dy. \eqno<$$><!--$

Hence,

$--><$$> {{\psi }_k}(k) = \frac{{\psi (0)\,{\rm{\, - \,}}\,G(0,k)}}{{1\,{\rm{\, - \,}}\,G(0,k)}}. \eqno<$$><!--$

Next, we consider the more general situation when u > k ≥ 0. Let $)(--><$> \bar{\psi }(u) = 1\,{\rm{\, - \,}}\,\psi (u) <$><$> {{\bar{\psi }}_k}(u) = 1\,{\rm{\, - \,}}\,{{\psi }_k}(u) <$><!--$ be the survival probabilities for the classical risk process and the modified risk process respectively. Conditioning on the amount of the first drop below level k, we have

$--><$$> {{\bar{\psi }}_k}(u) = \bar{\psi }(u\,{\rm{\, - \,}}\,k) + G(u\,{\rm{\, - \,}}\,k,k)\,{{\bar{\psi }}_k}(k), \eqno<$$><!--$

and therefore

$--><$$> \eqalign{ {{\psi }_k}(u) = \psi (u\,{\rm{\, - \,}}\,k)\,{\rm{\, - \,}}G(u\,{\rm{\, - \,}}\,k,k)\,(1\,{\rm{\, - \,}}\,{{\psi }_k}(k)) \cr = \psi (u\,{\rm{\, - \,}}\,k){\rm{\, - \,}}G(u\,{\rm{\, - \,}}\,k,k)\:\frac{{1\,{\rm{\, - \,}}\,\psi (0)}}{{1\,{\rm{\, - \,}}\,G(0,k)}}. \cr} \eqno<$$><!--$

For many claim size distributions we can easily find the components of ψ_k(u), and hence ψ_k(u) itself. See, for example, Gerber et al. (Reference Gerber, Goovaerts and Kaas1987) or Dickson (Reference Dickson2005).

3. Premium calculation for the reinsurer

Suppose that the insurer enters a reinsurance arrangement under which the reinsurer provides the funds needed to restore the surplus level to k every time the surplus falls between 0 and k. We denote the premium required by the reinsurer as Q(u, k), which is a function of the insurer's initial surplus u and the lower barrier k. Let the aggregate amount needed to restore the modified surplus process to k up to time t, given initial surplus u, be S_t _,_u _,_k.

In our numerical illustrations in the next section we consider premium principles for the reinsurance premium that are based on the first two moments of aggregate claims for the reinsurer, as well as a reinsurance premium based on the expected discounted claim payments by the reinsurer. We now derive formulae that can be used to calculate reinsurance premiums.

Let T_u,k denote the time of ruin under the modified process with initial surplus u and lower barrier k. Consider first E(S_u _,_k) where $)(--><$> {{S}_{u,k}} = {{S}_{{{T}_{u,k}},u,k}} <$><!--$ , i.e. the expected total claim amount for the reinsurer up to the time of ruin.

We start with the case u = k. Using ideas from Pafumi (Reference Pafumi1998), we can calculate E(S_k _,_k) as

$--><$$> \eqalign { E({{S}_{k,k}}) = {\int}_{\!\!\!\!0}^{k} (y + E({{S}_{k,k}}))\,g(0,y)\,dy \cr = {\int}_{\!\!\!\!0}^{k} y\:g(0,y)\,dy + E({{S}_{k,k}})\,G(0,k). \cr} \eqno <$$><!--$

Therefore,

$--><$$> E({{S}_{k,k}}) = \frac{{{\int}_{\!\!0}^{k} y\:g(0,y) \, dy}}{{1{\rm{\, - \,}}G(0,k)}}. \eqno<$$><!--$

When u > k, we have

(3.1)

$--><$$> \eqalignno { \qquad\qquad\qquad\qquad\qquad\qquad E({{S}_{u,k}}) = & {\int}_{\!\!\!\!0}^{k} (y + E({{S}_{k,k}}))\,g(u{\rm{\, - \,}}k,y)\,dy \cr = & {\int}_{\!\!\!\!0}^{k} y \, g(u\,{\rm{\, - \,}}\,k,y)\,dy + E({{S}_{k,k}})\,G(u{\rm{\, - \,}}k,k). <$$><!--$

Consider next calculation of $)(--><$> E(S_{{u,k}}^{2} ) <$><!--$ . The same idea gives

$--><$$> \eqalign { E(S_{{k,k}}^{2} ) = & {\int}_{\!\!\!\!0}^{k} ({{y}^2} + E(S_{{k,k}}^{2} ) + 2y \, E({{S}_{k,k}})) \, g(0,y) \, dy \cr = & {\int}_{\!\!\!\!0}^{k} {{y}^2} \, g(0,y)\,dy + E(S_{{k,k}}^{2} )\,G(0,k) + 2E({{S}_{k,k}}){\int}_{\!\!\!\!0}^{k} y \, g(0,y)\,dy, \cr} \eqno <$$><!--$

and therefore

$--><$$> E(S_{{k,k}}^{2} ) = \frac{{{\int}_{\!\!0}^{k} {{y}^2} \, g(0,y)\,dy + 2E({{S}_{k,k}}){\int}_{\!\!0}^{k} y \, g(0,y)\,dy}}{{1{\rm{\, - \,}}G(0,k)}}. \eqno<$$><!--$

Hence,

(3.2)

$--><$$> \eqalignno{ \qquad\qquad\qquad\qquad\qquad E(S_{{u,k}}^{2} ) = & {\int}_{\!\!\!\!0}^{k} ({{y}^2} + E(S_{{k,k}}^{2} ) + 2yE({{S}_{k,k}}))\,g(u{\rm{\, - \,}}k,y)\,dy \cr = & {\int}_{\!\!\!\!0}^{k} {{y}^2} g(u{\rm{\, - \,}}k,y)dy + E(S_{{k,k}}^{2} )G(u{\rm{\, - \,}}k,k) \cr & + 2E({{S}_{k,k}}){\int}_{\!\!\!\!0}^{k} yg(u\,{\rm{\, - \,}}\,k,y)dy. (3.2)<$$><!--$

We now consider the case when the reinsurer sets its premium based on the expected discounted value of the payments it will make until the time of ruin. Let $)(--><$> S_{{u,k}}^{\delta } <$><$> E(S_{{k,k}}^{\delta } ) <$><!--$ can be calculated as

$--><$$> \eqalign{ E(S_{{k,k}}^{\delta } ) = & {\int}_{\!\!\!\!0}^{\infty } {\int}_{\!\!\!\!0}^{k} {{e}^{{\rm{\, - \,}}\delta t}} \, (y + E(S_{{k,k}}^{\delta } )) \, w(0,y,t)\,dy\,dt \cr = & {\int}_{\!\!\!\!0}^{\infty } {\int}_{\!\!\!\!0}^{k} {{e}^{{\rm{\, - \,}}\delta t}} \, y \, w(0,y,t) \, dy\,dt \cr & + E(S_{{k,k}}^{\delta } ){\int}_{\!\!\!\!0}^{\infty } {\int}_{\!\!\!\!0}^{k} {{e}^{{\rm{\, - \,}}\delta t}} \, w(0,y,t) \, dy\,dt. \cr} \eqno<$$><!--$

Let

$--><$$> {{g}_\delta }(u,y) = {\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{\, - \,}}\delta t}} \, w(u,y,t) \, dt, \eqno<$$><!--$

denote the (defective) discounted p.d.f. of the deficit at ruin (y), with initial surplus u and force of interest δ. Also let G_δ(u,y) denote the corresponding c.d.f. so that

$--><$$> {{G}_\delta }(u,y) = {\int}_{\!\!\!\!0}^{y} {{g}_\delta }(u,x)dx. \eqno<$$><!--$

Hence $)(--><$> E(S_{{k,k}}^{\delta } ) <$><!--$ can be simplified as

(3.3)

$--><$$>\eqalignno{ \qquad\qquad\qquad\qquad\qquad\qquad\quad E(S_{{k,k}}^{\delta } ) = & \frac{{{\int}_{\!\!0}^{\infty } {\int}_{\!\!0}^{k} {{e}^{{\rm{\, - \,}}\delta t}} y \, w(0,y,t) \, dy \, dt}}{{1{\rm{\, - \,}}{\int}_{\!\!0}^{\infty } {\int}_{\!\!0}^{k} {{e}^{{\rm{\, - \,}}\delta t}} \, w(0,y,t) \, dy \, dt}} (3.3) \cr = & \frac{{{\int}_{\!\!0}^{k} y \, {{g}_\delta }(0,y) \, dy}}{{1{\rm{\, - \,}}{{G}_\delta }(0,k)}}. <$$><!--$

When u > k we have

(3.4)

$--><$$>\eqalignno{ \qquad\qquad\qquad\qquad\qquad\quad E(S_{{u,k}}^{\delta } ) = & {\int}_{\!\!\!\!0}^{\infty } {\int}_{\!\!\!\!0}^{k} {{e}^{{\rm{\, - \,}}\delta t}} \, (y + E(S_{{k,k}}^{\delta } )) \, w(u{\rm{\, - \,}}k,y,t) \, dy \, dt (3.4) \cr = & {\int}_{\!\!\!\!0}^{k} y \, {{g}_\delta }(u{\rm{\, - \,}}k,y) \, dy + E(S_{{k,k}}^{\delta } ) \, {{G}_\delta }(u{\rm{\, - \,}}k,k). <$$><!--$

Both w(u,y,t) and g_δ(u,y) can be found for certain claim size distributions (see, for example, Dickson & Drekic, Reference Dickson and Drekic2006 and Landriault & Willmot, Reference Landriault and Willmot2009), and we will use some of these results in our subsequent examples. We note that $)(--><$> E(S_{{u,k}}^{\delta } )\leq E({{S}_{u,k}}) <$><!--$ for all δ ≥ 0 and this relationship holds for all claim size distributions.

4. Minimizing the ultimate ruin probability

We now assume that the insurer holds an amount of capital, U, of which u is allocated as the initial surplus and Q(u, k) is used to buy reinsurance. Given a value of the initial surplus u and therefore a value of the reinsurance premium required (Q(u, k)), we can find the level of the lower barrier k. In our examples there is a minimum value of u such that the condition u ≥ k is satisfied. What will be of interest is whether there is a combination of u and k such that the ruin probability ψ_k(u) is minimized. That is, we are aiming to minimize ψ_k(u) subject to the constraints U = u + Q(u, k) and u ≥ k. Let u* and k* denote the optimal choices of u and k respectively, where by ‘optimal’ we shall always mean the ψ_k(u) is minimized. The minimum ruin probability is denoted $)(--><$> \psi _{k}^{\ast} (u) <$><!--$ .

Solving for u* and k* is thus a constrained optimization problem. Even in the simplest case (exponential claim sizes) we are unable to find explicit solutions for u* and k*. Hence, numerical techniques are required. In our examples in the next section, the values of u* and k* were found using Mathematica.

5. Examples

In this section, we consider two claim size distributions: exponential and a mixture of two exponentials. Under each of these claim size distributions, we investigate the optimal choice of u and k for given values of initial capital U, under different reinsurance premium scenarios. We also examine and compare the effectiveness of reinsurance in reducing the ruin probability under each circumstance.

5.1 Exponential claim sizes

Suppose that P(x) = 1−e ^−αx. It is well known (see, for example, Dickson, Reference Dickson2005) that

(5.1)

$--><$$>\psi (u) = \frac{\lambda }{{\alpha c}}{{e}^{{\rm{\, - \,}}(\alpha {\rm{\, - \,}}\lambda /c)u}}, \eqno<$$><!--$

(5.2)

$--><$$>g(u,y) = \psi (u)\alpha {{e}^{{\rm{\, - \,}}\alpha y}}, \eqno<$$><!--$

and

(5.3)

$--><$$>G(u,y) = \psi (u)(1\,{\rm{\, - \,}}\,{{e}^{{\rm{\, - \,}}\alpha y}} ).\eqno<$$><!--$

Formulae for both E(S_u _,_k) and $)(--><$> E(S_{{u,k}}^{2} ) <$><$> E(S_{{u,k}}^{\delta } ) <$><!--$ given below.

We now derive a formula for the expected present value of the reinsurance payments. From Gerber (Reference Gerber1979) the joint p.d.f. w(u, y, t) is

$--><$$> w(u,y,t) = \alpha {{e}^{{\rm{\, - \,}}\alpha y}} \, w(u,t). \eqno<$$><!--$

Hence,

$--><$$>\openup 5pt \eqalign{ E(S_{{k,k}}^{\delta } ) & = \frac{{{\int}_{\!\!0}^{\infty } {{e}^{{\rm{\, - \,}}\delta t}} w(0,t)dt{\int}_{\!\!0}^{k} y\alpha {{e}^{{\rm{\, - \,}}\alpha y}} dy}}{{1{\rm{\, - \,}}{\int}_{\!\!0}^{\infty } {{e}^{{\rm{\, - \,}}\delta t}} w(0,t)dt{\int}_{\!\!0}^{k} \alpha {{e}^{{\rm{\, - \,}}\alpha y}} dy}} \cr & = \frac{{E({{e}^{{\rm{\, - \,}}\delta {{T}_0}}} I({{T}_0} \lt \infty ))\frac{1}{\alpha }[1{\rm{\, - \,}}{{e}^{{\rm{\, - \,}}\alpha k}} (1 + \alpha k)]}}{{1{\rm{\, - \,}}E({{e}^{{\rm{\, - \,}}\delta {{T}_0}}} I({{T}_0} \lt \infty ))(1{\rm{\, - \,}}{{e}^{{\rm{\, - \,}}\alpha k}} )}}, \cr} \eqno<$$><!--$

where I is the indicator function.

Also from equation (3.4), we have

$--><$$> \eqalign{ E(S_{{u,k}}^{\delta } ) = {\int}_{\!\!\!\!0}^{\infty } {\int}_{\!\!\!\!0}^{k} {{e}^{{\rm{\, - \,}}\delta t}} (y + E(S_{{k,k}}^{\delta } ))w(u{\rm{\, - \,}}k,t)\alpha {{e}^{{\rm{\, - \,}}\alpha y}} dydt \cr = {\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{\, - \,}}\delta t}} w(u{\rm{\, - \,}}k,t)dt\left[ {{\int}_{\!\!\!\!0}^{k} y\alpha {{e}^{{\rm{\, - \,}}\alpha y}} dy + E(S_{{k,k}}^{\delta } ){\int}_{\!\!\!\!0}^{k} \alpha {{e}^{{\rm{\, - \,}}\alpha y}} dy} \right] \cr = E({{e}^{{\rm{\, - \,}}\delta {{T}_{u{\rm{\, - \,}}k}}}} I({{T}_{u{\rm{\, - \,}}k}} \lt \infty ))\left[ {\frac{1}{\alpha }[1{\rm{\, - \,}}{{e}^{{\rm{\, - \,}}\alpha k}} (1 + \alpha k)] + E(S_{{k,k}}^{\delta } )(1{\rm{\, - \,}}{{e}^{{\rm{\, - \,}}\alpha k}} )} \right]. \cr} \eqno<$$><!--$

We can evaluate this expression as we know from Gerber & Shiu (Reference Gerber and Shiu1998) that

$--><$$> E({{e}^{{\rm{\, - \,}}\delta {{T}_u}}} I({{T}_u} \lt \infty )) = (1{\rm{\, - \,}}{{R}_\delta }/\alpha ){{e}^{{\rm{\, - \,}}{{R}_\delta }u}}, \eqno<$$><!--$

where

$--><$$> {{R}_\delta } = \frac{{{\rm{\, - \,}}\lambda {\rm{\, - \,}}\delta + c\alpha + \sqrt {{{{(c\alpha {\rm{\, - \,}}\delta {\rm{\, - \,}}\lambda )}}^2} + 4c\delta \alpha } }}{{2c}}. \eqno<$$><!--$

Setting δ = 0 in the above expressions gives E(S_u _,_k).

We now show some numerical results under different reinsurance premium scenarios. For our numerical illustrations we set α = 1 so that the mean and the variance of the claim size distribution are both 1. Also, we set λ = 1 and c = 1.2, i.e. the premium loading factor for the insurer is θ ₁ = 0.2.

Example 5.1.1. Our first scenario is that Q(u, k) = 1.6E(S_u,k), i.e. the reinsurance premium is calculated using the expected value principle with loading factor θ₂ = 0.6. Figure 2illustrates how ψ_k(u) changes with u, given that U = 15. For this value of U, ψ(U) = 0.06840. The optimal choice of u and k is found to be u* = 10.05 and k* = 7.23 giving $)(--><$>\psi _{k}^{\ast} (u) = 0.00226<$><!--$ . Some values are shown in Table 1for different values of U, but we defer comment on these until after the next example.

Figure 2 ψ_k(u) (solid line) and ψ(U) (dotted line), U = 15, Q(u, k) = 1.6E(S_u _,_k), exponential claims

Table 1 Ruin probabilities, exponential claims

Example 5.1.2. For our second scenario we let Q(u,k) = E(S_u,k) + 2St.Dev.(S_u,k), i.e. the reinsurance premium is calculated by the standard deviation principle with loading factor θ ₃= 2. As a first illustration, consider the situation when the initial capital is U = 20, giving ψ(U) = 0.02973. The ruin probability ψ_k(u) is plotted in Figure 3for different values of u. We see in Figure 2in Example 5.1.1 that any combination of u and k (such that u + Q(u,k) = U) provides a lower ruin probability than under the original process. In Figure 3only certain combinations of u and k reduce the ruin probability compared with the original process. The minimum of ψ_k(u) is obtained when u* = 12.50 and k* = 4.28, giving $)(--><$>\psi _{k}^{\ast} (u) = 0.01645<$><!--$ .

Figure 3 ψ_k(u) (solid line) and ψ(U) (dotted line), U = 20, Q(u, k) = E(S_u _,_k) + 2St.Dev.(S_u _,_k), exponential claims

Table 1 shows the optimal values u* and k*, as well as the corresponding ruin probabilities under the scenarios described in Examples 5.1.1 and 5.1.2. It also shows the percentage reductions in the ruin probabilities, calculated as $)(--><$> (1{\rm{\, - \,}}\psi _{k}^{\ast} (u)/\psi (U))\times 100\% <$><!--$ , to illustrate the effectiveness of the lower barrier system. Consider the case when the initial capital is U = 11, so that the ruin probability under the original process is 0.13. When the reinsurance premium is calculated by the expected value principle with loading factor 0.6, the ruin probability is reduced by 61.04% to 0.05 when choosing the optimal combination u* and k*. When the reinsurance premium is calculated by the standard deviation principle, we find that the reinsurance premium exceeds the initial capital of U = 11 for any u and k such that 0 ≤ k ≤ u ≤ U. Hence the insurer would not buy reinsurance under this scenario. As U increases, the insurer is able to buy reinsurance under the scenario of Example 5.1.2 and we see that the ruin probability can be reduced considerably with an appropriate choice of u and k. Under each reinsurance premium scenario, the percentage reductions in ruin probabilities increase rapidly as U increases.

Example 5.1.3. As our third scenario, we set $)(--><$>Q(u,k) = 1.6E(S_{{u,k}}^{{0.01}} )<$><!--$ . Table 2shows the optimal values u* and k*, as well as the corresponding ruin probabilities both for this scenario and the case δ = 0 from Example 5.1.1. As the introduction of discounting reduces the reinsurance premium, we can see that under this scenario the insurer is able to retain more as the initial surplus and to set a higher value for k compared to our first scenario. Therefore, the ruin probabilities are further reduced under this scenario.

Table 2 Ruin probabilities, exponential claims

From the previous results, we see that the values of k can be quite high compared to the initial surplus u, and such situations may not be acceptable to reinsurers. For example, in Table 1, the ultimate ruin probability before reinsurance is close to 5% when U = 17. With k* being close to 9, the insurer's ruin probability is very small because the probability of a claim exceeding (at least) 9 is very small. The optimal choices of u* = 12.01 and k* = 9.19 may be a situation that is not acceptable to a reinsurer. To address this issue, we look at the effectiveness of the lower barrier system in reducing the ruin probability by setting k to reasonably low levels which should be acceptable to reinsurers. In Table 3, we first show the initial capital, U, needed so that ψ(U) is 1%, 2%, …, 5%. Having found the required U, we calculate the initial surplus level u by setting k = 2 and k = 3 with the reinsurance premium charged in Example 5.1.1. The ruin probability for each pair is then calculated.

Table 3 Results with fixed k, exponential claims

From Table 3, when U = 16.88, the ruin probability before reinsurance is 0.05. With k = 3, we find that the optimal initial surplus for the insurer is 16.32, and that ψ ₃(16.32) = 0.0216, which is a substantial reduction from 0.05.

Until now we have assumed that the insurer will try to use the capital U to purchase reinsurance to reduce the ruin probability. An alternative use of reinsurance is to release some of the insurer's funds without changing the ruin probability. For example, suppose that U is such that ψ(U) = 0.05. The idea now is that the insurer sets the barrier level k, then selects u such that ψ_k(U) = 0.05. Providing the arrangement is feasible, i.e. 0 ≤ k ≤ u ≤ U, the insurer can allocate the amount R_u _,_k = U−u−Q(u,k) to purposes other than reinsurance or the surplus process.

Example 5.1.4. Suppose that Q(u,k)=1.6E(S_u,k) and consider the values of U from Table 3. Table 4shows the amount of surplus required, u, to give the same ruin probability as ψ(U) for the cases k = 2 and k = 3. It also shows the amount R_u,k that is released for other purposes as a result of the reinsurance arrangement.

Table 4 Surplus required to maintain ruin probability and R_u _,_k, exponential claims

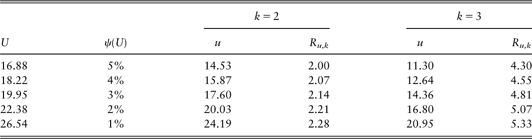
From Table 4we see that the amount of funds released increases as the ruin probability decreases, and that the amount released is larger in the case k = 3 for a given ruin probability. The percentage of U released ranges from 8.6% to 11.8% in the case k = 2, and from 20.1% to 25.5% in the case k = 3.

5.2. Mixed exponential claim sizes

We now assume that the individual claim amount distribution is a mixture of two exponential distributions, with p.d.f.

$--><$$> p(x) = \frac{1}{3}\;0.5{{e}^{{\rm{\, - \,}}0.5x}} + \frac{2}{3}\;2{{e}^{{\rm{\, - \,}}2x}} . \eqno<$$><!--$

This distribution has mean 1 and variance 1.5. Again, we let λ = 1 and set the premium rate as c = 1.2 in our numerical examples.

Using techniques described in Gerber et al. (Reference Gerber, Goovaerts and Kaas1987) we find that

$--><$$> \psi (u) = 0.79903{{e}^{{\rm{\, - \,}}{{R}_1}u}} + 0.03431{{e}^{{\rm{\, - \,}}{{R}_2}u}}, \eqno<$$><!--$

where R ₁ = 0.10685 and R ₂ = 1.55982, and

$--><$$> \eqalign { G(u,y) = \ & (0.07516(1{\rm{\, - \,}}{{e}^{{\rm{\, - \,}}2y}} ) + 0.72386(1\,{\rm{\, - \,}}\,{{e}^{{\rm{\, - \,}}0.5y}} )){{e}^{{\rm{\, - \,}}{{R}_1}u}} \cr & + (0.20262(1\,{\rm{\, - \,}}\,{{e}^{{\rm{\, - \,}}2y}} ){\rm{\, - \,}}0.16831(1\,{\rm{\, - \,}}\,{{e}^{{\rm{\, - \,}}0.5y}} )){{e}^{{\rm{\, - \,}}{{R}_2}u}} . \cr} \eqno<$$><!--$

As in the previous section we omit the details of formulae for E(S_u _,_k) and $)(--><$> E(S_{{u,k}}^{2} ) <$><$> E(S_{{u,k}}^{\delta } ) <$><!--$ . Dickson & Drekic (Reference Dickson and Drekic2006) show that when claims have a mixed exponential distribution with p.d.f.

$--><$$>p(x) = p\alpha {{e}^{{\rm{\, - \,}}\alpha x}} + q\beta {{e}^{{\rm{\, - \,}}\beta x}}, \eqno<$$><!--$

the p.d.f. w(u, y, t) is of the form

$--><$$> w(u,y,t) = {{\eta }_1}(u,t)\alpha {{e}^{{\rm{\, - \,}}\alpha y}} + {{\eta }_2}(u,t)\beta {{e}^{{\rm{\, - \,}}\beta y}}, \eqno<$$><!--$

but they do not identify η_i(u, t), for i = 1, 2. Substituting this expression into equation (3.4), we have

$--><$$> E(S_{{k,k}}^{\delta } ) = \frac{{{\int}_{\!\!0}^{\infty } {{e}^{{\rm{\, - \,}}\delta t}} \, {{\eta }_1}(0,t)\,dt{\int}_{\!\!0}^{k} y \, \alpha \, {{e}^{{\rm{\, - \,}}\alpha y}} \, dy + {\int}_{\!\!0}^{\infty } {{e}^{{\rm{\, - \,}}\delta t}} \, {{\eta }_2}(0,t)\,dt{\int}_{\!\!0}^{k} y \, \beta \, {{e}^{{\rm{\, - \,}}\beta y}} \, dy}}{{1{\rm{\, - \,}}{\int}_{\!\!0}^{\infty } {{e}^{{\rm{\, - \,}}\delta t}} \, {{\eta }_1}(0,t)\,dt{\int}_{\!\!0}^{k} \alpha \, {{e}^{{\rm{\, - \,}}\alpha y}} \, dy + {\int}_{\!\!0}^{\infty } {{e}^{{\rm{\, - \,}}\delta t}} \, {{\eta }_2}(0,t)\,dt{\int}_{\!\!0}^{k} \beta \, {{e}^{{\rm{\, - \,}}\beta y}} \, dy}}. \eqno<$$><!--$

An explicit formula for $)(--><$> {\int}_{\!\!0}^{\infty } {{e}^{{\rm{\, - \,}}\delta t}} {{\eta }_i}(u,t)dt <$><!--$ is given in Dickson & Drekic (Reference Dickson and Drekic2006). They show that

$--><$$> {\int}_{\!\!\!\!0}^{\infty } {{e}^{{\rm{\, - \,}}\delta t}} \, {{\eta }_i}(u,t) \, dt = {{\gamma }_i}(\delta ){{e}^{{\rm{\, - \,}}{{R}_{1\delta }} \, u}} + {{\sigma }_i}(\delta ){{e}^{{\rm{\, - \,}}{{R}_{2\delta }} \, u}}, \eqno<$$><!--$

for i = 1, 2, where ρ > 0, −R ₁_δ < 0 and −R ₂_δ < 0 are the solutions of Lundberg's fundamental equation

$--><$$> \lambda + \delta \,{\rm{\, - \,}}\,ct = \frac{{\lambda p\alpha }}{{\alpha + t}} + \frac{{\lambda q\beta }}{{\beta + t}}, \eqno<$$><!--$

and

$--><$$> \eqalign{ {{\gamma }_1}(\delta ) =\ & \frac{{(\alpha \,{\rm{\, - \,}}\,{{R}_{1\delta }})(\alpha \,{\rm{\, - \,}}\,{{R}_{2\delta }})(\beta \,{\rm{\, - \,}}\,{{R}_{1\delta }})}}{{\alpha ({{R}_{2\delta }}\,{\rm{\, - \,}}\,{{R}_{1\delta }})(\alpha \,{\rm{\, - \,}}\,\beta )}}, \cr {{\gamma }_2}(\delta ) = \ & {\rm{\, - \,}}\frac{{(\alpha \,{\rm{\, - \,}}\,{{R}_{1\delta }})(\beta \,{\rm{\, - \,}}\,{{R}_{1\delta }})(\beta \,{\rm{\, - \,}}\,{{R}_{2\delta }})}}{{\beta ({{R}_{2\delta }}\,{\rm{\, - \,}}\,{{R}_{1\delta }})(\alpha \,{\rm{\, - \,}}\beta )}}, \cr {{\sigma }_1}(\delta ) =\ & {\rm{\, - \,}}\frac{{(\alpha \,{\rm{\, - \,}}\,{{R}_{1\delta }})(\alpha \,{\rm{\, - \,}}\,{{R}_{2\delta }})(\beta \,{\rm{\, - \,}}\,{{R}_{2\delta }})}}{{\alpha ({{R}_{2\delta }}\,{\rm{\, - \,}}\,{{R}_{1\delta }})(\alpha \,{\rm{\, - \,}}\,\beta )}}, \cr {{\sigma }_2}(\delta ) = \ & \frac{{(\alpha \,{\rm{\, - \,}}\,{{R}_{2\delta }})(\beta \,{\rm{\, - \,}}\,{{R}_{1\delta }})(\beta \,{\rm{\, - \,}}\,{{R}_{2\delta }})}}{{\beta ({{R}_{2\delta }}\,{\rm{\, - \,}}\,{{R}_{1\delta }})(\alpha \,{\rm{\, - \,}}\,\beta )}}. \cr} \eqno<$$><!--$

Hence,

$--><$$> E(S_{{k,k}}^{\delta } ) = \frac{{({{\gamma }_1}(\delta ) + {{\sigma }_1}(\delta ))\left[ {1\,{\rm{\, - \,}}\,{{e}^{{\rm{\, - \,}}\alpha k}} (1 + \alpha k)} \right]/\alpha + ({{\gamma }_2}(\delta ) + {{\sigma }_2}(\delta ))\left[ {1\,{\rm{\, - \,}}\,{{e}^{{\rm{\, - \,}}\beta k}} (1 + \beta k)} \right]/\beta }}{{1\,{\rm{\, - \,}}\,({{\gamma }_1}(\delta ) + {{\sigma }_1}(\delta ))(1\,{\rm{\, - \,}}\,{{e}^{{\rm{\, - \,}}\alpha k}} ){\rm{\, - \,}}({{\gamma }_2}(\delta ) + {{\sigma }_2}(\delta ))((1\,{\rm{\, - \,}}\,{{e}^{{\rm{\, - \,}}\beta k}} ))}}, \eqno<$$><!--$

and therefore from equation (3.4) we have

$--><$$> \eqalign { E(S_{{u,k}}^{\delta } ) =\ & ({{\gamma }_1}(\delta ){{e}^{{\rm{\, - \,}}{{R}_{1\delta }}(u{\rm{\, - \,}}k)}} + {{\sigma }_1}(\delta ){{e}^{{\rm{\, - \,}}{{R}_{2\delta }}(u{\rm{\, - \,}}k)}} )\left[ {1{\rm{\, - \,}}{{e}^{{\rm{\, - \,}}\alpha k}} (1 + \alpha k)} \right]/\alpha \cr & + ({{\gamma }_2}(\delta ){{e}^{{\rm{\, - \,}}{{R}_{1\delta }}(u{\rm{\, - \,}}k)}} + {{\sigma }_2}(\delta ){{e}^{{\rm{\, - \,}}{{R}_{2\delta }}(u{\rm{\, - \,}}k)}} )\left[ {1{\rm{\, - \,}}{{e}^{{\rm{\, - \,}}\beta k}} (1 + \beta k)} \right]/\beta \cr & + E(S_{{k,k}}^{\delta } )\left( {({{\gamma }_1}(\delta ){{e}^{{\rm{\, - \,}}{{R}_{1\delta }}(u{\rm{\, - \,}}k)}} + {{\sigma }_1}(\delta ){{e}^{{\rm{\, - \,}}{{R}_{2\delta }}(u{\rm{\, - \,}}k)}} )(1{\rm{\, - \,}}{{e}^{{\rm{\, - \,}}\alpha k}} )} \right. \cr & + \left( {{{\gamma }_2}(\delta ){{e}^{{\rm{\, - \,}}{{R}_{1\delta }}(u{\rm{\, - \,}}k)}} + {{\sigma }_2}(\delta ){{e}^{{\rm{\, - \,}}{{R}_{2\delta }}(u{\rm{\, - \,}}k)}} )(1{\rm{\, - \,}}{{e}^{{\rm{\, - \,}}\beta k}} )} \right). \cr} \eqno<$$><!--$

In the examples below we apply the same reinsurance scenarios as in Examples 5.1.1 to 5.1.3.

Example 5.2.1. Firstly we assume that Q(u,k) = 1.6E(S_u,k). For U = 15, Figure 4shows the ruin probabilities ψ_k(u) for feasible combinations of u and k. The minimum ruin probability is $)(--><$>\psi _{k}^{\ast} (u) = 0.10448<$><!--$ when u* = 10.17 and k* = 5.62. Under the classical risk process ψ(15) = 0.16088, so reinsurance has reduced the ruin probability by 35.6% in this case. Note that under this reinsurance arrangement, we obtain ruin probabilities that are less than ψ(15), regardless of the choices of u and k.

Figure 4 ψ_k(u) (solid line) and ψ(U) (dotted line), U = 15, Q(u, k) = 1.6E(S_u _,_k), mixed exponential claims

Example 5.2.2. We now set Q(u,k) = E(S_u,k) + 2St.Dev.(S_u,k). For U = 30, Figure 5shows ruin probabilities for different combinations of u and k, as well as ψ(30) = 0.03239. As in Example 5.1.2, only certain choices of u and k provide a reduction in the ruin probability. The optimal choice is u* = 22.65 and k* = 18.10, giving $)(--><$>\psi _{k}^{\ast} (u) = 0.00024<$><!--$ .

Figure 5 ψ_k(u) (solid line) and ψ(U) (dotted line), U = 30, Q(u,k) = E(S_u _,_k) + 2St.Dev.(S_u _,_k), mixed exponential claims

Table 5 shows optimal values u* and k* for some values of U under the reinsurance premium arrangements of the previous two examples. Given these values, we are able to compare the effectiveness of reinsurance by looking at the reduction in ruin probabilities in percentage terms, as in Table 1. The percentage reduction in ruin probability increases rapidly when the reinsurance premium is calculated by the expected value principle, going from 35.06% when U = 15 to 98.89% when U = 29. When U is small and the reinsurance premium is calculated by the standard deviation principle, we find that reinsurance is too expensive, and therefore the insurance company should bear all the risk itself. When U is large enough, reinsurance becomes affordable and the ruin probability under reinsurance reduces from that under the original process.

Table 5 Ruin probabilities, mixed exponential claims

Example 5.2.3. As a third example, we assume $)(--><$>Q(u,k) = 1.6E(S_{{u,k}}^{\delta } )<$><!--$ with δ = 0.01. Table 6shows optimal values u* and k* for different values of U under scenarios 1 and 3, together with the ruin probabilities under each choice and the percentage reduction for each combination compared to the without reinsurance situation. When discounting is introduced, the premium charged by the reinsurer is lower, so the insurer is able to arrange reinsurance with larger k values, as well as retaining a greater initial surplus. Hence, the ruin probabilities are smaller under scenario 3 than under scenario 1.

Table 6 Ruin probabilities, mixed exponential claims

As in the case of exponential claims, we note that k* can be quite high. In Table 7 we show values of ψ_k(u) when k = 2 and k = 3. Compared to Table 3, the capital needed so that the pre-reinsurance ultimate ruin probabilities are 1%, 2%, …, 5% is much higher. This is because the claim size distribution has a larger variance compared to the exponential distribution. When ψ(U) = 5%, we found that U is 25.94. Having k = 3, the initial surplus level u is found to be 25.65 and ψ ₃(25.65) = 0.0386. The table shows that reinsurance works quite effectively even when we choose smaller k rather than the optimal k*.

Table 7 Results for fixed k, mixed exponential claims

Finally, we consider what happens when the ruin probability is unchanged.

Example 5.2.4. Suppose that Q(u,k) = 1.6E(S_u,_k) and consider the values of U from Table 7. Table 8shows the amount of surplus required, u, to give the same ruin probability as ψ(U) for the cases k = 2 and k = 3. It also shows the amount R_u,k that is released for other purposes as a result of the reinsurance arrangement.

Table 8 Surplus required to maintain ruin probability and R_u _,_k, mixed exponential claims

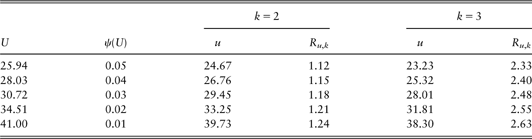
As in Table 4, the amount of funds released increases as the ruin probability decreases, and the amount released is larger in the case k = 3 for a given ruin probability. The percentage of U released ranges from 3.0% to 4.3% in the case k = 2, and from 6.4% to 9.0% in the case k = 3. Although these percentages are smaller than the corresponding values in Table 4, there is still a reasonable release of funds to the insurer.

6. Concluding remarks

We have seen from the examples of the previous section that the insurer can considerably reduce its ruin probability if it can allocate part of its capital to the surplus process and part as a reinsurance premium. However, the optimal barrier level may be sufficiently high to make a reinsurance contract unattractive to a reinsurer. However, even if the insurer has to settle for a level of reinsurance that is sub-optimal in terms of minimizing the ruin probability, the insurer can still create a meaningful reduction in its ruin probability by setting a relatively low value for the barrier.

An important point that distinguishes the reinsurance arrangement in this paper from other studies is that the reinsurance premium is paid for from the insurer's initial capital. In other studies (see, for example, Bowers et al., Reference Bowers, Gerber, Hickman, Jones and Nesbitt1997 or Centeno, Reference Centeno1986), it is assumed that the reinsurance premium is paid from the insurer's premium income. Our approach allows for the release of capital in a way that cannot occur if reinsurance is purchased from the insurer's premium income.

In our examples we have considered situations in which explicit formulae exist for the quantities of interest, such as ψ_k(u). In other situations, e.g. when the individual claim amount distribution is Pareto, explicit results do not exist. However, in such cases we can still find good approximations to quantities such as ψ_k(u) given the values of u and k using techniques described in Dickson & Waters (Reference Dickson and Waters1991, Reference Dickson and Waters1992). Unfortunately, a numerical approach is very computationally intensive to apply when we wish to find optimal values of u and k, and consequently we have not tried to construct an example using this approach.

References

Bowers, N.L., Gerber, H.U., Hickman, J.C., Jones, D.A., Nesbitt, C.J. (1997). Actuarial Mathematics, 2nd edition. Itasca, IL: Society of Actuaries.Google Scholar

Centeno, M.L. (1986). Measuring the effects of reinsurance by the adjustment coefficient. Insurance: Mathematics & Economics, 5, 169–182.Google Scholar

Dickson, D.C.M. (2005). Insurance Risk and Ruin. Cambridge: Cambridge University Press.CrossRef Google Scholar

Dickson, D.C.M., Drekic, S. (2006). Optimal dividends under a ruin probability constraint. Annals of Actuarial Science, 1, 291–306.CrossRef Google Scholar

Dickson, D.C.M., Waters, H.R. (1991). Recursive calculation of survival probabilities. ASTIN Bulletin, 21, 199–221.CrossRef Google Scholar

Dickson, D.C.M., Waters, H.R. (1992). The probability and severity of ruin in finite and in infinite time. ASTIN Bulletin, 22, 177–190.CrossRef Google Scholar

Dickson, D.C.M., Waters, H.R. (2004). Some optimal dividends problems. ASTIN Bulletin, 34, 49–74.CrossRef Google Scholar

Eisenberg, J., Schmidli, H. (2010). Minimising expected discounted capital injections by reinsurance in a classical risk model. Scandinavian Actuarial Journal, forthcoming.Google Scholar

Gerber, H.U. (1979). An Introduction to Mathematical Risk Theory. Philadelphia, PA: S.S. Huebner Foundation.Google Scholar

Gerber, H.U., Goovaerts, M.J., Kaas, R. (1987). On the probability and severity of ruin. ASTIN Bulletin, 17, 151–163.CrossRef Google Scholar

Gerber, H.U., Shiu, E.S.W. (1998). On the time value of ruin. North American Actuarial Journal, 2(1), 48–78.CrossRef Google Scholar

Landriault, D., Willmot, G.E. (2009). On the joint distributions of the time to ruin, the surplus prior to ruin, and the deficit at ruin in the classical risk model. North American Actuarial Journal, 13(2), 252–279.CrossRef Google Scholar