1 Introduction
Our aim in this paper and its accompanying paper, Hariyanto et al. (Reference Hariyanto, Dickson and Pitt2014a), referred to as Paper I, is to develop a method to estimate the probability of transition at individual ages between disability states as defined in the Survey of Disability, Ageing and Carers produced by the Australian Bureau of Statistics. In Paper I we describe the main tools (models) of the method and the estimation of the numbers of individuals in different disability categories at annual intervals from 1998 to 2003. In this paper we describe our method, followed by its implementation, discussion of results and graduation of the estimated transition probabilities.
In particular, we work through Steps 3 to 5 in Figure 1.1 of Paper I. In Sections 2 to 5 we deal with Step 3; we consider the calculation of net overseas migration in Sections 2 and 3, as part of our projection of the Australian population. The projected population is used in Sections 4 and 5 where we obtain our initial and refined estimates of one-year longitudinal disability data. Sections 5 and 6 deal with Step 4 in Figure 1. We outline the IPF procedure and its application in Section 5, then we estimate crude disability transition probabilities in Section 6. Finally, in Section 7 we complete Step 5 in Figure 1.1 by graduating the crude transition probabilities from Section 6.
2 Assumptions and Notation
In this paper, we assume that the population and overseas migrants who are aged x last birthday (where x is an integer) are aged exactly x + 0.5. We consider ages 60.5, 61.5, …, 109.5. In addition, we assume that only one transition is possible over a one-year period. We define the following notation.
•
$$$ NOM_{{x\, + \,0.5}}^{n} (t, \ t\, + \,1) $$$
denotes the number of net overseas migrants from the middle of year t to the middle of year t + 1 where the migrants are aged x + 0.5 and in state n (n = 0, 1,…, 4) when they migrate.•
$$$ I_{{x\, + \,0.5}}^{n} (t) $$$
denotes the number of net overseas migrants between the middle of years t − 1 and t who attain age x + 0.5 and are in state n (n = 0, 1,…, 5) at the middle of year t.•
$$$ N_{{x\, + \,0.5}}^{n} (t) $$$
denotes the size of population aged x + 0.5 and in state n (n = 0, 1,…, 4) at the middle of year t.•
$$$ {{\mathop{N}\limits^{{\rm{o}}}}}^{\vskip 6pt n} _{{x\, + \,0.5}} (t) $$$
denotes the size of population aged x + 0.5 and in state n (n = 0, 1,…,4) at the middle of year t assuming the absence of overseas migration between the middle of years t − 1 and t.•
$$$ {{D}_{x\, + \,0.5}}(t) $$$
denotes the number of deaths between the middle of years t − 1 and t from the population and net overseas migrants (those who migrate between the middle of years t − 1 and t) who are aged x − 0.5 at the middle of year t − 1.•
$$$ {{{\mathop{D}\limits^{{\rm{o}}}} }_{x\, + \,0.5}}(t) $$$
denotes the number of deaths between the middle of years t − 1 and t from the population aged x − 0.5 at the middle of year t − 1.•
$$$ N_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,\,t\, + \,1) $$$
denotes the size of the population aged x + 0.5 (for x = 60, 61,…, 108) and in state m (m = 0, 1,…, 4) at the middle of year t, and aged x + 1.5 and in state n (n = 0, 1,…, 5) at the middle of year t + 1. These are the real one-year longitudinal data.•
$$$ \bar{P}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,\,t\, + \,1) $$$
is the initial estimate of the probability that an individual aged x + 0.5 (for x = 60, 61,…, 108) and in state m (m = 0, 1,…, 4) at the middle of year t makes a transition to state n (n = 0, 1,…, 5) before reaching age x + 1.5. This probability is calculated from the conditional disability transition probabilities (i.e. probability of deteriorating, improving or staying in the same disability state conditional on survival) estimated in Section 4.3.3 of Paper I and the one-year death probability applicable at the middle of year t (discussed later).•
$$$ \hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,\,t\, + \,1) $$$
denotes the estimate of
$$$ N_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,\,t\, + \,1) $$$
calculated from
$$$ \bar{P}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,\,t\, + \,1) $$$
. This is the initial estimate of the one-year longitudinal data.•
$$$ \tilde{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,\,t\, + \,1) $$$
denotes the refined estimate of
$$$ N_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,\,t\, + \,1) $$$
(discussed later).
3 Estimation of Net Overseas Migration
In this section we describe the estimation of net overseas migration, 
$$$ NOM_{{x\, + \,0.5}}^{n} (t\,{\rm{ - }}\,1,\,t) $$$
, for n = 0, 1, …, 4 and t = 1999, 2000, …, 2003. From these estimates we calculate 
$$$ I_{{x\, + \,0.5}}^{n} (t) $$$
(for n = 0, 1, …, 5 and t = 1999, 2000, …, 2003). The data are from the overseas migration statistics published by the ABS (ABS, 2000, 2001, 2003, 2004b). Overseas migration consists of four components: permanent movement, long-term movement (arrivals and departures involving a period of 12 months or more), short-term movement (arrivals and departures involving a period of less than 12 months), and category jumping (the change between actual and intended duration of stay of travellers to and from Australia).
In adjusting the estimated disabled population for overseas migration, we only consider permanent and long-term movement (in line with the measurement of ERP). Estimates of permanent and long-term movement from one mid-year to the next from 1998 to 2002 are provided by the ABS. The estimates from 1998 to 2000 are not adjusted for category jumping (ABS, 2005). The net overseas migration (NOM) is calculated as total permanent and long-term arrivals minus total permanent and long-term departures. Table 3.1 presents the estimates of NOM in 1999 for males and females.
Table 3.1 NOM for the year ending 30 June 2000. Source: ABS (2001).
For ages 60 and over, the NOM is very small in comparison with the size of the disabled population (see Tables 5.2 and 5.3 of Paper I). Therefore, error in the estimation of NOM (including the error which arises from category jumping) is likely to have an insignificant effect on the estimated transition probabilities.
The NOM at single ages is estimated under the cumulation-differencing method using Sprague's formula. Regarding overseas migration, we assume the following.
(A1) Zero overseas migration for ages 95 and above.
(A2) Overseas migrants who migrate between the middle of years t and t + 1 have the same disability prevalence rates as the population at the same age at the middle of year t + 1.
(A3) Half of overseas migrations between the middle of years t and t + 1 occur at the middle of year t and half at the middle of year t + 1.
(A4) The probabilities
$$$ \bar{P}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,\,t\, + \,1) $$$
are applicable to the overseas migrants.
Therefore, 
$$$ I_{{x\, + \,0.5}}^{n} (t) $$$
(for n = 0, 1, …, 5 and t = 1999, 2000, …, 2003) are calculated according to
$$I_{{x\, + \,0.5}}^{n} (t)\, = \,\frac{1}{2}\mathop{\sum}\limits_{m\, = \,0}^4 \left( {NOM_{{x\,{\rm{ - }}\,0.5}}^{m} (t\,{\rm{ - }}\,1, \ t)\,\times \,\bar{P}_{{x\,{\rm{ - }}\,0.5,x\, + \,0.5}}^{{m,n}} (t\,{\rm{ - }}\,1, \ t)} \right)\, + \,\frac{1}{2}NOM_{{x\, + \,0.5}}^{n} (t\,{\rm{ - }}\,1, \ t).$$
The calculation of 
$$$ \bar{P}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t, \ t\, + \,1) $$$
and the estimation of 
$$$ \hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
are described in Section 4.
4 Initial Estimation of One-Year Longitudinal Data
In this section we describe the estimation of 
$$$ \hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
. Firstly, we calculate 
$$$ \bar{P}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
by incorporating a time trend into the one-year death probability, while the conditional disability transition probabilities (i.e. conditional on survival) are as estimated in Section 4.3.3 of Paper I. Specifically (for m = 0, 1,…, 4):
$${ \bar{P}_{{x\, + \,0.5,x\, & + \,1.5}}^{{m,n}} (t,t\, + \,1) = \left\{ {\matrix{ {\matrix{ {(1\,{\rm{ - }}\,Mortality(x\, + \,0.5,t,m))\,\times \,} \hfill \cr {\vskip4pt{Deteriorate(x\, + \,0.5,m,n)} \quad\qquad\qquad\qquad\qquad\quad\qquad {:\; \; m\, \lt \,n\,\leq \,4,}} \hfill \cr{\matrix{ {\vskip 4pt(1\,{\rm{ - }}\,Mortality(x\, + \,0.5,t,m))\,\times \,} \hfill \cr {\vskip3pt(1\,{\rm{ - }}\,Deteriorate\_From(x\, + \,0.5,m))\,\times \,} \hfill \ \ \ \quad\quad\qquad \ \ {:\; \; n\, = \,m,} \qquad\qquad\hfill \cr {\vskip3pt{(1\,{\rm{ - }}\,Improve\_From(x\, + \,0.5,m))} \hfill \hfill \\\end \hfill & }\hfill \cr {\matrix{\vskip3pt {(1\,{\rm{ - }}\,Mortality(x\, + \,0.5,t,m))\,\times \,} \hfill \cr {{(1\,{\rm{ - }}\,Deteriorate\_From(x\, + \,0.5,m))\,\times \,} \qquad\qquad\qquad{:\; \; 0\,\leq \,n\, = \,m\,{\rm{ - }}\,1,}} \hfill \cr \vskip-4pt{Improve\_From(x\, + \,0.5,m)} \hfill \hfill \\\end \hfill & \hfill \cr \vskip-4pt{Mortality(x\, + \,0.5,t,m)} \hfill \qquad\qquad\qquad \ \ \ \ {:\; \; n\, = \,5,} \hfill \cr \vskip-6pt0 \hfill \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \ \ {:\; \; n\, \lt \,m\,{\rm{ - }}\,1,} \hfill \\\end \right $$
where
$$$ Mortality(x\, + \,0.5,t,n) $$$
is the value of 
$$$ Mortality(x\, + \,0.5,n) $$$
applicable at the middle of year t, and
$$$ Deteriorate(x \, + \, 0.5,m,n) $$$
, 
$$$ Deteriorate\_From(x\, + \,0.5,m) $$$
and 
$$$ Improve\_From(x\, + \,0.5,m) $$$
are as estimated in Section 4.3.3 of Paper I.
The value of 
$$$ Mortality(x\, + \,0.5,t,n) $$$
is calculated by incorporating a time trend into the healthy mortality component of 
$$$ Mortality(x\, + \,0.5,n) $$$
(see Section 4.3.3 of Paper I) while the additional mortality due to the disability component is still assumed to be time invariant. Specifically (for n = 0, 1, …, 4):
$$ Mortality(x\, + \,0.5,t,n)\, = \,Overall\_Mort(x\, + \,0.5,t)\, + \, Additional\_Mort\,(x\, + \,0.5,n) \eqno $$
where
$$$ Overall\_Mort(x\, + \,0.5,t) $$$
is the value of 
$$$ Overall\_Mort(x\, + \,0.5) $$$
applicable at the middle of year t, and
$$$ Additional\_Mort(x\, + \,0.5,n) $$$
and its values are as described in Section 4.3.3 of Paper I.
$$$ Overall\_Mort(x\, + \,0.5,t) $$$
is estimated by matching the total number of deaths between the middle of years t and t + 1 from each disability category (where the one-year death probability of disability category n (for n = 0, 1, …, 4) is calculated according to (4.1)) with the total number of deaths if the whole population (total population across disability categories) experience mortality rates as specified in the Australian Life Table (ALT) in the relevant years (the ALTs are obtained from ABS (2008)). In the estimation, deaths from overseas migrants are considered (due to assumption (A3) of Section 3, we only need to consider those who migrate at the middle of year t). The one-year life table death probability (which is applicable to the whole population) from age x + 0.5 which is applicable at the middle of year t is calculated using
$$ q_{{x\, + \,0.5}}^{t} \, = \,1\,{\rm{ - }}\,p_{{x\, + \,0.5}}^{t} \, = \,1\,{\rm{ - }}\,{\rm{exp}}\left\{ {{\rm{ - }}0.5\,\times \,\left( {\mu _{{x\, + \,0.5}}^{t} \, + \,\mu _{{x\, + \,1.5}}^{{t\, + \,1}} } \right)} \right\} $$
where 
$$$ \mu _{x}^{t} $$$
is the force of mortality at age x which is estimated from the ALT applicable in year t. The forces of mortality at ages above 100 are extrapolated using Gompertz’ formula.
The 
$$$ \hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
are then calculated using (for m = 0, 1, …, 4 and n = 0, 1, …, 5)
$$\hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1)\, = \,N_{{x\, + \,0.5}}^{m} (t)\,\times \,\bar{P}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1).$$
The 
$$$ N_{{x\, + \,0.5}}^{m} (t) $$$
for m = 0, 1, …, 4 and t = 1998, 1999, …, 2003 are estimated in Paper I (note that we assume that the population who are aged x last birthday are aged x + 0.5 exact). From these estimates, we calculate 
$$$ \hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
for m = 0, 1, …, 4, n = 0, 1, …, 5 and t = 1998, 1999, …, 2002.
5 Refined Estimation of One-Year Longitudinal Data
In this section we obtain refinements 
$$$ \tilde{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
of the initial estimate of one-year longitudinal data calculated in Section 4. We begin by describing the outline of the procedure, then describe the actual steps of the estimation.
5.1 Outline
Consider the period from the middle of year t to the middle of year t + 1. Note that
$$ N_{{x\, + \,1.5}}^{n} (t\, + \,1)\, = \,\mathop{\sum}\limits_{m\, = \,0}^4 N_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1)\, + \,I_{{x\, + \,1.5}}^{n} (t\, + \,1) $$
for n = 0, 1,…, 4 and
$$ {{D}_{x\, + \,1.5}}(t\, + \,1)\, = \,\mathop{\sum}\limits_{m\, = \,0}^4 N_{{x\, + \,0.5,x\, + \,1.5}}^{{m,5}} (t,t\, + \,1)\, + \,I_{{x\, + \,1.5}}^{5} (t\, + \,1). $$
Adjusting 
$$$ N_{{x\, + \,1.5}}^{n} (t\, + \,1) $$$
and 
$$$ {{D}_{x\, + \,1.5}}(t\, + \,1) $$$
to exclude net overseas migrants who migrate between the middle of years t and t + 1 we have
$${\mathop{N}\limits^{ \circ }} _{{x\, + \,1.5}}^{\vskip 5pt n} (t\, + \,1)\, = \,N_{{x\, + \,1.5}}^{n} (t\, + \,1)\,{\rm{ - }}\,I_{{x\, + \,1.5}}^{n} (t\, + \,1)\, = \,\mathop{\sum}\limits_{m\, = \,0}^4 N_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1)$$
for n = 0, 1,…, 4 and
$${{{\mathop{D}\limits^{ \circ }} }_{x\, + \,1.5}}(t\, + \,1)\, = \,{{D}_{x\, + \,1.5}}(t\, + \,1)\,{\rm{ - }}\,I_{{x\, + \,1.5}}^{5} (t\, + \,1)\, = \,\mathop{\sum}\limits_{m\, = \,0}^4 N_{{x\, + \,0.5,x\, + \,1.5}}^{{m,5}} (t,t\, + \,1).$$
Equations (5.1) and (5.2) can be represented by Table 5.1 where, for convenience, we denote 
$$$ N_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
by 
$$$ N_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} $$$
, with 
$$$ {{R}_m}\, = \,N_{{x\, + \,0.5}}^{m} (t) $$$
, 
$$$ {{C}_n}\, = \,N_{{x\, + \,1.5}}^{n} (t\, + \,1) $$$
, 
$$$ {{C}_5}\, = \,{{{\mathop{D}\limits^{{\rm{o}}}} }_{x\, + \,1.5}}(t\, + \,1) $$$
and
Table 5.1 Annual population transition from the middle of year t to the middle of year t + 1.
$$ T\, = \,\mathop{\sum}\limits_{m\, = \,0}^4 {{R}_m}\, = \,\mathop{\sum}\limits_{n\, = \,0}^5 {{C}_n}. $$
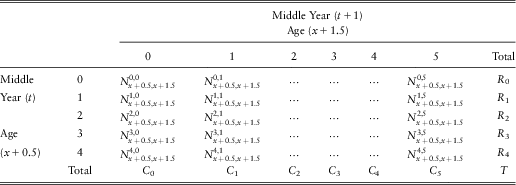
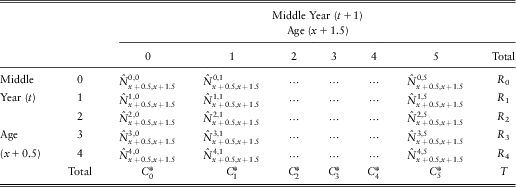
Table 5.2 is similar to Table 5.1 with the elements of Table 5.1 being replaced by the initial estimates of one year longitudinal data (
$$$ \hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
) calculated in Section 4.
Table 5.2 Estimate of annual population transition from the middle of year t to the middle of year t + 1.
Since the transition probabilities sum to one, we have
$${{R}_m}\, = \,N_{{x\, + \,0.5}}^{m} (t)\, = \,\mathop{\sum}\limits_{n\, = \,0}^5 \hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1)\quad {\rm for}\;\,m\, = \,0,1, \ldots, 4.$$
However, the following are unlikely to hold:
$${{C}_n}\, = \,{\mathop{N}\limits^{{\rm{o}}}} _{{x\, + \,1.5}}^{\vskip 5pt n} (t\, + \,1)\, = \,\mathop{\sum}\limits_{m\, = \,0}^4 \hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,\,t\, + \,1)\quad {\rm for}\,\,\,n\, = \,0,1, \ldots, 4,$$
$${{C}_5}\, = \,{{{\mathop{D}\limits^{{\rm{o}}}} }_{x\, + \,1.5}}(t\, + \,1)\, = \,\mathop{\sum}\limits_{m\, = \,0}^4 \hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,5}} (t,\,t\, + \,1).$$
Possible reasons why (5.4) and (5.5) may not hold are statistical variation and inaccurate estimation of the transition probabilities. However, if the exposures (
$$$ N_{{x\, + \,0.5}}^{n} (t) $$$
for n = 0, 1, …, 4) are large, the error due to statistical variation is likely to be small, and hence the remaining error is largely due to inaccurate estimation of the transition probabilities. Therefore, if we have accurate estimates of 
$$$ N_{{x\, + \,0.5}}^{n} (t) $$$
, 
$$$ {\mathop{N}\limits^{{\rm{o}}}} _{{x\, + \,1.5}}^{\vskip 6ptn} (t\, + \,1) $$$
(for n = 0, 1, …, 4) and 
$$$ {{{\mathop{D}\limits^{{\rm{o}}}} }_{x\, + \,1.5}}(t\, + \,1) $$$
for each single year of age, we are able to employ the IPF algorithm to refine our initial estimates of one-year longitudinal data (
$$$ \hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
) such that (5.4) and (5.5) hold (with (5.3) still holding). In doing so, we assume that the cross product ratios of 
$$$ \left\{ {\hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1)} \right\} $$$
are similar to the cross product ratios of 
$$$ \left\{ {N_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1)} \right\} $$$
(which is hopefully the case; in the implementation of the multiple state model as part of the estimation of 
$$$ \bar{P}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
, we have tried to be as realistic as the data allow). The refined estimates of one-year longitudinal disability data (
$$$ \tilde{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
) are maximum likelihood estimates (MLEs) under a saturated log-linear model with the state at the middle of year t as variable 1 and the state at the middle of year t + 1 as variable 2. Specifically (for i = 0, 1, …, 4 and j = 0, 1, …, 5)
• the main effect of variable 1 (u 1(i )) is estimated from {Ri},
• the main effect of variable 2 (u 2(j )) is estimated from {Cj}, and
• the interaction effect between variables 1 and 2 (u 12(ij )) is estimated from the cross product ratios of
$$$ \left\{ {\hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{i,j}} (t,t\, + \,1)} \right\} $$$
.
Therefore, in the application of the IPF algorithm we set:
•
$$$ {{x}_{i + }}\, = \,{{R}_i}\; \; \; \; for\,\;i\, = \,0,1, \ldots, 4 $$$
•
$$$ {{x}_{ + j}}\, = \,{{C}_j}\; \; \; \; for\;\,j\, = \,0,1, \ldots, 5 $$$
•
$$$ \hat{f}_{{ij}}^{{(0)}} \, = \,\hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{i,j}} (t,t\, + \,1)\,\quad {\rm for}\,\,i\, = \,0,1, \ldots, 4\;{\rm{and}}\quad j\, = \,0,1, \ldots, 5 $$$
.
Provided that the estimates of 
$$$ N_{{x\, + \,0.5}}^{n} (t) $$$
, 
$$$ N_{{x\, + \,1.5}}^{n} (t\, + \,1) $$$
and 
$$$ {{{\mathop{D}\limits^{{\rm{o}}}} }_{x\, + \,1.5}}(t\, + \,1) $$$
are accurate, and the cross product ratios of 
$$$ \left\{ {\hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1)} \right\} $$$
are similar to the cross product ratios of 
$$$ \left\{ {N_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1)} \right\} $$$
, at convergence we have 
$$$ {{\hat{f}}_{mn}}\, \approx \,N_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
(for m = 0, 1, …, 4 and n = 0, 1, …, 5). The convergence values under the above IPF algorithm are our refined estimates of one-year longitudinal data (i.e. 
$$$ \tilde{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1)\, = \,{{\hat{f}}_{mn}} $$$
).
In the following we describe the estimation steps for 
$$$ \tilde{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
.
5.2 Estimation Steps
The first step is to calculate 
$$$ {\mathop{N}\limits^{{\rm{o}}}} _{{x\, + \,1.5}}^{\vskip 5pt n} (t\, + \,1) $$$
(for n = 0, 1,…, 4) from the estimates of 
$$$ N_{{x\, + \,1.5}}^{n} (t\, + \,1) $$$
(see Section 5 of Paper I) and 
$$$ I_{{x\, + \,1.5}}^{n} (t\, + \,1) $$$
(Section 3) using equation (5.1). In this step, we calculate the first five column totals of Table 5.1 (i.e. C 0, C 1, …, C 4).
The second step is to estimate 
$$$ {{{\mathop{D}\limits^{{\rm{o}}}} }_{x\, + \,1.5}}(t\, + \,1) $$$
according to the following:
$$ {{{\mathop{D}\limits^{{\rm{o}}}} }_{x\, + \,1.5}}(t\, + \,1)\, = \,{{N}_{x\, + \,0.5}}(t)\,{\rm{ - }}\,{{N}_{x\, + \,1.5}}(t\, + \,1)\, + \,{{I}_{x\, + \,1.5}}(t\, + \,1) $$
where
$$ {{N}_{x\, + \,0.5}}(t)\, = \,\mathop{\sum}\limits_{n\, = \,0}^4 N_{{x\, + \,0.5}}^{n} (t)\,\,{\rm{and}}\,\,\,{{I}_{x\, + \,1.5}}(t\, + \,1)\, = \,\mathop{\sum}\limits_{n\, = \,0}^4 I_{{x\, + \,1.5}}^{n} (t\, + \,1). $$
In this step, we calculate the sixth column total of Table 5.1 (i.e. C 5).
Finally, from 
$$$ \left\{ {\hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1)} \right\} $$$
and the estimates of 
$$$ {\mathop{N}\limits^{{\rm{o}}}} _{{x\, + \,1.5}}^{\vskip 5pt n} (t\, + \,1) $$$
(for n = 0, 1, …, 4) and 
$$$ {{{\mathop{D}\limits^{{\rm{o}}}} }_{x\, + \,1.5}}(t\, + \,1) $$$
, we apply the IPF algorithm described in Section 5.1 to obtain 
$$$ \left\{ {\tilde{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1)} \right\} $$$
. We apply this procedure to obtain 
$$$ \left\{ {\tilde{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1)} \right\} $$$
for x = 60, 61, …, 108.
We apply the above procedures to the disabled population estimated in Paper I. The procedures are applied to the disabled population estimated at each pair of subsequent years (1998 and 1999, etc). Therefore, we obtain refined estimates of one-year longitudinal data from 1998 (i.e. from the middle of 1998 to the middle of 1999) to 2002. Specifically, we obtain 
$$$ \tilde{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
for x = 60, 61, …, 108, m = 0, 1, …, 4, n = 0, 1, …, 5 and t = 1998, 1999, …, 2002.
6 Estimation of Crude Transition Probabilities
The refined estimate of the one-year transition probability is calculated as:
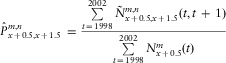$$\hat{P}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} \, = \,\frac{{\mathop{\sum}\limits_{t\, = \,1998}^{2002} \tilde{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1)}}{{\mathop{\sum}\limits_{t\, = \,1998}^{2002} N_{{x\, + \,0.5}}^{m} (t)}}$$
for m = 0, 1, …, 4 and n = 0, 1, …, 5 where 
$$$ \hat{P}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} $$$
is the refined estimate of the probability that an individual aged x + 0.5 and in live state m makes a transition to state n before reaching age x + 1.5, and 
$$$ \tilde{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
is the refined estimate of 
$$$ \hat{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
. Note that 
$$$ \hat{P}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} $$$
can only be regarded as a crude estimate, and hence graduation should take place.
From the refined estimates of one-year longitudinal disability data estimated in Section 5, we use formula (6.1) to calculate the refined estimates of one-year disability transition probabilities.
Figure 6.1 illustrates these crude probabilities for the no CAL category. In Figure 6.1, the transition data at ages above 85 are grouped into quinquennial age bands (discussed later).
Figure 6.1 One-year crude transition probabilities from able (no CAL) state.
There is a lack of randomness in the estimated crude probabilities as indicated by the systematic oscillation in the movement of the estimates from age to age. This is due to the various methods employed in estimating the annual disabled population at a single age (Paper I) and in deriving the initial estimate of one-year longitudinal data. While there is a lack of randomness, we believe the levels of estimated crude probabilities are indicative of the true levels of crude probabilities.
The patterns of the crude improvement probabilities, with the exception of improvement from mild CAL, are peculiar. Figure 6.2 shows the crude improvement probabilities from moderate CAL and from profound CAL for males. This peculiarity is because while in reality, improvement by more than one disability category is possible over the year, the initial transition probabilities do not allow this. Note that the accuracy of the results of the IPF procedure also depends on the accuracy of the initial probabilities used in the estimation. The crude improvement probabilities from moderate CAL show a more peculiar pattern than the crude improvement probabilities from either severe CAL or profound CAL as improvement by more than one category is more likely for the less disabled state.
Figure 6.2 Crude improvement probabilities from moderate CAL and from profound CAL, males.
For females, the following crude transition probabilities from mild CAL also have peculiar patterns:
(a) Mild CAL to mild CAL: non-decreasing at ages above 86.
(b) Mild CAL to moderate CAL: decreasing rapidly at ages above 86.
(c) Mild CAL to severe CAL: decreasing rapidly at ages above 86.
(d) Mild CAL to dead: lower than the crude death probabilities of no CAL at ages above 89.
Figure 6.3 shows the crude transition probabilities from mild CAL to mild CAL and from mild CAL to severe CAL for females. The peculiar patterns of these crude transition probabilities for females might be caused by the inaccuracy of the initial deterioration probabilities from mild CAL to moderate CAL and to severe CAL. The crude probabilities suggest that these deterioration probabilities should decrease with age at advanced ages. However, the initial deterioration probabilities are non-decreasing with age over this age range. If, in fact, these deterioration probabilities do decrease with age (which might be due to the rapid increase of deterioration to profound CAL and death probabilities), the inaccuracy of initial probabilities will distort the results of the IPF procedure at the relevant ages. Therefore, the decreasing pattern of (b) and (c) implied from the estimated crude probabilities might be too strong. The possible distortion might not be limited to the related probabilities (i.e. (a) and (d) might also be the result of distortion).
Figure 6.3 Selected crude transition probabilities from mild CAL, females.
The crude probabilities also suggest a decreasing pattern of the deterioration probabilities from no CAL to moderate CAL for females at ages above 86. However, since the decreasing pattern is evident for only one deterioration probability, the distortion is likely to be small. Other crude transition probabilities from no CAL for females generally behave as expected.
It is counter-intuitive for deterioration probabilities to decrease with age. However, the longitudinal disability data from the U.S. show that this could be the case. In Table 6 of Rickayzen and Walsh (2002), the disability transition rates from the National Long Term Care Surveys of 1982 and 1984 are presented. In that table, the transition probabilities from failing one ADL to failing two ADLs for males and from failing two ADLs to failing three or more ADLs for females are decreasing with age (although the stay probabilities (probabilities of staying at the same category) of these categories are high).
For some transition probabilities, the crude probabilities at ages above 85 or 90 are spurious. This is because of the difficulty in estimating the disabled population at these ages. In our graduation, we resolve this problem by grouping the data at high ages into quinquennial age bands and calculating crude probabilities at the weighted mean age.
We now make some observations on the estimated crude probabilities.
• Additional mortality due to disability is also experienced in the moderate CAL category.
• At very high ages, the observed mortality rates of the population are close to the crude mortality rates of profound CAL, while at younger ages they are close to the crude mortality rates of no CAL. This is in line with the reported disability prevalence rates at these ages.
• Generally, crude mortality rates are higher for males than for females across disability categories with the difference between genders being much less pronounced at very high ages. The difference between genders also seems to increase with the severity of disablement.
• For females, the crude mortality rates of mild CAL at ages above 89 are lower than the crude mortality rates of no CAL.
• The crude probabilities suggest lower mortality rates than the initial probabilities for no CAL and mild CAL at ages above 89. For females, the crude probabilities also suggest higher mortality rates for severe CAL and profound CAL at ages above 98.
We now make some observations about the crude deterioration probabilities.
• Generally, the crude deterioration probabilities are increasing with age with the increase slowing down at the very advanced ages. There are several exceptions to this. In particular, for females, the crude deterioration probabilities from no CAL to moderate CAL, and from mild CAL to moderate CAL and severe CAL are decreasing with age at ages above 86.
• Generally, deterioration is more likely into the less disabled states. However, crude deterioration probabilities into profound CAL are peculiar. Specifically, for males, deterioration into profound CAL is more likely than deterioration into severe CAL. For females, deterioration into profound CAL is more likely than deterioration into any less disabled state at ages above 80.
• Crude deterioration probabilities into a given disability state are higher for more disabled states than the less disabled ones.
• Crude deterioration probabilities are generally higher for females with the difference between genders seeming to increase with the severity of the disablement. The exceptions are deterioration into mild CAL (at ages 60 and above) and moderate CAL (at ages above 89).
• The crude deterioration probabilities suggest lower deterioration rates than the initial probabilities for deterioration into moderate CAL, severe CAL and profound CAL at ages above 89.
We now make some observations about the crude improvement probabilities.
• The crude improvement probabilities from moderate CAL are very spurious.
• Generally, crude improvement probabilities are decreasing with age (excluding improvement from moderate CAL; in the discussion below we exclude improvement from moderate CAL).
• For males, the crude improvement probabilities are generally decreasing with the severity of disablement.
• For females, at ages between 60 and 89, the improvement from mild CAL is the highest, while the improvements from severe CAL and profound CAL are broadly at similar levels. However, at ages above 89, the improvement from profound CAL is slightly higher than the improvement from either mild CAL or severe CAL.
• The improvements from mild CAL and severe CAL are broadly similar between genders at ages below 89 and higher for males at ages above 89. For profound CAL, the improvements are higher for males at ages between 60 and 70, slightly higher for females at ages between 70 and 90, and similar between genders at ages above 90.
• For males, the crude probabilities suggest higher improvement rates than the initial probabilities for mild CAL at ages above 89 and for profound CAL at ages between 60 and 70. For females, the crude probabilities suggest lower improvement rates from mild CAL at ages above 70 and from profound CAL at ages above 90.
We now make some observations about the crude stay probabilities.
• Generally, the crude stay probabilities are decreasing with age.
• At ages below 83, the crude stay probabilities of no CAL are the highest amongst the disability categories. At ages above 83, excluding profound CAL, the crude stay probabilities are decreasing with the severity of disablement (the crude stay probabilities of profound CAL are relatively high at these ages, at about a similar level as the crude stay probabilities of no CAL).
• The crude stay probabilities of no CAL and mild CAL are broadly at similar levels for males and females. The crude stay probabilities of moderate CAL and severe CAL are higher for males at ages above 89 (due to the higher likelihood of deteriorating into profound CAL for females). The crude stay probabilities of profound CAL are higher for females (due to the higher death probabilities for males).
• For males, the crude probabilities suggest higher stay probabilities than the initial probabilities for no CAL, mild CAL and moderate CAL at ages above 89. For females, the crude probabilities suggest higher stay probabilities for mild CAL and lower stay probabilities for moderate CAL at ages above 89.
7 Graduation of Disability Transition Probabilities
In this section, we graduate the crude disability transition probabilities calculated in Section 6. We begin by discussing the graduation method, then the graduation of the transition probabilities, and finally we assess the graduated probabilities.
7.1 Graduation Method
We consider graduation using Generalised Linear and Non-Linear models (GLM/NLM) and the Whittaker-Henderson (W-H) method. Graduation under GLM/NLM is discussed in Renshaw (Reference Renshaw1991) while the W-H method is discussed in Joseph (Reference Joseph1952). In the following we describe the adopted GLM/NLM.
Denote (for m = 0, 1,…, 4 and n = 0, 1,…, 5):
$$$ N_{{x\, + \,0.5}}^{m} \, = \,\mathop{\sum}\limits_{t\, = \,1998}^{2002} {N_{{x\, + \,0.5}}^{m} \,(t).} $$$
$$$ T_{{x\, + \,0.5,\,x\, + \,1.5}}^{{m,n}} $$$
: random variable for the number of transitions from state m to state n from the exposure 
$$$ N_{{x\, + \,0.5}}^{m} $$$
where the transitions occur over the age interval [x + 0.5, x + 1.5].
$$$ \hat{T}_{{x\, + \,0.5,\,x\, + \,1.5}}^{{m,n}} $$$
: sample value of 
$$$ T_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} $$$
obtained from the investigation from the middle of 1998 to the middle of 2003.
$$$ {\mathop{P}\limits^{ \circ }} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt m,n}} $$$
: graduated value obtained after smoothing 
$$$ \hat{P}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} $$$
.
Since we assume that only one transition is possible over a single year interval and that the population who are aged x last birthday are aged x + 0.5 exact, then the following is approximately true:
$$\hat{T}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} \, = \,\mathop{\sum}\limits_{t\, = \,1998}^{2002} \tilde{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1),\; \; m\, = \,0,1, \ldots, 4\,\,{\rm{and}}\,\,n\, = \,0,1, \ldots, 5.$$
The reason (7.1) is not exactly correct is because by definition 
$$$ \tilde{N}_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} (t,t\, + \,1) $$$
is affected by the transitions which occur at exact age x + 1.5. However, practically, this error is negligible.
We adopt the binomial distribution for the number of transitions:
$$ T_{{x\, + \,0.5,x\, + \,1.5}}^{{m,n}} \, \sim \,Bin\left( {N_{{x\, + \,0.5}}^{m}, \,{\mathop{P}\limits^{{\rm{o}}}} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt m,n}} } \right),\; \; m\, = \,0,1, \ldots, 4\,\,\,{\rm{and}}\,\,n\, = \,0,1, \ldots, 5 $$
where
$$ {\mathop{P}\limits^{{\rm{o}}}} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt m,n}} \, = \,GM_{\beta }^{{r,s}} (x\, + \,0.5)\,\,{\rm{or}}\,\,LGM_{\beta }^{{r,s}} (x\, + \,0.5), $$
$$GM_{\beta }^{{r,s}} (x\, + \,0.5)\, = \,\mathop{\sum}\limits_{i\, = \,1}^r {{\beta }_i}{{(x\, + \,0.5)}^{i\,{\rm{ - }}\,1}} \, + \,{\rm{exp}}\left\{ {\mathop{\sum}\limits_{i\, = \,r\, + \,1}^{r\, + \,s} {{\beta }_i}{{{(x\, + \,0.5)}}^{i\,{\rm{ - }}\,r\,{\rm{ - }}\,1}} } \right\}\;\;r,s\,\geq \,0,$$
$$LGM_{\beta }^{{r,s}} (x\, + \,0.5)\, = \,\frac{{GM_{\beta }^{{r,s}} (x\, + \,0.5)}}{{1\, + \,GM_{\beta }^{{r,s}} (x\, + \,0.5)}}\; \; r,s\,\geq \,0,$$
where GM denotes the Gompertz-Makeham formula and LGM denotes the logit Gompertz-Makeham formula. These formulae are often used in the graduation of mortality, disability and health data; see, for example, Leung (Reference Leung2006) and Pritchard (Reference Pritchard2006). Note that r = 0 implies the exponentiated polynomial term only, and s = 0 implies a polynomial term only.
The parameters 
$$$ \{ {{\beta }_1}, \ldots, {{\beta }_{r\, + \,s}}\} $$$
are estimated using maximum likelihood. Note that if both r and s are at least 1, we will have a non-linear predictor (GNLM). In this case, the parameters can be estimated by expanding the non-linear terms in the predictor using a Taylor series expansion; see Renshaw (Reference Renshaw1991). However, for convenience, we instead fit the GNLM by using the “gnm” function in R; see Turner (Reference Turner and Firth2011). Starting values for the iteration can be obtained using the weighted least squares (WLS) method.
For each transition probability, to determine a suitable model, we experiment with (7.2) and (7.3) with a variety of values of r and s.
As described in Section 6, some crude transition probabilities are spurious at ages above 85. For ages at which this is the case, we group the data at these ages into quinquennial age bands and calculate crude transition probabilities at the weighted mean age. The graduated probabilities are calculated from these recalculated crude probabilities.
Under the W-H method, the weights in the fitting are chosen to be the inverse of the variance of the crude probabilities. Under this method, in the case where the data are grouped, the graduated probabilities at a single age are obtained by fitting a polynomial to the graduated probabilities at the relevant ages. While this approach is not standard, for some transitions it produces satisfactory graduated values.
7.2 Graduation of Death Probabilities
For graduation of death probabilities, in addition to the methods described in Section 7.1, we also consider GLMs by targeting the force of mortality (
$$$ {{\mu }_{x\, + \,0.5}} $$$
) and graduation by reference to a standard table (Benjamin and Pollard (Reference Benjamin and Pollard1993)). In implementing the GLM by targeting 
$$$ {{\mu }_{x\, + \,0.5}} $$$
, we limit our investigation to the formula 
$$$ {{\mu }_{x\, + \,0.5}}\, = \,GM_{\beta }^{{0,s}} (x\, + \,0.5) $$$
for s ≥ 0.
Under graduation by reference to a standard table, the chosen standard tables are the Australian Life Tables 2000–02 (AGA, 2004). We consider a variety of possible relationships between the mortality rates of the standard table and the graduated mortality rates. The parameters of the graduation formula are estimated using the WLS method.
For females, the graduated mortality rates of mild CAL are lower than the graduated mortality rates of no CAL at the advanced ages. Note that this is because of the peculiarity of the crude rates. As discussed in Section 6, for females, there might be a distortion in the results of the IPF procedure for transitions from mild CAL at advanced ages. Comparing the crude mortality rates of no CAL with mild CAL, we find that at younger ages the crude mortality rates of these categories are similar. Therefore, for females, we decided to ignore the crude mortality rates of mild CAL at advanced ages and instead set the graduated mortality rates of mild CAL to be equal to the graduated mortality rates of no CAL.
7.3 Graduation of Improvement, Stay and Deterioration Probabilities
Improvement, stay and deterioration probabilities are graduated under the methods described in Section 7.1. Since for a given disability category, the transition probabilities sum to one, we only need to graduate two of the three transition probabilities as one can be set as residuals. Except for moderate CAL and profound CAL categories, the stay probabilities are set as residuals. For these categories, we instead set the improvement probabilities as residuals. This is because, as discussed in Section 6, the crude improvement probabilities from moderate CAL are spurious. For profound CAL, we find that by setting the improvement probabilities as residuals, more satisfactory graduated values can be obtained.
For some deterioration probabilities (e.g. 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{2,4}} $$$
for males and 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{0,1}} $$$
, 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{0,2}} $$$
, 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{0,3}} $$$
, 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{0,4}} $$$
, 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{2,3}} $$$
and 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{2,4}} $$$
for females), the methods described in Section 7.1 could not produce satisfactory graduated values over the entire considered age range. We resolved this problem using the following method. Firstly, we determined the optimal GM or LGM formula under ML estimation. For ages at which the chosen GM (or LGM) formula was unsuitable, we alternatively calculated the graduated values by fitting a suitable polynomial at these ages. The parameters of the polynomial were estimated using the ordinary least squares (OLS) method and chosen such that the polynomial curve is continuous from the GM (or LGM) curve at the transition age. Since the ages at which an alternative method is required are typically very high, a simple alternative method seems appropriate.
For females, in the graduation of 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{1,1}} $$$
, 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{1,2}} $$$
, 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{1,3}} $$$
and 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{1,4}} $$$
, we choose not to fully capture the pattern of the crude probabilities at ages above 86. For example, for 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{1,2}} $$$
and 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{1,3}} $$$
, we choose not to fully capture the rapidly decreasing pattern of the crude probabilities at these ages. This is because, for females, there is a possible distortion in the results of the IPF procedure for transitions from mild CAL at these ages as discussed in Section 6.
For some improvement probabilities (e.g. 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{1,0}} $$$
and 
$$$ P_{{x\, + \,0.5,x\, + \,1.5}}^{{3,2}} $$$
for females), the chosen graduation formula results in negative graduated values at extremely high ages. In this case, we simply replace the negative graduated values with zero. We could instead choose an alternative graduation formula which results in non-negative graduated values over the entire considered age range. This method is not preferable since the negative graduated values only occur at extremely high ages (and there will be more cost for switching into an alternative formula as it results in less optimal graduated values over the majority of ages).
Tables 7.1 and 7.2 present the graduated disability transition probabilities for males and females at a selection of ages.
Table 7.1 Males, graduated one-year disability transition probabilities.
Table 7.2 Females, graduated one-year disability transition probabilities.
7.4 Assessment of Graduated Transition Probabilities
To assess the graduated transition probabilities, we consider smoothness and goodness of fit tests. A smoothness test is required for graduation under the W-H method and in the case where we blend a polynomial with a GM (or LGM) formula in the graduation.
For smoothness, we adopt the criteria described in Barnett (Reference Barnett1985) and Benjamin and Pollard (Reference Benjamin and Pollard1993): the graduated probabilities should have third order smoothness (i.e. 
$$$ \left| {{{{\rm{\rDelta }}}^3} {\mathop{P}\limits^{{\rm{o}}}} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt m,n}} } \right|\,{{7}^3} \, \lt \,{\mathop{P}\limits^{{\rm{o}}}} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt m,n}} $$$
) over the majority of the age range. In all of our graduated probabilities, the proportion of ages which satisfy Barnett's (1985) third order smoothness criterion is higher than 50%.
We find that passing the χ 2 test is very difficult. Note that we do not have exposure data (at a single age) or the number of transitions. These quantities are estimated and there are estimation uncertainties. The unmodified implementation of the χ 2 test (i.e. by assuming that the estimated exposure at a single age is the real exposure and the estimated number of transitions is the real number of transitions) ignores these uncertainties and therefore heavily penalises the differences between crude and graduated probabilities. However, incorporation of these uncertainties into the χ 2 test is not straightforward. Therefore, for goodness of fit criteria, as in Leung (Reference Leung2006), we instead use the Theil Inequality Coefficient (TIC), Theil (Reference Theil1958), which is expressed as:
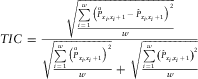$$ TIC\, = \,\frac{{\sqrt {\frac{{\mathop{\sum}\limits_{i\, = \,1}^w {{{\left( {{{{{\mathop{P}\limits^{{\rm{o}}}} }}_{{{x}_i},{{x}_i}\, + \,1}}\,{\rm{ - }}\,{{{\hat{P}}}_{{{x}_i},{{x}_i}\, + \,1}}} \right)}}^2} }}{w}} }}{{\sqrt {\frac{{\mathop{\sum}\limits_{i\, = \,1}^w {{{\left( {{{{{\mathop{P}\limits^{{\rm{o}}}} }}_{{{x}_i},{{x}_i}\, + \,1}}} \right)}}^2} }}{w}} \, + \,\sqrt {\frac{{\mathop{\sum}\limits_{i\, = \,1}^w {{{\left( {{{{\hat{P}}}_{{{x}_i},{{x}_i}\, + \,1}}} \right)}}^2} }}{w}} }} $$
where x 1, x 2,…, xw are ages considered in the graduation. The TIC lies between 0 and 1, with 0 being a perfect fit. The statistical properties of the TIC are discussed in Theil (Reference Theil1958). As in Leung (Reference Leung2006), we accept the graduated probabilities with a TIC of 10% or less. While our assessment of the goodness of fit does not consider the estimated exposure, it is taken into account in our graduation method (except in the case where the graduated probabilities are alternatively calculated under the OLS method where we blend a polynomial with the GM or LGM formula; however, this alternative method is only required at the very high ages as discussed previously).
In addition, due to the lack of randomness of the estimated crude probabilities, passing the individual standardised deviations, runs and serial correlations tests appears to be very difficult. However, most of the graduated probabilities pass both the cumulative deviations and sign tests (at the 5% significance level).
There are some cases where our graduated probabilities do not fully meet the goodness of fit criteria:
•
$$$ {\mathop{P}\limits^{ \circ }} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt 1,1}} $$$
,
$$$ {\mathop{P}\limits^{ \circ }} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt 1,2}} $$$
,
$$$ {\mathop{P}\limits^{ \circ }} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt 1,3}} $$$
,
$$$ {\mathop{P}\limits^{ \circ }} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt 1,4}} $$$
and
$$$ {\mathop{P}\limits^{ \circ }} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt 1,5}} $$$
for females. Note that for these transitions, we choose not to fully capture the pattern of the crude probabilities at ages above 86 in the graduation (as discussed before).•
$$$ {\mathop{P}\limits^{ \circ }} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt 2,1}} $$$
. Note that for this transition, the pattern of the crude probabilities is very spurious (discussed in Section 6) and, hence, the graduated probabilities of this transition are determined as a residual from other graduated transition probabilities from moderate CAL.•
$$$ {\mathop{P}\limits^{ \circ }} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt 4,3}} $$$
for males and
$$$ {\mathop{P}\limits^{ \circ }} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt 0,3}} $$$
,
$$$ {\mathop{P}\limits^{ \circ }} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt 2,2}} $$$
and
$$$ {\mathop{P}\limits^{ \circ }} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt 2,5}} $$$
for females. Due to the systematic oscillation, for some transitions, it is hard to pass both the cumulative deviations and sign tests. However, note that the TIC of these transitions are low indicating that, overall, the graduated probabilities are sufficiently close to the crude probabilities (the TIC of
$$$ {\mathop{P}\limits^{ \circ }} _{{x\, + \,0.5,x\, + \,1.5}}^{{\vskip 5pt 0,3}} $$$
for females is only marginally higher than 10%).
Figure 7.1 shows the crude and graduated transition probabilities from the mild CAL state for males. Note that the graduated probabilities capture the pattern of the crude probabilities. Similar qualities of fit are observed for other transition probabilities in cases other than discussed above. Lastly, generally, similar degrees of oscillation of the crude probabilities are observed in other transition probabilities.
Figure 7.1 Crude and graduated transition probabilities from mild CAL state, males.
8 Conclusion
In this paper, we propose a new estimation method for disability transition probabilities. The key contribution of our method is that we utilise data from both the 1998 SDAC and the 2003 SDAC, unlike previous analyses which rely on data from a single survey.
There are uncertainties in the estimation which are mainly due to our data. First, the SDAC data are survey data rather than census data. Second, these data are limited in that they are presented in age groups rather than at individual ages. However, reasonable estimates are obtained from which several informative observations emerged. The method is flexible (easily adjusted if desirable, for example, to suit better data) and will produce increasingly accurate results when better data become available.
There are several ways in which better data can be obtained. The obvious one is to increase the frequency of surveys. However, this is unlikely given the cost of conducting such a large scale national survey. A simple improvement to the survey that might materially improve the accuracy of the estimation is to present the estimate of disabled population at older age groups (say up to age 105, and over). Better data can also be obtained by measuring CAL with a similar scale as in the SDAC in regional longitudinal disability studies. If such data were available, we would be able to obtain more accurate initial transition probabilities (in the application of the IPF procedure) and hence, more accurate refined estimates of disability transition probabilities could be obtained. Note that the availability of such data would circumvent many of the modelling limitations associated with the estimation of initial transition probabilities. For example, it would allow a fuller set of recovery processes in the estimation. Furthermore, as a non-Markovian model can be constructed in the estimation of initial transition probabilities, this might open the possibility of constructing a non-Markovian (or proxy non-Markovian) model in the estimation of disability transition probabilities from national cross sectional datasets.
