RELATED WORK

Wars of attrition provide workhorse models for analyzing many different kinds of conflict. Applications include the study of exit in a declining industry (Fudenberg and Tirole Reference Fudenberg and Tirole1986; Ghemawat and Nalebuff Reference Nalebuff and Riley1985), strikes (Kennan and Wilson Reference Kennan and Wilson1989), economic stabilization (Alesina and Drazan Reference Alesina and Drazen1991; Cassella and Eichengreen Reference Cassella and Eichengreen1996), the provision of public goods (Bliss and Nalebuff Reference Bliss and Nalebuff1984), lobbying and vote buying (Dekel, Jackson, and Wolinsky Reference Dekel, Jackson and Wolinsky2008; Reference Dekel, Jackson and Wolinsky2009), and international bargaining (Fearon Reference Fearon1998).

Adding a third party to a war of attrition seems like a very natural point of departure for studying intervention. But third-party intervention in a war of attrition appears not to have been formally modelled before. The two most relevant studies are Bulow and Klemper (Reference Bulow and Klemperer1999) and Cassella and Eichengreen (Reference Cassella and Eichengreen1996). The former examines two versions of a generalized war of attrition in which p + m players compete for p prizes. In the case of a natural oligopoly of p firms, a firm pays a cost until it exits the market. By contrast, each firm continues to pay a cost for as long as the contest lasts when the firms are competing over setting industry standards since those standards are not set until all of the firms stop fighting. The latter is similar to the present model in that the third party cannot exit the game and its ultimate payoff depends on when the other players quit. A key difference is that the third party's decision affects the distribution of power between the players that are fighting which is not the case in the standards-setting model.

Cassella and Eichengreen (Reference Cassella and Eichengreen1996) study the effect of aid on stabilization. The aid, which arrives at an exogenously specified time, reduces the stakes by narrowing the gap between winning and losing. Whether or not aid accelerates or delays stabilization depends on when it arrives. Early arrival accelerates stabilization whereas late arrival delays it. The fundamental difference between that model and the present analysis is that what happens at the exogenous date is a strategic decision in the model studied here in that the third party decides what to do.

The present analysis is also related to two other areas: formal work on the causes and conduct of war and on alignment, intervention, and duration. As noted above, existing formal work on alignment usually lacks a dimension of time whereas work on duration generally centers on two-actor models. The present analysis begins to bridge this gap.

Nevertheless, two features of the standard war of attrition probably make it a more natural model of civil rather than interstate intervention. The first is the absence of bargaining. Most recent formal work on the causes and conduct of war frames the issue in terms of bargaining and a related inefficiency puzzle (Fearon Reference Fearon1995; Powell Reference Powell2006). Why does bargaining break down in costly conflict which is ex post inefficient? An important argument in the context of civil wars is that negotiated settlements, especially those calling on one of the factions to disarm, often entail very severe commitment problems (Fearon and Laitin Reference Fearon and Laitin2008; Walter Reference Walter2002; Reference Walter2009). As a result, civil-war outcomes often have the winner-take-all quality of wars of attrition.Footnote ⁴

Second, a state or faction can fight as long as it chooses to pay the cost. Neither can defeat the other. There are no battles which, if lost, result in the elimination of a state or faction. Nor is it possible for one belligerent to fight so long that the other runs out of resources and the ability to continue.Footnote ⁵

Although the model developed here is likely a better fit for civil war intervention, it still may provide useful insights into intervention into interstate conflict. Models often make strong, simplifying assumptions. They leave some important considerations out in order to focus on others. For example, interstate wars occur in the shadow of third parties that have a stake in the outcome, can intervene, and choose to do so in more than a quarter of the cases (Kyle, Ghosn, and Bayer Reference Joyce, Ghosn and Bayer2013). Yet the canonical models of bargaining and war (e.g., Fearon Reference Fearon1995; Powell Reference Powell1999) set intervention aside in order to focus on bargaining with two-actor bargaining models. The present approach sets bargaining aside and makes other strong assumptions in order to try to get some traction on the problem of intervention.

THE TWO-ACTOR BASELINE WAR OF ATTRITION

This section reviews some general results about wars of attrition which are needed to analyze the equilibria of the taking-sides game. The section then defines a baseline model by imposing four additional assumptions on a standard model. The first guarantees that the baseline model has a unique equilibrium. The second makes it possible to derive explicit, closed-form expressions for the equilibrium strategies. Having a unique, explicit equilibrium in the two-actor model simplifies the analysis when the third actor is introduced. The third and fourth assumptions are more substantively oriented. They ensure that one of the two main actors is stronger than the other. Taking one actor to be stronger than the other helps connect the present analysis to existing work in two ways. Governments are usually stronger than rebel groups, and some analyses rely on this (e.g., Gent Reference Gent2008). Still other work frames alignment decisions in terms of whether a third party balances by joining the weaker side or bandwagons by supporting the stronger side (e.g., Christia Reference Christia2012; Waltz Reference Waltz1979).

In a standard war of attrition, two actors, say 1 and 2, compete for a prize by deciding how long they will fight for it. The longer the fight lasts, the higher each faction's cost. The side that quits first loses. We can think of these actors as states or factions in the present context. More formally, faction 1 pays a marginal cost of c ₁ and a total cost of c ₁ t if the fight ends at time t. Winning brings a payoff of w ₁ while the losing brings zero. If the factions stop at the same time, each wins with probability 1/2.Footnote ⁶ Taking t_j ⩾ 0 to be the time at which j will stop fighting if the game has not already ended by this time and letting t_j = ∞ mean that j would fight forever, 1's payoff is

(1) $$\begin{equation} U_{1}(t_{1},t_{2})=\left\lbrace \arraycolsep5pt\begin{array}{ll}-c_{1}t_{1} & {\rm if}\,\,\, t_{1}<t_{2} \\ w_{1}/2-c_{1}t_{1} & {\rm if}\,\,\, t_{1}=t_{2} \\ w_{1}-c_{1}t_{1} & {\rm if}\,\,\,\, t_{1}>t_{2} \end{array} \right. \end{equation}$$

and similarly for U ₂(t ₁, t ₂). It proves convenient to reparametrize the model in terms of the cost ratio ρ₀ ≡ c ₁/c ₂ and the total (marginal) cost k ₀ = c ₁ + c ₂ via c ₁ = ρ₀ k ₀/(1 + ρ₀) and c ₂ = k ₀/(1 + ρ₀).

Each faction is unsure of the other's payoff to winning. Specifically, 1 believes 2's payoff w ₂ is distributed over $(\underline{w}_{2},\infty )$ with $\underline{w}_{2}\ge 0$ according to the cumulative distribution G ₂(w ₂). Similarly, 2 believes that w ₁ is distributed over $( \underline{w}_{1},\infty )$ with $\underline{w}_{1}\ge 0$ according to G ₁(w ₁).Footnote ⁷ A strategy for j is a function σ _j (w_j ) that specifies the time at which each type $w_{j}\in (\underline{w}_{j},\infty )$ stops.

The key to determining the equilibrium strategies is that a player type stops when the marginal gain from fighting a bit longer is just offset by the marginal cost. The marginal gain for type w ₁ is its payoff to winning, namely w ₁, times 2's hazard rate, i.e., the probability that 2 will quit in the next instant given that it has not already quit. The marginal cost is c ₁. Equating the marginal gain with the marginal cost for w ₁ and w ₂ yields two differential equations that the equilibrium strategies σ*₁(w ₁) and σ*₂(w ₂) must satisfy. (See the Appendix for the derivation of these strategies.)

The main equilibrium result is that the higher a state's or a faction's payoff to winning, i.e., the larger w_j , the longer the faction fights. More formally, σ*₁(w ₁) and σ*₂(w ₂) are continuous and strictly increasing at any σ* _j (w_j ) > 0. There are however infinitely many equilibria, and it is generally impossible to derive explicit closed-form expressions for the equilibrium strategies.Footnote ⁸

We make two assumptions to simplify the baseline model as much as possible before adding the third party. Assume first that there is an arbitrarily small probability that each faction is nonstrategic and fights forever and, second, that each faction believes the other faction's payoffs are exponentially distributed. The first assumption ensures that the two-actor baseline game has a unique equilibrium; the second makes it possible to derive explicit expressions for the factions’ strategies.Footnote ⁹ Formally, assume that w_j is distributed exponentially with $G_{j}(w_{j})=1-e^{\underline{w}_{j}-w_{j}}$ and that there exists a $ \overline{w}_{j}$ such that all $w_{j}>\overline{w}_{j}\,$ are nonstrategic types that fight forever.

It follows that the factions’ unique equilibrium stop times when $\underline{ w}_{1}=\underline{w}_{2}=0$ are

(2) $$\begin{eqnarray} \sigma _{1}^{\ast }(w_{1}) =\frac{\overline{w}_{1}\overline{w}_{2}}{k_{0}} \left( \frac{w_{1}}{\overline{w}_{1}}\right) ^{1+\rho _{0}},\vspace*{-11pt}\\ \sigma _{2}^{\ast }(w_{2}) =\frac{\overline{w}_{1}\overline{w}_{2}}{k_{0}} \left( \frac{w_{2}}{\overline{w}_{2}}\right) ^{1+1/\rho _{0}}\text{.} \end{eqnarray}$$

(See Equation (A3) for the more general expressions when $\underline{w}_{1}\ge 0$ and $\underline{w}_{2}\ge 0$ .)

The types of 1 and 2 that stop at the same time play an important role in the analysis. Solving σ*₁(w ₁) = σ*₂(w ₂) from Equations (2) or (A3) shows that w ₁ and $w_{2}=\overline{w }_{2}\left( w_{1}/\overline{w}_{1}\right) ^{\rho _{0}}$ stop at the same time. The curve θ(ρ₀) in Figure 1 traces out these points for $0\le w_{1}\le \overline{w}_{1}$ .

Figure 1 also illustrates the equilibrium dynamics. To see how the game unfolds over time, suppose that the pair of lowest-payoff types $(\underline{ w}_{1},\underline{w}_{2})$ is below or to the right of θ(ρ₀), e.g., at $(\underline{w}_{1}^{\prime },\underline{w}_{2}^{\prime })$ . Then the first thing that happens in equilibrium is that all types w ₂ between $\underline{w}_{2}^{\prime }$ and $\overline{w}_{2}\left( \underline{ w}_{1}^{\prime }/\overline{w}_{1}\right) ^{\rho _{0}}$ drop out at t = 0. Graphically, play moves vertically up from $(\underline{w}_{1}^{\prime }, \underline{w}_{2}^{\prime })$ to θ(ρ₀). Equilibrium play thereafter moves along θ(ρ₀) with w ₁ and $w_{2}= \overline{w}_{2}\left( w_{1}/\overline{w}_{1}\right) ^{\rho _{0}}$ dropping out at the same time until $\overline{w}_{1}$ and $\overline{w}_{2}$ simultaneously quit. If, by contrast, the lowest-payoff types are above or to the left of θ(ρ₀) at, say, $(\underline{w}_{1}^{\prime \prime },\underline{w}_{2}^{\prime \prime })$ , then play moves horizontally from $(\underline{w}_{1}^{\prime \prime },\underline{w}_{2}^{\prime \prime })$ to θ(ρ₀) with types w ₁ between $\underline{w} _{1}^{\prime \prime }$ and $\overline{w}_{1}\left( \underline{w}_{2}^{\prime \prime }/\overline{w}_{2}\right) ^{1/\rho _{0}}$ dropping out at t = 0. Subsequent play moves along θ(ρ₀).

FIGURE 1. Equilibrium Play in the Baseline Two-actor War of Attrition

Which player types drop out at the start of the game (t = 0) and why they do turns out to be crucial for understanding the equilibria of the three-actor game. A rough intuition begins with the observation that the lowest-payoff type of 2, $\underline{w}_{2}$ , is relatively small compared to the lowest-payoff type of 1, $\underline{w}_{1}$ , at points below or to the right of θ(ρ₀). As a result, low-payoff types of 2 are so pessimistic about their chances of prevailing when $(\underline{w}_{1}, \underline{w}_{2})$ is below θ(ρ₀) that they drop out immediately. The converse holds when the lowest-payoff types are above θ: the low-payoff types of 1 are so pessimistic about their chances that they quit at t = 0. Finally, if $(\underline{w}_{1},\underline{w}_{2})$ is on θ(ρ₀), the only types dropping out at t = 0 are $ \underline{w}_{1}$ and $\underline{w}_{2},$ and the probability that either faction drops out is zero.Footnote ¹⁰

It follows that the probability that a faction prevails in a war of attrition depends on the cost ratio but not on the total cost.Footnote ¹¹ For example, the probability that 1 prevails is the probability that it stops after 2, i.e., that σ*₁(w ₁) > σ*₂(w ₂). This in turn is the probability (w ₁, w ₂) lies below θ(ρ₀). Since θ(ρ₀) depends on ρ₀ but not k ₀, the probability that 1 wins depends on ρ₀ but not on k ₀. Both factions quit sooner when the total cost is higher as is clear from Equation (2) for the case when $\underline{w}_{1}=\underline{w}_{2}=0$ or Equation (A3) for the more general case. But a higher total cost does not affect the chances of prevailing as long as the cost ratio remains the same.

As noted above, the government is often stronger than the rebel group and assumed to be so in some work (e.g., Balach-Lindsay, Enterline, and Joyce Reference Balch-Lindsay, Enterline and Joyce2008; Gent Reference Gent2008; Regan Reference Regan2002). Other work frames third-party alignment decisions in both civil and interstate conflict in terms of a tradeoff between balancing or bandwagoning (e.g., Aydin and Regan Reference Regan and Aydin2008; Christia Reference Christia2012; Powell Reference Powell1999; Waltz Reference Waltz1979). A third party “balances power” when it joins, aligns with, or supports the weaker side. It “bandwagons” when it supports the stronger side. A third party faces a tradeoff between balancing and bandwagoning when it prefers the weaker side to win. Bandwagoning maximizes its chances of being on the winning side and obtaining the benefits that come with that. Balancing by contrast maximizes a third party's payoff conditional on being on the winning side.

In light of this work, it is useful to make one faction stronger than the other in the baseline model. Most simply, one faction is stronger than the other when it is more likely to prevail in the war of attrition. To formalize this, let Π _j (z ₁, z ₂, ρ) denote the probability that j prevails in the war of attrition with cost ratio ρ given that at least one faction is strategic and that z ₁ and z ₂ are the lowest-payoff types still active, i.e., all w ₁ ⩽ z ₁ and w ₂ ⩽ z ₂ have already dropped out.Footnote ¹² Then j is stronger than i at (z ₁, z ₂) when Π _j (z ₁, z ₂, ρ₀) > Π _i (z ₁, z ₂, ρ₀) or equivalently when Π _j (z ₁, z ₂, ρ₀) > 1/2.

As time passes and equilibrium play moves along θ, the probability that 1 prevails given that neither side has quit varies. Two assumptions ensure that 1 is always stronger than 2, i.e., everywhere along θ. Assume first that the cost ratio favors 1: c ₁ < c ₂ or ρ₀ < 1. This implies that 1 is stronger than 2 in an otherwise symmetric war of attrition where $\underline{w}_{1}=\underline{w}_{2}$ and $\overline{w}_{1}= \overline{w}_{2}$ . It implies in the asymmetric case that 1's probability of prevailing decreases as time goes on and play moves along θ. Indeed, the probability that 1 prevails decreases to $[1+\overline{w}_{1}/(\rho _{0} \overline{w}_{2})]^{-1}$ in the limit as all strategic types drop out and play approaches $(\overline{w}_{1},\overline{w}_{2})$ along θ. When this limit is less than 1/2, faction 1 may be stronger than 2 in the early phase of the war of attrition and then become weaker in the latter phase. The assumption that $\rho _{0}>\overline{w}_{1}/\overline{w}_{2}$ prevents this by guaranteeing that this limit is larger than 1/2 and therefore that faction 1 remains stronger than 2 throughout the conflict. Lemma 1 summarizes these results (see the Online Appendix for the proof).

Finally, it is important to note how changes in the cost ratio and in the total cost affect the outcome and duration of the conflict as these effects play a major role in determining which side the third party supports. The more the cost ratio favors one side in a war of attrition, the more likely that side is to prevail. To see why, note that as the cost ratio shifts in 1's favor (i.e., as ρ₀ = c ₁/c ₂ declines), θ(ρ₀) bows up, the area under it increases, and the probability that 1 prevails goes up. Similarly, the probability that 2 prevails increases as its relative cost of fighting goes down, i.e., Π₂ is increasing in ρ₀. And, as noted above, θ(ρ₀) is independent of k ₀, so shifts in the total cost have no effect on either faction's chances of winning as long as the cost ratio remains constant.

Turning to duration, the more symmetric the two factions’ costs, i.e., the closer ρ₀ is to one, the longer the fight. The model thus provides formal support for the familiar idea that “making the strength of the two parties more nearly equal” tends to make for longer conflicts (Deutsch Reference Deutsch and Harry1964). This idea, along with the presumption that the government is generally stronger than the opposition, underlies several empirical studies and leads to the hypothesis that intervention on the government's side tends to shorten conflicts whereas intervention on the rebels’ side tends to make them longer.

The total cost also affects the duration. As noted above, a higher cost k ₀ induces all types to stop sooner. This makes for shorter fights. Lemma 2 summarizes the results.

A MODEL OF TAKING SIDES

This section describes a game in which a third party, M, has preferences over which side prevails in the war of attrition between 1 and 2 and can affect the outcome by taking sides. More specifically, M can decide at an exogenously specified time T ⩾ 0 to support 1 or 2. Support for j shifts the distribution of power in j's favor and makes j more likely to win. More precisely, M's support for j shifts the cost ratio in j's favor in the continuation game between 1 and 2 that follows M's decision. As will be seen, this continuation game is itself a war of attrition, and Lemma 2 implies that the favorable shift in j's cost ratio increases its chances of prevailing.

To specify the effects of M's taking sides, let c _j|n denote j's cost of fighting if M supports n at T. For example, 1's cost of fighting after T is c _1|2 if M aligned with 2 and c _1|1 if M aligned with 1. Take ρ _n ≡ c _1|n /c _2|n to be the cost ratio between 1 and 2 if M joins n, and let k_n = c _1|n + c _2|n be the total (marginal) cost of fighting for 1 and 2. Then make the following assumption:

Part (i) formalizes the idea that M's support for j shifts the cost ratio in j's favor. If M aligns with 1, the cost ratio drops from ρ₀ to ρ₁ which makes 1 more likely to prevail (Lemma 2). Joining 2 increases the cost ratio from ρ₀ to ρ₂ and makes 2 more likely to prevail. This is the only part of the assumption needed to characterize the equilibria.

Part (ii) ensures that 1 is stronger than 2 regardless of M's actions. Part (ii) thus excludes the possibility that the third party can shift the distribution of power in 2's favor. Allowing for this would not change the equilibrium analysis but would add many more cases to the comparative-static analysis. Note that no assumption is being made about how M's support affects the total cost of fighting, i.e., whether k_j is larger or smaller than k ₀.

Faction 1's payoffs in the three-actor game are still given by Equation (1) if the game ends prior to T. To specify its payoff if the game ends at or after T, suppose for example that M joins 1 at T and that the game subsequently ends at t ⩾ T when 2 quits. Then 1's payoff is w ₁ − c ₁ T − c _1|1(t − T), and 2's is − c ₂ T − c _2|1(t − T). More concisely, suppose the game ends at t ⩾ T, the two factions’ stop times are t ₁ and t ₂, and M supports 1. The 1's payoff if M joins n at T is

(3) $$\begin{equation} U_{1|n}(t_{1},t_{2})=\left\lbrace \arraycolsep5pt\begin{array}{ll}-c_{1}T-c_{1|n}(t_{1}-T) & {\rm if}\,\,\, t_{1}<t_{2} \\ w_{1}/2-c_{1}T-c_{1|n}(t_{1}-T) & {\rm if}\,\,\, t_{1}=t_{2} \\ w_{1}-c_{1}T-c_{1|n}(t_{2}-T) & {\rm if}\,\,\, t_{1}>t_{2} \end{array} \right. \end{equation}$$

with analogous payoffs for 2. As in the baseline war of attrition, each faction is uncertain of the other's payoff to winning and believes it to be exponentially distributed.

Turning to M's payoffs, M gets v ₁ if 1 wins and v ₂ if 2 prevails. In addition to caring about who wins, M may also prefer to be on the winning side if it takes sides. That is, M's payoff if it aligns with j at T is v_j + γ if j subsequently prevails and v_i − γ if i ≠ j eventually wins where γ ⩾ 0 is the premium for being on the winning side. Note that if M prefers the weaker side 2 to prevail (v ₂ > v ₁), then M faces a tradeoff between bandwagoning by joining the stronger faction and balancing by aligning with the weaker side.

That longer conflicts are more costly for the protagonists is inherent in the notion of a war of attrition. Third parties, however, may have very different incentives as Deutsch (Reference Deutsch and Harry1964), Balch-Lindsay and Enterline (Reference Balch-Lindsay and Enterline2000), and Cunningham (Reference Cunningham2010) emphasize. Sometimes the third parties profit from conflict and are better off the longer it lasts. In still other cases, fighting imposes costs on the third party as well as the two protagonists. Formally, let f ₀ denote M's flow payoff prior to taking sides, and take f_j to be M's net flow payoff after supporting side j. M receives this flow for as long as the conflict lasts. Possible benefits accruing during the fighting include the gains from being able to exploit lootable resources, engage in smuggling or drug trafficking, or the direct side payments from j in return for M's support.Footnote ¹⁴ Possible costs include coming under more intense attack from the other faction, being sanctioned by other third parties, the cost of supplying arms or material to j, etc. The key distinction between f_j and v_j is that the former is contingent on the continuation of the fighting. M gets f_j for as long as the conflict lasts. This flow stops when a faction wins at which point M gets a final payoff of v ₁ or v ₂.

When f_j < 0, supporting j comes at a net cost which grows as the contest continues. In these circumstances, M prefers shorter conflicts to longer ones. By contrast, supporting j brings a positive flow of benefits when f_j > 0 and M prefers longer fights.Footnote ¹⁵ For example, the Central Intelligence Agency's history of the Yugoslav conflict reports that

In sum, M's payoff if j prevails at t < T is v_j + f ₀ t. M's payoff if it supports j at T and j subsequently wins at t ⩾ T is v_j + γ + f ₀ T + f_j (t − T). If the other faction wins at t ⩾ T, M gets v_i − γ + f ₀ T + f_j (t − T).

M has no private information about the factions. Its prior belief is that each faction's payoff to prevailing is distributed according to G_j (w_j ). M also believes that $w_{j}>\overline{w}_{j}$ are nonstrategic and fight forever.Footnote ¹⁶

THE EQUILIBRIA

This section provides a less technical overview of the perfect Bayesian equilibria (PBEs) of the game. (The formal derivation is in the Appendix.) An equilibrium of the taking-sides model turns out to have a very simple structure composed of three phases. The two factions fight a war of attrition with cost ratio ρ₀ and total cost k ₀ during the first phase. There follows an interval of pure fighting during which neither side ever quits. These first two phases last until T at which point M decides whether to support 1 or 2. The third phase follows and is again a war of attrition but now with the cost ratio and total cost determined by M 's actions. If for example M supports 1 at T, then 1 and 2 fight a war of attrition with cost ratio ρ₁ and total cost k ₁ during the last stage of the game.

To describe these phases more precisely, let (z ₁, z ₂) denote the pair of lowest-payoff types still active at T, i.e., all w ₁ < z ₁ and w ₂ < z ₂ will have dropped out during the first two phases before M decides what to do at T. Since M cannot intervene until t, all types that drop out prior to T are effectively playing a war of attrition with each other akin to the baseline war of attrition but with z ₁ and z ₂ rather than $\overline{w}_{1}$ and $\overline{w}_{2}$ being the highest-payoff strategic types.Footnote ¹⁷ Substituting z ₁ and z ₂ for $ \overline{w}_{1}$ and $\overline{w}_{2}$ in Equation (2) gives the stop times for w ₁ < z ₁ and w ₂ < z ₂ during this phase:

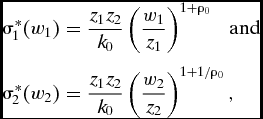(4) $$\begin{eqnarray} \sigma _{1}^{\ast }(w_{1})&=&\frac{z_{1}z_{2}}{k_{0}}\left( \frac{w_{1}}{z_{1}} \right) ^{1+\rho _{0}}\text{ \ \ and }\nonumber\\ \sigma _{2}^{\ast }(w_{2})&=&\frac{ z_{1}z_{2}}{k_{0}}\left( \frac{w_{2}}{z_{2}}\right) ^{1+1/\rho _{0}}, \end{eqnarray}$$

where we continue to assume $\underline{w}_{1}$ and $\underline{w}_{2}$ are zero. The first phase lasts until all of the w_j < z_j drop out or until time z ₁ z ₂/k ₀.Footnote ¹⁸

The second phase is an interval of pure fighting of length λ ⩾ 0 lasting from T − λ to T during which 1 and 2 never quit, i.e., no types drop out. An interval of pure fighting never occurs in a standard two-actor war of attrition. But it arises naturally in the three-actor game whenever M mixes, i.e., M supports 1 and 2 with positive probabilities.Footnote ¹⁹ The length of this interval is a function of z ₁ and z ₂ and will often be written as λ(z ₁, z ₂).Footnote ²⁰

The third phase follows M's decision and is a war of attrition with the cost ratio and total cost determined by M's action. If for instance M supports 1, then the continuation game between 1 and 2 following M's decision is a war of attrition with cost ratio ρ₁ and total cost k ₁. Types z ₁ and z ₂ are the lowest-payoff types during this phase and play a role analogous to $\underline{w}_{1}$ and $\underline{w} _{2}$ in the baseline two-actor war of attrition. The factions stop times in this phase are given by the more general expressions for σ*₁ and σ*₂ in the Appendix for the case in which the lowest-payoff types are not zero (see Equation (A3)).

Characterizing the equilibrium strategies of the taking-sides model thus amounts to finding z ₁ and z ₂ as well as the probability that M supports 1 at (z ₁, z ₂) which will be denoted by α₁. The pair (z ₁, z ₂) must satisfy two conditions, an incentive constraint for M and a timing constraint.

The incentive constraint follows from reasoning backwards from the end of the game, i.e., from the war of attrition played during the third phase following M's decision. The dynamics of this stage are illustrated in Figure 2. Recall that payoff types w ₁ and $w_{2}=\overline{w}_{2}(w_{1}/ \overline{w}_{1})^{\rho _{0}}$ quit at the same time in the baseline two-actor war of attrition when the cost ratio is ρ₀. The curves θ(ρ₁) and θ(ρ₂) depict the pair types (w ₁, w ₂) that stop at the same time in the two-actor baseline model when the cost ratios are ρ₁ and ρ₂ respectively. That is, $ w_{2}=\overline{w}_{2}(w_{1}/\overline{w}_{1})^{\rho _{j}}$ along θ(ρ _j ).

FIGURE 2. The Continuation Game when M Takes Sides

To see how the third phase plays out, assume that (z ₁, z ₂) is between θ(ρ₁) and θ(ρ₂) as in Figure 2 and that M supports 1 at (z ₁, z ₂). (Lemma 4 in the Appendix shows that (z ₁, z ₂) must lie on or between θ(ρ₁) and θ(ρ₂) in any equilibrium.) Since (z ₁, z ₂) is below θ(ρ₁), the low-payoff types of 2 are so pessimistic about their chances of prevailing when the cost ratio is ρ₁ that they drop out as soon as M joins 1. Play moves vertically up from (z ₁, z ₂) to θ(ρ₁) with $w_{2}\in [z_{2},\overline{w}(z_{1}/\overline{w} _{1})^{\rho _{1}}]$ quitting immediately after M joins 1. Subsequent play then moves along θ(ρ₁).

Suppose instead that M joins 2 at (z ₁, z ₂) and the cost ratio becomes ρ₂. The pair (z ₁, z ₂) is now above θ(ρ₂) and the low-payoff types of 1 are so pessimistic in light of this cost ratio that they drop out immediately after M aligns with 2. Play moves horizontally from (z ₁, z ₂) to θ(ρ₂) at T and then along θ(ρ₂) for the rest of the game.

Given that the continuation game following M's decision is a war of attrition, we can determine the factions’ strategies in that war and then use them to calculate M's payoffs to supporting 1 or 2 at (z ₁, z ₂). Let S ₁(z ₁, z ₂) and S ₂(z ₁, z ₂) respectively denote M's payoffs to supporting 1 or 2 and define Δ₁₂(z ₁, z ₂) ≡ S ₁(z ₁, z ₂) − S ₂(z ₁, z ₂) to be the difference between these payoffs.Footnote ²¹ Then M weakly prefers supporting 1 to aligning with 2 at (z ₁, z ₂) when the payoff to supporting 1 is at least as large as the payoff to supporting 2 or Δ₁₂(z ₁, z ₂) ⩾ 0. M weakly prefers 2 when Δ₁₂(z ₁, z ₂) ⩽ 0 and is indifferent between supporting 1 or 2 when Δ₁₂(z ₁, z ₂) = 0.

M's incentive constraint now follows. Result 1 (stated as Lemma 4 in the Appendix) establishes that (z ₁, z ₂) must be on or between θ(ρ₁) and θ(ρ₂). Moreover, M must support 1 for sure when (z ₁, z ₂) is on θ(ρ₁), support 2 for sure when (z ₁, z ₂) is on θ(ρ₂), and support both factions with positive probabilities (0 < α₁ < 1) when (z ₁, z ₂) is between θ(ρ₁) and θ(ρ₂). In order for these actions to be consistent with equilibrium play, M must at least weakly prefer supporting 1 when (z ₁, z ₂) is on θ(ρ₁), i.e., Δ₁₂(z ₁, z ₂) ⩾ 0 when (z ₁, z ₂) is on θ(ρ₁). M must also weakly prefer 2 if (z ₁, z ₂) is on θ(ρ₂), and M must be indifferent between 1 and 2 when (z ₁, z ₂) is between θ(ρ₁) and θ(ρ₂). Collectively these conditions on Δ₁₂(z ₁, z ₂) describe M's incentive constraint.

Result 1 is the key to characterizing the equilibria, and it is worth sketching the argument underlying part (iii). Claims (i) and (ii) follow from very similar arguments.

Proof (sketch): We argue by contradiction. That is, we first assume that M is sure to support 1, i.e., α₁ = 1, and then show that this leads to a contraction and hence to the conclusion that α₁ must be less than 1.

The first step in reaching a contradiction is to demonstrate that there is an interval (T − λ, T) for a λ > 0 during which 1 never quits, i.e., no player type w ₁ quits. We again argue by contradiction by assuming that there is no such interval and then demonstrate that this assumption this leads to a contradiction. More specifically, suppose that there are types w ₁ that do quit arbitrarily close to T. This leads to the contradiction that some of these types could profitably deviate from their equilibrium strategy of quitting before T by waiting until T to quit.

Suppose in particular that $\widehat{w}_{1}$ 's equilibrium strategy is to quit at T − ε where ε > 0 is arbitrarily small. Now compare $\widehat{w}_{1}$ 's payoff to quitting at T − ε to its payoff to waiting until T to quit. The net payoff to quitting at T − ε is zero: there are no further loses but there is also no chance of securing future gains when the other quits. If by contrast $\widehat{w} _{1}$ waits to quit until T, then M by assumption is sure to support 1 and as a result all w ₂ between z ₂ and θ(ρ₁) quit. This implies that $\,\widehat{w}_{1}$ 's payoff to waiting until T to stop is at least $\widehat{w}_{1}\alpha _{1}[e^{\underline{w}_{2}-z_{2}}-e^{ \underline{w}_{2}-\overline{w}_{2}(z_{1}/\overline{w}_{1})^{\rho _{1}}}]-c_{1}\varepsilon$ where α₁ = 1 by assumption and the expression in brackets is the prior probability that the w ₂ between z ₂ and θ(ρ₁) drop out.Footnote ²² The expression in brackets is sure to be positive because (z ₁, z ₂) is between θ(ρ₁) and θ(ρ₂) and, consequently, the payoff to this deviation is sure to be positive for ε small enough. This contradiction ensures that no w ₁ quits in (T − λ, T) for a λ > 0.

Given that no w ₁ quits in (T − λ, T) and α₁ = 1, the w ₂ between z ₂ and θ(ρ₁) that quit at T have no chance of winning after time T − λ. As a result, they would have done strictly better by quitting at T − λ than they do by fighting on until T. Having a profitable deviation from an equilibrium strategy is a contradiction, and it follows from this contradiction that α₁ must be less than one. An analogous argument yields α₁ > 0. Putting positive probably on supporting both 1 and 2 implies that M must be indifferent between them and Δ₁₂(z ₁, z ₂) = 0. $\hfill\square$

The pair (z ₁, z ₂) must also satisfy a timing constraint. The length of the war of attrition during the first phase plus the length of the interval of pure fighting must sum to T. As noted above, the war of attrition between types w ₁ < z ₁ and w ₂ < z ₂ ends at time z ₁ z ₂/k ₀. Hence, (z ₁, z ₂) must satisfy the timing constraint σ*₁(z ₁) + λ(z ₁, z ₂) = T or z ₁ z ₂/k ₀ + λ(z ₁, z ₂) = T. The points that do are illustrated in Figure 3.

FIGURE 3. The Timing Constraint

At least one pair (z ₁, z ₂) must satisfy both constraints. To verify this, suppose that Z′ in Figure 3 does not satisfy both constraints. Then M's incentive constraint must fail to hold. This implies that Δ₁₂(Z′) < 0 or, more substantively, that M strictly prefers supporting 2. Suppose further that Z″ does not satisfy both constraints and thus that M's incentive constraint fails to hold here too. This means that Δ₁₂(Z″) > 0. But if Δ₁₂(Z″) > 0 and Δ₁₂(Z′) < 0, then continuity ensures that Δ₁₂(z ₁, z ₂) must be zero and hence that M's incentive constraint must be satisfied somewhere along the timing constraint between Z′ and Z″.

Proposition 1 (which is formally stated in the Appendix) shows that a unique PBE is associated with each (z ₁, z ₂) that satisfies the two constraints.Footnote ²³ Suppose for example that Z* = (z*₁, z ₂*) in Figure 3 satisfies both constraints. Then w ₁ < z*₁ and w ₂ < z*₂ play a war of attrition with cost ratio ρ₀ and total cost k ₀. This first phase ends at z*₁ z ₂*/k ₀. There follows an interval of pure fighting lasting until T at which point M supports 1 with probability α₁. (See Proposition 1 for the expression for α₁.) If M supports j at T, then w ₁ > z*₁ and w ₂ > z*₂ fight a war of attrition with cost ratio ρ _j and total cost k_j during the final phase.

A numerical example helps fix ideas. Suppose that the initial cost ratio is ρ₀ = 1/2, decreases to ρ₁ = 3/7 if M joins 1, and increases to ρ₂ = 9/11 if M joins 2. To keep things simple, the total cost is assumed to remain the same with k ₀ = k ₁ = k ₂ = 1. Taking $\underline{w} _{1}=\underline{w}_{2}=0$ , $\overline{w}_{1}=5$ , and $\overline{w}_{2}=20$ satisfies Assumption 1 with $\overline{w}_{1}/\overline{w}_{2}<\rho _{1}<\rho _{0}<\rho _{2}<1$ . M's payoff if 1 prevails is v ₁ = −5 and v ₂ = 5 if 2 prevails. The payoff to being on the winning side conditional on having taken sides is γ = 1. M's flow payoff prior to taking sides is f ₀ = −20 which means fighting is costly and shorter fights are better. The cost is even higher after M takes sides with f ₁ = f ₂ = −40 . By way of calibrating the model, a marginal cost of 40 means that if M paid this while 1 and 2 fought the two-actor war of attrition, then M's expected cost would be 2.6 or 26 percent of the stakes |v ₁ − v ₂|. M decides what to do at T = 25. (Figures 1, 2, 3, and 5 are actually plots based on this example.)

In the unique equilibrium, the lowest-payoff types still active at T are z*₁ ≈ 1.9 and z*₂ ≈ 12.2. Types w ₁ ∈ (0, 1.9) and w ₂ ∈ (0, 12.2) fight a war of attrition with cost ratio ρ₀ = 1/2 during the first phase which ends at z*₁ z ₂*/k ₀ ≈ 21.1. There follows an interval of pure fighting lasting until T = 25 when M joins 1 with probability α₁ = 0.7 at T.

THE BOOMERANG EFFECT

The equilibrium strategies exhibit a boomerang effect when the stakes for M are not too large and fighting is costly, i.e., when |v ₁ − v ₂| is not too large and f ₁ and f ₂ are negative. The expectation that M is sure to support a given faction leads both factions to take actions that make it less likely that M will actually support that faction when the time comes. The formal effect of these forces is that M typically plays a mixed equilibrium strategy as is the case in the numerical example. The substantive import of the boomerang effect is that alignment patterns will often be unpredictable and coalitions dynamically unstable.Footnote ²⁴ Although identified in the specific context of a war of attrition, the boomerang effect seems likely to be present in any conflict in which there is uncertainty about each side's willingness to fight, more resolute types fight longer than less resolute types, and a third party's support advantages one side.

To develop some intuition for the boomerang effect and the forces inclining M to mix, suppose that both 1 and 2 expect M to join one of the factions, say 1, for sure. M's support for 1 at T will increase that faction's subsequent chances of prevailing. These better prospects will in turn induce some w ₁ that would have otherwise dropped out prior to T to fight on until at least T. By contrast, some w ₂ that would have fought until T drop out prior to T. The net effect is that there is a large set of types of w ₁ that have fought until T only because they expected M to support 1 at T. Realizing that they have been had, these types will immediately drop out if M supports 2 instead, thereby shortening the war of attrition fought in the third phase. The prospect of a shorter war in turn creates an incentive for M to support 2 when fighting is costly, and the larger incentive to support 2 tends to undermine the original expectation that M is sure to support 1. Formally, M's strategy of supporting 1 at T is not sequentially rational: M prefers to deviate by supporting 2 once play gets to T.

Figure 3 illustrates the boomerang effect graphically. The pair (z ₁, z ₂) must lie on θ(ρ₁) if M is expected to support 1 at T (Result 1). If, however, M actually supports 2, then all w ₁ between z′₁ and the point on θ(ρ₂) horizontally across from Z′ instantly drop out. This tends to shorten the war and creates an incentive for M to support 2 when fighting is costly.

To emphasize that it is the way 1 and 2 react to the expectation that M will support a given faction that undermines this expectation, assume that M has to decide what to do at the very start of the game (T = 0 ). Since M effectively moves before 1 and 2, neither faction can react in anticipation of M's action. Absent these anticipatory reactions, M is almost sure to strictly prefer supporting one side or the other. M will virtually never be indifferent and play a mixed strategy.Footnote ²⁵

Equilibrium forces play out differently when the stakes are high or M profits from the fighting (and we are back to the case in which T > 0). When M has a strong preference for one side, it supports that side and does not mix as will be seen below in the discussion of comparative statics. When fighting is profitable, M wants to prolong the conflict rather than shorten it. Now the fact that M's deviating from what it was expected to do tends to shorten the war makes M less rather than more inclined to deviate.

At the risk of pushing this result too hard, it suggests that coalition formation will be more predictable and coalitions will be more stable when fighting is profitable.

WHAT MAKES M MORE LIKELY TO SUPPORT A GIVEN FACTION?

The effects of changes in M's payoffs on the chances that M supports j turn out to be quite straightforward and intuitive. Anything that increases M's payoff to supporting a given faction makes M more likely to support that faction: The higher M's payoff if 1 prevails or the flow payoff it derives from supporting 1, the more likely M is to support 1. The higher M's payoff if 2 prevails or the higher M's flow payoff from supporting 2, the less likely M is to support 1. The effects of changes in the total cost that 1 and 2 pay if M supports a given faction, i.e., the effects of changes in k ₁ and k ₂, are also straightforward. The higher the total cost of fighting k_j , the shorter the war of attrition following M's decision to support j. Thus a higher cost k_j (and therefore a shorter third-phase war) makes supporting j more attractive when fighting is costly (f_j < 0) and less attractive when fighting is profitable (f_j > 0). As a result, an increase in k_j makes M is more likely to support j when fighting is costly (f_j < 0) and less likely when fighting is profitable (f_j > 0). The effects of changes in the payoff to being on the winning side are ambiguous.

These results are stated formally in Proposition 2 in the Online Appendix. The remainder of this section sketches the derivation, and readers less interested in the technical results may omit the rest of this section. The comparative statics follow from three observations. First, θ(ρ₁), θ(ρ₂), and the timing constraint T = z ₁ z ₂/k ₀ + λ(z ₁, z ₂, ρ₀, k ₀) are independent of M's payoffs v ₁, v ₂, γ, f ₀, f ₁, and f ₂ as well as the total costs k ₁ and k ₂.Footnote ²⁶ It follows that changes in these parameters have no effect on these curves. Second, Result 1 implies that α₁ = 0 at Z″ in Figure 3 where θ(ρ₂) and the timing constraint intersect. Result 1 also implies that α₁ = 1 at the other end of the timing constraint Z′. More generally, the farther the equilibrium pair (z ₁, z ₂) is from Z″ along the timing constraint, the higher α₁. This means that we can determine the effects of, say, an increase in v ₁ on α₁ by seeing how (z ₁, z ₂) moves along the timing constraint.

A qualification is in order before making the third observation. One might hope that the effects of a change in an underlying parameter would have the same directional effect in all of the equilibria when there are multiple equilibria. In a model of war, for example, one might hope that a change in the cost of fighting would make war less likely in all equilibria. Or, the higher the payoff if 1 wins in the present game, the more likely M is to support 1 in all equilibria.

Hope as one might, it is often the case that the direction of the effects of a parametric change vary across equilibria. Typically, a change in x makes y more likely in some equilibria and less likely in others. A less ambitious hope is that a parametric change has the same effect on, say, the probability that M supports 1 in the equilibrium in which M is least likely to support 1 as well as the equilibrium in which M is most likely to support 1. This is the approach take here. (See Ashworth and Bueno de Mesquita (Reference Ashworth and Bueno de Mesquita2006) for a discussion.)

Turning to the third observation, let μ be any parameter, e.g., 1's payoff to winning v ₁. Then the probability that M supports 1 in the equilibria in which M is most and least likely to support 1 is increasing in μ if Δ₁₂ is increasing in μ (i.e., if ∂Δ₁₂(z ₁, z ₂, μ)/∂μ > 0). Conversely, if Δ₁₂ is decreasing in μ, then M is less likely to support 1 (and hence more likely to support 2) in the equilibria in which M is most and least likely to support 1. To see why, consider Figure 4 which shows how Δ₁₂(z ₁, z ₂, μ) varies as we move along the timing constraint from Z″ where the timing constraint and θ(ρ₂) intersect (and α₁ = 0 by Result 1) to Z′ where the timing constraint and θ(ρ₁) intersect and α₁ = 1.Footnote ²⁷ By assumption, there are no pure strategy equilibria in the illustration. That is, M strictly prefers supporting 1 at Z″ (Δ₁₂(Z″) > 0) whereas equilibrium play would require it to support 2 (see Result 1). Analogously, M strictly prefers 2 at Z′ (Δ₁₂(Z′) < 0) whereas equilibrium play would have it support 1.

FIGURE 4. Δ₁₂ along the Timing Constraint

Rather than supporting either faction for sure, M mixes in the three equilibria depicted in Figure 4. More specifically, the incentive and timing constraints intersect wherever Δ₁₂ = 0 along the timing constraint. According to Proposition 1, a PBE corresponds to each of these intersections. Let $\underline{\alpha }_{1}$ and $\overline{\alpha }_{1}$ respectively denote the equilibria in which M is least and most likely to support 1. Clearly, an increase in μ to μ′ > μ that induces an upward shift in Δ₁₂ leads to an increase in both $ \underline{\alpha }_{1}$ and $\overline{\alpha }_{1}$ .

Given that α₁ is increasing in a parameter if Δ₁₂ is, it remains to be determined how Δ₁₂ varies with changes in the parameters. Recall that Π _j (z ₁, z ₂, ρ) is the probability that j prevails in the two-actor war of attrition given that z_j is the lowest-payoff type still active, the cost ratio is ρ, and given that at least one faction is strategic. Take D(z ₁, z ₂, ρ, k) to be the expected duration of this conflict. Then algebra and the Appendix show

$$\begin{eqnarray*} \Delta _{12}(z_{1},z_{2}) &=&(v_{1}-v_{2})[\Pi _{1}(z_{1},z_{2},\rho _{1})-\Pi _{1}(z_{1},z_{2},\rho _{2})]\\ &&+\,2\gamma [\Pi _{1}(z_{1},z_{2},\rho _{1})-\Pi _{2}(z_{1},z_{2},\rho _{2})] \\ &&+\,f_{1}D(z_{1},z_{2},\rho _{1},k_{1})-f_{2}D(z_{1},z_{2},\rho _{2},k_{2}), \end{eqnarray*}$$

where we use the fact that Π₁(z ₁, z ₂, ρ₁) + Π₂(z ₁, z ₂, ρ₁) = Π₁(z ₁, z ₂, ρ₂) + Π₂(z ₁, z ₂, ρ₂) = 1.

The effects of changes in v_j , f_j , and the total cost k_j for j ∈ {1, 2} are straightforward and unambiguous. The probability that 1 prevails is decreasing in the cost ratio, so Π₁(z ₁, z ₂, ρ₁) > Π₁(z ₁, z ₂, ρ₂). Δ₁₂ is therefore increasing in v ₁ and decreasing in v ₂. Thus the higher v ₁ and the lower v ₂, the more likely M is to support 1. Since durations are always nonnegative, a higher flow payoff to supporting 1 or a lower flow payoff to supporting 2 makes M more to support 1. Because duration is also decreasing in the total cost, a higher k ₁ makes M less likely to support 1 when fighting is profitable (f ₁ > 0) and more likely when it is costly (f ₁ < 0).

The effects of changes in the payoff to being on the winning side are ambiguous and depend on the sign of Π₁(z ₁, z ₂, ρ₁) − Π₂(z ₁, z ₂, ρ₂). The first term is the probability that 1 wins with M's support or, equivalently, the probability that M will be on the winning side if M supports 1. Analogously, Π₂(z ₁, z ₂, ρ₂) is the probability that M will be on the winning side if it supports 2. It follows that an increase in γ makes M more likely to join the side that is more likely to win when it has M's support. In symbols, an increase in γ makes M more likely to join 1 when Π₁(z ₁, z ₂, ρ₁) > Π₂(z ₁, z ₂, ρ₂) and more likely to join 2 when Π₁(z ₁, z ₂, ρ₁) < Π₂(z ₁, z ₂, ρ₂).

EMPIRICAL CHALLENGES

The theoretical model developed here and the resulting comparative statics have implications for empirical efforts to assess the effects of intervention. Many studies attempt to evaluate claims about the effects of intervention by estimating a duration model. Gent (Reference Gent2008), for example, uses a competing-risk model to test the hypothesis that third party support for the rebels increases their chances of prevailing. Balch-Lindsay and Enterline (Reference Balch-Lindsay and Enterline2000) and Balach-Lindsay, Enterline, and Joyce (Reference Balch-Lindsay, Enterline and Joyce2008) also use this approach to test their hypotheses about intervention. Regan (Reference Regan2002) estimates a Weibull duration model.

The present analysis shows that using duration models to evaluate the effects of intervention faces at least three formidable challenges. The most basic is that the likelihood that a faction prevails depends on the cost ratio but not on the total cost whereas the expected duration and hazard rate depend on both. Thus trying to infer changes in the likelihood of prevailing (i.e., in the cost ratio) from changes in the duration or hazard rate is problematic. A second challenge is that the hazard rate of equilibrium behavior may be very complicated even in a relatively simple model like this one. This casts doubt on the proportionality assumption of the Cox approach. Finally, there may be significant selection effects.

To illustrate these challenges, suppose we were trying to use a competing-risk proportional hazards model to test the hypothesis that third party support for the “rebel opposition” (i.e., for the weaker faction 2) makes that faction more likely to prevail. For each observation, the (hypothetical) data indicates whether the third party supported 1, supported 2, or stayed out; whether 1 or 2 ultimately prevailed; and the duration of the conflict (see below for the formal the analysis of the game when M has three options). Let X_j = 1 if M supports faction j and X_j = 0 otherwise for j ∈ {1, 2}. M stays out in cases where X ₁ = X ₂ = 0. Take H _2|k (t) to be 2's hazard rate of victory, i.e., the probability that 2 prevails in the next instant given that the conflict has lasted until t and that M supported k ∈ {0, 1, 2} where supporting “0” means staying out.

The Cox model assumes that the hazard rates of the different possible outcomes are proportional. In symbols, H _2|k (t) = H _2|0(t)e ^{β₁ X ₁ + β₂ X ₂} where H _2|0 is the baseline hazard rate, i.e., the chances that 2 prevails if M stayed out. The parameter β _j measures the effect on H _2|0 if M supports j. If, for example, M supports 2 in a given observation, then X ₁ = 0, X ₂ = 1, and the previous equation reduces to H _2|2(t) = H _2|0(t)e ^β₂ . This leaves H _2|2(t)/H _2|0(t) = e ^β₂ . The econometric challenge is to estimate β₁ and β₂. A positive estimate of β _j is generally taken to mean that M's support for j makes j more likely to win.

The model makes it possible to derive the hazard rates and this reveals other challenges. To derive the expression for H _2|2(t)/H _2|0(t), note that the probability that the fighting lasts until at least time t > T is the probability that both factions stop at t or later. The type w ₁ that stops at t given that M supported 2 is the inverse w ₁ = σ⁻¹ _1|2(t), so the probability that 1 has not yet quit at t is 1 − G(σ⁻¹ _1|2(t)) = e ^{−σ−1 _1|2(t)}. Similarly, the probability that 2 has not yet quit at t is 1 − G(σ⁻¹ _2|2(t)) = e ^{−σ−1 _2|2(t)}, and the probability neither faction has stopped by t is e ^{−σ−1 _1|2(t) − σ_2|2 −1(t)}. The chances that 2 prevails in the next instant is the probability that 1 quits in the next instant or d(1 − e ^{−σ−1 _1|2(t)})/dt. This yields a hazard rate of a rebel victory if M supports 2 of

$$\begin{eqnarray*} H_{2|2}(t)&=&\frac{\Pr \lbrace \text{1 quits in the next instant}\rbrace }{\Pr \lbrace \text{ neither faction quits before }t\rbrace }\\ &=&\frac{d(1-e^{-\sigma _{1|2}^{-1}(t)})/dt}{ e^{-\sigma _{1|2}^{-1}(t)-\sigma _{2|2}^{-1}(t)}}=e^{\sigma _{2|2}^{-1}(t)} \frac{d\sigma _{1|2}^{-1}(t)}{dt}\text{.} \end{eqnarray*}$$

Using the analogous expression for H _2|0(t),

(5) $$\begin{eqnarray} \frac{H_{2|2}(t)}{H_{2|0}(t)} &=&\frac{k_{2}}{1+\rho _{2}}\left[ \frac{k_{2} \widehat{t}}{\overline{w}_{1}\overline{w}_{2}}+\left( \frac{z_{1|2}}{ \overline{w}_{1}}\right) ^{1+\rho _{2}}\right] ^{\frac{-\rho _{2}}{1+\rho _{2}}}\nonumber\\ &&\times\, e^{\overline{w}_{2}\left[ \frac{k_{2}\widehat{t}}{\overline{w} _{1}\overline{w}_{2}}+\left( \frac{z_{1|2}}{\overline{w}_{1}}\right) ^{1+\rho _{2}}\right] ^{\frac{\rho _{2}}{1+\rho _{2}}}} \nonumber \\ &&\times\, \left( \frac{1+\rho _{0}}{k_{0}}\right) \left[ \frac{k_{0}\widehat{t }}{\overline{w}_{1}\overline{w}_{2}}+\left( \frac{z_{1|0}}{\overline{w}_{1}} \right) ^{1+\rho _{0}}\right] ^{\frac{\rho _{0}}{1+\rho _{0}}}\nonumber \\ &&\times\, e^{- \overline{w}_{2}\left[ \frac{k_{0}\widehat{t}}{\overline{w}_{1}\overline{w} _{2}}+\left( \frac{z_{1|0}}{\overline{w}_{1}}\right) ^{1+\rho _{0}}\right] ^{ \frac{\rho _{0}}{1+\rho _{0}}}} \end{eqnarray}$$

where $\widehat{t}=t-T$ is the time since intervention and z _1|k is the lowest payoff type of 1 still active at T given M supported k in equilibrium.

Three observations follow from this expression. First, the proportionality assumption is clearly violated. Indeed, the hazard-rate ratio varies in a complicated way over time. Second, there are likely to be selection effects. Consider an equilibrium in which M supports 2 for sure. Then the pair of lowest-payoff types active at T, (z _1|2, z _2|2), lies at the intersection of the timing constraint and θ(ρ₂). Both this pair and the corresponding hazard rate H _2|2 are well defined. But the pair of lowest-payoff types still active at T had M supported 1 or stayed out, that is, (z _1|1, z _2|1) and (z _1|0, z _2|0), are not defined. This in turn implies that the corresponding hazard rates H _2|1 and H _2|0 are not well defined. The numerical example illustrates a similar point. As shown below, M mixes over supporting 1 and 2 and never stays out when the numerical example is extended to allow M to choose not to take sides. Hence (z _1|1, z _2|1) = (z _1|2, z _2|2), and H _2|1 and H _2|2 are well defined and can be calculated. But what would have happened had M stayed out, that is, (z _1|0, z _2|0) and H _2|0, cannot.

Finally, suppose that despite all of these issues one could establish empirically that H _2|2(t)/H _2|0(t) > 1 at all t > T. That is, 2 at any t > T is always more likely to prevail in the next instant if M supported it than if M had stayed out. Could we infer from this that M's support makes 2 more likely to win? Is ρ₂/ρ₀ > 1 identified?

The answer is no. To establish this, we construct a counterexample in which M's support, by assumption, has no effect on either faction's chances of prevailing. Nevertheless, M's support increases the hazard rate of 2's prevailing, i.e., H _2|2(t)/H _2|0(t) > 1. Formally, suppose M's support has no effect on the cost ratio with $\overline{w}_{1}/\overline{w} _{2}<\rho _{0}=\rho _{1}=\rho _{2}<1$ where the inequalities ensure that 1 is always stronger than 2 regardless of what M does (see Assumption 1). Suppose further that M's support for the weaker side 2 (the rebels) increases the total marginal cost of fighting: k ₂ > k ₀. The Online Appendix shows that H _2|2(t)/H _2|0(t) > 1 at all t > T.

The counterexample illustrates the basic identification problem. The increased cost of fighting following M's decision to support 2 makes it more likely that the fighting will end in the next instant. But both sides are more likely to stop, and there is no change in the factions’ relative chances of prevailing since the cost ratio remains unchanged.

NOT TAKING SIDES

Until now M has had to take sides by supporting either 1 or 2. M could not decide to stay out. This section extends the model by giving M the three options of supporting 1 or 2 or staying out. We show that the equilibrium and comparative statics of the numerical example do not change when the option of staying out is added to the model. The basic reason is that M strictly prefers supporting 1 or 2 to staying out. Hence adding the third option of staying out with its lower payoff has no effect on equilibrium play. More generally, M will typically mix over two options when it has three alternatives as it does in the numerical example and the presence of the third option has no effect. But there may be cases in which M mixes over all three alternatives depending on the parameter values.

The analysis of the three-option game begins with an intermediate step in which M chooses between staying out or supporting 2. The analysis is fundamentally the same if M had the options of staying out or joining 1. Indeed, the main point of the intermediate step is that the equilibrium analysis is essentially the same when M only has two options regardless of what those options are. More importantly, the analysis shows that the equilibrium and comparative statics of the model when M only has two options is often an equilibrium of the model when M has three options.

To specify the model when M can stay out or support 2, assume that the cost ratio, total cost, and flow payoff remain ρ₀, k ₀ and f ₀ if M stays out (where the subscript “0” will be used for the option of staying out). They change to ρ₂, k ₂, and f ₂ if M supports 2. Let α₀ be the probability that M stays out. Take (z ₁, z ₂) to be the lowest-payoff types active at T and S ₀(z ₁, z ₂) to be M's payoff to staying out at (z ₁, z ₂).

Figure 5 illustrates the geometric similarly of the equilibrium analysis when M can stay out or support 2, or when when M can support 1 or 2. The lowest-payoff types (z ₁, z ₂) when M can support 0 or 2 must lie on or between θ(ρ₀) and θ(ρ₂) and satisfy an incentive constraint for M as well as a timing constraint. To specify the latter, note that the first phase of equilibrium play ends when z ₁ and z ₂ quit at time z ₁ z ₂/k ₀ (assuming $\underline{w}_{1}= \underline{w}_{2}=0$ ). Let λ₀₂(z ₁, z ₂) be the length of the interval of pure fighting that follows given that the cost ratio will be ρ₀ or ρ₂ after M decides what to do.Footnote ²⁸ This yields the timing constraint T = z ₁ z ₂/k ₀ + λ₀₂(z ₁, z ₂, ρ₀, ρ₂). Let TC ₀₂ denote the set of points satisfying this constrain. The points in TC ₀₂ are shown in Figure 5 as are the points satisfying the timing constraint TC ₁₂ when M could only support 1 or 2.

FIGURE 5. Taking Sides or Staying Out

M's incentive constraint follows from an analogue of Result 1: If (z ₁, z ₂) is on the upper edge θ(ρ₀), M must stay out (α₀ = 1) which in turn requires that M weakly prefer supporting 0, i.e., Δ₀₂(z ₁, z ₂) ≡ S ₀(z ₁, z ₂) − S ₂(z ₁, z ₂) ⩾ 0. (See the Appendix for the expression for Δ₀₂.) If (z ₁, z ₂) is on θ(ρ₂), M joins 2 for sure and must weakly prefer supporting 2 (Δ₀₂(z ₁, z ₂) ⩽ 0). Finally if (z ₁, z ₂) is strictly between θ(ρ₀) and θ(ρ₂), then M must be indifferent between supporting 0 or 2 so that M can mix in equilibrium (Δ₀₂(z ₁, z ₂) = 0). Let MIC ₀₂ be the set of points satisfying this incentive constraint.

It is straightforward to show that the analogue of Proposition 1 holds. At least one (z ₁, z ₂) satisfies TC ₀₂ and MIC ₀₂, and a virtually unique PBE is associated with any (z ₁, z ₂) satisfying both. Types $w_{1}\in (\underline{w}_{1},z_{1}]$ and $w_{2}\in (\underline{w} _{2},z_{2}]$ fight a war of attrition until time T − λ₀₂(z ₁, z ₂, ρ₀, k ₀) followed by a pure-fighting interval of length λ₀₂. M then decides what to do, and the war of attrition goes on with the cost ratio and total cost determined by M's action.

The comparative-static analysis parallels the argument in the case when M could support support 1 or 2. If Δ₀₂(z ₁, z ₂) is increasing in a parameter μ, then so are the chances that M will stay out in the equilibria in which M is most and least likely to stay out. It follows that the probability that M stays out are increasing in v ₁ and f ₀ and decreasing in v ₂ and f ₂. A higher total k ₂ decreases the expected duration of fighting if M supports 2.Footnote ²⁹ This in turn makes M more likely to support 2 when fighting is costly (f ₂ < 0) and less likely when it is profitable. The effects of changes in the payoff to being on the winning are however unambiguous in this case. M is less likely to be on the winning side if it supports 2, so an increase in γ makes M more likely to stay out.

Finally, what happens when M has the three options of staying out or supporting 1 or 2? Let TC ₁₂, TC ₁₀, and TC ₀₂ be the timing constraints if M has to choose between supporting 1 or 2, 1 or “0” , or “0” or 2, respectively. Take MIC_ij to be M's incentive constraints when M has to choose between joining i or j.

In the baseline numerical example where M must support 1 or 2, M mixes at the unique (z*₁, z ₂*) satisfying M's incentive and timing constraints with (z*₁, z ₂*) ≈ (1.9, 12.2). Moreover, M's payoff to supporting 1 or 2 at (z*₁, z ₂*) is strictly larger than its payoff to staying out. It follows that the numerical example described above when M can either support 1 or 2 is also an equilibrium when M has three options. The comparative static results for the equilibrium when M can only support 1 or 2 also hold for the equilibrium in which M can support 1 or 2 or stay out.

More generally suppose (z ₁, z ₂) satisfies the timing and incentive constraints when M's options are restricted to supporting i or j. The equilibrium of the two-option game will be an equilibrium of the three-option game as long as M weakly prefers supporting i or j to supporting the third option, say, n. In symbols, (z ₁, z ₂) is associated with an equilibrium in the three-actor game as long as min{S_i (z ₁, z ₂), S_j (z ₁, z ₂)} ⩾ S_n (z ₁, z ₂). The comparative statics of the equilibrium when M has three options are also the same as when M has two alternatives as long as the previous inequality is strict.

Of course, it may be the case that M always prefers to deviate to the third option n whenever (z ₁, z ₂) satisfies the incentive and timing constraints with respect to the other two options i and j. When this occurs, M must mix over all three options.

TAKING AND SWITCHING SIDES

What happens when M can take sides at time T′ and revisit the decision at a later time T″? The boomerang effect that tends to induce mixing and make alignment decisions unpredictable when M has one decision time tends to make M's decisions unpredictable at both times. As a result, M often mixes at both T′ and T″ when fighting is costly and the stakes are not too high. An outside observer looking at a set of cases would see instances in which M joins 1 at T′ and subsequently sticks with 1 at T″, M joins 1 at T′ and then switches to 2 at T″, M joins 2 at T′ and sticks with 2 at T″, or M joins 2 at T′ and switches to 1 at T″. In brief, almost anything can happen. This at least qualitatively is in keeping with recent empirical work on alliances in civil wars which finds that side switching is quite common (Christia Reference Christia2012; Seymour Reference Seymour2014).

To specify the extended model, add an additional decision time of T′ = 15 to the baseline numerical example where M could only support 1 or 2 at T″ = 25. In effect, M can now decide whether to support 1 or 2 at T′ and then stick with that faction at T″ or switch sides. The Appendix sketches the derivation of the equilibrium. The key to finding the equilibrium is using the fact that the equilibrium of the one-decision-time model is the equilibrium of the continuation game when M has two decisions.

The equilibrium probability that M joins 1 at T′ in the two-decision-time model is 0.52. Conditional on having joined 1 at T′, the probability that M continues to support 1 at T″ is 0.74. Conditional on supporting 2 at T′, the probability that M switches to supporting 1 is 0.84. The overall probability that M supports a side and then sticks with that side is 0.49. The probability that M switches sides is 0.51.

SUPPLEMENTARY MATERIAL

To view supplementary material for this article, please visit https://doi.org/10.1017/S0003055416000782