Political scientists are usually skeptical of blanket statements about the evils of special interest groups. Although corruption may explain some lobbying behavior (Grossman and Helpman Reference Grossman and Helpman2001), interest groups can also provide helpful policy information (Austen-Smith and Wright Reference Austen-Smith and Wright1994, Reference Austen-Smith and Wright1992; Wright Reference Wright1996), increase the work-capacity of legislators (Hall and Deardorff Reference Hall and Deardorff2006), and provide a connection between the public and the policy process. However, most campaigns focus on the potential negative effects of lobbying. It is hard to imagine a candidate emphasizing how her cozy relationship with lobbyists will make her more effective in office. In this article, we propose an alternative explanation for this contrast: a politician may try to signal that she is noncorrupt by taking a combative stance toward interest groups even when this adversely affects her ability to govern.
We develop a game-theoretic model of electoral competition in which two politicians vie for office, committing themselves to either banning or granting interest group access should they win. Politician choices over group access can inform voters about whether or not politicians are corrupt. Once a politician wins office an interest group, if access was granted, interacts with the winning politician. The group can engage in two types of lobbying by either providing policy-relevant information or initiating a quid pro quo. The type of politician in office dictates which lobbying tactic is most effective. The best-case scenario from voters’ perspectives is to elect an honest politician who grants interest group access for informational lobbying. However, voters are uncertain about which politicians are honest and which are corrupt and therefore use access decisions to attempt to screen out corrupt politicians. This comes at the cost of information as sincere politicians will often ban interest group access to attempt to communicate their sincerity to voters, a behavior we refer to as signaling with reform.
To illustrate our argument, consider a hypothetical election in which banking regulation is a central issue. During the campaign, the politicians can commit themselves to a policy which either allows or denies access to Wall Street interest groups. For instance, some politicians may indicate a need to work with the industry to develop effective regulations, whereas others may emphasize a belief that the regulatory process is rigged in favor of moneyed interests and promise a closed-door policy toward industry lobbyists. These politicians may even support similar regulations while maintaining different positions toward interest group participation. Now suppose that some proportion of politicians seek access to secure campaign contributions from Wall Street. These politicians will always grant access to interest groups and will ultimately act in the interests of the industry. The problem is that voters cannot tell the difference between politicians who grant access because they are corrupt and those who grant access to better serve the voters’ interests. Thus, sincere politicians may deny themselves the information needed to make good policy by shutting out interest groups to convince voters that they are not corrupt.
RELATED LITERATURE
Lobbying Tactics
Our model builds on the idea that lobbying includes multiple tactics with countervailing implications for voter welfare. We will focus on two well-studied lobbying tactics. We model socially unproductive lobbying as quid pro quo exchange between interest groups and politicians. Socially productive lobbying is modeled as policy-relevant information transmission. These two lobbying tactics are chosen because they have an important place in the lobbying literature and an unambiguous relationship to voter utility in our model. In principle, either quid pro quo or information transmission could be replaced by some other notion of lobbying and the main insights of the model would be similar. The most important assumptions needed are that (a) the socially productive lobbying method produces a good valued by the voter as well as by noncorrupt politicians, (b) socially destructive lobbying produces a good valued only by corrupt politicians and imposes costs on voters and noncorrupt politicians, and (c) the lobbying tactic chosen in equilibrium depends mainly on whether or not the elected politician is corrupt.
Quid Pro Quo Lobbying
Quid pro quo lobbying is most often modeled as an exchange of something valuable (e.g., money) in exchange for policy favors (Baron Reference Baron1989; Denzau and Munger Reference Denzau and Munger1986; Grossman and Helpman Reference Grossman and Helpman1994). Evidence of quid pro quo bargaining is necessarily indirect and varies across countries and contexts. For instance, outside of the United States, firms garner significant financial returns on political connections and pursue these connections more aggressively in countries where corruption is high (Faccio Reference Faccio2006; Fisman Reference Fisman2001).Footnote 1 Some theoretically informed research has focused on the question of whether legislators can credibly commit to deliver on promised policy favors after payments from interest groups have changed hands (McCarty and Rothenberg Reference McCarty and Rothenberg1996). We are interested in the implications of potential quid pro quo exchanges rather than the conditions under which they are possible, so we sidestep this issue by assuming that corrupt politicians have a preference for reciprocity (see Lambsdorff Reference Lambsdorff, Serra and Wantchekon2012).
The concept of corruption in our model should not be taken too literally. Corruption is a stand-in for any mode of lobbying that benefits the politician and interest group, but not the voter. For instance, lobbying is often seen as a way for interest groups to subsidize politicians’ efforts on their shared objectives (Hall and Deardorff Reference Hall and Deardorff2006). In cases where this distorts the policy agenda away from issues the voter cares about, this can harm voter welfare. Although this behavior does not constitute corruption, it fits in our model equally well.
Informational Lobbying
In information-based models, interest groups are influential to the extent that they transmit policy-relevant information to policy-makers. Potters and Van Winden (Reference Potters and Van Winden1990) demonstrate the effectiveness of informational lobbying in a dynamic game between one interest group and one legislator. Potters and Van Winden (Reference Potters and Van Winden1992) show how lobbying costs may expand the set of circumstances for which informational lobbying is credible. Austen-Smith and Wright (Reference Austen-Smith and Wright1992, Reference Austen-Smith and Wright1994) analyze models in which two interest groups attempt to persuade a policy-maker and draw implications for patterns of lobbying in the face of competition. Austen-Smith (Reference Austen-Smith1995) and Cotton (Reference Cotton2012) show how campaign contributions may be used to signal information which causes lobbies to be granted access for the purpose of informational lobbying. In these articles, information transmission improves the quality of the policy-makers’ decisions, as it does in our model.Footnote 2
Informational lobbying is a prominent explanation of lobbying behavior in empirical work. Interest group surveys show that a great deal of lobbyists’ time is spent conducting research and presenting arguments to elected officials (Baumgartner et al. Reference Baumgartner, Berry, Hojnacki, Leech and Kimball2009; Schlozman and Tierney Reference Schlozman and Tierney1986). Case studies also support informational lobbying. For instance, Hansen (Reference Hansen1991) argues that the farm lobby’s influence was attributable in large part to informational lobbying.
Much of the existing literature focuses on the conditions under which information transmission is credible in a lobbying environment. Our purpose is to build on existing theoretical and empirical work by focusing on the cases in which both quid pro quo and informational lobbying are possible and illustrating the resulting trade-offs that politicians face. To that end, our treatment of informational lobbying focuses on the case of verifiable information.Footnote 3
Mixed Lobbying Tactics
Several other papers juxtapose multiple lobbying tactics within a single game-theoretic model. In Wolton (Reference Wolton2016), political contributions are influential because they signal a group’s strength at grassroots lobbying. In Ellis and Groll (Reference Ellis and Groll2017), interest groups can engage in informational lobbying or give contributions in the form of legislative subsidy. Bennedsen and Feldmann (Reference Bennedsen and Feldmann2006) show how acquiring information creates externalities that raise the cost of bribing politicians. Dahm and Porteiro (Reference Dahm and Porteiro2008) analyze a model in which interest groups can provide information and apply political pressure and show how attitudes toward risk affect the choice of tactics. In contrast to these existing studies, we do not focus on the interest group’s choice of tactic, which in our model is a simple matter of matching the tactic to the type of politician. Instead, we focus on how the voter’s uncertainty about the type of lobbying solicited by politicians affects politicians’ incentives to signal to voters.
Pandering and Populism
This article also relates to the political economy literature on pandering. Pandering refers to a policy-maker’s decision to ignore relevant information and instead take the action ex ante preferred by the voters, often to bolster her reputation. Politicians may engage in this behavior to signal congruence with the voter (Maskin and Tirole Reference Maskin and Tirole2004; Morelli and Weelden Reference Morelli and Van Weelden2013; Morris Reference Morris2001) or to signal competence (Ashworth and Shotts Reference Ashworth and Shotts2010; Canes-Wrone, Herron, and Shotts Reference Canes-Wrone, Herron and Shotts2001; Prat Reference Prat2005). Our results are similar in that reputational concerns lead the politician to forgo acquiring information at all to signal that they are noncorrupt. However, the mechanisms driving our model differ from pandering. For instance, pandering occurs when the voter may see policy choices but not whether they were successful. In an extension we analyze a dynamic model to show that signaling with reform can be supported even when voters observe outcomes of policy choices.
In a related article, Coate and Morris (Reference Coate and Morris1995) develop an argument in which politicians engage in inefficient behavior to avoid revealing themselves as beholden to special interests. Inefficiencies may be introduced because of “bad” politicians mimicking “good” politicians by implementing public programs to transfer resources to special interests when a direct transfer would be more efficient. Similarly, good politicians may pool with bad politicians by not implementing public programs when their private information suggests they should. They do so to safeguard their already favorable reputations to maximize chances for reelection. Thus, inefficiency arises through politicians pooling to conceal their type. A related inefficiency arises in our model but through a separating equilibrium in which good politicians reveal themselves at some cost to efficiency. This difference is important in our welfare analysis, which turns on the relative benefits of screening out corruption versus good policymaking by noncorrupt politicians.
Acemoglu, Egorov, and Sonin’s (Reference Acemoglu, Egorov and Sonin2013) model of populism also features an argument similar to ours. In their model, corrupt politicians can be influenced by a wealthy elite with preferences to the right of the median voter. Honest politicians signal that they are incorruptible by choosing a policy to the left of the median voter. Thus, the desire to signal honesty can lead to policies that harm the welfare of the voter, as in our model.Footnote 4 We obtain a similar result, but the effects on voter welfare are driven by information acquisition rather than spatial preferences over policy. Overall, these previous models do not speak to information acquisition or direct decisions about interest group access, which are central to the insights in this article.
BASELINE MODEL
The model captures a situation in which an interest group lobbies for a policy which, depending on its private information, may or may not be in the best interests of the voters. Private information is captured by a variable θ which determines the policy preferred by a majority of voters. The interest group, however, would prefer the same policy no matter what it believed about θ. For instance, if it were known that unregulated financial derivatives would harm the economy, a majority would support regulation. However, a firm specializing in these derivatives would still like to keep them unregulated. The interest group can engage in one of two tactics, which we term “informational lobbying” (e.g., creating a white paper) or “bribes” (e.g., offering campaign contributions). The types of the politicians determine their susceptibility to each tactic, with sincere types persuaded by information and corrupt types persuaded by contributions. The behavior of the politicians is driven by their desire to demonstrate to the voters that they are sincere.
The players are two politicians (A and B), a representative voter V, and an interest group G. Politicians are either sincere or corrupt. During the campaign, politicians commit to platforms that effectively allow or deny access to the interest group. Once the winning politician takes office, he decides whether to enact a new policy. If the interest group has access to the politician, it may influence policy by either providing information or paying a bribe.
Sequence of Play
The sequence of play is as follows. First, nature draws each politician’s type τ i ∈ {S, C} (sincere or corrupt). The prior probability that a politician is sincere is π := Pr[τ i = S] and is private information. Nature also draws a state of the world θ ∈ {0, 1} that determines which policy is best for the voter. For instance, if the policy is a banking regulation, θ may represent information on how the new regulation will affect lending practices. The voter prefers regulation if it will not severely limit access to credit but not if it would make it too difficult for consumers to borrow money. Prior beliefs are that Pr[θ = 0] = q > 1/2. The state θ is private information to the interest group, which specializes in the policy area. Next, both politicians publicly announce their campaign platforms. Each politician can either run on a reform platform (p = 0) that effectively bans group access should the politician take office or an access platform (p = 1) that leads to interaction with the group after winning office. Following politician announcements, a representative voter elects politician A or B.
If the winning politician ran on a reform platform, then he will simply choose a policy x ∈ {0, 1} to implement. If the winning politician ran on an access platform, lobbying occurs before policy is chosen. In the lobbying stage, the interest group learns the politician’s type,Footnote 5 the interest group’s information about θ is revealed, and it can choose to offer the politician a bribe: b ∈ {0, 1} where b = 1 denotes a bribe.Footnote 6 If the politician in office ran on a reform platform, then b = 0 and the group’s information about θ is not revealed. The bribe may be interpreted as a literal bribe, an implied revolving door job offer, or anything else that materially benefits the politician but does not aid in policymaking. Substantive lobbying is captured through the verifiable information about θ that is revealed by the interest group through white papers or the like. Once the lobbying stage concludes, the politician updates her beliefs about θ and chooses a policy.
Preferences and Equilibrium
The voter wants the chosen policy to match the state of the world. Her preferences are given by the following utility function,
$${u_{\rm{V}}}\left( {x,\theta } \right) = - \left| {x - \theta } \right|.$$The interest group’s policy preferences are independent of the state: it always prefers x = 1 whether or not that policy is good for the voter. Furthermore, the interest group pays a cost, κ ∈ (0, 1), for bribes.Footnote 7 The interest group’s utility function is
$${u_{\rm{G}}}\left( {x,\theta ,b} \right) = x - \kappa b.$$Politician preferences depend on their types. Our assumptions about politician preferences are designed to make the contrast between types as stark as possible: sincere types only want to choose the policy that is best for the voter and corrupt types only want to pursue exchanges with the group.Footnote 8 Accordingly, politician preferences are represented by the utility function,
$${u_i}\left( {x,\theta ,b} \right) = \left\{ {\matrix{ { - \left| {x - \theta } \right|} \hfill & {{\rm{if}}\;{\tau _i} = S,} \hfill \cr {bx - \left( {1 - b} \right)x} \hfill & {{\rm{if}}\;{\tau _i} = C.} \hfill \cr} } \right.$$We analyze symmetric pure strategy perfect Bayesian equilibria in weakly undominated strategies.Footnote 9 We also focus on equilibria that satisfy the Intuitive Criterion (Cho and Kreps Reference Cho and Kreps1987).
Interest Group Access and Informed Policymaking
To begin the analysis, note that any time interest group access was banned all politicians set x = 0. Corrupt politicians choose x = 0 because they are not bribed and sincere politicians choose x = 0 because their prior beliefs place a higher probability on θ = 0. This further implies that with probability 1 – q, the wrong policy, from the voter’s perspective, will be implemented.
When the interest group does have access policy choices vary. Consider a corrupt politician that won office after running on an access platform. He is solely motivated by rent-seeking and therefore will choose the group’s preferred policy, x = 1, only if he receives a bribe, b = 1, and implements x = 0 otherwise. The group understands this and therefore knows that a bribe will lead to its most preferred policy. In equilibrium, when the interest group learns a corrupt politician has won office it optimally pays the bribe. Sincere politicians’ policy choices respond to information, not bribery. Thus, the interest group has no incentive to bribe sincere politicians. When a sincere politician runs on an access platform and wins he learns θ because the group’s private information is verifiable. This allows him to match policy to the state, x(θ) = θ, an outcome that is optimal for both him and the voter. The foregoing analysis yields a unique equilibrium to the lobbying stage of the game.
Proposition 1. The unique equilibrium to the lobbying stage consists of the following collection of strategies when access was granted.
• The interest group reveals θ to sincere politicians and bribes corrupt politicians, b = 1.
• Corrupt politicians implement the interest group’s preferred policy, x = 1, only if b = 1 and implement x = 0 otherwise.
• Sincere politicians implement the interest group’s preferred policy, x = 1, only if they learn θ = 1 and implement x = 0 otherwise.
To summarize Proposition 1, when access was granted, the interest group always bribes a corrupt politician and always reveals θ to a sincere politician. A corrupt politician sets x = 1 if and only if he is bribed and a sincere politician sets x = θ after learning θ.
Signaling with Reform
In this section, we characterize platform decisions. There are two types of equilibria. A reform equilibrium is a separating equilibrium, in which sincere politicians run on reform platforms and corrupt politicians run on access platforms. Voters can infer sincerity in this case and screen out corrupt politicians, but sincere politicians sacrifice policy-relevant information by banning group participation. An access equilibrium is a pooling equilibrium in which all politicians run on access platforms. In this case, the voter cannot infer politician types, but if a sincere politician wins office, he is able to make informed policy choices. Therein lies the fundamental trade-off at the heart of this article: improved screening for corruption comes at the cost of informed policymaking.
Equilibrium Voting
The voter attempts to elect sincere over corrupt politicians. In a reform equilibrium, she can perfectly infer politician types. If both politicians run on reform and ban group access, then she is indifferent because both are sincere and x = 0 is implemented regardless of who she elects. If both politicians run on access, then she knows that both are corrupt and is again indifferent because x = 1 will ultimately be implemented. Finally, when one politician is sincere and runs on reform and one is corrupt and runs on access, she votes for the sincere politician who will implement x = 0 over the corrupt politician who will implement x = 1. Because θ = 0 is ex ante more likely this choice yields higher expected utility than electing a corrupt politician.
In an access equilibrium, the voter cannot infer politician types and retains her prior belief, implying that either politician is equally likely to be sincere. In that case, the voter can do no better than voting for either politician with equal probability. She expects to lose nothing on policy with probability π because in that case the politician is sincere and policy is implemented to match the state. In contrast, with probability 1 – π, the winning politician is corrupt and x = 1 is implemented for sure, leading to an expected policy loss proportional to the probability that θ = 0.
Equilibrium Platforms
To illuminate the issues at stake when considering platform decisions, consider again the case of banking regulation discussed in the introduction. For corrupt politicians, public office is seen as an avenue for private rents and, therefore, will always grant access to banking groups and subsequently choose policy that is favorable to those groups. For sincere politicians, there is a trade-off involved. Granting access to banking groups (i.e., enlisting their advice in crafting policy) carries significant informational benefits. In fact, the informational advantage of those in the banking industry is often seen as an important reason for these groups to be included in the regulatory process (e.g., Omarova Reference Omarova2010). However, consulting with interest groups may lead voters to question whether the politician is sincere. When will sincere politicians eschew policy-relevant information by running on reform in pursuit of revealing that they are sincere?
Consider first the incentives of corrupt politicians. Because they only respond to bribes, the maximum payoff for running on reform is zero because that precludes the group’s ability to pay bribes. In contrast, if corrupt politicians run on access platforms, depending on the type of their opponents, they may win office and receive a bribe from the group. Thus, it is always beneficial for corrupt politicians to run on an access platform.
Sincere politicians have different incentives because they pursue policy rather than bribes. Consider the reform equilibrium environment. Corrupt politicians run on access, whereas sincere politicians run on reform. A sincere politician’s expected payoff for banning access in this environment is given by
$$E{U_i}\left( {p_i^ * = 0{\rm{|}}{\tau _i} = S,p_{ - i}^ * ,{x^ * }} \right) = - \left( {1 - q} \right).$$The implemented policy outcome when two sincere politicians compete against one another is the same: both will set x = 0 because neither receives information from the interest group. This yields an expected payoff of −(1 − q).Footnote 10 If instead he faces a corrupt politician, he wins the election for sure but receives no information because lobbying is banned. He therefore sets x = 0, which again yields an expected payoff of −(1 − q). Thus, regardless of his opponent’s type, a sincere politician’s expected payoff is −(1 − q) when he runs on reform.
If instead a sincere politician deviates and runs on access his expected payoff is
$$E{U_i}\left( {{p_i} = 1|{\tau _i} = S,p_{ - i}^*,{x^*}} \right) = - \pi \left( {1 - q} \right) - {1 \over 2}\left( {1 - \pi } \right)q.$$If he deviates, he loses when he runs against another sincere politician because now his platform signals to the voter that he is corrupt. In this case, the politician expects to lose −(1 − q) because that is the likelihood the uninformed sincere politician who won office will fail to match policy to the state. If he faces a corrupt politician, then the voter elects either with equal probability because she believes both are corrupt. If the sincere politician wins, then he is able to perfectly match policy to the state because the group has access and provides information about θ. If he loses, then the corrupt winner will implement x = 1 which will fail to match the state with probability q.
It is incentive compatible for a sincere politician to run on a reform platform if
$$- \left( {1 - q} \right) \ge - \pi \left( {1 - q} \right) - {1 \over 2}\left( {1 - \pi } \right)q,$$which is satisfied for all π ∈ (0, 1) when 
$q \,\ge\, {2 \over 3}$. Combined with the fact that corrupt politicians always run on access in this environment, this yields the necessary and sufficient condition to support a reform equilibrium: 
${q^{{\rm{Reform}}}}\left( \pi \right): = {2 \over 3}$. So long as q ≥ q Reform(π)—the probability that θ = 0 is sufficiently high—there is a reform equilibrium.
Now consider the access equilibrium environment in which all politicians run on access. The upside to this situation is that sincere politicians, if they win, are able to make fully informed policy choices. The downside is that the voter cannot differentiate politicians and therefore may elect a corrupt politician. Corrupt politicians have even stronger incentive to run on access in this case because they no longer lose with certainty when facing a sincere politician.
Sincere politicians would prefer to run on access for its informational value, conditional on winning the election. However, doing so precludes the sincere politician from revealing he is sincere and therefore he risks losing the election to a corrupt politician. A sincere politician’s expected payoff from running on access in this case is
$$E{U_i}\left( {p_i^ * = 1{\rm{|}}{\tau _i} = S,p_{ - i}^ * ,{x^ * }} \right) = - {1 \over 2}\left( {1 - \pi } \right)q.$$If he faces another sincere politician, then regardless of who wins policy is implemented to match the state and he receives zero. If he runs against a corrupt politician, then he runs the risk of losing and having x = 1 implemented for sure, which will mismatch the state with probability q, yielding his expected policy losses in that case. If a sincere politician instead deviates to running on reform and banning access, he foregoes the opportunity to make informed policy should he win, but ensures that he will win the election with certainty because the voter correctly believes he is sincere.Footnote 11 This deviation yields the following expected payoff:
$$E{U_i}\left( {{p_i} = 0{\rm{|}}{\tau _i} = S,p_{ - i}^ * ,{x^ * }} \right) = - \left( {1 - q} \right).$$Regardless of what type of politician his opponent is, the sincere politician will win the election but will learn nothing about θ. Thus, he will follow his prior information, implement x = 0, and policy will not match the state with probability 1 − q. To support the posited sincere politician behavior in the access equilibrium, incentive compatibility requires that
$$- {1 \over 2}\left( {1 - \pi } \right)q \,\ge\, - \left( {1 - q} \right),$$which is satisfied for all π ∈ (0, 1) when 
$q \in \left( {{1 \over 2},{2 \over {3 - \pi }}} \right]$. Because corrupt politicians always run on access platforms, this incentive compatibility condition is necessary and sufficient to support an access equilibrium. Define this condition as 
${q^{{\rm{Access}}}}\left( \pi \right): = {2 \over {3 - \pi }}$. As long as q ≤ q Access(π)—the probability that θ = 0 is sufficiently low—there is an access equilibrium.
The conditions on q that support the separating reform and the pooling access equilibria are not distinct. In fact for any π ∈ (0, 1), there exists a region in which both reform and access equilibria are possible: q ∈ [q Reform(π), q Access(π)].
Proposition 2. Define 
${q^{Reform}}\left( \pi \right): = {2 \over 3}$ and 
${q^{Access}}\left( \pi \right): = {2 \over {3 - \pi }}$. Then for all π ∈ (0, 1) we have the following equilibria conditional on the magnitude of q.
• If q Reform(π) ≤ q Access(π) < q, then the separating reform equilibrium is unique.
• If q < q Reform(π) ≤ q Access(π), then the pooling access equilibrium is unique.
• If q Reform(π) < q < q Access(π), then both the separating reform and the pooling access equilibria can be supported.
The range of q in which reform and access equilibria both exist varies in the likelihood of corruption, π. Specifically, q Access(π) is increasing in π, which yields the following corollary.
Corollary 1. As π → 0 corruption is almost certain and we have either a reform equilibrium or an access equilibrium depending on whether 
$q \gtrless {2 \over 3}$. As π → 1, there is little chance of corruption and an access equilibrium always exists, whereas a reform equilibrium only exists if 
$q \ge {2 \over 3}$.
As corruption becomes increasingly likely, there is little overlap in the regions that support both reform and access equilibria. That is, when it is almost certain that politicians are corrupt either there is a reform equilibrium, if q is sufficiently high, or an access equilibrium, if q is sufficiently low. Substantively, this implies that when information is highly valuable, all politicians prefer to run on access to preserve the possibility of learning about θ from the interest group, whereas when information is not particularly valuable, sincere politicians prefer to identify themselves by running on reform and banning group access. Conversely, as corruption becomes highly unlikely, there is almost always an access equilibrium although the conditions to support a reform equilibrium remain unchanged. As it becomes more likely that all politicians are sincere, there are weaker incentives to signal sincerity through reform. Sincere politicians and the voter prefer access to be granted for informational purposes conditional on there being no corruption in the political system. Figure 1 displays the results from Proposition 2 and Corollary 1 graphically.
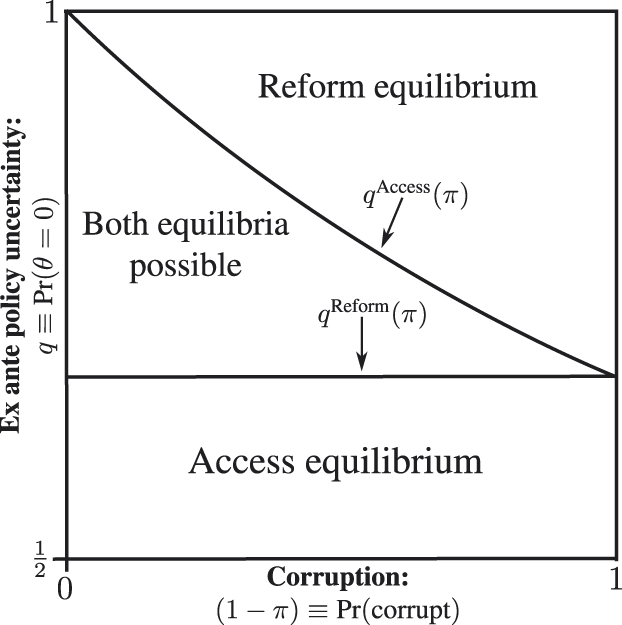
FIGURE 1. Equilibrium Regions
Note: The y-axis denotes q = Pr[θ = 0]. Policy uncertainty decreases as q increases. The x-axis denotes (1 − π) = Pr[τ i = C]. Likelihood of corruption is increasing left-to-right.
Voter Welfare: When is Reform Better than Access?
Our analysis so far suggests that, for many situations, there are two plausible equilibria with very different political behavior. In one equilibrium, all politicians run on access, so sincere politicians will have good information if they are elected, but voters cannot distinguish sincere from corrupt politicians. In another equilibrium, sincere politicians signal their types to voters by running on reform, so voters know whether or not politicians are sincere, but sincere politicians lack valuable information that they could have obtained from interest groups. Thus, we turn our attention to a key normative question: under what circumstances will one equilibrium improve voter welfare relative to the other?
The welfare implications of the equilibria are not obvious because both types of equilibria provide different advantages to voters. For instance, in the case of banking regulation, the voter has two interests. First, the voter may want help in distinguishing between politicians who are truly interested in which regulations most benefit consumers from those seeking private office rents. In this way, the reform equilibrium is good for the voter because it perfectly sorts these types of politicians. Second, the voter is interested in sincere politicians’ ability to make good policy once in office. For this purpose, the voter would benefit from having sincere politicians and banking industry representatives in the same room to discuss market conditions and match regulations to the current economic climate. In this way, the access equilibrium is good for the voter because it allows sincere politicians to take full advantage of industry expertise when making decisions. The welfare implications of a reform versus an access equilibrium depend on the relative weight placed on these two forces, as we further explain below.
To begin the analysis, consider the voter’s welfare from the reform equilibrium:
$$W_{\rm{V}}^{{\rm{Reform}}}\left( {p,x} \right) = - \left( {{\pi ^2} + 2\left( {1 - \pi } \right)\pi } \right)\left( {1 - q} \right) - {\left( {1 - \pi } \right)^2}q.$$Because the voter can perfectly infer sincerity, her ex ante welfare simply depends on whether a sincere politician is running for office. This occurs with probability π 2 + 2(1 − π)π. In this case, the voter elects a sincere politician, but still expects policy to mismatch the state with probability 1 − q because access was denied and the interest group cannot reveal θ. With probability (1 − π)2, both politicians are corrupt and the winner will receive a bribe and implement x = 1, which mismatches the state with probability q.
In comparison, the voter’s welfare in an access equilibrium is
$$W_{\rm{V}}^{{\rm{Access}}}\left( {p,x} \right) = - \left( {1 - \pi } \right)q.$$Because the voter cannot differentiate between sincere and corrupt politicians, she elects either politician with equal probability. If the winning politician is sincere, then there is zero policy loss because a sincere politician who wins office learns θ from the interest group and sets policy accordingly. However, with probability 1 – π, the winning politician will be corrupt. In this case, the interest group bribes the corrupt politician to implement x = 1, which in expectation does not match the state with probability q. Thus, the voter can expect to lose utility equal to the product of the probability, given a politician is corrupt and the probability that policy will not match the state.
Taken together, these two expressions imply that a reform equilibrium is preferred to an access equilibrium from the perspective of voter welfare if,
$$- \left( {{\pi ^2} + 2\pi \left( {1 - \pi } \right)} \right)\left( {1 - q} \right) - {\left( {1 - \pi } \right)^2}q > - \left( {1 - \pi } \right)q.$$Which equilibrium is preferred depends on the relative importance of screening out corruption (π) compared with the value of information in policymaking (q).
Proposition 3. Define 
${q^{Welfare}}\left( \pi \right): = {{\pi - 2} \over {2\pi - 3}}$. From the perspective of ex ante voter welfare, the reform equilibrium is preferred to the access equilibrium if q > q Welfare(π), otherwise the access equilibrium is welfare-preferred to the reform equilibrium. Moreover, 
${d \over {d\pi }}\left( {{q^{Welfare}}\left( \pi \right)} \right) > 0$.
Figure 2 displays the result in Proposition 3 graphically. Which equilibrium benefits the voter depends on the relationship between q and π. To see the intuition behind the result consider what q and π jointly represent from the voter’s perspective. When q is sufficiently high, information is relatively less valuable and the voter benefits from improved ability to screen politicians. Thus, the separating reform equilibrium is welfare-preferred. However, when q is relatively low, information is more valuable and the voter benefits from risking election of corrupt politicians in exchange for improved policymaking when sincere politicians take office. Moreover, q Welfare(π) is increasing in π, which implies that the value of information has to decrease as the threat of corruption increases for the benefits of improved screening to outweigh the benefits from informed policymaking.
FIGURE 2. Voter Welfare in Reform Versus Access Equilibria
Note: 
${q^{{\rm{Welfare}}}}\left( \pi \right): = {{\pi - 2} \over {2\pi - 3}}$. If q > q Welfare(π) the voter prefers reform equilibrium and if q < q Welfare(π) the voter prefers access equilibrium.
Interest Group Self-Regulation
Our model provides an instrumental foundation for why interest groups may support legislation that strengthens lobbying regulations, as well as why it may be beneficial to join trade associations with more stringent internal enforcement. Because the possibility of bribery may lead sincere politicians to ban special interest participation, interest groups can benefit from supporting policies that effectively remove the possibility of bribery to induce sincere politicians, whom the group wants to influence with information, to allow special interests a seat at the table. This may help explain why lobbyists themselves have at various times organized to advocate for stronger transparency and lobbying regulation (Leech Reference Leech2013, chap. 1). When might interest groups benefit from self-regulating and committing to not bribing corrupt politicians?
In an access equilibrium, the interest group never benefits from self-regulating. In this case, the only thing that self-regulation does is preclude the ability to induce corrupt politicians to implement x = 1, with no effect on sincere politicians that win office. Thus, the group only loses utility from self-regulation in an access equilibrium. However, in a reform equilibrium, the interest group can benefit from policies that preclude bribery. This follows from the effects self-regulation has on sincere politician incentives. Corrupt politicians still have no strict incentive to run on reform. Sincere politicians benefit from abandoning reform and running on access when groups self-regulate because the risk of x = 1 always being implemented because bribery is removed. There is only upside to sincere politicians deviating to access platforms when groups self-regulate because it increases the likelihood they can match policy to the state.
Accordingly, in a reform equilibrium, the interest group’s choice to self-regulate depends on whether it benefits from sincere politicians running on reform or access. Consider the group’s welfare if they do not self-regulate and politicians play reform equilibrium strategies,
$${W_{\rm{G}}}\left( {{\rm{Bribes|Reform}}} \right) = {\left( {1 - \pi } \right)^2}\left( {1 - \kappa } \right).$$If a sincere politician wins office, then the group receives zero because in this case the politician ran on reform, banned group access, and always implements x = 0. However, with probability (1 − π)2, both politicians are corrupt, ensuring a corrupt politician wins office. The group then bribes the politician to implement x = 1, yielding a payoff of 1 − κ.
In contrast, group welfare from self-regulating and inducing access equilibrium behavior is
$${W_{\rm{G}}}\left( {{\rm{No}}\;{\rm{bribes|Access}}} \right) = \pi \left( {1 - q} \right).$$In this case, either politician wins with equal probability. The winning politician is sincere with probability π and, because the group has access, the politician implements x(θ) = θ, which benefits the group when θ = 1 and yields an expected payoff of (1 − q). If a corrupt politician wins office, then the group receives zero because it cannot bribe. Combining these expressions yields the condition for the group to benefit from self-regulation,
$$\pi \left( {1 - q} \right) > {\left( {1 - \pi } \right)^2}\left( {1 - \kappa } \right),$$which is satisfied when 
${1 \over 2}\left( {{{2\kappa + q - 3} \over {\kappa - 1}} - \sqrt {{{\left( {q - 1} \right)\left( {4\kappa + q - 5} \right)} \over {{{\left( {\kappa - 1} \right)}^2}}}} } \right): = \pi _{\rm{G}}^{{\rm{Regulate}}}\left( {q,\kappa } \right) \lt \pi \lt 1.$
Proposition 4. Suppose politicians play reform equilibrium strategies when the interest group can bribe. The group benefits from self-regulation if 
$\pi > \pi _G^{Regulate}\left( {q,\kappa } \right)$. Moreover, 
$\pi _G^{Regulate}\left( {q,\kappa } \right)$ is increasing in q and decreasing in κ.
Proposition 4 shows the interest group benefits from self-regulation when the probability of sincere politicians, π, is sufficiently high. The key trade-off for the group is having access to sincere politicians, which allows them to provide information and get their preferred policy when θ = 1, versus precluding their ability to bribe corrupt politicians. The less likely it is that a given politician is corrupt, the more the group benefits from self-regulation because it induces sincere politicians to grant access. Thus, so long as the probability of a politician being corrupt is sufficiently low the group prefers tying its own hands so that sincere politicians will grant access.Footnote 12 Additionally, as q increases, the condition is less likely to be satisfied, implying that the more likely it is that θ cuts against group interests the less likely it is the group will self-regulate. Intuitively, the more costly bribery becomes, the more likely it is that the group benefits from self-regulation. Figure 3 displays these intuitions graphically.
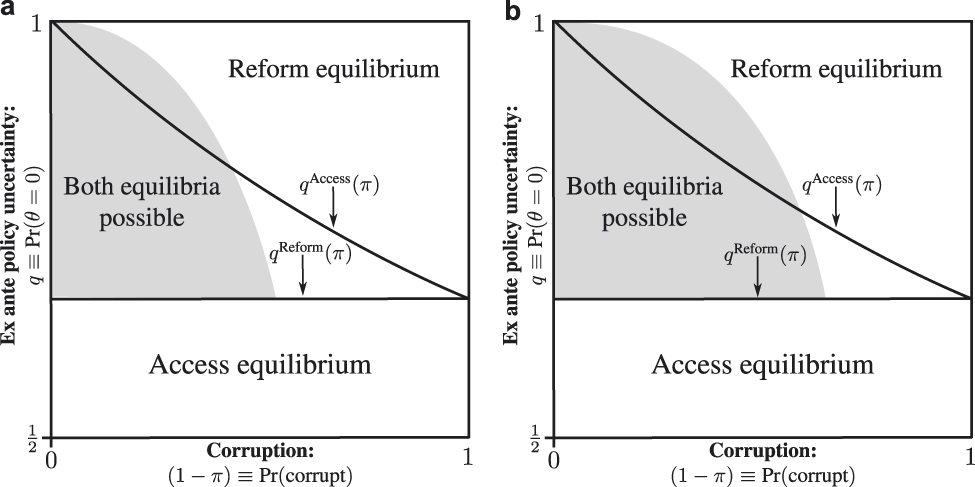
FIGURE 3. Interest Group Self-Regulation.
Note: (a) Low cost of bribery: 
${\kappa } \,\equals {1 \over 4}$. (b) High cost of bribery: 
${\kappa } \equals {3 \over 4}.$ Shaded areas represent regions in which the interest group benefits from self-regulation given a reform equilibrium.
RELAXING PLATFORM COMMITMENT
In the baseline model, we assumed that politicians could commit to platforms that ban interest group access following the election. Although that facilitates concise communication of our main insights, full commitment is a strong assumption. In this section, we relax this assumption and show that our main insights continue to hold. First, we analyze a model that replaces platform commitment with costly campaign announcements. Second, we analyze a dynamic model without campaign announcements and instead analyze incumbent choices regarding interest group access.
One related concern that is not directly addressed in the extensions below is that sincere politicians could consult with interest groups and allow them to provide information without voters learning they had done so. In this way, the key assumption is verifiability of access rather than commitment. However, the issue of access verifiability does not pose major problems for our results. Although politicians could allow interest groups to provide information without being detected, they could not act on that information without revealing they had done so. Furthermore, if these contacts are not verifiable, then the voters cannot readily tell whether the politician changed her mind because of information or bribes. Thus, the possibility of clandestine interaction with interest groups does not free sincere politicians from the need for costly signaling.
Costly Campaign Announcements
In this section, we analyze an alternative model that does not assume platform commitment. Instead, we model platforms as costly campaign announcements. Politician platform choice affects the cost of access that interest groups must pay to interact with incumbents. Access costs are higher when the politician in office ran on a reform platform.Footnote 13 This makes platform choices costly to politicians by lowering the probability they will interact with the interest group if they take office after running on reform, which harms sincere politicians’ ability to learn policy-relevant information and corrupt politicians’ ability to solicit exchanges. The group’s access costs can be understood as absorbing reputational costs that politicians must bear if they meet with special interests after running on reform. This is consistent with a competitive lobbying market in which interest groups subsidize any costs politicians must bear to meet with them in exchange for access.
As in the baseline model, the game begins with Nature drawing politician types and the state of the world with the same prior probabilities, π = Pr(τ i = S) and q = Pr(θ = 0) > 1/2. Then, politicians announce reform or access platforms, p i ∈ {0, 1}, followed by the voter electing one of the politicians. In contrast to the baseline model, once a politician takes office Nature draws a cost of access, 
${\alpha _G} \,\sim\, U\left[ {0,\bar{\alpha }} \right]$ with 
$\bar{\alpha } > 1$. This stochastic cost allows the interest group to buy access even if the winning politician ran on reform. Formally, the interest group chooses whether to access the politician (a G = 1) or not (a G = 0). If the group chooses a G = 1, then it pays (1 − p i)α G. If the politician ran on an access platform, p i = 1, then the group can access the politician without paying α G and if the politician ran on a reform platform, p i = 0, then the group must pay α G for access. The likelihood that access costs will be realized low enough that the group will pay to access a politician that ran on a reform platform depends on the magnitude of the upper bound of the α G distribution, 
$\bar{\alpha }$. The probability that α G is realized low enough that the group pays to access politicians that ran on reform is decreasing as 
$\bar{\alpha }$ increases.Footnote 14 Once a politician takes office, the interest group observes his type and chooses whether to pay for access. If it does, then θ is revealed and the group can choose to offer a bribe, as before. Following this interaction (or lack thereof), the politician sets policy, x ∈ {0, 1}, as in the baseline.
Only the interest group’s utility function differs from the baseline model. Incorporating the group’s access choice and platform-conditional access cost its utility function is
$${u_{\rm{G}}}\left( {x,\theta ,b,{\alpha _{\rm{G}}}} \right) = x - {a_{\rm{G}}}\left( {1 - {p_i}} \right){\alpha _{\rm{G}}} - \kappa b.$$We again analyze symmetric pure strategy perfect Bayesian equilibrium.
Interest Group Access and Informed Policymaking
Politician policymaking behavior is equivalent to the baseline model. Sincere politicians match policy to the state when they learn θ and implement x = 0 otherwise. Corrupt politicians implement x = 1 if bribed, and x = 0 otherwise. In contrast to the baseline model, the interest group can now pay to access politicians following the election even if they ran on reform platforms.
When the winning politician ran on an access platform, access is costless. If the winner is corrupt, the interest group is strictly better off gaining access and paying a bribe to induce x = 1. If the winner is sincere, then the interest group is strictly better off gaining access and providing information when θ = 1. When θ = 0, the outcome does not depend on whether or not the interest group provides information because an uninformed sincere politician would set x = 0 anyway.
Access dynamics change when the politician in office ran on a reform platform because now the group must pay α G for access. If a sincere politician wins office when θ = 1, then the group will pay for access provided the cost of doing so does not exceed the benefit of revealing θ to induce x = 1, which requires that 1 > α G. If θ = 0, then the group strictly prefers to eschew access, but if 1 > α G, then the politician infers θ from the group’s decision not to pursue access. Thus, the sincere politician learns θ when α G is less than 1. If a corrupt politician wins office, then the interest group will pay for access only if after paying α G it can still afford to pay κ and bribe the corrupt politician to implement x = 1. Access is useless for the group unless it can also bribe and have their preferred policy implemented. This implies that the group pays for access to corrupt politicians only if 1 > α G + κ, which is a more demanding condition than when a sincere politician is in office.
The conditions for the group to buy access also yield the ex ante probabilities of sincere politicians learning θ and corrupt politicians being bribed after running on reform platforms. Because α G is distributed uniform over 
$\left[ {0,\bar{\alpha }} \right]$, the ex ante probability sincere politicians learn θ after running on reform is 
$\Pr \left( {{\alpha _G} \le 1{\rm{|}}\bar{\alpha }} \right) = {1 / {\bar{\alpha }}}$ and the ex ante probability corrupt politicians are bribed after running on reform is 
$\Pr \left( {{\alpha _{\rm{G}}} \le 1 - \kappa {\rm{|}}\bar{\alpha },\kappa } \right) = {{\left( {1 - \kappa } \right)} / {\bar{\alpha }}}$. Sincere politicians have a higher probability of learning θ even after running on reform than corrupt politicians have of being bribed, which is due to the additional cost of bribery.
Equilibrium Campaign Announcements
The reform equilibrium and access equilibrium from the baseline also exist in this model, but we can now support a third equilibrium that we refer to as an anti-interest group equilibrium. The anti-interest group equilibrium is a pooling equilibrium in which both types of politicians run on reform platforms. As before, in the reform equilibrium, the voter can perfectly infer politician types and in either pooling equilibrium the voter learns nothing about politician types. Thus, equilibrium voting behavior is equivalent to the baseline model.
Assuming corrupt politicians run on access platforms, the incentives for sincere politicians are similar to those in the baseline model. When information is relatively less valuable (i.e., q is sufficiently high), sincere politicians are willing to trade off the likelihood of acquiring information about θ to credibly signal their sincerity and improve their electoral prospects by running on reform platforms. Similarly, when information is relatively more valuable (i.e., q is sufficiently low), sincere politicians are willing to run on access platforms and trade off their electoral prospects for learning θ when they win office. Additionally, as the probability of corruption decreases, sincere politicians are more likely to value running on access platforms to increase the probability they learn θ when they win office. The magnitude of 
$\bar{\alpha }$ strengthens the commitment-like properties of campaign announcements: As 
$\bar{\alpha }$ increases, it becomes harder to support sincere politicians running on reform but easier to prevent corrupt politicians from mimicking.
In contrast to the baseline, it is not always optimal for corrupt politicians to run on access platforms because there is now a positive probability they will be bribed after running on reform. Assuming sincere politicians run on reform platforms, corrupt types would deviate and mimic sincere types by choosing reform if π is too high relative to the likelihood of gaining access after choosing reform. If π is large then it is likely a corrupt politician will run against a sincere politician, which leads to electoral loss. In this case, corrupt politicians prefer to mimic sincere politicians to improve their probability of taking office even though it reduces the probability they will be bribed should they win. As the probability that corrupt politicians will be bribed after running on reform decreases, which occurs when 
$\bar{\alpha }$ and/or κ increases, this condition is easier to satisfy.
Finally, consider the anti-interest group equilibrium in which all politicians run on reform platforms. In this case, politicians who deviate to running on access lose the election for sure because voters infer politicians who deviate to access are corrupt. Sincere politicians have no incentive to deviate to an access platform as sticking with reform preserves a positive probability of winning the election and learning θ, because now the interest group may still gain access. Corrupt politicians also have no incentive to deviate because if they do they lose with certainty, cannot be bribed, and receive nothing, whereas if they stick with reform, then there is a positive probability of winning the election and being bribed.
In the baseline model, this equilibrium was ruled out by the requirement that in equilibrium players only play weakly undominated strategies. In an environment in which sincere politicians ran on reform corrupt politicians were indifferent between running on a reform platform and an access platform. If they were to run on an access platform, then they would lose with certainty to a sincere politician and therefore could not be bribed. If they instead ran on reform, then they might win, but because running on reform is a commitment to ban group access, they still could not be bribed, which rendered them indifferent. By replacing platform commitments with costly campaign announcements, this model opens the door for the anti-interest group equilibrium.
Proposition 5 formalizes the preceding arguments.Footnote 15 Figure 4 illustrates equilibrium regions.
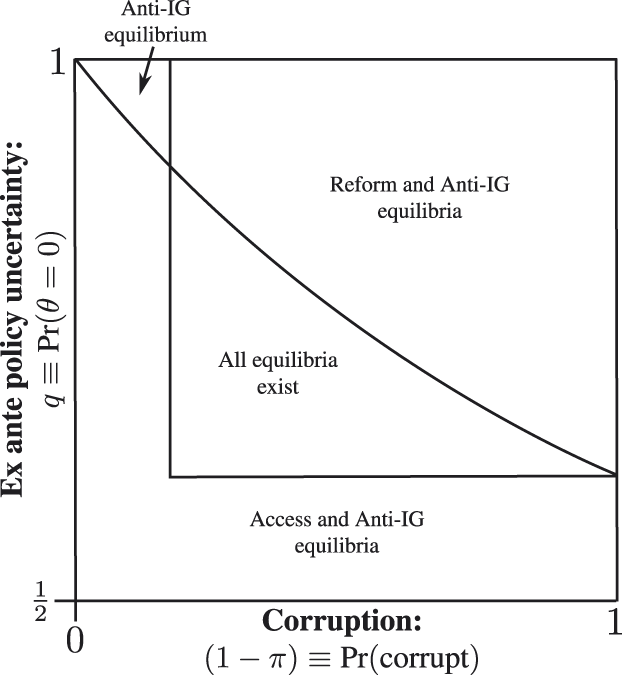
FIGURE 4. Equilibrium Regions when 
$\bar{\boldalpha } \,\boldequals\, \bf5$ and κ = 1/4
Proposition 5. In the costly campaign announcements game, the set of equilibria are determined as follows:
• A separating reform equilibrium exists if
$q \,\,\ge\,\, {{2\bar{\alpha } - 2} \over {3\bar{\alpha } - 2}}$, $\pi \,\,\le\,\, {{\bar{\alpha } + 2\kappa - 2} \over {\bar{\alpha } + \kappa - 1}}$, and $\kappa > {{2 - \bar{\alpha }} \over {\bar{\alpha }}}$.• A pooling access equilibrium exists if
$\bar{\alpha } \,\,\ge\,\, {2 \over {1 + \pi }}$, $q \,\,\lt\,\, {{2\bar{\alpha } - 2} \over {3\bar{\alpha } - 2 - \bar{\alpha }\pi }}$, and $\kappa \,\,\ge\, {{2 - \bar{\alpha }} \over 2}$.
Additionally, a pooling anti-interest group equilibrium in which both sincere and corrupt politicians run on reform platforms always exists.
Voter Welfare
Similar to the baseline model, sometimes the voter benefits from the reform equilibrium and other times benefits from politicians pooling on campaign platforms. Proposition 6 states the main welfare result and Figure 5 provides graphical illustration.
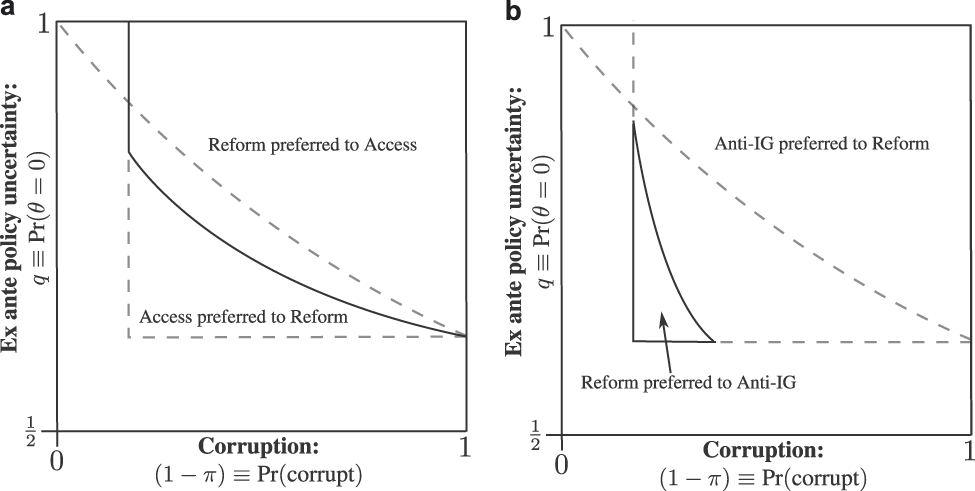
FIGURE 5. Voter Welfare Comparisons when 
$\bar{\boldalpha } \,\boldequals\, \bf5$ and 
${\boldkappa } \,\boldequals \bf{1 \over 4}$.
Notes: (a) Voter welfare in reform versus access equilibria. (b) Voter welfare in reform versus anti-IG equilibria.
Proposition 6. In terms of ex ante voter welfare, reform equilibrium is preferred to access equilibrium when both exist if 
$\pi \,\,\lt\,\,\, {{2\left( {1 - \bar{\alpha }} \right) + q\left( {3\bar{\alpha } - 2} \right)} \over {1 - \bar{\alpha } + q\left( {2\bar{\alpha } - 1} \right)}}$ and reform equilibrium is preferred to anti-interest group equilibrium when both exist if 
$\pi >\, {{1 + 2q\left( {\bar{\alpha } + \kappa - 1} \right) - \bar{\alpha } - \kappa } \over {1 + q\left( {2\bar{\alpha } - 1} \right) - \bar{\alpha }}}$.
As in the baseline model, whether the voter prefers a reform or access equilibrium depends on the value of information relative to improved screening. As q increases, the relative value of information decreases and the voter is more likely to benefit from the improved screening facilitated by reform equilibrium. Conversely, as q decreases information becomes more valuable and the voter is more likely to benefit from access equilibrium. As π decreases it is more likely that a given politician is corrupt, which increases the likelihood the voter prefers reform equilibrium and the improved screening it provides. These dynamics are amplified by the fact that sincere politicians may learn θ even after running on reform. As 
$\bar{\alpha }$ decreases the probability sincere politicians learn θ after running on reform increases, which improves the likelihood the voter benefits from the reform equilibrium because she is better able to screen out corruption without sacrificing as much in terms of information. Figure 5a presents these intuitions graphically.
The implications of reform versus anti-interest group equilibria for voter welfare are two-fold. First, the reform equilibrium helps the voter screen out corrupt politicians and the anti-interest group equilibrium does not. Second, the anti-interest group equilibrium limits bribery of corrupt politicians when they do take office, whereas the reform equilibrium does not. The voter’s preference between these equilibria depends on the relative importance of these two factors. When π is large, the reform equilibrium tends to be preferred because screening becomes very effective and the risk of bad behavior by corrupt politicians is relatively small. In addition, the voter is more likely to prefer the anti-interest group equilibrium as 
$\bar{\alpha }$ increases because it lowers the probability corrupt politicians are bribed should they win office. Figure 5b illustrates these dynamics.
This model relaxed the commitment assumption from the baseline model by adding costly campaign announcements. Next, we analyze a dynamic model with no campaign announcements, and therefore no commitment.
Dynamic No-Commitment Game
In this section, we analyze a model of repeated elections with lobbying. This version of the model falls into the category of political agency models with adverse selection and moral hazard.Footnote 16 The players are the same as in the baseline model and elections occur over an infinite horizon, with time periods indexed by t = 1, 2,…. The first time period begins with a randomly selected incumbent. The sequence of play in each time period is as follows:
1. Nature chooses the state of the world θ t for period t, with
$\Pr \left[ {{\theta _t} = 0} \right] = q > {1 \over 2}.$ If the incumbent is sincere, Nature makes him corrupt with some probability ε ∈ (0, min{π, 1 − π}).2. The incumbent chooses whether to grant access (p t = 1) or not (p t = 0).
3. The state of the world θ t and the incumbent’s type are revealed to the interest group. If p t = 1, then lobbying occurs. Lobbying strategies do not substantially change, so we simply assume that if p t = 1 and the incumbent is sincere then θ is revealed and if p t = 1 and the incumbent is corrupt then a bribe is paid. We set b t = 1 if a bribe is offered. If p t = 0, then the game simply moves to the next step with no lobbying.
4. The incumbent chooses a policy x t ∈ {0, 1}. An outcome (i.e., the voter’s utility) is u V(x t, θ t) = 1 − |x t − θ t|.
5. The voter learns the incumbent’s access choice. With probability r, she also learns the policy choice and her utility (with probability 1 − r she learns neither policy nor her utility).Footnote 17
6. Nature chooses whether the challenger is sincere (with probability π) or corrupt (with probability 1 − π). The voter (without observing the challenger’s type) decides whether to retain the incumbent or replace her with the challenger.
Stage-game preferences are similar to the baseline model. The voter and sincere politicians receive a payoff of 1 if θ t = x t and 0 otherwise.Footnote 18 When they are in office, corrupt politicians receive a payoff of 1 if they are offered a bribe and choose the interest group’s preferred policy x = 1, and zero otherwise. An issue that did not arise in the one-shot game but is relevant to the dynamic model is what payoff politicians receive when they are not in office. We assume that, regardless of type, politicians are identical to the voter when they are not in office, receiving a payoff of 1 if the policy matches the state and 0 otherwise. The results are similar if politicians receive a constant payoff once out of office. The utility of the voter and politician i in time t are denoted u V(x t, θ t) and u i(x t, θ t, b t), respectively. At any time period, the players maximize the discounted present value of their utilities: 
$\sum\limits_{t = 1}^\infty {{\delta ^{t - 1}}{u_{\rm{V}}}\left( {{x_t},{\theta _t}} \right)}$ for voters and 
$\sum\limits_{t = 1}^\infty {{\delta ^{t - 1}}{u_i}\left( {{x_t},{\theta _t},{b_t}} \right)}$ for politicians, where δ ∈ (0, 1) is a discount factor. We characterize stationary perfect Bayesian equilibria in weakly undominated strategies.
Remarks on Modeling Assumptions
We have made two major alterations to the baseline model beyond extending the time horizon and eliminating the commitment assumption. First, we allow for the possibility that sincere politicians may be corrupted at some point in the future if they remain in office. This serves two substantive purposes. First, it captures the idea that politicians may become entrenched in powerful networks and lose sight of their constituents’ welfare the longer they are in office. This effect does not need to be particularly large, and in fact we will consider what happens in the limit as the probability of this occurring goes to zero. Second, it ensures that the voters’ beliefs about the incumbent’s type will not be degenerate after one period of signaling. This serves the technical purpose of creating some value to signaling in each time period. It also adds to the realism of the model because it is unlikely that voters’ information sets are ever so perfect that there is no more they could learn. The second purpose could also be satisfied by some other source of noise, like errors in politicians’ actions or in voters’ observations of those actions without much change in results.
The second departure from the baseline model is that the voter observes policy choices and outcomes with probability r. The purpose of this parameter is to highlight how the welfare comparisons between equilibria depend on the quality of voters’ information. This also adds realism to the model: the quality of voters’ information on a particular issue depends on its salience in the news media, the transparency of the policymaking process in the relevant committee or executive agency, the quality of inter-branch oversight, and a number of other variables that may change over time for reasons that are outside the model.
Reform and Access Equilibria
In a reform equilibrium, sincere politicians choose p t = 0 at all t and corrupt politicians choose p t = 1. This implies that the voter always learns the incumbent’s type on the path of play. Therefore, the voter always retains the incumbent when p t = 0 and never retains the incumbent when p t = 1. Existence of a reform equilibrium is driven by the same factors as in the baseline: when q is sufficiently high and π sufficiently low, sincere politicians consider the risk of being replaced by a corrupt politician high enough and the returns to policy information low enough to deny access in exchange for reelection. Because there is no commitment in this game, signaling is driven by the expectation of staying in office in the future, so existence of reform equilibrium also depends on agents being sufficiently patient and on the probability that the sincere politician is corrupted while serving in office.
One key difference between the dynamic model and the baseline model is that the access equilibrium always exists. In this equilibrium profile, both politician types grant access and voter decision-making is based solely on observed policy outcomes. If the voter does not observe outcomes, which happens with probability 1 − r, then she simply retains the incumbent. If instead she does observe outcomes then she retains the incumbent when she learns her utility in that period is 1 and replaces the incumbent when she learns her utility in that period is 0. Finally, if the voter observed an incumbent who denied access off the path-of-play, she would believe that incumbent is sincere and therefore retain. This is required by the Intuitive Criterion because denying access is equilibrium-dominated for corrupt politicians. In turn, there is no reason for either politician type to deviate from granting access. The argument for corrupt politicians in the separating equilibrium implies that they would not deviate to denying access even if it guaranteed them reelection. For sincere politicians, granting access guarantees the best policy outcome in the current period. Furthermore, because the voter updates solely on policy outcomes (and retains when she learns nothing), this guarantees reelection for sincere politicians. Thus, regardless of type, no politician has an incentive to deviate to banning access.
Proposition 7. Define 
$q_D^{Reform}\left( {\pi ,\delta ,\varepsilon } \right): \,\,= {{\delta \left( {\varepsilon - 1} \right) + 1} \over {\left( {\delta + 1} \right)\left( {\delta \left( {\varepsilon - 1} \right) + 1} \right) + \left( {\delta - 1} \right)\delta \pi }}.$ A separating reform equilibrium to the dynamic no-commitment game exists if 
$q \,\ge\, q_D^{Reform}\left( {\pi ,\delta ,\varepsilon } \right).$ Additionally, an access equilibrium always exists.
Universal existence of an access equilibrium hinges on the knife-edge assumption that the probability a challenger is sincere is the same as for incumbents. This assumption implies that the voter is indifferent between retaining and replacing the incumbent when she does not learn policy outcomes in the access equilibrium. If some incumbents were considered more likely to be corrupt than a random challenger—perhaps because politicians who serve in office longer are more likely to be corrupt—then they would not be retained in an access equilibrium when voters do not learn about outcomes prior to voting. Therefore, when r is small, sincere incumbents would have a strict incentive to reveal their sincerity to stay in office and the access equilibrium would no longer survive the equilibrium refinements applied in the baseline model. This caveat means that the universal existence of access equilibria is not a strong positive prediction of the dynamic game. That said, because our focus is on the welfare comparisons across reform and access equilibria, this case serves as a useful baseline for analyzing voter welfare.
Before turning to voter welfare comparisons, we briefly discuss comparative statics on the threshold for reform equilibrium: 
$q_{\rm{D}}^{{\rm{Reform}}}\left( {\pi ,\delta ,\varepsilon } \right)$. First, 
$q_{\rm{D}}^{{\rm{Reform}}}\left( {\pi ,\delta ,\varepsilon } \right)$ is increasing in the probability a given incumbent is sincere, π. Because 
$q_{\rm{D}}^{{\rm{Reform}}}$ is a lower bound on q for existence of a reform equilibrium, reform is less likely when most politicians are sincere. The reason for this is that sincere politicians are policy-motivated and therefore have a stronger desire to hold office when their opponent is more likely to be corrupt. Second, 
$q_{\rm{D}}^{{\rm{Reform}}}\left( {\pi ,\delta ,\varepsilon } \right)$ is decreasing in δ which means reform equilibria become more likely with patience. This is because, by choosing reform, sincere politicians forgo better policymaking in the current period to stay in office in the future. Finally, 
$q_{\rm{D}}^{{\rm{Reform}}}\left( {\pi ,\delta ,\varepsilon } \right)$ is decreasing in ε, which means separating equilibria become more likely as sincere politicians become more likely to be corrupted in the future. The main reason for this is that forward-looking politicians weigh their potential future payoffs for becoming corrupt and accepting a bribe, which adds to the expected value of retaining office.
Voter Welfare
In this section, we compare voter welfare in the reform and access equilibria when both exist in the dynamic no-commitment game. As in the baseline and costly campaign announcement models, we show that either equilibrium may be welfare-preferred from the voter’s perspective. Proposition 8 states the main welfare result. First, Proposition 8 shows that the reform equilibrium is only preferred to the access equilibrium for sufficiently high values of q, holding the other parameters constant. The intuition for this is similar to the intuition for the baseline model. As q → 1/2, two things happen. First, a sincere politician who denies access is not much better than a corrupt politician who grants access. Second, information about θ t becomes increasingly valuable. Both of these factors favor the access equilibrium over the reform equilibrium because learning about θ t becomes relatively more valuable than screening. Conversely, as q increases, screening politicians becomes very important and information about θ t becomes less valuable, which favors the reform equilibrium. This logic leads to a cutoff for q such that the reform equilibrium is preferred by the voter if q is above the cutoff and the access equilibrium is preferred otherwise.
Additionally, Proposition 8 clarifies the impact of r, the probability that the voter learns the policy choice and outcome prior to the next election, on the comparison of the reform and access equilibrium. The parameter r tells us how much moral hazard exists with respect to policy. As r → 0 the voter faces a severe moral hazard problem and can never update on the incumbent’s type in the access equilibrium. As r → 1, there is very little moral hazard and the voter can very effectively remove corrupt politicians from office in the access equilibrium. The welfare comparison of the reform and access equilibria at extreme values of r follows closely from this logic. If r = 0, then the voter can only remove corrupt politicians from office through signaling with reform dynamics, so the reform equilibrium is always preferred. If r = 1, then the voter is very effective at throwing corrupt politicians out of office without signaling so the access equilibrium is always preferred.
Proposition 8. There exists a cutoff 
$q_D^W\left( {\pi ,\delta ,\varepsilon ,r} \right)$ such that the reform equilibrium produces a higher ex ante expected utility to the voter than the access equilibrium if and only if 
$q \,\ge\, q_D^W\left( {\pi ,\delta ,\varepsilon ,r} \right).$ Furthermore, when the reform equilibrium exists, this condition always holds as r → 0 and never holds as r → 1.
To highlight how the dynamics of the expanded model relate to those of the baseline model, we illustrate the results by fixing parameters other than π and q and visualizing the regions under which reform equilibria exist and are preferred to the access equilibrium. Specifically, in Figure 6, we fix δ = 0.95, set the value of r at two different intermediate values (1/4 and 3/4), and visualize the limit of equilibria as ε → 0.Footnote 19 The lower left region in each plot represents the lowest levels of corruption (high levels of π) and of policy certainty. In this region, the reform equilibrium does not exist. The upper right regions represent the highest levels of corruption and the highest levels of certainty that θ t = 0. In this region, both equilibria exist and the reform equilibrium is preferred by the voter. The middle region represents the region for which both equilibria exist and the reform equilibrium is dominated by the access equilibrium. Consistent with our intuition from Proposition 8 about moral hazard in the access equilibrium, increasing r also increases the size of the region in which the access equilibrium dominates. In the region where the access equilibrium dominates reform, we can think of signaling with reform as an accountability trap. This is true despite the fact that corrupt politicians may stay in office for multiple periods in the access equilibrium and never in the reform equilibrium. The policy cost incurred to separate sincere from corrupt politicians is simply not worth the benefits to the voter.
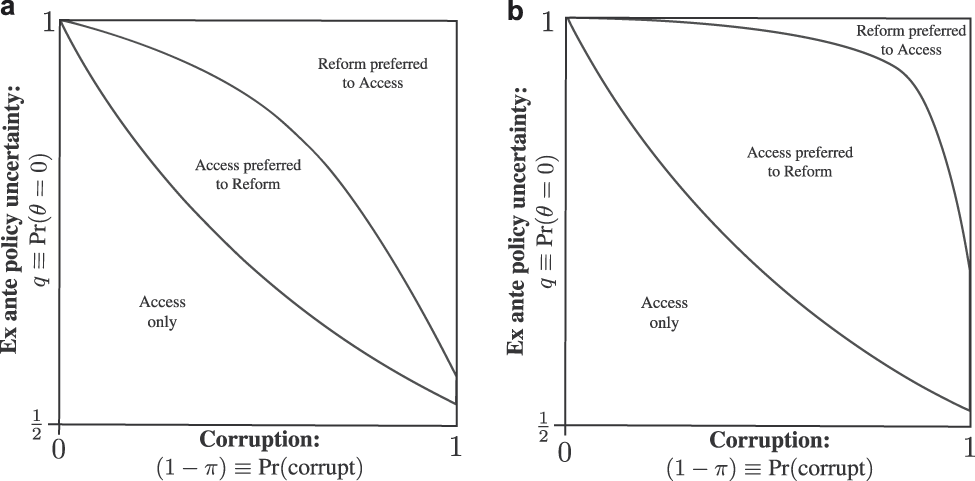
FIGURE 6. Voter Welfare Comparisons.
Notes: (a) Low probability of revelation: 
$r \,\boldequals \bf{1 \over 4}$. (b) High probability of revelation: 
$r \,\boldequals \bf{3 \over 4}.$
The relationship between the quality of the voter’s information about incumbent performance (r) and the welfare effects of reform is instructive. When voters are unable to fully evaluate policy outcomes before making reelection decisions, costly signaling that harms policy information may be good for voters. Conversely, when voters can discriminate between sincere and corrupt politicians reasonably well from observing their behavior in office, the voters are better off without such signals. This can be related to policy variables such as the rate at which government audits occur. From this perspective, increasing the rate of audits (i.e., increasing r) can have two good effects for voters: the direct effect is to improve voters’ information to select good politicians and the indirect effect is to reduce the need for politicians to engage in inefficient signaling.
CONCLUSION
We have analyzed a series of models in which interest group influence may take two forms. If lobbying is directed toward sincere politicians, then it may provide valuable policy information that benefit voters. If lobbying is directed toward corrupt politicians, then it may take the form of an economic exchange that tempts the politician away from the policy most likely to benefit voters. The voter’s problem is that she does not know whether a given politician is sincere or corrupt and therefore cannot always predict whether lobbying will be beneficial or harmful. This informational problem gives sincere politicians an incentive to signal their type by running on campaign platforms advocating restrictions to special interests’ role in the policymaking process. Notably, equilibria of this sort exist even when the probability of corruption is quite small. Thus, our model describes one rationale for why politicians may run campaigns on their freedom from lobbyists’ influence even in cases where lobbyists’ influence is primarily positive. Put another way, the substantive insights we provide in this article suggest one explanation for why politicians seem to find it beneficial to run against special interests: they benefit from signaling they are not the sort of politicians who will be corrupted by those interests and that they share voters’ concerns about the corrupting influence of those interests. Furthermore, the model shows why some reform-themed campaigns for getting money out of politics may work to the detriment of voters, whereas others may improve their welfare by helping them select sincere politicians.
Our results highlight yet another social cost of corruption in democratic societies: the perception of corruption and the desire to signal to voters may eliminate avenues for socially productive relationships between interest groups and noncorrupt politicians. This may have particularly troubling normative consequences because institutional factors such as low legislative professionalism have been associated with higher corruption (Meier and Holbrook Reference Meier and Holbrook1992), as well as increased demand for information provision by interest groups (Berkman Reference Berkman2001). The trade-off between preventing corruption and allowing socially productive lobbying should be an ongoing subject of theoretical and empirical research.
SUPPLEMENTARY MATERIAL
To view supplementary material for this article, please visit https://doi.org/10.1017/S0003055419000169.
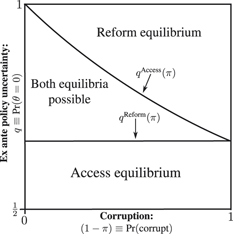
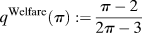
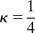
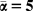
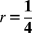
Comments
No Comments have been published for this article.