Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-21T22:04:16.092Z Has data issue: false hasContentIssue false
  • English
  • Français

Legislatures, Bureaucracies, and Distributive Spending

Published online by Cambridge University Press:  10 May 2012

MICHAEL M. TING
MICHAEL M. TING*
Affiliation:
Columbia University
*
Michael M. Ting is Professor of Political Science and Public Affairs, Columbia University, 420 West 118th Street, New York NY 10027 (mmt2033@columbia.edu).
Rights & Permissions [Opens in a new window]

Abstract

This article develops a theory of bureaucratic influence on distributive politics. Although there exists a rich literature on the effects of institutions such as presidents, electoral systems, and bicameralism on government spending, the role of professional bureaucrats has yet to receive formal scrutiny. In the model, legislators bargain over the allocation of distributive benefits across districts. The legislature may either “politicize” a program by bargaining directly over pork and bypassing bureaucratic scrutiny, or “professionalize” it by letting a bureaucrat approve or reject project funding in each district according to an underlying quality standard. The model predicts that the legislature will professionalize when the expected program quality is high. However, politicization becomes more likely as the number of high-quality projects increases and under divided government. Further, more competent bureaucrats can encourage politicization if the expected program quality is low. Finally, politicized programs are larger than professionalized programs.

Type
Research Article
Information
American Political Science Review , Volume 106 , Issue 2 , May 2012 , pp. 367 - 385
Copyright
Copyright © American Political Science Association 2012

A familiar piece of conventional wisdom, reaching back at least as far as Weber (Reference Weber, Gerth and Mills1946), is that the professional judgment of bureaucrats is essential for good governance. Bureaucrats typically possess the information and processing capacity that politicians inevitably lack. Thus nonpolitical actors routinely handle responsibilities such as choosing contractors, evaluating scientific projects, arresting criminal suspects, and setting various regulatory policies. As many studies have articulated, these activities can have pronounced distributive consequences, across both groups in society and geographic regions.Footnote 1 These consequences naturally evoke the issue of legislative consent (e.g., Arnold Reference Arnold1979). Due to the need to maintain electoral support or other political reasons, legislators may be hesitant to forego benefits aimed at their districts for the sake of “good” policy. Thus, there is an inherent tension between using an expert bureaucracy to allocate public spending and simply appropriating public money directly through the legislature.

To take a familiar example, in the United States most federally funded academic research is channeled through institutions such as the National Science Foundation and National Institutes of Health. There, projects are evaluated according to nonpolitical criteria by a combination of professional experts and external peer reviewers. On the merits, this system has been widely regarded as successful (e.g., Nelson and Rosenberg Reference Nelson, Rosenberg and Nelson1993). But as de Figueiredo and Silverman (Reference de Figueiredo and Silverman2006) document, a rapidly growing share of academic research—almost 10% by 2001—is “earmarked,” or directly appropriated to specific universities by Congress. Such spending is not scrutinized by the peer review process and is instead allocated directly through legislative bargaining.Footnote 2

This article analyzes the legislature's decision whether to distribute public funds directly via detailed legislation or indirectly via the bureaucracy. The focus on distributive politics (i.e., the allocation of public funds) means that I cannot use off-the-shelf models. On one hand, existing models of legislative delegation to the bureaucracy (e.g., Gailmard Reference Gailmard2002; Huber and Shipan Reference Huber and Shipan2002) explicitly focus on left-right or spatial politics, not distributive politics. On the other hand, existing models of distributive legislation, many of which belong to a family derived from Baron and Ferejohn (Reference Baron and Ferejohn1989), have no strategic role for bureaucrats.Footnote 3

The theory developed here therefore combines a basic model of distributive politics with a simple model of bureaucratic decision making. The setting is one in which a legislature and a bureaucrat jointly determine a policy outcome across multiple legislative districts, each represented by a single legislator. Each district has a single project with an unknown characteristic that the bureaucrat cares about. This characteristic may be thought of as the project's technical merit or quality (either high or low). A project may correspond to any entity that could qualify for public spending, such as an infrastructure proposal, a licensing or siting application, or a request for public welfare assistance. Legislators maximize their districts’ budget allocations, or pork. They do not care explicitly about the quality of the projects, thus presumptively biasing the results away from expert allocation. The projects are costly, with total costs divided evenly among legislators as a tax. The marginal cost of the legislation is increasing in the total budget allocation, which might reflect the deadweight loss of taxation.

The basic game begins with a vote over two alternative institutional mechanisms, which I term politicization and professionalization. After this choice, legislators bargain in a finite-horizon variant of the closed rule Baron-Ferejohn game. Under politicization, legislators bargain in a “divide the dollar” fashion, essentially distributing public spending in an earmark-like process. Legislative proposals are vectors of allocations that may differ across districts. If passed, these allocations bypass bureaucratic evaluation and flow directly to their designated districts.

By contrast, professionalization removes the ability to dictate district-specific allocations. Instead, legislators bargain over a uniform “national” project budget that applies to every district.Footnote 4 Once this budget is passed, a bureaucrat decides whether to fund each district's project. Districts (and legislators) only receive the money upon bureaucratic approval. Intuitively, professionalization transforms the bargaining space from a divide-the-dollar game to a “median voter” game where districts vary according to ideal budgets. One theoretical contribution of the model is therefore the integration of spatial and divide-the-dollar bargaining within the same legislative framework.

Under professionalized allocation, the bureaucrat's decision problem works as follows. She begins with a prior belief about the quality of the project in each district. There are two types of districts, where high-type districts are more likely ex ante to have high-quality projects than low-type districts. The bureaucrat may decide whether to investigate each project by collecting an additional noisy quality signal at a cost. She then approves or rejects the project, with approval yielding the district the legislatively mandated budget. The bureaucrat is motivated by career concerns and receives utility for granting or denying benefits according to an exogenous standard. This standard, and the ability to apply it, may reflect prevailing professional norms, the influence of nonlegislative actors in a separation of powers system, civil service protections, monitoring problems, or standing legislation.Footnote 5

The game has a unique symmetric subgame perfect equilibrium. The central tensions in the equilibrium can be illustrated by considering the position of a legislator who is uncertain whether the bureaucrat would approve her district's project. Politicization can help her by eliminating quality considerations from whether her district receives money. But it also introduces competition over the distribution of benefits. In this environment she cannot demand more than any other legislator in a winning coalition, and even worse, she may be excluded from a winning coalition altogether. Additionally, the ability to exploit proposal power inevitably results in highly inegalitarian and inefficiently large programs. By contrast, professionalization gives a greater claim on government spending to high-type districts and reduces competition-induced uncertainty for both types. The relative uniformity of bureaucratic decisions forces proposers to internalize program costs and therefore results in smaller programs and lower taxation.

The first prediction is that professionalization occurs when projects are of sufficiently high expected quality. This is intuitive, because projects of low expected quality are unlikely to pass muster with the bureaucrat. Professionalization therefore beats politicization when it is likely to provide benefits to a sufficiently broad coalition.Footnote 6 The basic result holds regardless of which district type has a legislative majority; high types will actually prefer politicization if their projects are unlikely to be of high quality. Notably, this finding is consistent with some previous empirical work linking project quality with professionalization (e.g., Anagnoson Reference Anagnoson1982; Reference Anagnoson1983; Law and Tonon Reference Law and Tonon2006).

The basic model also generates several more subtle findings. A legislative majority consisting of high-type districts becomes more inclined to politicize as the size of the majority increases, whereas the reverse is true for a majority consisting of low-type districts. Both of these relationships follow from the higher tax costs of funding many high-quality projects. Next, the effect of increasing the quality of bureaucrats, in the sense of more accurate investigations, depends on expected project quality. When projects are expected to be of high quality, then better bureaucrats raise the payoffs from professionalization. Yet better bureaucrats are also better at sniffing out low-quality projects, and so legislators facing this prospect will be more tempted to politicize.

A key extension to the model considers an alternative bureaucratic decision-making process in which an executive player can exercise managerial control over the agency (McCubbins, Noll and Weingast Reference McCubbins, Noll and Weingast1987; Moe Reference Moe, Chubb and Peterson1989). In a separation of powers system, this player might be a president, who can control agency procedures through the Office of Management and Budget, or a governor. The executive can control whether the bureaucrat investigates, but not her approval decision. Through this simple procedural tool, she may affect the distribution of benefits across districts and also the initial politicization choice (Berry, Burden and Howell Reference Berry, Burden and Howell2010; Gordon Reference Gordon2011). The results here depend on the objectives pursued by the executive. If the executive attempted to enforce a higher project standard than the bureaucrat, then the bureaucrat's lower probability of acceptance will encourage the legislature to politicize. A low standard will reverse this relationship. Thus politicization may be more likely when there is an executive who is ideologically opposed to a legislature's program, as might be expected under divided government. By contrast, an executive with “distributive” preferences will professionalize when her constituency matches that of the legislative majority.

This article engages a number of disparate literatures. Numerous empirical studies have documented the consequences of politicized actors in areas as varied as infrastructure policy (Gerber and Gibson Reference Gerber and Gibson2009, Rauch Reference Rauch1995), state economic projections (Krause, Lewis, and Douglas Reference Krause, Lewis and Douglas2006), broad categories of federal programs (Lewis Reference Lewis2008), and distributive spending (Berry and Gerson Reference Berry and Gersen2010). Additionally, Hird (Reference Hird1991) finds that both political factors and quality played roles in the selection of Army Corps of Engineers projects. By linking project quality with agency design, the model's predictions may be useful for guiding future empirical work on the determinants of agency spending patterns.

Theoretically, the model complements a long-standing body of work on the institutional basis of the distribution of government resources. In various forms, legislatures have long been at the center of the study of distributive politics (e.g., Ansolabehere, Gerber, and Snyder Reference Ansolabehere, Gerber and Snyder2002; Collie Reference Collie1988; DelRossi and Inman Reference DelRossi and Inman1999; Lee Reference Lee2000; Levitt and Snyder Reference Levitt and Snyder1995; Lowi Reference Lowi1964; Shepsle and Weingast Reference Shepsle and Weingast1981; Stein and Bickers Reference Stein and Bickers1995). Numerous studies over the years have also linked legislative politics with specific agencies or policy areas, such as water (Ferejohn Reference Ferejohn1974; Maass Reference Maass1951), taxes (Manley Reference Manley1970), military bases (Arnold Reference Arnold1979), local government grants (Rich Reference Rich1989), the postal service (Kernell and McDonald Reference Kernell and McDonald1999), higher education (Balla et al. Reference Balla, Lawrence, Maltzman and Sigelman2002), and labor and defense department contracts (Bertelli and Grose Reference Bertelli and Grose2009). Finally, agency-specific studies have also emphasized the role played by internal agency procedures and expertise in determining outcomes (e.g., Hird Reference Hird1990; Maor Reference Maor2007).

The simple model of bureaucratic decision making used here resembles in spirit those of Prendergast (Reference Prendergast2003) and Carpenter and Ting (Reference Carpenter and Ting2007), where the bureaucrat is asked to approve or reject a project of uncertain quality on behalf of a principal. However, the models do not consider the difference between professional and politicized allocation. The origins and implications of this distinction have received recent theoretical attention, in the contexts of elected versus unelected officials (Maskin and Tirole Reference Maskin and Tirole2004), bureaucrats versus politicians (Alesina and Tabellini Reference Alesina and Tabellini2007) and political versus civil service appointments (Gailmard and Patty Reference Gailmard and Patty2007). Finally, a number of models examine the legislature's role in funding government agencies, focusing primarily on information asymmetries (e.g., Banks Reference Banks1989; Bendor, Taylor, and Van Gaalen Reference Bendor, Taylor and Gaalen1987; Miller and Moe Reference Miller and Moe1983). Although each of these strands has contributed to the bureaucratic questions raised by this article, none has focused on legislative and distributive politics. To my knowledge, this model is the first that explicitly addresses the role of bureaucracies in distributive politics.Footnote 7

The model also joins a substantial literature on legislative bargaining in the Baron and Ferejohn (Reference Baron and Ferejohn1989) family. As with this article, the basic framework has been applied to common institutional variations, such as legislative procedures with pork barrel programs (Baron Reference Baron1991), a presidential veto player (McCarty Reference McCarty2000), bicameralism (Ansolabehere, Snyder, and Ting Reference Ansolabehere, Snyder and Ting2003) and public goods (Volden and Wiseman Reference Volden and Wiseman2007). Perhaps most similarly to the politicized process studied in this article, Norman (Reference Norman2002) studies a finite-horizon variant of the Baron-Ferejohn game. Richer versions of the “unidimensional” professionalized bargaining process are examined by Baron (Reference Baron1996) and Cho and Duggan (Reference Cho and Duggan2005).

The remainder of the article is organized as follows. The next sections describe the model and examine the bureaucrat's project approval problem. The following section then derives legislative strategies in both bargaining subgames. The main results about distribution, professionalization, and budgetary implications follow. A section on extensions then examines the effects of executive intervention, the quality of bureaucrats, and endogenous program standards. The final section discusses some implications of the results.

MODEL

The model combines bureaucratic decision making and legislative bargaining. The outcome of the game is an allocation of funding across n ≥ 5 (odd) districts. There are two kinds of players. A single bureaucrat B may decide whether to approve a project in each district. There are also n legislators, each representing one district, who wish to maximize their district's expected funding. It will be occasionally convenient to label the legislature collectively as L.

Each district i has a single project of unknown quality, denoted $\theta _i \in \lbrace \underline{\theta }, \overline{\theta }\rbrace$, where $\underline{\theta }< \overline{\theta }$. There are two types of districts, high and low (denoted τ = h and τ = l), where ex ante, quality level $\overline{\theta }$ occurs with probability p τ, with pl < ph. Let n τ denote the number of type τ districts. In what follows, both legislators and districts are referred to according to type.

The bureaucratic decision-making part of the model is a simple decision problem of choice under technical uncertainty. If given the opportunity by L, B's job is to decide whether to fund each district's project at L's specified level or to cancel it. To do so, B can first choose whether to investigate the project, acquiring a signal σi ∈ {0, 1}, where $\Pr \lbrace \sigma _i = 0\, |\, \theta _i = \underline{\theta }\rbrace = \Pr \lbrace \sigma _i = 1\, | \,\theta _i = \overline{\theta }\rbrace = q > 1/2$. When there is no investigation, it will be convenient to let σi = ∅. Thus, q is a measure of the precision of the signal, which may be due to B's expertise. The signal is independently distributed across districts, and each investigation imposes a cost c ≥ 0 on B. B must then approve or reject the project. B's payoff from the district i project decision is

$$ \left\lbrace\!\!\arraycolsep4pt\begin{array}{ll}\pi (\theta _i - s) & \mathrm{for\ approval} \\[4pt] 0 & \mathrm{for\ rejection} \end{array} \right. $$

Here s represents an exogenous standard. Throughout the article, I adopt the obvious interpretation of s as a technical quality standard or cost-benefit ratio, but it may also usefully demarcate other underlying dimensions, such as ideology. The parameter π > 0 is the extent to which B is motivated by project quality. Thus, rather than being a budget maximizer, B wishes to approve only projects that are “better” than s. The extensions section considers one extension in which an “executive” player (such as a governor or president) can costlessly determine whether B investigates, and another extension where s is endogenous.

The legislative bargaining part of the model is a variant of the Baron-Ferejohn (Reference Baron and Ferejohn1989) game, with T > 1 (finite) rounds of bargaining. The proposal space used by legislators depends on whether L chooses to “politicize” or “professionalize” the process by which districts are funded. This choice is denoted by I ∈ {B, L}, where B corresponds to professionalization, or using bureaucratic expertise, and L corresponds to politicization, or using direct legislative appropriations.

Bargaining proceeds via closed-rule majority rule. In each bargaining period t ∈ {1, . . ., T}, a legislator is recognized to make a proposal with probability 1/n. Under politicization, a proposal is a vector bt of non-negative benefits for each legislator or district. The legislature then votes on the proposal. If passed, district i's project is automatically funded with budget bi = b t,i, with no intervention from B. Under professionalization, a proposal is simply some non-negative bt, which is a uniform project budget for all districts that meet the national standard s. If passed, b = bt is allocated to each district on approval by B.Footnote 8 Under both institutional mechanisms, a rejected proposal results in another legislator being recognized to make a proposal until all T rounds are exhausted. The status quo allocation, which is adopted if no proposal is passed within T periods, is 0 if I = L and 0 if I = B.

A project gives each legislator utility equal to the realized budget in her district. This means that under professionalization, a legislator receives no benefit unless the project is approved. Additionally, legislators are taxed uniformly for the cost of the total benefits. Letting xj denote the realized benefit level in district j, the total cost of the legislation is then k(∑nj = 1xj)2 (where k > 0), which is distributed evenly across districts as a tax. Legislator i's realized payoff is then

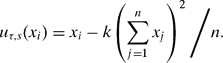
$$ u_{\tau,s}(x_i) = x_i - k\left(\sum _{j=1}^{n} x_j\right)^{2}\Bigg/n. $$

A stylized sequence of the game is as follows. All player moves are perfectly observable.

  1. 1. Institutional Choice. Each legislator i casts a vote w i,0 ∈ {B, L} to determine professionalization or politicization, with the outcome determined via majority rule.

  2. 2. Bargaining — Recognition. At each round t, Nature recognizes one legislator with probability 1/n, independently and identically distributed across periods.

  3. 3. Bargaining — Proposal. At each round t, if I = L, then the recognized legislator proposes an allocation bt ∈ ℜn+ for each district. If I = B, then the recognized legislator proposes a national project budget bt ∈ ℜ+.

  4. 4. Bargaining — Voting. At each round t, each legislator casts a vote w i,t ∈ {y, n} on the proposal, with the outcome determined via majority rule. If the proposal passes or fails at round T, then bargaining ends. Otherwise, bargaining proceeds to round t + 1.

  5. 5. Administration. In each district i, if I = B, B makes an investigative choice ai ∈ {investigate, noinvestigate}, yielding σi ∈ {0, 1, ∅}. B then forms posterior beliefs μi(σi) and makes an approval decision, di ∈ {y, n}.

I derive a symmetric subgame perfect equilibrium (SSPE) in pure strategies. This equilibrium treats all legislators of the same type identically under professionalization, and all legislators identically under politicization. Equilibrium strategies consist of five elements. First, each legislator has a vote w i,0 ∈ {B, L} over the institutional mechanism. Second, for each I, each legislator i has a proposal strategy mapping the set legislative histories H r,i leading to her recognition to a proposal. This mapping is βi:H r,i→ℜ+ if I = B and βi:H r,i→Δ(ℜn+) if I = L, where Δ(ℜn+) is the set of probability distributions over ℜn+. Third, each legislator i has a voting strategy wi:Hp→{y, n} mapping the set of legislative histories Hp leading to a proposal to a vote. Fourth, B's investigative strategy a:Hb→{investigate, noinvestigate}n maps the set of legislative histories under I = B leading to a passed budget to investigative choices in each district. Finally, B's approval strategy a:Hb×{0, 1, ∅}n→{y, n}n maps the set of histories leading to investigative results to approval decisions in each district. These decisions are based on her posterior beliefs μi(σi) about the probability that project i is of type $\overline{\theta }$. As the subsequent development shows, the SSPE is unique.

BUREAUCRATIC CHOICE

This section derives the bureaucrat's approval strategy in a professionalized setting. The analysis here yields each district type's probability of project acceptance under professionalization, which will affect the legislature's choice in the next section. It will be useful to restrict attention to a single district of arbitrary type; thus, notation for district i and type τ is suppressed here.

In choosing whether to investigate, B weighs the implications of the possible investigative outcomes. Thus, given ex ante probability p of a high-quality project, B's posterior belief that the project is of high quality when there is no investigation is simply μ(∅) = p. On investigating and seeing favorable (σ = 1) or unfavorable (σ = 0) investigative evidence, Bayes’ Rule implies that the posterior is

$$ \mu (\sigma ) = \left\lbrace \arraycolsep4pt\begin{array}{ll}\displaystyle\frac{qp}{qp + (1 - q)(1 - p)} & \mathrm{if}\ \sigma = 1, \\[14pt] \displaystyle\frac{(1-q)p}{(1-q)p + q(1 - p)} & \mathrm{if}\ \sigma = 0. \end{array} \right. $$

To identify the standards of interest to B, it is helpful to define the interval ${\mathcal P} = [\underline{\mathcal P}, \overline{\mathcal P}]$ as follows:

$$ {\mathcal P} \equiv [ \mu (0) \overline{\theta }+ (1 - \mu (0)) \underline{\theta }, \mu (1) \overline{\theta }+ (1 - \mu (1)) \underline{\theta }]. $$

This is the set of standards s for which the result of an investigation would be pivotal in B's decision whether to approve or reject. That is, if $s \in {\mathcal P}$, then a negative signal implies an unacceptable project in expectation. The unconditional probability of acceptance when there is an investigation is then pq + (1 − p)(1 − q), which is increasing in q if p > 1/2.

When will the bureaucrat collect this extra information? Without an investigation, B will accept the project if $s \le p \overline{\theta }+ (1 - p) \underline{\theta }$ and will reject it otherwise. Clearly, the signal is not worth acquiring if it would not affect the expected value of the project relative to s; that is, $s \not\in {\mathcal P}$. Otherwise, s is intermediate and the bureaucrat would benefit from additional information, but may not be willing to pay for it. Comparing expected payoffs and simplifying, B acquires the signal if

\begin{eqnarray*} &&qp \overline{\theta }+ (1 - q)(1 - p) \underline{\theta }- [q p + (1 - q)(1 - p)] s - c / \pi\\ &&\quad\ge \max \lbrace p \overline{\theta }+ (1 - p) \underline{\theta }- s, 0 \rbrace. \end{eqnarray*}

This expression reduces to

$$ \left\lbrace \arraycolsep4pt\begin{array}{l} -(1 - q) p (\overline{\theta }- s) - q(1 - p) (\underline{\theta }- s) \ge c / \pi \\[6pt] \quad \mathrm{if } \, p \overline{\theta }+ (1 - p) \underline{\theta }- s > 0\\ qp (\overline{\theta }- s) + (1 - q)(1 - p) (\underline{\theta }- s) \ge c / \pi \\ \quad \mathrm{otherwise.} \\ \end{array} \right. $$

These conditions hold if the expected upside bonus or the avoided downside loss from collecting the signal is sufficiently large. This will be true for some values of p if

(1)
\begin{equation} (2q - 1) \frac{(\overline{\theta }- s)(s - \underline{\theta })}{\overline{\theta }- \underline{\theta }} \ge \frac{c}{\pi }. \end{equation}

These expressions allow a complete characterization of B's acceptance and investigation strategy. When (1) holds, B investigates when $s \in {\mathcal S} = [\underline{\mathcal S}, \overline{\mathcal S}]$, where

(2)
\begin{eqnarray} {\mathcal S} &\equiv& \left[ \frac{(1-q)p \overline{\theta }+ q (1 - p) \underline{\theta }+ c/\pi }{(1-q)p + q(1 - p)}, \right.\nonumber\\ &&\left.\frac{qp \overline{\theta }+ (1 - q)(1 - p) \underline{\theta }- c/\pi }{qp + (1 - q)(1 - p)} \right] , \end{eqnarray}

or equivalently, $p \in [ \frac{c/\pi - (1 - q)(\underline{\theta }- s)}{q(\overline{\theta }- s) - (1-q)(\underline{\theta }- s)}, \frac{q(\underline{\theta }- s) + c/\pi }{q(\underline{\theta }- s) - (1-q)(\overline{\theta }- s)} ]$. Note that ${\mathcal S} \subseteq {\mathcal P}$, so that B investigates for a subset of standards for which more information would sway her decision. As intuition would suggest, the size of ${\mathcal S}$ is decreasing in the cost of investigation, c, and increasing in B's career motivation π.

The bureaucrat therefore investigates when s or p is “moderate,” which reflects its payoff-weighted incentive to investigate when uncertainty is high. For lower values of p (respectively, s) outside the interval, B simply rejects (respectively, accepts) the project outright, and for higher values B accepts (respectively, rejects) without investigation.

LEGISLATION

Politicized Allocation

I begin the analysis of legislative bargaining with the case of politicized allocation. Under this institutional mechanism, the standard s is irrelevant and legislators are able to appropriate projects directly to districts, so that xi = bi for all i. As is standard for this type of game, the recognized proposer in any period t must offer enough to make (n − 1)/2 legislators indifferent between the proposal and their continuation payoffs. By symmetry, coalition partners are randomly and fairly chosen and must be given the same amount.

The SSPE of the bargaining game is derived in a straightforward manner. At period T, the default allocation gives zero to each legislator, and so the proposer can give zero to (n − 1)/2 legislators and just enough to the remainder to cover their tax costs. Before period T, the proposer must give coalition partners a net payoff equal to their expected value of continuing the game to the next round. The amount received by partners is higher than in period T because it reflects the possibility that partners may become future proposers. This proposal is passed with the support of all coalition partners. The following remark summarizes the equilibrium proposal and players’ expected utilities. The proofs of this and other results are located in the Appendix.

Remark 1 Politicized Allocation. A legislator i recognized at t = 1 proposes $b_{1,i} = \frac{1}{2 k}$for herself, $b_{1,j} = \frac{1}{k (n + 1)}$for (n − 1)/2 randomly selected coalition partners, and b 1,j = 0 for all other legislators. L approves the budget. Each legislator's expected utility is $\nu^P = \frac{1}{k (n + 1)^2}$.

As is standard in Baron-Ferejohn style games, the proposing legislator's ex post share is quite high. Furthermore, aggregate spending is almost double that which would maximize the legislators’ collective welfare, or $\frac{1}{2k}$. However, legislation is not socially inefficient: Aggregate benefits exceed aggregate costs, although of course noncoalition partners receive negative payoffs ex post.

Two other features of this equilibrium are worth noting. First, it can be demonstrated that the period t = 1 strategies would also obtain in a stationary equilibrium of a version of this game where T is infinite. Second, although the bureaucratic project standard s plays no role under politicization, the assumption that the legislature can earmark funds directly for districts is equivalent to letting B apply a minimal standard $s < \underline{{\mathcal S}}_l$ and allowing bargaining to proceed according to the politicized process. Such a standard ensures that each legislator receives exactly the allotted bi, while a higher standard (for example, $s \in {\mathcal P}_{\tau }$) might require a larger budget to buy a type τ legislator's vote. From a proposer's perspective, a minimal standard would be optimal under politicization because of the concavity of the legislators’ utility functions.

Professionalized Allocation

Now consider the bargaining environment in which the bureaucrat's professional expertise is invoked by the legislation. Legislators cannot discriminate between projects that the bureaucrat considers acceptable, so budgets are simply the (uniform) size of each funded project and must respect the fixed “national” standard s.

It is useful to begin with a simplifying observation about bureaucratic standards. Because the bureaucrat faces two types of districts and has three actions (investigate, approve without investigation, and reject without investigation), she must treat many possible standards identically. In particular, there can be only one of five strategies for any given s. First, for any $s > \overline{{\mathcal S}}_h$, B's standard is very high and all projects are rejected without investigation. Second, for $s \in (\max \lbrace \overline{{\mathcal S}}_l, \underline{{\mathcal S}}_h\rbrace , \overline{{\mathcal S}}_h]$, B rejects in type l districts and investigates in type h districts. Third, either $s \in (\overline{{\mathcal S}}_l, \underline{{\mathcal S}}_h]$ or $s \in (\underline{{\mathcal S}}_h, \overline{{\mathcal S}}_l]$. Under the former, B rejects in type l districts and accepts in type h districts, both without investigation, whereas under the latter, B investigates both district types. Fourth, for $s \in (\underline{{\mathcal S}}_l, \min \lbrace \overline{{\mathcal S}}_l, \underline{{\mathcal S}}_h\rbrace ]$, B investigates in type l districts and approves in type h districts without investigation. Fifth, for any $s \le \underline{{\mathcal S}}_l$, B has a very low standard and approves all projects without investigation. For simplicity, I therefore label s 1, . . ., s 5 as arbitrary standards in each of these five respective intervals. Each s∈[0, 1] is thus in an equivalence class with exactly one of s 1, . . ., s 5. Figure 1 illustrates the set of possible standards.

FIGURE 1. Bureaucratic Standards and Investigation Strategies

Notes: For each type τ, ${\mathcal P}_{\tau }$ is the set of standards for which an additional signal would be pivotal in B's approval decision. ${\mathcal S}_{\tau }$ is the set of standards for which B would be willing to pay the cost of an investigation. All standards within a region s j induce the same investigative behavior. At s = s 3, for example, B rejects type l projects and approves type h projects without investigation, because $\overline{{\mathcal S}}_l < \underline{{\mathcal S}}_h$.

Given a standard, it is straightforward to derive legislators’ ideal budgets. Some additional notation is helpful for this purpose. Let ρτ,s denote the probability that B approves a project given standard s and district type τ, as determined in the previous section. Also let ντ denote the random variable for the number of approved projects in type τ districts. Thus νl+νh, the number of approvals of both types, is distributed according to a bivariate binomial distribution. Denote by Δ the expected squared number of project successes induced by this distribution:

\begin{eqnarray*} \Delta &\equiv& n_l \rho _{l,s} (1 - \rho _{l,s}) + n_h \rho _{h,s} (1 - \rho _{h,s})\\ && +\, (n_h \rho _{h,s} + n_l \rho _{l,s})^2. \end{eqnarray*}

A type τ legislator's expected payoff for a budget b can then be written as

$$ \rho _{\tau ,s} b - \frac{k b^2}{n} E[ (\nu _l + \nu _h)^2 ] = \rho _{\tau ,s} b - \frac{k b^2}{n} \Delta. $$

Straightforward maximization of this objective gives the following expressions for the optimal project budget and the expected utility it yields for a type τ proposer:

(3)
\begin{equation} \hat{b}_{\tau ,s} = \frac{n \rho _{\tau ,s}}{2 k \Delta }. \end{equation}
(4)
\begin{equation} E[ u_{\tau ,s}(\hat{b}_{\tau ,s}) ] =\frac{n \rho _{\tau ,s}^2}{4 k \Delta }. \end{equation}

The optimal budget is zero for type h proposers at s = s 1, and for type l proposers at s = s 1, s 2, and s 3 when $\underline{{\mathcal S}}_h > \overline{{\mathcal S}}_l$. At these standards, the proposer type in question is excluded from enjoying project benefits. For example, type l legislators receive a negative payoff if a positive budget is passed when s = s 2. For both types, lower standards induce positive optimal budgets. Neither the optimal budget nor the proposer's expected utility from it is monotonic in s, because lower standards also increase the overall cost of the legislation.

In standard fashion, the bargaining equilibrium is derived by considering final-period offers and then using backwards induction, ultimately deriving the proposals that each type of legislator will offer in the first period. To preview the outcomes of this game, consider two simple cases where legislators agree on the optimal budget. This occurs when s is such that the bureaucrat treats both district types identically. If s = s 1, then all projects are rejected without investigation ($\rho _{\tau , s_1} = 0$). The payoff to all districts is zero, as is the budget. Thus the only meaningful proposal is $\hat{b}_{\tau , s_1} = 0$, and all districts receive zero, which is worse than the politicization payoff of $\frac{1}{(n+1)^2k}$. Likewise, if s = s 5, then all projects are approved without investigation ($\rho _{\tau , s_5} = 1$). Applying (3) yields $\hat{b}_{\tau , s_5} = \frac{1}{2kn}$ for both proposer types. This results in an expected payoff of $\frac{1}{4kn}$ for each legislator, which is better than that under politicization. In fact, professionalization under this standard maximizes the legislators’ collective and individual welfare. Relative project quality remains important for the three intermediate standards as well, even though they induce B to treat different types differently.

As the subsequent subsections describe, there are two types of equilibria, depending on whether a majority of districts are of type h or l. For convenience, I adopt the following notation. Let $v_{\tau }^* = E[ u_{\tau ,s}(\hat{b}_{\tau ,s}) ]$ denote type τ's period T expected payoff, conditional on recognition (this is, in many cases, simply the payoff generated by type τ's ideal budget), and let $\tilde{v}_{\tau }^* = E[ u_{\tau ,s}(\hat{b}_{-\tau ,s}) ]$ be her period T payoff conditional on recognition of the other type. Additionally, let b τ,t denote the proposal bt offered by a type τ legislator. Finally, denote the continuation value for type τ at period t by v τ,t.

High-quality Majority

In the first case, most districts have high-quality projects, so that nh > (n − 1)/2. The intuition for the equilibrium can be seen by considering when legislators can successfully propose their ideal budgets, starting with period T. Because type h legislators are a majority, their optimal budgets will automatically win a majority. Type l legislators’ optimal budgets will win unanimous support, because type h legislators benefit at least as much as type l legislators in expectation from any given budget. Thus both types propose their ideal budgets at period T ($b_{\tau , T} = \hat{b}_{\tau ,s}$), yielding payoffs $v_{\tau }^* = \frac{n \rho _{\tau ,s}^2}{4 k \Delta }$ and $\tilde{v}_{\tau }^* = \frac{n \rho _{-\tau ,s} (2 \rho _{\tau ,s} - \rho _{-\tau ,s})}{4 k \Delta }$. The two types’ continuation values at period T are then

(5)
\begin{equation} v_{h, T} = \frac{n_h}{n} v_h^* + \frac{n_l}{n} \tilde{v}_{h}^* = \frac{n \rho _{h,s}^2 - n_l (\rho _{h,s} - \rho _{l,s})^2}{4 k \Delta }. \end{equation}
(6)
\begin{equation} v_{l, T} = \frac{n_h}{n} \tilde{v}_l^* + \frac{n_l}{n} v_{l}^* = \frac{n \rho _{l,s}^2 - n_h (\rho _{h,s} - \rho _{l,s})^2}{4 k \Delta }. \end{equation}

At period T − 1, a type h proposer can clearly offer other type h legislators more than v h,T by again proposing her ideal budget. All type h legislators would vote for the proposal, which would then pass. However, a type l proposer cannot propose $\hat{b}_{l,s}$, because this provides less utility than needed to gain type h legislators’ votes. A type l proposer must increase b T − 1 above $\hat{b}_{l,s}$ so that type h legislators can receive their reservation value of v h,T.

More generally, at all periods before T, type h proposers can continue to propose $b_{h,t} = \hat{b}_{h,s}$. This budget will obviously attract majority support. A type l proposer must offer a budget that makes type h indifferent between it and continuing to the next period, when a type h member might be recognized. In particular, for all r ≥ 1, type h must receive the following expected payoff under the proposed budget:

(7)
\begin{equation} v_{h,T-r} = \frac{n_h}{n} v_h^* + \frac{n_l}{n} v_{h,T-r+1}. \end{equation}

Expression (7) defines an iterative relationship for type h's continuation value. It also provides an intuition for type l proposers’ strategies. To satisfy the type h majority's demands, the type l proposal in any given period must lie between the ideal budgets $\hat{b}_{l,s}$ and $\hat{b}_{h,s}$. Unlike the politicized process, the time horizon now matters. Because a longer time horizon increases the type h legislators’ chances of eventual recognition, the type l budget proposal will approach the type h ideal as T increases. Thus, a minority will tend to benefit from bargaining environments where proposal rights are highly constrained.

The next remark uses this relation to characterize the relevant features of the unique equilibrium under a high-quality majority.

Remark 2 High-Type Majority. If nh > (n − 1)/2, then in period 1 type l legislators offer $b_{l,1} = \frac{n \rho _{h,s} - n \left( n_l/n \right)^{(T-1)/2} (\rho _{h,s} - \rho _{l,s})}{2 k \Delta }$, type h legislators offer $b_{h,1} = \frac{n \rho _{h,s}}{2 k \Delta }$, and L approves the budget. Expected utilities are

\begin{eqnarray*} v_{l, 1} &=& \frac{n \rho _{l,s}^2 - [n_h + n_l (1 - (n_l/n)^{\frac{T-1}{2}})^2 ] (\rho _{h,s}- \rho _{l,s})^2}{4 k \Delta }. \\ v_{h, 1} &=& \frac{n \rho _{h,s}^2 - n (n_l/n)^T (\rho _{h,s}- \rho _{l,s})^2}{4 k \Delta }. \end{eqnarray*}

It is clear from this discussion that, by controlling the bargaining process, the high types will typically do quite well, with v h,1→v*h as T → ∞. With probability greater than one-half, they receive their ideal policy outcome, and at the very worst the outcome is simply the low type's ideal budget, from which they receive higher utility than the low types themselves. However, the expected payoff may not induce h legislators to prefer professionalization to politicization. Low types may do poorly in this environment. Remark 2 also makes it evident that v l,1<0 when ρl,s is sufficiently low. Thus professionalization may result in worse outcomes for the low type than either politicization or the status quo.

Low-quality Majority

In the second case, nh ≤ (n − 1)/2. Although this case is similar to that of the high-quality majority, one difference lies in the asymmetry between proposals by high- and low-quality types. Whereas at period T type h legislators would accept the type l ideal budget of $\hat{b}_{l,s}$ because of their higher valuation of project budgets, type l legislators might not accept the type h ideal budget of $\hat{b}_{h,s}$. As intuition might suggest, this occurs because type l legislators are taxed for the high budgets but expect little benefit when their projects are of much lower expected quality. Obviously, this distinction becomes relevant when type l legislators are able to reject the proposed budget.

In particular, when ρl,s<ρh,s/2, a recognized type h legislator must propose a lower period T budget of $\frac{n \rho _{l,s}}{k \Delta }$ to satisfy type l's reservation value of $\tilde{v}_{l}^* = 0$ and hence secure passage. This change also affects the budgets that type h legislators can propose in earlier periods. For all ρl,s, however, there is again a unique budget proposal between $\hat{b}_{l,s}$ and $\hat{b}_{h,s}$ at each period. By contrast, type l legislators can continue to propose $\hat{b}_{l,s}$ and win majority support in all periods. Thus, both legislator types have unique proposal strategies that ensure passage in period 1.

In all other respects, the equilibrium derivation closely resembles that of the high-quality majority case. The next remark summarizes the main features of the equilibrium.

Remark 3 Low-Type Majority. If nh ≤ (n − 1)/2, then in period 1 type l legislators offer $b_{l,1} = \frac{n \rho _{l,s}}{2 k \Delta }$, type h legislators offer $b_{h,1} = \frac{n \rho _{l,s} + n \left( n_h/n \right)^{(T-1)/2} (\rho _{h,s} - \rho _{l,s})}{2 k \Delta }$if $\rho _{l,s} \ge \frac{\rho _{h,s}}{2}$and $b_{h,1} = \frac{n (1 + \left( n_h/n \right)^{(T-1)/2}) \rho _{l,s}}{2 k \Delta }$if $\rho _{l,s} < \frac{\rho _{h,s}}{2}$, and L approves the budget. Expected utilities are

(8)
\begin{eqnarray} v_{l, 1} &=& \left\lbrace \arraycolsep4pt\begin{array}{ll} \displaystyle\frac{n \rho _{l,s}^2 - n (n_h/n)^T (\rho _{h,s} - \rho _{l,s})^2}{4 k \Delta } & \mathrm{if } \, \rho _{l,s} \ge \displaystyle\frac{\rho _{h,s}}{2}. \\[10pt] \displaystyle\frac{n ( 1 - (n_h/n)^T ) \rho _{l,s}^2}{4 k \Delta } & \mathrm{if } \, \rho _{l,s} < \displaystyle\frac{\rho _{h,s}}{2}. \end{array} \right. \nonumber\\ \end{eqnarray}
(9)
\[ v_{h, 1} = \] {\fontsize{8.5}{10}\selectfont{\begin{eqnarray} %&&v_{h, 1} =\nonumber\\ \left\lbrace{\!\!} \arraycolsep4pt\begin{array}{l} \displaystyle\frac{n \rho _{h,s}^2 - [ n_l + n_h (1 - (n_h/n)^{\frac{T-1}{2}})^2] (\rho _{h,s} - \rho _{l,s})^2}{4 k \Delta } \\ \quad \mathrm{if } \, \rho _{l,s} \ge \displaystyle\frac{\rho _{h,s}}{2}.\\[8pt] \displaystyle\frac{[2n \rho _{h,s} - n_l \rho _{l,s} + 2 n_h \rho _{h,s} (n_h/n)^{\frac{T-1}{2}} - n_h \rho _{l,s} (1 + (n_h/n)^{\frac{T-1}{2}})^2 ] \rho _{l,s}}{4 k \Delta } \\ \quad \mathrm{if } \, \rho _{l,s} < \displaystyle\frac{\rho _{h,s}}{2} .\\ \end{array} \right. \nonumber\\[-28pt] \nonumber \end{eqnarray}}}

As before, the majority type does well under the expert allocation, although because of their higher acceptance probabilities the type h minority does even better. In contrast to the high-quality majority case, type l legislators can now ensure that they receive strictly positive payoffs. Again, however, this payoff may not induce l legislators to prefer professionalization to politicization.

It is worth observing finally that, under either type of legislative majority, equilibrium proposals and expected payoffs converge to the majority's ideal as T increases. For majority members, limT → ∞v τ,1→v*τ, and for minority members, $\lim _{T \rightarrow \infty } b_{\tau ,T-r} = \hat{b}_{-\tau ,s}$ and $\lim _{T \rightarrow \infty } v_{\tau ,1} \rightarrow \tilde{v}_{\tau }^*$. In fact, Remarks 2 and 3 extend straightforwardly to the case where the number of potential bargaining rounds is infinite (T = ∞), as is normally assumed in the bargaining literature. In this environment, members of a majority of type τ could obviously ensure the passage of their ideal budget $\hat{b}_{\tau ,s}$ by proposing it whenever they are recognized. Further, without discounting, majority members would be willing to block any proposal that is not $\hat{b}_{\tau ,s}$. Thus the only outcome in a stationary SSPE of this game is for the approved budget to reflect the majority's ideal. The next remark summarizes the relevant properties of this game. Note that that expected payoffs could be obtained by substituting T = ∞ into Remarks 2 and 3.

Remark 4 Bargaining with an Infinite Horizon. For T = ∞, there exists a stationary SSPE such that in period 1: (i) if nh > (n − 1)/2, then all legislators offer $b_{\tau ,1} = \frac{n \rho _{h,s}}{2 k \Delta }$and receive expected utilities $v_{h, 1} = \frac{n \rho _{h,s}^2}{4 k \Delta }$and $v_{l, 1} = \frac{n \rho _{h,s} (2 \rho _{l,s} - \rho _{h,s})}{4 k \Delta }$; (ii) if nh ≤ (n − 1)/2, then all legislators offer $b_{\tau ,1} = \frac{n \rho _{l,s}}{2 k \Delta }$and receive expected utilities $v_{l, 1} = \frac{n \rho _{l,s}^2}{4 k \Delta }$and $v_{h, 1} = \frac{n \rho _{l,s} (2 \rho _{h,s} - \rho _{l,s})}{4 k \Delta }$.

Main Results

The first result provides conditions for the central institutional choice of politicization versus professionalization. Broadly speaking, professionalization allows legislators to avoid the uncertainty induced by coalition-building. A nonpolitical bureaucracy treats similar districts similarly, thus neutralizing the inefficiently large proposer advantage that occurs under politicization. A majority will therefore professionalize if its members’ probabilities of project approval are high, and it will politicize if those probabilities are low.Footnote 9

An example of politicization under a low-quality majority is easily seen by substituting ρl,s = 0 (satisfied at s = s 1, s 2, and possibly s 3) into (8): Legislators whose projects stand no chance of approval before an expert evaluation would prefer to allocate through legislative bargaining. An example of professionalization under a high-quality majority can be derived by comparing the payoffs expected by type h legislators under both procedures. Using Remarks 1 and 2, expert allocation is preferred if

(10)
\begin{equation} \frac{n \rho _{h,s}^2 - n (n_l/n)^T (\rho _{h,s}- \rho _{l,s})^2}{4 k \Delta } \ge \frac{1}{k (n + 1)^2}. \end{equation}

For ρh,s = 1 and ρl,s = 0 (occurring at s = s 3, when the investigation regions do not overlap), this condition is easily shown after some manipulation to hold for any n ≥ 8 or T sufficiently large.

Proposition 1 Project Quality and Institutional Choice. (i) L chooses politicized allocation if

$$ \left\lbrace \arraycolsep4pt\begin{array}{ll}\rho _{h,s} < \displaystyle\frac{4 n_h}{n (n+1)^2 - 4 n_h (n_h - 1)} & \mathrm{if } \, n_h > (n - 1)/2 .\\[18pt] \rho _{l,s} < \displaystyle\frac{4}{n^2 - 2 n + 5} & \mathrm{if } \, n_l > (n - 1)/2 . \end{array} \right. $$

(ii) L chooses professionalized allocation if

{\fontsize{8}{10}\selectfont{$$ \left\lbrace \arraycolsep4pt\begin{array}{l}\rho _{h,s} > \displaystyle\frac{4n}{(n+1)^2 n_h + 4 n - 4 n^2} \\[10pt] \quad \mathrm{if } \, n_h > (n - 1)/2. \\[6pt] \rho _{l,s} > \displaystyle\frac{2 \left[ 1 + 2 n_h + \sqrt{(1 + 2 n_h)^2 + n_h^2(n^2 + 2 (n_h - n_l) + 5)/n_l} \right]}{n^2 + 2 (n_h - n_l) + 5} \\[10pt] \quad \mathrm{if } \, n_l > (n - 1)/2 .\\ \end{array} \right. $$}}

(iii) For types τ ∈ {h, l}, there exist ρ*τ,s∈[0, 1] such that a typeτ majority politicizes if ρτ,s<ρ*τ,sand professionalizes if ρτ,s > ρ*τ,s.   ■

Parts (i) and (ii) of Proposition 1 provide some easily checked sufficient (interior) conditions for each choice. Observe in particular that for high-type majorities, the quadratic denominator in part (ii) implies that professionalization is “easy” when the legislature is large. Note also that these conditions do not take into account the constraint that ρl,s ≤ ρh,s. Thus a sufficiently low value of ρh,s would imply that no feasible ρl,s could be high enough to induce a type l majority to professionalize. Likewise, a high ρl,s may imply that ρh,s cannot be low enough for a type h majority to politicize.

Part (iii) of Proposition 1 complements these conditions by establishing that the comparative statics on the majority's success probability are well behaved: For any ρτ,s for which L politicizes (respectively, professionalizes), then it must politicize for lower (respectively, professionalize for higher) values of ρτ,s. Thus, despite the fact that v l,1 and v h,1 are non-monotonic, L's institutional choice obeys a sensible “cutpoint” rule.Footnote 10

The second result establishes the main effect of district composition on politicization. This effect works in opposite directions for the two different district types. For type h majorities, the tendency to politicize will increase with the size of the majority. This occurs because a larger number of high types induces greater spending for the proposer, and hence greater taxation. This in turn increases the relative appeal of politicizing the process. The result may not hold for low values of T because higher values of nh also reduce the probability that a type l legislator can make a proposal. This proposal power effect for type l legislators goes to zero as T increases. For type l majorities, the result is simpler: Larger majorities lead to more professionalization, because they reduce the expected number of successful projects to be funded. Thus, the proposal power effect and the expected cost effect work in the same direction, for all T.

Propositions 1 and 2 are both illustrated in Figure 2.

FIGURE 2. Professionalization, Project Quality, and Legislative Composition

Notes: Let n = 5 and T = 20. Horizontal and vertical axes are the probabilities of acceptance in high- and low-type districts (ρh,s and ρl,s, where ρh,s > ρl,s), respectively. Shaded areas indicate where L prefers professionalization, given the indicated majority size. In the left illustration, there is a type h majority. Professionalization becomes preferred as ρh,s increases and as the majority size decreases. In the right illustration, there is a type l majority. Professionalization becomes preferred as ρl,s increases and as the majority size increases.

Proposition 2 Majority Size and Politicization. Holding n constant, when ρh,s > ρl,s > 0,

(i) If nh > (n − 1)/2, then v h,1is decreasing in nh for T sufficiently large.

(ii) If nl > (n − 1)/2, then v l,1is increasing in nl.   ■

Although Proposition 2 establishes that the relative payoff from professionalization is piecewise decreasing in nh, it does not imply that type h majorities are always more inclined to politicize than type l majorities. Because the payoff from professionalization also depends on ρτ,s, higher quality districts will expect higher payoffs when the expected total budget costs are similar. As a result, type h legislators expect higher payoffs under a bare majority than type l legislators would. The next remark follows from straightforward manipulation of v h,1 and v l,1 and is stated without proof.

Remark 5 Small Majorities and Professionalization. v h,1is higher under a type h majority of size nh = (n + 1)/2 than v l,1under a type l majority of size nl = (n + 1)/2.

These results can be usefully mapped to a relation with partisan politics, if party representation is correlated with project quality and parties are able to vote cohesively. After gaining a close majority, a party that represented predominantly high-quality projects would tend to professionalize, whereas a party that represented predominantly low-quality projects would tend to politicize. Moreover, politicization becomes more likely as the high-quality party's majority increases or as the low-quality party's majority decreases.

The third result is that politicized programs typically distribute more, and hence are more costly than their professionalized counterparts. Interestingly, this is true not only in equilibrium but also across the entire range of parameter values. In other words, professionalization reduces expected spending, whether it is chosen by the legislature or imposed from outside.

Proposition 3 Project Size. For any ρl,s and ρh,s, if (i) nh > (n − 1)/2, or (ii) nl > (n − 1)/2 and either a type l legislator is recognized at t = 1 or T is sufficiently large, then the total allocation under politicization is strictly higher than the expected allocation under professionalization.   ■

The intuition for Proposition 3 is that under politicization, the proposer gives herself an inefficiently large allocation while spreading costs over the rest of the legislature. Professionalization curbs this tendency by forcing a more uniform distribution of public goods, which internalizes the costs of higher project budgets. Interestingly, the exception occurs when type h legislators are a minority and have proposal power, as this produces relatively inefficient allocations similar to those under politicization. In the same vein, alternative bargaining models that do not feature large proposer allocations (such as an open-rule variant of the Baron-Ferejohn game) would probably reduce the overall size of politicized programs.

It is finally worth exploring the robustness of these results with respect to assumptions about the legislators’ utility functions. In particular, project costs in the model are not additively separable, thus calling into question the interpretation of the bureaucrat's activities as district-by-district cost-benefit analyses. Changing the overall cost of legislation to the sum of squared project allocations (i.e., from k(∑nj = 1xj)2 to k(∑nj = 1x 2j)) results in the loss of straightforward closed-form solutions in the politicization game. However, it can be shown numerically that the payoff to politicization typically increases more than the payoff to professionalization, but not enough to make politicization unambiguously preferred. The intuition is fairly straightforward: Because costs are convex, district-by-district aggregation reduces the relative inefficiency of the proposer's large share in the politicization game. Importantly, results such as Proposition 2 and Remark 5 continue to hold, with slight modifications. Thus, convex nonseparable costs and a bargaining process that awarded large ex post proposer benefits both appear to drive the relative inefficiency of politicization.Footnote 11

EXTENSIONS

Executive Procedures

In a separation of powers system, executives such as governors or presidents can exercise considerable authority over bureaucratic discretion. Derthick (Reference Derthick1990), for example, describes the Reagan administration's attempt to reduce the rolls of the Social Security Administration's (SSA) Disability Insurance (DI) program. In the absence of legislation to tighten eligibility for DI, the White House ordered the SSA to perform annual reevaluations of every recipient. Given the SSA had previously reviewed only 4% of cases, this move reduced the number of people who could remain as enrollees, fraudulently or otherwise.

A clear implication of the legislative bargaining game is that the probability that the agency accepts candidate projects will affect both the scale of legislation and the institutional mechanism used to deliver it. By ordering the bureaucrat to pursue (or halt) an investigation, the executive can either raise or lower the acceptance probability relative to what the bureaucrat would have achieved on her own. Here I combine these ideas to derive several implications of executive intervention. This intervention is modeled simply by giving an executive player E control over whether B investigates projects. Investigations continue to impose cost c on B but are costless to E, and E does not investigate when she is indifferent. Thus, E has a narrow “management” role and cannot intervene in B's choice to accept or reject a project.Footnote 12

I examine two variants of executive power, corresponding to objectives that are “bureaucratic” and “legislative” in nature. In the first, E's objective, like B's, is based on quality. E's utility function is identical to B's, with the exception that she wishes to implement a standard sE. Observe that B's standard s still matters: In a type τ district, if $s \not\in {\mathcal P}_{\tau }$, then E cannot gain from her authority, because an investigation would not affect B's approval decision. Attention may therefore be restricted to “intermediate” bureaucratic standards, or $s \in {\mathcal P}_{\tau }$, where failed investigations result in rejection and successful investigations in acceptance.

There are three cases, depending on the location of sE. First, if $s^E \in {\mathcal P}_{\tau }$, then E would want the same investigated projects to be accepted as B. Because she does not bear the cost of investigations, it is straightforward to see that E would always order an investigation. When c > 0, this means that B may be compelled to investigate when she would not have done so if choosing on her own.

Second, if $s^E > \overline{\mathcal P}_{\tau }$, then E would want the project rejected regardless of any investigative outcome. There are two subcases. If $s < p_{\tau } \overline{\theta }+ (1 - p_{\tau }) \underline{\theta }$, then B is favorably predisposed toward the project and would accept in the absence of further information. E therefore orders an investigation because doing so will induce a rejection probability of p τ(1 − q) + (1 − p τ)q. Note that when B's standard is very low ($s < \underline{{\mathcal S}}_{\tau }$), she would not have investigated on her own, whereas if $s > \underline{{\mathcal S}}_h$, the two players would have agreed on investigating. By contrast, if $s \ge p_{\tau } \overline{\theta }+ (1 - p_{\tau }) \underline{\theta }$, then B is predisposed toward rejection, which E can secure with certainty by ordering no investigation. Now if B's standard is very high ($s > \overline{{\mathcal S}}_{\tau }$) both players would want no investigation, whereas if $s < \overline{{\mathcal S}}_{\tau }$, E essentially cancels B's investigation. Thus, relative to the case where B had exclusive investigative authority, E overrides B's favored choices in some instances, and makes the same choice in others. The overall effect is to shift the quality of the set of investigated projects upward.

Finally, if $s^E < \underline{{\mathcal P}}_{\tau }$, then E wants the project approved regardless of the investigative outcome. This case is symmetrical with the second case: When B would accept the project without further information then E orders no investigation, and if B would reject without further information then E orders an investigation. The following remark summarizes the conditions under which the executive orders investigations.

Remark 6 Executive Intervention in Agency Decision Making. E orders an investigation in a type τ district if and only if

$$ \left\lbrace \arraycolsep4pt\begin{array}{l}s, s^E \in {\mathcal P} .\\[6pt] s \in {\mathcal P}, s < p_{\tau } \overline{\theta }+ (1 - p_{\tau }) \underline{\theta }, s^E > \overline{\mathcal P}_{\tau } .\\[6pt] s \in {\mathcal P}, s > p_{\tau } \overline{\theta }+ (1 - p_{\tau }) \underline{\theta }, s^E < \underline{{\mathcal P}}_{\tau } . \end{array} \right. $$

The remark implies that an executive with a sufficiently high standard could generate lower acceptance probabilities than a bureaucrat would. Proposition 1 then suggests that such an executive would reduce the relative payoff of professionalization, and thereby encourage politicization. The next result formalizes this intuition. Let I*E denote the institutional choice under executive intervention. Then under some basic conditions executive intervention can induce a change in institutional choice (I*E ≠ I*) in only one direction. If E's standard is high, then only a shift from professionalization to politicization is possible. The reduction in B's acceptance probabilities will tend to reduce the payoffs to professionalization (even as they reduce its overall cost). Likewise, if E's standard is low, then the higher probability of acceptance makes the reverse shift possible.

Proposition 4 Executive Standards and Politicization. For a majority of type τ ∈ {l, h}, if $s \not\in {\mathcal P}_{-\tau }$then

(i) If $s^E > \overline{\mathcal P}_{\tau }$, then I*E ≠ I* only if I* = B.

(ii) If $s^E < \underline{{\mathcal P}}_{\tau }$, then I*E ≠ I* only if I* = L.   ■

Three features of Proposition 4 are worth noting. First, although the result is stated in terms of necessary conditions, it is easy to find examples where the executive would affect institutional choice.Footnote 13 Second, the condition that $s \not\in {\mathcal P}_{-\tau }$ is sufficient (but not necessary) to ensure that E's investigative choice does not affect the acceptance probability of the non-majority's districts. As Remarks 2 and 3 make clear, this probability can affect the payoffs to professionalization. It is straightforward to show, however, that this effect vanishes for sufficiently large T, and the proposition would then hold for all s. Finally, the effects of “intermediate” standards, in which $s^E \in {\mathcal P}_{\tau }$, are ambiguous. Here, E would always order an investigation, and so the effect would depend on the location of s.

The second executive objective is distributive in nature, as in the McCarty (Reference McCarty2000) bargaining model. Suppose that E uses its managerial authority to maximize the expected payoff of a subset M of the legislature. Let mh and ml denote the number of type h and l districts in M, respectively. To simplify the analysis, the executive's managerial authority is modeled as a commitment to an investigative strategy in each type of district. Investigations cannot discriminate by district. This choice is made after the legislature's choice to professionalize a program, but before a budget is passed. Thus E's policy might correspond to general federal policies over rule-making, such as Ronald Reagan's Executive Order 12866 and its successors that mandated cost-benefit analyses for federal rules.

The next result establishes restrictions on the ways in which the configuration of M can affect the decision to professionalize. Again, a key intuition is that E may be able to increase or decrease a project's acceptance probability relative to what B would have done. For example, if s were such that B investigated projects in type h districts but would accept in the absence of further information, then E could raise the professionalization payoff in those districts by ordering no investigations. This would encourage a type h majority to professionalize. Of course, depending on the location of s, E may be unable to affect B's acceptance probability, and so executive intervention alone is not sufficient to change each district's expected payoff.

Proposition 5 Executive Constituencies and Professionalization. For a majority of type τ ∈ {l, h} and T sufficiently large, there exists a finite $\overline{m}_{\tau }$such that if $m_{\tau }/m_{-\tau } > \overline{m}_{\tau }$then I*E ≠ I* only if I* = L.   ■

The implication of this result is that a “distributive” executive will tend to encourage professionalization when the composition of her constituency coincides with the legislative majority. Specifically, the executive does this by helping to approve projects of the majority's type and helping to reject projects of the non-majority's type. When the conditions are not met, E may instead induce politicization by increasing taxes without providing a commensurate increase in the majority's acceptance probabilities.Footnote 14

Propositions 4 and 5 show that managerial control exerted by executives (or perhaps other external actors) can affect politicization in both directions. With some limitations, they yield clear empirical predictions. Propositions 4 might correspond to a policy area with a strong ideological component, such as welfare assistance. The executive's standard sE may serve as a proxy for an ideological preference, with a high standard indicating opposition and a low standard indicating support. An executive who opposes a legislative program will then have the effect of politicizing its implementation, whereas a supportive executive will encourage professionalization. Thus professionalization might be more likely under unified than divided government. Proposition 5 might correspond better to less ideologically charged issues, such as transportation or agriculture spending. Here the composition of the executive's party or faction and the distribution of district types determine the legislature's incentive to professionalize.

The Quality of Bureaucrats

A reasonable conjecture is that the quality of bureaucrats should affect whether agencies are politicized. Because the model links the probability of a project's acceptance to legislative payoffs from professionalization, it is possible to ask how the quality of bureaucratic analysis, embodied by q, matters. The next result shows that the effects of better qualified personnel or greater administrative capacity are not entirely straightforward.

Increasing q has two effects. Suppose that a majority of legislators is of quality type τ. First, it increases the probability of acceptance conditional on an investigation when p τ > 1/2, and reduces it otherwise (i.e., good projects are more likely to be approved). Second, it shifts the set of projects that will be inspected (${\mathcal S}_{\tau }$), as the range of projects B would accept or reject without investigation shrinks.

Combining the two effects, a higher probability of acceptance under an investigation and an upward shift in $\overline{\mathcal S}_{\tau }$ will increase type τ's acceptance probabilities. If in addition the change in q does not affect the non-majority type's probability of acceptance, the legislative majority will benefit under professionalization. Similarly, a lower probability of acceptance under an investigation and a downward shift in $\underline{\mathcal S}_{\tau }$ can reduce the majority's payoff from professionalization.

Proposition 6 formalizes this logic by establishing that the effect of q depends on project quality p τ. The result does not depend on which type has the legislative majority. High values of p τ can cause the payoff to professionalization to be increasing in q, and low values of p τ can cause the reverse, for sufficiently large T. Thus, as intuition might suggest, professionalization is better under high-quality bureaucrats when projects are likely to be approvable. Symmetrically, a perverse form of professionalization can occur with low-quality bureaucrats, who are more likely to approve low-quality projects. The relationship between professionalization and q also depends on s. For example, if s is either very high or very low, then a higher quality bureaucrat may increase or decrease acceptance probabilities, respectively, by scrutinizing projects that a lower quality bureaucrat would not have investigated.

Proposition 6 Bureaucrat Quality and Politicization. Suppose the majority is of type τ ∈ {l, h} and $s \not\in {\mathcal S}_{-\tau }$for all q . For T sufficiently large, the expected payoff for majority legislators under professionalization is

(i) weakly increasing in q if p τ > 1/2 and $s \ge \underline{{\mathcal S}}_{\tau }$.

(ii) weakly decreasing in q if p τ < 1/2 and $s \le \overline{{\mathcal S}}_{\tau }$.   ■

The parameter q may serve as an indicator for the quality of a civil service system or the level of training of a specific agency. The somewhat surprising implication of the result is that the outside option of politicization may cause high-quality bureaucrats not to exercise their professionalism. Rather, “slam dunk” projects will be professionalized when bureaucrats are of high quality, and questionable projects will be professionalized when bureaucrats are of low quality. In other, “intermediate” cases, a legislature might be more inclined to attempt politicized allocation. A further implication might then be that legislatures (or bureaucrats themselves) would be less willing to invest in administrative capacity in these intermediate cases.

The Choice of Standard

Thus far, it has been assumed that the bureaucrat's standard s is fixed. In one respect, the assumption is natural: The extensive formal and informal literatures on bureaucratic politics are based on the assumption that legislatures cannot easily dictate the preferences or actions of bureaucratic agents. Thus, a legislature might face significant agency losses if it attempted to impose standards in complex policy areas. For example, a bureaucrat may respond by nominally applying a low standard but channeling resources toward more desirable projects. One reason for fixed standards is that legislative programs may be constrained in the short run to exploit existing agencies and laws—accepting their capabilities, methods, and limitations. In the longer run a legislature could perhaps design an agency more to its liking, but this could be prove to be expensive. In presidential systems, the separation of powers also drives the agency problem. For example, through appointment powers or the Office of Management and Budget, presidents can bargain over or obstruct legislative instructions to the bureaucracy. As the extensions on executive intervention illustrate, an executive can to some degree manipulate the effective standard using only “management” techniques.

Another important source of limitations on the legislature's ability to dictate s is career concerns. Some bureaucrats may respond to professional incentives that cannot be easily dictated by politicians. This might especially be the case for peer-reviewed programs, where the career prospects of experts depend more on the evaluation of peers than on those of legislators. This autonomy is further enhanced by some common institutional features, such as civil service protections and agencies insulated from political pressure through complex appointment structures.

Nevertheless, legislators have incentives to change s, and it is therefore worth asking how they would do so. I adopt the simplest assumption for how the standard is chosen, which is to let a member of the majority type unilaterally specify s prior to game play. The resulting game represents a polar opposite view of the source of standards from the basic model, and it perhaps approximates the practice of setting geographically based allocation formulas. Procedures with similar effects could of course be built into the bargaining game in various ways.

In general, each legislator type does better by minimizing the success probability of the other legislator type, which reduces overall costs. Each type also prefers a standard at s 5 to s 1. Remarks 2 and 3 clearly show that the majority receives positive payoffs under s 5, and zero under s 1. Type l legislators are at a disadvantage because higher standards discriminate more against them than against type h legislators. An optimal standard for type l legislators is then s 5. By contrast, type h legislators benefit from somewhat higher standards. It is straightforward to show that a type h majority would do best under s 3 when $\overline{\mathcal S}_l < \underline{{\mathcal S}}_h$, as this maximizes benefits for type h and excludes type l. Otherwise, when $\overline{\mathcal S}_l > \underline{{\mathcal S}}_h$, s 3 is dominated by s 2 and a type h majority may also prefer s 4.

Regardless of which type holds the majority, the ability to choose a project standard for the agency will induce L to professionalize the program.

Remark 7 Professionalization under an Endogenous Standard. If the legislature can choose s, then I* = B.

This result follows directly from Proposition 1(ii), which implies that if ρτ,s = 1, then professionalization yields an expected payoff for the legislative majority exceeding that of politicization. Because there is always at least one standard ensuring ρτ,s = 1 for either type, both types can benefit from professionalization. Note finally that because type h legislators receive strictly higher benefits than type l legislators for a given s, type h legislators automatically prefer professionalization if type l legislators do so as well. Thus a roll call vote on professionalization should be unanimous under a type l majority. The same does not necessarily hold for a type h majority, which may prefer a standard that excludes some type l legislators.

DISCUSSION

Virtually all public money in advanced democracies is channeled through bureaucratic agencies. As a result, legislators face prominent but seemingly opposing incentives in a distributive politics setting. They may wish to control spending directly by earmarking funds for constituents. Or they may wish to involve bureaucratic experts in distributing public resources. There has been little theoretical work that reconciles these incentives.

The model developed here fuses bureaucratic decision making with distributive politics. Unlike the prevailing models of bureaucratic delegation, the model explicitly addresses questions that arise in a divide-the-dollar context. The key insight is that purely pork-oriented legislators may collectively choose to professionalize a program when it is likely to receive widespread bureaucratic endorsement. When a project is “good,” an apolitical bureaucrat can offer a higher probability of receiving funding than the normal legislative coalition-building process. In addition, bureaucratic allocation reduces the inefficiencies associated with proposer rents in legislative bargaining. Professionalization also becomes more appealing to legislators when high-quality districts are a relatively small majority, when an executive player supports the project or represents the same constituency as the legislative majority, and when the quality of bureaucrats and the quality of the majority's projects are either both high or both low.

Perhaps the most important empirical implication to be examined is the link between legislative representation, project quality and policy outcomes at the program level. In the U.S. context, program politicization can be measured through both direct earmarks and agency leadership. Expert decision making is likely to be facilitated by leadership structures that give more control to career civil servants and less to political appointees (e.g., Berry and Gersen Reference Berry and Gersen2010). As an example, U.S. state transportation departments vary considerably in their appointment structures, with some giving power to geographically based boards. The underlying quality of projects is sometimes measured directly by the agencies themselves (e.g., Hird Reference Hird1991) or can in some cases be proxied by variables such as population growth.

The extensions to the model also offer potential cross-national predictions. The results on executive intervention suggest an important role for executive autonomy from the legislature. Higher autonomy will lead to more politicization under divided government, and more professionalization under unified government. Autonomy may be crudely measured by whether a system is presidential, semi-presidential, or parliamentary, whereas professionalization might be captured by a measure of restraints on executive power (e.g., Besley and Persson Reference Besley and Persson2011). The extensions on bureaucrat quality and endogenous standards imply that the autonomy and quality of bureaucrats will also affect policy implementation. In political systems where bureaucrats have only minimal autonomy, the model would predict a perverse form of professionalization, whereby bureaucrats apply legislatively driven standards. Where bureaucrats do enjoy some autonomy, a higher quality civil service system (e.g., Rauch and Evans Reference Rauch and Evans2000) will induce professionalization when the expected quality of the majority's projects is high, and will instead induce politicization when that quality is low.

The model deliberately used the simplest possible assumptions to reach its conclusions, and several modifications can affect the balance between the two institutional forms. First, the inefficiency of politicization arises in part from the high ex post share earned by the proposer. This effect may be ameliorated by using supermajority voting thresholds or open amendment rules. Both would spread benefits more evenly and increase the efficiency of politicized allocation. Second, professionalization would become more desirable if legislators cared about maximizing project quality. This suggests a potentially important public interest role for voters or interest groups in shaping legislative preferences. Third, politicization might become more desirable to legislators who cared directly about credit claiming, because voters may hold them more accountable for earmarks than for agency decisions. Fourth, the model does not consider the possibility of local externalities. These could affect both the attractiveness of different districts as coalition partners and the appeal of using a bureaucrat to distinguish between good and bad projects.

Finally, one prediction that this model misses is that government programs often feature both politicization and professionalization. Examples include grant programs from the National Institutes of Heath and National Science Foundation, and Community Development Block Grants. The model does, however, suggest how such hybrid programs might arise. Suppose that a purely professionalized program could achieve the support of a significant minority of districts. A legislator who could propose hybrid programs might then offer to earmark sufficient funds to other legislators to complete a majority coalition. Similarly, supporters of politicization could buy the support of other legislators by setting aside some funds for bureaucratic allocation. Thus, partial politicization might be the norm in policy areas where projects are highly heterogeneous in quality across legislative districts.

APPENDIX

Proof of Remark 1. Consider an arbitrary period t. By symmetry, let vt denote a legislator's ex ante payoff at t. Clearly, a proposer i promises positive benefits to exactly (n − 1)/2 coalition partners, and symmetry implies that partners are chosen with equal probability and vote for a proposal if they receive allocation b t,j = v t + 1+kx 2/n, where x is the total benefit promised to all players. The proposer's objective is then

$$ x - \frac{n - 1}{2} \left( \nu_{t+1} + \frac{k x^2}{n} \right) - \frac{k x^2}{n}. $$

Performing the straightforward optimization yields $x = \frac{n}{k (n + 1)}$. This implies that $b_{t,j} = v_{t+1} + \frac{n}{k (n + 1)^2}$.

By symmetry, $x = \frac{n-1}{2} b_{t,j} + b_{t,i}$, and hence $b_{t,i} = \frac{n (n + 3)}{2 k (n + 1)^2} - \frac{n - 1}{2} v_{t+1}$. Ex post, the proposer receives $\frac{n (n + 3)}{2 k (n + 1)^2} - \frac{n - 1}{2} v_{t+1} - \frac{n}{k (n + 1)^2} = \frac{n}{2 k (n + 1)} - \frac{n - 1}{2} v_{t+1}$, coalition partners receive v t + 1, and nonpartners receive $-\frac{n}{k (n + 1)^2}$. Summing over recognition and coalition partner probabilities, each player's ex ante expected value is $v_t = \frac{1}{k (n + 1)^2}$ for all t.

At t = T, the default allocation gives 0, so the proposer pays $b_{T,j} = \frac{n}{k (n + 1)^2}$ to partners. For all periods t < T, substituting $v_t = \frac{1}{k (n + 1)^2}$ into the above budget expressions generates the proposal.   ■

Proof of Remark 2. As established in the text, the type h budget proposal in all periods is simply $\hat{b}_{h,s}$. To derive the type l budget, equation (7) simplifies to the following expression for type h's continuation value at period T − r:

(11)
\begin{equation} v_{h,T-r} = \left( 1 - \left( \frac{n_l}{n} \right)^{r+1} \right) v_h^* + \left( \frac{n_l}{n} \right)^{r+1} \tilde{v}_{h}^*. \end{equation}

Rewriting (11) by expanding v h,T − r and substituting from (3) and (4), the type l budget proposal that would induce type h legislators to vote in favor is characterized by

(12)
\begin{eqnarray} &&\rho _{h,s} b_{l,T-r} - \frac{k b_{l,T-r}^2}{n} \Delta \nonumber\\ &&\quad = \frac{\left( 1 - \left( \frac{n_l}{n} \right)^{r} \right) n \rho _{h,s}^2 + \left( \frac{n_l}{n} \right)^{r} n \rho _{l,s} (2 \rho _{h,s} - \rho _{l,s})}{4 k \Delta } \nonumber \\ b_{l,T-r} &=& \frac{\rho _{h,s} \pm \sqrt{\rho _{h,s}^2 - 4 (k \Delta /n) \frac{\left( 1 - \left( \frac{n_l}{n} \right)^{r} \right) n \rho _{h,s}^2 + \left( \frac{n_l}{n} \right)^{r} n \rho _{l,s} (2 \rho _{h,s} - \rho _{l,s})}{4 k \Delta }}}{2 k \Delta /n} \nonumber \\ &=& \frac{n \rho _{h,s} - n \left( n_l/n \right)^{\frac{r}{2}} (\rho _{h,s} - \rho _{l,s})}{2 k \Delta }. \end{eqnarray}

The lower root of the quadratic formula is the only plausible solution for b l,T − r. Thus (12) is the minimum budget that is acceptable to type h legislators. Straightforward manipulation reveals that $b_{l,T-r} < (n_l/n) b_{l,T-r+1} + (n_h/n) \hat{b}_{h,s}$ for all r, which implies that a type l proposer cannot do better by proposing a budget that type h would vote against.

Equation (12) thus gives a unique period 1 budget proposal b l,1 for type l legislators that will be approved. Each type τ's expected payoff is then given simply by substituting b l,1 and b h,1 into each type's expected payoff, given by $v_{\tau ,1} = \frac{n_{\tau }}{n} E[ u_{\tau ,s}(b_{\tau ,1}) ] + \frac{n_{-\tau }}{n} E[ u_{\tau ,s}(b_{-\tau ,1}) ]$.   ■

Proof of Remark 3. First consider period T proposals. A recognized type l legislator can propose her optimal budget $b_{l,T} = \hat{b}_{l,s}$, which would automatically receive a majority of votes because nl > nh. This yields utility $v_l^* = \frac{n \rho _{l,s}^2}{4 k \Delta }$ for type l. A type h proposer may propose $b_{h,T} = \hat{b}_{h,s}$ and win approval if for type l legislators $\rho _{l,s} \hat{b}_{h,s} - \frac{k \Delta }{n} \hat{b}_{h,s}^2 \ge 0$, or $\rho _{l,s} \ge \frac{\rho _{h,s}}{2}$. When this holds, the expressions for v h,T and v l,T remain as in (5) and (6), and $\tilde{v}_{l}^* = \frac{n \rho _{h,s} (2 \rho _{l,s} - \rho _{h,s})}{4 k \Delta }$.

When $\rho _{l,s} < \frac{\rho _{h,s}}{2}$, the optimal type h budget $\hat{b}_{h,s}^{\prime }$ is at a corner and must satisfy $\tilde{v}_{l}^* = 0$; this implies $\rho _{l,s} \hat{b}_{h,s}^{\prime } - \frac{k \Delta }{n} (\hat{b}_{h,s}^{\prime })^2 = 0$, or $b_{h,s}^{\prime } = \frac{n \rho _{l,s}}{k \Delta }$. Thus, the period T budget offer by type h is

$$ b_{h,T} = \min \left\lbrace \frac{n \rho _{h,s}}{2 k \Delta }, \frac{n \rho _{l,s}}{k \Delta } \right\rbrace. $$

At the corner solution the reduced budget offered by type h proposers yields the following:

\begin{eqnarray*} v_{h, T} &=& \frac{4 n_h \rho _{l,s} (\rho _{h,s} - \rho _{l,s}) + n_l \rho _{l,s} (2 \rho _{h,s} - \rho _{l,s})}{4 k \Delta } .\\ v_{l, T} &=& \frac{n_l \rho _{l,s}^2}{4 k \Delta }. \end{eqnarray*}

For all periods t < T, recognized type l legislators can still propose $\hat{b}_{l,s}$, which a majority would approve. Type h proposers must offer budgets giving type l legislators their continuation values in order to receive their vote. For all r ≥ 1, the continuation value can be written as

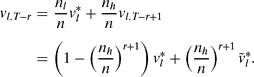
\begin{eqnarray*} v_{l,T-r} &=& \frac{n_l}{n} v_l^* + \frac{n_h}{n} v_{l,T-r+1} \\ &=& \left( 1 - \left( \frac{n_h}{n} \right)^{r+1} \right) v_l^* + \left( \frac{n_h}{n} \right)^{r+1} \tilde{v}_{l}^*. \end{eqnarray*}

The corresponding budget must then satisfy

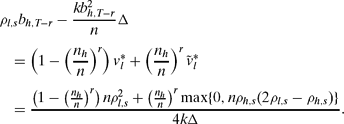
\begin{eqnarray*} &&\rho _{l,s} b_{h,T-r} - \frac{k b_{h,T-r}^2}{n} \Delta \\ &&\quad= \left( 1 - \left( \frac{n_h}{n} \right)^{r} \right) v_l^* + \left( \frac{n_h}{n} \right)^{r} \tilde{v}_{l}^* \\ &&\quad = \frac{\left( 1 - \left( \frac{n_h}{n} \right)^{r} \right) n \rho _{l,s}^2 + \left( \frac{n_h}{n} \right)^{r} \max \lbrace 0, n \rho _{h,s} (2 \rho _{l,s} - \rho _{h,s}) \rbrace }{4 k \Delta }. \end{eqnarray*}

Solving for the budget in both cases yields:

(13)
\begin{eqnarray} &&b_{h,T-r} \nonumber\\ &&= \frac{\rho _{l,s} \pm \sqrt{\rho _{l,s}^2 - 4 (k \Delta /n) \frac{\left( 1 - \left( \frac{n_h}{n} \right)^{r} \right) n \rho _{l,s}^2 + \left( \frac{n_h}{n} \right)^{r} \max \lbrace 0, n \rho _{h,s} (2 \rho _{l,s} - \rho _{h,s}) \rbrace }{4 k \Delta }}}{2 k \Delta /n} \nonumber \\ && = \left\lbrace \arraycolsep4pt\begin{array}{ll} \displaystyle\frac{n \rho _{l,s} + n \left( n_h/n \right)^{\frac{r}{2}} (\rho _{h,s} - \rho _{l,s})}{2 k \Delta } & \mathrm{if } \, \rho _{l,s} \ge \displaystyle\frac{\rho _{h,s}}{2}. \\[8pt] \displaystyle\frac{n (1 + \left( n_h/n \right)^{\frac{r}{2}}) \rho _{l,s}}{2 k \Delta } & \mathrm{if } \, \rho _{l,s} < \displaystyle\frac{\rho _{h,s}}{2} . \end{array} \right. \end{eqnarray}

For both the interior and corner cases, the upper roots of the quadratic formula are the only plausible solutions for b h,T − r. Thus (13) is the maximum budget acceptable to type l legislators. Straightforward manipulation reveals that $b_{h,T-r} > (n_l/n) \hat{b}_{l,s} + (n_h/n) b_{h,T-r+1}$ for all r, which implies that a type h proposer cannot do better by proposing a budget that type l would vote against.

Equation (13) thus gives a unique period 1 budget proposal b h,1 for type h legislators that will be approved. Note that $b_{h,1} < \hat{b}_{h,s}$. The period 1 value functions follow immediately by substituting b l,1 and b h,1 into each type's expected payoff, given by $v_{\tau ,1} = \frac{n_{\tau }}{n} E[ u_{\tau ,s}(b_{\tau ,1}) ] + \frac{n_{-\tau }}{n} E[ u_{\tau ,s}(b_{-\tau ,1}) ]$.   ■

Proof of Proposition 1. (i) When nh > (n − 1)/2, then by Remark 2 L politicizes if:

(14)
\begin{equation} \frac{n \rho _{h,s}^2 - n (n_l/n)^T (\rho _{h,s}- \rho _{l,s})^2}{4 k \Delta } < \frac{1}{(n+1)^2k}. \end{equation}

Clearly, the left-hand side of (14) is bounded from above at T = ∞, and thus it is sufficient to derive conditions under which $\frac{n \rho _{h,s}^2}{4 k \Delta } < \frac{1}{(n+1)^2k}$, or equivalently

(15)
\begin{eqnarray} &&4 [ n_l \rho _{l,s} (1 - \rho _{l,s}) + n_h \rho _{h,s} (1 - \rho _{h,s}) + (n_h \rho _{h,s} + n_l \rho _{l,s})^2 ]\nonumber\\ &&\quad -\, (n+1)^2 n \rho _{h,s}^2 > 0. \end{eqnarray}

Because Δ is increasing in ρl,s, letting ρl,s = 0 gives a lower bound on the left-hand side of (15), yielding 4[nhρh,s(1 − ρh,s) + n 2hρ2h,s]−(n + 1)2nρ2h,s > 0, or

\begin{eqnarray*} \rho _{h,s} < \frac{4 n_h}{n (n+1)^2 - 4 n_h (n_h - 1)}. \end{eqnarray*}

If nl > (n − 1)/2, then by Remark 3 L politicizes if

(16)
\begin{eqnarray} \left\lbrace \arraycolsep4pt\begin{array}{ll}\displaystyle\frac{n \rho _{l,s}^2 - n (n_h/n)^T (\rho _{h,s} - \rho _{l,s})^2}{4 k \Delta } < \displaystyle\frac{1}{(n+1)^2k} & \mathrm{if } \, \rho _{l,s} \ge \displaystyle\frac{\rho _{h,s}}{2}. \\[10pt] \displaystyle\frac{n ( 1 - (n_h/n)^T ) \rho _{l,s}^2}{4 k \Delta } < \displaystyle\frac{1}{(n+1)^2k} & \mathrm{if } \, \rho _{l,s} < \displaystyle\frac{\rho _{h,s}}{2} \end{array} \right. \nonumber\\ \end{eqnarray}

As in the previous case, the left-hand side expressions of (16) are bounded from above at T = ∞, and thus it suffices to derive conditions under which $\frac{n \rho _{l,s}^2}{4 k \Delta } < \frac{1}{(n+1)^2k}$, or equivalently

(17)
\begin{eqnarray} &&4 [ n_l \rho _{l,s} (1 - \rho _{l,s}) + n_h \rho _{h,s} (1 - \rho _{h,s}) + (n_h \rho _{h,s} + n_l \rho _{l,s})^2 ] \nonumber\\ &&\quad-\, (n+1)^2 n \rho _{l,s}^2 > 0. \end{eqnarray}

As Δ is increasing in ρh,s, letting ρh,s = ρl,s gives a lower bound on the left-hand side of (17). This reduces to 4[nρl,s(1 − ρl,s) + n 2ρ2l,s]−(n + 1)2nρ2l,s > 0, or

\begin{eqnarray*} \rho _{l,s} &<& \frac{4}{n^2 - 2 n + 5}. \end{eqnarray*}

(ii) When nh > (n − 1)/2, then by Remark 2 L professionalizes if

(18)
\begin{equation} \frac{n \rho _{h,s}^2 - n (n_l/n)^T (\rho _{h,s}- \rho _{l,s})^2}{4 k \Delta } > \frac{1}{(n+1)^2k}. \end{equation}

Clearly, the left-hand side of (18) is minimized at T = 1, and thus I derive conditions under which $\frac{n \rho _{h,s}^2 - n_l (\rho _{h,s} - \rho _{l,s})^2}{4 k \Delta } > \frac{1}{(n+1)^2k}$, or equivalently

(19)
\begin{eqnarray} &&(n+1)^2 [n \rho _{h,s}^2 - n_l (\rho _{h,s} - \rho _{l,s})^2] > 4 [ n_l \rho _{l,s} (1 - \rho _{l,s}) \nonumber\\ &&\quad+\, n_h \rho _{h,s} (1 - \rho _{h,s}) + (n_h \rho _{h,s} + n_l \rho _{l,s})^2 ]. \end{eqnarray}

To derive a condition on ρh,s, note that a lower bound for the left-hand side (respectively, upper bound for the right-hand side) of (19) is achieved by letting ρl,s = 0 (respectively, ρl,s = ρh,s), thus giving (n + 1)2nhρ2h,s > 4[nρh,s(1 − ρh,s) + n 2ρ2h,s], or

\begin{eqnarray*} \rho _{h,s} > \frac{4n}{(n+1)^2 n_h + 4 n - 4 n^2}. \end{eqnarray*}

If nl > (n − 1)/2, there are two cases. First, if $\rho _{l,s} \ge \frac{\rho _{h,s}}{2}$ (the interior case), then L professionalizes if

(20)
\begin{equation} \frac{n \rho _{l,s}^2 - n (n_h/n)^T (\rho _{h,s} - \rho _{l,s})^2}{4 k \Delta } > \frac{1}{(n+1)^2k}. \end{equation}

As before, the left-hand side of (20) is minimized at T = 1, and thus it suffices to derive conditions under which $\frac{n \rho _{l,s}^2 - n_h (\rho _{h,s} - \rho _{l,s})^2}{4 k \Delta } > \frac{1}{(n+1)^2k}$, or equivalently

(21)
\begin{eqnarray} &&(n+1)^2 [n \rho _{l,s}^2 - n_h (\rho _{h,s} - \rho _{l,s})^2] > 4 [ n_l \rho _{l,s} (1 - \rho _{l,s}) \nonumber\\ &&\quad+\, n_h \rho _{h,s} (1 - \rho _{h,s}) + (n_h \rho _{h,s} + n_l \rho _{l,s})^2 ]. \end{eqnarray}

To obtain an upper bound on the right-hand side of (21), let ρh,s = 1. To obtain a lower bound on the left-hand side of (21), note that ρh,s ≤ 2ρl,s for the interior case, so let ρh,s = 2ρl,s. These substitutions yield (n + 1)2nlρ2l,s−4[nlρl,s(1 − ρl,s) + (nh + nlρl,s)2]>0. Because this expression is convex in ρl,s, it is satisfied for

\begin{eqnarray*} \rho _{l,s} > \frac{2 \left[ 1 + 2 n_h + \sqrt{(1 + 2 n_h)^2 + n_h^2(n^2 + 2 (n_h - n_l) + 5)/n_l} \right]}{n^2 + 2 (n_h - n_l) + 5}. \end{eqnarray*}

Second, if nl > (n − 1)/2 and $\rho _{l,s} < \frac{\rho _{h,s}}{2}$ (the corner case), then L professionalizes if

(22)
\begin{equation} \frac{n ( 1 - (n_h/n)^T ) \rho _{l,s}^2}{4 k \Delta } > \frac{1}{(n+1)^2k} \end{equation}

Again, the left-hand side of (22) is minimized at T = 1, and thus it suffices derive conditions under which $\frac{n_l \rho _{l,s}^2}{4 k \Delta } > \frac{1}{(n+1)^2k}$, or (n + 1)2nlρ2l,s > 4[nlρl,s(1 − ρl,s) + nhρh,s(1 − ρh,s) + (nhρh,s+nlρl,s)2]. Letting ρh,s = 1 to obtain an upper bound on the right-hand side, this is the same condition as in the interior case, and the condition on ρl,s is therefore identical.

(iii) When nh > (n − 1)/2, L politicizes (respectively, professionalizes) if (14) (respectively, (18)) holds; simplifying yields

(23)
\begin{eqnarray} &&n (n + 1)^2 [\rho _{h,s}^2 - (n_l/n)^T (\rho _{h,s} - \rho _{l,s})^2] - 4 [ n_l \rho _{l,s} (1 - \rho _{l,s}) \nonumber\\ &&\quad+\, n_h \rho _{h,s} (1 - \rho _{h,s}) + (n_h \rho _{h,s} + n_l \rho _{l,s})^2 ] < (>)\, 0. \end{eqnarray}

I first show that (23) is convex. Because (23) is quadratic in ρh,s, it is convex if

$$ n (n+1)^2 (1 - (n_l/n)^T) + 4n_h - 4n_h^2 > 0. $$

This expression holds for all T if it holds at T = 1, which reduces the expression to (n + 1)2 > 4(nh − 1), which clearly holds for any n.

Now observe that at ρh,s = 0, expression (23) is nonpositive. The convexity of (23) then implies that it has a unique non-negative maximal root ρ′. If ρ′ ≤ ρl,s, then let ρ*h,s = ρl,s. If ρ′≥1, then let ρ*h,s = 1. Otherwise, let ρ*h,s = ρ′. Then by (23) a type h majority politicizes (professionalizes) if ρh,s<(>)ρ*h,s.

The calculation for ρ*l,s is almost identical and is therefore omitted.   ■

Proof of Proposition 2. (i) For nh > (n − 1)/2, I show that $\lim _{T \rightarrow \infty } \frac{d v_{h,1}}{d n_h} < 0$. I rewrite v h,1 by letting n − nh = nl and using Δ(nh) to express the dependence of Δ on nh. Applying the quotient rule and simplifying, $\frac{d v_{h,1}}{d n_h} < 0$ if and only if

(24)
\begin{eqnarray} &&\left[ T \left( \frac{n - n_h}{n} \right)^{T-1} (\rho _{h,s} - \rho _{l,s})^2 \right] \Delta (n_h) \nonumber\\ &&\quad-\, n \left[ \rho _{h,s}^2 - \left( \frac{n - n_h}{n} \right)^T (\rho _{h,s} - \rho _{l,s})^2 \right] \Delta ^{\prime }(n_h) < 0. \end{eqnarray}

Now observe that by L'Hopital's rule, $\lim _{T \rightarrow \infty } T ( \frac{n - n_h}{n} )^{T-1} = \lim _{T \rightarrow \infty } 1 / [ ( \frac{n}{n - n_h} )^{T-1} \ln \frac{n}{n - n_h} ] = 0$. Substituting, the limit of (24) as T → ∞ becomes:

$$ - n \rho _{h,s}^2 [ 1 - \rho _{h,s} - \rho _{l,s} + 2 (n_h \rho _{h,s} + (n - n_h) \rho _{l,s}) ] (\rho _{h,s} - \rho _{l,s}) < 0. $$

This clearly holds and is bounded away from zero for any ρh,s > ρl,s, establishing the result.

(ii) For nl > (n − 1)/2, I show that $\frac{d v_{l,1}}{d n_l} > 0$ in both the interior case (where ρh,s ≤ 2ρl,s) and the corner case (ρh,s > 2ρl,s). In the interior case, I rewrite v l,1 by letting n − nl = nh and using Δ(nl) to express the dependence of Δ on nl. Applying the quotient rule and simplifying, $\frac{d v_{l,1}}{d n_l} > 0$ if and only if

(25)
\begin{eqnarray} &&\left[ \frac{T (n-n_l)^{T-1}}{n^T} (\rho _{h,s} - \rho _{l,s})^2 \right] \Delta (n_l) \nonumber\\ &&\quad-\, \left[ \rho _{l,s}^2 - \left( \frac{n-n_l}{n} \right)^T (\rho _{h,s} - \rho _{l,s})^2 \right] \Delta ^{\prime }(n_l) > 0. \end{eqnarray}

When ρh,s > ρl,s, the first term of (25) is clearly positive, and the bracketed part of the second term is also positive when ρh,s ≤ 2ρl,s. Thus (25) holds if Δ′(nl) ≤ 0, or

(26)
\begin{eqnarray} [ 1 - \rho _{h,s} - \rho _{l,s} + 2 (n_l \rho _{l,s} + (n - n_l) \rho _{h,s}) ] (\rho _{l,s} - \rho _{h,s}) \le 0 . \nonumber\\ \end{eqnarray}

The bracketed expression in (26) is clearly positive and ρl,s<ρh,s, thus establishing the result.

In the corner case, I rewrite v l,1 as earlier with nh = n − nl and Δ(nl). Applying the quotient rule and simplifying, $\frac{d v_{l,1}}{d n_l} > 0$ if and only if

(27)
\begin{eqnarray} &&\left[ T \left( \frac{n-n_l}{n} \right)^{T-1} \rho _{l,s}^2 \right] \Delta (n_l)\nonumber\\ &&\quad -\, \left[ n \left( 1 - \left( \frac{n-n_l}{n} \right)^T \right) \rho _{l,s}^2 \right] \Delta ^{\prime }(n_l) > 0. \end{eqnarray}

The first term of (27) and the bracketed part of the second term are clearly positive for ρl,s > 0. Thus (27) holds if Δ′(nl) ≤ 0, which was established earlier for the interior case.   ■

Proof of Proposition 3. The result holds trivially when ρh,s = 0; thus, suppose ρh,s > 0.

(i) Suppose nh > (n − 1)/2. By Remark 2, the maximum budget that can be offered in equilibrium is $b_{h,1} = \frac{n \rho _{h,s}}{2 k \Delta }$. Using Remark 1 and aggregating across districts, a politicized budget exceeds the expected budget under professionalization if

(28)
\begin{eqnarray} &&\frac{n}{k (n + 1)}\nonumber\\ &&\quad > \frac{(n_h \rho _{h,s} + n_l \rho _{l,s}) n \rho _{h,s}}{2 k [n_l \rho _{l,s} (1 - \rho _{l,s}) + n_h \rho _{h,s} (1 - \rho _{h,s}) + (n_h \rho _{h,s} + n_l \rho _{l,s})^2]} . \nonumber\\ \end{eqnarray}

The right-hand side of (28) is bounded from above by $\frac{n \rho _{h,s}}{2 k (n_h \rho _{h,s} + n_l \rho _{l,s})}$ (this also follows from the fact that (E[νl+νh])2<E[(νl+νh)2]). Substituting into (28) and simplifying yields 2(nhρh,s+nlρl,s)≥(n + 1)ρh,s, or equivalently 2nlρl,s+nhρh,s≥(nl + 1)ρh,s, which holds whenever nh > nl.

(ii) Let nl > (n − 1)/2. If a type l legislator is recognized, then by Remark 3 the equilibrium budget is $b_{l,1} = \frac{n \rho _{l,s}}{2 k \Delta }$. The proof is symmetrical with case (i) and is therefore omitted. If a type h legislator is recognized, then using Remark 3 and the upper bound from case (i) the professionalized budget is bounded from above by some $\frac{n \rho _{l,s} + n f(T)}{2 k (n_h \rho _{h,s} + n_l \rho _{l,s})}$, where f(T) is positive and decreasing and limT → ∞f(T)=0. Then the politicized budget is larger if $\frac{n}{k (n + 1)} \ge \frac{n \rho _{l,s} + n f(T)}{2 k (n_h \rho _{h,s} + n_l \rho _{l,s})}$, or equivalently nlρl,s+2nhρh,s≥(nh + 1)ρl,s+(n + 1)f(T). Thus for T sufficiently large, it is straightforward to verify that this condition holds whenever nl > nh.   ■

Proof of Proposition 4. Denote by ρEτ,s the probability of acceptance under executive intervention. Note that $s \not\in {\mathcal P}_{-\tau }$ implies that B's investigation decision for type −τ is independent of sE; thus, ρE−τ,s = ρ−τ,s and I focus on the relationship between ρEτ,s and ρτ,s.

(i) If $s^E > \overline{\mathcal P}_{\tau }$, then E minimizes ρEτ,s. There are three subcases. First, if $s \not\in {\mathcal P}_{\tau }$, then B's approval decision does not depend on σ, and thus E cannot affect the acceptance probability: ρEτ,s = ρτ,s. Second, if $s \in {\mathcal P}_{\tau }$ and $s < p_{\tau } \overline{\theta }+ (1 - p_{\tau }) \underline{\theta }$, then B would accept if there were no investigation. E therefore orders an investigation, so that ρEτ,s = p τq + (1 − p τ)(1 − q) ≤ ρτ,s, with the inequality strict for $s < \underline{{\mathcal S}}_{\tau }$. Third, if $s \in {\mathcal P}_{\tau }$ and $s > p_{\tau } \overline{\theta }+ (1 - p_{\tau }) \underline{\theta }$, then B would reject if there were no investigation. E therefore orders no investigation, so that ρEτ,s = 0 ≤ ρτ,s, with the inequality strict for $s < \overline{{\mathcal S}}_{\tau }$. Because ρEτ,s ≤ ρτ,s for all $s \not\in {\mathcal P}_{-\tau }$, Proposition 1(iii) implies that if I* = L, then I*E = L. Thus I*E ≠ I* only if I* = B.

(ii) If $s^E < \underline{{\mathcal P}}_{\tau }$, then E maximizes ρEτ,s. There are again three subcases. First, if $s \not\in {\mathcal P}_{\tau }$, then B's approval decision does not depend on σ, and thus E cannot affect the acceptance probability: ρEτ,s = ρτ,s. Second, if $s \in {\mathcal P}_{\tau }$ and $s < p_{\tau } \overline{\theta }+ (1 - p_{\tau }) \underline{\theta }$, then B would accept if there were no investigation. E therefore orders no investigation, so that ρEτ,s = 1≥ρτ,s, with the inequality strict for $s > \underline{{\mathcal S}}_{\tau }$. Third, if $s \in {\mathcal P}_{\tau }$ and $s > p_{\tau } \overline{\theta }+ (1 - p_{\tau }) \underline{\theta }$, then B would reject if there were no investigation. E therefore orders an investigation, so that ρEτ,s = p τq + (1 − p τ)(1 − q)≥ρτ,s, with the inequality strict for $s > \overline{{\mathcal S}}_{\tau }$. Because ρEτ,s≥ρτ,s for all $s \not\in {\mathcal P}_{-\tau }$, Proposition 1(iii) implies that if I* = B, then I*E = B. Thus I*E ≠ I* only if I* = L.   ■

Proof of Proposition 5. Let e = mhv h,1+mlv l,1 denote E's objective. I establish comparative statics for e with respect to ρl,s and ρh,s to derive E's investigation strategy and its effects on the majority's expected payoff from professionalization.

I first establish that (a) $\lim _{T \rightarrow \infty } \frac{d v_{\tau ,1}}{d \rho _{\tau ,s}} > 0$, and (b) $\lim _{T \rightarrow \infty } \frac{d v_{\tau ,1}}{d \rho _{-\tau ,s}} < 0$ under a majority of type τ. I consider only τ = h; the result for τ = l is almost identically derived and is therefore omitted. To establish (a), I rewrite v h,1 by letting Δ(ρτ,s) express the dependence of Δ on ρτ,s. Applying the quotient rule and simplifying, $\frac{d v_{h,1}}{d \rho _{h,s}} > 0$ if and only if

\begin{eqnarray*} &&2 \left[ n \rho _{h,s} - n (n_l/n)^T (\rho _{h,s}- \rho _{l,s}) \right] \Delta (\rho _{h,s}) \\ &&\quad-\, \left[ n \rho _{h,s}^2 - n (n_l/n)^T (\rho _{h,s}- \rho _{l,s})^2 \right] \Delta ^{\prime }(\rho _{h,s}) > 0. \end{eqnarray*}

Taking the limit as T → ∞ yields 2nρh,sΔ(ρh,s) − nρ2h,sΔ′(ρh,s)>0, or equivalently

(29)
\begin{eqnarray} 2 n_l \rho _{l,s} (1 - \rho _{l,s}) + n_h \rho _{h,s} + 2 (n_l n_h \rho _{l,s} \rho _{h,s}+ n_l^2 \rho _{l,s}^2) > 0 . \nonumber\\ \end{eqnarray}

Because each term of (29) is strictly positive, the condition always holds, thus establishing (a).

To show (b), note simply that $\frac{d v_{h,1}}{d \rho _{l,s}} < 0$ if and only if

(30)
\begin{eqnarray} &&2 n (n_l/n)^T (\rho _{h,s} - \rho _{l,s}) \Delta (\rho _{l,s}) \nonumber\\ &&\quad-\, \left[ n \rho _{h,s}^2 - n (n_l/n)^T (\rho _{h,s}- \rho _{l,s})^2 \right] \Delta ^{\prime }(\rho _{l,s}) < 0. \end{eqnarray}

Taking the limit as T → ∞, the first term in (30) is clearly zero, while the bracketed expression is positive. This establishes (b).

It is easily verified that the derivatives of v h,1 and v l,1 with respect to both ρh,s and ρl,s are always finite. Because E's objective is linear, there exists some $\overline{m}$ such that if $m_{\tau }/m_{-\tau } > \overline{m}_{\tau }$, e is increasing in ρτ and decreasing in ρ−τ. Thus if T is sufficiently large and $m_{\tau }/m_{-\tau } > \overline{m}_{\tau }$, then E's investigative strategy maximizes acceptances in type τ districts (i.e., investigate iff $s \in {\mathcal P}_{\tau }$ and $s \ge p_{\tau } \overline{\theta }+ (1 - p_{\tau }) \underline{\theta }$). E also minimizes acceptances in type −τ districts (i.e., investigate iff $s \in {\mathcal P}_{\tau }$ and $s < p_{-\tau } \overline{\theta }+ (1 - p_{-\tau }) \underline{\theta }$). Intervention by E then weakly increases the payoff to professionalization for type τ. Because type τ legislators are decisive in the choice of I, I*E ≠ I* only if I* = L.   ■

Proof of Proposition 6. I derive comparative statics on v τ,1 as T → ∞. As established in the proof of Proposition 5, for a majority of type τ, $\lim _{T \rightarrow \infty } \frac{d v_{\tau ,1}}{d \rho _{\tau ,s}} > 0$. Thus it will be sufficient to establish conditions under which ρτ,s is weakly increasing or weakly decreasing in q.

As a preliminary step, I derive the signs of $\frac{d \underline{{\mathcal S}}_{\tau }}{d q}$ and $\frac{d \overline{{\mathcal S}}_{\tau }}{d q}$. Differentiating, $\frac{d \underline{{\mathcal S}}_{\tau }}{d q} > 0$ if and only if

\begin{eqnarray*} &&({-}p_{\tau } \overline{\theta }+ (1 - p_{\tau }) \underline{\theta }) [(1-q)p_{\tau } + q(1 - p_{\tau })] \\ &&\quad>\![(1-q)p_{\tau } \overline{\theta }+ q (1 - p_{\tau }) \underline{\theta }+ c/\pi ] (1 - 2p_{\tau }) \nonumber\\ &&\quad\Leftrightarrow p_{\tau } > \overline{p} \equiv \frac{1}{2} - \frac{2c/\pi - \sqrt{(\overline{\theta }- \underline{\theta })^2 + 4c^2/\pi ^2}}{2(\overline{\theta }- \underline{\theta })} .\nonumber \end{eqnarray*}

By a similar calculation, $\frac{d \overline{{\mathcal S}}_{\tau }}{d q} > 0$ if and only if $p_{\tau } > \underline{p} \equiv \frac{1}{2} + \frac{2c/\pi - \sqrt{(\overline{\theta }- \underline{\theta })^2 + 4c^2/\pi ^2}}{2(\overline{\theta }- \underline{\theta })}$; note that $0 < \underline{p} < 1/2 < \overline{p} < 1$.

(i) Suppose $p_{\tau } > \overline{p}$. Then $\frac{d \overline{{\mathcal S}}_{\tau }}{d q} > 0$ and $\frac{d \underline{{\mathcal S}}_{\tau }}{d q} > 0$. Note that ρτ,s = 0 for $s > \overline{{\mathcal S}}_{\tau }$ and ρτ,s = 1 for $s < \underline{{\mathcal S}}_{\tau }$. Further, because $\overline{p} > 1/2$, $\frac{d \rho _{\tau ,s}}{d q} > 0$ for $s \in {\mathcal S}_{\tau }$. Thus for any s, ρτ,s is weakly increasing in q. By assumption $s \not\in {\mathcal S}_{-\tau }$ for all q, which implies $\frac{d \rho _{-\tau ,s}}{d q} = 0$. Thus, v τ,1 is weakly increasing in q for a type τ majority.

Next, suppose $p_{\tau } \in (1/2, \overline{p}]$. Then $\frac{d \overline{{\mathcal S}}_{\tau }}{d q} > 0$ and $\frac{d \underline{{\mathcal S}}_{\tau }}{d q} < 0$. The preceding proof then applies for any $s > \overline{{\mathcal S}}_{\tau }$ and $s \in {\mathcal S}_{\tau }$, or equivalently $s \ge \underline{{\mathcal S}}_{\tau }$.

(ii) Suppose $p_{\tau } < \underline{p}$. Then $\frac{d \overline{{\mathcal S}}_{\tau }}{d q} < 0$ and $\frac{d \underline{{\mathcal S}}_{\tau }}{d q} < 0$. Note that ρτ,s = 0 for $s > \overline{{\mathcal S}}_{\tau }$ and ρτ,s = 1 for $s < \underline{{\mathcal S}}_{\tau }$. Further, because $\overline{p} < 1/2$, $\frac{d \rho _{\tau ,s}}{d q} < 0$ for $s \in {\mathcal S}_{\tau }$. Thus for any s, ρτ,s is weakly decreasing in q. By assumption $s \not\in {\mathcal S}_{-\tau }$ for all q, which implies $\frac{d \rho _{-\tau ,s}}{d q} = 0$. Thus, v τ,1 is weakly decreasing in q for a type τ majority.

Next, suppose $p_{\tau } \in [\underline{p}, 1/2)$. Then $\frac{d \overline{{\mathcal S}}_{\tau }}{d q} > 0$ and $\frac{d \underline{{\mathcal S}}_{\tau }}{d q} < 0$. The preceding proof then applies for any $s < \underline{{\mathcal S}}_{\tau }$ and $s \in {\mathcal S}_{\tau }$, or equivalently $s \le \overline{{\mathcal S}}_{\tau }$.   ■

Footnotes

1 These studies are far too numerous to list here, but see Wilson (Reference Wilson2000) for an overview. A few prominent examples are Kaufman (Reference Kaufman1960), Muir (Reference Muir1977), Weaver (Reference Weaver1977), Wilson (Reference Wilson1978), Quirk (Reference Quirk and Wilson1980), and Carpenter (Reference Carpenter2001).

2 There are many other sources of earmarks. According to the U.S. Office of Management and Budget, the 110th Congress was responsible for 11,524 earmarks totaling $16.5 billion in fiscal year 2008 (http://earmarks.omb.gov/2008_appropriations_earmarks_110th_congress.html accessed August 20, 2009). This is almost certainly an undercount of the total of public spending distributed according to political criteria.

3 As de Figueiredo and Silverman (Reference de Figueiredo and Silverman2006) show, another explanation for politicization is interest group lobbying. This argument is not incompatible with a distributive politics framework, because lobbied legislators ultimately must traverse the full proposal and voting process modeled in this article.

4 For example, the 2010 Patient Protection and Affordable Care Act established an Independent Payment Advisory Board that would order Medicare spending cuts when per capita costs exceeded a target rate, starting in 2014. Congress could overturn these cuts only by passing a law that achieved the same reductions. Previously, Congress was relatively free to set geographically specific reimbursement rates. See Shailagh Murray, “Obama Eyes the Purse Strings for Medicare,” Washington Post, July 16, 2009.

5 As an example of an agency evaluation standard, the Federal Aviation Administration's Airport Improvement Program (AIP), which has been active since 1982, assigns proposed projects a National Priority Rating score between 0 and 100. The normal passing threshold for projects is 41, whereas for stimulus projects sponsored by the 2009 American Recovery and Reinvestment Act it is 62 (see http://www.faa.gov/airports/aip/grant_histories/airport_projects/ accessed July 3, 2011). A 2009 study sponsored by the Pew Charitable Trusts showed that 17% of AIP projects between fiscal years 2005 through 2009 had scores below 41 (http://subsidyscope.org/transportation/aip/ accessed July 3, 2011).

6 Bickers and Stein (Reference Bickers and Stein1997) argue that an agency can effectively randomize the allocation of a project with a narrowly geographic focus, thus allowing legislators to broaden its coalition of supporters. This view of professionalization is more similar to politicization in my model, because proposers in the bargaining game are chosen at random.

7 One partial exception is Bertelli and Grose (Reference Bertelli and Grose2009), who argue informally that senators who are ideologically closer to agencies are more likely to receive grants.

8 Given that the bureaucrat in this model cares only about approving deserving projects, she is indifferent over how money is distributed across deserving projects. Note however that if legislators could vary district budgets under professionalization, then they could achieve a result similar to that under politicization by assigning districts budgetary certainty equivalents. Thus, the inability of legislators to control district-specific allocations is essential to professionalization.

9 The argument bears some similarities to the universalism arguments of Shepsle and Weingast (Reference Shepsle and Weingast1981). Note that while the bureaucrat will typically create more efficient programs in equilibrium, the programs may not be universalistic, depending on her standard and the size of the majority.

10 It can be shown easily that as T → ∞, v τ,s for the majority faction is monotonic.

11 Relatedly, substituting square root for linear benefit utility and linear for quadratic costs also generated some interesting results. Under this variation, costs are separable, whereas utility over benefits is concave. Closed form solutions under politicization were again unobtainable, though the professionalization game remained similar to the basic game. Numerical simulations showed that the basic ideas of Proposition 2 and Remark 5 continued to hold, but the payoffs to politicization were typically much lower, resulting in a consistent legislative preference for professionalization. One conjecture for the difference in results is that because marginal benefits decline very quickly for the proposer, she must extract more from non-coalition partners, thus amplifying the inefficiency of the proposer bonus. Concave benefit utility therefore seems also to encourage professionalization.

12 The ability of a president to affect agency decisions and thereby change the distribution of resources is consistent with the findings of Berry, Burden, and Howell (Reference Berry, Burden and Howell2010). The executive power modeled here might be viewed as a conservative take on the extent of executive power. In some environments the executive could have the ability to cancel projects or contracts outright or may also have these powers even under politicization.

13 For example, when a majority is indifferent between politicization and professionalization, $s \in {\mathcal S}_h \cup {\mathcal S}_l$ and ${\mathcal P}_h \cap {\mathcal P}_l = \emptyset$, there exist values of sE that would induce I* ≠ I*E.

14 The condition on T ensures that v τ,1 is increasing in ρτ,s and decreasing in ρ−τ,s, though for a range of parameter values the result also holds for T = 1.

References

REFERENCES

Alesina, Alberto, and Tabellini, Guido. 2007. “Bureaucrats or Politicians? Part I: A Single Policy Task.” American Economic Review 97 (1): 169–79.CrossRefGoogle Scholar
Anagnoson, J. Theodore. 1982. “Federal Grant Agencies and Congressional Election Campaigns.” American Journal of Political Science 26 (3): 547–61.CrossRefGoogle Scholar
Anagnoson, J. Theodore. 1983. “Bureaucratic Reactions to Political Pressures: Can a Grant Agency “Manage” Its Political Environment?” Administration & Society 15 (1): 97–118.CrossRefGoogle Scholar
Ansolabehere, Stephen, Gerber, Alan, and Snyder, James M.. 2002. “Equal Votes, Equal Money: Court-Ordered Redistricting and Public Expenditures in the American States.” American Political Science Review 96 (4): 767–77.Google Scholar
Ansolabehere, Stephen, Snyder, James M., and Ting, Michael M.. 2003. “Bargaining in Bicameral Legislatures: When and Why Does Malapportionment Matter?” American Political Science Review 97 (3): 471–81.CrossRefGoogle Scholar
Arnold, R. Douglas. 1979. Congress and the Bureaucracy. New Haven, CT: Yale University Press.Google Scholar
Balla, J. Steven, Lawrence, D. Eric, Maltzman, Forrest, and Sigelman, Lee. 2002. “Partisanship, Blame Avoidance, and the Distribution of Legislative Pork.” American Journal of Political Science 46 (3): 515–25.Google Scholar
Banks, Jeffrey S. 1989. “Agency Budgets, Cost Information, and Auditing.” American Journal of Political Science 33 (3): 670–99.Google Scholar
Baron, David P. 1991. “Majoritarian Incentives, Pork Barrel Programs, and Procedural Control.” American Journal of Political Science 35 (1): 57–90.Google Scholar
Baron, David P. 1996. “A Dynamic Theory of Collective Goods Programs.” American Political Science Review 90 (2): 316–30.CrossRefGoogle Scholar
Baron, David P., and Ferejohn, John A.. 1989. “Bargaining in Legislatures.” American Political Science Review 83: 1181–1206.CrossRefGoogle Scholar
Bendor, Jonathan, Taylor, Serge, and Gaalen, Roland Van. 1987. “Politicians, Bureaucrats, and Asymmetric Information.” American Journal of Political Science 31 (4): 796–828.CrossRefGoogle Scholar
Berry, Christopher R., Burden, Barry C., and Howell, William G.. 2010. “The President and the Distribution of Federal Spending.” American Political Science Review 104 (4): 783–99.CrossRefGoogle Scholar
Berry, Christopher R., and Gersen, Jacob E.. 2010. “Agency Design and Distributive Politics.” Unpublished manuscript, University of Chicago.CrossRefGoogle Scholar
Bertelli, Anthony M., and Grose, Christian R.. 2009. “Secretaries of Pork? A New Theory of Distributive Public Policy.” Journal of Politics 71 (3): 926–45.CrossRefGoogle Scholar
Besley, Timothy, and Persson, Torsten. 2011. Pillars of Prosperity: The Political Economics of Development Clusters. Princeton, NJ: Princeton University Press.Google Scholar
Bickers, Kenneth N., and Stein, Robert M.. 1997. “Building majority Coalitions for Sub-majority Benefit Distributions.” Public Choice 91 (3/4): 229–49.CrossRefGoogle Scholar
Carpenter, Daniel P. 2001. The Forging of Bureaucratic Autonomy: Reputations, Networks, and Policy Innovation in Executive Agencies, 1862–1928. Princeton, NJ: Princeton University Press.Google Scholar
Carpenter, Daniel P., and Ting, Michael M.. 2007. “Regulatory Errors with Endogenous Agendas.” American Journal of Political Science 51 (4): 835–52.Google Scholar
Cho, Seok-ju, and Duggan, John. 2005. “Bargaining Foundations of the Median Voter Theorem.” Unpublished manuscript, University of Rochester.Google Scholar
Collie, Melissa P. 1988. “The Legislature and Distributive Policy Marking in Formal Perspective.” Legislative Studies Quarterly 13: 427–58.Google Scholar
de Figueiredo, John M., and Silverman, Brian S.. 2006. “Academic Earmarks and the Returns to Lobbying.” Journal of Law and Economics 49 (2): 597–626.CrossRefGoogle Scholar
DelRossi, Alison F., and Inman, Robert P.. 1999. “Changing the Price of Pork: The Impact of Local Cost Sharing on Legislators’ Demands for Distributive Public Goods.” Journal of Public Economics 71: 247–73.CrossRefGoogle Scholar
Derthick, Martha. 1990. Agency under Stress. Washington, DC: Brookings Institution.Google Scholar
Ferejohn, John A. 1974. Pork Barrel Politics: Rivers and Harbors Legislation, 1947–1968. Stanford, CA: Stanford University Press.Google Scholar
Gailmard, Sean. 2002. “Expertise, Subversion, and Bureaucratic Discretion.” Journal of Law, Economics, and Organization 18 (2): 536–55.CrossRefGoogle Scholar
Gailmard, Sean, and Patty, John W.. 2007. “Slackers and Zealots: Civil Service, Policy Discretion and Bureaucratic Expertise.” American Journal of Political Science 51 (4): 873–89.Google Scholar
Gerber, Elisabeth R., and Gibson, Clark C.. 2009. “Balancing Regionalism and Localism: How Institutions and Incentives Shape American Transportation Policy.” American Journal of Political Science 53 (3): 633–48.CrossRefGoogle Scholar
Gordon, Sanford C. 2011. “Politicizing Agency Spending Authority: Lessons from a Bush-era Scandal.” American Political Science Review 105 (4): 717–34.CrossRefGoogle Scholar
Hird, John A. 1990. “Superfund Expenditures and Cleanup Priorities: Distributive Politics or the Public Interest?” Journal of Policy Analysis and Management 9 (4): 455–83.CrossRefGoogle Scholar
Hird, John A. 1991. “The Political Economy of Pork: Project Selection at the U.S. Army Corps of Engineers.” American Political Science Review 85 (2): 429–56.CrossRefGoogle Scholar
Huber, John D., and Shipan, Charles R.. 2002. Deliberate Discretion? The Institutional Foundations of Bureaucratic Autonomy. New York: Cambridge University Press.Google Scholar
Kaufman, Herbert. 1960. The Forest Ranger, A Study in Administrative Behavior. Baltimore: Johns Hopkins Press.Google Scholar
Kernell, Samuel, and McDonald, Michael P.. 1999. “Congress and America's Political Development: The Transformation of the Post Office from Patronage to Service.” American Journal of Political Science 43 (3): 792–811.CrossRefGoogle Scholar
Krause, George A., Lewis, David E., and Douglas, James W.. 2006. “Political Appointments, Civil Service Systems, and Bureaucratic Competence: Organizational Balancing and Executive Branch Revenue Forecasts in the American States.” American Journal of Political Science 50 (3): 770–87.CrossRefGoogle Scholar
Law, Marc T., and Tonon, Joseph M.. 2006. “The Strange Budgetary Politics of Agricultural Research Earmarks.” Public Budgeting and Finance 26 (3): 1–21.CrossRefGoogle Scholar
Lee, Frances. 2000. “Senate Representation and Coalition Building in Distributive Politics.” American Political Science Review 94 (1): 59–72.CrossRefGoogle Scholar
Levitt, Steven D., and Snyder, James M. Jr. 1995. “Political Parties and the Distribution of Federal Outlays.” American Journal of Political Science 39 (4): 958–80.CrossRefGoogle Scholar
Lewis, David E. 2008. The Politics of Presidential Appointments: Political Control and Bureaucratic Performance. Princeton, NJ: Princeton University Press.CrossRefGoogle Scholar
Lowi, Theodore J. 1964. “American Business, Public Policy, Case Studies, and Political Theory.” World Politics 16: 677–715.CrossRefGoogle Scholar
Maass, Arthur. 1951. Muddy Waters: The Army Engineers and the Nation's Rivers. Cambridge, MA: Harvard University Press.CrossRefGoogle Scholar
Manley, John T. 1970. The Politics of Finance. Boston: Little, Brown.Google Scholar
Maor, Moshe. 2007. “A Scientific Standard and an Agency's Legal Independence: Which of These Reputation-Protection Mechanisms Is Less Susceptible to Political Moves.” Public Administration 85 (4): 961–78.CrossRefGoogle Scholar
Maskin, Eric, and Tirole, Jean. 2004. “The Politician and the Judge: Accountability in Government.” American Economic Review 94 (4): 1034–54.CrossRefGoogle Scholar
McCarty, Nolan. 2000. “Presidential Pork: Executive Veto Power and Distributive Politics.” American Political Science Review 94 (1): 117–29.Google Scholar
McCubbins, Mathew D., Noll, Roger G., and Weingast, Barry R.. 1987. “Administrative Procedures as Instruments of Political Control.” Journal of Law, Economics, and Organization 3 (2): 243–77.Google Scholar
Miller, Gary J., and Moe, Terry M.. 1983. “Bureaucrats, Legislators, and the Size of Government.” American Political Science Review 77 (2): 297–322.Google Scholar
Moe, Terry M. 1989. “The Politics of Bureaucratic Structure.” In Can the Government Govern?, eds. Chubb, J. E. and Peterson, P. E.. Washington, DC: Brookings Institution, 267–329.Google Scholar
Muir, William K. 1977. Police: Streetcorner Politicians. Chicago: University of Chicago Press.Google Scholar
Nelson, Richard R., and Rosenberg, Nathan. 1993. “Technical Innovation and National Systems.” In National Innovation Systems, ed. Nelson, R. R.. New York: Oxford University Press.CrossRefGoogle Scholar
Norman, Peter. 2002. “Legislative Bargaining and Coalition Formation.” Journal of Economic Theory 102: 322–53.CrossRefGoogle Scholar
Prendergast, Canice. 2003. “The Limits of Bureaucratic Efficiency.” Journal of Political Economy 111 (5): 929–58.Google Scholar
Quirk, Paul. 1980. “Food and Drug Administration.” In The Politics of Regulation, ed. Wilson, J. Q.. New York: Basic Books, 191–235.Google Scholar
Rauch, James E. 1995. “Bureaucracy, Infrastructure, and Economic Growth: Evidence from U.S. Cities during the Progressive Era.” American Economic Review 85 (4): 968–79.Google Scholar
Rauch, James, and Evans, Peter B.. 2000. “Bureaucratic Structure and Bureaucratic Performance in Less Developed Countries.” Journal of Public Economics 75 (1): 49–71.Google Scholar
Rich, Michael J. 1989. “Distributive Politics and the Allocation of Federal Grants.” American Political Science Review 83 (1): 193–213.Google Scholar
Shepsle, Kenneth A., and Weingast, Barry R.. 1981. “Political Preferences for the Pork Barrel: A Generalization.” American Journal of Political Science 25: 96–111.CrossRefGoogle Scholar
Stein, Robert M., and Bickers, Kenneth N.. 1995. Perpetuating the Pork Barrel: Policy Subsystems and American Democracy. New York: Cambridge University Press.Google Scholar
Volden, Craig, and Wiseman, Alan E.. 2007. “Bargaining in Legislatures over Particularistic and Collective Goods.” American Political Science Review 101 (1): 79–92.Google Scholar
Weaver, Suzanne. 1977. Decision to Prosecute. Cambridge, MA: MIT Press.Google Scholar
Weber, Max. 1946. “Bureaucracy.” In Essays in Sociology, eds. Gerth, H. H. and Mills, C. Wright. New York: Oxford University Press, 196–233.Google Scholar
Wilson, James Q. 1978. The Investigators: Managing FBI and Narcotics Agents. New York: Basic Books.Google Scholar
Wilson, James Q. 2000. Bureaucracy: What Government Agencies Do and Why They Do It. 2nd ed.New York: Basic Books.Google Scholar
Figure 0

FIGURE 1. Bureaucratic Standards and Investigation StrategiesNotes: For each type τ, ${\mathcal P}_{\tau }$ is the set of standards for which an additional signal would be pivotal in B's approval decision. ${\mathcal S}_{\tau }$ is the set of standards for which B would be willing to pay the cost of an investigation. All standards within a region sj induce the same investigative behavior. At s = s3, for example, B rejects type l projects and approves type h projects without investigation, because $\overline{{\mathcal S}}_l < \underline{{\mathcal S}}_h$.

Figure 1

FIGURE 2. Professionalization, Project Quality, and Legislative CompositionNotes: Let n = 5 and T = 20. Horizontal and vertical axes are the probabilities of acceptance in high- and low-type districts (ρh,s and ρl,s, where ρh,s > ρl,s), respectively. Shaded areas indicate where L prefers professionalization, given the indicated majority size. In the left illustration, there is a type h majority. Professionalization becomes preferred as ρh,s increases and as the majority size decreases. In the right illustration, there is a type l majority. Professionalization becomes preferred as ρl,s increases and as the majority size increases.

Submit a response

Comments

No Comments have been published for this article.