2.1. Main issues in teaching creative engineering

What is at stake in creative engineering is the way engineers deal with problems such as those described above. These problems are usually characterized as “ill-defined” (Simon, Reference Simon1969) or “wicked” problems (Rittel & Webber, Reference Rittel and Webber1972; Dunne & Martin, Reference Dunne and Martin2006) with “figural complexity” (Schön, Reference Schön and Howard1990). With such problems, engineers' traditional methods of reasoning are not enough as the situation is radically different from classical optimization and modeling. In such situations, engineers have also to collaborate with other designers, such as industrial designers or architects, who also reason in a very different way from optimizing and modeling. Hence, the issue for teaching is to help engineers acquire this capacity for innovative design reasoning. This requires more than just adding a new science to the engineering sciences (McMahon et al., Reference McMahon, Ion and Hamilton2003).

It is interesting that the history of engineering has already been through periods where new forms of innovation have required major changes in teaching: the first industrial revolution forced engineers to be able to deal with complex machines for various applications, and this led to the invention of parametric design at the German Technische Hochschule (Redtenbacher, Reference Redtenbacher1852; König, Reference König1998). The second industrial revolution forced engineers to deal with “science-based products” (electrical engineering, chemical engineering, etc.), and this led to the invention of systematic design (Rodenacker, Reference Rodenacker1970; Pahl & Beitz, Reference Pahl and Beitz1977; Heymann, Reference Heymann2005).

What issues are involved in teaching innovative design? Following Dym et al. (Reference Dym, Agogino, Eris, Frey and Leifer2005), they can be summarized as teaching divergent thinking (DT) and convergent thinking (CT) in a collaborative, controlled manner. First, teaching DT consists in making people able to formulate original propositions. As observed by Loch et al. (Reference Loch, De Meyer and Pich2006), this is much more than being able to act in uncertain situations. In uncertain situations, alternatives are known and only their probability is unknown, whereas DT consists in acting in situations where the nature of the alternative is unknown, where new, original worlds have to be created. This creation requires the capacity to break existing generative rules (Boden, Reference Boden1990) and to create alternatives. It is also accepted that designers should not only be able to use existing knowledge but also have to ask so-called “generative design questions” (Eris, Reference Eris2003, Reference Eris2004).

Second, teaching CT does not consist in teaching the engineering sciences, but rather in teaching the capacity to use knowledge, for instance through “deep reasoning questions,” that is, with a capacity to activate expertise, to transform it into usable skills, and to be able to link existing, abstract engineering science models to so-called “hardware” situations (Brereton, Reference Brereton1999). This is different from the capacity to optimize and is closer, for instance to the capacity to formulate relevant “estimates” (Linder, Reference Linder1999; Dym et al., Reference Dym, Agogino, Eris, Frey and Leifer2005), that is, knowledge relevant for a particular situation.

Third, teaching DT and CT (DTCT) also aims at making designers able to switch regularly from one mode into the other (Eris, Reference Eris2004; Dym et al., Reference Dym, Agogino, Eris, Frey and Leifer2005). Several works have emphasized interesting challenges of this DTCT design process. The process of iteration should be cumulative and lead to language expansion (Mabogunje & Liefer, Reference Mabogunje and Leifer1997). Iterations should keep cyclical semantic coherence (Song et al., Reference Song, Dong and Agogino2003). This kind of process could be evaluated by using creativity metrics suggested by Shah et al. (Reference Shah, Vargas-Hernandez and Smith2003): a DTCT process should lead to originality and variety but also to robust, feasible solutions.

Fourth, designers, especially engineers, have to be able to follow an innovative design process in a collaborative manner. One goal is therefore to enable them to follow DTCT processes with users (von Hippel, Reference von Hippel2001; Magnusson, Reference Magnusson2003) from varied disciplines, with different “types” of people: either different Myers–Briggs Type Indicator profiles (Reilly et al., Reference Reilly, Lynn and Aronson2002) or different design traditions (architects, industrial designers, engineers, etc.; Rice, Reference Rice1994; Savanovic & Zeiler, Reference Savanovic and Zeiler2007).

Fifth, teaching innovative design should also enable people to control whether or not they are following the process correctly. This criteria of controllability is mentioned regularly in design teaching (Pahl & Beitz, Reference Pahl and Beitz2006). It was theorized by Argyris and Schön (Schön, Reference Schön1983; Argyris & Schön, Reference Argyris and Schön1996) in the notion of double-loop learning, in which designers have to be able not only to use the “espoused theory” but also to change it to identify new ways of doing things in the so-called theory in use. In the case of DTCT, people should be taught to control when they should switch from DT to CT or from CT to DT. They should learn to control the balance between creative thinking and resources for exploring and learning, and they should be able to control whether their group of designers is in a design process and the quality of their work at all times.

The literature provides us with several insights into the goals of teaching innovative design. It also identifies the main questions for teaching. First, how do we evaluate the capacity for DT? As observed by Dym et al. (Reference Dym, Agogino, Eris, Frey and Leifer2005), it is difficult to design and grade an exam to test whether students are able to formulate undecidable propositions: “how to evaluate something that is neither true nor false?” Second, how do we teach the balance between DT and CT? It is possible to teach methods of inquiry and creativity, but how can they be combined? Third, how can the “process” be evaluated? Innovative design usually tends to be taught with a “PBL” model (see Dym et al., Reference Dym, Agogino, Eris, Frey and Leifer2005). The teaching aims precisely to help students learn to design in a creative, collective, and controllable way. However, as observed by Dym et al. (Reference Dym, Agogino, Eris, Frey and Leifer2005), this raises a number of questions. What is an “authentic situation”? Teaching, and even more so evaluation, should concern the process itself and not merely the output. How do we evaluate whether the process is under control? How do we ensure that the team is varied enough? How do we check the capacity to design collectively? It is not by forcing people to work together in multidisciplinary teams that their collective work is necessarily effective in terms of innovative design?

2.2. Analyzing the obstacles encountered by learners: Four forms of FE

Having outlined the main issues and the questions they raise for teaching, we must try to gain a clearer picture of the main obstacles that designers meet when learning innovative design. Some of the requirements of innovative design may be met by natural aptitude, others through regular teaching. However, recent works on cognition and psychology help to clarify some obstacles that apparently almost everybody is likely to face in innovative design situations. In the literature we have identified four main obstacles that can be characterized as four types of FE: FEs in the generation of alternatives, FEs in knowledge acquisition, FEs in collaborative creativity, and FEs in creativity processes. We will now clarify these four main obstacles in a view to establishing a framework for analyzing innovative design teaching methods, which should help overcome at least one of these FEs.

1. 1. Works on creative cognitionFootnote ¹ have analyzed the cognitive factors that can limit creativity (Ward et al., Reference Ward, Smith, Finke and Sternberg1999). They show that the number of ideas is not necessarily the main issue, although it is often used as an estimation of creativity. However, the ability to meet the criterion of “variety” is a major issue. A first series of works showed that people always tend to generate ideas in the same “family,” showing “fluency” but limited variety. This was described for instance in Ward's experiments (Ward, Reference Ward1994) that show how people in creative exercises tend to follow the “path of least resistance”: when told to draw imaginary animals, people tend to draw animals with legs, heads, and eyes. Originality is also limited in creative experiments. Although people are expected to break the rules (Boden, Reference Boden1990), that is, to rediscuss the knowledge they have, they tend rather to reuse knowledge and, more specifically, to reuse recently activated knowledge (Jansson & Smith, Reference Jansson and Smith1991; Smith et al., Reference Smith, Ward and Schumacher1993). A first criterion for teaching innovative design therefore emerges here: it should help to overcome the FE in the “generation of alternatives.”

2. 2. These works also help identify a second cognitive factor that limits creative cognition: people have difficulty making an effort to learn during a creative process, for instance by observing uses or by making “crazy prototypes.” Although it has been shown that learning, modeling, scanning or, more generally speaking, competence building, greatly accelerates creativity (Alexander, Reference Alexander1964; Sutton & Hargadon, Reference Sutton and Hargadon1996; Cropley, Reference Cropley2006), there is a tendency to focus on existing knowledge or to use the knowledge specific to the goal and task to be met (Finke, Reference Finke1990). The issue is not that designers learn to produce knowledge, but that they produce knowledge that is used in the design reasoning. This leads us to suggest a second criterion for innovative design teaching: it should help to overcome the “K acquisition” FE.

3. 3. Another stream of works has emphasized the cognitive and psychological difficulties involved in collaborative creativity. It is well known that groups using brainstorming methods (Osborn, Reference Osborn1957) generate significantly fewer ideas than the combined total of ideas generated by the same number of individuals brainstorming alone (called the nominal group; Diehl & Stroebe, Reference Diehl and Stroebe1987; Mullen et al., Reference Mullen, Johnson and Salas1991; Paulus & Dzindolet, Reference Paulus and Dzindolet1993). Several research projects have studied this “productivity gap,” providing evidence of a FE in “collective creativity” in brainstorming. Various social causes of production blocking have been identified, such as divided attention (Mulligan & Hartman, Reference Mulligan and Hartman1996; Paulus & Yang, Reference Paulus and Yang2000), social pressure of ex post evaluation (social anxiousness; Camacho & Paulus, Reference Camacho and Paulus1995), the effect of perceived expertness on creativity (Collaros & Anderson, Reference Collaros and Anderson1969), and a lack of recognition causing loafing and free riding. Cognitive factors have attracted renewed interest in recent years, with a focus on the risk of similarity in idea associations: the idea associations tend to follow the rule of similarity, meaning that the ideas generated from one idea tend to be in the same category as the initial idea (Brown et al., Reference Brown, Tumeo, Larey and Paulus1998; Paulus et al., Reference Paulus, Brown, Ortega, Purser and Montuori1999, Reference Paulus, Larey, Dzindolet and Turner2000). This is coherent with the individual FE reported by cognitive psychologists (Ward et al., Reference Ward, Smith, Finke and Sternberg1999) mentioned above. Moreover, unique ideas have poor association value: they initiate fewer ideas because the knowledge required for generation is not shared by the participants (Stasser & Birchmeier, Reference Stasser, Birchmeier, Paulus and Nijstad2003). Other works have insisted on the risk of not fully exploring the full range of ideas (Stewart & Stasser, Reference Stewart and Stasser1995; Gigone & Hastie, Reference Gigone and Hastie1997; Paulus, Reference Paulus2000) and the risk of cognitive load (each individual follows his or her own idea generation process while following the collective exchanges). Finally, there have been studies of phenomena regarding the limitations of knowledge expansion, such as the convergence of a group of people drawing on a common knowledge base (Stewart & Stasser, Reference Stewart and Stasser1995). Such phenomena illustrate a “collaborative creativity” FE and help identify a third criteria for innovative design teaching: it should help people to overcome this effect by “creatively” building on the others' ideas and using the knowledge provided by them.

4. 4. Finally, an FE has been reported in the process itself: when studying DTCT processes, it appears that designers tend to organize a two-step process (Shah et al., Reference Shah, Vargas-Hernandez and Smith2003; Eris, Reference Eris2004; Plety & Cremet, Reference Plety and Cremet2007), with an initial period of divergence in which a single “good” idea is usually selected and then developed during the convergence process. Students in design processes tend to identify a first phase of problem framing (or problem setting) and a second phase of problem solving. Schön's description of the “reflective practitioner” (Schön, Reference Schön1983) and Sutton and Hargadon's (Reference Sutton and Hargadon1996) description of IDEO creative processes show processes where designers are able to shift regularly from DT to CT and from CT to DT. A fourth criteria for teaching innovative design therefore emerges: it should help to overcome the “creativity process” FE.

It is interesting to note that history has provided us with several methods for overcoming some of the FEs listed here. We can illustrate how a teaching method overcomes one of these FEs with a few examples. For instance, one striking example in industrial design tradition is the educational program of the Bauhaus school (Droste, Reference Droste2002). It was based on powerful theoretical works by Gropius, Itten, and others. In his introductory course, Itten (Reference Itten1975) did not follow the classical teaching pattern of the Beaux Arts (i.e., copy the models) but taught “the fundamental laws of colours, forms, composition and creation” (p. 31). Students then had to do three types of projects: studies of nature and materials, analyses of old masters (such as the Issenheim Altarpiece), and nudes. He taught a grammar of shapes, colors, contrasts, rhythms, and materials, showing the different materials' essential and contradictory aspects.

Engineering design has also done a great deal of work on teaching innovative design. One archetype reported by König (Reference König1999) is Peter Klimentitsch von Engelmeyer (1855–1939), a Russian–German engineering design professor and theoretician who proposed the first integrated engineering design theory that linked intuition and knowledge creation into a design process. Klimentisch built a “Theorie der kreativen Arbeit” (1912; see also Engelmeyer, Reference Engelmeyer1895) and deduced from it a scaffolded process of PBL. He defined three types of projects, which can be characterized by different levels of expansion: designing a variant of an existing machine (a computing problem only), improving a function of a machine (applying scientific knowledge when the main working principles are known), and new construction (an Edison-like project, requiring the investigation of new physical principles to address emerging needs).

Even if they address different types of designers, both teaching processes share common principles: they insist on knowledge acquisition for creative design (grammar of shapes, study of old masters, reverse engineering, etc.); they underline the limits of existing knowledge (exercises to explore new combinations of shapes, colors, and materials, projects to improve machines or even to explore new phenomena, etc.) and they train students to face unknown design situations (Bauhaus teaching program, Klimentitsch's innovative projects). In this way, they address the FEs in “the generation of alternatives” and in “knowledge acquisition.”

To summarize, our literature review has helped to build a framework for the main criteria used to evaluate innovative design teaching methods. Such a method should meet the following four criteria:

1. 1. Overcome FEs in “the generation of alternatives”: The method should help to generate “varied” and “original” alternatives.

2. 2. Overcome FEs in “knowledge acquisition”: The method should help to generate and acquire relevant knowledge.

3. 3. Overcome FEs in “collaborative creativity”: The method should help to use the other actors' knowledge and build on their ideas.

4. 4. Overcome FEs in the “creativity process”: The method should help to combine problem setting and problem solving in a nonlinear process.

This analysis of the FEs encountered by students learning innovative design helps to characterize the issue of teaching: classical methods of “teaching” creativity usually control the output of the creative process. This control is grounded on criteria derived from Guilford or Torrance criteria, taking into account specific aspects of engineering (Guilford, Reference Guilford1950, Reference Guilford1985; Torrance, Reference Torrance and Sternberg1988; Shah et al., Reference Shah, Vargas-Hernandez and Smith2003). But the above-mentioned analyses of collective creative processes show that the final performance is actually impeded by FEs: hence, the issue is to devise a teaching method that helps to control and manage this “process” variable, which is often widely uncontrolled. In this perspective, the students are not only be evaluated on the outputs but also on the process: the evaluation should control the students' capacity to control and overcome the FEs during the innovative design process.

3.1. Elements of C-K theory

C-K theory (Hatchuel & Weil, Reference Hatchuel and Weil2003, Reference Hatchuel and Weil2007) was initially developed to support innovative design teaching. We will now see how it meets the requirements of an innovative design theory. Defining K as the space containing all established (true) propositions (the available knowledge), a C-K design process begins with a proposition that is undecidable in K (neither true nor false in K) about some partially unknown objects x. Concepts are all of the following form: “There exists an object x, for which a group of properties P1, P2, Pk hold in K.”

Concepts can only be partitioned or included, not searched or explored. If we add new properties (K → C), we partition the set into subsets; if we subtract properties we include the set in a set that contains it. Nothing else can be done. After partitioning or inclusion, concepts may still remain concepts (C → C), or move to propositions of K (C → K). The two spaces and four operators (including the K → K) are shown in Figure 1.

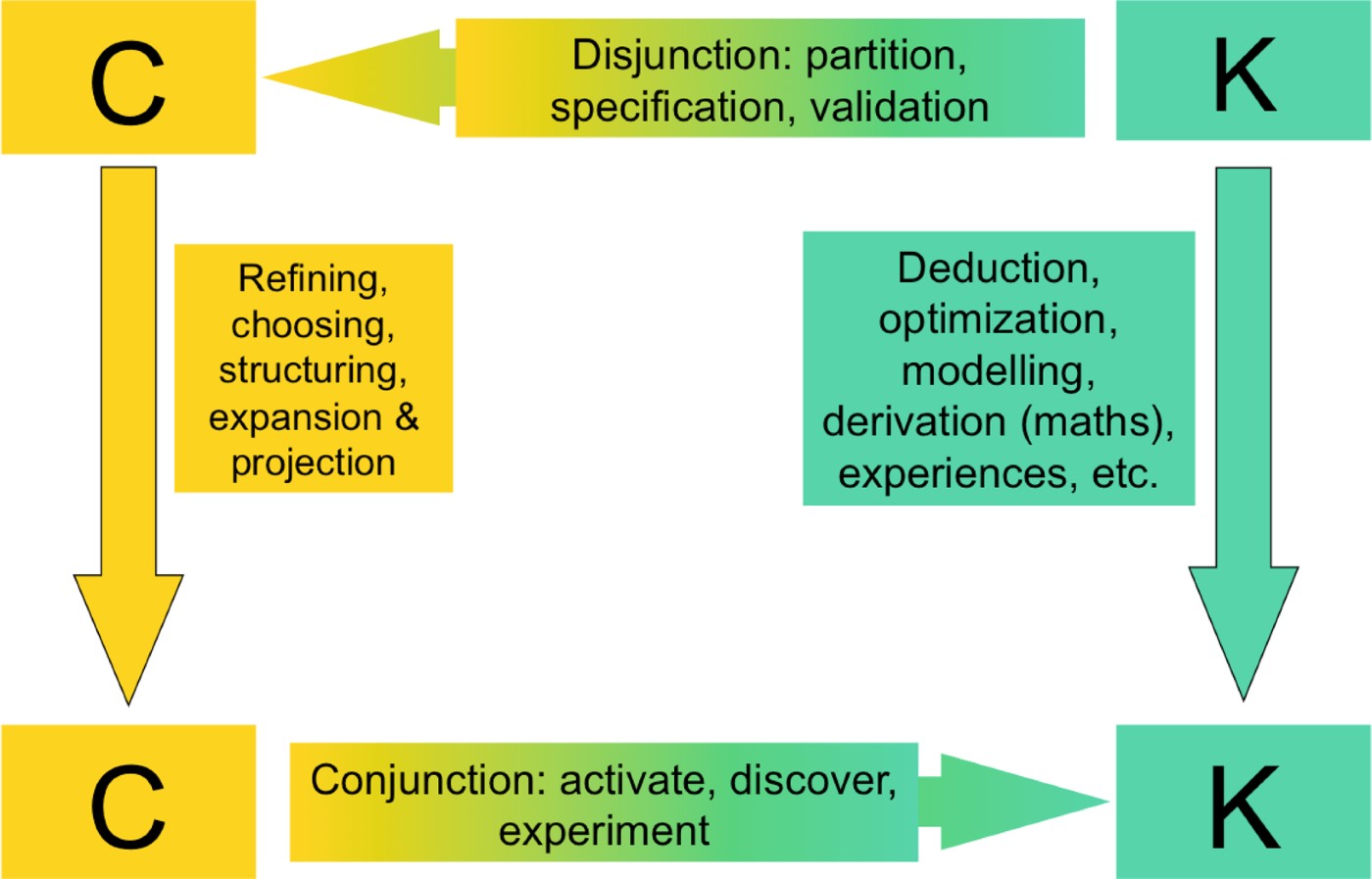
Fig. 1. The four operators of concept–knowledge theory (Hatchuel & Weil, Reference Hatchuel and Weil2003). C, concept; K, knowledge. [A color version of this figure can be viewed online at journals.cambridge.org/aie]

Any design project intends to transform an undecidable proposition (concept)—its “brief”—into a true proposition of K by adding new properties to C coming from the space of knowledge K and by producing new knowledge guided by conceptual issues. These partitions of the concepts can be either restrictive or expansive. If the partition expands the definition of an object with a new property, it is called an expanding partition (e.g., a flying house). Conversely, if the partition relies on an existing definition of the object, it is called a restrictive partition (speaking of “a house with a red roof” is a restrictive partition if “houses with red roofs” are already known in K).

Creativity is the result of expansive partitions of concepts (Hatchuel et al., Reference Hatchuel, Le Masson and Weil2008). Another view of C-K dynamics is given in Figure 2. Because of the partitioning process, the C-structure is necessary as a tree structure, whereas the structure in K could be completely different. We also see in this picture that any expansion in C is dependent on K and vice versa. Any choice to expand or not to expand in C is K dependent. Design begins with a disjunction and will only end if a conjunction exists and is judged as an acceptable solution.

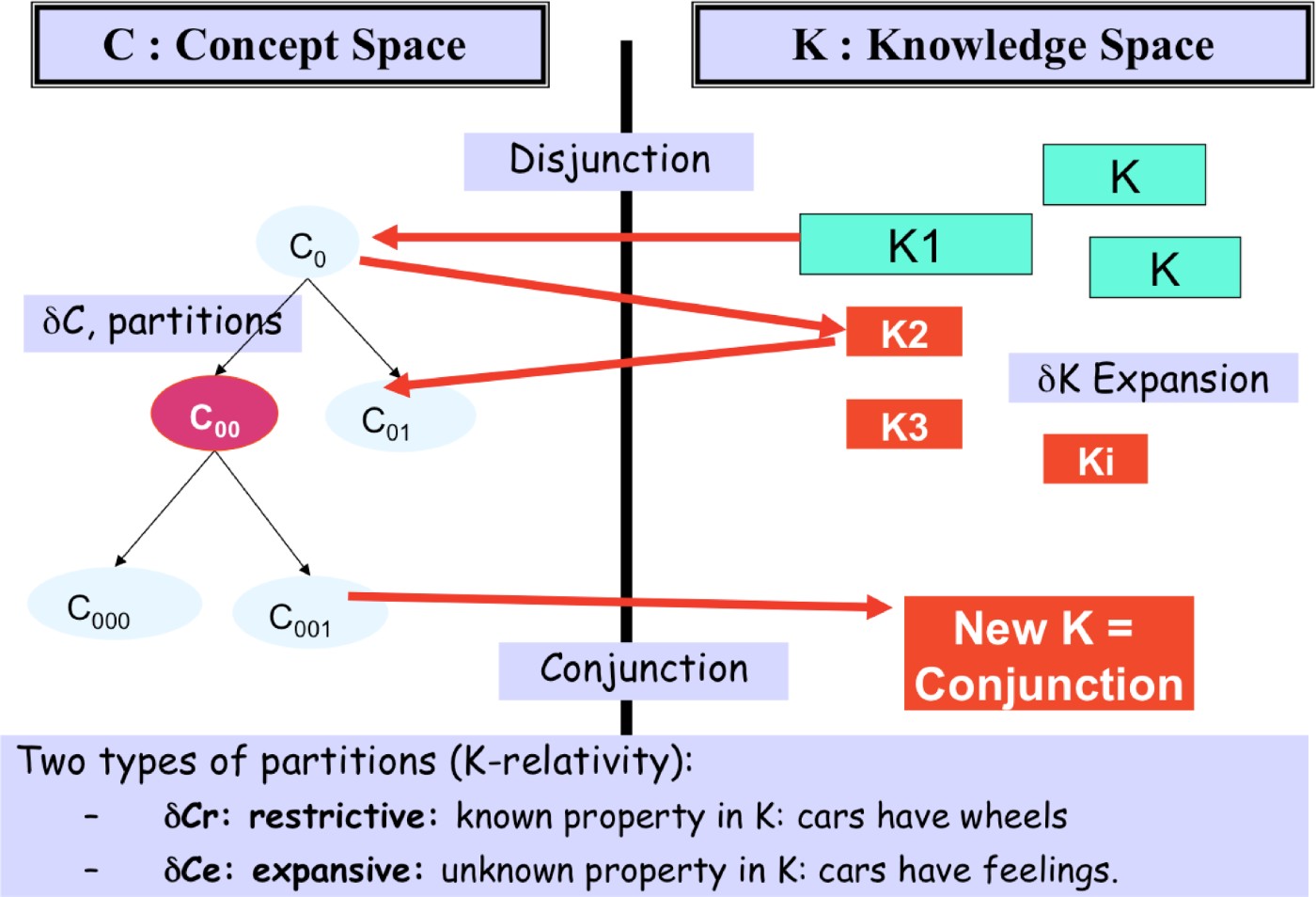
Fig. 2. The concept–knowledge dynamics (Hatchuel et al., 2004). [A color version of this figure can be viewed online at journals.cambridge.org/aie]

As in the Bauhaus and Klimentitsch cases, C-K theory combines the classical engineering design emphasis on knowledge and knowledge creation with the requirement for creativity to venture into the unknown (C0) and break the (right) rules to create new, original artifacts (expanding partition; Boden, Reference Boden1990; Le Masson et al., Reference Le Masson, Hatchuel and Weil2007; Hatchuel et al., Reference Hatchuel, Le Masson and Weil2008).

3.2. How C-K helps to control and overcome FEs

Let us now see how C-K addresses the four issues of design teaching identified above. We show that the theory helps to teach students in two ways: it clarifies the performance to be achieved and the means of action to achieve it and, more specifically, it enables students to clarify what “fixes” them and to make sure that they overcome the problem.

3.2.1. C-K and FEs in the generation of alternatives

In C-K, the FE in the generation of alternatives can be modeled as a limitation of C expansion because of the preservation of a stable K structure, with a stable set of generative rules in K (see Fig. 3).

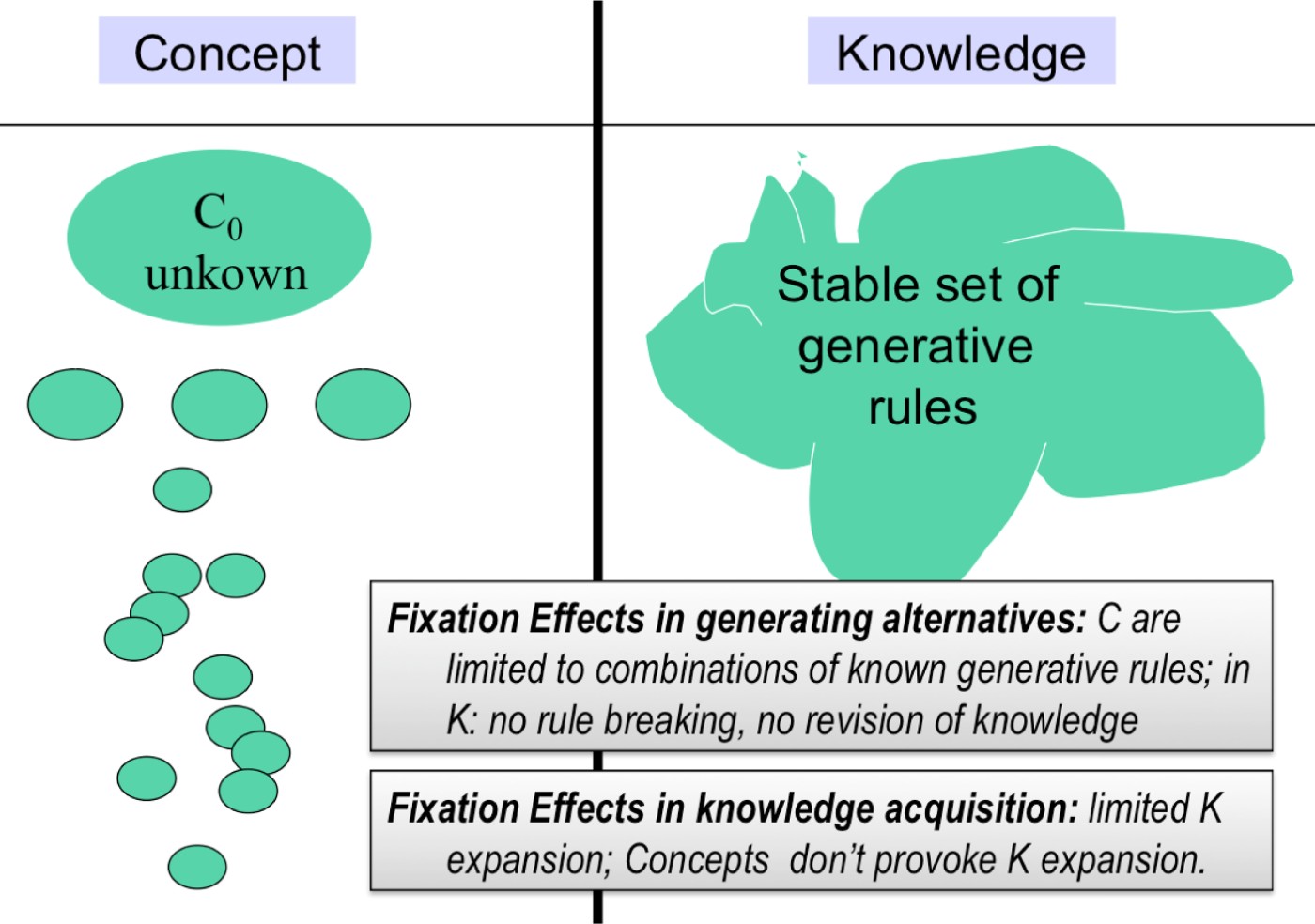
Fig. 3. A representation of the fixation effects in the generation of alternatives and in knowledge acquisition. C, concept; K, knowledge. [A color version of this figure can be viewed online at journals.cambridge.org/aie]

The operators of C-K, described above, directly enable the generation of design paths. More precisely, it is possible to evaluate “variety” by analyzing the structure of C and the variety of K bases that students mobilize for generating design paths. It is also possible to check whether or not the ideas are original. Following the definition of “originality” given by Boden (Reference Boden1990), an idea is original if it breaks a design rule; this corresponds to an expansive partition in C-K (Hatchuel et al., Reference Hatchuel, Le Masson and Weil2008). Hence, we see how C-K theory can help students to generate alternatives and to control whether these alternatives are varied (number of partitions and variety of knowledge bases mobilized in these partitions) and original (number of expansive partitions).

Moreover, C-K intrinsically allows for a control on the FEs in idea generation: C-K process helps identify and position all the “classical ideas” generated by using “common knowledge” and classical “generative rules”; this common knowledge and these generative rules must be shown in the space K. C-K therefore clarifies what fixes the designer; it also offers a self-evident way of overcoming this type of FE: as soon as a “classical generative rule” is identified, the student can “break” it, that is, can generate a concept in C that negates the generative rule.

For instance, in anticipation of the illustrations below (Section 4), when students are told to design a “smart shopping cart” using C-K theory, they identify that one generative rule is “a physical cart containing the goods the shopper wants to buy” (written in K). Hence, K-base contains a classical design rule. Immediately, they can break this rule by writing in C: “a smart shopping cart that is a physical shopping cart that doesn't contain the goods.” Building on this idea, they will go back and forth between C and K to finally expand the smart shopping cart into “a scanner that only ‘selects’ the items, in a supermarket that is redesigned as a showroom.”

3.2.3. C-K and the FEs in “collective creativity”

In C-K, the FEs in collective creativity appear in several ways. In a group, the C-K diagram of the group will tend to only represent the common knowledge base; consequently, the concepts will only be based on this knowledge (see Fig. 4). Seen from the point of view of one member of the group, this observation means that the student does not use knowledge that he did not have beforehand, as it was provided by another student of the group; similarly the student is unable to provide knowledge on a concept proposed by someone else. The group maintains a common knowledge base in K, that is, everybody uses this knowledge base, and concepts that could lead to the expansion or rediscussion of this knowledge base are neglected by the group.

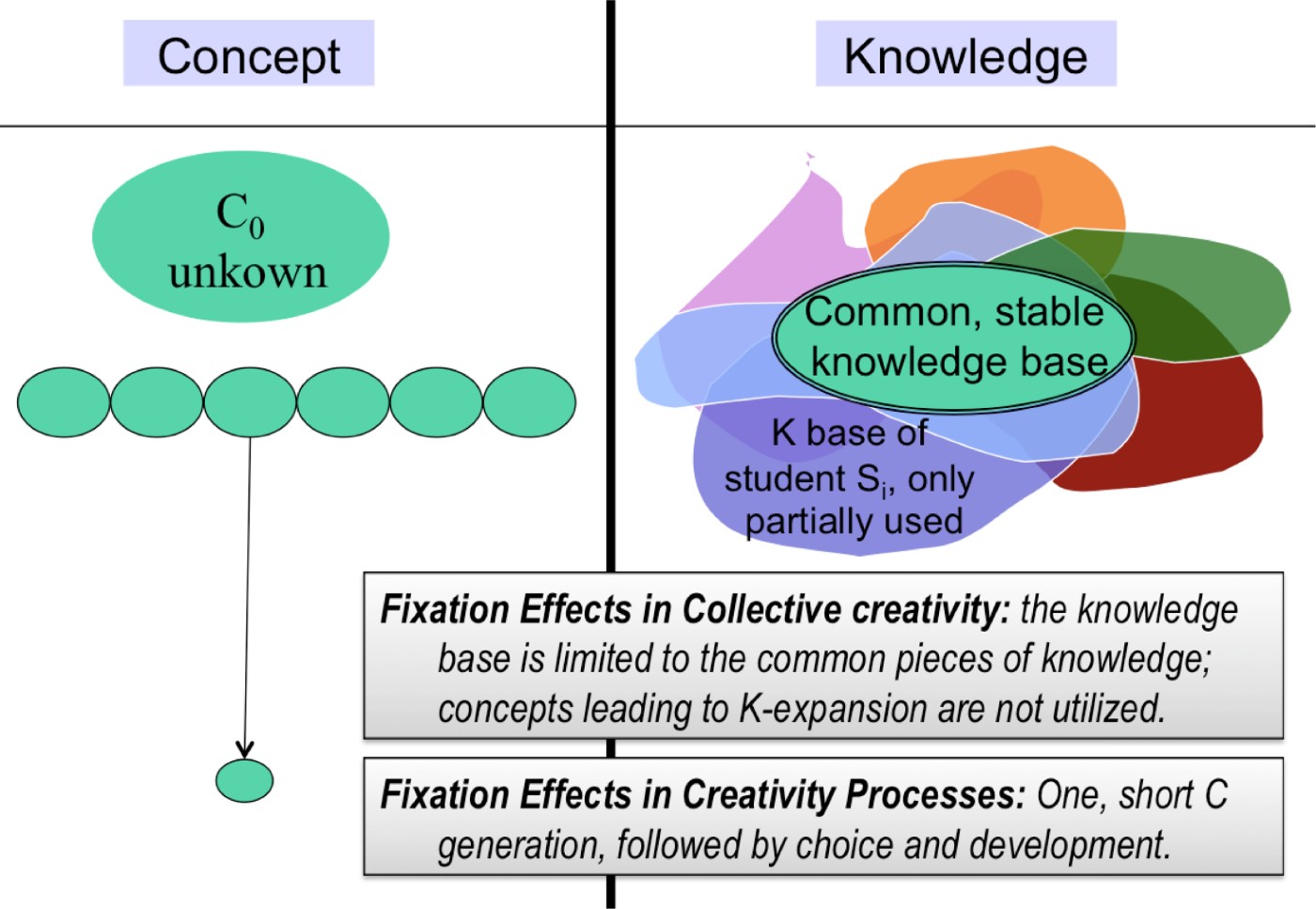
Fig. 4. A representation of the fixation effects in collective creativity and creativity processes. C, concept; K, knowledge. [A color version of this figure can be viewed online at journals.cambridge.org/aie]

C-K not only helps to make the “collective creativity” FE visible, but also helps to overcome it in several ways. First, the C-K diagram helps to provide an overview of the group's reasoning. By clarifying the design paths and the available knowledge bases, it helps students to make use of the knowledge provided by others or to provide knowledge on concepts proposed by others. Second, it becomes possible to give simple guidelines to create ideas that could only emerge in a group: for instance, ask individual students to identify a piece of knowledge that is new to them and to make use of it in one of their concepts and, conversely, ask them to provide one piece of knowledge on a concept that is new to them.

It can also help to make heterogeneous designers work together while still respecting the variety of their talents. For instance, C-experts and K-experts can be identified. To simplify, industrial designers are more likely to be C-experts, whereas engineers are more likely to be K-experts. The collective creativity FE would predict that engineers would have difficulty explaining and setting out their knowledge and designers would refrain themselves from breaking design rules. By clarifying the contributions of C-experts and K-experts, C-K helps them to collaborate.

3.3. Remarks on PBCL

When it comes to design teaching, and more precisely to innovative design teaching, PBL is often advocated as a means of learning about types of action. C-K-based learning might seem to be a distinct approach, but actually it merely makes some implicit hypotheses of the PBL approach more explicit. Recent debates on PBL (Kirschner et al., Reference Kirschner, Sweller and Clark2006; Hmelo-Silver et al., Reference Hmelo-Silver, Duncan and Chinn2007) show that PBL is a “scaffolded” process, relying on expert guidance, based on “particular reasoning strategies” (Hmelo-Silver et al., Reference Hmelo-Silver, Duncan and Chinn2007). Hence, teaching innovative design in PBL requires a better understanding of design thinking (Dym et al., Reference Dym, Agogino, Eris, Frey and Leifer2005). A theory of design thinking is extremely useful for design teaching, because it can be taught and learned in a relatively short time, in controllable processes, with evaluation and exercises to improve creative efficiency.

A design theory provides a means of organizing the learning process and orienting it toward the most critical points to be learned. Based on a design theory, it is possible to organize what we propose to call PBCL, which consists of teaching a design theory that can be related to critical cognitive and organizational issues and organizing, on this theoretical backbone, a curriculum that encompasses classical teaching (i.e., the disciplinary content in engineering science) and projects.

This process combines the advantages of classical PBL (collective experience of ventures into the unknown, motivation, real-life or quasi real-life situations, etc.) and the advantages of a theoretical approach (offering an integrated framework, supporting the discovery of complex and nonintuitive reasoning, avoiding student manipulation by enabling discussion and criticism of the process, etc.). It should be noted that Bauhaus' teaching, Peter Klimentitsch von Englemeyer's teaching or, more generally speaking, “engineering design teaching” (Erkens, Reference Erkens1928; Pahl & Beitz, Reference Pahl and Beitz1977), were actually a combination of theoretical teaching and PBL.

In a more general sense, it seems logical to base the learning concerning an action (learning to design) on the action itself (learning based on design projects), but learning about action can also be scaffolded by a theory. For instance, learning to act in uncertainty can be done by playing lotto; but this learning can also be enhanced by teaching probability theory or teaching statistical decision-making theory (Raïffa, Reference Raïffa1968; Savage, Reference Savage1972). What is the advantage of teaching a theory of the action? At the very least, it can help students realize that they think differently and do not approach uncertainty as predicted by probability theory. Students might also understand that probability theory performs better than human common sense in some uncertain situations. In both cases, the existence of a precise, rigorous theory offers students an increased capacity for reflexivity to face risk. Let us examine the advantages of decision-making theory:

1. 1. It increases the understanding of the “quality” of the outputs (what is a “good” decision? A decision made on a clear set of alternatives with well-identified criteria or, technically speaking, utility functions).

2. 2. It increases the means for action (clarify the value of new information, build subjective probabilities, etc.).

3. 3. It supports reflexivity (clarify counterintuitive notions, avoid the intuition traps; i.e., clarify the hazard decision tree and avoid the intuitive but misleading representation of “hazard decision”).

When describing the advantages of C-K in creative design, we found precisely the same types of advantages: a “good” innovative design is a design that has expansive partitions and varied alternatives, based on robustness and value criteria; “breaking the rules” and “learning” can be considered as essential means of action; students should be attentive to all kinds of FEs, from the “path of least resistance” to difficulty in staying in C and in structuring C without choosing and validating.

4.1. Type 1 case studies: Revealing the FEs in creative projects

This case study, named Artem, was conducted as a joint program for an art school (Ecole nationale supérieure d'art de Nancy), an engineering school (Ecole nationale supérieure des mines de Nancy) and a business school (Ecole de management de Nancy). Over a period of 1 year, groups of four to eight students from the three schools were asked to carry out various types of innovative projects. To assess the educational and creative aspects of the projects, six of them were studied by an educational psychologist, Robert Plety, and a professor of engineering. The research method used various empirical materials including video recording of the students' project meetings. C-K theory was selected by the team as a potential framework to assess the “creative” aspects of the students. The researchers received a short oral presentation of the theory and had access to the main papers about it. The authors of this paper had no contact with the Artem projects and only became acquainted with the findings through the research reports (Plety & Cremet, Reference Plety and Cremet2007). The main findings are as follows:

• • Combining design and creativity in the projects: Projects were initiated by a “brief” from a company, which left full freedom to the students. The integration of both design and creativity was completely natural to the students.

• • Concept formation and expansion: the students tended to call “concept,” not the first design brief, but the “feasible project goal,” derived from the brief agreed upon by the group after the first intensive discussions. Hence, the role of space C was entirely implicit and appeared in the form of intense work on the elaboration of the “concept.” As a result, there was no formal building of a set of concept variants with several degrees of elaboration. Nonetheless, the notion of concept expansion describes the students' activity very well.

• • Knowledge activation and generation: The development of the concept was obtained through a knowledge process where both activation and generation of new knowledge were intensive. Students had to go far beyond their own skills and managed several inquiries in areas that they had known nothing of beforehand. Moreover, the positive relationship between the expanding power of the concept and the intensity of the new knowledge generated was clearly observed see also Mabogunje and Leifer (Reference Mabogunje and Leifer1997). It is interesting that this knowledge acquisition process is often driven by the “feasible project goal.”

• • Two distinct project phases—Co-elaboration and cooperation: The project seemed to follow a linear sequence of two phases that were not linear themselves.

  1. 1. The first phase was described as “co-elaboration” by Plety and Cremet (Reference Plety and Cremet2007) and clearly corresponds to the period of intensive discussion, knowledge expansion and the generation of the “concept.” It can be interpreted as the phase of creative design.

  2. 2. The second phase was described as “cooperation.” It corresponds to the gradual elaboration of the concept, but Plety and Cremet (Reference Plety and Cremet2007) insist on the fact that the work division in this phase closely followed the students' curricula: engineering students behaved as engineers, art students as artists, and business students as managers. Thus, the project was more like a development program. It was also clearly observed that only during the creative design phase did all students behave very similarly, and it was difficult to recognize who was studying which curricula. It was as if the logic of creative design were universal and common to all the professional traditions.

• • Informal conceptual expansion: Case study 1 strongly supports the fact that “spontaneous” creative design is impeded by FEs: students tended to reduce, oversimplify or neglect the structuring of C, had difficulty in generating knowledge for “idea generation” and preferred to produce knowledge to realize the “feasible project goal.” The collective work focused on a single, consensual “solution” and did not divide up the exploration work. Finally, the group spontaneously divided the work into two phases, corresponding to the classical DT and CT phases.

Other case studies support this first analysis. Several groups of students, from two design schools (the Strate College industrial design school and the ENSAM engineering school) were asked to propose creative alternatives for a smart shopping cart. They had access to Internet. They had received no previous education in C-K. The students presented their results as a list of proposals, each proposal being more or less detailed with illustrations and technical and/or functional details. We authors have presented the proposals in the C-K framework to identify the concepts and the knowledge used to produce the concepts, giving the following archetypal pattern (see Fig. 5).

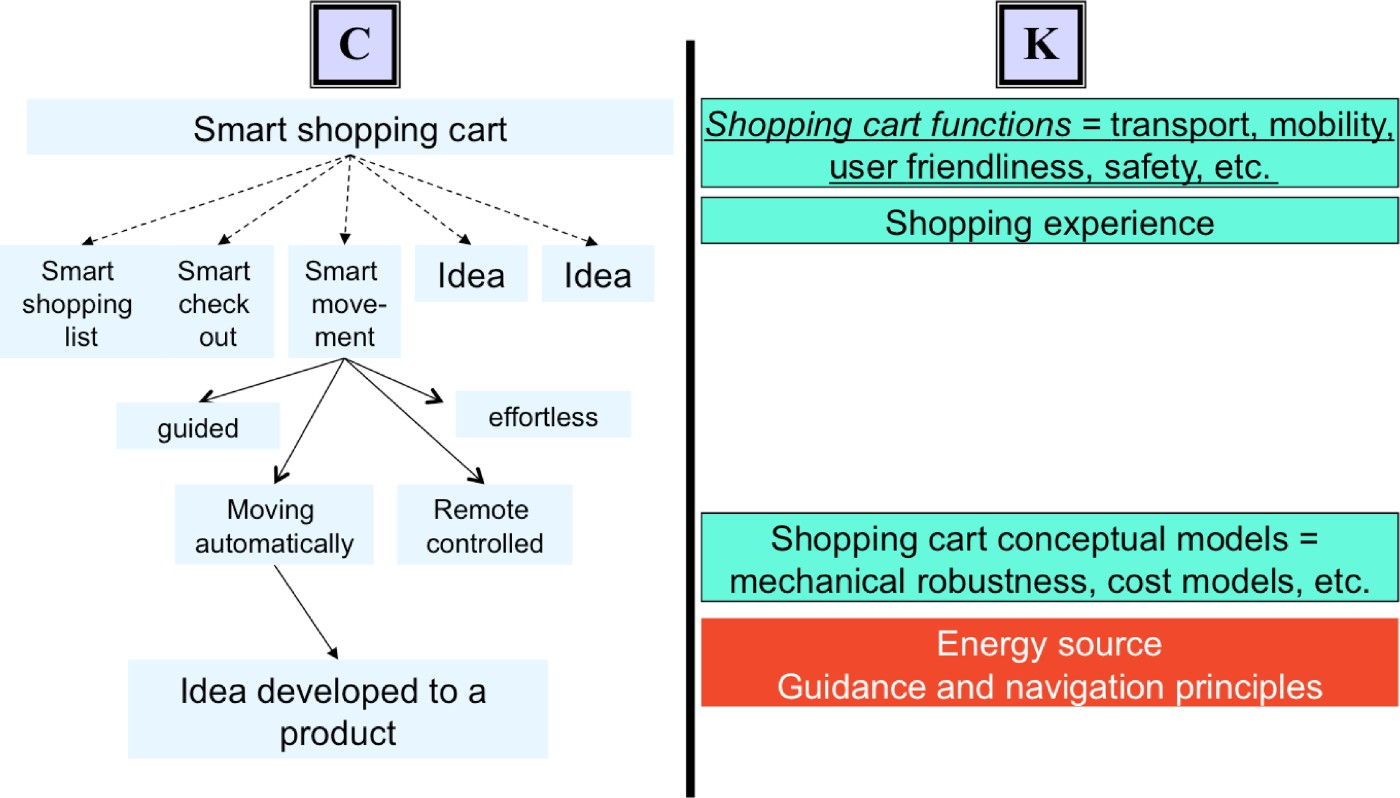
Fig. 5. The archetypal pattern of collective creativity without a concept–knowledge (C-K) scaffold. The white letters on a dark background in K indicates knowledge expansion, that is, knowledge acquired during the process (mainly through Internet connections). [A color version of this figure can be viewed online at journals.cambridge.org/aie]

This pattern illustrates the different forms of FEs:

1. 1. FE in the generation of alternatives: The divergence occurs as a first series of ideas; then the idea generation focuses on one main aspect (in this case, smart movement); finally, the idea generation process stops with the selection of one main idea that is then developed into a feasible product.

2. 2. FE in knowledge acquisition: Students make use of the knowledge they have but do not use Internet in the first phase; when the “feasible project goal,” that is, the “good” idea is selected, they use Internet to find means of implementing the idea (in this case, energy sources, techniques and guidance principles for driving a shopping cart automatically into a supermarket). Hence, knowledge is acquired, but mostly “after” the divergence phase.

3. 3. FE in collaborative creativity: There is no division of work during the generation of alternatives, when the whole team works together; the students share common knowledge and do not bring individual, specific knowledge to the group. In this process, students build on the others' ideas and move in the same main direction (in this case, different alternatives for smart movement).

4. 4. FE in creative processes: the group spontaneously organizes a two-phase process. In the first phase, students “diverge” to generate several ideas; in the second phase, students select an idea and try to develop it (CT).

What would have been the impact if the students had received preliminary training in C-K theory or if C-K theory had been given as a normative framework for the design work? Ideally, it would have been highly valuable to have Artem groups with and without training in C-K theory, but this was not possible. Case Study 2 nonetheless gave us interesting indications of the impact of C-K theory as a prescriptive guide to creative design.

4.2. Type 2 case studies: Controlling and overcoming the FEs

In this second type of case study, groups of students trained in C-K theory were required to use it to design a smart shopping cart. The only available source of new knowledge was free Internet access. The work was done in a very limited time of 2 h as a severe test of the power of the method. The case study was carried out eight times with groups of four students among engineering design, industrial design, and management students. It is important to note that the students were not told to be “creative” but to try to build the greatest possible expansion in both C and K. The final results consisted in complete C-K diagrams and not just one concept or a list of ideas. This brief was chosen to follow the IDEO experiment broadcast by ABC News in 1999 on the same brief. The broadcast was unknown to the students who took part in the case study.

These workshops were led by one or two coaches (professors). The role of the coach was strictly defined: they could only help students to apply the theory: they help to clarify whether a student's proposition is a concept or a piece of knowledge, they ask for clarification of the operators used to go from C to K and K to C, they suggest to go to C when students were blocked in K and vice versa. They did not provide any knowledge and did not formulate any C-proposition.

We start with the main observations, insisting on the contrast with the type 1 case studies.

Use of the method—Space C case: Despite its abstract aspect, C-K theory seemed easily accepted by the students. However, in practice, it was constantly observed that there was a spontaneous focus on discussions in space K and neglect in structuring space C. The coaches had to intervene to refocus on a thorough structuring of space C. In comparison to case study 1, it is interesting to find the same spontaneous behavior that tends to neglect working directly on the conceptual alternatives that are precisely the source of expanding partitions. It is as if it were true that analogy, metaphors and other “good ideas” come through pure serendipity. Once asked to clearly model space C, the students were themselves surprised by the power of the partitions generated by the simple interplay of the mechanisms alone.

Easy generation of original ideas: The mandatory use of the dual expansion process systematically generated a wide range of novel and surprising ideas including examples of rule-breaking creativity, where the notion of the “cart” was greatly enlarged and finally questioned in some cases far more than in the standard creativity process described above in the first type of case studies.

Fig. 6. The first example of a concept–knowledge (C-K) diagram completed by a group of students educated in C-K. The white letters on a dark background in K indicates knowledge expansion, that is, knowledge acquired during the process (mainly through Internet connections); the white letters on a dark background in C indicates an expansive partition in C, that is, partitions that add unusual attributes to the concept (e.g., the shopping cart is always provided by the supermarket, but the concept considers that part of the shopping cart is not provided by the supermarket). [A color version of this figure can be viewed online at journals.cambridge.org/aie]

Fig. 7. The second example of concept–knowledge (C-K) diagram prepared by students educated in C-K. The white letters on a dark background in K indicates knowledge expansion, that is, knowledge acquired during the process (mainly through Internet connections); the white letters on a dark background in C indicates an expansive partition in C, that is, partitions that add unusual attributes to the concept (e.g., the shopping cart is always provided by the supermarket, but the concept considers that part of the shopping cart is not provided by the supermarket). [A color version of this figure can be viewed online at journals.cambridge.org/aie]

C-K as a systematic method for innovative design: Finally, the type 2 case studies strongly support the idea that the creative process, which aims at novelty and value, corresponds to a systematic type of reasoning that is correctly captured by C-K theory. Training the students in this type of reasoning helps avoid any reference to a strange creative process believed to produce ideas coming from nowhere, without any clear process. In addition, students are often skeptical about the level of novelty they can reach by themselves or through a “creative effort” on their part. When they are convinced by the power of C-K theory, they usually feel far more at ease when faced with innovative projects.

These examples also illustrate how C-K serves to control and overcome the FEs:

1. 1. FEs in the generation of alternatives: A first evaluation of the capacity to overcome such FEs consists in measuring variety and originality. More precisely, the C-K diagrams enable students to find the “classical” solutions in C (Internet shopping cart, display added to a cart, etc.) and encourage them to explore alternatives to these classical alternatives. One way of doing so consists precisely in breaking the rules that lead to classical information (see the example of breaking the rule “owned by the supermarket”). This makes it possible to propose “strange” alternatives that are apparently “nonsensical” or, more precisely, are propositions without a logical status (the shopper goes to choose but does not bring goods home or, conversely, the shopper does not go to choose but brings things home!). It helps to keep them alive without killing them too fast and, above all, to begin to give them a logical status (showroom).

2. 2. FE in knowledge acquisition: A quantitative evaluation consists in measuring robustness and value criteria (i.e., knowledge on certain “killer tests” such as costs or reliability) and, more precisely, the number of criteria that were not usually associated to a shopping cart. More precisely, the C-K process makes it possible to carry out a rigorous, enriched state of the art review, including use analysis, stakeholders' interests (not only the shopper but also the supermarket or the goods manufacturer), modeling of shopping concepts (analyze a supermarket as a compromise between a logistics centre and a showroom) and provocative examples (analyze IKEA as a separation of these two supermarkets, the showroom on the one hand, the logistics center on the other hand). The acquisition of knowledge contributes to the generation of alternatives.

3. 3. FEs in collaborative creativity: FEs appear when there is a strict relationship of one participant—one concept—one knowledge base (often only the initial, common knowledge base). Because the students were obliged to work using the C-K method, they had to clarify their knowledge base and their concept, meaning that other students were able to use the clarified knowledge base or to build upon the explicit concept. We controlled this process by following how a piece of knowledge (respectively a concept) was initially proposed (explored) by one student or a group of students and then reused by another for exploring a concept (respectively activating another knowledge base). More generally, it appears that one piece of knowledge is used for several concepts and one concept leads to multiple knowledge bases: such a tight, coupled pattern is a symptom of the capacity to overcome the collective creativity FE.

4. 4. FEs in creativity processes: Following C-K theory, the students use the operators (C → K, K → C, K → K, C → C) that provide a better understanding of the creative process. We see phases of “in-depth” exploration in C (refinement of a concept) or in K (clarification of a knowledge base) or “in-breadth” exploration in C (generation of varied alternatives, based on a rigorous, often abstract model in K) or in K (generate a general model that helps to separate contrasted alternatives). Instead of two phases, we even saw quite complex divisions of work: certain teams were able to split into subgroups exploring alternative paths (in this case, one group explored the showroom, another worked on the other stakeholders). Some of these explorations led to new knowledge (in this case, the value of manufactured goods explored from the stakeholders perspective) that was used by the other subgroup (a showroom that helps the manufacturers to enhance the value of their products).

4.3. Conclusion and discussion on the evaluation of PBCL and its relevance

In this paper, we began with a summary of how recent advances on creativity help clarify the objectives of methods teaching how to be creative in engineering design. Whereas classical objectives strictly concern the outputs (creativity criteria), these works identify process criteria and focus teaching on the capacity to overcome the factors that limit creativity during the process. We identified four types of FEs (in the generation of alternatives, knowledge acquisition, collective creativity, and creativity process). We then showed how the C-K theory can help to teach how to overcome the FEs: C-K theory enables students to model the FEs, to identify and control them in the process, and finally, to overcome them. We illustrated this process with two types of educational case studies, based on a type of PBL that is strongly scaffolded by a theory.

It is interesting to note that the method helps to address design issues that are not easily address in the classical Simonian approach: in “wicked problems” (following Rittel & Webber, Reference Rittel and Webber1972) with “figural complexity” (following Schön, Reference Schön and Howard1990), certain design solutions are not easily connected to the design starting point. Our reading of the FE literature clarified what “easily” means: we identified four “obstacles,” that is, four FEs. In front of these FEs C-K is not a “mechanical” process; C-K theory provides the designer with a means to be self-reflective: C-K theory helps the practitioner to become aware of his own fixations and to overcome them. Hence, it should make him more able to make connections between pieces of knowledge that are not easy to connect.

We emphasize the need to address two strong issues of PBL in innovative design: evaluation and relevance.

Evaluation may be difficult if one has to evaluate “propositions that are neither true nor false.” However, the evaluation must account for the capacity to overcome the four types of FEs. It is not the C-proposition in itself that should be evaluated but the distribution of the C-propositions, related to the knowledge base. This is why four types of criteria can be used:

1. 1. for FEs in the generation of alternatives: variety, originality, capacity to find the classical solutions, and position original ones;

2. 2. for FEs in knowledge acquisition: robustness, value, capacity to build a rigorous state of the art review that does not neglect any aspect of the concept (science, uses, innovation competition, etc.) and includes provocative examples;

3. 3. for FEs in collaborative creativity: capacity to divide the work, to conduct contrasted explorations that will help each other (through sharing the newly acquired knowledge); and

4. 4. for FEs in the creativity process: capacity to maintain broad exploration at all levels in C and also to work on “quick and fast solutions” to speed up the innovation process.

One of the recurrent issues in PBL is to ensure that the case is relevant. Is the chosen project “real” enough? One way to assess this is to compare the educational project and real-life projects. For instance, we can compare the educational concept (smart shopping cart) with other industrial cases. The IDEO case shows that the concept was actually an acceptable concept for an industrial design firm. We can also compare the type of knowledge bases available in “real life” and the type of knowledge bases available in our cases: the students are not experts in shopping carts and have no education in this kind of product. However, this situation is quite credible because, in most companies, innovative design briefs make the actors go far beyond company expertise. Finally, we can compare the type of organizations in both cases. This is certainly the strongest difference, because no particular organization is specified in the C-K exercise, whereas companies often have strongly structured organizational processes. However, in both cases the professionals, as well as students, have to more or less invent a new form of organization. In this sense, the learning situation is doubtless quite realistic! Note that MINES Paristech has developed another way to address this question: one educational solution consists in organizing C-K interventions within companies, with company experts, and within their organizational setups (this educational method is not described here).

However, the issue of realism should be based on the criterion to be met by teaching, namely, “do students overcome the FEs?” The question becomes: does the exercise realistically illustrate the FE? In this perspective, one interest of the C-K-based PBCL is precisely to clarify the FEs to which students were submitted and then to analyze whether these FEs are realistic or not. In the case of the shopping cart, this gives the following analysis:

• • FEs in the generation of alternatives: The FE appeared when the display was seen as an accessory mounted on the shopping cart (solved by providing the plug for the user's own display device) or the shopping cart for the supermarket of today (solved by the showroom shopping cart). The students were hence “fixed” by the fact that the environment (the supermarket) was not in the scope of the work and that the firm's product (the shopping cart) had to be improved upon rather than significantly changed. This seems quite realistic, in the sense that engineers in a company would probably also be “fixed” in a similar way. Note that it helps to answer one critical question: is the initial brief “realistic”? It could be argued that the initial brief (smart shopping cart) tended to provoke the FE; and also that a brief like “a smart system to help the shopper to shop in a supermarket” would diminish the FE. It is difficult to answer this question without clarifying what the FE in the second case would be. However, we understand that, in an educational perspective, the real issue is not whether the brief “provokes” an FE but that the FE itself is realistic.

• • FE in knowledge acquisition: The FE appeared through the clarification of the initial knowledge base. The students apparently knew rather less than shopping cart designers. This means that the FE is somewhat weaker for students than for experts. The exercise therefore tends to underestimate the “knowledge acquisition FE.”

• • FE in collaborative creativity: It appeared when participants were reluctant to break away from the “legitimate” knowledge base or to propose “crazy concepts” and preferred to only build on the common knowledge base and work on their own ideas. In the exercise, there was no real issue in the “legitimacy” of expertise and in the risks taken by “rule breakers.” Hence, the exercise also minimized the collective creativity FE.

• • FE in the creativity process: It appeared when participants tended to use the classical “funnel” pattern, with a first phase of idea generation and a second phase of “development.” In this case as well, the exercise underestimates this type of FE.

This analysis helps to qualify the extent to which the smart shopping cart exercise was realistic, showing that it is more realistic when addressing the two first FEs than the last two.