1. INTRODUCTION
The built environment is considered at two distinct scales: the boundary conditions exemplified by building shells and urbanized territories and the embedded circulation systems of corridors and streets. Analytical models that consider interrelations between the two scales are especially important for the study of building types where the two have different life spans. For example, although office layouts are modified frequently due to changes in organizational models, their design and planning take into consideration the constraining effect of the permanent building shells (Duffy, Reference Duffy1974). Exhibition curators face similar issues, reconciling the ever-changing layout strategies and artifact contents with the permanent shells of museums and art galleries (Zamani, Reference Zamani2008). Such interrelations are also worth studying because boundary conditions and circulations systems are influenced by specific factors of distinct origin. Although building shells are affected by structural, environmental, and construction systems, interior layouts take into account factors that range from ergonomics to organizational models.
The effect of boundary on contained spatial systems has been an inquiry within architectural discourse for quite some time. In 1928, Krasil'nikov (Cooke, Reference Cooke1975) proposed a mathematical model to explain the relation between the geometry of floorplate and the travel time from the entrance to workplaces in a building. Floorplate shapes have been shown to affect the distance of travel between internal locations (Willoughby, Reference Willoughby1975; Tabor, Reference Tabor and March1976) and travel distance between day-lit strips in buildings (Steadman, Reference Steadman2003). Floorplate shapes in office buildings have been shown to affect the spatial integration (a measure of directional distance) of layouts (Shpuza & Peponis, Reference Shpuza and Peponis2008). Similarly, urban shapes have been shown to affect the integration of street networks in cities (Shpuza, Reference Shpuza2007).
Research in space syntax (Hillier & Hanson, Reference Hillier and Hanson1989; Hillier, Reference Hillier1996; Peponis & Wineman, Reference Peponis, Wineman, Bechtel and Churchman2002) has primarily studied contained space. This configurational approach scrutinizes relational patterns among discrete components of building interiors and public spaces in cities to explain the built environment as a social product. A substantial body of empirical research has demonstrated strong affinities between underlying configurational features of space and various aspects of spatial cognition, behavioral patterns, and social function. Originally, studies in space syntax assessed topological characteristics of space to evaluate its social function; the early work did not consider geometric shape. More recent developments in space syntax theory augment original topological descriptions of space with metrics for shape (Hillier, Reference Hillier1996). Street networks have been conceptualized as independent systems with their own internal logic tied to patterns of street connectivity, which evolve by resolving the paradoxes of centrality and visibility (Hillier, Reference Hillier1996, Reference Hillier1999). Experiments in partitioning grids have illustrated the dependence of grids on topological relations and explained the emergence of the street geometry of deformed grids. However, with the exception of the torus shape (Hillier, Reference Hillier1996), no attention has been given to the mutual effect of the boundary and structural pattern it contains in built environments. For example, the street structures of London and New York reflect not only patterns of the deformed wheel and the Manhattan grid, respectively, but also the cropping effect of Thames, Hudson, and East Rivers.
In summary, the effect of embedded circulation systems on boundary conditions is little understood. This study is aimed at testing the hypothesis that boundary shapes exhibit characteristics that are intrinsically tied to the generative principles underlying the circulation systems they contain, over and above the influences of site context. As a corollary, such features support morphological classifications in the built environment.
This study is aimed at describing boundary conditions in the built environment according to their two-dimensional (2-D) shape. The boundary shape is considered as a diagram of forces (Thompson, Reference Thompson1959) that originate from inside and outside the boundary, and results in a state of fit (Alexander, Reference Alexander1964). In buildings, these forces are exemplified by requirements for space use, accommodation of layouts, daylight, natural ventilation, building systems, structural limitations, and site constraints. In cities, they represent growth pressures, zoning regulations, the constraining effect of terrains, and the cost of travel between locations. For the purpose of this argument, the built environment is considered from the viewpoint of the social function of space (Hillier & Hanson, Reference Hillier and Hanson1989). Accordingly, the study tackles the understanding of boundary shape according to internal forces related to patterns of movement, co-presence, co-awareness, and encounter, without considering external forces such as the constraining effects of building sites and terrains. Shapes are regarded as byproducts of the potential internal movement, thus making it possible to gauge in turn the mutual interaction between boundary shapes and contained circulation systems.
The floorplate shape, or the 2-D shape of the slab of a particular floor, is defined according to the conventions used in architectural design. Building cores, shafts, stairs, ramps, atria, courtyards, and light wells are not part of floorplate shapes, and when located inside buildings, they constitute holes in its shape. The floorplate is one of the most permanent among building elements and is often tied to the structural integrity of the building. Holes are considered an integral part of a floorplate and remain unchanged as they provide vertical circulation, light, ventilation, and passage of conduits. Because of their permanence, for the purpose of this argument, floorplate shapes are considered only in their actual state and not according to shape hulls (i.e., ignoring holes).
The urban shape, or the 2-D shape of the urbanized territory, is defined according to the contiguity of its built form, disregarding administrative boundaries, and following two rules as follows. First, notwithstanding obvious physiographic barriers, one has reached the urban boundary when traveling outward from the city center one reaches the point where there are no buildings but only undeveloped land in both sides of a road. Second, roads that provide short-cut connections between outlying peripheral fringes are included in the urbanized territory. Holes in the urban shape are defined as areas located inside the urbanized territory unused for buildings, recreation, or industrial production. Examples of shape holes include agricultural land in the fringes of urban shapes; areas unsuitable for building such as rivers, ravines, steep slopes, bays, lagoons, ponds; and man-made features like canals and railroads. The shape hull results from removing the holes from the urban shape. In contrast to buildings, where the floorplate shape remains unchanged over the years, urban shapes are in continuous flux. Urban growth involves two kinds of processes: the outbound extension of urban shapes, and the infilling of shape holes. From the viewpoint of environmental protection, energy, and commuting time, the infill development of urban holes takes priority to the outbound urban extension. Therefore, the study considers the urban environments according to both the actuality of their urban shape and the potentiality of their shape hulls.
The argument is developed in four parts. First, a review of theories and methods of shape description examines applications suitable for the analysis of boundary shapes in the built environment. Second, two shape descriptions are proposed based on the human experience of moving through space. Third, samples of various classes of boundary shape in the built environment and nature are analyzed according to two measures. Fourth, a discussion addresses the typological classifications of boundaries in the built environment in general and the different states of covariance between two measures according to underlying circulation in particular.
2. METHODS OF SHAPE DESCRIPTION
In the review of methods for describing the compactness of shape, MacEachern (1985) identifies two main approaches for quantifying shape. The first includes methods that address shape uniqueness according to which no shapes that differ from each other can have equal descriptions. These methods employ multiple parameters and complex mathematical models for defining shape. Bunge (Reference Bunge1966) proposed a system of unique shape classification based on distances between selected vertices of a polygon. Similarly, the application of dual-axis Fourier analysis to shape analysis (Moellering & Rayner, Reference Moellering and Rayner1981) suggests a unique description of shape. More recently, the trivariate shape definition (Wentz, Reference Wentz2000) demonstrated that when three indices of edge, elongation, and perforation are used to describe shape, no two different shapes have the same set of numbers.
The second approach includes a vast array of methods that address specific aspects of shape, such as compactness, elongation, and indentation. In general, the indices used by geographers regard various relations among metric distances between shape vertices, perimeter points, and centroids; ratios between actual areas and areas of yardstick shapes; and perimeter (Haggett & Chorley, Reference Haggett and Chorley1969; March & Steadman, Reference March and Steadman1971; Austin, Reference Austin, Gaile and Willmott1984; MacEachern, 1985). Compactness is the single most considered aspect that has been formalized in a wide range of indices (Clark & Gaile, Reference Clark and Gaile1973; MacEachren, Reference Maceachren1985). Shape compactness, measured as the ratio between area and perimeter, has been employed widely by architects as a simple empirical measure for describing building plans (March & Steadman, Reference March and Steadman1971). However, this metric has limited accuracy. For example, it can be easily proven that a perimeter jagged in the small scale of local indentations may coincide with a compact shape. Overall, the application of geographical indices based on discrete metric elements for the analysis of the built environment is problematic because discrete elements characterize either local features of shapes or global features that are not related to the human perception of space.
Another class of methods for describing shape is based on infinitesimal representations. A shape is represented with modular units, and specific relations among all units are aggregated into an overall index. According to Blair and Biss (Reference Blair and Biss1967), a shape is divided into infinitesimal elements, and distances between all shape units to the center of gravity are aggregated to calculate an index of compactness. It is argued that this method overcomes the problems of dealing with cases of high degree of fragmentation, dispersion into islands, gross distortions, and punctured shapes. Taylor (Reference Taylor1971) uses the statistical distribution of metric distances within shapes to gauge the effects of elongality, puncturedness, fragmentation, and indentation.
Only a few methods proposed by research in space syntax address the properties of shape. The descriptions of architectural plans with s-partitions and e-partitions emphasize the importance of shape for determining the definition of elemental convex partitioning (Peponis et al., Reference Peponis, Wineman, Rashid, Hong Kim and Bafna1997). The inner spatial structure is considered an effect of bounding shape. Psarra and Grajewski (Reference Psarra and Grajewski2001) propose a robust description of space based on the visibility between tessellated units of the enclosing perimeter. However, the indices proposed by these two methods remain unchanged after affinity transformation of shape (parallelism, cross-ratio, and neighborliness) and therefore cannot be used for describing shape.
Recent studies have utilized representations of architectural and urban plans flood-filled with small tessellated units and have proposed spatial descriptions based on patterns of co-visibility between the units (Batty, Reference Batty2001; Conroy, Reference Conroy2001; Turner et al., Reference Turner, Doxa, O'Sullivan and Penn2001). Of particular interest to this argument are Turner et al.'s two indices, mean shortest path distance, calculated as the aggregate shortest path metric distance between all modular units, and visual mean depth, calculated as the aggregate of directional changes between all units. However, these methods describe spatial complexes according to properties of specific locations and regions in a spatial complex without compiling any overall shape index.
For the purpose of describing shapes in the built environment, the modular methods have a threefold advantage: first, these methods enable direct associations of representational units with continuous qualities of space, which is essential for describing large unpartitioned boundary spaces. Second, modular representations allow gauging the spatial qualities of the built environment in a configurational manner by considering relations among all shape units. Third, modular methods take into account dimensional aspects of shape and thus allow weighing the configurational analysis with metrics of size and distance.
From the viewpoint of understanding the effect of circulation systems on boundary shapes, configurational methods can be used to formulate descriptions that are compatible with configurational descriptions of circulation systems in buildings and cities. Movement has been recognized as a basic premise for understanding the built environment (Piaget & Inhelder, Reference Piaget and Inhelder1967; Gibson, Reference Gibson1979). Two measures of shape based on the human experience of moving through space, previously developed by Shpuza (Reference Shpuza2001) and Shpuza and Peponis (Reference Shpuza and Peponis2008), are enhanced for the purpose of this study.
3. RELATIVE DISTANCE (RD)
The first measure, RD, is an index of universal metric distance. It corresponds to the potential energy needed to cover distances between locations inside a shape. In contrast to analytical models that consider distance as an effect of shape, here, distances between points are used to characterize a shape. Shape is considered according to the structure of the field and as a derived entity of space (Koenderink, Reference Koenderink1990) whereby distance is used to define a particular aspect of shape according to an inside to outside approach. A shape is represented with modular square units, and shortest path inner shape distances are computed between pairs of units. The overall distance D for a shape is the sum of aggregated shortest path distances.

where d ij is the shortest path distance between two units i and j, and n is the number of units in a shape (Fig. 1).
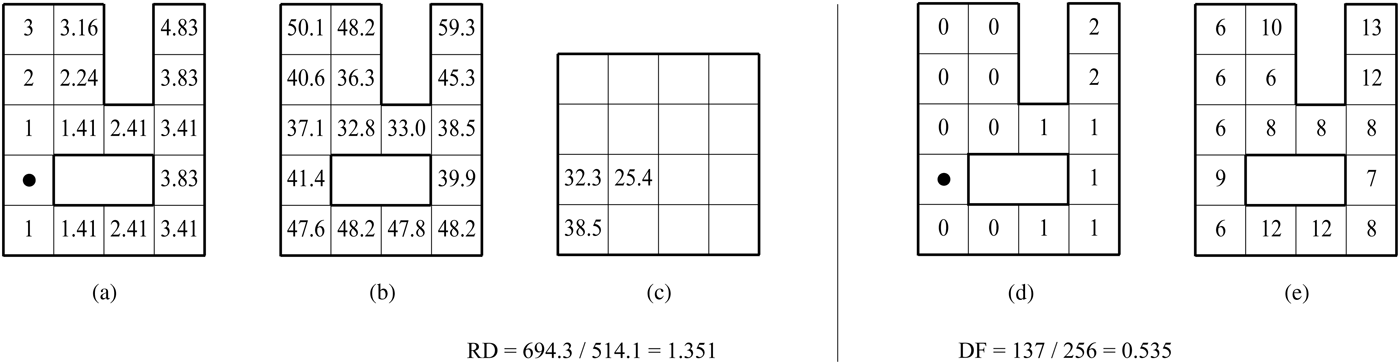
Fig. 1. Measures of shape: (a) short path metric distances from a particular unit in the shape, (b) aggregate distances for all units in the shape, (c) aggregate distances in the equal area square, (d) directional depth from a particular unit in the shape, and (e) aggregate directional depths for all units in the shape.
The measure of RD is expressed as the overall distance for the entire shape D normalized by the overall distance in an equal area square D eas (Fig. 1c).
Because shapes are not always represented with a number of units equal to a square, D eas is obtained by the linear interpolation between distances of the two closest square shapes D □. For example, for a shape represented with 110 units, D eas equals 66,690 after the interpolation between D □(100) = 51,615 and D □(121) = 83,272. The value of RD for a square therefore equals 1, whereas for a circle it equals 0.980. The RD increases as shapes become elongated or fragmented into wings or by holes.
For the square shape, when taxicab distance δ is used, the overall distance Δ□ is a function of the number of units used for representing the square (Shpuza, Reference Shpuza2006; Shpuza & Peponis, Reference Shpuza and Peponis2008). In contrast, when shortest path distance is used, the overall distance D □ follows a fuzzy logic and cannot be expressed as a function of representation units. However, in a square mapped with 4 units, the ratio Δ□/ D □ equals 1.172, for a square with 16 units it equals 1.245, whereas for fine representations of more than 3000 units, the ratio settles at 1.279.

Calculations with fine representations of large samples of shape indicate that RD ratios yield almost identical results when computed with taxicab distances and shortest path distances.
4. DIRECTIONAL FRAGMENTATION (DF)
The second measure is DF. This is an index of the universal change of direction of travel between locations in a shape and corresponds to the kinetic inertia of movement. Directional changes are measured according to visibility graph distances (Turner et al., Reference Turner, Doxa, O'Sullivan and Penn2001). The index is normalized for size by dividing the aggregate distance by the shape area.

where v ij is the visual depth or directional distance between two units i and j, and n is the number of units in a shape (Fig. 1d and e). The visual depth between two co-visible points is established as 0; therefore, DF equals 0 for a convex shape. The index varies slightly when a shape is represented with different numbers of units; however, it stabilizes for fine representations. The index yields almost identical results between calculating with visibility depth and overlapping convex depth as demonstrated by the strong correlation (r 2 = 0.926) for a sample of 50 urban shapes (Shpuza, Reference Shpuza2007). Fragmentation in shapes is achieved in two ways: by adding wings and increasing the jaggedness of the perimeter; by adding holes and increasing the size of holes in the shape.
For the purpose of this study, shapes are represented with fine meshes generally of 3000–8000 units, and with 29,000 units for a very complex shape such as Venice. The calculation of the two shape measures is carried out using the Java application Qelizë, which in its enhanced version supports the calculation of RD with both shortest path distance and taxicab distance, and DF with both visual depth and overlapping convex depth.
5. MORPHOSPACE OF COUPLED SHAPE MEASURES
A 2-D morphospace is proposed based on joint use of the developed measures of distance RD and directionality DF. Originating from studies in biology, the concept of morphospace has been used for the classification of built form based on topological characteristics of shape (Steadman & Mitchell, Reference Steadman and Mitchell2010). For the purpose of this study, the morphospace is defined according to the scatterplot between RD values of shape in the horizontal x axis, and DF values of shape in the vertical y axis. The morphospace bridges between two main disciplines of shape description. It conveys quantitative descriptions of two features of shape, thus belonging to morphometry. At the same time, the combined state of the measures produce qualitative topological classifications of shape, and thus also belongs to morphology.
Each shape occupies a specific position according to RD and DF pairs. As a corollary, the study tests the hypothesis that the coupled measures represent a unique description of shape; that is, no two different shapes have the same pair of RD and DF values. The morphospace characterizes both topological and dimensional features of shape, given the definition of the two measures. Its dimensionality is fixed and minimal, requiring only two shape indices. From this conceptual viewpoint, it differs from methods that utilize large numbers of arbitrary shape attributes for formal classification of built forms (Hanna, Reference Hanna and Gero2010).
The two proposed measures gauge distinct aspects of shape while showing a complex relationship with each other. On the one hand, an increase in shape fragmentation (i.e., higher DF) is always followed by a decrease in compactness (i.e., higher RD). The inverse of this relation is not possible; no fragmented shape can have the same compactness as the square, as illustrated by the lack of data points in the wedge region between the limit line and y axis (Fig. 2a). The definition of the equation of the line bounding the area of possible combinations of RD and DF is a mathematical problem sui generis that remains to be solved.

Fig. 2. (a) Series of polyomino shapes (n = 1 to 6) in morphospace; (b) scatterplot of sample of 48 decomino shapes including all (○) 16 cases with topological holes, (Δ) 16 cases with nontopological holes, and (•) 16 cases without holes.
However, on the other hand, it is possible to endlessly elongate a convex shape, thus increasing its RD, while keeping a constant DF of 0, thus occupying positions in the lower area of the plot along the x axis. The asymmetrical relationship between the two measures explains in part the preference for the concept of compactness by most geographical studies in the past. At the same time, this discussion illustrates how one measure alone cannot suffice to fully describe the complexity of shape.
6. THEORETICAL SHAPES
Boundary shapes of polyomino arrangements (Golomb, Reference Golomb1996) are analyzed for the purpose of understanding the potential covariance between the two measures. Starting with an elementary square tile, the increase of number of tiles, or polyomino order, produces combinations of contiguous shapes that can represent any actual shape. Polyomino families (n = 1 to 6; Fig. 3) are shown in morphospace with lines connecting data points ranked according to RD values (Fig. 2a). The higher order polyominoes include increasingly complex shapes. Although their family lines become progressively more jagged, they maintain an overall inverted “U” contour and offset incrementally up and toward the right, thus filling the area to the right of the limit line. However, most data points in each family are located along the left half of the inverted “U” lines, spanning between the origin and the apex; considered separately, these cases show high positive correlations between the two measures. This leads to the speculation that although it is possible to produce shapes that can occupy any position to the right of the limit lines in morphospace, most shapes occupy a narrower region with a positive correlation between the two measures starting at the (RD = 1, DF = 0) origin and extending toward the upper right.

Fig. 3. Polyomino shapes (n = 1 to 6) listed according to ascending relative distance values for each group.
The further increase of polyomino order generates shapes that contain holes. A second sample of theoretical shapes is constructed as a subset of 4655 decominoes (n = 10) containing all 16 instances with topological disc holes (Myers, Reference Myers2010), 16 cases randomly selected from 179 decominoes with nontopological holes, and 16 cases from compact shapes. The location of data points in the scatterplot reinforces the above trend with regard to the inverted “U” scatter and the accumulation of most data points along the left half of the crescent (Fig. 2b). Shapes with topological disc holes occupy a specific area in morphospace along the upper extremity of the scatter, the nontopological holes have a wider spread while maintaining a linear scatter, whereas the solid shapes fall across the entire span of the crescent. This raises the possibility that, when compared to solid shapes, shapes with holes represent distinct correlations between RD and DF. Theoretically possible correlations between the two measures are likely to have different specific actualizations in boundary shapes of various types of built form.
Mazes are another class of theoretical shapes that are generated by arranging square tiles according to compositional rules of a topological nature. Here, the boundary shapes of mazes are analyzed in order to understand the effect of underlying generative principles on the relationship between compactness and fragmentation of shape. Four kinds of mazes—braid, cavern, crack and perfect—are considered as examples of different rules concerning dead-ends, loops, junctions, inaccessible areas, walls, and passages. They are generated using Daedalus software (Pullen, Reference Pullen2011) in four series, including five shape groups of 3 × 3, 4 × 4, 5 × 5, and 6 × 6 sizes, totaling 80 cases (Fig. 4).

Fig. 4. Mazes generated according to crack, cavern, braid, and perfect algorithms in sizes 3 × 3, 4 × 4, 5 × 5, and 6 × 6, respectively. Shapes are listed according to ascending relative distance values for each group.
For each series, shape groups are shown in morphospace with lines connecting data points ranked according to RD (Fig. 5). The increase of DF indicates higher maze complexity. The relative positioning of the four-maze series in morphospace illustrates that complexity increases from crack to cavern, to braid, to perfect. In addition, the increase of maze size leads to more complex shapes as indicated by the higher location of incremental size groups in the plot. In crack mazes, the offset among groups is smaller and confined to comparable RD values, thus indicating small increase of complexity due to size increase, and that complexity is achieved while maintaining rather stable compactness. In contrast, size increase in perfect mazes leads to a rapid increase in complexity that is equally matched by increased elongation of shape. Considered together, the 80 mazes show a strong and significant correlation (r = 0.843, p < 0.001). Unlike polyominoes, the morphogenetic rules in mazes are manifested in a close relationship between RD and DF of boundary shapes. This raises the premise that various types in the built environment occupy distinct regions of morphospace with specific correlations between compactness and fragmentation.

Fig. 5. Morphospace plots of series of crack, cavern, braid, and perfect mazes, generated with 3 × 3, 4 × 4, 5 × 5, and 6 × 6 sizes, respectively. For clarity, only braid series are labeled.
7. ACTUAL BOUNDARY SHAPE CLASSES
Six samples of boundary shapes from various classes in the built environment and physical geography are analyzed with the twofold purpose of understanding their position in the proposed morphospace and inquiring into the effect of underlying circulation structures on boundary shape conditions.
Houses are a built type with elementary circulation, in both topological and metric terms, that links rooms and open plan components. The requirement for easy access between spaces often leads to compact forms. A sample of 50 detached houses is selected based on 20th century design masterpieces (Davies, Reference Davies2006; Table 1, Fig. 6). House floorplates are analyzed according to RD and DF. The plot between the two measures shows a weak correlation, suggesting that elementary circulation systems are associated with a wide range of conditions of boundary shapes that lack a clear relationship between compactness and fragmentation (Fig. 13a).

Fig. 6. The sample of 50 house floorplates listed according to ascending relative distance values.
Table 1. Catalogue of the sample of 50 houses listed according to ascending relative distance values

Office buildings represent a built type with a close relationship between main circulation and floorplate geometry (Shpuza, Reference Shpuza2006; Shpuza & Peponis, Reference Shpuza and Peponis2008). Office floorplates are, to some degree, offset projections of the main circulation system given specific depths of leasing space and rooms (differences between open plan and cellular configurations not withstanding). It is thus to be expected that office floorplates exhibit strong typological features that position them in distinct areas of morphospace. This study recognizes two fundamental categories of main circulation in offices: ring and linear. Ring circulation systems are those where there exists at least a second alternative path between two positions along the main circulation system. By contrast, linear circulation systems offer only one path between such locations. A subsample of 50 ring office buildings (Table 2, Fig. 7; Pile, Reference Pile1976; Bedarida & Milatović, 1991; Duffy & Powell, Reference Duffy and Powell1997; Myerson & Ross, Reference Myerson and Ross1999; Various authors, 2004–2009; Hascher et al., Reference Hascher, Jeska and Klauck2002; Shpuza, Reference Shpuza2006; Gregory, Reference Gregory2008; van Meel, 2010; Weston, Reference Weston2010) and a subsample of 50 linear office buildings (Table 3, Fig. 8; Pile, Reference Pile1976; Duffy & Powell, Reference Duffy and Powell1997; Bedarida & Milatović, Reference Bedarida and Milatović1991; Myerson & Ross, Reference Myerson and Ross1999; Albrecht & Broikos, Reference Albrecht and Broikos2000; van Meel, Reference van Meel2000; Hascher et al., Reference Hascher, Jeska and Klauck2002; Blaser, Reference Blaser2003; Shpuza, Reference Shpuza2006; Futagawa, Reference Futagawa2008; Gregory, Reference Gregory2008; Weston, Reference Weston2010) was selected based on best practice examples of office buildings from 1904 to the present. There exist strong and significant correlations between RD and DF for both ring office floorplates (r = 0.811) and linear ones (r = 0.846). However, the correlation decreases (r = 0.674) when the two subsamples (100 cases) are analyzed together. The data points from each subsample occupy separate regions in morphospace as illustrated by the marginal overlap between them (Fig. 9). The linear regressions of the two subsamples exhibit a significant inequality (Zar, Reference Zar2009), thus confirming that the two categories of office buildings constitute different ways of correlating compactness and fragmentation. Ring offices show a greater variety of shape fragmentation, whereas linear offices show a greater variety of shape compactness. Topological differences between the two kinds of underlying main circulation systems are therefore materialized in striking morphological disparities between two classes of floorplate shape.

Fig. 7. The sample of 50 office floorplates with ring circulation listed according to ascending relative distance values.

Fig. 8. The sample of 50 office floorplates with linear circulation listed according to ascending RD values.

Fig. 9. Fifty ring office floorplates (gray) and 50 linear office floorplates (black) compared according to relative distance and directional fragmentation.
Table 2. Catalogue of the sample of 50 office floor plates with ring circulation listed according to ascending relative distance values

Table 3. Catalogue of the sample of 50 office floor plates with linear circulation listed according to ascending relative distance values

Urban shapes are generated upon circulation structures of street networks according to the process of filling urban blocks. Street networks are complex systems with high degree of connectivity and choice. A sample of 50 urban shapes was selected from the Adriatic and Ionian littoral zones (Google Earth, 2006–2010). It includes some of the largest populated centers and a few towns of historical significance on the Italian coast, and 25 urban centers with populations greater than 10,000 on the coast of Slovenia, Croatia, Montenegro, Albania, and Greece. These cities display a wide diversity of urban shapes affected by various physiographic conditions of bays, lagoons, deltas, islands, promontories, and narrow strips of land bound by the shoreline and hilly terrains (Fig. 10). The analysis of actual urban shapes shows a weak and insignificant (r = 0.225) covariance between the two indices. However, when urban shape hulls are analyzed (i.e., holes in the urban shapes are ignored), a strong and significant (r = 0.690) correlation emerges (Fig. 13b). This indicates that urban forms internalize the effect of holes to exert a strong balance between compactness and fragmentation and overcome apparently insurmountable obstacles of the terrain.

Fig. 10. The sample of 50 urban shapes of Adriatic and Ionian coastal cities listed according to ascending shape hull relative distance values.
Two samples of boundary shape from physical nature are analyzed for the purpose of inquiring into the relationship between RD and DF. One includes the shapes of the 50 largest islands in the world (Fig. 11), and the other includes the shapes of world's 50 largest lakes with stable water levels (Fig. 12). Island and lake shapes are obtained from the Natural Earth (2010) database using conformal WGS 1984 projections according to specific UTM zones. Despite a seemingly wide variety of shapes that lack human order, the two samples combined reveal ambivalent relationships between the two measures. Although island shapes show a weak correlation between RD and DF (Fig. 13e), lake shapes show a strong and significant correlation (r = 0.711; Fig. 13f). The correlation for lake shapes improves further (r = 0.764) if the outlier, Lake Saimaa, is excluded. The explanation of this discrepancy between island and lake shapes, if indicative of any geophysical phenomenon, falls to the domain of physiographic studies. For this argument, of interest the fact that correlations between RD and DF are not limited to types in the built environment, but also include classes in nature.

Fig. 11. The shapes of the 50 largest islands in the world listed according to ascending relative distance values.

Fig. 12. The shapes of the 50 largest stable lakes in the world listed according to ascending relative distance values.

Fig. 13. Scatterplots between relative distance and directional fragmentation for six classes of boundary shape.
The morphospace constructed according to the two measures is used for the comparative study of form. Each class from the built environment and nature is represented with a polygon that is drawn according to the convex hull of data points in the scatterplot (Fig. 14). In general, class polygons are positioned in the zone with a positive correlation between RD and DF, just to the right of the limit line thus illustrating an overall balance between distance and directionality for actual shapes. The correlation between RD and DF for 300 combined actual shapes of houses, cities, offices, islands, and lakes is r = 0.679 (p < 0.001), and for 380 cases including mazes is r = 0.901 (p < 0.001). No class extends to the wedge region on the lower right alongside the x axis, which would include extremely elongated convex shapes. Houses are positioned in the lower left corner of the morphospace and include compact and simple floorplate shapes. The small extent of this polygon denotes little variance among house shapes. Urban shape hulls are positioned further above along the y axis. Two subsamples of office buildings, shown in gray, extend further on both directions to include a wide range of forms that are still bound inside distinct wedgelike regions. Mazes are positioned up and to the right and include the most complex shapes. Lakes include a wider variety of shapes than islands as indicated by the extent of the polygon high and to the right in the morphospace.

Fig. 14. The position of boundary shape classes in morphospace.
8. DISCUSSION
This study contributes a configurational approach situated within the discipline of space syntax for analyzing shape based on two elemental experiences of moving through space: covering distances and changing direction of travel. Boundary shapes are considered according to a balanced diagram of forces, of which the internal forces exerted by circulation systems in buildings and street networks in cities is given priority. The study is developed on the premise that the dialogue between centrality and visibility (Hillier, Reference Hillier1996) in circulation systems and street networks affects boundary shapes to maintain a close relationship between compactness and fragmentation and manifest features of emergence and dynamic order in the built form (Hillier et al., Reference Hillier, Penn, Hanson, Grajewski and Xu1993; Hillier, Reference Hillier1999). The proposed method of describing shape takes into account dimensional aspects of form and weighs the configurational analysis with metrics. It contributes normalized shape indices that do not depend on the number of representational units. In contrast to measures of shape based on the description of perimeter, here a space to shape approach is used whereby conditions or each location in space contribute to the shape description.
This paper suggests important implications for the study of form. First, the simultaneous description of shape according to RD and DF suggests a “unique” approach to shape description. The empirical analysis of 484 shapes in eight samples shows that no two shapes have the same pair of values for RD and DF. The claim remains to be tested further with empirical studies of larger data sets of shapes.
Second, it is shown that actual boundary shapes of various classes in the built environment occupy distinct regions in morphospace and utilize a specific portion of combinations that are theoretically possible.
Third, from the viewpoint of the interaction between boundary shape and embedded circulation, it is suggested that specific conditions of shape for various classes are mediated by the configuration of the underlying main circulation. Elementary circulation systems, such as for detached houses, show weak correlations between compactness and fragmentation of floorplate shapes. In contrast, developed circulation systems in offices and cities are matched by strong correlations between distance and directionality of floorplate shapes and urban shapes. Furthermore, configurational disparities between ring and linear circulation systems in office buildings are manifested in distinct classes of floorplate shapes that occupy separate regions in morphospace. This economy of balancing various degrees of distance and directionality points to the application of “principles of least action” (Mayer, Reference Mayer1877) underlying the generation of man-made boundaries.
The study contributes unique descriptive measures of shape, a morphospace of coupled shape measures, and a comparative approach to the study of built environment and nature. The paper raises theoretical implications for understanding the intricate relationship between boundary and circulation in the built environment and for supporting experimental and generative algorithms in aid of design and planning.
ACKNOWLEDGMENTS
The author thanks Sean Hanna and the anonymous reviewers for their constructive recommendations, John Peponis for the criticism that led to a wider scope of argumentation for the study, Martin Scoppa, who facilitated the projection of geographical shape files, and Fisnik Shpuza, who generously programmed the latest version of Qelizë.
Ermal Shpuza is an Associate Professor of architecture at Southern Polytechnic State University. He teaches architectural and urban design studios and courses on spatial morphology, urban design theory, and environmental technology. He is a registered architect with many years of practice experience. His research interests span architectural and urban morphology, workplace environments, Mediterranean postindustrial urban history, and design computing.



















