Introduction
Background and objective of study
In recent years, there has been an increasing concern about the mobility needs of the ageing population in many developed countries (Bedard et al. Reference Bedard, Isherwood, Moore, Gibbons and Lindstrom2004, Reference Bedard, Porter, Marshall, Isherwood, Riendeau, Weaver, Tuokko, Molnar and Miller-Polgar2008; Korner-Bitensky et al. Reference Korner-Bitensky, Kua, von Zweck and van Benthem2009; Marshall et al. Reference Marshall, Spasoff, Nair and van Walraven2002; Mayhew, Simpson and Ferguson Reference Mayhew, Simpson and Ferguson2006; McCarthy Reference McCarthy2003a, Reference McCarthy2005; Nasvadi and Vavrik Reference Nasvadi and Vavrik2007; Owsley, Stalvey and Phillips Reference Owsley, Stalvey and Phillips2003; Tay Reference Tay2006, Reference Tay2008; Weaver et al. Reference Weaver, Bédard, McAuliffe and Parkkari2009). The demographic profile and thus, the profile of drivers in many countries, are undergoing significant changes. In most developed countries, the population is ageing as the baby-boomer generation matures. Furthermore, the new generation of seniors is expected to drive more frequently and continue to drive longer than their previous counterparts.
The expected increase in the number of ageing drivers on the road has generated much concern among some road safety researchers and policy makers because of their anticipated decrease in driving ability and the disproportionate attention given to their age by the media when they are involved in a crash (Tay Reference Tay2006, Reference Tay2008). These perceptions, supported by numerous studies on their driving performance, have generated frequent calls in many countries for policy makers to tighten the licence renewal process of ageing drivers (di Stefano and Macdonald Reference di Stefano and Macdonald2003; Dulisse Reference Dulisse1997; Evans Reference Evans2004; Langford et al. Reference Langford, Fitzharris, Koppel and Newstead2004; Lyman et al. Reference Lyman, Ferguson, Braver and Williams2002; Molnar et al. Reference Molnar, Byszewski, Marshall and Hing2005; Owsley, Stalvey and Phillips Reference Owsley, Stalvey and Phillips2003; Road Safety Committee 2003; Rock Reference Rock1998; Transportation Research Board 1994).
A rational approach to policy making requires that the effects of different licence renewal requirements on road safety be well understood and any policy recommendations be based on scientific evidence. Despite the extensive literature examining the physical and cognitive attributes that contribute to the performance of ageing drivers, there are only a limited number of scientific studies that examine the impact of different re-testing and licence renewal policies on crashes among ageing drivers. Many studies have found that the ability to drive has a significant effect on the wellbeing of our senior citizens (Fildes et al. Reference Fildes, Lee, Kenny and Foddy1994; Liddle, McKenna and Broome Reference Liddle, McKenna and Broome2004; Marottoli et al. Reference Marottoli, Mendes de Leon, Glass and Williams1997, Reference Marottoli, Marottoli, Mendes de Leon, Glass, Williams, Cooney and Berkman2000; Organisation for Economic Cooperation and Development 2001; Oxley and Charlton Reference Oxley and Charlton2009; Ragland, Satariano and Macleod Reference Ragland, Satariano and Macleod2005) and efforts need to be invested in ensuring that their driving privileges are not restricted unnecessarily.
The purpose of this paper is to examine the relationship between different re-testing and licence renewal policies and the crash rates among ageing drivers. Using licensing and crash data from five Canadian provinces from 1998 to 2004, this study aims to test if more stringent licensing policies are correlated with lower crash rates. It should be noted that the policy implications from this study may be applicable to other developed countries with similar ageing populations and mobility profiles that are also grappling with this difficult policy issue.
To provide some more background on this important policy issue, a review of the relevant literature will be provided next, followed by an overview of the ageing driver policies and practices in Canada. In the second section, a conceptual framework relating licensing policies and practices to crash rates will be presented, followed by a description of the data used and the methodology employed in this study. The results of the data analysis will then be discussed, and some concluding remarks will be provided in the final section.
Literature review
In an early and frequently cited study that examined the effectiveness of different testing and licence renewal policies for ageing drivers, Levy, Vernick and Howard (Reference Levy, Vernick and Howard1995) assessed the relationship between drivers' licence renewal policies and fatal crashes involving drivers 70 years or older. Using data from the United States of America (USA) between 1985 and 1989, Poisson regression models were estimated to isolate the effects of mandatory vision tests, and/or road tests on fatal crashes involving senior drivers. Their study found that state-mandated vision screening was associated with lower fatal crash risks for senior drivers. In contrast, the knowledge test and on-road test provided no significant reduction in crashes.
In another early study that was widely cited, Rock (Reference Rock1998) examined the effects of increased restrictions and testing for seniors in the American State of Illinois. In late 1989, Illinois revised the length of licence terms and renewal requirements for older drivers. The term was shortened from four to two years for those aged 81–86 and one year for those above the age of 86. A mandatory road test, which had been required at renewal for all drivers aged 69 and over, was eliminated for those who were 69–74 in age. He concluded that eliminating the road test for those aged 69–74 did not appear to have any negative impact. He also concluded that the more frequent renewal periods for those above 80 years old did not appear to produce any benefit.
Using data from January 1990 to December 2000 from the Fatality Analysis Reporting System, Grabowski, Campbell and Morrisey (Reference Grabowski, Campbell and Morrisey2004) performed regression analyses to estimate the effects of state-level driver licensure laws, such as in-person renewal, vision tests, road tests and frequency of licence renewal, on older driver fatalities in the USA. The authors concluded that in-person licence renewal was related to a significantly lower fatality rate among the oldest drivers (85 and above) but not the two younger groups of ageing drivers (65–74 and 75–84), and state laws mandating vision tests, road tests, and more frequent renewals were not associated with a lower fatality rate among older drivers.
In a study using state-level data from Australia between 1994 and 1998, Langford et al. (Reference Langford, Fitzharris, Koppel and Newstead2004) simply compared the number of fatal crashes per population and number of serious crashes per population in different states. The authors computed the relative fatal crash risk and relative serious crash risk for ageing drivers who were 80 years of age and older using the State of Victoria as the reference. The authors concluded that older drivers in jurisdictions with age-based mandatory assessment programmes were not safer than drivers in a jurisdiction without mandatory assessment. In another study, Langford et al. (Reference Langford, Bohensky, Koppel and Newstead2008) compared the number of fatalities per licensed driver between the Australian states of Victoria which had very few restrictions and New South Wales which had more restrictions. The authors concluded that age-based mandatory assessment programmes did not have demonstrable safety benefits.
Ageing population and driver licensing in Canada
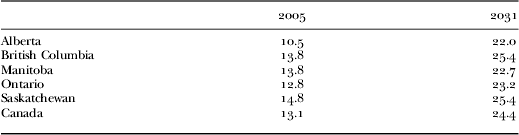
Canada's population is ageing and the number of older drivers is increasing rapidly as a result of lower birth rates, baby boomers’ maturation and increased longevity. Between 1981 and 2005, the proportion of older persons in Canada grew from 10 to 13 per cent. In all the projection scenarios, the proportion of older people would increase more rapidly in the coming decades, reaching between 23 and 25 per cent in 2031 and between 25 and 30 per cent in 2056 (Statistics Canada 2005). Table 1 shows the predicted changes in proportions of ageing population in Canada and its five large provinces: Alberta, British Columbia, Manitoba, Ontario and Saskatchewan.
As the proportion of senior citizens in the Canadian population increases, the proportion of ageing drivers on the roads is also expected to increase and will comprise a substantial group of the driving population. Since ageing drivers have a relatively higher crash rate per distance travelled, there has been considerable interest in the testing and renewing of driving licences for ageing drivers (Bedard et al. Reference Bedard, Isherwood, Moore, Gibbons and Lindstrom2004, Reference Bedard, Porter, Marshall, Isherwood, Riendeau, Weaver, Tuokko, Molnar and Miller-Polgar2008; Scialfa et al. Reference Scialfa, Ference, Boone, Tay and Hudson2010; Tay Reference Tay2008).
The regulation of driver licensing for ageing drivers, however, is a sensitive issue with many political, social, equity, financial as well as health and wellness considerations. Hence, different provinces have adopted different policies that are deemed to best meet their local needs. It is thus insightful to compare the licensing procedures for some of the main provinces like Alberta, British Columbia, Saskatchewan, Manitoba and Ontario. A sample of the different licensing policies for ageing drivers in five Canadian provinces is presented in Table 2.
Table 2. Licensing requirements for ageing drivers in five Canadian provinces

Note: SGI: Saskatchewan Government Insurance.
Source: National Highway Traffic Safety Administration (2003).
From Table 2, it is quite clear that British Columbia has a more lenient licensing policy towards ageing drivers than Alberta, and Ontario appears to have a more stringent licensing policy than Alberta. Both Saskatchewan and Manitoba require the driver to pass a visual acuity test while Manitoba also requires a visual test for horizontal field. These test requirements appear to be slightly more restrictive than Alberta and they both have a shorter renewal cycle of one year. Overall, Ontario appears to have the strictest and British Columbia appears to have the most lenient licensing policy for ageing drivers in the five major provinces in mid and western Canada, with Alberta, Saskatchewan and Manitoba positioned somewhere in the middle.
Methodology, data and approach
Conceptual framework and hypotheses
Theoretically, the safety relationship between licensing requirements and collision rates is hypothesized to involve two elements. First, if licensing requirements become more stringent due to an increase in the number of tests or a reduction in licensing period, for example, this change will increase the cost of renewing a licence. As the cost increases, demand for a driving licence is expected to decrease due to the Law of Demand in Economics. This reduction will decrease the level of exposure and hence, reduce the expected collision rate. Second, if the additional tests introduced are reliable and valid, then they are supposed to reduce the number of high-risk drivers on the roads. Hence, the average number of collisions per driver is expected to decrease, thereby resulting in fewer collisions. All else held constant, as licensing becomes more stringent for drivers in general and ageing drivers in particular, the collision rate is expected to decrease.
However, this relationship is moderated or mediated by several factors. Many ageing drivers self-regulate and decrease their exposure by driving less frequently (Abdel-Aty, Chen and Radwan Reference Abdel-Aty, Chen and Radwan1999; Newbold et al. Reference Newbold, Scott, Spinney and Kanaroglou2005; Owsley, Stalvey and Phillips Reference Owsley, Stalvey and Phillips2003; Raitanen et al. Reference Raitanen, Tormakangas, Mollenkopf and Marcellini2003; Tay Reference Tay2006, Reference Tay2008). They also reduce their risk levels by driving less at night, driving slower, driving during off-peak hours and driving only in familiar environments (Abdel-Aty, Chen and Radwan Reference Abdel-Aty, Chen and Radwan1999; Newbold et al. Reference Newbold, Scott, Spinney and Kanaroglou2005; Owsley, Stalvey and Phillips Reference Owsley, Stalvey and Phillips2003; Raitanen et al. Reference Raitanen, Tormakangas, Mollenkopf and Marcellini2003). These self-regulatory actions will reduce the effectiveness of the externally imposed licensing requirements and regulations. This behavioural adaptation may explain why several studies have found little or no correlation between test performance and crash outcomes (Anstey et al. Reference Anstey, Wood, Lord and Walker2005; Scialfa et al. Reference Scialfa, Ference, Boone, Tay and Hudson2010).
Moreover, the choice of licensing policies and practices may not be totally independent or exogenous. Often, jurisdictions with a more severe social issue may be able to implement tougher policies and practices than jurisdictions that do not have the same level of the problem. Similarly, it is quite likely that provinces with higher crash rates may be more likely to impose more restrictions on licence re-testing and renewal than provinces with lower crash rates. If this is the case, then a positive relationship may be observed between stricter licensing policies and crash rates among the different provinces.
Although a stricter testing and licensing regime may prevent some at-risk drivers from driving, and thus reduce the overall crash risk, it may also have some unintended consequences on some of the drivers who are able to renew their licences. For example, it may induce some drivers to be over-confident and thus compensate by driving more frequently or driving in more risky situations. A stricter testing and licensing regime may reduce the incentive of some drivers to self-regulate their driving. This behavioural adaption is consistent with the risk compensation hypothesis in economics (McCarthy and Talley Reference McCarthy and Talley1999; Peltzman Reference Peltzman1975; Tay Reference Tay2006) and risk homeostasis theory in psychology (Wilde Reference Wilde1994).
Data collection
Data on licensing and crashes from 1998 to 2004 were extracted from the official reports published by the departments of transportation in five large provinces in the middle and western regions of Canada: Alberta, British Columbia, Manitoba, Ontario and Saskatchewan. Of the 13 provinces and territories in Canada, these five accounted for 68.9 per cent of the Canadian population. Besides the main variables of interest, several proxy variables were used to capture the effect of exposure. These variables included unemployment rates, gasoline sales and population. These data were collected from various reports published by Statistics Canada over the years.
In addition to the above secondary data collection, a simple survey was also conducted to check the rating of the licensing requirements done by the research team. The description of the licensing requirements for ageing drivers were presented to 35 participants of a road safety course and the participants were asked to rank the different requirements using a five-point scale, with one being the least restrictive (easiest to get a licence) and five being most restrictive (hardest to get a licence). The main reason for using this sample was convenience. An added advantage of using this sample was that participants in the sample possessed some basic knowledge of road safety, making them an informed group to do the rating.
Descriptive analysis
One simple and straightforward descriptive analysis that can provide a basic understanding of the collision risk among the different provinces is to compare the number of collisions per licensed drivers for drivers who are 65 years or older. The mean collision rates from 1998 to 2004 will then be compared and the province with the lowest mean collision will be assigned a rank of one whereas the province with the highest mean collision will assigned a rank of five.
While we acknowledge that there are many factors contributing to the collision risks, it is still insightful to examine the crash rates for ageing drivers to see if there is any obvious correlation between more stringent licence renewal requirements and lower crash rates. First, the mean collision rates for the different provinces can be compared with the rankings of their licensing scheme in a simple graph to see if there is any obvious relationship. Next, a simple t-test will be conducted to test for any correlation between the rankings on crash rates and licensing schemes. Since the simple t-test of correlation coefficients requires the variables to be normally distributed, a non-parametric test with no assumption on the distribution, the Spearman rank correlation test, will also be conducted to confirm the existence or non-existence of a relationship between licensing schemes and crash rates.
Development of empirical model
In order to control for the influences of other external factors when examining the effect of different licensing requirements, an appropriate multivariate analysis should also be performed. Since the number of crashes, y, is a count data and likely to follow a Poisson distribution in theory, the Poisson regression model has been widely used in many road safety analyses (Jovanis and Chang Reference Jovanis and Chang1986; Kattan, Acharjee and Tay Reference Kattan, Acharjee and Tay2009; Miaou and Lum Reference Miaou and Lum1993; Michener and Tighe Reference Michener and Tighe1992; Tay Reference Tay2001, Reference Tay2003a, Reference Tay2005b, Reference Tay2005c, Reference Tay2006). However, some researchers are concerned about the assumption in the Poisson regression model that the mean and variances are equal because this assumption is often violated in practice. Since over-dispersion of data (variance larger than mean) is present in our data, the Negative Binomial (NB) model is then more appropriate (Abdel-Aty and Radwan Reference Abdel-Aty and Radwan2000; Dee, Grabowski and Morrisey Reference Dee, Grabowski and Morrisey2005; Miaou Reference Miaou1994; Noland and Oh Reference Noland and Oh2004; Noland and Quddus Reference Noland and Quddus2004; Poch and Mannering Reference Poch and Mannering1996; Rifaat et al. Reference Rifaat, Tay, Perez and de Barros2009; Shankar, Mannering and Barfield Reference Shankar, Mannering and Barfield1995; Tay Reference Tay2004, Reference Tay2005d). The general form of the negative binomial model is given below:
where y i is the number of crashes involving ageing drivers; μi is the expected number of crashes; β0, β1, …, βk are the parameters to be estimated; x i1, x i2, …, x ik are the explanatory variables; α is the dispersion parameter.
If α is zero, then the NB model reduces to the Poisson regression model. In this way, the Poisson regression model is nested within the NB and a t-test for α=0 can be used to evaluate the significant presence of over-dispersion in the data. Estimation of the model can be done using the standard maximum likelihood method in STATA version 9.0.
Since the objective of this study is to examine the relationship between stricter licensing requirements and crash rates, the dependent variable will be the number of crashes per year in each of the five provinces from 1998 to 2004 and the main independent variable of interest is the ranking of the licensing requirements in the five provinces.
In addition to the main independent variable, we also include several covariates that have been found in the literature to be significant in influencing the number of crashes at a macro level and have data that are publicly available. First, a time trend is included in the model to capture any temporal effects across the nation. This variable is a continuous variable that simply ranges from one for the first year (1998) to seven for the last year (2004) of data used. This variable is also included in the model to account for the influence of gradual and longer-term improvements in the road environment and vehicle safety (Joksch Reference Joksch1984; Tay Reference Tay2005a, Reference Tay2005b, Reference Tay2005c). Second, four dummy variables are created to capture any province-specified factors that are not explicitly controlled for in the model, with the Province of Alberta used as a reference or base case.
Third, the influence of exposure has to be controlled for in the model. As the number of vehicles on the roads increases, the chances of vehicle conflicts and collisions also increase. Note that the risk of collision is increased for all drivers, including older and non-older drivers, because we all drive on the same road system. To capture older driver-specific risks due to exposure, the share of older drivers will be included as one of the control variables in the model.
Measuring exposure at a macro level, however, is complicated. While data for vehicle kilometres travelled are generally available for specified segments of major roads, they are not available at the regional or provincial levels. The latter forms of data are often estimated using population and employment statistics of the regions included in the analyses (Dee, Grabowski and Morrisey Reference Dee, Grabowski and Morrisey2005; Institute of Transportation Engineers 2003; Morrisey and Grabowski Reference Morrisey and Grabowski2005; Rifaat, Tay and de Barros Reference Rifaat, Tay and de Barros2010; Tay Reference Tay2005c, Reference Tay2009, Reference Tay2010). Therefore, we have included both population and unemployment rate in our model as surrogate measures of exposure. Finally, since the focus of this paper is on ageing drivers, the percentage of the driving population that comprises the ageing drivers is included in the model to control for the effect of this specific type of exposure.
Note that the level of economic activities has two opposing effects (Tay Reference Tay2003b, Reference Tay2005c, Reference Tay2010). As economic activities increase, the amount of travel and transportation of goods will increase, which will result in a larger number of crashes. However, the level of economic activities also has an income effect and its increase will reduce the number of crashes since safety is assumed to be a normal good in which its demand will increase as income increases. To better differentiate between these two effects, another measure of travel and transportation of goods is also included in the model. The quantity of gasoline sold in each province is assumed to be a good proxy measure to capture the amount of traffic on the roads.
Results
Confirmation of rating for licensing scheme
As shown in Table 3, both the mean and mode produced the same ranking for the different provinces with respect to the restrictiveness of their licensing systems. More importantly, these rankings were consistent with the rankings done by the research team, confirming the reliability and validity of the ranking used in this study.
Table 3. Ranking of licensing systems
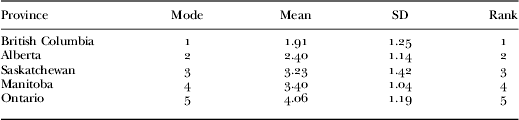
Notes: SD: standard deviation. Lower number in rank represents less-restrictive licensing system.
Results of descriptive analyses
The collision rates (collision per licensed driver) are reported in Table 4. It is clear from the table that the collision rates for ageing drivers are quite constant over the seven years for most provinces, except for Saskatchewan which seems to be experiencing an increasing trend. Also, 1999 appears to be an abnormal year for Manitoba which experienced a spike in the collision rate. Moreover, it appears from Table 4 that the collision rates for ageing drivers vary considerably across the five provinces.
Table 4. Ageing drivers collision rates
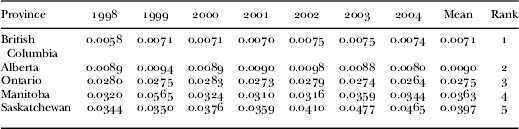
Note: Rank assigned based on mean collision rates.
The one-way analysis of variance procedure rejected the null hypothesis that the means were equal to one another, implying that the collision rates were not the same across provinces and the differences observed could not be attributed to random chance. In addition, paired-wise t-tests used to compare the mean collision rates also rejected the equality of means between all pairs except one (Manitoba and Saskatchewan). Therefore, it could be concluded that British Columbia had the lowest crash rate, followed by Alberta, then Ontario, and finally by Manitoba and Saskatchewan.
The average collision rates for ageing drivers in the five provinces are shown in Figure 1. The provinces are arranged according to the ranking of the stringency of their licensing system from the least restrictive system on the left to the most restrictive on the right. It is clear from the figure that there does not appear to be any clear association between stringency in licensing policies and collision rates. British Columbia, which has the most lenient policy, has the lowest collision rate but Ontario, which has the most stringent licensing policy, has a higher collision rate. On the other hand, Alberta, Manitoba and Saskatchewan which have relatively moderate licensing policies, have rather diverse collision rates. Therefore, there is no obvious relationship between stringency in licensing policies and collision rates.
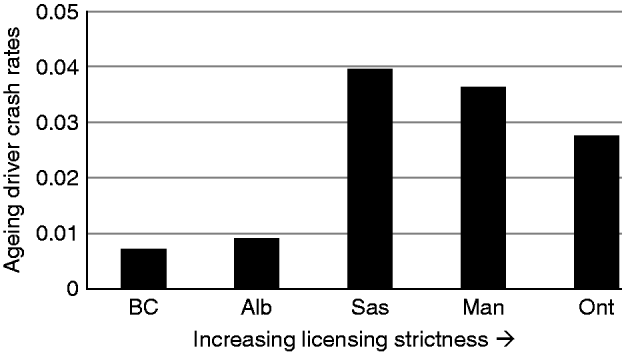
Figure 1. Average ageing driver collision rates.
In addition, a simple correlation test is performed using the mean ranks of the different provinces with respect to their licensing stringency and their mean crash rates. The estimated coefficient is positive (ρ=0.77), indicating that provinces with more stringent licensing requirements are associated with higher crash rates. However, this relationship is not statistically significant (p=0.128). Moreover, a rank correlation test is also performed using the ranking of the different provinces with respect to the crash rates (Table 4) and stringency of licensing policies (Table 3). The Spearman rank correlation coefficient estimated is 0.4, indicating that more stringent licensing policies are associated with higher crash rates. Again, this coefficient is not statistically significant (p=0.212).
Estimates for empirical model
The estimation results for the negative binomial model are reported in Table 5. In general, the model fits the data very well, with a relatively large pseudo R 2 and chi-square goodness-of-fit statistics. We are more than 99.99 per cent confident that the model has some explanatory power. Compared to Alberta, the province of British Columbia appears to have a higher average number of crashes involving ageing drivers whereas the provinces of Saskatchewan and Manitoba have lower averages, all other factors held constant.
Table 5. Results of negative binomial model
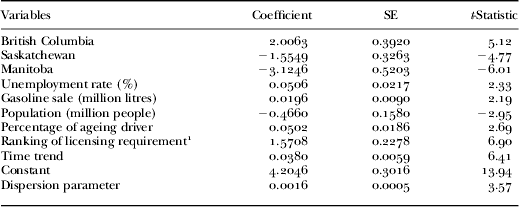
Notes: Number of observations: 35; pseudo R 2: 0.3287; χ2: 199.39; p<0.0001. SE: standard error. 1. Larger numbers indicate stricter licensing requirements.
As expected, the number of crashes involving ageing drivers exhibits an increasing trend over the seven-year period as shown by the positive and significant coefficient for the time trend variable in the model. This finding confirms the concerns in the road safety profession about the effects of the ageing driving population.
Our results showed that an increase in unemployment would increase the number of motor vehicle crashes involving ageing drivers, which supported the hypothesis of safety as a normal good with significant income effect. Also as expected, the number of crashes involving ageing drivers would increase as the quantity of gasoline sold increased, due to an increase in traffic on the roads. In contrast, an increase in the population while holding traffic constant would decrease the number of crashes.
With respect to the ranking of licensing requirements, our results showed that an increase in the stringency of licensing for ageing drivers was associated with an increase in the number of crashes involving older drivers. However, unlike the univariate analyses, this correlation was significant in the multivariate regression model.
Discussions and conclusions
There are few attempts to harmonise the licensing policies for ageing drivers in Canada because of the sensitivity of the issues involved, including political, social, equity, financial as well as health and wellness considerations. As a result, policies regarding the re-testing and renewal of licences for ageing drivers vary considerably across the provinces. A search of the publicly available literature finds only a few papers on the relative effectiveness of the different licensing practices for ageing drivers in general and no evaluation report for Canada in particular.
Main finding and policy recommendation
Using an established procedure (Langford et al. Reference Langford, Fitzharris, Koppel and Newstead2004), a simple comparison of the stringency of the licensing policies in five provinces in western and central Canada with their corresponding collision rates for ageing drivers did not find any obvious relationship. In addition, correlation tests between the rating on the stringency of the licensing requirements and crash rates revealed a positive relationship, indicating that more stringent policies were associated with higher crash rates although these correlations were not statistically significant. Hence, there is no clear evidence that having a stricter licensing policy will improve safety. Therefore, without further evidence, we cannot recommend having a stricter licensing policy for ageing drivers or introducing more mandatory re-testing policies in Canada.
Moreover, a multivariate analysis using a negative binomial regression model found that the stringency of licensing for ageing drivers was associated with an increase in the number of crashes involving ageing drivers and this relationship was found to be statistically significant. This finding did not support our initial hypothesis of a negative relationship based on the proposition that more stringent licensing requirements would result in fewer at-risk drivers on the roads and hence fewer crashes. However, it supported our alternate hypothesis of a positive relationship due to self-regulation and risk compensation behaviour among ageing drivers as well as our proposition that provinces with higher crash rates tended to impose stricter requirements in an effort to improve safety.
It should be noted that the above result is not surprising given the assumptions needed to produce the hypothesised negative relationship. The potential safety gains from more stringent licensing requirements are predicated on the assumption that the additional tests required are valid and reliable in predicting crash involvement and that unlicensed drivers will not drive. Although the second assumption is fairly valid for older drivers, the first assumption is not. Extant research has shown that many of the widely used tests have low predictive validity (Anstey et al. Reference Anstey, Wood, Lord and Walker2005; Scialfa et al. Reference Scialfa, Ference, Boone, Tay and Hudson2010). If the additional tests and procedures lack efficacy, then their requirement may simply make things worse instead of producing a safety benefit.
Limitation of study and future research
Note that we are able to establish only correlations and not causality in the statistical analyses. The relationship between the stringency in licensing policies and crash rates may be affected by several opposing influences like the validity of the tests imposed by the government, the likelihood of imposing such restrictions being influenced by the collision rates and risk compensation by drivers who are able to renew their licences under a more stringent licensing scheme. Hence, care should be exercised when interpreting our main finding.
Owing to the difficulty in obtaining data, many of the smaller provinces and territories in Canada have not been included in the analysis. Although the five provinces included in this study make up more than two-thirds of the population in Canada, future research should endeavour to include all the other provinces and territories to get a more complete picture. Moreover, we are not able to differentiate and test the different specific licensing requirements to uncover their individual efficacies due to paucity of the licensing data.
Future research should also consider using more years of data to increase the likelihood of including some temporal differences in the licensing policies and practices. Data on changes in policies and practice over time will enable researchers to obtain a firmer basis to infer causal effect. More research is therefore needed to discover better methods of licensing drivers that have a significant safety benefit.
Finally, since the focus of this study is on the effect of stricter licensing policies and practices on traffic safety, only a few external influences or covariates have been included in the model. The inclusion of other influences such as differences in enforcement intensity, weather, quality of roads, and vehicle fleet across different provinces will improve the estimates of the model.
Acknowledgements
Financial support from the Alberta Motor Association Traffic Safety Foundation and the Social Science and Humanities Research Council of Canada are gratefully acknowledged. However, the views expressed by the author do not necessarily reflect those of the funding agencies.