3.1 Theoretical background of TO

The TO method can be used to find an optimised material distribution over a given design wing space. Material that is significant for the structure is retained while eliminating the undesired weight, thus resulting in the best structural load distribution. The TO approach in the numerical codes is used to respect the given constraints by defining objectives. To ensure that the design requirements are met, minimum material thicknesses are set and exclusion areas defined. The objective of TO is to minimise the compliance, i.e. maximise the stiffness, while satisfying the design constraints.

The material density is considered as a variable of the objective function. For every finite element, the pseudo-density x _i may vary between 0 and 1, 0 ≤ x _i ≤ 1, where 0 represents void material and 1 represents solid material. The pseudo-density variable can be expressed a shown in Equation (1)^{(Reference Tamta and Saxena32)}:

(1) \begin{equation}{x_i} = \frac{{{\rho _i}}}{{{\rho _0}}}\end{equation}

where x _j is the pseudo-density of the ith element, $\rho$ _i is the density of the ith element and $\rho$ ₀ represents the density of the base material. The effect of the pseudo-density on the stiffness properties can be described as

(2) \begin{equation}{E_{\left( {{x_i}} \right)}} = {E_{{\rm{soild}}}}{\left( {{x_i}} \right)^p}\end{equation}

(3) \begin{equation}{E_{\left( {{x_i}} \right)}} = {E_{{\rm{void}}}} + {x_i}^p\left( {{E_{{\rm{solid}}}} + {E_{{\rm{void}}}}} \right)\;\;\;\;\;\;\;\;\;\;\;\;p \ge 1\end{equation}

where ${E_{{\rm{void}}}}$ is a very low Young’s modulus allocated to void regions, ${E_{{\rm{solid}}}}$ is the Young’s modulus of solid regions and ${E_{\left( {{x_i}} \right)}}$ is Young’s modulus of each element.

The penalty parameter, expressed by the exponent p, has a value greater than 1 (in this paper, p = 3), therefore in combination with the pseudo-densities, it will have a great effect on the optimisation results. The stiffness often approaches 0 as the density $\rho$ _i gets close to 0 as well. In the Solid Isotropic Material with Penalisation (SIMP) approach, if the intermediate densities approach 0, then the rate of reduction of the modulus of elasticity ${E_{\left( {{x_i}} \right)}}$ is low. Otherwise, if the intermediate densities p reach 1, the rate of growth in the modulus of elasticity ${E_{\left( {{x_i}} \right)}}$ increases considerably^{(Reference BendsØe and Sigmund33,Reference Gunwant and Misra34)} . The total volume can be represented as the volume of all units with their relevant pseudo-densities, as shown in Equation (3):

(4) \begin{equation}V = \mathop \sum \limits_{i = 1}^n {x_i}{V_i}\end{equation}

where V is the total volume, x _i is the pseudo-density of the ith element and V _i is the volume of the ith element.

The TO objective function is to minimise the compliance and maximise the stiffness of the structure while meeting the design constraints. The objective function can be described mathematically as

(5) \begin{align}{\mathop {\min }\limits_x:c(x)} &= {U^T}KU = \mathop \sum \limits_{e = 1}^N {{\left( {{x_i}} \right)}^P}u_e^T{k_0}{u_e}\nonumber\\[3pt]{\rm{subject\;to}}:{\rm{\;}}\;\frac{{V(x)}}{{{V_0}}} &= f\nonumber\\[3pt]:KU &= F\nonumber\\[3pt]:0 \lt {x_{{\rm{min}}}} &\le {x_i} \le 1\end{align}

The function of the design variable vector x is called c(x). The volume fraction is expressed as $\;\frac{{V\left( X \right)}}{{{V_0}}} = f$ , where f is the load vector, V is the final volume and V ₀ is the initial volume. F is the force vector, U is the global displacement, and K is the global stiffness matrix in the displacement KU = F. Meanwhile, u _e represents the displacement vector and k ₀ the elemental stiffness matrix.

The shape of the density filter is chosen in our mathematical optimisation as explained by Sigmund^{(Reference Sigmund and Petersson35)}. The physical relative density filtering is donated by $\widetilde{x_{\iota}}$ and can be expressed as

(6) \begin{equation}\widetilde{x_i}=\frac{\sum_{{j\in {\mathbb N}}_e}{w(r_i)v_j{\tilde{x}}_j}}{\sum_{{j\in {\mathbb N}}_e}{w(r_i)v_j}}\end{equation}

where ${N_e} = \left\{ {i|{r_i} - {r_e} \le R} \right\}$ is a neighbourhood set with filter radius R. Here, r _i and r _e are the filter radii about the centre of elements i and e, respectively. Also, $w(r_{i},r_{e})=R-\|r_{i}-r_{e}\|$ is the weighting function, and v _i is the volume of element i ^{(Reference Aage, Andreassen, Lazarov and Sigmund36)}.

The global stiffness of the structure is maximised by applying a given load. Thus, the optimisation problem is solved by minimising the compliance of the Three-Dimensional (3D) morphing wing while constraining its volume.

The compliance optimisation problem can be formulated as

(7) \begin{equation}C = \mathop \smallint \limits_V^{} fu\;{\rm{d}}V + \mathop \smallint \limits_S^{} tu\;{\rm{d}}S + \mathop \sum \limits_i^n {F_i}{u_i}\end{equation}

where f is the distributed body force, u is the displacement area, t is the traction force, F _i is the point load on the ith node, u _i is the ith displacement degree of freedom, V is the volume of the continuum and S is the surface area of the continuum.

3.2 Parameterisation formulation of the TO problem

The aim of the discrete TO of the structural design problem is to maximise the stiffness while minimising the weight. Density-based approaches are applied here, and the optimisation problem is solved using the static linear method. The topology design problem can be described using the following mathematical formulation:

(8) \begin{align}\min f(x) = f( {{x_1},{x_2}, \ldots \ldots ,{x_n}})\nonumber\\{{g_j}(x) \le 0,}\quad {j = 1, \ldots \ldots ,m}\\{{x_{{i_{{\rm{min}}}}}} \le {x_i} \le {x_{{i_{{\rm{max}}}}}}}\quad {i = 1, \ldots \ldots ,n}\nonumber\end{align}

where the design variables x are the independent variables of the f(x) objective function, g(x) are the constraints and x _max and x _min are the upper and lower bound constraints, respectively.

In this investigation, solid elements are used, and the optimisation process is performed using linear analysis^{(Reference Lee and Park37)}. The calculation of the given constraints whose gradients are required can be facilitated by utilising the constraints screening process to differentiate between active and idle constraints, thereby limiting the number of responses within the optimisation problem that form a representative set. The optimisation algorithm, which is written and run in numerical codes, is applied in combination with the approximate method.

The Optimality Criteria (OC) approach is applied to a robust algorithm that can reliably solve the problem by using a large set of design variables. Therefore, iterative optimisation methods are commonly employed to solve this problem.

The analysis process minimises the compliance of the variable-span morphing wing while meeting the given constraints using the minimal volume of material. Clearly, this iterative process continues until reaching convergence^{(Reference Tamta and Saxena32,Reference Jankovics, Gohari, Tayefeh and Barari38)} .

4.1 Material selection

The wing design concept of the MVSTW was discussed in Section 2.1. For the first optimisation process, aluminium alloy 2024-T3 was selected. Aluminium 2024-T3 is an isotropic material with good versatility; it is easy to work with this, due to its high mechanical strength. Commonly used for structural applications, this material is quite prevalent in the aerospace industry. Its material properties are described in Table 4.

4.2 Load estimation and pre-processing approach

The load was calculated at the maximum speed and sea level for a full-extension wingspan. A load factor of 3g (three times the acceleration due to gravity) and a safety factor of 1.5 were applied. The solid wing was modelled in 3D using aluminium alloy 2024-T3. The numerical analysis was performed separately on the two wing segments of the basic structure. The basic wing structure of the MVSTW represents the initial solid wing of the moving and fixed segments before the optimisation process. Figure 3 shows the geometry wing planform for both segments.

Table 3 Lift forces at sea level for various speeds and wingspan extensions

Table 4 Material data for aluminium alloy 2024-T3

Table 5 The parameters used in the TO

Figure 3. Wing planform: (a) fixed part, (b) moving part.

The procedure was implemented for both the fixed and moving wing segments, and is presented in the next paragraphs. The basic structure and physical configuration for both wing shapes of the design were defined as shown in Fig. 3.

The data were processed at zero angle-of-attack. The study parameters of the semi wing-span were selected at the extreme flight conditions to ensure compliance through all flight phases as presented in Table 5.

4.3 Finite element model of the MVSTW

The numerical analyses of the MVSTW were implemented using a static structure within ANSYS Workbench, which can predict the performance of a product under a real-world environment by incorporating all the occurring physical phenomena with very good accuracy^{(Reference Ghosh, Ghosh, Ghimire and Barman41)}. Structural analysis is one of the most common applications of FEA. The process for static analysis involves meshing, boundary conditions and loading.

In this simulation study, the following procedures were adopted for the static analysis and TO:

• • The geometrical shape and physical outlines of the design for the fixed and moving segments were defined, as illustrated in Fig. 3.

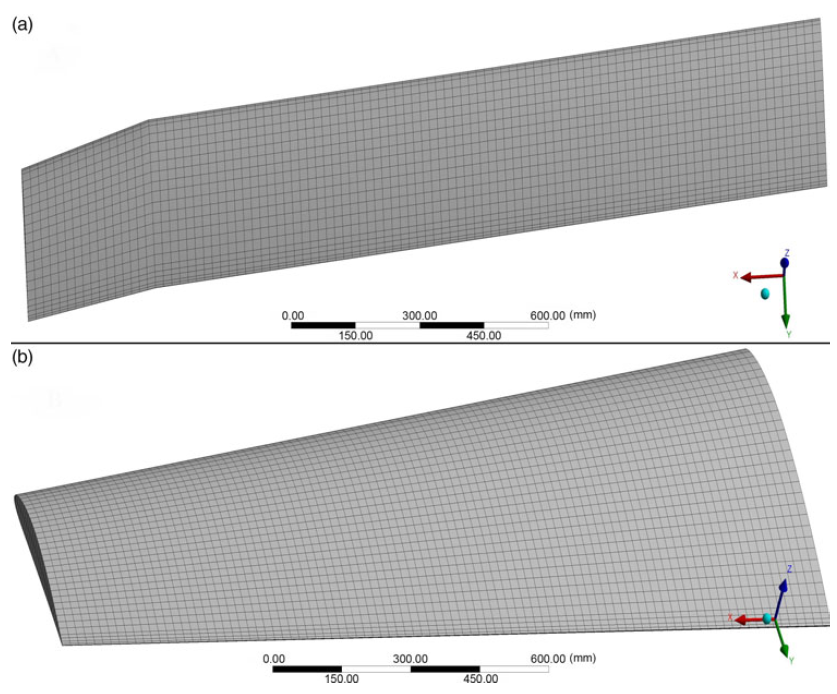
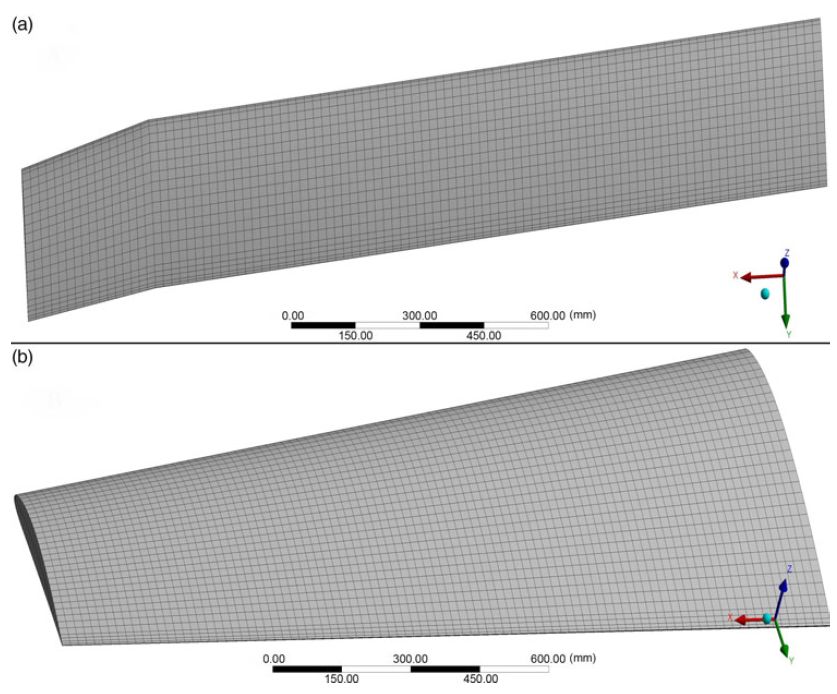
• • Mesh generation by the ANSYS solver offers efficient and high-quality grid partitions for both wing shapes. Two meshing elements types were used in the FEM and TO methodologies. The meshing elements are high-quality hexahedral and tetrahedral. The total number of nodes and elements for the fixed segment were 54,185 and 10,152, respectively, while for the moving segment their total numbers were 25,077 and 4,704, respectively. Figure 4 shows the meshed models of the fixed and moving span morphing wing segments.

  

  Figure 4. Meshing model of (a) moving and (b) fixed wing segment.

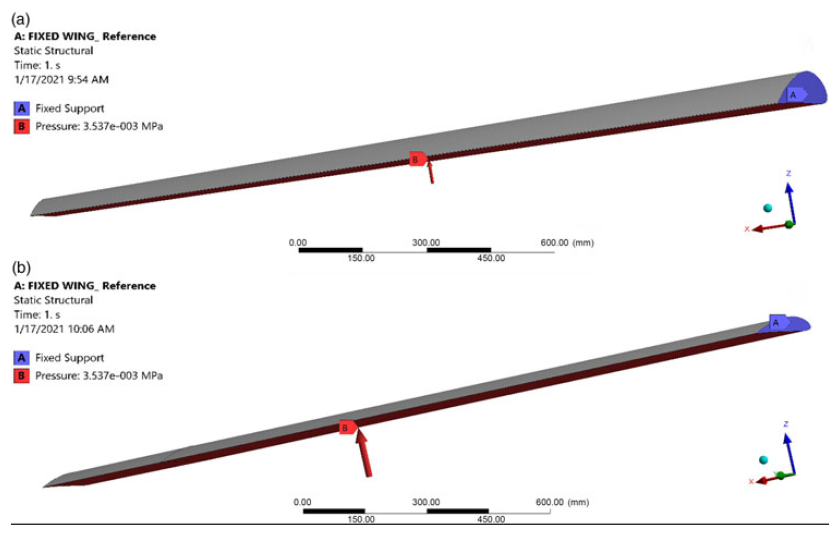
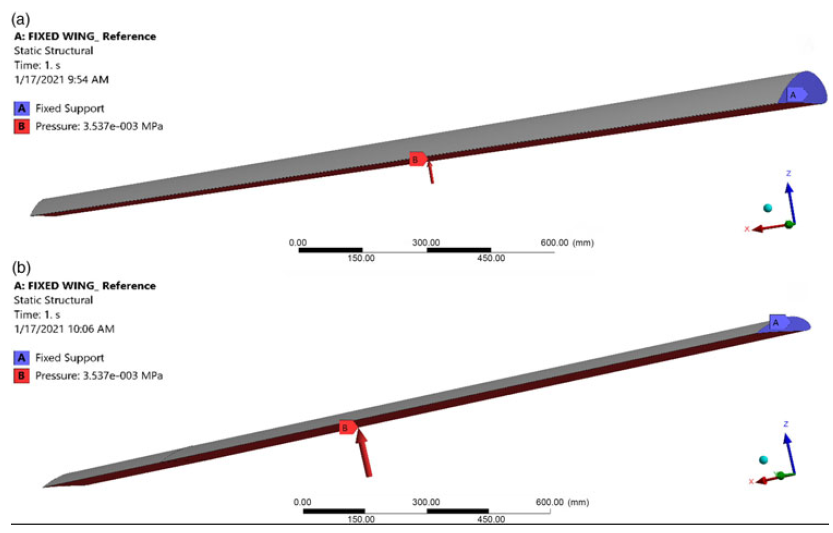
• • The boundary conditions expressed by the desired mechanical behaviour and properties (material properties definition, analysis settings and loading conditions) were defined. The variable span morphing wing was mounted on the aircraft fuselage, with the moving segment sliding inside the fixed segment. The boundary conditions, fixed supports and the load applications for both wing segments are shown in Fig. 5. Static structural analysis was performed for the fixed and moving segments by enforcing identical boundary conditions. Therefore, in the static structural domain, a fixed support was inserted at the root chord for both segments. The load is distributed uniformly on all nodes situated on the bottom surfaces of the moving and fixed wing segments. This load is applied with the same values along the Y direction for both segments. To apply the load on the wing segments. The pressure calculated following the aerodynamic results was considered to apply the load on the wing segments, and the magnitude of the load was 3,537Pa^{(Reference Elelwi, Kuitche, Botez and Dao24,Reference Chethan, Zuber, Shenoy and Kini42)} .

  Table 6 Results for the three parameters (deformation, stress and strain) for fixed and moving segments at ultimate pressure

  
  

  Figure 5. Boundary condition, fixed support and loading application for (a) fixed and (b) moving segments.

• • Post-processing was applied after solving the equations of the structural calculations such as stress, deformation and strain to obtain the converged solution. The static analysis solver allows contour plots, vector plots, 2D and 3D surface schemes to be designed, and to visualise the finite element analysis results. It can also offer animation to display the results dynamically.

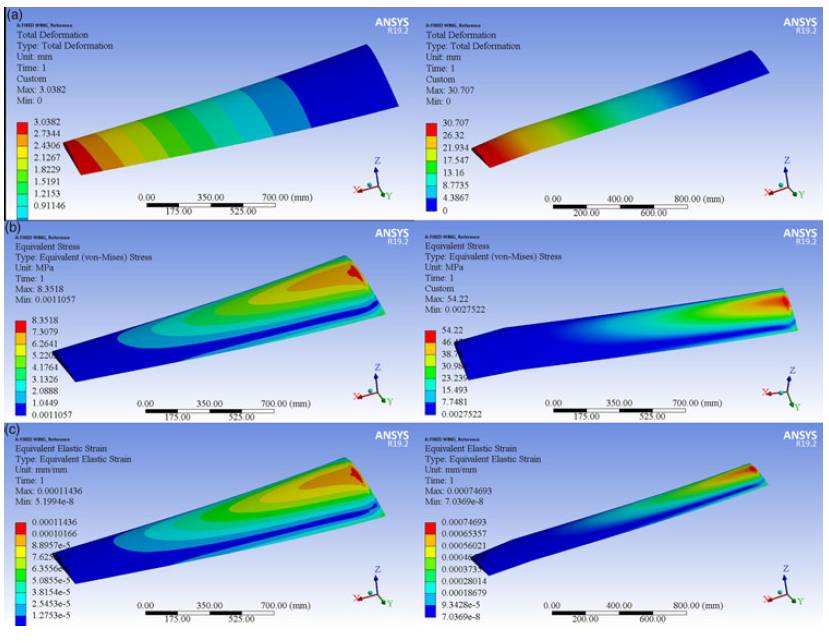
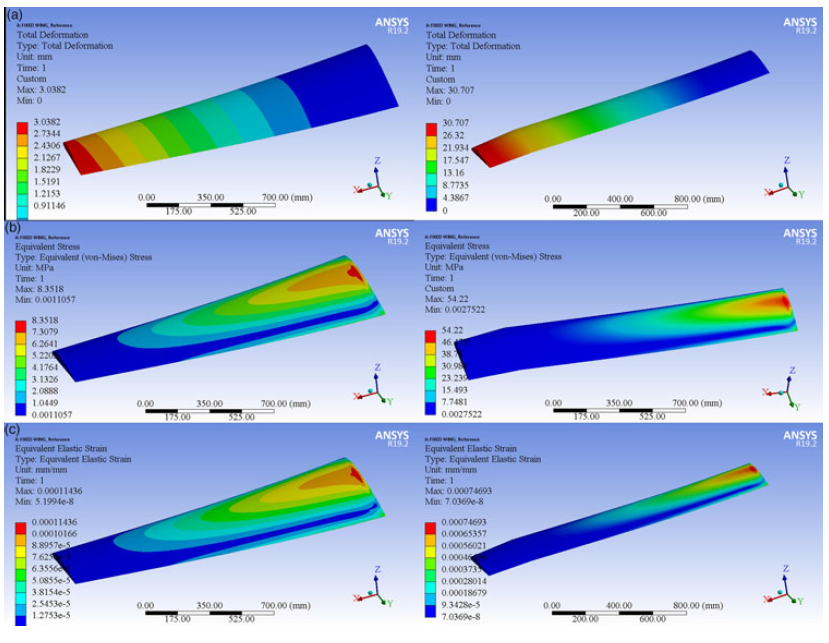
• • The results are obtained by static structural analysis. Following the optimisation process, von Miss stresses, stresses and deformation values are obtained from the static structural analysis. The FEM results, expressed in terms of deformation, stress and strain, for the morphing wing segments respect the safety limits of the selected material’s mechanical properties. The FEA results obtained on the considered wing segments are described in Table 6 and further shown in Figs. 6(a), (b) and (c).

  

  Figure 6. (A) Total deformation, (B) von Mises stress and (C) elastic strain for (a) fixed, and (b) moving segments of the variable-span morphing of a tapered wing aerofoil.

6.1 FEM based on TO

The described approach based on the simulation-based TO method can provide a detailed structural design of the variable-span morphing wing. This offers a new way to reduce the aircraft’s structural weight. The redesign based on the TO method suggested a variable-span morphing wing model consisting of a thin skin, twin spars, seven ribs and multiple support elements, as shown in Figs. 9 and 10. The baseline design consists of the external surface skin to sustain the aerodynamic loads and distribute the aerodynamic loads to the internal components, such as spars, ribs and stringers. The main function of the two spars is to support the multiple loads acting on the wing, including the bending moment and shear force, as well as to support the wing structure against any torsion created by load lifting. The ribs are used to retain the geometrical shape of the wing section with the aim of distributing the external loads evenly on the wing skin and thereby prevent undesired wing deformation. The stringers are applied in the design to enhance the wing’s rigidity^{(Reference Zhang, Zhao and Si45)}.

To achieve a stiffened and reliable variable-span morphing wing, the main parameters of its fixed and moving wing segments components are defined as follows:

• • A wing skin thickness of 2mm for both segments

• • A spar thickness of 6mm for both segments

• • A rib thickness of 6mm for both segments

• • Flat stringers with thickness of 4mm for the fixed segments, and round stringers with diameter of 3mm and thickness of 1mm.

• • A stringer thickness of 8mm for the moving segment.

Furthermore, as they are parallel, the distance between the two spars is defined as 351.56mm for the fixed segment and 163.38mm for the moving segment of the wing.

The objective for designing such a wing is to enhance the capabilities of the Unmanned Aerial Vehicle (UAV) to accomplish multiple missions during the same flight. This UAV is mainly used for surveillance and security purposes, as it can cover all its targets in one flight by reaching its intended destination rapidly while expanding the flight range without refuelling.

The variable-span morphing wing shapes for various wingspan extensions and different flight speeds were re-analysed using the CFD calculations. The static analysis parameters for the optimised wing were selected for four flight speeds at all three wingspan extensions to ensure compliance throughout each flight phase, as described in Table 8.

The same material properties were selected as explained in the previous analysis for the solid wing segments, as described in Table 4. Hexahedral meshing was performed using the MultiZone mesh method with the aim of obtaining highly accurate results. The mesh size was selected to be the same for both wing segments: 15mm for the wing skin, 6mm for wing spars and 3mm for the ribs and stringers. The total number of nodes was equal to 836,885, and the total number of elements was equal to 243,976 for the entire wing. Figure 11 shows the meshing of the wing structure and its components.

The same methodology as mentioned in Section 6 was used in this case study. The boundary conditions applied on the variable-span morphing wing were defined. The root chord of the variable-span morphing wing was fixed, and the load was applied for wingspan extensions of 50% and 75%, at a speed of 17m/s, and for the wingspan extension of 0% (original) and 25% at a speed of 51m/s, as shown in Fig. 12.

Table 8 FEA specifications for MVSTW at all span extensions and different flight speeds

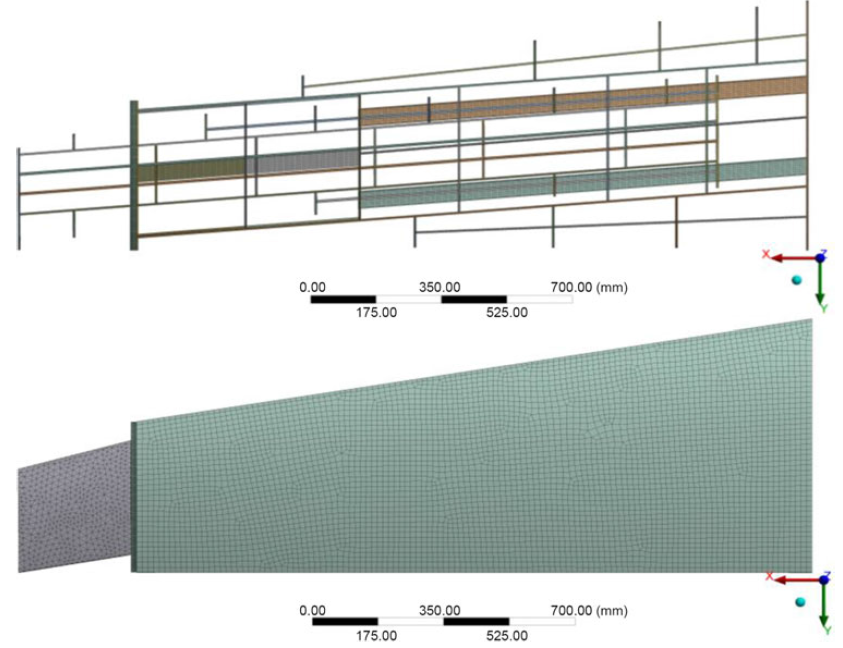
Figure 11. Grid meshing of the variable-span morphing tapered wing and its components.

Table 9 Results for the three characteristics (deformation, stress and strain) at selected wingspan extensions and flight speeds

Figure 12. Boundary conditions for variable morphing for wingspan extensions of (a) 50% and 75% at 17m/s and (b) 0% and 25% at 51m/s.

The given loads for the multiple wingspan extensions and speeds were applied along the Y direction for the variable-span morphing wing, with the pressures calculated according to the aerodynamic results described in Table 8.

6.2 Evaluations of the static structural analysis of the optimised MVSTW

Static analysis was performed to evaluate the optimised MVSTW. The loads were defined as per the lift forces that were obtained for the various wingspan extensions and flight speeds. The same boundary conditions were also considered in this investigation and the safety factor, as given in Table 8.

The results of the static structural analysis are expressed in terms of deformations, von Mises stresses and strains for eight selected cases (Table 9); the results are illustrated in Figs. 13, 14 and 15.

Figure 13. Total deformation of the MVSTW for (a) Wing extension of 50% and speed of 17m/s, (b) wing extension of 75% and speed of 17m/s, (c) wing extension of 50% and speed of 34m/s, (d) wing extension of 75% and speed of 34m/s, (e) wing extension of 0% and speed 51m/s, (f) wing extension of 25% and speed of 51m/s, (g) wing extension of 0% and speed of 68m/s and (h) wing extension of 25% and speed of 68m/s.

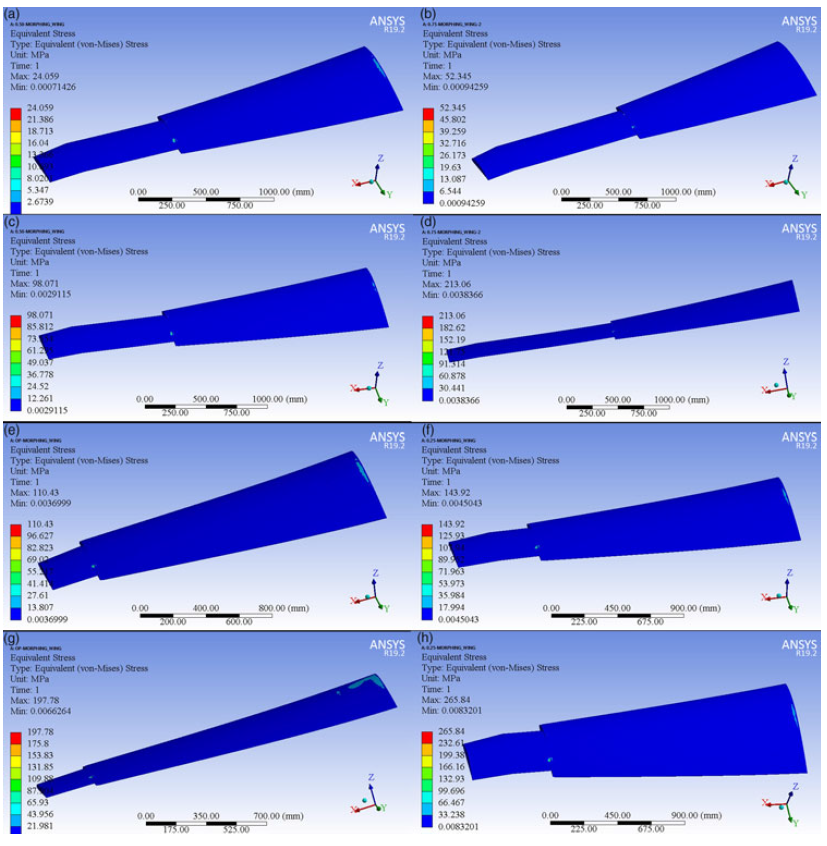
Figure 14. von Mises stress of the MVSTW for (a) wing extension of 50% and speed of 17m/s, (b) wing extension of 75% and speed of 17m/s, (c) wing extension of 50% and speed of 34m/s, (d) wing extension of 75% and speed of 34m/s, (e) wing extension of 0% and speed of 51m/s, (f) wing extension of 25% and speed of 51m/s, (g) wing extension of 0% and speed of 68m/s and (h) wing extension of 25% and speed of 68m/s.

Figure 15. Equivalent strain of the MVSTW for (a) wing extension of 50% and speed of 17m/s, (b) wing extension of 75% and speed of 17m/s, (c) wing extension of 50% and speed of 34m/s, (d) wing extension of 75% and speed of 34m/s, (e) wing extension of 0% and speed of 51m/s, (f) wing extension of 25% and speed of 51m/s, (g) wing extension of 0% and speed of 68m/s and (h) wing extension of 25% and speed of 68m/s.

The results obtained from the MVSTW simulations are depicted in Figs. 13, 14 and 15, and in Table 9. Note that the values of the mechanical properties, that is, the deformation, stress and strain, increased with increasing aerodynamic loads. Meanwhile, the aerodynamic loads increase with the wingspan extension (increasing the wing surface area) and also changes in the flight speed^{(Reference Ajaj, Friswell, Saavedra Flores, Keane, Isikveren, Allegri and Adhikari46)}. The mechanical properties increase dramatically at the large wingspan extensions of 50% and 75%, and at increased cruise and maximum flight speeds. Therefore, the wingspan extensions of 50% and 75% are suggested only for the minimum speed and loiter phases. The main benefit of symmetric wingspan extension is to increase the aerodynamic efficiency for maximised range flight, and to reduce the take-off and landing distances. The wingspan at the original position without extension (0%) and at 25% extension can be used to ensure high manoeuvrability, and to reduce the flight time, as the mechanical properties remain within the safe domain of the wing’s resistance to failure.

According to the FEA results, it is clear that the morphing of the structure of the designed wing is suitable for the rolling control strategy using the asymmetric span morphing technique. However, the optimum rolling mechanism should consider that both sides of the wing’s span must expand gradually and symmetrically. In addition, the wingspan should extend smoothly and effectively to avoid structural fatigue, since the results obtained for the changes of the deformation, stress, and strain show dramatic increases, being severely affected by the aerodynamic loads. An example of these increases is presented in Table 9 for a wingspan extended from its original position to 75% of its length.

The structural optimisation of the MVSTW under stiffness requirements is used to predict the perfect layouts of the wing components within the design space. The TO results suggest that the best possible weight values of the MVSTW for both segments are the following: the optimised weight of the fixed segment is 16.3kg, and the optimised weight of the moving segment is 10.3kg, compared with the calculated values of 112 and 45kg for both solid wing segments, respectively. The structural layouts based on the mechanical characteristics, such as stiffness and strength, involve two-spar and seven-rib configurations. Moreover, to achieve the multi-mission requirements, additional support parts, such as stringers and stiffeners, are added to overcome mechanical fatigue (Fig. 10) by enhancing the structural integrity and avoiding structural failure. The proposed arrangement and allocation of wing components was proved to attain the robustness and integrality required for the MVSTW, and to achieve important weight reductions through the topological optimisation^{(Reference Amendola, Dimino, Amoroso and Pecora47)}.