1.0 INTRODUCTION
Research and development on active flutter suppression systems has been ongoing since the 1970s. However, the problem of flutter still persists, particularly in the transonic flow domain. The importance of the flutter problem in the transonic flow regime was underscored by Mykytow(Reference Mykytow1) in a review as early as 1977. A subsequent review by Bendiksen(Reference Bendiksen2) also highlighted the importance of the transonic flow regime.
One of the first in-flight demonstrations of an active flutter suppression system was by Roger et al.(Reference Roger, Hodges and Felt3) in 1975. One of the earliest efforts to synthesise control laws for active flutter suppression based on optimal linear–quadratic Gaussian regulator theory was reported by Lyons et al.(Reference Lyons, Vepa, McIntosh and Debra4). Motivated by the need to compute the unsteady aerodynamic loads due to arbitrarily moving aerofoils and assess the associated flight dynamics and aeroelasticity, Vepa(Reference Vepa5) developed finite-state unsteady aerodynamic models. The use of matrix Padé approximants, which are rational polynomials whose matrix coefficients are found by least-squares curve fitting of the aerodynamic loads computed over a finite range of frequencies, was proposed by Vepa(Reference Vepa6). This approach reduces the number of so-called augmented states needed to model the various unsteady aerodynamic transfer functions arising from the generalised forces due to the motion of the structural modes, by requiring that all the transfer functions share common poles, which are determined numerically. In a series of papers, Nissim and co-workers(Reference Nissim7–Reference Nissim11) developed the aerodynamic energy method to synthesise control laws for several aircraft wings based on an analytical dynamic model. The control law synthesis technique was validated using classical concepts of Nyquist plots, and the robustness of the controllers was established. The energy-based method has some useful interpretations and is useful for understanding the role of the feedback controller. Livne(Reference Livne12) presents an overview of over fifty years of research and development in the active flutter suppression area.
Recognising the importance of flutter in the transonic flow regime, NASA Langley Research Center initiated the Benchmark Models Program (BMP) program and sponsored the design of a series of models which were used to study different aeroelastic phenomena and to validate computational fluid dynamics codes. The Benchmark Active Controls Technology (BACT) model was a part of the BMP. The primary objective of BACT testing was to obtain steady and unsteady loads, accelerations and aerodynamic pressures due to control surface activity to calibrate unsteady Computational Fluid Dynamics (CFD) codes and active control design tools. A review on active control using the BACT model is given by Mukhopadhyay(Reference Mukhopadhyay13-Reference Mukhopadhyay15). Mukhopadhyay(Reference Mukhopadhyay16) also presented details of the transonic flutter suppression control law design and related wind-tunnel validation test results. Results and data related to the modelling of the BACT wing were presented by Scott et al.(Reference Scott, Hoadley, Wieseman and Durham17) and Waszak(Reference Waszak18), while Svoboda and Hromcik(Reference Svoboda and Hromcik19) and Adams et al.(Reference Adams, Christhilf, Waszak, Mukhopadhyay and Srinathkumar20) presented details of control laws obtained by the application of several different synthesis methods.
The primary difficulty in the case of a wing in the transonic flow regime is that the equations describing the flow are fundamentally non-linear and the computation of the aerodynamic loads is generally carried out numerically using one of the available computational methods. The primary computation approaches generally adopted in the unsteady, transonic flow regime are based on (i) the Navier–Stokes formulation, which is associated with high computational and labour cost and requires the use of a “turbulence model”, (ii) the Euler formulation, which is also associated with high computational cost but can give a fairly complete picture, (iii) the full potential equation formulation, and (iv) the Transonic Small Disturbance (TSD) potential formulation. In these cases, it is nearly impossible to compute any augmented state models, and it is probably best to avoid such augmentation of the state vector. The situation is further complicated due to the transonic dip, as demonstrated numerically by Isogai(Reference Isogai21). There have been a number of studies on the stability of a wing with active control surfaces in a transonic flow, with the aerodynamic loads being computed numerically by Batina and Yang(Reference Batina and Yang22), Guruswamy et al.(Reference Guruswamy, Tu and Goorjian23), Guruswamy and Tu(Reference Guruswamy and Tu24), Guruswamy(Reference Guruswamy25), Ominsky and Ide(Reference Ominsky and Ide26), Bendiksen et al.(Reference Bendiksen, Hwang and Piersol27), Silva and Bennett(Reference Silva and Bennett28), Stephens et al.(Reference Stephens, Arena and Gupta29) and Djayapertapa and Allen(Reference Djayapertapa and Allen30,Reference Djayapertapa and Allen31) . Comparisons of the results of different computational approaches were provided by Edwards and Thomas(Reference Edwards and Thomas32). Bennet and Edwards(Reference Bennett and Edwards33) provided an overview of developments in computational aeroelasticity up to the end of the last millennium. A more recent review by Henshaw et al.(Reference Henshaw, Badcock, Vio, Allen, Chamberlain, Kaynes, Dimitriadis, Cooper, Woodgate, Rampurawala, Jones, Fenwick, Gaitonde, Taylor, Amor and Eccles34) surveyed the application of nonlinear aeroelastic computations to aircraft. Newsom et al.(Reference Newsom, Robertshaw and Kapania35) addressed the problem of control system design based on a computational model derived in the flow domain. They developed a methodology, based on the eigensystem realisation algorithm, for designing active control laws in a computational aeroelasticity environment. The methodology was based on a systems identification technique to develop an explicit state-space model for control law design from the output of a computational aeroelasticity code. The linear quadratic Gaussian control law design technique was employed to design a control law. A major difficulty with the eigensystem realisation algorithm is that it is difficult to identify a state-space model that corresponds completely with the structural dynamic model because the state-space representations obtained by the application of the algorithm are not unique. Probably, the one important achievement of Newsom et al.(Reference Newsom, Robertshaw and Kapania35) was to dispense with the need for added or augmented states. A related approach is to use a reduced-order model for the synthesis of a control law. Using a high-fidelity computational approach, Allen et al.(Reference Allen, Taylor, Fenwick, Gaitonde and Jones36) discussed a systematic method for constructing a reduced-order model and successfully predicted the open-loop flutter boundary, and then synthesised control laws for flutter suppression for the case of a two-dimensional aerofoil. Silva and Raveh(Reference Silva and Raveh37) developed state-space models for the unsteady aerodynamics from computationally obtained responses to pulse inputs. Dowell and Hall(Reference Dowell and Hall38) presented a comprehensive review of modelling approaches to study the aerodynamics by aeroelastic analysis. Waite et al.(Reference Waite, Stanford, Bartels, Silva and Massey39) used the eigensystem realisation algorithm along with a fully unstructured Reynolds-averaged Navier–Stokes code coupled with reduced-order modelling methods to derive an explicit state-space model and the associated control laws. They also used linear models defined by using the DLM and structural dynamics model to synthesise an initial set of control laws. Mukhopadhyay(Reference Mukhopadhyay40) synthesised a flutter suppression controller for an active flexible wing model by using the linear quadratic Gaussian theory. Furthermore, based on the unified linear quadratic Gaussian and minimax method, Mukhopadhyay(Reference Mukhopadhyay16) proposed a flutter suppression controller, which was tested in the NASA Langley Transonic Dynamics Tunnel. Zhang and Ye(Reference Zhang and Ye41) used an Euler code coupled with a reduced-order modelling method to synthesise control laws for a wing in transonic flow. Nie et al.(Reference Nie, Yang and Zhang42) used a computational method for the synthesis of the aerodynamic loads and coupled it with a reduced-order modelling method to synthesise control laws for a wing in the transonic domain by the application of both linear quadratic Gaussian control and sliding mode control. They were able to show that sliding mode control can force the response of the closed-loop system to decay to a stable equilibrium more rapidly than when using the linear quadratic Gaussian control method.
Batina and Yang(Reference Batina and Yang22) were perhaps the first to include a feedback control law in a computational analysis of wing flutter using the TSD theory. They were able to assess the effect of a constant-gain control law on the time-domain responses with displacement, velocity and acceleration feedback. They also compared their results with corresponding results obtained by using a linear subsonic theory, revealing that the frequency and damping values at the onset of flutter differed significantly. However, they were able to effectively incorporate a control law into their code and show that the feedback was effective for suppressing transonic flutter. Djayapertapa et al.(Reference Djayapertapa, Allen and Fiddes43) also included a typical control law in their high-fidelity model and demonstrated an increase in the flutter speed, albeit in the case of a two-dimensional aerofoil. Thus, given a feedback control law, it is possible in principle to assess its capacity to actively suppress flutter in the transonic flow domain by incorporating it into a transonic flutter analysis code that also includes the TSD potential prediction code. It therefore becomes extremely important to establish an initial set of optimal control laws, which is discussed in the next sub-section.
In this paper, the problem of synthesising an active flutter suppression system for a fluttering wing in the transonic domain using a computational model, such as the transonic, small-disturbance, non-linear, potential analysis method, is considered. A trailing-edge control surface, in the form of a part-span flap, was used only to modify and control the unsteady aerodynamic loading on the wing. The flap rotation was used to provide feedback, which consisted of a weighted linear combination of the amplitudes of the principal modes of the structure, referred to as the control law. Given a feedback control law, it is possible in principle to assess its capacity to actively suppress flutter in the transonic flow domain by using a servo-controlled control surface to modify the unsteady aerodynamic loads on the wing. Thus, it becomes essential to construct first a set of feasible control laws. In this paper, this is done by applying the doublet lattice method (DLM) and extracting the low-frequency quasi-steady loads. Only the aerodynamic stiffness and damping, obtained from the low-frequency asymptote, are used, thereby avoiding the need for any augmented states. Note that ignoring the augmented states is completely equivalent to assuming that their dynamics is relatively fast, which justifies this simplification, especially for establishing an initial set of optimal control laws. The aerodynamic loads are computed for all the available structural modes, and no attempt is made to reduce the order of the model. It was decided at the outset not to introduce any reduced-order modelling, to ensure that there was no increase in the flutter speed. Once a set of control laws are available, they are evaluated by using a complete non-linear computational model in the transonic flow regime, and the most suitable set of control laws are selected on the basis of the desired performance and the stability margins. The methodology is applied to several benchmarking wing models, revealing that the design of near-optimal control laws for active flutter suppression is feasible. A systematic search for an optimal or near-optimal control law, such as the one proposed herein, has not been reported in literature. The two important contributions of this paper are the systematic search for a near-optimal controller and the inadequacy of relatively small control inputs. In the case of linear optimal control, one can design a range of control laws that are expected to be suitable. However, in reality, it is shown that relatively small control inputs, that is, control laws requiring small control surface deflections, may not be adequate for suppressing flutter, in certain planforms at transonic speeds, but not in all.
2.0 ESTABLISHING AN INITIAL SET OF OPTIMAL CONTROL LAWS
In this sub-section, the formulation for the prediction of the linearised, quasi-steady subsonic aerodynamic loads is briefly revisited to explain how a preliminary linear state-space model and a set of optimal control laws can be established. Generally, if one uses the DLM, given a reference length such as the root chord
![]() ${c_r}$
, the free stream density
${c_r}$
, the free stream density
![]() ${\rho _\infty }$
and the free stream flow velocity
${\rho _\infty }$
and the free stream flow velocity
![]() ${U_\infty }$
, one can construct the generalised aerodynamic forces matrix defined by
${U_\infty }$
, one can construct the generalised aerodynamic forces matrix defined by
where
![]() ${z_j}$
is the vibration mode shape of the structure in the
${z_j}$
is the vibration mode shape of the structure in the
![]() ${j^{th}}$
mode,
${j^{th}}$
mode,
![]() ${S^ * }$
is the non-dimensional planform area,
${S^ * }$
is the non-dimensional planform area,
![]() ${x^ * }$
and
${x^ * }$
and
![]() ${y^ * }$
are the non-dimensional coordinates of a point in the planform,
${y^ * }$
are the non-dimensional coordinates of a point in the planform,
![]() $k$
is the reduced frequency and
$k$
is the reduced frequency and
![]() ${M_\infty }$
is the free stream Mach number, the ratio of the free stream flow velocity to the local speed of sound. In the above equation for the generalised aerodynamic force matrix, the integration is performed over the planform surface area. The modal displacements and slopes at the sending and receiving points in the DLM code are obtained by spline interpolation of the modal displacements at nodes of the structural model. The matrix
${M_\infty }$
is the free stream Mach number, the ratio of the free stream flow velocity to the local speed of sound. In the above equation for the generalised aerodynamic force matrix, the integration is performed over the planform surface area. The modal displacements and slopes at the sending and receiving points in the DLM code are obtained by spline interpolation of the modal displacements at nodes of the structural model. The matrix
![]() ${\bf{Q}}\left( k \right)$
is generally complex. If one assumes a matrix Padé approximant representation, the matrix
${\bf{Q}}\left( k \right)$
is generally complex. If one assumes a matrix Padé approximant representation, the matrix
![]() ${\bf{Q}}\left( k \right)$
may approximated as
${\bf{Q}}\left( k \right)$
may approximated as
where
![]() ${{\bf{Q}}_0}$
and
${{\bf{Q}}_0}$
and
![]() $ik{{\bf{Q}}_1}$
are the steady-state and low-frequency asymptote, which can be computed independently from the steady-state and low-frequency asymptotes of the subsonic kernel function as outlined by Vepa(Reference Vepa5). If one assumes that the augmented poles are relatively fast, which is usually the case, then it is possible to set
$ik{{\bf{Q}}_1}$
are the steady-state and low-frequency asymptote, which can be computed independently from the steady-state and low-frequency asymptotes of the subsonic kernel function as outlined by Vepa(Reference Vepa5). If one assumes that the augmented poles are relatively fast, which is usually the case, then it is possible to set
![]() ${{\bf{Q}}_p} \approx {\bf{0}}$
. Consequently,
${{\bf{Q}}_p} \approx {\bf{0}}$
. Consequently,
Generally, the matrices
![]() ${{\bf{Q}}_r}$
(the residue matrix) and
${{\bf{Q}}_r}$
(the residue matrix) and
![]() ${{\bf{Q}}_p}$
(the matrix related to the poles corresponding to the augmented states) are constructed by matching the matrix
${{\bf{Q}}_p}$
(the matrix related to the poles corresponding to the augmented states) are constructed by matching the matrix
![]() ${\bf{Q}}\left( k \right)$
to the coefficient matrices in the matrix Padé approximant representation at some low value of the reduced frequency
${\bf{Q}}\left( k \right)$
to the coefficient matrices in the matrix Padé approximant representation at some low value of the reduced frequency
![]() $k = {k_f}$
close to the estimated flutter reduced frequency. Then, assuming that
$k = {k_f}$
close to the estimated flutter reduced frequency. Then, assuming that
![]() $k$
is small, it follows that
$k$
is small, it follows that
Thus
![]() ${\bf{Q}}\left( k \right)$
, computed by the DLM, may be approximated by the quasi-steady approximation, which corresponds to the zeroth-order matrix Padé approximant and is given by
${\bf{Q}}\left( k \right)$
, computed by the DLM, may be approximated by the quasi-steady approximation, which corresponds to the zeroth-order matrix Padé approximant and is given by
The approximation involves no augmented states and can be used to construct a linear state-space model of the aeroelastic system. Thus, given the mass matrix
![]() ${\bf{M}}$
, the stiffness matrix
${\bf{M}}$
, the stiffness matrix
![]() ${\bf{K}}$
, of the structural system, assuming a suitable model for the structural damping factor
${\bf{K}}$
, of the structural system, assuming a suitable model for the structural damping factor
![]() $g$
, so the structural damping matrix is
$g$
, so the structural damping matrix is
![]() ${\bf{C}} = g{\bf{K}}$
, and that any control surface that may be present is locked in its equilibrium position, the equations of motion of the wing in terms of the vector of generalised modal displacement amplitudes
${\bf{C}} = g{\bf{K}}$
, and that any control surface that may be present is locked in its equilibrium position, the equations of motion of the wing in terms of the vector of generalised modal displacement amplitudes
![]() ${\bf{q}} = {\left[ {{q_j}} \right]^T}$
are
${\bf{q}} = {\left[ {{q_j}} \right]^T}$
are
When the modal displacements are normalised by the square root of the generalised masses, the mass matrix is given by
![]() ${\bf{M}} = {\bf{I}}$
and the coordinates
${\bf{M}} = {\bf{I}}$
and the coordinates
![]() ${\bf{q}}$
are the principal coordinates. In the presence of a control surface such as a trailing-edge partial-span flap, assuming that the flap is actuated relatively slowly, the equations of motion defined by equations (6) are now extended to include the quasi-steady generalised aerodynamic forces due to the flap angular displacement
${\bf{q}}$
are the principal coordinates. In the presence of a control surface such as a trailing-edge partial-span flap, assuming that the flap is actuated relatively slowly, the equations of motion defined by equations (6) are now extended to include the quasi-steady generalised aerodynamic forces due to the flap angular displacement
![]() $\eta $
and expressed as
$\eta $
and expressed as
The equations of motion defined by equations (7) may then be cast in state-space form, where the state vector is the combination of both
![]() ${\bf{q}}$
and
${\bf{q}}$
and
![]() ${\dot{\bf{q}}}$
, and written as
${\dot{\bf{q}}}$
, and written as
Now it is completely feasible to construct an optimal control law based on the above model formulation, defined by equation (8). The optimal control is assumed to minimise a cost function of the form
where
![]() $r$
is a scalar used to alter the control weighting matrix
$r$
is a scalar used to alter the control weighting matrix
![]() ${\bf{R}}$
in the formulation of the optimal control law synthesis,
${\bf{R}}$
in the formulation of the optimal control law synthesis,
![]() ${{\bf{Q}}_x}$
is the state vector weighting matrix, and
${{\bf{Q}}_x}$
is the state vector weighting matrix, and
![]() ${{\bf{Q}}_f}$
is the weighting matrix for the state vector at the final time
${{\bf{Q}}_f}$
is the weighting matrix for the state vector at the final time
![]() $t = {t_f}$
. For the single input case,
$t = {t_f}$
. For the single input case,
![]() ${\bf{R}} = 1$
. The steady-state control law takes the form
${\bf{R}} = 1$
. The steady-state control law takes the form
where
![]() ${{\bf{P}}_\infty }$
satisfies an algebraic Riccati equation. Thus, given a range of monotonically increasing free stream Mach numbers
${{\bf{P}}_\infty }$
satisfies an algebraic Riccati equation. Thus, given a range of monotonically increasing free stream Mach numbers
![]() ${M_{\infty ,j}}$
,
${M_{\infty ,j}}$
,
![]() $j = 1,2, \cdots ,$
as well as a set of values for the relative weighting scaling parameter
$j = 1,2, \cdots ,$
as well as a set of values for the relative weighting scaling parameter
![]() $r$
, one can construct families of control laws with differing closed-loop stability characteristics. Each of these control laws may then be used with the open-loop dynamics, reformulated in the transonic domain based on the TSD theory, to study the closed-loop behaviour of the aeroelastic system. The control laws, however, are no longer optimal and can at best be considered as near optimal. To match the control laws to the transonic dynamic model and the TSD theory, the control law calculations are carried out at a set of specific flight conditions.
$r$
, one can construct families of control laws with differing closed-loop stability characteristics. Each of these control laws may then be used with the open-loop dynamics, reformulated in the transonic domain based on the TSD theory, to study the closed-loop behaviour of the aeroelastic system. The control laws, however, are no longer optimal and can at best be considered as near optimal. To match the control laws to the transonic dynamic model and the TSD theory, the control law calculations are carried out at a set of specific flight conditions.
The parameter r, in accordance with optimal control theory, is the ratio of the maximum magnitude of an element in the state vector to the maximum magnitude of the control input. It is a measure of the performance that is expected or delivered by the optimal control law. When r is large, the maximum magnitude of the control input relative to the magnitude of the state is very small. In this case, the magnitude of the largest element in the state vector is large; it asymptotically tends to the case when there is no or a small control input. On the other hand, when r is small, the control input is significant as a large control input must be used. The case of
![]() $r \approx 1$
represents the balanced case where the magnitude of the control used is of the same order of magnitude as the state vector. In this paper, it provides us with a single scalar parameter that we can vary to obtain a large distribution of control laws, which we could use to find a near-optimal solution, as our problem is essentially non-linear.
$r \approx 1$
represents the balanced case where the magnitude of the control used is of the same order of magnitude as the state vector. In this paper, it provides us with a single scalar parameter that we can vary to obtain a large distribution of control laws, which we could use to find a near-optimal solution, as our problem is essentially non-linear.
Alternative methods for synthesising the preliminary control law, such as transonic linear small perturbation theory, time-domain fitting of the unsteady loads, eigensystem realisation algorithm and the transonic linear full potential method, were also explored. However, the doublet lattice method coupled with the zeroth-order matrix Padé approximant provided the fastest method for synthesising the large number of preliminary control laws needed to make an informed choice of the final control law. By using a linear model such as the DLM, the search for a suitable control law is essentially carried out over a one- rather than multi-dimensional space.
3.0 CONTROL LAW VALIDATION IN THE TRANSONIC DOMAIN
In the transonic domain, based on the TSD formulation, the equations of motion of the vibrating wing, including the partial-span trailing-edge flap, take the form
where the vectors
![]() ${{\bf{Q}}_{tsd}}\left( {{\bf{q}},{\rm{ }}{\dot{\bf{q}}},{M_\infty }} \right)$
and
${{\bf{Q}}_{tsd}}\left( {{\bf{q}},{\rm{ }}{\dot{\bf{q}}},{M_\infty }} \right)$
and
![]() ${{\bf{Q}}_{tsd,\eta }}\left( {{\bf{q}},{\rm{ }}{\dot{\bf{q}}},{M_\infty }} \right)$
are obtained numerically using a code based on the TSD formulation(Reference Kwon, Kim and Lee44). When the feedback control law developed in the preceding section is used, the corresponding closed-loop equations of motion take the form
${{\bf{Q}}_{tsd,\eta }}\left( {{\bf{q}},{\rm{ }}{\dot{\bf{q}}},{M_\infty }} \right)$
are obtained numerically using a code based on the TSD formulation(Reference Kwon, Kim and Lee44). When the feedback control law developed in the preceding section is used, the corresponding closed-loop equations of motion take the form
It must be emphasised that, in the above equations (11) and (12), the aerodynamic load vectors are computed by the use of the TSD theory, while the control gain vector
![]() ${{\bf{K}}_f}$
, in equation (12), is obtained by using a linear model of the aeroelastic system based on the DLM. However, the DLM is also a linear potential flow-based method, although it is also a boundary element method based on the linearised kernel function formulation of the potential function.
${{\bf{K}}_f}$
, in equation (12), is obtained by using a linear model of the aeroelastic system based on the DLM. However, the DLM is also a linear potential flow-based method, although it is also a boundary element method based on the linearised kernel function formulation of the potential function.
To match the control laws to the transonic model, the response calculations were carried out at the same set of specific flight conditions as used earlier for the computation of the control laws. As the model used for the synthesis of the linear control laws and the model used for the closed-loop validation are different, the control laws can, at best, be only considered to be sub-optimal, although it is possible to show in principle, on the basis of the solution of the inverse optimal control problem, that there exists an optimising cost function associated with the closed-loop model. The numerical solution of the closed-loop equation (12) is obtained by a time-marching method. By proceeding monotonically from the open-loop stable case, for lower values of
![]() ${M_\infty }$
, to the open-loop unstable cases corresponding to higher values of
${M_\infty }$
, to the open-loop unstable cases corresponding to higher values of
![]() ${M_\infty }$
, the responses are obtained quite quickly. The closed-loop characteristics are assessed, and from the responses, the decay rate and oscillation frequency are obtained. By suitable interpolation, when the decay rate is equal to zero, the flutter Mach number and the flutter frequency are then obtained, provided they lie within the envelope of the cases considered. In most cases, the closed-loop response was adequately stable and the corresponding flutter Mach number and flutter frequency are beyond the aircraft’s desired flight envelope.
${M_\infty }$
, the responses are obtained quite quickly. The closed-loop characteristics are assessed, and from the responses, the decay rate and oscillation frequency are obtained. By suitable interpolation, when the decay rate is equal to zero, the flutter Mach number and the flutter frequency are then obtained, provided they lie within the envelope of the cases considered. In most cases, the closed-loop response was adequately stable and the corresponding flutter Mach number and flutter frequency are beyond the aircraft’s desired flight envelope.
4.0 APPLICATION TO BENCHMARKING EXAMPLES
The methodology was applied to two benchmarking examples, the first a low-aspect-ratio wing and the second a moderately high-aspect-ratio wing. The first is the AGARD 445.6 wing model, proposed by Yates(Reference Yates45), which is a standard aeroelastic configuration used for validation purposes. Experimentally obtained transonic flutter characteristics of a similar wing planform were reported earlier.
The AGARD 445.6 wing is a swept-back wing, with a quarter-chord sweep angle of 45° and a NACA 65A004 aerofoil cross-section, as shown in Fig. 1. It has a panel aspect ratio of 1.65 and a taper ratio of 0.66. In the DLM code, it is modelled as a flat plate. Continuous representations of the first four mode shapes of the AGARD 445.6 planform, obtained after splining the discrete mode shape data using the infinite plate surface (IPS) spline method proposed by Harder and Desmarais(Reference Harder and Desmarais46), which assumes a set of discrete data points lying within an infinite flat plate, are shown in Fig. 2.
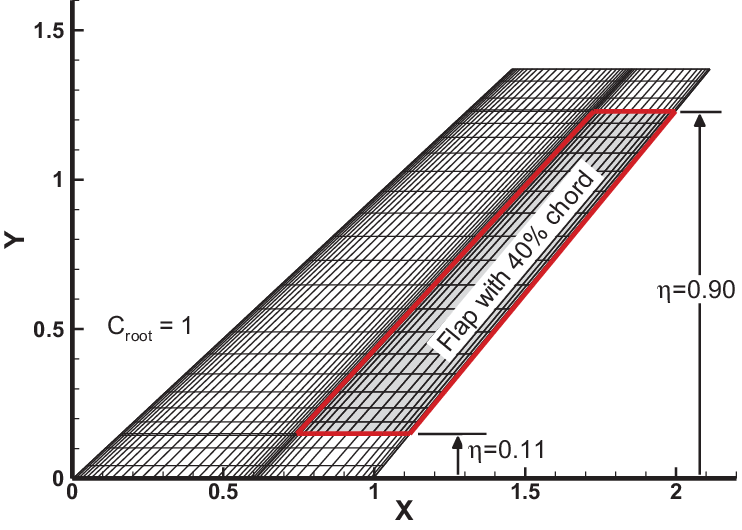
Figure 1. The AGARD 445.6 planform with trailing-edge flap and the aerodynamic grid.
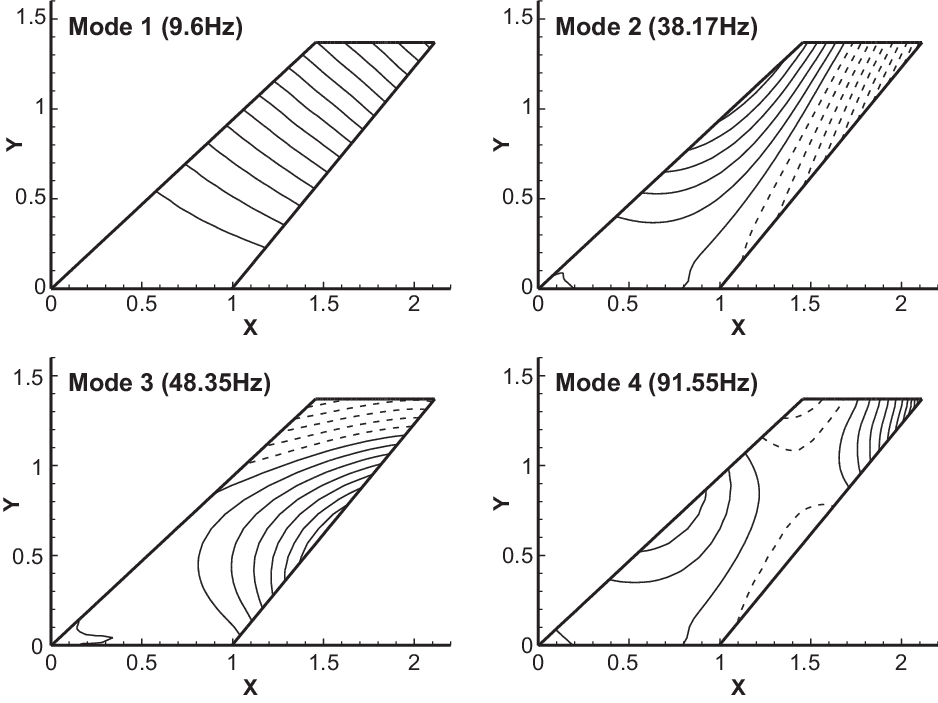
Figure 2. Illustration of the first four mode shapes of the AGARD 445.6 wing smoothed by the IPS method.
The nominal flight condition for this example is an altitude of 10,000m. The corresponding atmospheric density, temperature and the speed of sound were estimated from the properties of the international standard atmosphere. The structural damping factor was assumed to be
![]() $g = 0.03$
, as it is particularly important to damp the higher-frequency modes.
$g = 0.03$
, as it is particularly important to damp the higher-frequency modes.
The second benchmarking model used for validation is the NASA Common Research Model (CRM), which consists of a contemporary supercritical transonic wing (and a fuselage). The CRM is designed for a cruise Mach number of
![]() ${M_\infty } = 0.85$
. The corresponding design coefficient of lift is
${M_\infty } = 0.85$
. The corresponding design coefficient of lift is
![]() ${C_L} = 0.5$
. The aspect ratio of the wing planform is equal to 9.0, and the quarter-chord sweep angle is 35°.
${C_L} = 0.5$
. The aspect ratio of the wing planform is equal to 9.0, and the quarter-chord sweep angle is 35°.
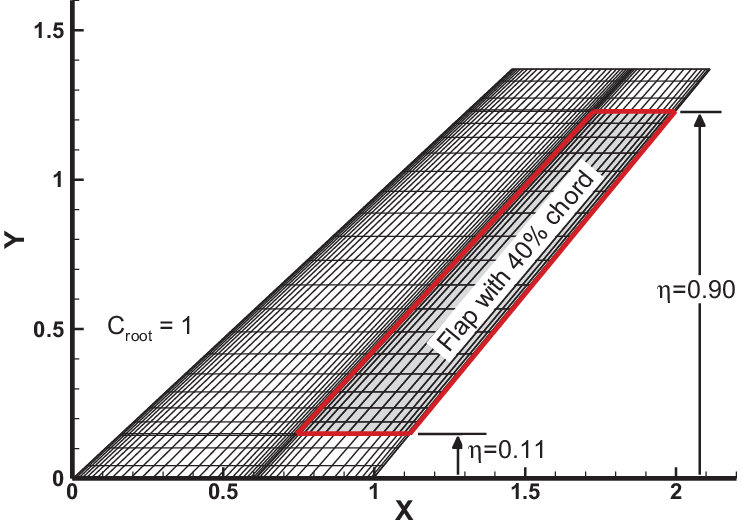
Initially, the structural modes of the wing models were computed using a matching structural grid and the finite element method and verified with published data, provided in the paper. The primary modification introduced was the inclusion of a servo-controlled flap, which was assumed to be deflected relatively slowly. The flap was used only to modify the unsteady aerodynamic loading on the wing. When any modifications were made to the wing, the structural modes were re-computed using a similar matching structural grid and the finite element method with the flap actuator fixed rigidly, so the flap remained without any rotation in its initial equilibrium position. The same method was used for all the benchmarking models that were considered. In the second example, the flap was assumed to be much smaller relative to the wing than in the first example, but it is more realistic. The non-dimensional CRM planform is illustrated in Fig. 3. The geometry and model files are available in the public domain(Reference Rivers47).

Figure 3. Non-dimensional CRM planform with a flap of 23% wing chord.
5.0 TYPICAL RESULTS AND DISCUSSION
The first example was the AGARD 445.6 three-dimensional wing. In this example, to capture the closed-loop flutter point, the response calculations were done at several sets of flight Mach number, corresponding to the range of values of the flutter speed index
![]() ${U_\mu }$
, and the cost function relative weighting scaling parameter
${U_\mu }$
, and the cost function relative weighting scaling parameter
![]() $r$
, defined earlier in equations (9) and (10). Based on the quasi-steady DLM, the wing flutters in open loop, at
$r$
, defined earlier in equations (9) and (10). Based on the quasi-steady DLM, the wing flutters in open loop, at
![]() ${M_\infty } = 0.86$
.
${M_\infty } = 0.86$
.
Based on the nonlinear TSD aerodynamics, the onset of flutter without any control inputs occurs at about
![]() ${M_\infty } = 0.56$
. Recall that the non-dimensional flutter speed index
${M_\infty } = 0.56$
. Recall that the non-dimensional flutter speed index
![]() ${U_\mu }$
was defined in Cunningham et al.(Reference Cunningham, Batina and Bennett48) and earlier by Yates(Reference Yates45) in terms of the chosen reference length
${U_\mu }$
was defined in Cunningham et al.(Reference Cunningham, Batina and Bennett48) and earlier by Yates(Reference Yates45) in terms of the chosen reference length
![]() ${b_0}$
, the first torsional natural frequency
${b_0}$
, the first torsional natural frequency
![]() ${\omega _\alpha }$
and the ratio of the wing mass to the mass of air in the truncated cone that encloses the wing, denoted by
${\omega _\alpha }$
and the ratio of the wing mass to the mass of air in the truncated cone that encloses the wing, denoted by
![]() $\mu $
, as
$\mu $
, as
Thus, the flutter speed index and the Mach number are proportional to each other for a specific wing and flight condition. So, for a particular flutter speed index, there is a corresponding Mach number, which is referred to as the matched point. Thus, the Mach number of
![]() ${M_\infty } = 0.56$
corresponds to a matched flutter point with a flutter speed index equal to
${M_\infty } = 0.56$
corresponds to a matched flutter point with a flutter speed index equal to
![]() ${U_\mu } = 0.67$
for the wing and flight condition under consideration.
${U_\mu } = 0.67$
for the wing and flight condition under consideration.
An initial set of optimal control laws, synthesised for
![]() ${M_\infty } = 0.85$
(based on the DLM) and for a set of 20 different values for the weighting parameter r, in the range
${M_\infty } = 0.85$
(based on the DLM) and for a set of 20 different values for the weighting parameter r, in the range
![]() $0.1 \le r \le 500$
, were used to evaluate the closed-loop performance using the TSD aerodynamics. The responses of the flap and wing in closed loop, obtained for different r values at a typical nominal cruise Mach number of
$0.1 \le r \le 500$
, were used to evaluate the closed-loop performance using the TSD aerodynamics. The responses of the flap and wing in closed loop, obtained for different r values at a typical nominal cruise Mach number of
![]() ${M_\infty } = 0.85$
and
${M_\infty } = 0.85$
and
![]() ${U_\mu } = 0.44$
, are compared in Fig. 4.
${U_\mu } = 0.44$
, are compared in Fig. 4.
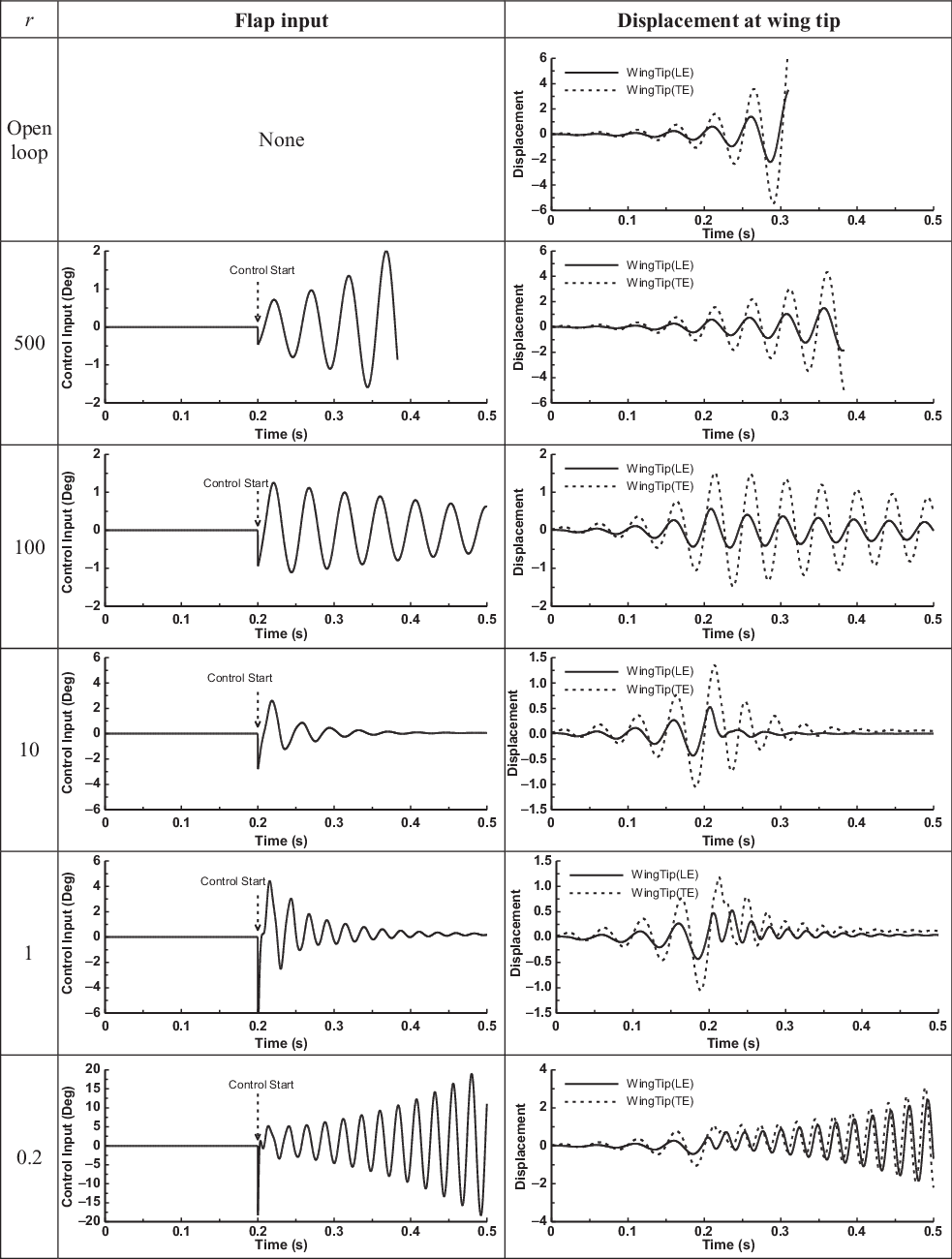
Figure 4. Closed-loop responses for different r values at
![]() ${M_\infty } = 0.85$
and
${M_\infty } = 0.85$
and
![]() ${U_\mu } = 0.44$
.
${U_\mu } = 0.44$
.
Initially, the transonic aerodynamic calculations, which use a set of non-dimensional parameters, were performed at a lower value of the flutter speed index
![]() ${U_\mu } = 0.44$
than the actual matched point value of
${U_\mu } = 0.44$
than the actual matched point value of
![]() ${U_\mu } = 0.67$
. Computations of both the control laws and the TSD aerodynamics were repeated for a range of cruise Mach numbers from 0.5 to 0.95. The results obtained in the open- and closed-loop cases were qualitatively similar to those of Lai and Lum(Reference Lai and Lum49), who presented a flutter prediction approach using a combination of full-order computational aeroelastic techniques and reduced-order modelling methods, which were applied to closed-loop and nonlinear Hopf bifurcation analysis of the benchmark transonic aeroelastic AGARD 445.6 wing.
${U_\mu } = 0.67$
. Computations of both the control laws and the TSD aerodynamics were repeated for a range of cruise Mach numbers from 0.5 to 0.95. The results obtained in the open- and closed-loop cases were qualitatively similar to those of Lai and Lum(Reference Lai and Lum49), who presented a flutter prediction approach using a combination of full-order computational aeroelastic techniques and reduced-order modelling methods, which were applied to closed-loop and nonlinear Hopf bifurcation analysis of the benchmark transonic aeroelastic AGARD 445.6 wing.
Under transonic flow conditions, high-aspect-ratio wings can exhibit Limit-Cycle Oscillations (LCOs). Trailing-edge flaps can exhibit transonic buzz, an instability driven by aerodynamic nonlinearities. Control surface buzz is an LCO type of aeroelastic instability observed in trailing-edge control surfaces(Reference Dowell, Edwards and Strganac50). However, Allen et al.(Reference Allen, Jones, Taylor, Badcock, Woodgate, Rampurawala, Cooper and Vio51) confirmed that the calculations of the flutter instability boundaries of the AGARD 445.6 wing based on linear analysis techniques provided reasonably accurate results because of the simplicity of the planform shape. Thus, from the responses obtained numerically, the range of r values for which one could expect closed-loop stability at a desired value of the cruise Mach number are determined.
Now, it is possible to focus on a lower range of values of the relative weighting parameter r and increase the value of the flutter speed index
![]() ${U_\mu }$
. The closed-loop flap and wing responses obtained for different r values at the typical nominal cruise Mach number of
${U_\mu }$
. The closed-loop flap and wing responses obtained for different r values at the typical nominal cruise Mach number of
![]() ${M_\infty } = 0.85$
and a flutter speed index
${M_\infty } = 0.85$
and a flutter speed index
![]() ${U_\mu } = 0.66$
are compared in Fig. 5. An optimum choice is
${U_\mu } = 0.66$
are compared in Fig. 5. An optimum choice is
![]() $r \approx 1$
, which implies that the magnitudes of both the modal amplitudes and the flap deflections are of equal importance in the cost function.
$r \approx 1$
, which implies that the magnitudes of both the modal amplitudes and the flap deflections are of equal importance in the cost function.
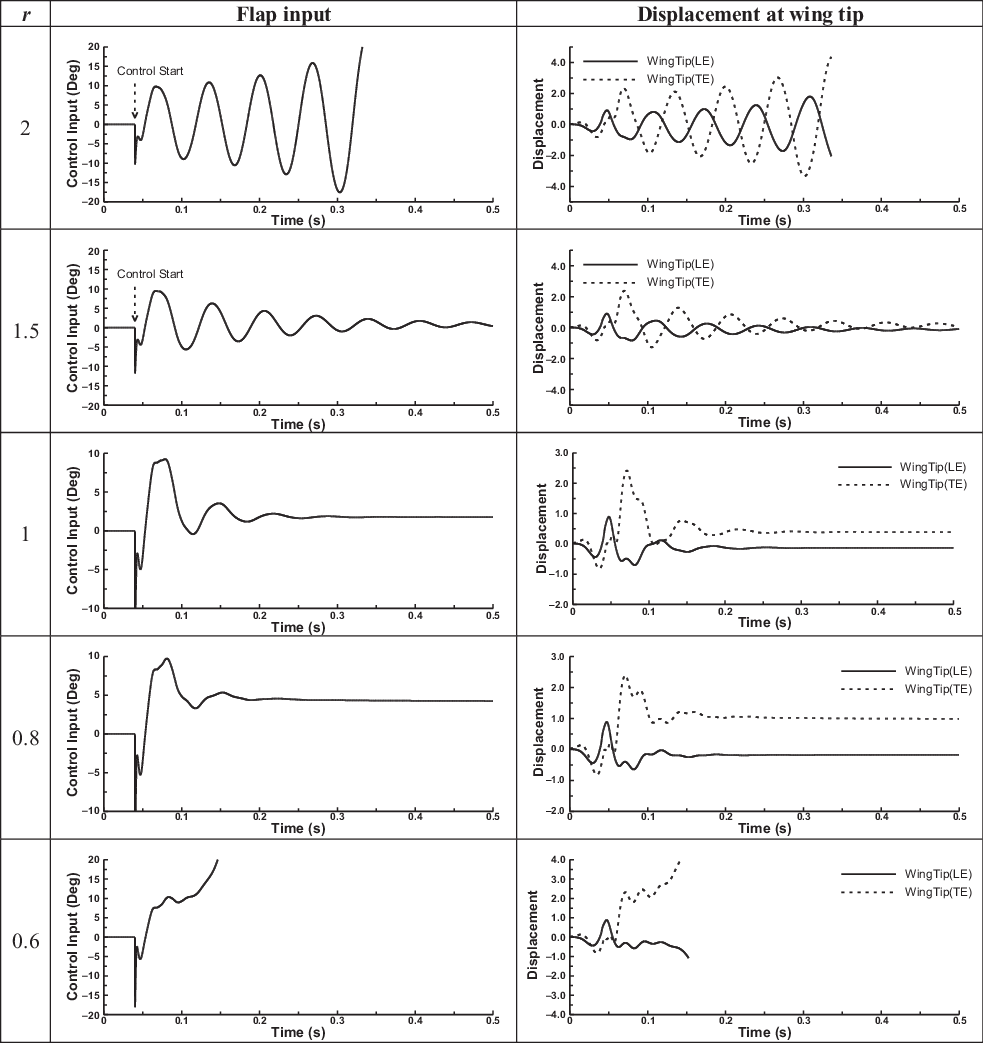
Figure 5. Closed-loop flap and wing responses for different r values at
![]() ${M_\infty } = 0.85$
and
${M_\infty } = 0.85$
and
![]() ${U_\mu } = 0.66$
.
${U_\mu } = 0.66$
.
The closed-loop flutter point, with the initial control law computed as explained above and with
![]() $r = 1$
, is now established. The Mach number at the onset of flutter, corresponding to the matched flutter point, is just over
$r = 1$
, is now established. The Mach number at the onset of flutter, corresponding to the matched flutter point, is just over
![]() ${M_\infty } = 0.85$
, corresponding to a flutter speed index of
${M_\infty } = 0.85$
, corresponding to a flutter speed index of
![]() ${U_\mu } = 0.67$
, which is only marginally higher than in Fig. 5. The open- and closed-loop matched point responses at
${U_\mu } = 0.67$
, which is only marginally higher than in Fig. 5. The open- and closed-loop matched point responses at
![]() ${M_\infty } = 0.6$
and
${M_\infty } = 0.6$
and
![]() ${M_\infty } = 0.85$
, respectively, are compared in Fig. 6. Also shown in Fig. 7 are plots of the flutter speed index and the flutter frequency versus the Mach number. The open-loop results are compared with the experimental results of Yates(Reference Yates45) and the results obtained by Lee-Rausch and Batina(Reference Lee-Rausch and Batina52) using the numerical solution of the Euler equations.
${M_\infty } = 0.85$
, respectively, are compared in Fig. 6. Also shown in Fig. 7 are plots of the flutter speed index and the flutter frequency versus the Mach number. The open-loop results are compared with the experimental results of Yates(Reference Yates45) and the results obtained by Lee-Rausch and Batina(Reference Lee-Rausch and Batina52) using the numerical solution of the Euler equations.
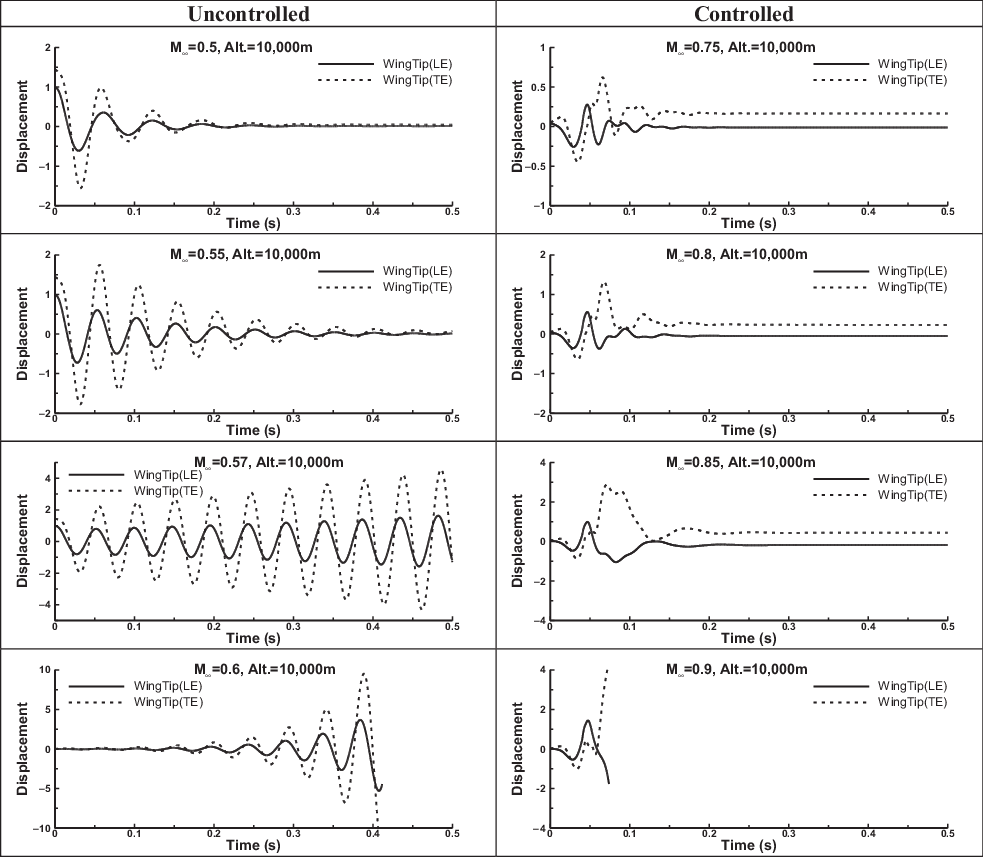
Figure 6. Open and closed-loop responses for
![]() $r = 1$
.
$r = 1$
.
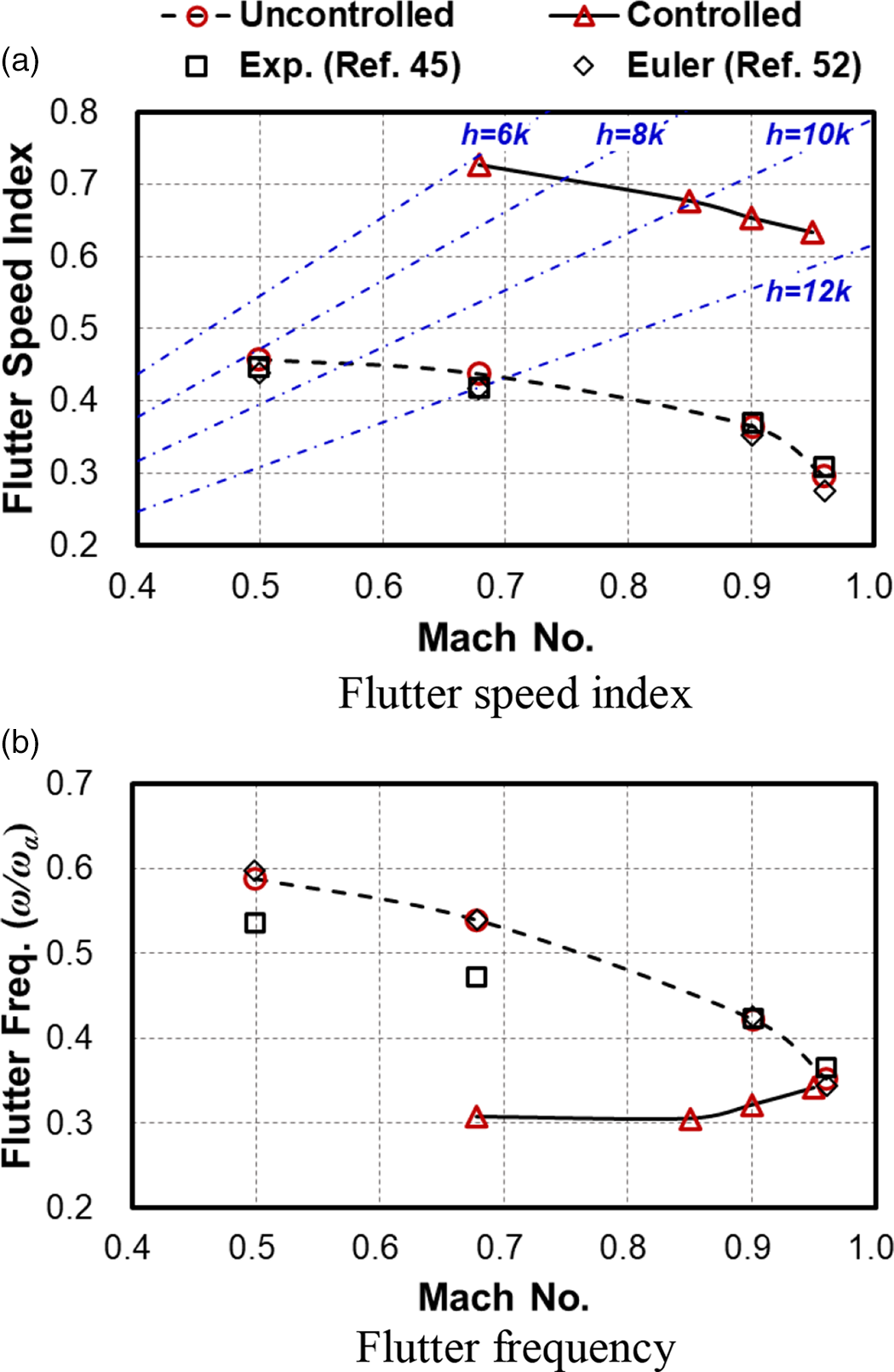
Figure 7. (a) Flutter speed index and (b) flutter frequency versus the Mach number.
The second example considered is the CRM three-dimensional wing with a free stream Mach number ranging from
![]() ${M_\infty } = 0.65$
to
${M_\infty } = 0.65$
to
![]() ${M_\infty } = 0.96$
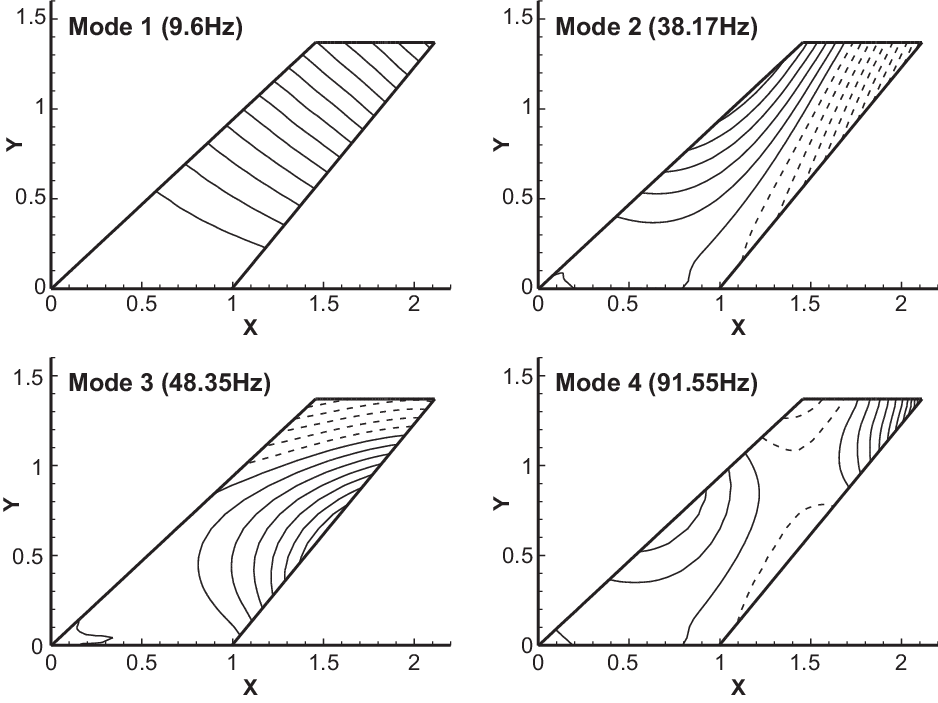
. Initially, 20 modes were used to perform the flutter analysis. The non-dimensional flutter speed was computed. The number of modes used was reduced to 18, and the non-dimensional flutter speed was re-computed. There was no perceptible change in the flutter speed, which meant that the higher modes did not play a role in determining the flutter speed. This process was continued, and the optimum set of modes to describe the open-loop dynamics was then established. After analysing with several other modal combinations as well, it was decided that the first eight modes were adequate for the synthesis of the control laws. These modes and their shapes are shown in Fig. 8. The open-loop flutter boundaries with a structural damping factor of
${M_\infty } = 0.96$
. Initially, 20 modes were used to perform the flutter analysis. The non-dimensional flutter speed was computed. The number of modes used was reduced to 18, and the non-dimensional flutter speed was re-computed. There was no perceptible change in the flutter speed, which meant that the higher modes did not play a role in determining the flutter speed. This process was continued, and the optimum set of modes to describe the open-loop dynamics was then established. After analysing with several other modal combinations as well, it was decided that the first eight modes were adequate for the synthesis of the control laws. These modes and their shapes are shown in Fig. 8. The open-loop flutter boundaries with a structural damping factor of
![]() $g = 0.03$
are compared with the closed-loop flutter boundaries in Fig. 9. The frequencies are reported in Hz for ease of comparison with the modes in Fig. 8 and as reported in ref. (Reference Rivers47).
$g = 0.03$
are compared with the closed-loop flutter boundaries in Fig. 9. The frequencies are reported in Hz for ease of comparison with the modes in Fig. 8 and as reported in ref. (Reference Rivers47).
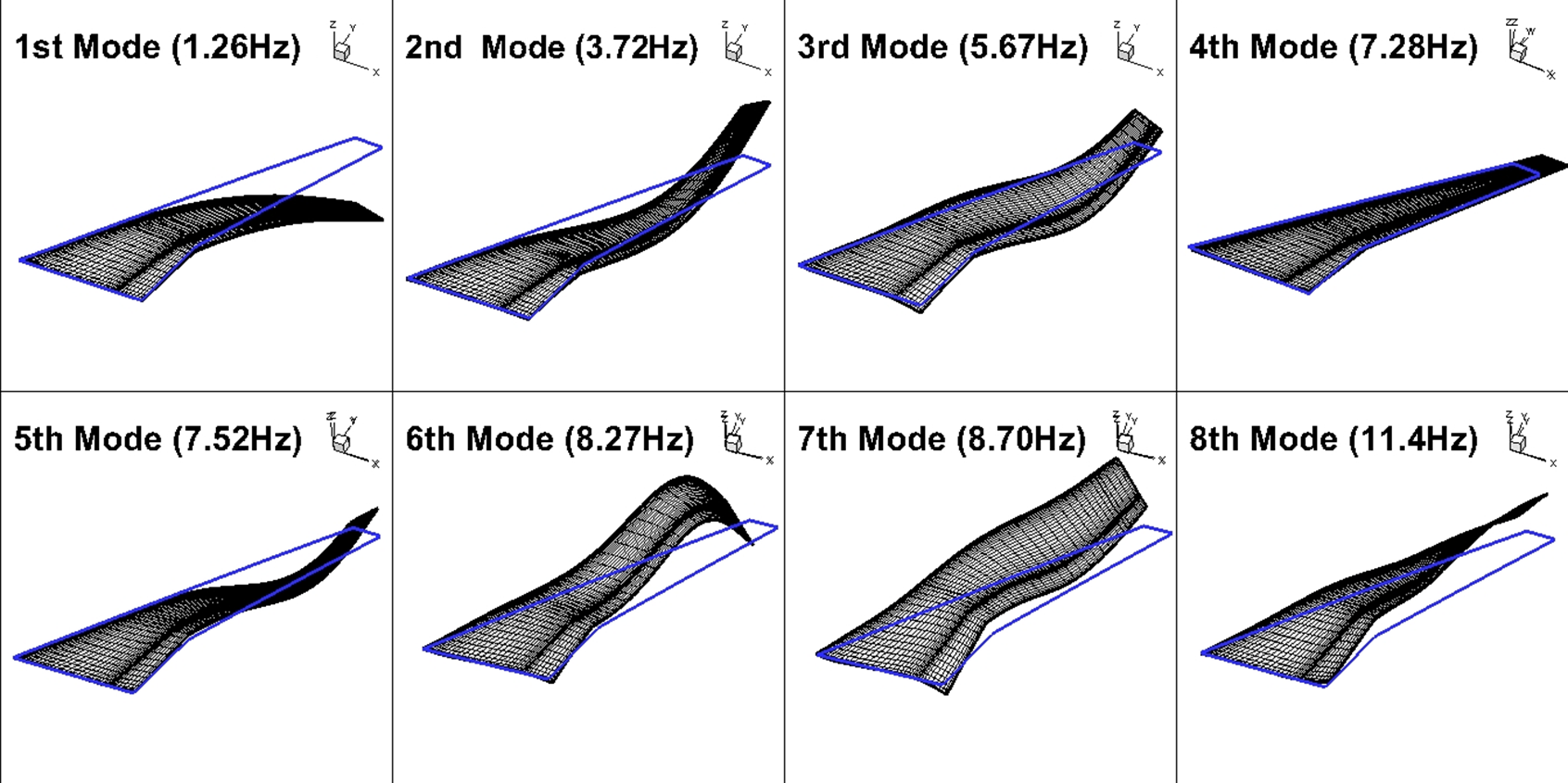
Figure 8. Structural mode shapes and frequencies of the CRM wing-box v15 model.
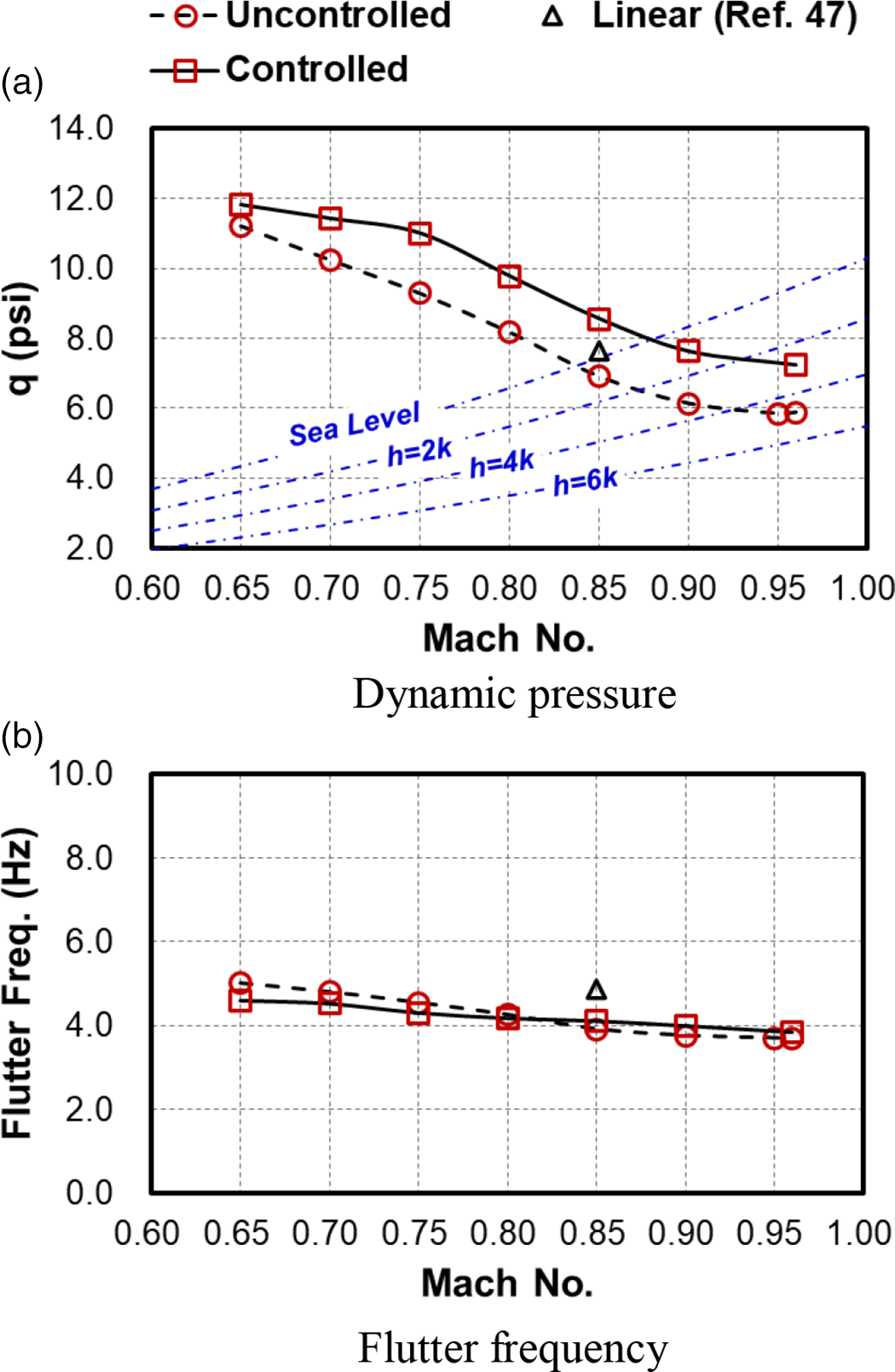
Figure 9. Plots of the open- and closed-loop (a) flutter dynamic pressure and (b) flutter frequency versus the Mach number for the CRM planform.
The initial set of control law gains for the 16 states in the model were first computed for several free stream Mach numbers given by,
![]() ${M_\infty } = 0.65, \cdots ,{\rm{ }}0.85,0.88,0.90, \cdots ,0.96$
, and for
${M_\infty } = 0.65, \cdots ,{\rm{ }}0.85,0.88,0.90, \cdots ,0.96$
, and for
![]() $r$
values ranging from 1 to 10, representing over 200 gain vector sets to facilitate a wide search. The lowest gain magnitudes were obtained for
$r$
values ranging from 1 to 10, representing over 200 gain vector sets to facilitate a wide search. The lowest gain magnitudes were obtained for
![]() ${M_\infty } = 0.65$
with
${M_\infty } = 0.65$
with
![]() $r = 10$
, and the highest for
$r = 10$
, and the highest for
![]() ${M_\infty } = 0.96$
with
${M_\infty } = 0.96$
with
![]() $r = 1$
. A systematic search amongst these gain vector sets was then performed to identify the best gain vector sets, both in terms of optimality and to ensure feasibility of physical implementation, using the nonlinear TSD aerodynamics to compute the closed-loop characteristics. After establishing the trends in the changes in the flutter speeds, the search was restricted to a much smaller number of selected gain vector sets.
$r = 1$
. A systematic search amongst these gain vector sets was then performed to identify the best gain vector sets, both in terms of optimality and to ensure feasibility of physical implementation, using the nonlinear TSD aerodynamics to compute the closed-loop characteristics. After establishing the trends in the changes in the flutter speeds, the search was restricted to a much smaller number of selected gain vector sets.
The closed-loop computations were performed over a much larger time frame as compared with the earlier example, with a similar time step, as the frequencies of vibration were significantly smaller in this example. So, the computations took much longer. The closed-loop response computations and analysis were also performed for
![]() ${M_\infty } = 0.65, \cdots ,{\rm{ }}0.96$
. Since the CRM is a high-aspect-ratio wing, it is important to ensure that the occurrence of control surface buzz of the LCO type is avoided. Figure 10 compares the open- and closed-loop responses of the wing at
${M_\infty } = 0.65, \cdots ,{\rm{ }}0.96$
. Since the CRM is a high-aspect-ratio wing, it is important to ensure that the occurrence of control surface buzz of the LCO type is avoided. Figure 10 compares the open- and closed-loop responses of the wing at
![]() ${M_\infty } = 0.85 - 0.96$
with
${M_\infty } = 0.85 - 0.96$
with
![]() $r = 1$
and with a dynamic pressure equal to q = 6.52 psi to 7.17psi. The increase in the closed-loop flutter speed is more than 16%. Increasing the r value from 1 to about 5 did not have a significant effect on the closed-loop flutter speed. Thus, the key feedbacks and modal quantities could be identified.
$r = 1$
and with a dynamic pressure equal to q = 6.52 psi to 7.17psi. The increase in the closed-loop flutter speed is more than 16%. Increasing the r value from 1 to about 5 did not have a significant effect on the closed-loop flutter speed. Thus, the key feedbacks and modal quantities could be identified.
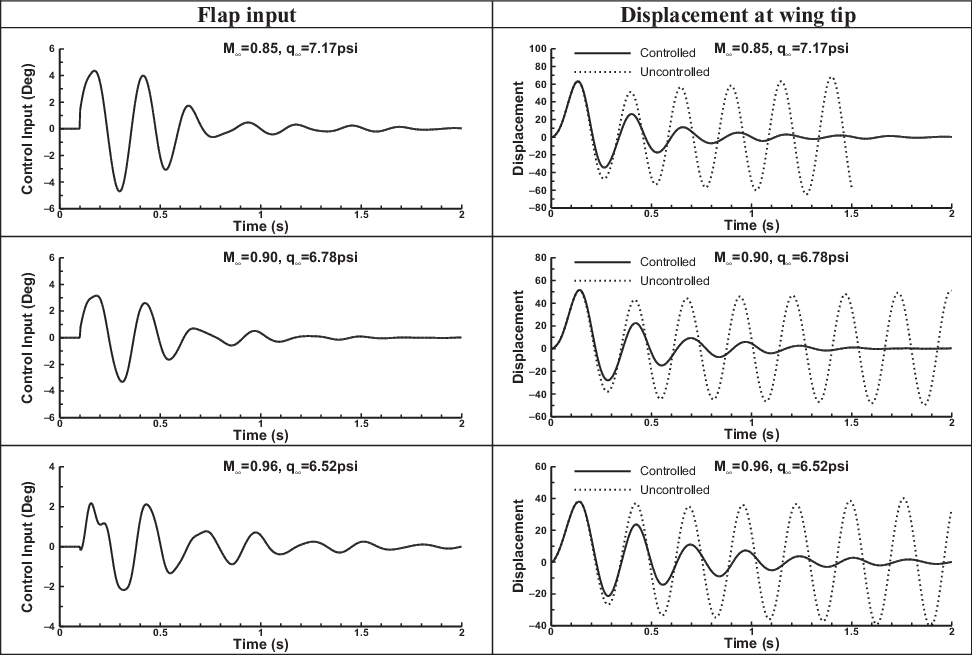
Figure 10. Comparison of open- and closed-loop responses at
![]() ${M_\infty } = 0.85,{\rm{ 0}}{\rm{.90, 0}}{\rm{.96}}$
with
${M_\infty } = 0.85,{\rm{ 0}}{\rm{.90, 0}}{\rm{.96}}$
with
![]() $r = 1$
.
$r = 1$
.
6.0 CONCLUSIONS
The present work introduces a systematic technique for the synthesis of near-optimum control laws for active flutter suppression for three-dimensional wing configurations based on a computational model. In the first instance, an AGARD 445.6 wing planform was considered and it is shown that the flutter Mach number could be raised from 0.6 to 0.85 by using an appropriate linear state feedback control law. It was decided that the closed-loop flutter Mach number should not exceed 0.85, as one could encounter the transonic dip region and the difficulties associated with it. It was also decided to stay away from the domains exhibiting LCOs and control surface buzz. The design objectives were successfully achieved in this validation example.
The open-loop flutter speed obtained by using the DLM-based aerodynamics was significantly higher than the corresponding open-loop flutter speed obtained by using the nonlinear TSD-based aerodynamics, clearly showing the unreliability of the DLM. Although it is possible to reduce this gap by modifying the potential function equation, as the flow approaches
![]() ${M_\infty } \to 1$
, it may not be worth the effort. Nevertheless, the sets of linear control laws obtained by using the aerodynamic loads as calculated by the DLM were extremely useful in the search for a suitable control law that is capable of delivering the desired closed-loop performance. While a linear aeroelastic system with the DLM-based aerodynamics, with or without augmented states, can be stabilised for all values of the cost function relative weighting parameter r, it is seen that, with the nonlinear TSD aerodynamics, the aeroelastic system is stabilised only for a small range of r values. Moreover, as the flight velocity or free stream velocity approaches the closed-loop flutter speed, this range rapidly decreases, although the control gains were re-computed for those particular flight velocities as well as the values of r. This suggests that there is an upper limit (in terms of the flight or free stream Mach number) beyond which a control law computed with the linear aerodynamics and a suitable r value is unable to stabilise the aeroelastic system with the non-linear TSD aerodynamics. This clearly points to the fact that a relatively small control input is inadequate; that is, control laws requiring small control surface deflections may not be adequate for suppressing flutter beyond a certain Mach number. In this example, this seems to occur around
${M_\infty } \to 1$
, it may not be worth the effort. Nevertheless, the sets of linear control laws obtained by using the aerodynamic loads as calculated by the DLM were extremely useful in the search for a suitable control law that is capable of delivering the desired closed-loop performance. While a linear aeroelastic system with the DLM-based aerodynamics, with or without augmented states, can be stabilised for all values of the cost function relative weighting parameter r, it is seen that, with the nonlinear TSD aerodynamics, the aeroelastic system is stabilised only for a small range of r values. Moreover, as the flight velocity or free stream velocity approaches the closed-loop flutter speed, this range rapidly decreases, although the control gains were re-computed for those particular flight velocities as well as the values of r. This suggests that there is an upper limit (in terms of the flight or free stream Mach number) beyond which a control law computed with the linear aerodynamics and a suitable r value is unable to stabilise the aeroelastic system with the non-linear TSD aerodynamics. This clearly points to the fact that a relatively small control input is inadequate; that is, control laws requiring small control surface deflections may not be adequate for suppressing flutter beyond a certain Mach number. In this example, this seems to occur around
![]() ${M_\infty } = 0.95$
. While this does limit the usefulness of the method, there is still a large range of flight conditions over which a feasible set of control gains can be obtained and validated. Nevertheless, it is very clear that one cannot rely purely on the calculations of the linear control laws obtained from a linear aerodynamic model, and validation with one or more non-linear aerodynamic predictions is vital.
${M_\infty } = 0.95$
. While this does limit the usefulness of the method, there is still a large range of flight conditions over which a feasible set of control gains can be obtained and validated. Nevertheless, it is very clear that one cannot rely purely on the calculations of the linear control laws obtained from a linear aerodynamic model, and validation with one or more non-linear aerodynamic predictions is vital.
Considering the second example, the stability characteristics of the CRM wing obtained by using the linear DLM for computing the aerodynamic loads differed significantly from the stability characteristics obtained by using the non-linear TSD-based aerodynamic loads. The CRM wing underscores the importance of using properly matched nonlinear aerodynamic loads in the computation of its stability characteristics as well as the inadequacy of the DLM. Yet the control laws computed using the linear DLM-based state-space model provided a large one-parameter varying set of control gain vectors which could be rapidly assessed to establish a feasible closed-loop controller for enhancing the flight envelope of the aircraft. From the preliminary set of control gain vectors, a near-optimum set of gains were chosen to increase the flutter speed to a value close to the sonic Mach number. The flap used in this case was of a realistic chord and span. Furthermore, in this example, it was possible to increase the r value to 5 and still be able to obtain a feasible control law over the Mach numbers of interest. Thus, it has been successfully demonstrated that a feasible near-optimum linear control law could be designed for increasing the closed-loop flutter speed of an aircraft wing in the transonic domain, by employing the nonlinear TSD theory as a validation tool.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the support provided by the Agency for Defence Development, South Korea, through the award of a post-doctoral fellowship to the second author while at Queen Mary, University of London, UK, as part of the Commissioned Continuing Education programme (2019-personnel appointments (Ga)-110).