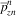2.1 Damage tolerance approach

The modern damage tolerance approach accepted for airframe composite structures requires that any impact damage in the composite structure either should be detected or should not reduce the structural strength below ultimate load capability. This approach is described in advisory circulars^{( 7 , 8 )} and based on the five category classification of the damage potentially expected in operation. Damage is classified depending on the detectability, or more specifically – depending on the operating time needed for reliable detection of this damage within the accepted aircraft maintenance program. For each category, the requirements for static and fatigue loads are established, in which the damaged structure must withstand while operating up until the moment of damage detection. The Category 1 addresses non-detectable damages and limited by two thresholds: threshold of detectability (known as barely visible impact damage) and energy threshold (‘realistic’ energy level) whichever comes first. The Categories 2 and 3 address visible impact damages and damages caused by the severe impacts.

There are at least two ways to identify which energy level can be considered as ‘realistic’ and each one is recognised as applicable according to Advisory Circulars of FAA^{( 7 )} and EASA^{( 8 )}.

According to the deterministic approach, the energy thresholds are to be evaluated based on the prescribed impact parameters: impacted zone of structure, impact energy and frequency of event. First, this approach was applied by Cook⁽ Reference Cook, Adami, Digenova and Maass ^{1 )} for the zoning of a UH-60A Black Hawk helicopter: for each zone of the fuselage, the impact energy exceedance curves were generated and taken as damage tolerance criteria (the considered impact threat scenarios were mostly related to mistakes during standard maintenance procedures). Later this approach was developed by Kan et al.⁽ Reference Kan, Cordero and Whitehead ^{2 )} who investigated the relationship between low-velocity impacts energies and damage sizes in wing panels of different thickness. As a result of these studies, the value of 100 ft-lbs (136 J) was adopted for the realistic energy threshold.

Probabilistic approach proposed by Rouchon⁽ Reference Rouchon ^{9 )} implies the determination of the realistic energy level on the basis of in-service statistical data relevant to actual operating conditions. This approach was used in the current study for the estimation of wing damage tolerance parameters.

2.2 Field survey

Design of MS-21 aircraft with full composite wing has led to urgent need of an advanced certification approach⁽ Reference Dubinskii and Safonov ^{10 )}. As a part of this approach the in-house studies on impact threat scenarios typical for local operational conditions were initiated.

On the first stage of those studies, Feygenbaum and Dubinskii⁽ Reference Feygenbaum and Dubinskiy ^{11 )} performed the analysis of 1258 damage events registered in operation and during maintenance of a commercial fleet. The work was continued by the team of experts from industry research institutes and airlines who collected and analysed data on accidental damages registered between year 2000 and 2016. The data came from periodic reviews of structure for airworthiness, operator’s reports, maintenance checks, failure registration cards, manufacturer databases, reports on structural condition assessment needed for service life extension and other documents containing relevant information (see the sources of information breakdown in Fig. 1.)

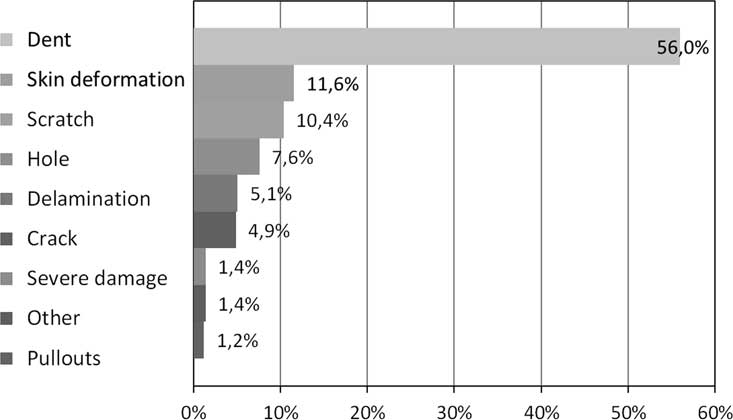
Figure 1. Breakdown of field damage data sources.

About 30 thousand documents related to 35 aircraft types were reviewed to identify approximately 5,300 damage incidents of various source and nature from barely visible surface deformations and scratches to very large damage causing a real threat to the structural integrity of airframe. Of these, about 2,000 damage records were made on local fleet aircraft types (Ilyushin, Antonov, Tupolev and Yakovlev) and about 3,300 records on Boeing aircraft used by local operators. The operating time of the considered fleet resembled about 4 m flight cycles (F.C.) and 10 m flight hours (F.H.)

More than 80% of damages were related to errors during ground handling: falling baggage, dropped tools, collisions with airfield infrastructure and ground service vehicles. The ground hail, wind gusts and snow/sand storms caused about 10% of damage. Other 10% of damage sources were foreign objects impacts: runway debris, uncontained rotor burst, bird strike and tire explosion⁽ Reference Fеygenbaum, Sokolov, Bozhevalov and Arepev ^{12 )}.

The types of damages were classified according to the breakdown shown in Fig. 2. The dent appeared to be the most frequent type (more than 50%), with depth sizes ranging from 0.1 mm to 50 mm. Out of this breakdown for the purposes of current study, only the wing skin surface dents (Fig. 3) were taken into consideration since this type of damage provides possibility to recover impact energy from dent geometry that is required for damage tolerance analysis.

Figure 2. Breakdown of damage type.

Figure 3. Wing skin metal dent examples.

2.3 Probabilistic model

In order to evaluate the probability of accidental in-service impact into the wing of commercial aircraft, the following simple probabilistic model was used.

The in-service damageability of the aircraft is considered as a random stream of events taking place in time one after another. It is assumed that damage events occur independently (the occurrence of one event does not affect the probability that a second event will occur), that damage events occur at constant rate and that two events cannot occur at exactly the same instant. Under those assumptions, the exponential distribution can be applied⁽ Reference Feller ^{13 )}:

(1) $$f(t){\equals}{\rm \lambda e}^{{{\minus}{\rm \lambda }t}} ,$$

and the damage probability function P _D can be expressed as

(2) $$P_{D} (t){\equals}(1{\minus}{\rm e}^{{{\minus}{\rm \lambda }t}} )$$

Here, t is the time, λ is the damage events intensity (parameter, inverse to average flight time until damage event T measured in F.H. or F.C.):

(3) $${\rm \lambda }{\equals}1\,/\,T $$

The damage intensity for the given aircraft type averaged on the fleet is

(4) $${\rm \bar{\lambda }}_{i} {\equals}N_{i} \,/\,T_{{\Sigma i}} $$

Here, N _i is the total number of registered damage events for all aircraft of type i, T _Σi – total flight time measured in F.H. or F.C. In Table 1 the average flight time until damage and damage intensity for 16 aircraft types is presented.

Table 1 Average flight time until damage and damage intensity for different aircraft types

It follows from Table 1 that the damage events intensity per F.H. averaged over the full data set makes

(5) $$\bar{\lambda }{\equals}\mathop{\sum}\limits_{i{\equals}1}^n {N_{i} } \,/\,\mathop{\sum}\limits_{i{\equals}1}^n {T_{{\Sigma i}} } {\equals}5.43{\times}10^{{{\minus}4}} $$

For the qualitative characterisation of wing damageability, it was proposed to divide aircraft wing into zones and determine the impact threat for each one. The generic wing structure of commercial aircraft consists of wingbox, leading edge, trailing edge, wing to body fairing, flaps, slats, ailerons, interceptors, airbrakes and wingtips. Where applicable, the inboard/central/outboard parts of each element were allocated and for each part the top and bottom surface were considered separately. In total, it made N _z =34 zones of the wing, see Table 2.

Table 2 Conditional probability of wing element impact damage for different aircraft types

The impact threat for each zone was estimated by methods of conditional probability analysis (the conditional probability is a measure of the probability of an event given that another event has occurred ⁽ Reference Ross ^{14 )}). In the current case, it means that in order to evaluate the conditional probability of the impact into given zone of the wing element $\bar{p}_{z}^{n} $ , one should take into account the following probabilities:

• ∙ averaged probability $\bar{p}_{e} $ that the wing element is damaged given that the airframe damage occurred;

• ∙ averaged probability $\bar{p}_{{{\rm dent}}} $ that the wing element is impacted (damage has the form of surface dent) given that the wing element is damaged;

• ∙ probability $p_{{{\rm sq}}}^{n} $ that zone n is impacted given that the wing element containing zone n is impacted

(6) $$\bar{p}_{z}^{n} {\equals}\bar{p}_{e} \cdot \bar{p}_{{{\rm dent}}} \cdot p_{{{\rm sq}}}^{n} $$

(7) $$\bar{p}_{e} {\equals}n_{e} \,/\,N_{{\rm \Sigma }} \,\bar{p}_{{{\rm dent}}} {\equals}n_{{{\rm dent}}} \,/\,N_{{\rm e}} \,p_{{{\rm sq}}}^{n} {\equals}s_{n} \,/\,S_{{{\rm element}}} $$

Here, n _e is the number of wing damage events, N _Σ is the total number of damage events, n _dent is the number of dents on the wing element, N _e is the total number of damage of all types registered on the element, s _n is the area of the zone n and S _element is the total area of the wing element containing zone n.

The conditional probabilities of the accidental impact into the allocated zones of the wing averaged on all considered aircraft types are presented in Table 2. Here $\bar{p}_{{zn}}^{n} $ is the $\bar{p}_{z}^{n} $ normalised per unit.

For the further analysis, in order to establish the realistic impact energy level and compare it to the similar estimations made by other authors, it is necessary, in accordance with Rouchon model^{( 8 )}, to determine the probability of impact into wing. The superposition theorem for homogeneous processes⁽ Reference Kingman ^{15 )} gives for wing damage events intensity $\bar{\lambda }_{{{\rm wing}}} {\equals}\bar{\lambda } \cdot \mathop \sum\limits_{n{\equals}1}^{N_{z} {\equals}34} \bar{p}_{z}^{n} $ . Then the conditional probability of whole wing structure impact damage, derived from Equation (2) for t=1 F.H. and for the sum of $\bar{p}_{z}^{n} $ presented in Table 2 becomes

(8) $$P_{{{\rm impact}}} {\equals}(1{\minus}{\rm exp}({\minus}\bar{\lambda }_{{{\rm wing}}} )){\equals}(1{\minus}{\rm exp}({\minus}{\rm \bar{\lambda }} \cdot 0.2097))\,\cong\,10^{{{\minus}4}} $$

The distribution of $\bar{p}_{{zn}}^{n} $ over the wing structure provides possibility to have the picture of wing relative damageability and understand in which zones of the wing the impact threats are more likely. In Fig. 4, one can see the qualitative distribution of impact intensity over the top and bottom surfaces of the generic wing.

Figure 4. Wing relative damageability $\bar{p}_{{zn}}^{n} $ .

It follows from Fig. 4 that the wing panels are the least prone to damage, as the main risk of collision with objects is related to wing edges. Slat and inboard flap are most damaged elements of the wing: the damage comes from flight hail, runway debris, errors during taxiing, collisions with ground service equipment (GSE) and aerodrome structures.

Those observations and the impact distribution data presented in Table 2 and in Fig. 4 were obtained on aircraft types of different airframe configuration, see Table 1. Nevertheless, the facts that wing of generic transport category aircraft possesses a certain number of standard elements, (wingbox, high-lift device, ailerons and air brakes) and that the commercial fleet nowadays goes through very similar field maintenance procedures lead to the assumption that the generic accidental impact scenarios needed on the stage of preliminary design can successfully be taken from the above analysis. The evaluation of impact threats and corresponding structural damage related to the specific aircraft type should be done on the late development stage addressing the detailed design scheme and expected operating conditions.

2.4 Impact energy distribution

Statistical data on accidental impact damage collected on metal aircraft skins can be used for damage tolerance evaluation of similar composite structures. In order to do, this it is necessary to convert the metal dent depth into impact energy. For this purpose, the original analytical method⁽ Reference Dubinskiy, Zharenov, Pavlov and Ordyntsev ^{16 )} based on the establishment of three-dimensional relationship between the impact energy, dent depth and thickness of the skin was developed. The relationship for duralumin alloy 1163 that is used in skin panels of most aircraft types, mentioned above, was generated and validated experimentally. The impact cases valid for conversion were selected from the damage database and translated into impact energy survey. The resulting energy range covered three orders of magnitude, from a few joules to several thousand joules.

Unlike the Northrop and MCAir survey analysed by Kan et al.⁽ Reference Kan, Cordero and Whitehead ^{2 )}, the TsAGI and GosNII GA database includes a significant number of high energy impact events. For damage tolerance analysis, it would be reasonable to make the same data extraction as in Northrop and MCAir study where the depth of registered metal dents did not exceed 0.1 in (2.5 mm). The cumulative probability distributions (probability to encounter the impact energy E or less) for full and for limited data samples are shown in Figs 5 and 6.

Figure 5. Cumulative impact energy probability for full data sample (Lognormal scale).

Figure 6. Cumulative impact energy probability for limited data sample (Weibull scale).

The empirical distribution of full data sample (Fig. 5) is very close to a logarithmically linear function. The hypothesis, that impact energies are distributed according to logarithmically normal law, was checked by nω² criterion for two unknowns⁽ Reference Martynov ^{17 )}. The calculated statistic value nω²=0.1215 appeared to be less than the criterion value (nω²)_α=0.125 taken at the accepted significance level α=0.05⁽ Reference Casella and Berger ^{18 )}. Thus, the hypothesis about normality of experimental data has been confirmed at a significance level of 5% or more. The Weibull function established from the same data does not agree with the empirical distribution (Fig. 5).

The distribution of limited empirical data sample agrees neither with Lognormal nor with Weibull distribution: both hypotheses have too low significance level α<0.001 by the Anderson-Darling criterion⁽ Reference Lawless ^{19 )}. It follows from Fig. 6 that the left-hand side is better described by the Weibull distribution and the right-hand side – by Lognormal law. Thus for the limited data sample of the given survey there is no definite distribution law, it can only be stated that Weibull distribution can be reasonably used for small energies while Lognormal distribution is more suitable for moderate energy impacts consideration.

The R-squared regression errors for the fitted distributions are given in Table 3.

Table 3 R ² regression errors for Lognormal and Weibull distributions

2.5 Impact energy characterisation for damage tolerance analysis

Although it is reasonable to assume that for the determination of realistic impact energy level the use of limited data sample is more adequate than the use of full data sample which includes such unrealistic events as serious collision with airfield buildings, equipment, GSE and other aircraft, for the purposes of damage tolerance analysis, both data samples were considered. The reason for full data sample analysis importance is that the sampling criteria taken from the Northrop and MCAir survey, in which dents larger than 2.5 mm were not registered at all, may be not always be valid for composites, (for their impact sensitivity and brittle behavior). If one assumes that at least one high energy impact event remains unreported or ignored by technical personnel during aerodrome maintenance, it is reasonable to make estimation on the full data sample.

According to the Rouchon model⁽ Reference Rouchon ^{9 )} and the approach presented in Handbook^{( 20 )}, the probability P(E) to encounter an impact in operation with an energy exceeding E is the product of two independent probabilities: the probability of obtaining an impact in operation P _impact and the probability of exceeding a certain level of energy P _E (E):

(9) $$P(E){\equals}P_{{{\rm impact}}} \cdot P_{E} (E)$$

The empirical distributions of P(E) determined on the basis of TsAGI and GosNII GA impact energy survey for two P _impact estimations (the first one P _impact=10⁻⁴ derived above from local field data, see Equation (8), and the second one P _impact=10⁻³ taken from Gary ⁽ Reference Gary and Riskalla ^{3 )} and Airbus ⁽ Reference Morteau and Fualdes ^{4 )} studies) are shown on Figs 7 and 8. The full and limited data sample distribution functions were approximated, respectively, by Lognormal and Weibull laws.

Figure 7. Probability to encounter in operation an impact with an energy exceeding E for full data sample (Lognormal law).

Figure 8. Probability to encounter in operation an impact with an energy exceeding E for limited data sample (Weibull law).

According to the advanced non-conservative damage tolerance methodology presented in Refs 4,9,18 the ‘realistic’ and ‘severe’ energy levels can be derived from energy distribution function under the following assumptions.

The impact with ‘realistic’ or higher energy aircraft may experience not more often than once per lifetime. Taking service life of modern aircrafts for 10⁵ F.H., the probability of ‘realistic’ energy level can be determined as P(E _realistic)=10⁻⁵ F.H. The ‘severe’ or ‘maximum possible’ energy level may be determined by criterion of almost improbable event, namely 10⁻⁹: P(E _maximum)=10⁻⁹ F.H.

Using the relationships in Figs 7 and 8, the energy levels corresponding to those probabilities were determined, and the summary results are presented in Table 4.

Table 4 ‘Maximum’ and ‘Realistic’ energy levels determined according to probabilistic approach^{( 8 )}

‘Unrealistic’ scenarios (Fig. 7): Under the assumption that any damage in the wing structure may remain undetected for considerably long time comparable with heavy inspection interval, the full data sample can be applied for damage tolerance analysis. In the conservative case (P _impact=10⁻³), the ‘threshold’ energy exceeds thousand joules and the probability of exceeding of 136 J makes only 10⁻⁴, which means that the aircraft can encounter an impact with energy over 136 J about 10 times per service life.

‘Realistic’ scenarios (Fig. 8): Under the assumption that all high energy impacts are immediately reported, the limited data sample should be used for damage tolerance analysis. The impact energy which aircraft may encounter during its lifetime determined for conservative case P _impact=10⁻³ makes E _realistic=36 J. This figure matches Airbus threshold value E _realistic=35 J⁽ Reference Morteau and Fualdes ^{4 )} which was determined under the same assumptions but on very different data set, namely Northrop and MCAir survey of US Navy fighters. The P(E) distribution calculated for US Navy data⁽ Reference Kan, Cordero and Whitehead ^{2 )} is also shown for comparison. The trend lines in Fig. 8 confirm that impact of 136 J accepted as a threshold value in Boeing damage tolerance methodology⁽ Reference Fawcett and Oaks ^{21 )} can be considered as a remote event.