NOMENCLATURE
- ADS-B
Automated Dependant Surveillance - Broadcast
- BVLOS
Beyond Visual Line of Sight
- CAA
Civil Aviation Authority
- GNSS
Global Navigation Satellite Systems
- GSM
Global System for Mobile communications
- IMU
Inertial Measurement Unit
- NOTAM
Notice to Airmen
- UAS
Unmanned Aircraft Systems
- VLOS
Visual Line of Sight
- A
Elements of air environment awareness
- C
An available communication channel
- E
An arbitrary element
- G
Elements of ground awareness
- I
Elements of internal awareness
- SA
Situation Awareness
- X
Elements of position awareness
- H
Corresponding to a human operator
- HT
Corresponding to a human team
- S
Corresponding to that shared between vehicle and human operators
- V
Corresponding to a vehicle
Acronyms
Symbols
Subscripts
1.0 INTRODUCTION
Approval to routinely operate an Unmanned Aircraft System (UAS) Beyond Visual Line of Sight (BVLOS) requires that the system be capable of at least an equivalent level of safety to Visual Line of Sight (VLOS) operation(Reference Veres, McAree and Aitken16). In this case, the system includes the aircraft itself, any communications and ground control equipment and the human operator(s). Removal of the aircraft from the visual field of the operator inevitably reduces their ability to directly attain adequate situation awareness of the vehicle and its surroundings. Situation awareness is a prerequisite to rational decision making and reflects a human’s ability to perceive elements in their environment, comprehend their meaning and project their state into the future(Reference Endsley6).
In complex system configurations, the need for the operator to maintain an understanding of the situation is critical in ensuring safety(Reference Aitken, Alexander and Kelly2). As situations develop, the operator is required to make decisions. Without good awareness of the situation, the ability to make decisions is diminished. Indeed, as Klein states, decisions often are not made, but rather are “recognition-primed”; that is to say, familiarity with the situation provides everything necessary to make a good decision(Reference Klein10). Any inaccuracy with the representation of the situation will then propagate into the decision-making process. When adding automation and other processes in order to increase situational awareness, it is important to take into account the operator and the possibility that they may be unfamiliar with the technology or uncertain over its capability(Reference Dzindolet, Peterson, Pomranky, Pierce and Beck4,Reference Dzindolet, Pierce, Beck, Dawe and Anderson5,Reference Stanton, Salmon, Jenkins, Walker, Rafferty and Revell15) . Unnecessary complexity adds to operator confusion as it changes the context of operator interaction(Reference Cameron, Aitken, Collins, Boorman, Chua, Fernando, McAree, Martinez-Hernandez and Law3), and over-reliance can skew the decision-making process(Reference Lee and Moray11). These factors point to the statistical/probabilistic nature of UAS qualities.
To maintain an equivalent level of safety in Beyond Visual Line of Sight (BVLOS) operation, it is necessary to maintain an equivalent level of situation awareness in the system. The inevitable reduction in operator awareness must, therefore, be augmented by the vehicle itself(Reference Adams1). The majority of UAS possess very little in the way of on-board situation awareness at present; therefore, new systems will need to be designed to meet this requirement. In designing such artificial situation awareness systems(Reference Liu, Coombes, Li and Chen12-Reference McAree and Chen14), it is beneficial to quantify the current level of awareness in VLOS operation.
Measurement of situation awareness to date has focused on understanding human operators(Reference Endsley7-Reference Endsley9). These techniques have predominantly performed a qualitative assessment of individuals, leading to quantitative results once a population has been analysed. This approach does not readily transfer to the analysis of an artificial situation awareness system, which instead requires a quantitative assessment from the start.
In this paper, we introduce a new model for quantifying the situation awareness of an UAS under the control of at least one (and possible more) human operator(s). In the next section, we review a traditional, qualitative process for assessment of situation awareness and apply it to a simple VLOS operation, demonstrating its limitations when applied to a non-human component of the system. Section 3 then introduces a new, quantitative method for modelling the situation awareness of a system by considering the probability with which each element of awareness is known. Section 4 provides an example usage of the proposed model for assessing VLOS operation and comparing the safety of BVLOS. Finally, Section 5 will provide some concluding remarks and consider how this model should be used in future work.
2.0 QUALITATIVE SITUATION AWARENESS
The principle of situation awareness of a team of human operators and an unmanned vehicle is introduced in Ref. 1 as a set of elements known either by the vehicle or one of its human operators. Specifically, the total situation awareness of a system can be expressed as
$$\begin{equation}
SA_{S} = SA_{HT} \cup SA_{V},
\end{equation}$$
where SA V is the situation awareness of the vehicle itself and SA HT is the awareness of the human team, defined as
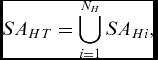$$\begin{equation}
SA_{HT} = \bigcup \limits _{i=1}^{N_H} SA_{Hi},
\end{equation}$$
where N H is the number of human operators in the team.
This definition is sufficient for a qualitative assessment of the systems awareness (Reference Endsley7-Reference Endsley9). Formally, situation awareness consists of the following components.
Definition 1. A set of critical elements of situation awareness are SAcrit = {I, X, A, G}, where
• I = {IB, IM, IS, IA} is the internal state of the vehicle consisting of battery level, planned mission, sensor and actuator health
• X is the position of the vehicle
• A = {AT, AR, W} is the air environment surrounding the vehicle consisting of air traffic, airspace restrictions and weather
• G = {GS, GM, GR} is the ground environment surrounding the vehicle consisting of static obstacles, moving obstacles and restrictions
Here, X is based on Global Navigation Satellite Systems (GNSS) positioning or observation of the pilot and I is dependant on sensors and signal processing to obtain the operational state of on-board devices. The awareness of a simple UAS under VLOS with a qualified pilot (H1) and a competent observer (H2) can be expressed as
$$\begin{equation}
SA_V & = & \lbrace X_V, I\rbrace
\end{equation}$$\\
$$\begin{equation}
SA_{H1} & = & \lbrace X_1, I, A_1, G_1\rbrace
\end{equation}$$ \\
$$\begin{equation}
SA_{H2} & = & \lbrace X_2, A_2, G_2\rbrace
\end{equation}$$
Analysis of the intersections of SA V, SA H1 and SA H2 provides insight into the elements, which are known by multiple parties, illustrative of the degree of redundancy in the system. For example, under GNSS failure, SA V becomes SA′V = SAV∖XV, but as SA H1 and SA H2 are unaffected (as they can physically see the location of the vehicle), the system is still safe.
The above analysis is a formal description of the process used by the UK Civil Aviation Authority (CAA) to approve VLOS operations. A pilot qualification is necessary to ensure that {X, A}⊂SA H, a site assessment and flight plan are required before each flight to ensure that G⊂SA H, and a pre-flight inspection of the aircraft is required to ensure SA V = {X, I}, thereby completing SA crit.
For simple systems operating in VLOS environments, the above analysis may be sufficient to understand its situation awareness and, therefore, operational safety. In more complex situations, however, its utility breaks down. Consider, for example, a UAS operating BVLOS with a single operator who possesses a telemetry link to the vehicle. The aircraft has a map of the environment and is equipped with an Automated Dependant Surveillance - Broadcast (ADS-B) receiver capable of detecting traffic aircraft (and assume no ground traffic is present due to the nature of the environment). Performing the same analysis as above, we have
$$\begin{equation}
SA_V = SA_{H} = \lbrace I, X, A, G\rbrace ,
\end{equation}$$
as all information possessed by the vehicle is shared with the operator via the telemetry link.
At first glance, it would appear that the system is safe as SA S = SA crit. Consider GNSS failure, however, leading to SA′V = SAV∖XV and SA′H = SAH∖XV (as the operator has no independent means of determining the vehicles position); therefore, SA S = SA crit∖X and the system is no longer safe under BVLOS. In this qualitative assessment, we have lost any information about the dependence of elements of situation awareness on one another, such as the dependence of the operator’s position awareness on the vehicle’s position awareness in this example. These dependencies may be introduced by communication links between vehicle and operator or by systematic dependency, such as an ADS-B system’s need for a functioning GNSS system.
The next section introduces a probabilistic, quantitative model of mission safety in terms of robustness against on-board and environmental failures and variations, whilst capturing the inherent interdependency between elements of situation awareness.
3.0 QUANTITATIVE SITUATION AWARENESS
The previous section demonstrated the utility in traditional qualitative situation awareness assessment for simple VLOS operation. To properly assess BVLOS operation, however, we require a more quantitative approach which considers not only the attainment of elements of awareness but their quality and reliability also. Due to the inherent uncertainty in quantifying these properties, we no longer seek to make concrete statements such as SA S = SA crit, but instead, to calculate a probability of loss of situation awareness, 
$P(\overline{SA})$. We state that the probability of a system possessing adequate situation awareness of an element E is P(E); conversely, the probability of not possessing adequate awareness is 
$P(\overline{E}) = 1 - P(E)$.
The concept of adequate situation awareness is based on the accuracy with which the system has knowledge of a particular quantity or set of quantities. For example, adequate position awareness may be defined as knowledge of the position of the vehicle to within 5 m of the ground truth value laterally and 20 ft vertically. This paper does not attempt to define these performance criteria, or even strictly specify how a particular element should be assessed, as this is likely to be highly system and operation specific. Instead, we present a probabilistic model which quantifies the awareness of a vehicle in abstract terms. By applying this model to existing VLOS operation, it is then possible to determine the performance criteria which, when enforced for BVLOS systems, should ensure an equivalent level of performance.
For very simple UAS, with no on-board awareness capability, we can write that
$$\begin{equation}
P(\overline{SA}) = P(\overline{SA}_{HT}),
\end{equation}$$
which states that the probability of loss of awareness of the system is given by the probability of loss of awareness of the human team. Such systems must be evaluated solely from a human factors engineering perspective. As UAS become more autonomous on the route to regular BVLOS operation, a degree of awareness by the vehicle itself is necessary.
Theorem 1. The probability of loss of an element of situation awareness E by a UAS (either the vehicle or human team) is given by
$$\begin{equation}
P(\overline{E}) = P(\overline{E}_V) + P(E_V)\left( P(\overline{E}_{HT} | E_V, C_E) P(C_E) + P(\overline{E}_{HT} | \overline{C}_E) P(\overline{C}_E)\right)
\end{equation}$$
provided P(EV) > 0, where
• P(EV) is the probability of adequate situation awareness by the vehicle
•
$P(\overline{E}_{HT} | E_V, C_E)$ is the probability of loss of adequate situation awareness by the human team, given adequate situation awareness of the vehicle and the presence of a communication channel between the vehicle and the human team• P(CE) is the probability of a communication channel between the vehicle and the human team to transmit E
•
$P(\overline{E}_{HT} | \overline{C}_E)$ is the probability of loss of adequate situation awareness by the human team, given no communication channel between the vehicle and the human team.
Proof. The probability of loss of an element E of situation awareness by the UAS, in terms of loss of awareness by the vehicle 
$P(\overline{E}_V)$ and the human team 
$P(\overline{E}_{HT})$, is
$$\begin{equation}
P(\overline{E}) = P(\overline{E}_V) + P(\overline{E}_{HT}) - P(\overline{E}_V \cap \overline{E}_{HT})
\end{equation}$$
The final term represents co-occurence and possible coupling between the human team’s and the vehicle’s awareness. Considering the situation where awareness information is passed from the vehicle to the human team, necessarily, this requires P(E V) > 0; therefore we can write
$$\begin{equation}
P(\overline{E}_V \cap \overline{E}_{HT}) = P(\overline{E}_{HT} | \overline{E}_V) P(\overline{E}_V),
\end{equation}$$
where 
$P(\overline{E}_{HT} | \overline{E}_V)$ represents the probability of loss of awareness by the human team, given loss of awareness of the vehicle. This quantity in its own right may be difficult to quantify; therefore, we exploit the fact that 
$P(\overline{E}_{HT}) = P(\overline{E}_{HT} | \overline{E}_V) P(\overline{E}_V) + P(\overline{E}_{HT} | E_V) P(E_V)$ and write Equation (10) as
$$\begin{equation}
P(\overline{E}_V \cap \overline{E}_{HT}) = P(\overline{E}_{HT}) - P(\overline{E}_{HT} | E_V) P(E_V)
\end{equation}$$
The term 
$P(\overline{E}_{HT} | E_V)$ now reflects the probability of loss of awareness of the human team, given that the vehicle has adequate awareness. This situation can arise in one of two ways; either
1. The awareness of the human team is reliant on information passed from the vehicle via communication channel C E, and C E is not available; or
2. The awareness of the human team is not reliant on the communication channel C E but fails for another reason, such as the operating becoming distracted
These situations are captured by decomposing 
$P(\overline{E}_{HT} | E_V)$ into
$$\begin{equation}
P(\overline{E}_{HT} | E_V) = P(\overline{E}_{HT} | E_V, C_E) P(C_E | E_V) + P(\overline{E}_{HT} | E_V, \overline{C}_E) P(\overline{C}_E | E_V)
\end{equation}$$
Given that the availability of the communication channel is independent of state of awareness of the vehicle, P(C E|E V) = P(C E) and 
$P(\overline{C}_E | E_V) = P(\overline{C}_E)$, therefore
$$\begin{equation}
P(\overline{E}_{HT} | E_V) = P(\overline{E}_{HT} | E_V, C_E) P(C_E) + P(\overline{E}_{HT} | E_V, \overline{C}_E) P(\overline{C}_E)
\end{equation}$$
Finally, under the condition of 
$\overline{C}_E$, the 
$\overline{E}_{HT}$ and E V are independent; therefore,
$$\begin{equation}
P(\overline{E}_{HT} | E_V) = P(\overline{E}_{HT} | E_V, C_E) P(C_E) + P(\overline{E}_{HT} | \overline{C}_E) P(\overline{C}_E)
\end{equation}$$
Substituting Equations (14) and (11) into Equation (9) yields an expression for 
$P(\overline{E})$.□
The following sections discuss the application of Theorem 1 to each element of situation awareness, including examples of how terms can be evaluated for different system configurations.
3.1 Internal awareness
By applying Theorem 1 to the internal awareness of the system, we have
$$\begin{equation}
P(\overline{I}) = P(\overline{I}_V) + P(I_V)\left( P(\overline{I}_{HT} | I_V, C_I) P(C_I) + P(\overline{I}_{HT} | \overline{C}_I) P(\overline{C}_I)\right)
\end{equation}$$
In a complete UAS system, 
$P(\overline{I})$ itself will need breaking down into its constituent elements (e.g. battery monitoring, sensor and actuator health modelling). Consider here, however, a simplified example of a UAS with on-board battery voltage measurement, but no forecasting of remaining flight time. Such a system relies on communicating the battery level to the human operator, and this operator then predicting remaining flight time. For such a system,
•
$P(\overline{I}_V)$ is the probability that the voltage measurement circuit fails•
$P(\overline{I}_{HT} | I_V, C_I)$ is the probability that the human operator is aware of the battery voltage, but incorrectly predicts the remaining flight time. This can be thought of as the failure of a closed-loop system, where the operators prediction is informed by a feedback loop.• P(C I) is the probability that the telemetry system communicates the battery voltage to the human operator
•
$P(\overline{I}_{HT} | \overline{C}_I)$ is the probability that the human operator incorrectly predicts the remaining flight time, without any communicated knowledge of the battery voltage. This can be thought of as the failure of an open-loop system, where the operators prediction is based on heuristics (e.g. “The battery was fully charged at the start of the flight. The battery endurance is usually 15 minutes. The flight has lasted 5 minutes; therefore, the remaining flight time is 10 minutes.”)
3.2 Position awareness
By applying Theorem 1 to position awareness of the system, we have
$$\begin{equation}
P(\overline{X}) = P(\overline{X}_V) + P(X_V)\left( P(\overline{X}_{HT} | X_V, C_X) P(C_X) + P(\overline{X}_{HT} | \overline{C}_X) P(\overline{C}_X)\right)
\end{equation}$$
Once again, by way of example, consider a VLOS UAS with on-board GNSS positioning and a telemetry link to the human operator.
•
$P(\overline{X}_V)$ is the probability of failure of GNSS positioning. It is possible to further decompose this term by considering the factors which can contribute to GNSS failure, such as interference or proximity to buildings.•
$P(\overline{X}_{HT} | X_V, C_X)$ is the probability of human operator losing awareness of the vehicles position, given a working telemetry link. This probability could be relatively high, if the telemetry information was available to the pilot only in text based form (e.g. latitude, longitude, altitude), as they may be unable to readily interpret this data. The use of a moving map display to inform the pilot of the vehicles position will significantly reduce the failure probability.• P(C X) is the probability that the telemetry system communicated the vehicle’s position to the human operator
•
$P(\overline{X}_{HT} | X_V, \overline{C}_X)$ is the probability that the human operator loses awareness of the vehicle position without a working telemetry link. This corresponds to the likelihood of the operator failing to adequately determine the vehicle’s position by visual acquisition. Clearly, if such a system were operated under BVLOS, this value would be very high.
3.3 Air environment awareness
Air environment awareness consists of the sub-elements of air traffic (AT), airspace restrictions (AR) and weather awareness (W). Failure of any one of these components constitutes a failure of awareness; therefore,
$$\begin{equation}
P(\overline{A}) = P(\overline{AT} \cup \overline{AR} \cup \overline{W})
\end{equation}$$
or,
$$\begin{equation}
P(\overline{A}) \le P(\overline{AT}) + P(\overline{AR}) + P(\overline{W})
\end{equation}$$
We can now apply either Equation (7) or Theorem 1 to the terms in Equation (18), dependent on whether the system possesses any form of on-board awareness. For example, a typical VLOS UAS with geo-fencing capability but no on-board air traffic or weather awareness can be represented as
$$\begin{eqnarray}
P(\overline{A}) & \le & P(\overline{AT}_{HT}) \nonumber\\
&& +\, P(\overline{W}_{HT}) + P(\overline{AR}_V) + P(AR_V)\Big( P(\overline{AR}_{HT} | AR_V, C_{AR}) P(C_{AR}) \nonumber\\
&& +\, P(\overline{AR}_{HT} | \overline{C}_{AR}) P(\overline{C}_{AR})\Big),
\end{eqnarray}$$
where
•
$P(\overline{AT}_{HT})$ and $P(\overline{W}_{HT})$ are the probabilities of loss of air traffic and weather awareness by the human operators, respectively•
$P(\overline{AR}_V)$ is the probability of loss of geo-fencing information by the vehicle, possibly due to the failure of Global System for Mobile communications (GSM)•
$P(\overline{AR}_{HT} | AR_V, C_{AR})$ is the probability of loss of airspace restriction awareness by the human operators, given the vehicle is communicating its geo-fencing information• P(C AR) is the probability that the vehicle is communicating its geo-fencing information to the human operators
•
$P(\overline{AR}_{HT} | \overline{C}_{AR})$ is the probability of loss of airspace restriction awareness by the human team, without communication of geo-fencing information from the vehicle. This could be due to the human operator’s lack of knowledge of aviation regulation, or a temporary Notice to Airmen (NOTAM) in the area
3.4 Ground environment awareness
Ground environment awareness consists of the sub-elements of static obstacles (GS), moving obstacles (GM) and restrictions (GR). Failure of any one of these components constitutes a failure of awareness, therefore
$$\begin{equation}
P(\overline{G}) = P(\overline{GS} \cup \overline{GM} \cup \overline{GR})
\end{equation}$$
It is likely that a system which detects static obstacles will also detect moving obstacles; therefore, we should not assume these elements are mutually exclusive. Instead, we could write
$$\begin{equation}
P(\overline{G}) \le P(\overline{GS}) + P(\overline{GM}) + P(\overline{GR}) - P(\overline{GS} \cap \overline{GM})
\end{equation}$$
A detailed discussion of how to assess the interdependency of systems, such as evaluating 
$P(\overline{GS} \cap \overline{GM})$, is beyond the scope of this paper as it is highly dependent on the configuration of a particular UAS. The following section discusses how some interdependencies can arise and provides options for evaluation.
3.5 Interdependency in situation awareness
The previous sections have given an insight into the evaluation of the individual elements of situation awareness. Given expressions for the probability of failure of each element, we can bound the failure of situation awareness by
$$\begin{equation}
P(\overline{SA}) \le P(\overline{SA})_{upper} = P(\overline{I}) + P(\overline{X}) + P(\overline{A}) + P(\overline{G})
\end{equation}$$
To gain a less conservative failure probability, we must evaluate the potential interdependencies between I, X, A and G. The probability of loss of situation awareness by a UAS is
$$\begin{eqnarray}
P(\overline{SA}) & = & P(\overline{SA})_{upper} \nonumber\\
&& -\, P(\overline{I} \cap \overline{X}) - P(\overline{I} \cap \overline{A}) - P(\overline{I} \cap \overline{G}) - P(\overline{X} \cap \overline{A}) - P(\overline{X} \cap \overline{G}) - P(\overline{A} \cap \overline{G}) \nonumber \\
&& +\, P(\overline{I} \cap \overline{X} \cap \overline{A}) + P(\overline{I} \cap \overline{A} \cap \overline{G}) + P(\overline{X} \cap \overline{A} \cap \overline{G}) \nonumber \\
&& -\, P(\overline{I} \cap \overline{X} \cap \overline{A} \cap \overline{G}),
\end{eqnarray}$$
where P(E 1∩. . .∩E n) represents the joint probability of events E 1 to E n occurring. If these events are independent, then computation of the joint terms is trivial; however, dependency between events is likely in a number of cases making their evaluation more involved. Examples of interdependence between events include
•
$\overline{X}$, $\overline{A}$ and $\overline{G}$ are all likely to depend on $\overline{I}$ because if a system is unable to correctly assess the health of its hardware, it is unable to have any confidence in the sensor measurements•
$\overline{A}$ is likely to depend on $\overline{X}$ if the air traffic awareness of a system is based on position broadcasts from other vehicles (such as from ADS-B). In such a system, a UAS cannot know the relative position of traffic without accurate knowledge of its own position•
$\overline{G}$ could also depend on $\overline{X}$ if the system is avoiding collisions with ground-based obstacles based on some global map information. Once again, such a system cannot know its relative position to obstacles without accurate knowledge of its own position
It is possible that many other interdependencies will exist in any particular UAS, dependent on the particular hardware and software components of the system. It is beyond the scope of this paper to consider the evaluation of each of these combinations in detail. This is left to the designer of a particular UAS in order to achieve a less conservative failure probability estimate than that afforded by Equation (22).
4.0 EXAMPLE USAGE
To demonstrate the application of the quantitative probabilistic model introduced in the previous section, we consider a UAS operated under both VLOS and BVLOS. In each case, we assume a single human operator in command of a UAS equipped with a single telemetry link, dual redundant Inertial Measurement Units (IMUs) and GNSS receivers and a single ADS-B receiver. We assume that no ground hazards are present due to the nature of the environment, the weather is good and there are no airspace restrictions.
4.1 VLOS
We first assess the performance of the UAS under VLOS conditions, using representative failure probabilities. The result of this analysis will provide an upper bound on the situation awareness failure probability for VLOS operation. This value can be used as a benchmark to assess the safety of BVLOS operation with the same UAS.
4.1.1 Internal awareness
Assuming the vehicle monitors its battery state, the health of its communication link and each of its sensor systems, but not its actuators, the terms of Equation (15) are
$$\begin{equation}
P(\overline{I}_V) = P(\overline{I}_{B_V} \cup \overline{I}_{C_V} \cup \overline{I}_{I1_V} \cup \overline{I}_{I2_V} \cup \overline{I}_{G1_V} \cup \overline{I}_{G2_V} \cup \overline{I}_{A_V})
\end{equation}$$
where the subscripts B, C, I1, I2, G1, G2, A refer to the battery state, the health of the communication link, the first and second IMUs, the first and second GNSS receivers and the ADS-B receiver, respectively.
$$\begin{equation}
P(\overline{I}_H | I_V, C) = P(\overline{I}_{B_H} \cup \overline{I}_{C_H} \cup \overline{I}_{I1_H} \cup \overline{I}_{I2_H} \cup \overline{I}_{G1_H} \cup \overline{I}_{G2_H} \cup \overline{I}_{A_H} | I_V, C),
\end{equation}$$
where the subscript HT has been reduced to H to indicate a single operator and C I is reduced to C to indicate the presence of a single communications link for all situation awareness information.
Given the VLOS nature of the flight, we assume the human operator is able to reason about the internal state of the vehicle without any telemetry communication. However, this ability is fairly limited in comparison with telemetry-based reasoning; therefore, a high failure probability is assumed
$$\begin{equation}
P(\overline{I}_H | \overline{C}) = 5 \times 10^{-2}
\end{equation}$$
If we consider the failure of each monitoring system to be 10−6, and each system to be mutually exclusive, we have
$$\begin{equation}
P(\overline{I}_V) = 7\times 10^{-6}
\end{equation}$$
Assuming failure of the human operator in assessing each system based on telemetry data is 10−4 and a communications failure rate of 10−3, we have
$$\begin{equation}
P(\overline{I}_H | I_V, C) = 7\times 10^{-4}
\end{equation}$$
and from Equation (15)
$$\begin{equation}
P(\overline{I}) = 7\times 10^{-6} + (1 - 7\times 10^{-6})( 7\times 10^{-4} (1 - 10^{-3}) + 5 \times 10^{-2} \times 10^{-3}) \approx 7.6 \times 10^{-4}
\end{equation}$$
4.1.2 Position awareness
Under VLOS, the system attains position awareness both from the vehicle’s on-board GNSS receivers and by the visual perception of the human operator. Assuming the GNSS receivers are independent, we can evaluate 
$P(\overline{X}_V)$ as
$$\begin{equation}
P(\overline{X}_V) = P(\overline{X}_{G1_V} \cap \overline{X}_{G2_V} | GNSS) P(GNSS) + P(\overline{GNSS}),
\end{equation}$$
where 
$P(\overline{X}_{G1_V} \cap \overline{X}_{G2_V}|GNSS)$ is the probability of loss of position awareness from both GNSS receivers, assuming GNSS is available and 
$P(\overline{GNSS})$ is the probability that the GNSS system is unavailable (e.g. due to interference). Assuming the failure rate of each receiver is 10−6 and mutually exclusive, and the failure rate of the GNSS system is 10−3, we have
$$\begin{equation}
P(\overline{X}_V) = 1\times 10^{-12} (1 - 10^{-3}) + 10^{-3} \approx 10^{-3}
\end{equation}$$
Assuming a skilled operator, their visual perception ability should be comparable with GNSS; therefore, we assume
$$\begin{equation}
P(\overline{X}_H | \overline{C}) = 10 ^{-3}
\end{equation}$$
With the addition of a working telemetry link, it is anticipated that the operators performance would improve markedly; therefore, we assume
$$\begin{equation}
P(\overline{X}_H |X_V,C) = 10 ^{-6}
\end{equation}$$
If the vehicle uses the same telemetry link as internal awareness, the same failure rate of 10−3 is used; therefore, by Equation (16)
$$\begin{equation}
P(\overline{X}) = 10^{-3} + (1-10^{-3})(10^{-6}(1-10^{-3}) + 10 ^{-3} \times 10^{-3}) \approx 10^{-3}
\end{equation}$$
4.1.3 Air environment awareness
In this example, the only relevant component of air environment awareness is air traffic. Assuming that both the ADS-B receiver and human operator have a failure rate of 10−6, both with and without telemetry, we have
$$\begin{equation}
P(\overline{A}) = 10^{-6} + (1-10^{-6})(10^{-6}(1-10^{-3}) + 10^{-6} \times 10^{-3}) \approx 2 \times 10^{-6}
\end{equation}$$
4.1.4 System failure probability
The upper bound on the probability of loss of situation awareness of the UAS under VLOS is given by
$$\begin{equation}
P(\overline{SA})_{upper} \approx 7.6 \times 10^{-4} + 10 ^ {-3} + 2 \times 10^{-6} \approx 1.76 \times 10^{-3}
\end{equation}$$
4.2 BVLOS
Consider the same UAS as in the previous section but now under BVLOS operation. The implication of this change is that the human operator is no longer able to attain any situation awareness without the provision of a telemetry communication link; therefore, 
$P(\overline{\bullet } _H | \overline{C}) = 1$. All other probabilities remain unchanged.
4.2.1 Internal awareness
Replacing 
$P(\overline{I}_H | \overline{C}) = 1$, we have
$$\begin{equation}
P(\overline{I}) = 7\times 10^{-6} + (1 - 7\times 10^{-6})( 7\times 10^{-4} (1 - 10^{-3}) + 10^{-3}) \approx 1.7 \times 10^{-3}
\end{equation}$$
4.2.2 Position awareness
Replacing 
$P(\overline{X}_H | \overline{C}) = 1$, we have
$$\begin{equation}
P(\overline{X}) = 10^{-3} + (1-10^{-3})(10^{-6}(1-10^{-3}) + 10^{-3}) \approx 2 \times 10^{-3}
\end{equation}$$
4.2.3 Air environment awareness
Replacing 
$P(\overline{AT}_H | \overline{C}) = 1$, we have
$$\begin{equation}
P(\overline{A}) = 10^{-6} + (1-10^{-6})(10^{-6}(1-10^{-3}) + 10^{-3}) \approx 10^{-3}
\end{equation}$$
4.2.4 System failure probability
The upper bound on the probability of loss of situation awareness of the UAS under BVLOS is given by
$$\begin{equation}
P(\overline{SA})_{upper} \approx 1.7 \times 10^{-3} + 2 \times 10^{-3} + 10^{-3} \approx 4.7 \times 10^{-3}
\end{equation}$$
4.3 Discussion
The previous sections have illustrated the benefit of the proposed quantitative probabilistic model of situation awareness in comparison with traditional qualitative techniques. Firstly, unlike the qualitative assessment in Section 2, the quantitative model captures the significant decrease in safety associated with the BVLOS operation of the VLOS system, characterised by an increase in the failure probability of situation awareness of 267%. Secondly, an in-depth analysis of the equations leading to these results enables the designer to discover which aspects of their systems contribute most to the result. In this example, the presence of a single telemetry communication link presented the BVLOS case with a single point of failure with relatively high failure probability. Introducing redundancy to this communications link would significantly improve the result.
Finally, additional insight into the system may be achieved by parametrising various probabilities on continuous states of the environment. For example, in practice, 
$P(\overline{X}_H | \overline{C})$, the probability of loss of position awareness of the human operator assuming no communication link to the vehicle, is likely to be an increasing function of the distance between the operator and the vehicle. Likewise, 
$P(\overline{GNSS})$, the probability that the GNSS system is not available, is likely to be a decreasing function of the distance between the vehicle and obstacles which could interfere with the GNSS signals (e.g. tall buildings). By formulating the probabilistic model as a function of variables such as these, it can be used to assess the safe environmental operating envelope for the system.
5.0 CONCLUSIONS
This paper considers quantifying the situational awareness of UAS. The relationship to current manned systems has been investigated and a modelling approach has been employed that lays new foundations to extend operational areas of Unmanned Aircraft Systems (UAS). Traditional system deployments operate under VLOS conditions where a pilot plays a crucial role in determining the conditions both around and onboard the UAS.
Situational awareness of the system, either by the pilot or based on its on-board computers, consists of awareness of the conditions of internal components, aircraft position, air environment, ground environment and interdependent aspects. In order to extend operation to the BVLOS operation, the pilot will no longer be able to maintain unaided eye contact with the UAS. Responsibility for the situational awareness will pass partly to the UAS and it will need to be adequately communicated back to the pilot to achieve a similar level of awareness as with Visual Line of Sight (VLOS).
This paper initially reviews a traditional set-theoretic approach which allows qualitative measurement of situation awareness. Whilst this provides a useful grounding in determining the factors that play a role in situational awareness, it does not provide the depth of analysis required to be able to understand the true operation of a system.
A formal framework is presented, which can be used to probabilistically quantify the situational awareness of a UAS, both with and without a human in the control loop. It identifies and provides an open and flexible mathematical description of the sources of situational awareness in both VLOS and Beyond Visual Line of Sight (BVLOS) scenarios, where the responsibility shifts between human and vehicle. An example of using the probabilistic model has been presented to illustrate its benefits in the assessment of both VLOS and BVLOS systems.
The new framework will allow the accommodation of new technologies emerging in on-board device safety, in communication systems and in the development of artificial on-board awareness systems. New technologies can, in the future, be assessed against the probabilities needed for safety in the framework presented in this paper. Hence, the framework will provide an assessment framework for the safety of awareness in both VLOS and BVLOS operations.
ACKNOWLEDGEMENTS
This research was supported by EPSRC Grant No. EP/L024942/1 held by Professor Veres at the University of Sheffield, and Innovate UK Grant No. 132303 on ”Verification of UAS decisions in complex environments” held by SysBrain Ltd., Southampton, UK.
