NOMENCLATURE
- AAF
cross section area of an aerofoil, m2
- AR
aspect ratio
- b
wing span, m
- c
mean wing chord, m
- cR, cT
root and tip chord of a wing respectively, m
- cd
coefficient of profile drag of an aerofoil based on c
- CD
coefficient of drag of the entire aircraft based on S
- cl
coefficient of lift of an aerofoil based on c
- CL
coefficient of lift of the entire aircraft based on S
- D
total drag, N
- e
span efficiency factor
- fAF
aerofoil area fraction, fraction an aerofoil occupies within a rectangular envelope
- fPT
planform transformation factor, transforming the wing box planform
- fPTE
factor to transform the wing box to an elliptical planform
- fPTT
factor to transform the wing box to a tapered planform
- g
gravitational acceleration, taken as 9.81 m/s2
- IF
inflation factor
- L
aircraft lift, N
- m
aircraft mass, kg
- Ma
Mach number
- n
manoeuvring load factor
- Re
Reynolds number
- S
wing planform area, used as reference area for coefficients, m2
- t
relative aerofoil thickness as % of chord, c
- V
true air speed of flight, m/s
- VolAC
total volume of an aircraft, enclosed by its wetted surface, m3
- VolIW
volume of the ideal wing, enclosed by its wetted surface, m3
- VolWB
volume of the wing box, m3
- VolWing
volume of a wing, m3
- Z
taper ratio
- ρ
air density at flight altitude, kg/m3
- ρAC
mean density of an aircraft, kg/m3
- ρIW
mean density of the ideal wing, kg/m3
- ρWing
mean density of a wing based on aircraft mass and wing volume, kg/m3
- μ
the dynamic viscosity, kg/ms
- ν
the kinematic viscosity, m2/s
1.0 HISTORICAL CONTEXT
In 1904, as powered aviation got off the ground, Ludwig Prandtl introduced the notion of the boundary layer and offered explanations for the phenomenon of viscous drag(Reference Prandtl1). With power plants of marginal power densities, early aircraft required low wing loading to find their power match. External bracings and biplane configurations offered successful structural solutions for the fledgling domain of heavier-than-air aviation. With better comprehension of drag, it was soon recognised that thicker wings could offer useful volume with little penalty in aerofoil drag. The structures of unbraced wings could hide within this volume. Though heavier, and penalised by induced drag, its lower parasitic drag allowed for faster flight. As the understanding of inviscid drag consolidated through the work of Lanchester and Prandtl, the trade-off between viscous and inviscid drag became the topic of perhaps the most persistent debate in aviation.
Hugo Junkers committed to the opportunity of useful wing volume in the year before Prandtl's landmark clarification of induced drag in 1911 when he sealed this conviction into his ‘Volume Patent’ in 1910(Reference Junkers2,Reference Horton and Selinger3) . He therein suggested that not just the wing structure but also the engines, their fuel, the crew and the payload should eventually reside inside the wing. He thus hinted that the Flying Wing could be the aircraft configuration of the future. The Junkers G 38 airliner began to enact this idea into service in the decade leading to the Second World War. In 1930 Junkers incorporated the idea fully into the design of a 100-ton flying wing intended (but never built) for transatlantic air travel(Reference Horton and Selinger3).
The internal wing structure is part of the solution that has by now dominated aircraft design for almost a century. Though fuel or ballast also commonly reside inside the wing, the fuselage has never disappeared entirely into it, and engines seldom have. From early on, a dedicated fuselage holding tail wings (the empennage) formed part of a robust solution to the challenges of stability and control. Although the Horton brothers and many others demonstrated long ago that such tail wings can be considered redundant(Reference Horton and Selinger3,Reference Nickel, Wohlfahrt and Brown4) , they remain part of the dominant solution today, together with the rather long and slender fuselage that holds them.
Proponents for alternatives to the current dominant aircraft configuration cast serious doubt on its supremacy by claims that superior solutions exist in terms of flight efficiency(Reference Liebeck, Page and Rawdon5–Reference Gur, Schetz and Mason7). Much research is motivated by this speculation(Reference Dénos8). It also remains common practice in aircraft design to dedicate substantial efforts to the choice of the configuration(Reference Torenbeek9–Reference Roskam11) despite the existence of the well-established dominant solution. If the aircraft configuration space were divided into only two broad families, one could follow Stinton's(Reference Stinton12) classification of aeroplanes into a classical family and an integrated family. The classical arrangement has distinguishable lifting and non-lifting parts as in the current dominant configuration, often called the ‘tube-and-wings’ configuration. The integrated family is characterised by the attempt to avoid exposure of any non-lifting aircraft surfaces to the air, and the Volume Patent is thus at the core of such arrangements. The continuing debate should at least attempt to answer to which family the aircraft of the future will belong.
Nickel and Wohlfahrt(Reference Nickel, Wohlfahrt and Brown4) offer an example to dismiss the pure flying wing as a solution to the flight objective of a well-known large transport aircraft. They demonstrate that the volume requirement of this specific flight objective cannot be practically met by a pure flying wing and conclude that a commercially viable all-wing airliner seems unfeasible with the technology of the time. However, it is not clear from such an isolated example how sensitive this conclusion might be to changes in the flight objective parameters, or to what extent a useful integrated arrangement would deviate from the pure flying wing.
Torenbeek(Reference Torenbeek9,Reference Torenbeek13) explores the matter of volume requirement more broadly by investigating variations of the ratio of fuselage volume to wing volume by also allowing two operational parameters (cruise speed and density) to vary. Thus, the variation from the classical arrangement towards the integrated arrangement is considered as the fuselage relinquishes an increasing amount of its volume to the wing. A variety of integrated arrangements were compared against an existing large conventional baseline without a conclusive statement.
In Torenbeek's analysis(Reference Torenbeek9,Reference Torenbeek13) , no special consideration is given to the payload grain size, which is part of a practical volume requirement. Also, that work was performed in the context of the large transport aircraft, the only significant domain in which the integrated arrangement is seriously considered as an attractive proposition for high-altitude cruise at perhaps reduced speed.
Proposals by Burnelli in the early 1920s to shape a dedicated fuselage as a lifting body have also not found sustained implementation(Reference Wood14). However, in recent decades such concepts have been reconsidered in many different variants with many different blended-wing bodies (BWBs) studied in the USA, initiatives like the VELA in Europe and TsAGIs integrated wing body, lifting body, and flying wing in Russia, as summarised by Lowther(Reference Lowther15).
As a contrasting alternative it is proposed that wings should be thinner and of higher aspect ratio. Such wings would also require less sweep but would need external bracings(Reference Gundlach, Tetrault, Gern, Nagshineh-Pour, Ko, Schetz, Mason, Kapania, Grossman and Haftka6,Reference Gur, Schetz and Mason7) . These braced wings then have particularly little volume and thus inevitably belong to the classical family of dedicated wing and body.
The above gives a superficial overview of the debate surrounding wing volume, which is a core configuration issue. Mason observes that ‘a simple, easy-to-understand analysis’ to gauge when wing volume can and cannot be useful is still missing(Reference Mason16,Reference Torenbeek9) . In response, a simple and general notion is here introduced, with two new parameters, the Wing Density and the Inflation Factor.
2.0 THE FLIGHT OBJECTIVE, THE IDEAL WING, WING DENSITY AND THE INFLATION FACTOR
In order to formulate a hypothetical ideal to serve as an evaluation reference, it is necessary to consider the physical limitations of aerodynamics independent of operational compromises and limitations. The notion of the Ideal Wing is here used as such a baseline. Any real aircraft design inevitably must offer a compromise suitable for a large variation in objectives. To avoid the need to compromise, one must derive a unique objective from the large scope of variation. The notion of the Flight Objective is here used to give focus to a specific objective. It is then possible to derive a unique ideal wing for any given flight objective. Its mass and volume then define the ideal Wing Density. Relating this wing density to the average aircraft density of a corresponding real solution yields the Inflation Factor. This factor serves as a measure of discrepancy between a practical solution and its aerodynamically possible ideal.
2.1 About the flight objective
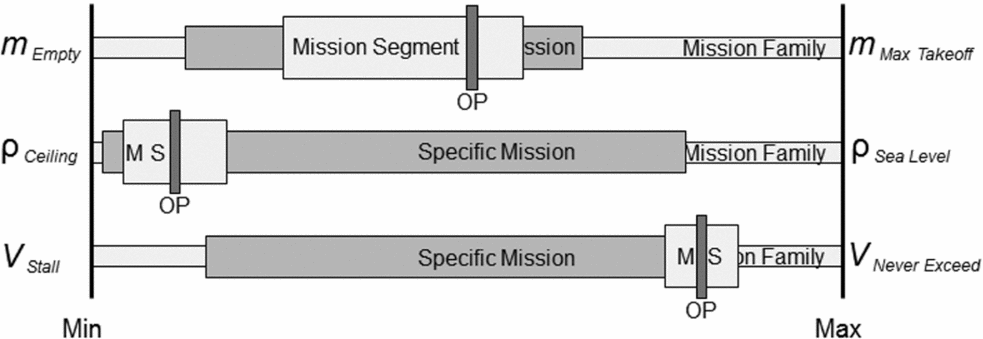
Each aircraft is designed for a family of missions. Every flight represents a specific mission. Each mission is composed of a sequence of mission segments (Fig. 1), each segment having one specific performance objective. This performance objective, together with the operational parameters, define the Flight Objective of the segment.

Figure 1. Any mission is a sequence of mission segments, each having a specific performance objective.
The mission family defines the overall scope of Operational Parameters of aircraft mass m, the load factor n, air density ρ and the flight speed V, and all the Performance Objectives relating for example to range, endurance or rate of climb. Each specific mission narrows down the scope of operational parameters while all the performance objectives may still be of relevance. Each mission segment further narrows down the variation of operational parameters (as illustrated in Fig. 2) and now only one specific performance objective is relevant. The performance objective and the operational parameters are now specific, and an aircraft specialised for only one such specific flight objective can be without compromise. Such a hypothetical aircraft forms the basis of the ideal wing described here.

Figure 2. The Operational Parameters (OP) are narrowed down from the overall scope of variation of the Mission Family first by the Specific Mission and further by the Mission Segment (MS) to give focus to the operational parameters for a given flight objective.
Besides the operational parameters and the performance objective, the flight objective is also concerned with other requirements. The volume requirement and the demands concerning stability and control may be applicable to all segments. Other special requirements like cabin pressure or radar signature may be associated only with some segments. Such additional requirements are then ignored since, by the definition of the ideal wing, only the operational parameters and the performance objectives are of interest.
It is normally the objective to perform any mission with the best overall flight economy and this therefore also applies to each mission segment. Overall mission optimisation and operational constraints will of course influence the choice of the operational parameters but it is here unimportant how these parameters have been chosen. The flight objective may now be defined as:
the objective to operate the aircraft at the parameters of choice (m, n, ρ and V) at the best flight economy for the given performance objective.
2.2 The ideal wing
Presuming that the physics of flight require a dynamic interaction between the flight body and its surrounding viscous medium to provide the lifting force for heavier-than-air flight, such a lifting device is taken to be a wing (a fixed wing, given the domain under consideration). A wing is then an inevitable necessity and it would be best if the aircraft needed nothing else. By ignoring the requirements for volume, stability and control, and other special requirements of the flight objective, the aircraft can be reduced to the Ideal Wing. Thus:
the Ideal Wing is the hypothetical aircraft which offers the best aerodynamic efficiency for a given flight objective by containing the entire aircraft in only a wing of ideal aerodynamic shape and size.
Each flight objective defines a unique ideal wing and this is without compromise, as the flight objective is specific. It serves as a reference to compare practical solutions for a given flight objective with the hypothetical ideal.
2.2.1 The shape of the ideal wing
‘Ideal’ in the present context relates only to the physics of lift and drag, and thus considers only the transfer of energy from the flight body to the surrounding medium while changing its momentum to provide the required lift. Thus, the ideal wing is shaped and sized to provide the required lifting force in a way that would shed the least amount of energy to the wake to achieve the desired flight objective. In terms of the induced drag, all ideal wings will therefore operate with the best span efficiency, e = 1. To keep the model of the ideal wing simple, the classical approximation of the elliptical planform without twist is adopted here, and nonplanar or multi-component wings are not considered.
It is the purpose of the ideal wing to serve as a baseline for size comparisons only, and by the definition offered here, issues of stability and control and of compressibility are ignored, together with the volume- and other requirements. Thus, sweep and dihedral features are neglected, but without implying that the ideal wing is necessarily without such features. The size parameters of interest for the ideal wing are insensitive to these neglected geometric characteristics. Furthermore, these size parameters are not needed with any great accuracy and therefore some simplifying assumptions are permitted to arrive at consistent parametric estimates.
The detail of the shape of the ideal wing can be debated(Reference Wakayama and Kroo17,Reference McGeer18) . However the proposed representation needs to be seen not as the confirmed actual ‘ideal’, but rather as a reasonable geometric representation for a comparative baseline. The baseline properties of interest are the wing volume, VolIW, its maximum thickness, tcR, and later (not discussed here) its wetted surface. These parameters need not be known with great accuracy, as long as they are uniquely defined in terms of the operational parameters.
2.2.2 The mass of the ideal wing
As a comparative reference, the mass of its corresponding real aircraft within the mission segment under consideration is used for the ideal wing. For existing designs, this mass (and its variation during the segment) is known. Otherwise, if only payload mass is known, it is common practice to derive estimates from existing designs with similar objectives. The mass may be considered as if distributed ideally along the span such that no consideration needs to be given to the structure of the ideal wing.
2.2.3 The aerofoil of the ideal wing
The three-dimensional consequences of wing geometry can quite reliably be derived from the results of classical wing theory, given the geometric simplicity and rather high AR of the ideal wing. However, this requires information on the local circulation strength along the span as produced by the aerofoils and reflected by the operational coefficients of lift cl and the corresponding profile drag cd. The physical limitations of these parameters depend on the quality of the aerofoil, which affects the viscous interactions within the boundary layer.
While the notion of the ideal wing can be applied to any mission segment, the focus is here on segments in which the greatest efficiency is desired. That excludes operations involving deliberate flow separation and implies that the best advantage is taken of laminar flow. In terms of maximum aerofoil efficiency, only one effective angle of attack is then of interest for such mission segments – that at which the wing CL/CD is the highest. Then, also a high maximum aerofoil cl/cd is of interest and the design CL may then typically be rather close to the cl for (cl/cd)max. Best aerofoil efficiency is usually associated with a large amount of laminar flow, and this reduces rather abruptly beyond a critical lift coefficient(Reference Boermans19–Reference Althaus and Xaver22). Thus, the aerofoil of the ideal wing is considered (where suitable) to be a laminar aerofoil.
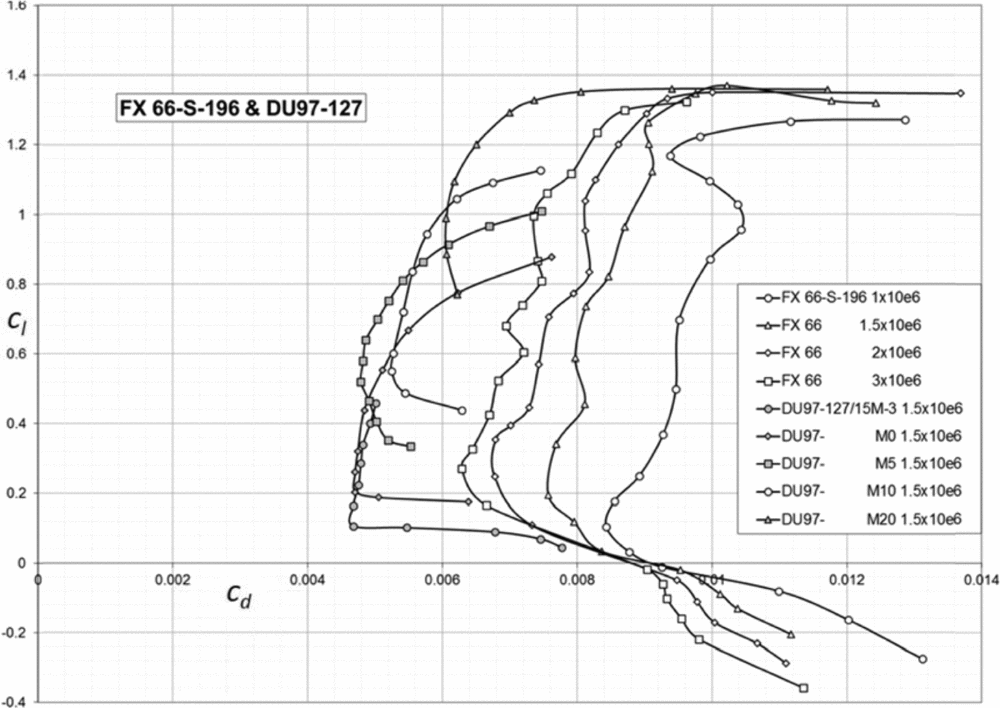
Historically, one can observe a trend of improvement of the best aerofoil cl/cd even after the prominent jump linked to the emergence of laminar flow aerofoils during the Second World War. Fig. 3 shows properties of an early laminar flow aerofoil against those of a more recent one. One example clearly shows the influence of Re. The other shows how a flap can be used to compose a useful range of cl for low drag operation.

Figure 3. Experimental data of the Wortmann FX 66 aerofoil(Reference Althaus and Xaver22) at different Reynolds numbers and the Delft DU97 aerofoil(Reference Boermans19) at different flap settings. For each polar curve, only the laminar ‘drag bucket’ is shown.
For a true ‘ideal’ reference, the physical limit towards which this trend is converging should be applied to the ideal wing. As long as this physical limit may be unknown, realistic values for cl and cd of the current best aerofoils at the given operational Reynolds (Re) and Mach (Ma) numbers should be used, assuming that these are not far off this physical limit.
Any form of active boundary layer control reliant on external energy would form part of a propulsion system and is therefore not considered in this definition of the ideal wing. However, boundary layer control continues the trend of improving best aerofoil cl/cd and therefore needs to be considered in the wing volume debate. The corresponding augmented ideal wing offers even less wing volume.
2.2.4 The size of the ideal wing
Given the assumption of constant downwash (as implied by e = 1) and the rather high AR of the ideal wing, the operational lift coefficient of the entire wing, CL, is approximately the same as the constant local coefficients of its aerofoils, cl. Then the size of the ideal wing follows directly from the operational parameters m, ρ and V and from the aerofoil operational lift coefficient cl. The flight speed would typically be that for minimum total drag (where the total drag is the sum of profile and induced drag only). Since there are important mission segments associated with curved flight, it is necessary to include the load factor n so that
Once the AR or wing span b is known, the root chord of the elliptical wing can be derived from the mean chord c by cR = 4/πc, with the maximum thickness of the wing then being cRt. This parameter reflects the upper vertical limit within the useful volume of the ideal wing.
To compensate for variations in the operational parameters as fuel is consumed and air density changes with altitude, the flight speed could in principle be changed so that mn/ρV 2 remains constant. To operate at a constant speed, the rate of climb should be balanced with the fuel consumption such that the displacement volume mn/ρ remains constant. Either way, the aircraft would operate at the best CL throughout the mission segment for a fixed wing area. Thus, the flight objective can in principle define a unique ideal wing of fixed size despite large parameter variations during the mission segment. This approach deliberately neglects practical limitations of operation in controlled airspace to remain consistent with the underlying laws of physics rather than with artificial rules and procedures.
2.2.5 The aspect ratio of the ideal wing
The wing of infinite span (and thus AR) represents the hypothetical case without induced drag. Any real wing must have a finite AR, but which AR would be ideal for the ideal wing? Since the flight objective defines the flight speed and altitude of choice (and thus the viscosity, density and Ma), the wing area follows directly from any choice of lift coefficient as shown by Equation (1).
Now, since:
where ν = μ/ρ, then, given the relationship between the chord, c, area, S and aspect ratio, AR,
from Equations (1) and (2) we may write:
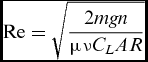 $$\begin{equation}
{\mathop{\rm Re}\nolimits} = \sqrt {\frac{{2mgn}}{{\mu \nu {C_L}AR}}}
\end{equation}$$
$$\begin{equation}
{\mathop{\rm Re}\nolimits} = \sqrt {\frac{{2mgn}}{{\mu \nu {C_L}AR}}}
\end{equation}$$and hence:
The product of dynamic and kinematic viscosity, μν, has units of force and increases with altitude. Recalling the approximation CL≅cl, then an estimate of cd can be made from measured or computed drag polars. In particular, numerical codes such as XFOIL/XFLR5 can be used to generate a series of polars for varying cl, at given Re and Ma, and Equation (5) may then be used to compute AR. The total drag is the sum of profile and induced components:
and so the dimensionless drag to lift ratio is:
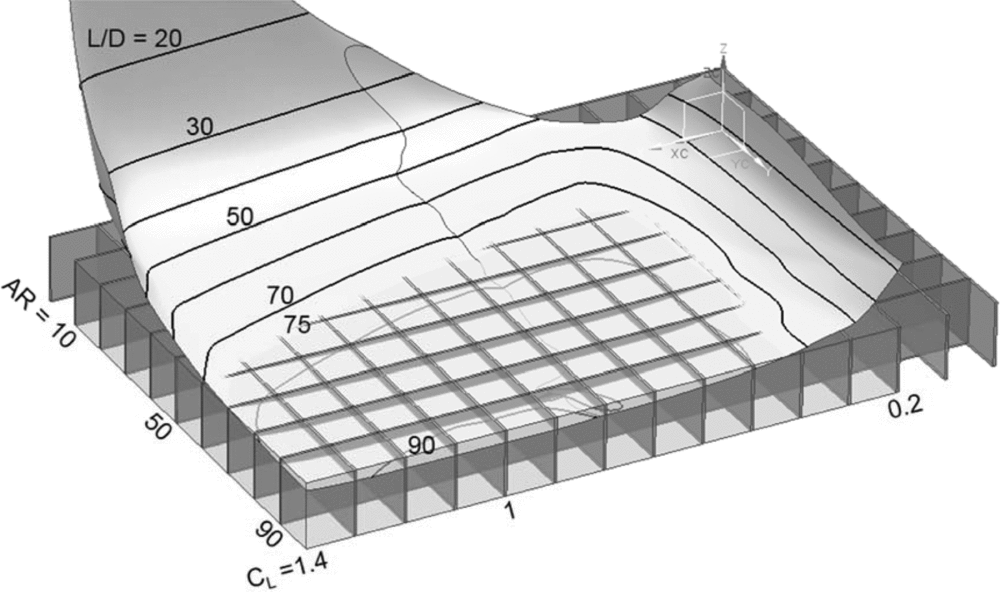
C D/C L can now be shown as a surface over the variables CL and AR, as in Fig. 4 for one example case. Here the aerofoil is based on the DU97-127 on an imagined sailplane of m = 600 kg, at a density altitude of ρ = 1 kg/m3. Such surfaces would ideally be compiled from properties of aerofoils specialised for any given CL and Re at a given Ma, and a unique set of surfaces could in principle be derived by a rigorous process of aerofoil optimisation for the single objective of minimising aerofoil drag in their design points. The minimum point on such a surface would then define the ideal lift coefficient and AR for a given flight objective.

Figure 4. The surface of D/L as a function of AR and CL shows, by means of the L/D contours, how CL and AR should increase to get to the best performance (with the lowest region offering the best L/D). The fissure in the otherwise smooth surface separates two different flap settings.
This optimisation exercise is not part of this work and the surface of Fig. 4 is offered as an example, numerically derived from only a single base geometry. No attempt at aerofoil specialisation has been made for this example other than including two flap settings. The surface does not reflect operational relationships but design relationships. A large CL implies a small wing. It can be seen that the design landscape allows a large variation of CL for a given AR without much change in the performance. The region around the optimum is a rather weak function of CL and AR and the optimum is found at rather high values of CL and AR (on the order of CL = 1 and AR beyond 100 in this example). This example is used to show how such surfaces may be constructed so as to offer a baseline for the notion of the ideal wing.
2.3 Wing density
Wing density may be added to the list of useful parameters such as wing loading or span loading that characterise an aircraft. Although the absolute wing volume is of interest, a more generalised parameter results from normalising the volume with the aircraft mass to either become the specific volume (m3/kg) or a density (kg/m3). The latter form has been chosen here as it compares more easily with the densities of fuel and ballast. Wing density is then simply the aircraft mass m over its wing volume VolWing:
This represents the mean density of the aircraft as if it were compressed into its wing. Comparing it with the actual mean aircraft density:
where VolAC is the total volume of the aircraft, one obtains a generic parameter to gauge the usefulness of the wing volume.
2.3.1 The wing volume
The wing volume can be approximated from the primary wing geometry parameters, S and AR or span b, the planform, and the aerofoil geometry. The Wing Box is here presented as the scalable volume, VolWB, which is later expressed in terms of the operational parameters. This box is then transformed to account for the actual planform of the wing by means of the Planform Transformation, fPT. The wing occupies only a fraction of the wing box proportional to the Aerofoil Area Fraction, fAF, and the relative aerofoil thickness t so that:
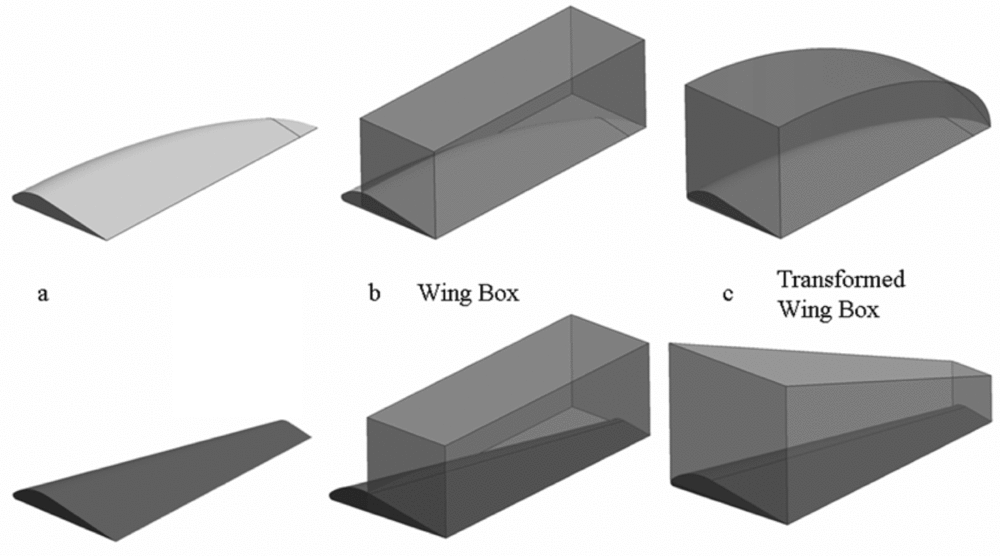
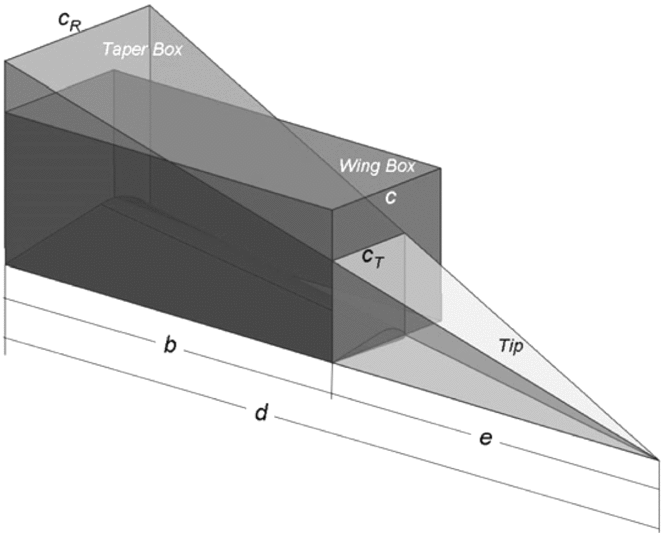
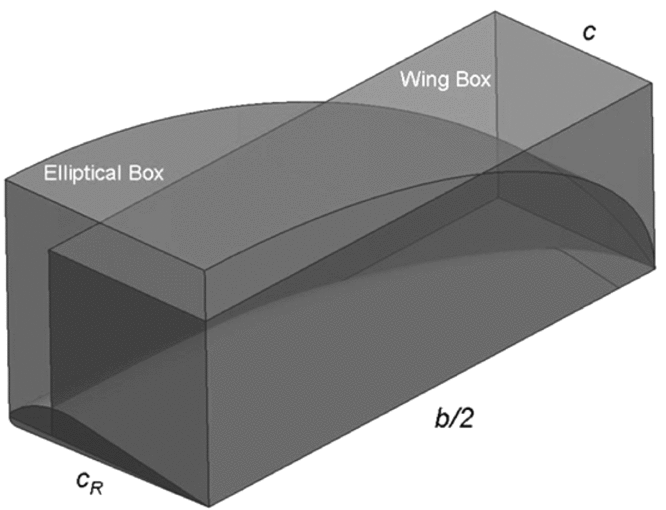
Equation (10) shows how the wing box volume can be scaled to any specific, real geometry through transformations fPT, fAF and t to allow quantitative statements to be made on wing volume and density by simply considering the wing box volume. Illustrations of the scaling transformations are given in Fig. 5 for an elliptic and a tapered wing.

Figure 5. Wing box transformations to estimate the volume of an elliptical and a tapered wing.
2.3.2 The wing box
The wing box can be viewed as a rectangular box having the same base area S as the wing and having a square longitudinal cross section. It is the rectangular box in Fig. 5(b) of span b with a square cross section c 2 (with c the mean chord of the wing), such that its volume:
The wing box volume can also be expressed in various ways, using S = bc and AR = b/c = b 2/S, so that:
The last expression illustrates best how an increase in AR reduces the wing volume for a given wing area. The next step is to make the specific transformations of this generic shape for particular geometries.
2.3.3 The planform transformation, fPT
The dimensionless factor, fPT, transforms the wing box to have the same planform as the wing. The transformed wing box retains the square longitudinal cross sections, but the chord varies with spanwise location, c = c(y). For a wing with single taper, the Planform Transformation (Taper), fPTT, is:
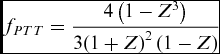 $$\begin{equation}
{f_{PTT}} = \frac{{4\left( {1 - {Z^3}} \right)}}{{3{{\left( {1 + Z} \right)}^2}\left( {1 - Z} \right)}}
\end{equation}$$
$$\begin{equation}
{f_{PTT}} = \frac{{4\left( {1 - {Z^3}} \right)}}{{3{{\left( {1 + Z} \right)}^2}\left( {1 - Z} \right)}}
\end{equation}$$
with the taper ratio ![]() $Z = \frac{{{c_{Tip}}}}{{{c_{Root}}}}$. This expression, derived in Appendix A1, is undefined for a rectangular wing (Z = 1), but for such a wing, no transformation is needed (or fPT = 1). The maximum taper transformation adds 33% (fPTT = 4/3) to the volume of a wing when the taper ratio is at its minimum of 0, while a taper ratio of 0.5 adds only 3.7% when compared with the rectangular wing of the same wing area.
$Z = \frac{{{c_{Tip}}}}{{{c_{Root}}}}$. This expression, derived in Appendix A1, is undefined for a rectangular wing (Z = 1), but for such a wing, no transformation is needed (or fPT = 1). The maximum taper transformation adds 33% (fPTT = 4/3) to the volume of a wing when the taper ratio is at its minimum of 0, while a taper ratio of 0.5 adds only 3.7% when compared with the rectangular wing of the same wing area.
The Planform Transformation (Elliptical), fPTE, transforms the wing box into a volume with an elliptical planform and locally square longitudinal cross sections. For an elliptical wing of mean chord c, the wing root chord cR = 4/πc = 1.27c. As derived in Appendix A2, the elliptic transformation inflates the wing box by:
This means that the elliptical wing has a 27% larger root chord and is 27% thicker at the root than its rectangular equivalent of the same wing area, and it also has 8% more volume. This is about the same as the volume of a comparable tapered wing with Z = 1/3.
2.3.4 The aerofoil area fraction, fAF
The cross-sectional area AAF of an aerofoil is proportional to its chord length c and thickness ct (with relative thickness t expressed as a fraction of c). It also depends on the aerofoil geometry for which the Area Fraction is illustrated in Fig. 6, and defined as:

Figure 6. An aerofoil comparable to the DU97 of thickness t = 12.7% has an area fraction fAF = 68.4%.
The aerofoil area fraction based on the square cross section of the wing box, c 2, is then:
which would also be the volume fraction of a rectangular wing in its wing box, which is typically on the order of 10%.
2.3.5 The ideal wing density
From Equations (10) and (12), a general geometric expression for the wing volume is:
Substituting Equation (1) for S here introduces the operational parameters of choice together with the proposed lift coefficient and AR, so that:
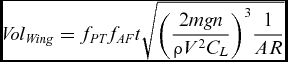 $$\begin{equation}
\textit{Vol}_{\scriptsize\textit{Wing}} = {f_{\scriptsize\textit{PT}}}{f_{\scriptsize\textit{AF}}}t\sqrt {{{\left( {\frac{{2mgn}}{{\rho {V^2}{C_L}}}} \right)}^3}\frac{1}{{AR}}}
\end{equation}$$
$$\begin{equation}
\textit{Vol}_{\scriptsize\textit{Wing}} = {f_{\scriptsize\textit{PT}}}{f_{\scriptsize\textit{AF}}}t\sqrt {{{\left( {\frac{{2mgn}}{{\rho {V^2}{C_L}}}} \right)}^3}\frac{1}{{AR}}}
\end{equation}$$As a reference, the density of the ideal wing gives the highest wing (or aircraft) density for a given flight objective. Inserting the above into Equation (8) and using the elliptical planform transformation fPTE gives the ideal wing density as
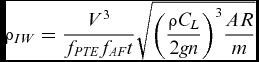 $$\begin{equation}
{\rho _{IW}} = \frac{{{V^3}}}{{{f_{\scriptsize\textit{PTE}}}{f_{\scriptsize\textit{AF}}}t}}\sqrt {{{\left( {\frac{{\rho {C_L}}}{{2gn}}} \right)}^3}\frac{{AR}}{m}}
\end{equation}$$
$$\begin{equation}
{\rho _{IW}} = \frac{{{V^3}}}{{{f_{\scriptsize\textit{PTE}}}{f_{\scriptsize\textit{AF}}}t}}\sqrt {{{\left( {\frac{{\rho {C_L}}}{{2gn}}} \right)}^3}\frac{{AR}}{m}}
\end{equation}$$ This can be rearranged into a parameter relating to the design choice ![]() $\sqrt {C_L^3AR}$, a parameter relating to the wing and aerofoil geometry
$\sqrt {C_L^3AR}$, a parameter relating to the wing and aerofoil geometry ![]() ${1}/{{{f_{\scriptsize\textit{PTE}}}{f_{\scriptsize\textit{AF}}}t}}$ (in which fPTE = 1.08) and an operations related parameter
${1}/{{{f_{\scriptsize\textit{PTE}}}{f_{\scriptsize\textit{AF}}}t}}$ (in which fPTE = 1.08) and an operations related parameter ![]() ${V^3}\sqrt {{{( {{\rho }/{{2gn}}} )}^3}{1}/{m}}$, and so expressed, with the constants combined into K = 0.0106 as:
${V^3}\sqrt {{{( {{\rho }/{{2gn}}} )}^3}{1}/{m}}$, and so expressed, with the constants combined into K = 0.0106 as:
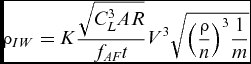 $$\begin{equation}
{\rho _{IW}} = K\frac{{\sqrt {C_L^3AR} }}{{{f_{\scriptsize\textit{AF}}}t}}{V^3}\sqrt {{{\left( {\frac{\rho }{n}} \right)}^3}\frac{1}{m}}
\end{equation}$$
$$\begin{equation}
{\rho _{IW}} = K\frac{{\sqrt {C_L^3AR} }}{{{f_{\scriptsize\textit{AF}}}t}}{V^3}\sqrt {{{\left( {\frac{\rho }{n}} \right)}^3}\frac{1}{m}}
\end{equation}$$2.4 The inflation factor
With the ideal wing representing the smallest and most efficient wing capable of meeting the flight objective regardless of the volume requirement, the additional volume needed for any real solution can be quantified by means of the Inflation Factor. This is defined as the ratio of the total aircraft volume to the volume of its corresponding ideal wing for the given flight objective:
Since m of the hypothetical ideal wing has been chosen to be the same as that of the aircraft at the time for which it has been derived, the inflation factor can also be expressed as the density ratio:
Thus, for any existing or planned aircraft design, an inflation factor can be associated with any given flight objective.
If one imagines that the entire aircraft could be compressed into its ideal wing, then it would have to inflate by the inflation factor before its volume would be sufficient for the required original payload density and grain size.
Any aircraft design, existing or planned, implicitly has a unique inflation factor for a given flight objective. Since any real design solution, planned or existing, provides for a variety of flight objectives, there will be a range of inflation factors associated with any real design. With the ideal wing regarded as the hypothetical aerodynamic ideal, the inflation factor is a measure of design quality as it reflects the departure from the ideal. The inflation factor should strive towards 1, and for small deviations from 1, the flying wing could be a practical solution. Junkers’ Volume Patent gives priority to such solutions. Therefore, to evaluate the merit of this idea, one needs only to estimate the inflation factor of real flight objectives.
Real solutions deviate from the ideal due to technical constraints. A wing of lower AR than that of the ideal wing is inflated due to the lower AR and the operation at a lower CL. Deviation from the elliptical planform may lead to inflation if a small taper ratio is used. A general equation for wing density is (combining Equations (8), (10) and (12)):
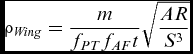 $$\begin{equation}
{\rho _{\scriptsize\textit{Wing}}} = \frac{m}{{{f_{PT}}{f_{AF}}t}}\sqrt {\frac{{AR}}{{{S^3}}}}
\end{equation}$$
$$\begin{equation}
{\rho _{\scriptsize\textit{Wing}}} = \frac{m}{{{f_{PT}}{f_{AF}}t}}\sqrt {\frac{{AR}}{{{S^3}}}}
\end{equation}$$3.0 INTERPRETATION
When considering an existing aircraft design (or one in development) the aircraft volume is in principle known and the range of mean aircraft density is simple to derive. From the corresponding ideal wing density the inflation factor can then be derived for a given flight objective. The inflation factor can then be used directly to establish which combination of cruise speed and air density would offer an inflation factor of 1 (or close to 1) for the wing volume to be useful. If the resulting operational parameters are acceptable, implementation of Junkers’ Volume Patent may be considered for the given flight objective. More important, however, may be to observe the historic trend in technological capabilities and operational preferences to ascertain whether aircraft development is moving towards or away from the idea of the Volume Patent. This will reveal the favoured family (i.e. classical or integrated) from which the aircraft of the future may emerge.
The significant parameters of wing density will now be discussed in terms of their historical trends. Trends increasing the wing density of real wings drive development away from the idea of Junkers’ Volume Patent. With ![]() ${\rho _{\scriptsize\textit{Wing}}} = f( {{{\sqrt {C_L^3AR} }}/{t}} )$, the trend in aerofoil development does just that.
${\rho _{\scriptsize\textit{Wing}}} = f( {{{\sqrt {C_L^3AR} }}/{t}} )$, the trend in aerofoil development does just that.
Improvements in laminar aerofoils favour a higher design CL and offer a lower design cd and tend towards lower thickness t. These improvements call for an increase in the design AR which technological advances in materials and structural strategies also allow. Together such implementations impose a strong penalty on wing volume.
Even more diverting has been the increase in cruising speeds given that ρWing = f(V 3). Early flight was limited to lower speeds. The gas turbine then pushed the common cruise speed to the fringes of the compressibility limit, where it is likely to stay. Given the profound effect of cruise speed on wing density, the integrated aircraft configuration may take advantage if the hurry-up-and-wait staccato of current air travel improves in other contributors to total travel time, to permit a slower flying speed in favour of more comfortable travel and arrival times with better flight economy.
Only the trends towards flight at lower air density at higher altitudes and towards heavier aircraft act in favour of the Volume Patent with ![]() ${\rho _{\scriptsize\textit{Wing}}} = f( {\sqrt {{{{\rho ^3}}}/{m}} } )$. This explains why the integrated approach is mostly considered for large-capacity aircraft cruising at high altitude.
${\rho _{\scriptsize\textit{Wing}}} = f( {\sqrt {{{{\rho ^3}}}/{m}} } )$. This explains why the integrated approach is mostly considered for large-capacity aircraft cruising at high altitude.
4.0 EXAMPLES
In this section, the parameters of ideal wing density and the inflation factor are used by example in two different ways. In one case, taken from the discipline of gliding, they are used to show how diverse the ideal wings can be for different mission segments within the same mission. A trend is noted and later related to the second example. This other example shows the domain in which the airline industry would have to operate efficient, integrated solutions.
4.1 The sailplane
The sport of gliding holds a special place in aviation development. Gliders were the first aircraft in human aviation and are still often used in aircraft development projects. Furthermore, the discipline of gliding still serves as an incubator for many developments in aviation. A sailplane has a particularly challenging mission family because the typical gliding flight frequently alternates mission segments having conflicting flight objectives. Most other aircraft can be specialised for their principal flight objective, but in gliding, such specialisation is not practical. The absence of an on-board power system makes the glider very relevant to the notion of the ideal wing in which the issues of propulsion are not addressed. Even though the energy for gliding flight is almost free, aircraft efficiency is of prominent importance in the context of competition flying. Gliding competitions, in turn, present an unrivalled platform for overall evaluation of design quality in which the full spectrum of quality issues is reflected.
What role can the idea of the ideal wing play in understanding the shape and the evolution of the sailplane? Consider the following questions: What does the ideal wing look like for the best rate of climb in a column of rising air? How does this wing compare to the ideal wing for the best straight gliding distance at high speed? How much space for the pilot (the occupants) or ballast would these ideal wings offer? How do real solutions compare to the various ideal wings? What trends may be expected for the future of the sailplane? To which aircraft family does the sailplane of the future belong?
In line with the approach of dividing the mission into isolated mission segments, the take-off, the powered climb and the landing can be ignored, as the typical competition mission has its important mission segments between the start and the finish gate. Taking a flat-land distance task in convective conditions as an example, there are two distinct mission segments which are alternately flown during the task. During the segment of climb in rising air, when the glider is taking aboard environmental energy, the flight objective is to exploit a local region of best rising air most efficiently. In terms of the competition objective, to cover the task distance within the shortest time, it is then the rate of climb that matters. The lower the flight speed and mass, the better. During the run segment, the best glide distance should be achieved in the shortest time and thus high speed and mass are of interest.
Operationally, the performance objectives of the two segments differ in that the climb should be flown at the speed for minimum sink rate, while the run should be flown at the speed for minimum drag. However, if specialising a wing by design for a specific desired speed, in both cases minimum drag is the design objective. That means that only the wing area (and thus the wing loading) will differ for the ideal wings of the different mission segments. The aerofoil can then be essentially the same, as Re does not vary, and thus the design cl and cd will also be the same. The only compensation needed is for Ma within the regime under consideration. The parameters as derived from Fig. 4 can then be used in this example.
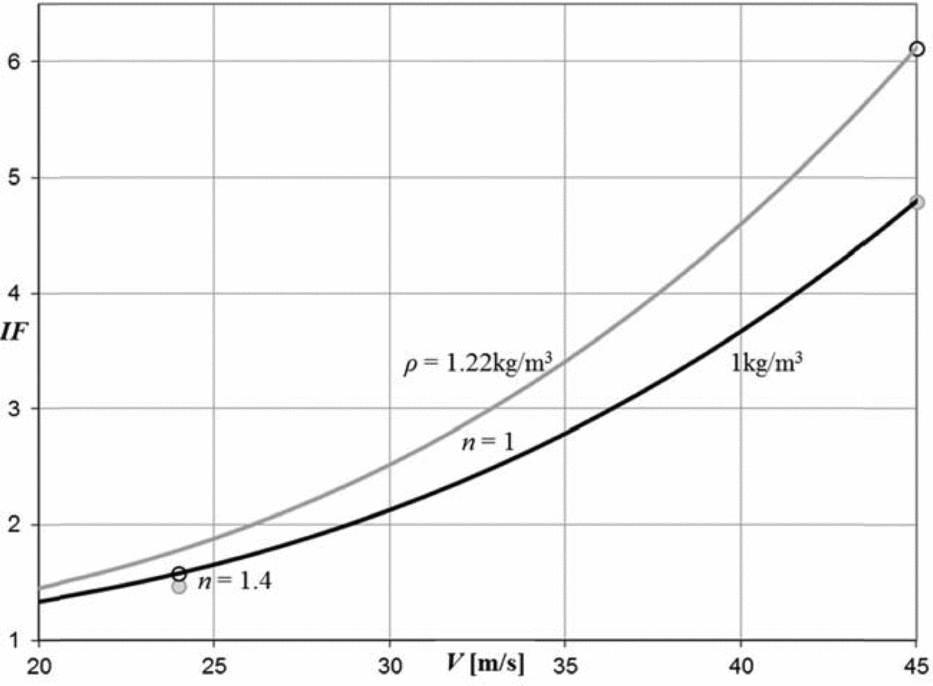
All-up mass can be reduced by dumping ballast (if available), but no means of increasing it in flight is in common use. Therefore, the all-up mass is considered here to be the same for both mission segments, taking m = 600 kg. Thus, in this example only V, ρ and n remain as operational variables. The wing density (or the expected inflation factor) can then be plotted against speed as in Fig. 7, with typical low-speed flight shown at n = 1.4 (45° bank angle), while the high-speed flight is shown at n = 1 (straight flight). Air density is taken to vary between sea level density and that at 2000 m (1.22 and 1 kg/m3, respectively).

Figure 7. Inflation factor (IF) as a function of the design flight speed V for different air densities ρ and load factors n (based on the aerofoil parameters offered in the previous figures).
The aspect ratio of 100 is the same for all such ideal wings and the largest root chord is then <200 mm, evidently insufficient for an occupant. Adding the minimum volume of about 0.5 m3 required for an occupant to the volume of the ideal wing gives the inflation factor as plotted in Fig. 7.
The attractor towards low wing loading for the climb segment pulls the ideal wing towards the idea of the Volume Patent, while the opposing attractor for high wing loading pulls far from it. The low inflation factor solution is interesting in weak conditions when no record-breaking flights can be expected, while the dense wing can achieve record results in strong conditions, thereby setting the trend. This is demonstrated by unique sailplane developments like the Concordia and the eta that have AR tending towards that of their ideal wings with 50.3 and 48, respectively, unbraced! Their wings clearly show that the wing is useless for the occupant; their volumes are not even sufficient for the desired ballast (as can also be derived from the wing density).
The Horton H IV glider had remarkable performance under certain conditions when compared with other gliders of its time(Reference Horton and Selinger3). The H IV was one of very few implementations of the idea of Junkers’ Volume Patent, as the fuselage was essentially contained within the wing. However, its approach was not repeated when tailless gliding was given another chance with the SB 13, which instead offered a dedicated fuselage(Reference Nickel, Wohlfahrt and Brown4).
From these observations it would appear that the sailplane of the future will remain within the classical family.
A further comment can be made when considering the two extreme ideal wings of gliding. One might enquire why area-extending flaps are not common features on modern sailplanes(Reference Johl23), and, how and whether one might reconfigure a wing in flight for the two opposing flight objectives. This issue was at the heart of the projects fs 29 of the Akaflug Stuttgart and the SB 11 of the Akaflug Braunschweig(Reference Thomas24). The fs 29 used a telescopic wing to increase wing area and AR for slow flight while the SB 11 used area-extending flaps by which, however, AR decreases as the wing area enlarges. The notion of the ideal wing suggests that the shape of the wing should ideally remain the same for both flight objectives; only its size should change. Implementation of such a strategy of in-flight wing adaptation is highly impractical. Therefore, either span or chord changes are considered independently for real solutions, and as long as this will be the case, consensus cannot be reached on which is the better compromise.
4.2 The airliner
Here, a modern commercial airliner, the Boeing 787–800, is taken as an example. Its fuselage volume is estimated to be about 1230 m3 and its total volume is about 1585 m3 (excluding the engines). With an all-up mass of 228,000 kg and an empty mass of 118,000 kg, the mean aircraft density will not exceed 144 kg/m3 or be less than 74 kg/m3. Taking the cruise segment of the mission as the principal mission segment and assuming that the displacement volume m/ρAir is about 553,900 m3 while cruising at a constant true airspeed of 254 m/s, the mean aircraft density could vary between 132 and 92 kg/m3 during the principal mission segment as fuel is burned off. In contrast, the density of the representative ideal wing for this flight objective varies between 550 and 383 kg/m3. The inflation factor is then about 4.1 and this is a fixed value given that the flight objective defines an ideal wing of unique size. Thus, the volume of the ideal wing, like that of the real aircraft, is constant. An ideal wing useful for this flight objective would require ideal wing densities of the same order of magnitude as those of the real aircraft for the inflation factor to be 1 (or close to 1). With all else remaining the same, such a wing would have to cruise at ![]() ${{{V_{787}}}}/{{\sqrt[3]{{IF}}}} = 0.62{V_{787}}$, or at about 158 m/s, to have a wing volume sufficient to include the entire aircraft with its payload. Alternatively, the aircraft should cruise with a displacement volume of
${{{V_{787}}}}/{{\sqrt[3]{{IF}}}} = 0.62{V_{787}}$, or at about 158 m/s, to have a wing volume sufficient to include the entire aircraft with its payload. Alternatively, the aircraft should cruise with a displacement volume of ![]() $\sqrt[3]{{I{F^2}}} = 2.57$ times larger. This could be achieved by cruising about 6000 m higher and at the same speed. The ideal wing would then have a root aerofoil thickness of about 3 m, perhaps sufficient for the payload grain size. These findings are in line with those of Torenbeek(Reference Torenbeek9), who goes further in an exercise of optimisation to find the best combination of speed and density at which the flying wing could in principle be suitable.
$\sqrt[3]{{I{F^2}}} = 2.57$ times larger. This could be achieved by cruising about 6000 m higher and at the same speed. The ideal wing would then have a root aerofoil thickness of about 3 m, perhaps sufficient for the payload grain size. These findings are in line with those of Torenbeek(Reference Torenbeek9), who goes further in an exercise of optimisation to find the best combination of speed and density at which the flying wing could in principle be suitable.
5.0 CONCLUSIONS
While it may be qualitatively obvious how wing area, span, and aspect ratio influence the wing volume, the expressions for the volume of the wing box in Equation (12) help to quantify these dependencies explicitly. In surveying modern aircraft configurations, one will intuitively be inclined to dismiss the idea of Junkers’ Volume Patent. However, alternatives to the current dominant configuration continue to be proposed and debated. The notion of the inflation factor as a property of a specific flight objective is useful in understanding the relative importance of wing and fuselage volume, and it may be the most decisive figure of merit for the choice of aircraft configuration. Indeed, it can easily be used as the single variable by which ‘genetic’ relationships between various configurations can be established. Its historic trend then also gives clear indications as to where aircraft development is heading or where it should go.
Inflation factors of the typical current flight objectives are much too high for Junkers’ Volume Patent to be of interest. The technological trend in terms of structure and the design CL are not expected to reduce the inflation factor. On the other hand, environmental and/or economic pressures may force the cruise velocity and air density to be lowered and mass to be increased in favour of lower inflation factors. Propulsion technology is likely to lead the way to lower cruise air densities. However, with the majority of principal flight objectives related to maximum range, it is extremely unlikely that the wing density will ever become compatible with payload density for any significant number of flight objectives. It is therefore concluded here that the prediction implicit in the Volume Patent will never be confirmed in an economically significant way. The majority of flight solutions of the future will require inflation factors significantly beyond 1 even though several future flight objectives are expected to have low inflation factors (given that miniaturisation of payloads is a prominent trend in unmanned aviation). Wing volume will remain useful for structure, fuel, and ballast, and elements of the propulsion system are likely to find their way into the wing, but bulky payload is expected to remain in a dedicated container of suitable shape.
The campaign for braced wings respects the attractor towards high AR and acknowledges that the volume of the ideal wing is rather limited – not even sufficient for the entire wing structure.
The magnitude of typical inflation factors hints that the classical dedicated wing body family is more likely to hold the configuration for the aircraft of the future. On this side of the binary configuration divide also resides the current dominant configuration and all proposed braced-wing configurations.
At the time that Junkers filed his patent, the gas turbine had not been foreseen, laminar flow aerofoils were not yet known, and material properties were far less advanced, so the inflation factors of the time were therefore much smaller and even showed a downward trend as aircraft grew in mass and size. Junkers therefore had all the right reasons for filing this patent. He would, however, most likely not have done so today.
ACKNOWLEDGEMENT
We would like to thank Loek Boermans (TU Delft) for his valuable comments and suggestions. We also thank referees for careful and constructive comments.
6.0 APPENDIX A
6.1. Planform transformation for tapered wings
With the wing box having the same base area of the wing S = bc and a square longitudinal cross section (with longitudinal here making reference to the aircraft coordinate convention), its volume is:
and the transformed tapered box having the same base area S and retaining the square cross sections, the taper transformation factor is their volume ratio:
with the planform taper ratio being the ratio of the tip chord to the root chord Z = cT/cR = e/d and, from Fig. A1, e = d − b = Zd d = b/1 − Z and e = bZ/1 − Z
The mean chord is c = cR + cT/2 or c = cR(1 + Z)/2 so that cR = 2c/1 + Z and cT = ZcR
The volume of the tapered box is what remains of the pyramid after subtracting its tip:
so that the taper transformation factor becomes:
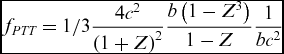 $$\begin{equation*}
{f_{\scriptsize\textit{PTT}}} = {{1/3}}\frac{{4{c^2}}}{{{{\left( {1 + Z} \right)}^2}}}\frac{{b\left( {1 - {Z^3}} \right)}}{{1 - Z}}\frac{1}{{b{c^2}}}
\end{equation*}$$
$$\begin{equation*}
{f_{\scriptsize\textit{PTT}}} = {{1/3}}\frac{{4{c^2}}}{{{{\left( {1 + Z} \right)}^2}}}\frac{{b\left( {1 - {Z^3}} \right)}}{{1 - Z}}\frac{1}{{b{c^2}}}
\end{equation*}$$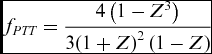 $$\begin{equation*}
{f_{\scriptsize\textit{PTT}}} = \frac{{4\left( {1 - {Z^3}} \right)}}{{3{{\left( {1 + Z} \right)}^2}\left( {1 - Z} \right)}}
\end{equation*}$$
$$\begin{equation*}
{f_{\scriptsize\textit{PTT}}} = \frac{{4\left( {1 - {Z^3}} \right)}}{{3{{\left( {1 + Z} \right)}^2}\left( {1 - Z} \right)}}
\end{equation*}$$6.2. Planform transformation for elliptical wings
The elliptic transformation transforms the rectangular wing box to a volume with an elliptical planform and square longitudinal cross sections (as above).

Figure A1. Wing box and the transformed wing box of a tapered wing.
If i, j and k are the principal dimensions of an arbitrary ellipsoid, then i and j could be the root chord cR and k the span b of a round ellipsoid derived from a wing of elliptical planform. The volume of this ellipsoid would be:
The cross-section area of this ellipsoid in the plane of the wing has the same area as the elliptical planform of the wing, S = bc with c the mean chord, thus:
The area of a square enclosing a circle of diameter d is larger than the circle area by the factor:
Then, the volume of the round ellipsoid transformed to the elliptical box, a body of elliptical base section and square longitudinal cross sections is:

Figure A2. shows the wing box and the transformed wing box of an elliptical wing.
and, by definition:
Then, the planform transformation factor to transform the wing box to the elliptical box is: