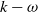Nomenclature
- a
-
impact acceleration
-
${C_p}$
-
pressure coefficient
- DOF
-
degree of freedom
- g
-
gravitational acceleration
- HRIC
-
high-resolution interface capturing
- M
-
mass
- p
-
pressure
- r
-
wetted length
- RMSE
-
root mean square error
- S
-
shape factor
- SPH
-
smoothed particle hydrodynamics
- SIMPLE
-
semi-implicit pressure linked equations
- t
-
time
-
${u_i}$
,
${u_j}$
-
time-averaged velocity components
-
$\upsilon $
-
penetration velocity
- V
-
volume of the cell
- VOF
-
volume of fluid
- WIG
-
wing in ground
-
${x_i}$
,
${x_j}$
-
spatial coordinate componentsv
- z
-
penetration depth
Greek symbol
-
$\alpha $
-
volume fraction
-
$\beta $
-
deadrise angle
-
$\gamma $
-
pile-up coefficient
-
$\theta $
-
pitching angle
-
$\kappa $
-
ratio of corresponding velocity and initial velocity
-
$\nu $
-
fluid kinematic viscosity
-
$\rho $
-
density
-
$\varphi $
-
physical properties
1.0 Introduction
Due to limited resources in inland areas, significant attention has been directed toward the exploration of ocean resource by numerous researchers. To efficiently conduct missions over the sea, flight vehicles, such as amphibious aircraft, helicopters and wing-in-ground (WIG) craft, have been widely used for transportation, with most operations taking place over water. It has led to a focus on investigating emergency water landings, commonly known as ditching [Reference Howson1, Reference Pérez, Benítez, Oliver and Climent2]. Unlike impacts on rigid floor [Reference Ren and Xiang3], ditching involves more complex phenomena, including over-pressure, air cushion effects, cavitation and suction, etc. [Reference Hughes, Vignjevic, Campbell, Vuyst, Djordjevic and Papagiannis4].
A wide range of parameters affecting the dynamic behaviour of flight vehicles ditching have been extensively studied. For instance, a generic aircraft, as reported in NACA TN2929 [Reference McBride and Fisher5], was investigated to assess the effect of rear-fuselage shape, including changes in longitudinal curvature, rear-fuselage cross section and fuselage fineness ratio, on ditching behaviour through experimental study. The conclusion deduced from the work is the minimum longitudinal curvature and circular cross section are optimal for high landing speeds, while moderate longitudinal curvature with moderately curved cross section is preferable for lower speeds. Additionally, a higher fineness ratio contributes to a safer ditching process. Subsequent research shifted to studying the effects of aerodynamic configurations, including wings, horizontal tails and flaps, using the finite volume method coupled with the volume of fluid model [Reference Qu, Hu, Guo, Liu and Agarwal6]. The significant influence of aerodynamic loads was highlighted by comparing the dynamic behaviour of pure fuselage, wing-body combination, wing-body-horizontal tail combination and the complete configuration with deflected flaps. The effect of initial pitching angle on the ditching performance of a low-mid wing civil aircraft was demonstrated numerically by Guo et al. [Reference Guo, Liu, Qu and Wang7]. It indicated that the initial pitching angle has significant effect on the normal load, except for the maximum longitudinal load and maximum pressure on the fuselage. To reduce the load, an incident angle between 10 and 12 deg has been recommended during ditching for similarly configured aircraft. Xiao et al. [Reference Xiao, Lu and Deng8] presented a smoothed-particle hydrodynamics (SPH) study on helicopter ditching, examining both vertical and horizontal motion on calm water, and also investigated the effect of the initial pitching angle. The ditching of a WIG craft with different velocity components was simulated by Cheng et al. [Reference Cheng, Ming, Sun, Wang and Zhang9] using the SPH method. It concluded that the maximum impacting acceleration occurs during the first sliding stage and is mainly influenced by the vertical velocity rather than the horizontal velocity. It was showed that the acceleration increases significantly with higher vertical velocity.
Furthermore, the dynamic behaviour of a helicopter ditching on wavy water, where the effects of ditching positions, i.e., rising, crest, falling and trough, was comprehensively evaluated by Xiao et al. [Reference Xiao, Lu, Deng, Zhi, Zhu and Chen10]. Ditching on crest of wave exhibited the best performance in terms of angular, vertical and horizontal acceleration, whereas ditching on the trough location experienced the most severe overload. This is because the largest impacting area of the helicopter provides a relatively large reactive force to decelerate the descending motion of the helicopter. The wave resistance of amphibious aircraft planing in waves was investigated by Zhou et al. [Reference Zhou, Hu, Mao, Sun and Cao11], focusing on the effect of different wave elements and planing speeds on the motion response. A certain regularity was observed in the heave and pitch motion responses of amphibious aircraft with varying wave conditions. Particularly, when the wavelength reaches 1.38–2.76 times the length of the fuselage, the aircraft is more likely to experience jumping motions with high speeds and large wave steepness.
The ditching process is typically divided into four phases: approach, impact, landing and flotation [Reference Siemann, Schwinn, Scherer and Kohlgruber12]. Among these, the impact phase is particularly important, as the structure undergoes rapid changes in vertical acceleration, similar to what occurs during water entry scenario [Reference Wang, Lugni and Faltinsen13]. The hydrodynamic forces experienced during water impact have been extensively studied. Gong et al. [Reference Gong, Liu and Wang14] investigated a series of cases on a wedge with various initial entering velocities, deriving fitting formulas for both the maximum force on the wedge and the corresponding time based on the initial entry velocity. In the work of Abraham et al. [Reference Abraham, Gorman, Reseghetti, Sparrow, Stark and Shepard15], it was found that the drag-coefficient of a sphere impacting water is independent of factors, such as sphere velocity, surface tension, flow regime and Reynolds number. Algebraic expressions of the drag coefficient versus the dimensionless depth were then established using two fitted polynomials. Yu et al. [Reference Yu, Shen, Zhen, Tang and Wang16] further analysed the effects of impact velocity, radius and mass on the impact force and acceleration. Through fitting the relationship between peak values of non-dimensional force and mass, they obtained simplified expressions for maximum force and acceleration. The slamming force decomposition concept was explored for 2D wedged shapes by Sun et al. [Reference Sun, Sui, Korobkin, Zou and Zong17]. The total slamming force can be represented in three components, such as velocity, acceleration and gravity part, which can be characterised by the corresponding coefficient. Wen et al. [Reference Wen, Liu, Del Buono, Qu and Iafrati18, Reference Wen, Del Buono, Liu, Qu and Iafrati19] formulated the slamming force acting on the wedges during both slamming and transition stages for constant and varying speed impacts, with deadrise angles ranging from
${5^ \circ }$
to
${70^ \circ }$
. For the constant speed impact, the hydrodynamic force is described as a combination of the similitude of the declining forces in the transition stage and the linear increasing forces in the slamming stage. For the varying speed impact, the hydrodynamic force component caused by the acceleration effect in the transition stage is formulated by an added mass coefficient with an average increase of 27.13
${\rm{\% }}$
compared with that of slamming stage.
When managing the results derived from changes in the investigated parameters, similar hydrodynamic characteristics are consistently observed. In fact, such recurring phenomenon is commonly summarised as scaling laws [Reference Mivehchi, Zhong, Kurt, Quinn and Moored20]. However, despite previous pioneering works, the connection between the hydrodynamic phenomenon and scaling laws remains unidentified. In other words, few direct investigations have presented reasonable scaling laws to govern the prediction of hydrodynamics. In the previous study on V-shaped cross-sections of bodies impacting on water [Reference Lu, Del Buono, Xiao, Iafrati, Deng and Xu21], including 2D wedge, 3D cabin section and amphibious aircraft, it was found that the maximum vertical acceleration can be scaled by the square of the initial vertical impacting velocity. For helicopters, the longitudinal section is similar to a V-shaped geometry when ditching with a pitching angle. Thus, it is essential to theoretically evaluate the availability of initial downward velocity on describing peak vertical acceleration and other kinematic parameters when maximum vertical acceleration is achieved. Moreover, the effect of deadrise angle on predicting the maximum vertical acceleration and related parameters was further investigated for wedge impacting [Reference Lu, Del Buono, Xiao, Iafrati, Xu, Deng and Chen22]. In the case of helicopter ditching, different pitching angles can be treated as equivalent to different deadrise angles on either side of a V-shaped section, though this differs slightly from the symmetric case. Consequently, the scaling laws derived from the symmetric wedge need to be extended to asymmetric one. Following this extension, the effect of pitching angle on accelerations for helicopter ditching is then discussed based on the theoretical scaling laws.
Therefore, the main objective of present study is to theoretically establish a comprehensive understanding and evaluation of ditching characteristics with the help of numerical simulation. The primary investigated initial conditions are downward velocity and pitching angle, as these parameters are of utmost concern during ditching. A three-dimensional scaled model of a helicopter was chosen for studying ditching on still water. This paper is organised as follows: the theoretical and numerical methods are introduced in Section 2, while Section 3 subsequently presents the simulation results and analysis of the helicopter ditching, followed by conclusions drawn in Section 4.
2.0 Methodology and computational setup
2.1 Theoretical approach
Based on the extended von Karman’s momentum theory [Reference Lu, Del Buono, Xiao, Iafrati, Deng and Xu21] for wedge impacting scenario (see Fig. 1), it is possible to compute the maximal impact acceleration and the corresponding penetration depth, velocity and time when acceleration reaches its peak value, using the initial parameters:
\begin{align}{a_{z{\rm{max}}}} = \upsilon _{z0}^2{\left( {\frac{5}{6}} \right)^3}\frac{\gamma }{{{\rm{tan}}\!\left( \beta \right)}}\sqrt {\frac{{2\pi \rho }}{{5M}}} \\[-24pt] \nonumber \end{align}
\begin{align}{z^{\rm{*}}} = \sqrt {\frac{{2M}}{{5\pi \rho {\gamma ^2}}}} {\rm{tan}}\!\left( \beta \right) \\[-24pt] \nonumber \end{align}
\begin{align}\upsilon _z^{\rm{*}} = \frac{5}{6}{\upsilon _{z0}} \\[-24pt] \nonumber \end{align}
\begin{align}{t^{\rm{*}}} = \frac{1}{{{\upsilon _{z0}}}}\frac{{16}}{{15}}\sqrt {\frac{{2M}}{{5\pi \rho {\gamma ^2}}}} {\rm{tan}}\!\left( \beta \right) \end{align}
Figure 1. Wedge water entry scenario.
As mentioned in previous study on wedge water entry [Reference Lu, Del Buono, Xiao, Iafrati, Xu, Deng and Chen22], the scaling laws for acceleration, velocity, penetration depth and time have been established based on variations in initial velocity, deadrise angle and mass, as described by Equation (1). Similar behaviours could be concluded in helicopter ditching events, where changes in initial parameters lead to corresponding variations in kinematic parameters. Moreover, looking at the longitudinal plane of the helicopter, it can be seen as a wedge-shaped body to some degree, which supports the applicability of the theoretical approach used for wedge water entry. However, defining the equivalent and suitable deadrise angle
$\beta $
, pile-up coefficient
$\gamma $
and mass
$M$
for the helicopter ditching scenario is hard to determine. Thus, the formula of maximal acceleration can be rewritten as:
\begin{align}{a_{z{\rm{max}}}} = {\left( {\frac{5}{6}} \right)^3}\sqrt {\frac{{2\pi \rho }}{5}} \cdot S\!\left( {\gamma, \beta, M} \right) \cdot \upsilon _{z0}^2 \end{align}
where
$S\left( {\gamma, \beta, M} \right)$
is defined as shape factor, involving the combined effect of
$\beta $
,
$\gamma $
and
$M$
.
Then, the corresponding penetration depth
${z^{\rm{*}}}$
and time
${t^{\rm{*}}}$
can be expressed by the shape factor:
\begin{align}{z^{\rm{*}}} = \sqrt {\frac{2}{{5\pi \rho }}} \cdot \frac{1}{{S\!\left( {\gamma, \beta, M} \right)}} \\[-24pt] \nonumber \end{align}
\begin{align}{t^{\rm{*}}} = \frac{1}{{{\upsilon _{z0}}}}\frac{{16}}{{15}}\sqrt {\frac{2}{{5\pi \rho }}} \cdot \frac{1}{{S\!\left( {\gamma, \beta, M} \right)}} \end{align}
It is interesting to discuss the validity of Equations (2), (3) and (4) on predicting the hydrodynamic characteristics for helicopter ditching problem.
2.2 Numerical method
In the present study, the unsteady incompressible Reynolds-averaged Navier-Stokes equations along with a standard
$k - \omega $
two-equation turbulence model, are solved by the finite volume method. The governing equations for continuity and momentum conservation are expressed as follows:
\begin{align}\frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 \\[-24pt] \nonumber \end{align}
\begin{align}\rho \frac{{\partial {u_i}}}{{\partial t}} + \rho \frac{\partial }{{\partial {x_j}}}\left( {{u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\nu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \overline {u{{\rm{'}}_i}u{{\rm{'}}_j}} } \right) + \rho {g_i} \end{align}
where
${u_i}$
and
${u_j}$
(
$i,j$
= 1,2,3) represent the time-averaged velocity components,
${x_i}$
and
${x_j}$
(
$i,j$
= 1,2,3) are the spatial coordinate components,
$\rho $
is the fluid density,
$p$
is the fluid pressure,
$\nu $
is the fluid kinematic viscosity,
$ - \rho \overline {u{{\rm{'}}_i}u{{\rm{'}}_j}} $
denotes the Reynolds stress and
${g_i}$
is the gravitational acceleration in the
$i$
-th direction.
The Semi-Implicit Pressure Linked Equations (SIMPLE) algorithm is employed to achieve an implicit coupling between pressure and velocity, with the gradient reconstructed using the Green-Gauss Node-Based method. For volume fraction transport, the modified High-Resolution Interface Capturing (HRIC) scheme is adopted. Convection and diffusion terms are treated as algebraic parameters using second-order upwind and second-order central methods, respectively. The unsteady terms are discretised in the time domain using a second-order implicit scheme.
The volume of fluid (VOF) scheme, originally proposed by Hirt et al. [Reference Hirt and Nichols23], is used in the present computational framework to capture the water-air interface. It involves introducing a variable,
${\alpha _{\rm{w}}}$
, referred to as the volume fraction of water in the computational cell, which varies between 0 (air) and 1 (water) and is defined as:
\begin{align}{\alpha _{\rm{w}}} = {V_{\rm{w}}}/V, \end{align}
where
${V_{\rm{w}}}$
is the volume of water in the cell and
$V$
is the volume of the cell. The volume fraction of the air in a cell can be computed as:
\begin{align}{\alpha _{\rm{a}}} = 1 - {\alpha _{\rm{w}}}. \end{align}
The volume of fraction is governed by the following equation:
\begin{align}\frac{\partial \alpha}{{\partial t}} + {u_i}\frac{{\partial \alpha }}{{\partial {x_i}}} = 0. \end{align}
The effective value
${\varphi _{\rm{m}}}$
of any physical properties, such as density, viscosity, etc., of the mixture of water and air in the transport equations is determined by:
\begin{align}{\varphi _{\rm{m}}} = {\varphi _{\rm{w}}}{\alpha _{\rm{w}}} + {\varphi _{\rm{a}}}\!\left( {1 - {\alpha _{\rm{w}}}} \right). \end{align}
To accurately capture the dynamic behaviour and the loads generated during the water-entry process, the motion of the body induced by fluid forces and moments is determined using a six degree-of-freedom (6DOF) model. The 6DOF model solves the equations governing the rotation and translation of the centre of mass of the body. The translation equation is formulated within the global inertial coordinate system:
\begin{align}M \cdot \frac{{{\rm{d}}\boldsymbol{\upsilon} }}{{{\rm{d}}t}} = \boldsymbol{F}, \end{align}
and the rotation of the body is solved in the body local coordinate system by:
\begin{align}\boldsymbol{L}\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} + \omega \times \boldsymbol{L}\omega = \boldsymbol{M}. \end{align}
For the current study, the hydrodynamic requirement of
$y + $
could be 10 times as large as the aerodynamic
$y + $
, due to the difference in density and viscosity between water and air. Based on the discussion in Duan’s work [Reference Duan, Sun, Chen, Wei and Yang24], it is practical to set the aerodynamic
$y + $
within the value of 10 and the hydrodynamic y+ within the value of 100. In the present study, the prismatic boundary layer cells around the helicopter model were generated according to an aerodynamic
$y + $
of 10, which are believed to be fine enough for both aerodynamics and hydrodynamics. A dynamic mesh strategy [Reference Xiao, Lu, Deng, Zhi, Zhu and Chen10] was used to handle the relative motion between the fluid and the impacting objects. This approach moves or rotates the entire computational mesh rigidly with the object at each time step, based on the solution of the 6DOF model. Since neither mesh deformation nor regeneration was used, the high quality of the initial mesh remained unchanged throughout the whole simulation. As a result, the solution accuracy of both flow field and water-air interface was not degraded, even for such unsteady problems involving significant relative motion.
3.0 Results and discussion
Figure 2 presents the initial flow field of helicopter ditching on still water. In the present study, the helicopter performs a three-degree-of-freedom landing motion, involving pitch, horizontal and vertical displacement, while ignoring the lift of rotor during this process. To optimise computational efficiency, a half model is employed for the present numerical simulation. Furthermore, to simplify the model, the effects of the rotor and other components are not omitted. Detailed dimensions of the helicopter model are summarised in Table 1.
Figure 2. Computational domain and boundary conditions.
Table 1. Parameters of the helicopter model
The dimension of the computational domain and the boundary conditions for the helicopter ditching scenario are depicted in Fig. 2. The computational domain is configured as a cuboid with a size of
$4 \times 1 \times 4L$
in length, width and height, respectively. To accurately capture the water-air interface, the Cartesian grid, due to its inherent high orthogonality and anisotropic features, is a better choice compared with other grid types, especially for complex-shaped models. Consequently, the region around the helicopter and meshes near the air-water interface are particularly refined in
$x - $
and
$z - $
directions for the sake of capturing the interface more accurately. In the previous study [Reference Xiao, Lu, Deng, Zhi, Zhu and Chen10], hydrodynamic characteristics of a helicopter ditching on both still and wavy water were numerically investigated. The verification and validation of the numerical method were already performed as part of that work. Specifically, the high-speed three-dimensional flat plate ditching experiment [Reference Iafrati, Grizzi and Olivieri25] was employed to validate the feasibility and accuracy of the numerical method. The mesh resolution of the water-air interface was determined through verification of the wave generation, and the appropriate time-step size was selected based on the temporal convergence study for ditching on still water. As a continuous investigation of the previous one, the computational model, grid resolution and time-step size adopted in the present work are same. Thus, meshes inside the refined zone are 0.0525 m (
${\rm{\Delta }}x$
) and 0.0125 m (
${\rm{\Delta }}z$
), with
${\rm{\Delta }}t = 5 \times {10^{ - 4}}$
s. The total number of grid is approximately 10 m. Additionally, to compare the dynamic behaviour of the helicopter ditching for various initial velocities and pitching angles in a consistent way, the initial drop height of the helicopter ditching on still water is confined to the same small distance.
3.1 Effect of initial downward velocity
Firstly, the effect of initial downward velocity on the hydrodynamic characteristics of helicopter ditching is discussed. Note that the initial pitch angle of the helicopter
${\theta _0}$
is set at
${6^ \circ }$
and the initial downward velocity
${\upsilon _{z0}}$
varies from 1 to 4m/s, with intervals of 1m/s. While the actual variation range of
${\upsilon _{z0}}$
is relatively narrow, we intentionally extend the range of
${\upsilon _{z0}}$
during simulation to assess the validity of the theoretical relationship comprehensively.
The comparison of vertical acceleration
${a_z}$
for different
${\upsilon _{z0}}$
is shown in Fig. 3(a). Note that Lowess smoothing methods are employed herein, since it is particularly effective for detecting trends in noisy data, especially when dealing with a large number of data points. Depending on the data distribution in different cases, the proportion for span varies from 0.03 to 0.2. Due to the presence of small wings on both sides of the helicopter, there are slight variations in acceleration at the early stage. However, the overall trend still adheres to the principles of free-falling water entry motion. It can be observed that
${a_z}$
increases with
${\upsilon _{z0}}$
and achieves its maximum value in a shorter duration. Then, the peak vertical acceleration
${a_{z{\rm{max}}}}$
is extracted from Fig. 3(a) and associated with
${\upsilon _{z0}}$
, as presented in Fig. 3(b). It is worth noting that
${a_{z{\rm{max}}}}$
exhibits a linear relationship with the square of the initial downward velocity
$\upsilon _{z0}^2$
, expressed as
${a_{z{\rm{max}}}} = 10.0841\upsilon _{z0}^2 - 1.5655$
. Furthermore, by combining the theoretical relationship (Equation 2 mentioned in Section 2.1), the shape factor
$S\left( {\gamma, \beta, M} \right)$
is obtained as 4.1311, which will be used in the following discussions concerning other kinematic parameters.
Figure 3. Effect of initial downward velocity on vertical acceleration for helicopter ditching with
${\theta _0} = {6^ \circ }$
. (a) time histories of
${a_z}$
, and (b) relationship between
${a_{z{\rm{max}}}}$
and
${\upsilon _{z0}}$
.
Figure 4 presents the effect of initial downward velocity on other kinematic parameters (
${t^{\rm{*}}}$
,
${z^{\rm{*}}}$
,
$\upsilon _z^{\rm{*}}$
, and
$\kappa $
) when maximum vertical acceleration is achieved. As shown in Fig. 4(a), it is evident that the corresponding time
${t^{\rm{*}}}$
is a linear function of
$\upsilon _{z0}^{ - 1}$
. In addition, substituting the shape factor
$S\left( {\gamma, \beta, M} \right) = 4.1311$
into Equation (4), the expression of
${t^{\rm{*}}}$
is derived as
${t^{\rm{*}}} = 0.0245{\upsilon _{z0}}$
. Comparing the theoretical predictions with the numerical results, as shown in Fig. 4(a), a good agreement can be observed with the error
$\mu $
being less than 10
${\rm{\% }}$
.
Figure 4. Effect of initial downward velocity on variable dynamic parameters for helicopter ditching with
${\theta _0} = {6^ \circ }$
. (a)
${t^{\rm{*}}}$
, (b)
${z^{\rm{*}}}$
, (c)
$\upsilon _z^{\rm{*}}$
, and (d)
$\kappa $
.
Observing the corresponding penetration depth
${z^{\rm{*}}}$
in Fig. 4(b), it can be seen that as
${\upsilon _{z0}}$
increases,
${z^{\rm{*}}}$
shows a gradually decreasing trend and eventually approaches a constant value. Particularly, in the case of small
${\upsilon _{z0}}$
, the gravity effect can be observed, which is similar to the findings of Lu et al. [Reference Lu, Del Buono, Xiao, Iafrati, Deng and Xu21]. By substituting the shape factor
$S\left( {\gamma, \beta, M} \right) = 4.1311$
into Equation (3), the corresponding penetration depth
$z_{{\rm{theory}}}^{\rm{*}} = 0.0229$
is obtained, which is slightly different from the present numerical results shown in Fig. 4(b). In general, the prediction accuracy of
${z^{\rm{*}}}$
using the theoretical formula in Equation (3) is adequate, with an error of less than 10
${\rm{\% }}$
.
Another parameter describing the ditching performance of the helicopter, the corresponding downward velocity
$\upsilon _z^{\rm{*}}$
, is shown in Fig. 4(c). It can be seen that
$\upsilon _z^{\rm{*}}$
exhibits a linear relationship with the initial downward velocity
${\upsilon _{z0}}$
, expressed as
$\upsilon _z^{\rm{*}} = 0.8027{\upsilon _{z0}} + 0.1041$
. Since the theoretical relationship between these two parameters remains unaffected by the shape parameters, the theoretical solution
$\upsilon _z^{\rm{*}} = 5{\upsilon _{z0}}/6$
is illustrated by a blue dashed line in Fig. 4(c). It can be observed that the theoretical solution aligns closely with the numerical results. The variation of
$\kappa $
, as depicted in Fig. 4(d), can be further used to investigate this linear relationship. As
${\upsilon _{z0}}$
increases, the value of
$\kappa $
gradually decreases, and when
${\upsilon _{z0}}$
is greater than 2.5m/s,
$\kappa $
gradually approaches the theoretical value 5/6. It is worth noting that at low initial downward velocity, the numerical results of
$\kappa $
and
${z^{\rm{*}}}$
significantly deviate from the respective approaching values, indicating the presence of gravity effect observed in the two-dimensional scenario [Reference Lu, Del Buono, Xiao, Iafrati, Deng and Xu21], also prevalent in the case of the three-dimensional helicopter ditching with low velocity.
Furthermore, the comparison of variation in the pitching angle
$\theta $
for different
${\upsilon _{z0}}$
cases is shown in Fig. 5(a). It can be observed that the pitching angle of helicopter initially decreases and then increases after contacting the water. The initial decrease in pitching angle occurs because the first landing point of the body is behind the centre of gravity. Consequently, due to the combination of fluid force and gravity, a negative angular acceleration is generated, as shown in Fig. 5(b). Looking at both Fig. 5(a) and (c), it becomes apparent that when
${a_z}$
reaches its maximum value, the corresponding pitching angle and horizontal velocity for all cases are almost identical, differing only in the corresponding downward velocity
$\upsilon _z^{\rm{*}}$
(see Fig. 4c).
Figure 5. Effect of initial downward velocity on pitching angle and horizontal velocity for helicopter ditching with
${\theta _0} = {6^ \circ }$
. (a) time histories of
$\theta $
, (b)
${\dot \omega _y}$
, and (c)
$\upsilon _x^{\rm{*}}$
.
Pressure distribution and water deformation for different initial downward velocities of the helicopter when
${a_z}$
reaches its maximum are presented in Fig. 6, where the pressure coefficient
${C_p}$
is defined as
${C_p} = \left( {p - {p_0}} \right)/\left( {0.5\rho \upsilon _{x0}^2} \right)$
. Note that
$\upsilon _x^{\rm{*}}$
is relatively small for all cases, thus
${\upsilon _{x0}}$
is used herein. Because it can be seen that the small wings on the two sides of the body participate in the ditching process, providing static buoyancy in the case of a shallow draft. This observation can also elucidate the slight discrepancies between the numerical and theoretical results regarding
${z^{\rm{*}}}$
(see Fig. 4b). Additionally, comparing Fig. 6(a) and (f), it is notable that bubbles are generated at the bottom of the body during high-velocity ditching, whereas they are less prominent at low-velocity ditching. It is worth noting that, despite variation in magnitude, a similar pressure distribution phenomenon can be observed on the bottom surface of the fuselage under different conditions, that is an over-pressure appeared in the front area and a negative pressure formed in the rear area. The presence of the negative pressure zone leads to a gradual increase in the angular acceleration
${\dot \omega _y}$
(see Fig. 5b), consequently resulting in an increase in the pitching angle of the helicopter. This phenomenon also explains the initial decrease and subsequent increase in the pitching angle described in Fig. 5(a).
Figure 6. Pressure distribution and water deformation for different initial downward velocities of helicopter when
${a_z}$
reaches its maximum.
To gain a better understanding of the negative pressure, the distributions of downward and horizontal velocities on the longitudinal section for different initial downward velocities of the helicopter when
${a_z}$
reaches its maximum are presented in Figs 7 and 8, respectively. Note that both the downward and horizontal velocities are dimensionless, relative to the initial downward and horizontal velocities for each condition.
Figure 7. Downward velocity distribution on longitudinal section for different initial downward velocity of helicopter when
${a_z}$
reaches its maximum.
Figure 8. Horizontal velocity distribution on longitudinal section for different initial downward velocities of helicopter when
${a_z}$
reaches its maximum.
Regarding the downward velocity distribution, due to the motion of the fuselage, the fluid below the bottom surface of the fuselage acquires a body-following downward velocity, while the fluid on both sides moves along the body’s surface. At this moment, the body can be considered as an asymmetric wedge entering the water. Since the angle between the body surface and the free surface on the left side is larger than the right side, the fluid tends to move upward along the left side surface, especially during the water entry of the asymmetric wedge with horizontal velocity. In addition, from the magnitude and distribution of downward velocity, the darker colour in the smaller velocity condition indicates a larger ratio of
${\upsilon _z}/{\upsilon _{z0}}$
. However, in the case of larger velocities (such as in Fig. 7d, e and f), the distribution of downward velocity is nearly same, which is consistent with the change of
$\kappa $
shown in Fig. 4(d).
Moving to horizontal velocity distribution (see Fig. 8), the direction of horizontal motion points to the right side. A similar phenomenon can be observed in the fluid at the front part of the bottom surface of the fuselage, consistent with the flat plate ditching scenario [Reference Iafrati26]. However, in the rear area, due to the upward contraction of the longitudinal section line of the fuselage, the nearby fluid has more space to develop and quickly escapes in the opposite direction of the body motion, generating a larger relative velocity compared with the velocity of fuselage. In general, a larger relative motion velocity in both vertical and horizontal directions is generated near the rear part, while the front area exhibits relative velocity mainly in the vertical direction. It can be concluded that the formation of the negative pressure area is primarily related to the relative motion between the fluid and the body, that is, a larger relative velocity is more likely to generate a negative pressure area. For the helicopter ditching event, the negative pressure is mainly concentrated in areas where longitudinal section curve of the fuselage changes drastically. Therefore, reasonable control of the longitudinal section curve can effectively suppress or utilise the negative pressure area.
Due to the helicopter ditching with an initial horizontal velocity, it is necessary to further discuss the horizontal acceleration
${a_x}$
. Time histories of
${a_x}$
for different cases of
${\upsilon _{z0}}$
are presented in Fig. 9(a). It can be observed that
${a_x}$
increases with
${\upsilon _{z0}}$
, reaching its peak value in a relatively short time period, similar to the behaviour of
${a_z}$
(see Fig. 3(a)). The maximum accelerations
${a_{x{\rm{max}}}}$
are then collected and associated with the initial downward velocity
${\upsilon _{z0}}$
, as shown in Fig. 9(b). It is found that
${a_{x{\rm{max}}}}$
is a linear function of
${\upsilon _{z0}}$
itself, which contrasts with the law observed in the wedge oblique entry scenario, where
${a_{x{\rm{max}}}}$
is linearly related to
$\upsilon _{z0}^2$
[Reference Lu, Del Buono, Xiao, Iafrati, Deng and Xu21]. A reasonable explanation for this difference is that the three-dimensional effect and the negative pressure at the rear part of the fuselage collectively weaken the hydrodynamic forces.
Figure 9. Effect of initial downward velocity on horizontal acceleration for helicopter ditching with
${\theta _0} = {6^ \circ }$
. (a) time histories of
${a_x}$
, and (b) relationship between
${a_{x{\rm{max}}}}$
and
${\upsilon _{z0}}$
.
Besides, comparing the time instants when
${a_{z{\rm{max}}}}$
and
${a_{x{\rm{max}}}}$
occur, as shown in Fig. 10(a), it is found that
${a_{x{\rm{max}}}}$
appears later than
${a_{z{\rm{max}}}}$
, and the interval time
${\rm{\Delta }}{t^{\rm{*}}}$
between the two peak values gradually shortens with the increase of
${\upsilon _{z0}}$
. Combined with Figs 5(a) and 10(b), it can be observed that when the horizontal acceleration reaches its maximum value, the pitching angle
$\theta $
, corresponding horizontal velocity
$\upsilon _x^{\rm{*}}$
, and corresponding penetration depth
${z^{\rm{*}}}$
for all cases are nearly the same, which is consistent with the behaviour observed in the case of
${a_{z{\rm{max}}}}$
.
Figure 10. Effect of initial downward velocity on variable dynamic parameters for helicopter ditching with
${\theta _0} = {6^ \circ }$
when
${a_x}$
reaches its maximum. (a)
${\rm{\Delta }}{t^{\rm{*}}}$
, and (b)
$\upsilon _x^{\rm{*}}$
and
${z^{\rm{*}}}$
.
3.2 Effect of initial pitching angle
When the helicopter attempts to ditch on the water surface with different initial pitching angles, the front and rear angles between the bottom surface of the fuselage and the free surface also change accordingly. Viewed from the longitudinal plane, its initial situation resembles that of an asymmetric wedge water entry problem, as shown in Fig. 11. Therefore, the study on the impact of pitching angle on helicopter ditching begins with analysing the hydrodynamic characteristics of the asymmetric wedge vertical water entry, aiming to explain the effect of pitching angle on hydrodynamic load. Moreover, in order to mimic the water landing process of the helicopter with different pitching angles as accurately as possible, an asymmetric wedge is constructed with a constant vertex angle, height
$h$
and mass
$M$
. Only the deadrise angles on both sides of the wedge are altered, with the left and right deadrise angles denoted as
${\beta _{\rm{L}}}$
and
${\beta _{\rm{R}}}$
, respectively.
Figure 11. Relation between helicopter ditching and asymmetric wedge impacting.
3.2.1 Simplification in asymmetric wedge
Note that only vertical motion is considered for the asymmetric wedge, with an initial vertical velocity of 5.5m/s and a mass
$M$
=4.6842kg/m [Reference Lu, Del Buono, Xiao, Iafrati, Xu, Deng and Chen22]. Time histories of
${a_z}$
are shown in Fig. 12. It can be observed that the larger the difference between
${\beta _{\rm{L}}}$
and
${\beta _{\rm{R}}}$
, the higher
${a_{z{\rm{max}}}}$
becomes. Particularly, when
${\beta _{\rm{L}}}$
equals
${\beta _{\rm{R}}}$
, the value of
${a_{z{\rm{max}}}}$
is the smallest one for all cases. It can be further explained through the pressure distribution around the wedge, as shown in Fig. 13. Turning to helicopter ditching scenario with different pitching angles, the body with a larger pitching angle could attain a moderate vertical acceleration to some extent. However, in practical engineering problems, when aiming for a smaller landing acceleration, the range of pitching angles will be restricted by other factors, such as pitching moment and the safety distance between the tail wing and the water surface, et al.
Figure 12. Effect of deadrise angle
$\beta $
on
${a_z}$
for asymmetric wedge impacting.
Figure 13. Pressure distribution for different deadrise angle of asymmetric wedge when
${a_z}$
reaches its maximum.
By observing the relationship between
${a_{z{\rm{max}}}}$
and the deadrise angles on both sides (
${\beta _{\rm{L}}}$
and
${\beta _{\rm{R}}}$
) in Fig. 12, and referring to the combined method for symmetric wedge water entry proposed by Lu et al. [Reference Lu, Del Buono, Xiao, Iafrati, Xu, Deng and Chen22], it becomes meaningful to extend the combined method to the study of an asymmetric wedge. This extension aims to quantitatively analyse the relationship among
${a_{z{\rm{max}}}}$
,
${\beta _{\rm{L}}}$
and
${\beta _{\rm{R}}}$
. Based on the assumption of the combined method, the definition of added mass mainly depends on the semi-wet width
$r$
of the wedge. However, for the asymmetric wedge, the wet widths
${r_{\rm{L}}}$
and
${r_{\rm{R}}}$
on both sides are not the same. To address this, the concept of the average semi-wet width, proposed by Ghadimi et al. [Reference Ghadimi, Tavakoli, Dashtimanesh and Taghikhani27], can be introduced:
\begin{align}\mathop r\limits^\_ = \frac{1}{2}\left( {{r_{\rm{L}}} + {r_{\rm{R}}}} \right) \end{align}
According to the relation of
$r$
and
$z$
in the case of wedge water entry (see Fig. 1), Equation (13) can be rewritten as:
\begin{align}\frac{z}{{{\rm{tan}}\mathop \beta \limits^\_ }} = \frac{1}{2}\left( {\frac{z}{{{\rm{tan}}\,{\beta _{\rm{L}}}}} + \frac{z}{{{\rm{tan}}\,{\beta _{\rm{R}}}}}} \right) \end{align}
where
$\bar \beta $
represents the average deadrise angle. Removing the parameter
$z$
, it can be expressed as:
\begin{align}{\rm{tan}}\,\bar \beta {\rm{ }} = \frac{{2 \cdot {\rm{tan}}{\beta _{\rm{L}}} \cdot {\rm{tan}}{\beta _{\rm{R}}}}}{{{\rm{tan}}{\beta _{\rm{L}}} + {\rm{tan}}{\beta _{\rm{R}}}}} \end{align}
At this point, considering both the influence of
${\beta _{\rm{L}}}$
and
${\beta _{\rm{R}}}$
, Equation (15) provides a new quantitative relationship to unify the two different deadrise angles. For
${\beta _{\rm{L}}}$
and
${\beta _{\rm{R}}}$
respectively, according to Dobrovol’skaya’s theoretical solution [Reference Dobrovol’skaya28, Reference Zhao and Faltinsen29], the relationship between
$\gamma $
and deadrise angle
$\beta $
in Fig. 14(a) is obtained. However, it is challenging to obtain an effective pile-up coefficient for the asymmetric wedge. Referring to the theoretical formula of the pile-up coefficient mentioned in the work of Lu et al. [Reference Lu, Del Buono, Xiao, Iafrati, Xu, Deng and Chen22], and substituting the average deadrise angle
$\bar \beta $
, the average pile-up coefficient
$\bar \gamma $
is obtained as follow:
\begin{align} \mathop \gamma \limits^\_ = \frac{{{a_{z{\rm{max}}}}}}{{\upsilon _{z0}^2{{\left( {\frac{5}{6}} \right)}^3}\sqrt {\frac{{2\pi \rho }}{{5M}}} }} \cdot {\rm{tan}}\!\left( {\mathop \beta \limits^\_ } \right) \end{align}
Figure 14. Relationship between average pile-up coefficient
$ \bar \gamma $
and average deadrise angle
$\bar \beta $
for asymmetric wedge. (a)
$\gamma $
and
$\beta $
, and (b)
$\bar \gamma $
and
$\bar \beta $
.
By substituting the peak acceleration values obtained from present CFD results (seen in Fig. 12) into Equation (16), the relationship between
$ \bar \gamma $
and
$\bar \beta $
applicable for the water entry of the asymmetric wedge is derived, as shown in Fig. 14(b). The fitting relationship is expressed as
$ \mathop {\,\gamma }\limits^\_ = - 0.3245\,{\rm{tan}}\!\left( {\mathop \beta \limits^\_ } \right) + 1.3841 $
, exhibiting behaviour similar to that observed in the case of symmetric wedge water entry as described in Ref. (Reference Lu, Del Buono, Xiao, Iafrati, Xu, Deng and Chen22). Similarly, the expression for
${a_{z{\rm{max}}}}$
for the asymmetric wedge can be derived, as well as
${z^{\rm{*}}}$
,
$\upsilon _z^{\rm{*}}$
, and
${t^{\rm{*}}}$
:
\begin{align}{a_{z{\rm{max}}}} = \upsilon _{z0}^2{\left( {\frac{5}{6}} \right)^3}\frac{{\bar \gamma }}{{{\rm{tan}}\!\left( {\bar \beta } \right)}}\sqrt {\frac{{2\pi \rho }}{{5M}}} \\[-24pt] \nonumber \end{align}
\begin{align}{z^{\rm{*}}} = \sqrt {\frac{{2M}}{{5\pi \rho {{\bar \gamma }^2}}}} {\rm{tan}}\!\left( {\bar \beta } \right) \\[-24pt] \nonumber \end{align}
\begin{align}\upsilon _z^{\rm{*}} = \frac{5}{6}{\upsilon _{z0}} \\[-24pt] \nonumber \end{align}
\begin{align} {t^{\rm{*}}} = \frac{1}{{{\upsilon _{z0}}}}\frac{{16}}{{15}}\sqrt {\frac{{2M}}{{5\pi \rho {{\bar \gamma }^2}}}} {\rm{tan}}\!\left( {\bar \beta } \right) \end{align}
Figure 15 shows the effect of average deadrise angle
$\bar \beta $
on the maximal vertical acceleration
${a_{z{\rm{max}}}}$
and the corresponding parameters, such as the penetration depth
${z^{\rm{*}}}$
, velocity
$\upsilon _z^{\rm{*}}$
and time
${t^{\rm{*}}}$
. As it can be seen in Fig. 15(a),
${a_{z{\rm{max}}}}$
is a linear function of
$\bar \beta $
, and the numerical results are highly consistent with the theoretical estimates. Note that the average pile-up coefficient
$\bar \gamma $
used in the theoretical estimates is obtained from the fitting relationship
$\bar \gamma = - 0.3245\,{\rm{tan}}\!\left( {\bar \beta } \right) + 1.38415$
in Fig. 14(b). In Fig. 15(b), the numerical results of
$\kappa $
float around the theoretical value of 5/6, with a root mean square error (RMSE) of 0.004. Similarly, the numerical results of
${t^{\rm{*}}}$
and
${z^{\rm{*}}}$
fluctuate near the theoretical solution. It can be concluded that the validity and accuracy of the proposed theoretical Equation (17) for the asymmetric wedge are sufficient.
Figure 15. Effect of average deadrise angle on variable dynamic parameters for asymmetric wedge impacting. (a)
${a_{z{\rm{max}}}}$
, (b)
$\kappa $
, (c)
${t^{\rm{*}}}$
, and (d)
${z^{\rm{*}}}$
.
3.2.2 Case for helicopter
Based on the aforementioned research on the hydrodynamic characteristics of helicopter ditching on still water with varying initial downward velocities and asymmetric wedge water entry with different deadrise angles, the effect of the initial pitching angle
${\theta _0}$
on the ditching performance of the helicopter with various initial downward velocities
${\upsilon _{z0}}$
is fully discussed, as shown in Fig. 16. In Fig. 16(a), it can be observed that for different cases of
${\theta _0}$
,
${a_{z{\rm{max}}}}$
still maintains a linear quantitative relationship with
$\upsilon _{z0}^2$
, with the slope value of the linearity decreasing as
${\theta _0}$
increases. Specifically, under the same value of
${\upsilon _{z0}}$
, a relatively larger
${\theta _0}$
can result in a smaller
${a_{z{\rm{max}}}}$
, which is consistent with the phenomenon observed in the case of the asymmetric wedge. Since
${a_{z{\rm{max}}}}$
varies with
${\theta _0}$
, the time history of acceleration changes accordingly, impacting the time integral term of acceleration (water entry velocity). It can be used to explain the fluctuation behaviour of
$\kappa $
in Fig. 16(b).
Figure 16. Effect of
${\theta _0}$
and
${\upsilon _{z0}}$
on acceleration for helicopter ditching. (a)
${a_{z{\rm{max}}}}$
, and (b)
$\kappa $
.
Taking
${\upsilon _{z0}}$
=2 m/s as an example case, the influence of
${\theta _0}$
on the angular acceleration
${\dot \omega _y}$
and horizontal acceleration
${a_x}$
of the helicopter during the water landing process is further analysed, as shown in Fig. 17(a) and (b). A more gentle variation in
${\dot \omega _y}$
can be observed with a relatively larger
${\theta _0}$
, while the tendency of
${a_x}$
is quite different. This observation highlights the significance of considering the influence of the initial pitching angle on both vertical and horizontal accelerations comprehensively in practical engineering problems, and the initial pitching angle should be as large as possible within a reasonable range, as discussed by Xiao et al. [Reference Xiao, Lu, Deng, Zhi, Zhu and Chen10].
Figure 17. Effect of
${\theta _0}$
in the case of
${\upsilon _{z0}}$
=2 m/s. (a)
${\dot \omega _y}$
, and (b)
${a_x}$
.
Figure 18 shows the comparison of the numerical results and theoretical solutions of
${t^{\rm{*}}}$
and
${z^{\rm{*}}}$
during the water landing process of the helicopter with different initial pitching angles
${\theta _0}$
. As can be seen,
${t^{\rm{*}}}$
remains a linear function of
$1/{\upsilon _{z0}}$
, and
${z^{\rm{*}}}$
trends towards a constant value. Referring to the theoretical relationship mentioned in Section 2.1 and Fig. 16(a), the fitting relationships of
${a_{z{\rm{max}}}}$
in terms of
$\upsilon _{z0}^2$
with shape factors
$S\left( {\gamma, \beta, M} \right)$
are listed in Table 2. An increasing trend can be observed in
$S\left( {\gamma, \beta, M} \right)$
with the increase of the initial pitching angle, indicating the effectiveness of the shape factor. Subsequently, the theoretical values of
${z^{\rm{*}}}$
are computed. The comparison between the numerical and theoretical values reveals that the RMSE of
${z^{\rm{*}}}$
is very small, indicating that the theoretical solution has a high prediction accuracy.
Table 2. Comparison of theoretical results for helicopter ditching with different
${\theta _0}$
Figure 18. Comparison of theoretical solutions and numerical results. (a)
${t^{\rm{*}}}$
, and (b)
${z^{\rm{*}}}$
.
4.0 Conclusion
In the present study, effects of initial downward velocity and pitching angle on hydrodynamic behaviour during helicopter ditching have been investigated numerically and theoretically. Contributions and findings can be summarised as:
-
(1) The vertical acceleration
${a_{z{\rm{max}}}}$
exhibits a linear relationship with the square of the initial downward velocity
$\upsilon _{z0}^2$
. This linearity is consistent across various initial pitching angle
${\theta _0}$
. Besides, a higher initial pitching angle
${\theta _0}$
results in a reduced vertical acceleration
${a_{z{\rm{max}}}}$
for a given
${\upsilon _{z0}}$
, aligning with the asymmetric wedge water entry behaviour. -
(2) The theoretical approach, incorporating the shape factor
$S\left( {\gamma, \beta, M} \right)$
, effectively predicts the maximum vertical acceleration
${a_{z{\rm{max}}}}$
. The accuracy of the theoretical approach is validated by the small RMSE between numerical and theoretical values of
${z^{\rm{*}}}$
. The value of
${t^{\rm{*}}}$
as a linear function of
$1/{\upsilon _{z0}}$
and the constancy of
${z^{\rm{*}}}$
provide further validation of the theoretical predictions. -
(3) Taking the theoretical method into asymmetric wedges, the average semi-wet width and average pile-up coefficient are introduced to account for differing deadrise angles (
${\beta _{\rm{L}}}$
and
${\beta _{\rm{R}}}$
), supporting the extension of theoretical approach from symmetric wedges to asymmetric situations. -
(4) Detailed pressure distributions and velocity fields provide a foundation for designing helicopter fuselages that minimise negative pressure areas, thereby improving ditching performance.
Acknowledgements
This work has been supported by the Aeronautical Science Foundation of China (No. 20220023052001 and No. 20230023052001).
