Acronym List
- CFD
Computational Fluid Dynamics
- CIRA
Italian Center for Research in Aerospace
- CRIAQ
Consortium for Research and Innovation in Aerospace in Quebec
- CRNC
Canadian National Research Council
- ETS
Ecole de Technologie Superieure
- MDO
Multi-Disciplinary Objective
- IR
Infrared thermography
- UAV/UAS
unmanned aerial vehicle/system
NOMENCLATURE LIST
- λ
laminar to transition flow boundary parameter
- Ci
case number i
- Cd
drag coefficient
- Cl
lift coefficient
- Cp
pressure coefficient
- Count
1e−3
- Ff
fitness function
- γ
intermittency variable
- τ
transition to turbulent flow boundary parameter
- Re
reynolds number
- Trerror
absolute transition error
- UpTr
upper surface transition
- Wi
fitness function weight
- x/c
chord distribution
- y+
wall condition
1.0 INTRODUCTION
The air transportation industry is a key contributor to economic development around the world. Since the beginning of civil aviation, there has been a steady increase in the number of passengers using airplanes as a fast and safe transportation method, with airlines carrying almost three billion passengers worldwide in 2014 alone. This achievement has also transformed the air transport industry into a non-negligible source of pollution. In 2014, over 2% of the worldwide carbon dioxide emissions were attributed to commercial airline companies(1).
Today, researchers compete to find the best solutions to be applied to solve the emission problem, both on long and short terms. One such solution is the morphing of the aircraft. Aircraft morphing is not a new concept, as it was applied by the military aviation on some of their more renowned aircrafts, such as the Grumann F-14(2), the North American Aviation XB-70 Valkyrie prototype(Reference Talay3) and the AFTI/F-111 ‘Mission Adaptive Wing’(Reference Bonnema and Smith4). Recently, the concept of aircraft morphing started being researched for civil and unmanned aviation as well.
A morphing wing could allow the aircraft to fly at optimal lift-to-drag ratios for any condition encountered during flight by changing some of its wing characteristics. Researchers have proposed different technological solutions for obtaining the desired wing adaptability, and some of the concepts have achieved important theoretical performance improvements compared to the baseline design. However, the technology is still in the early stages of development, its technological readiness level is still low, and only a few concepts have sufficiently progressed to reach wind-tunnel testing, and even fewer have actually been flight tested.
For the Unmanned Aerial Vehicles, research was conducted by many teams. Some of the most interesting morphing applications were described by Sofla et al(Reference Sofla, Meguid, Tan and Yeo5) and Barbarino et al(Reference Barbarino, Bilgen, Ajaj, Friswell and Inman6) in their literature review papers. Interesting research on the effect of morphing of the UAV and UAS wing related to their aerodynamic performances was conducted by Sugar Gabor. et al(Reference Sugar Gabor, Koreanschi and Botez7,Reference Sugar Gabor, Koreanschi and Botez8) .
Pecora et al(Reference Pecora, Barbarino, Concilio, Lecce and Russo9) demonstrated the effectiveness of replacing the conventional segmented flap with a morphing compliant high-lift device, in the case of a regional transport aircraft. Bilgen et al(Reference Bilgen, Kochersberger, Diggs, Kurdila and Inman10,Reference Bilgen, Kochersberger and Inman11) also presented the concept of replacing the wing trailing-edge devices with a morphing surface, capable of achieving continuous camber variations instead of rigid deflections. The morphing system was designed to replace the ailerons of an UAV, for which it used rapid, electrical actuation mechanisms. Both wind-tunnel experiments and preliminary flight test were performed, and demonstrated the effectiveness of the concept at providing accurate roll control. Pankonien and Inman(Reference Pankonien and Inman12) presented a concept for morphing ailerons designed to replace the conventional wing control surfaces of an UAV. The aerodynamic performance of the system was evaluated using wind-tunnel testing. The experimental measurements focused on the drag coefficient penalties associated with classic control surface deflections at off-design flight conditions. The use of the morphing trailing edge achieved drag reductions of up to 20% compared to its original design, thus justifying its increased mass and complexity.
A project that was dedicated to developing a new concept of morphing wing for civil aviation was the CRIAQ 7.1 project(Reference Botez, Molaret and Laurendeau13,Reference Mamou, Mébarki, Khalid, Genest, Coutu, Popov, Sainmont, Georges, Grigorie, Botez, Brailovski, Terriault, Paraschivoiu and Laurendeau14) . This project was developed under partnership between Bombardier Aerospace, Thales Avionics Canada, Ecole de Technologie Superieure, Ecole Polytechnique and the Canadian National Research Council (CNRC). The purpose of the project was the development of a wing model capable of deforming its upper surface using controlled movement of two lines of shape-memory alloy actuators installed on the upper surface skin(Reference Grigorie, Popov, Botez, Mamou and Mébarki15,Reference Grigorie, Popov, Botez, Mamou and Mébarki16) . The morphing upper surface skin itself was developed through optimisation techniques as Carbon-Kevlar composite. The model's capabilities were tested at the CNRC subsonic wind tunnel in Ottawa, and the objective of the tests was to observe the behaviour of the flow transition with the aim to delay it. The results have shown that the wing model achieved high transition delays and the balance measurements have read drag coefficient reductions of up to 20%(Reference Coutu, Brailovski and Terriault17). A subsequent aeroelastic study proved that the morphing technique would not induce flutter phenomena during wind-tunnel testing(Reference Courchesne, Popov and Botez18). In addition, many breakthroughs were achieved in active open-loop(Reference Popov, Botez, Grigorie, Mamou and Mebarki19) and closed-loop(Reference Popov, Labib, Fays and Botez20) control using PID(Reference Popov, Botez, Grigorie, Mamou and Mebarki21), fuzzy logic and neural network controllers in wind-tunnel testing(Reference Grigorie and Botez22,Reference Grigorie, Botez and Popov23) under the auspices of this same project.
The research presented in this paper was conducted in the frame of the CRIAQ MDO 505 project ‘Morphing Architectures and Related Technologies for Wing Efficiency Improvement’. This project was an international collaboration between Canadian and Italian industry, academic and research teams. The Canadian partners were Bombardier Aerospace, Thales Canada, Ecole de Technologie Superieure (ETS), Canadian National Research Council (CNRC) and Ecole Politechnique. The Italian partners were Alenia Aermacchi, the University of Naples Federico II (UNINA) and the Italian Center for Research in Aerospace (CIRA). The purpose of the project was to develop a full-size wing-tip structure equipped with a morphing upper surface and two types of ailerons: a conventional rigid aileron and a morphing aileron. The objective of the development of such a wing tip was threefold: 1) through upper surface morphing and aileron morphing change the shape of the wing and influence its aerodynamic performances towards delay of the transition of the flow between laminar and turbulent states; 2) through optimisation of the structure and of the upper surface composite skin, maintain a wing structure that respects structural requirements for certification and remains similar to a real aircraft wing-tip structure(Reference Michaud, Joncas and Botez24,Reference Koreanschi, Henia, Guillemette, Michaud, Tondji, Gabor and Salinas25) ; and 3) demonstrate that an integrated control system for the morphing upper surface and ailerons can achieve the desired shapes obtained during numerical optimisation(Reference Kammegne, Nguyen, Botez and Grigorie26,Reference Kammegne, Belhadj, Nguyen and Botez27) .
2.0 GENERAL DETAILS ON THE MORPHING WING MODEL
The full-scale morphing wing model, as shown in Figs 1 and 2, is a structure with a 1.5 m span and a 1.5 m root chord, a taper ratio of 0.72, and leading and trailing edges sweep angles of 8°. The chord distribution of the wing model follows the one of the real wing-tip section, while the sweep angle and the spanwise twist distribution were modified (smaller twist and sweep angle) in order to reduce the structure's complexity and to obtain a flatter surface between the ribs to better observe and measure the upper surface deformation. The wing box and its internal structure (spars, ribs, and lower skin) were manufactured from aluminum alloy material, while the adaptive upper surface, which was positioned between 20% and 65% of the wing chord, was manufactured using carbon fibre composite materials(Reference Michaud28).
The deformation of skin shape, driven by actuators placed inside the wing box structure, is a function of the flight condition (defined in terms of Mach number, Reynolds number and angle-of-attack). These actuators were specifically designed and manufactured to meet the project requirements. Four electrical actuators were installed on two actuation lines; two actuators each, placed at 37% and 75% of the wing span, were fixed to the ribs and to the composite skin. Each actuator has the ability to operate independently from the others, and has a displacement range between ±3.5 mm. On each actuation line, the actuators were positioned at 32% and 48% of the local wing chord.
The aileron hinge articulation was located at 72% of the chord. Two ailerons were designed and manufactured. One aileron was structurally rigid, while the other one represented a new morphing aileron concept. Both ailerons were designed to be attached to the same hinge axis of the wing box, and both are able to undergo a controlled deflection between −7° and +7°. This interval was more restricted than the normal deflection range of an aileron, but it was considered sufficient to demonstrate the proof of concept for the morphing aileron. This restriction was determined by the available space inside the NRC wind tunnel and by the load limits of the wind tunnel balance. Figure 3 presents the morphing wing model concept as it would be mounted and tested in the NRC subsonic wind tunnel.
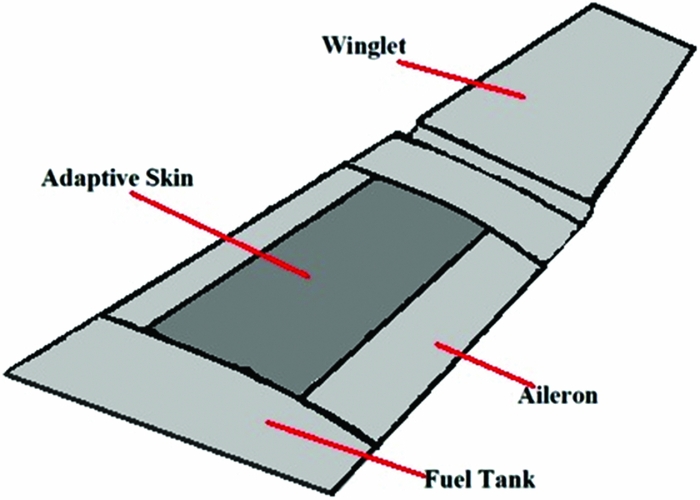
Figure 1. The layout of the morphing skin on the aircraft wing.
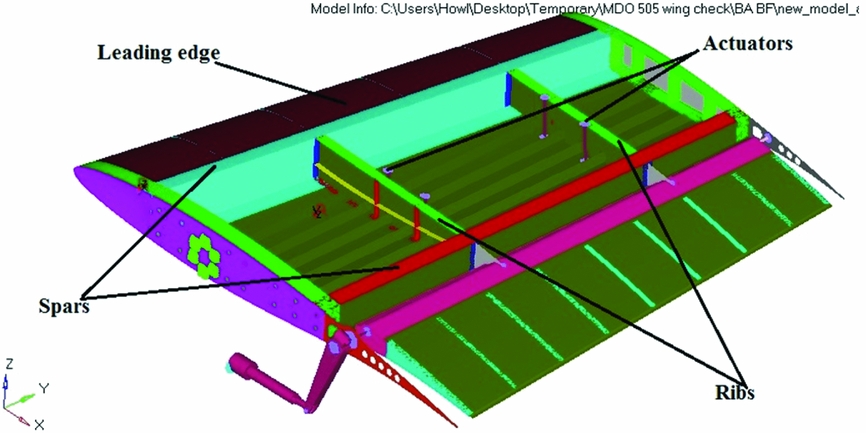
Figure 2. The structural elements of the CRIAQ MDO 505 morphing wing box (the morphing skin is not shown in the figure).
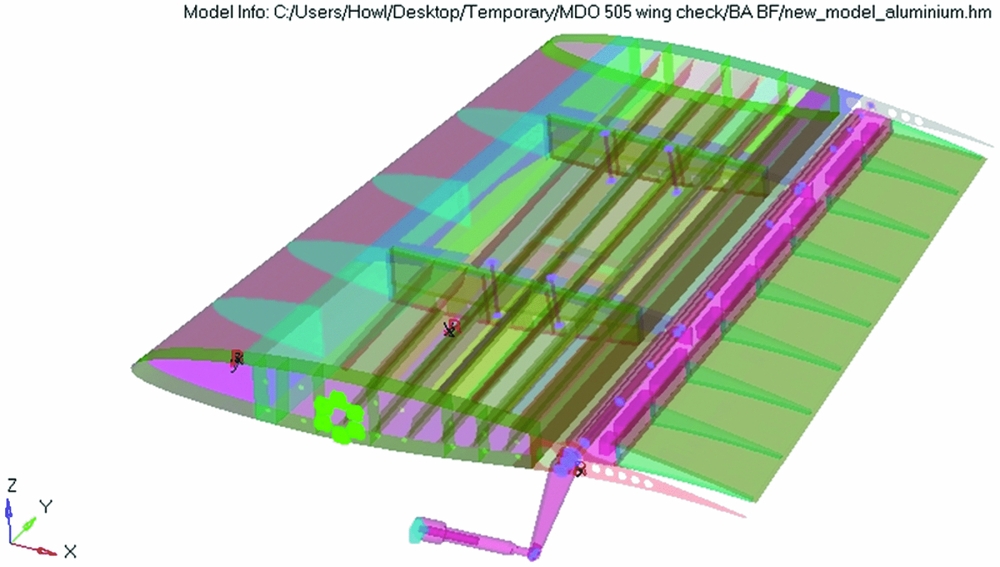
Figure 3. CRIAQ MDO 505 morphing wing model.
The control of the actuators was realized with four various controllers – PID, Fuzzy Logic and two Neural Network methods – that were integrated with the measurement systems incorporated into the model. Figure 4 presents an overview of the morphing wing control system.
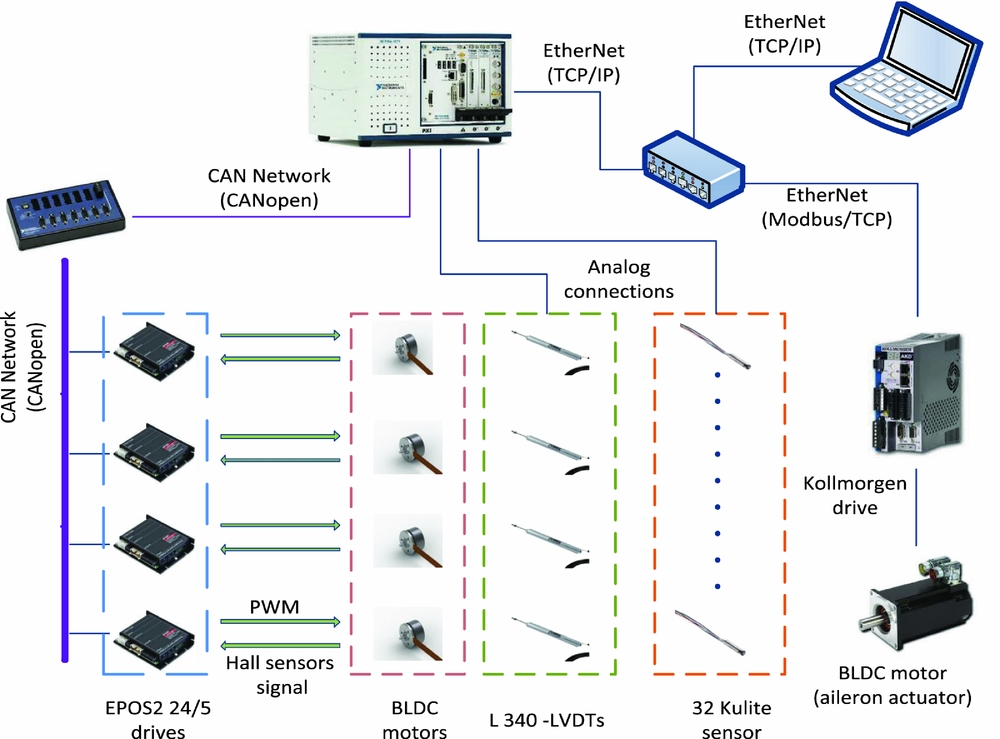
Figure 4. Overview of the morphing-wing control system.
The wing was equipped with 32 kulite pressure sensors installed on two parallel staggered lines at 60 cm from the root of the wing. Three accelerometers were installed on the wing: one each on the wing box, aileron and balance shaft, for safety purposes, by monitoring the vibration behaviour of the wing during wind-tunnel tests.
The wing tip was manufactured at NRC and ETS, and complied with the technological requirements demanded by the industrial partners.
2.1. Morphing aileron
An important component of the wing tip, with high impact on its aerodynamic performances, was the aileron. The conventional aileron, found on most aircraft wings, has a disadvantage that emboldened the research for a concept to replace it. The disadvantage of the conventional aileron lies in the manner in which it changes the camber of the wing. The aileron rotates around its hinge point, and thus creates a discontinuity of the slope of the aerofoil camber line that should be considered over the upper and lower surfaces. For high-deflection angles, this discontinuity can lead to premature boundary-layer separation and a loss of efficiency for the aileron.
Therefore, the concept of a morphing aileron has been developed to replace the conventional rigid aileron, and thus to avoid the problem of the discontinuity. In their paper, Pecora et al(Reference Pecora, Amoroso, Magnifico, Dimino and Concilio29) have demonstrated the potential of a kinematic rib-based morphing structural system for a shape changing trailing-edge device of a medium range aircraft. Dimino et al(Reference Dimino, Concilio and Pecora30) have studied the safety and reliability aspects associated with the use of morphing trailing-edge device in a flying aircraft. Also, Barbarino et al(Reference Barbarino, Pecora, Lecce, Concillio, Ameduri and De Rosa31) and Ameduri et al(Reference Ameduri, Brindisi, Tiseo, Concilio and Pecora32) have shown the possibilities of using the SMA materials when developing shape changing devices by using an aerofoil morphing model and a morphing flap device equipped with SMA actuators. Diodati et al(Reference Diodati, Concilio, Ricci, de Gaspari, Liauzun and Godard33) have analysed the performances towards fuel consumption reduction of an adaptive trailing edge for a medium-size aircraft.
Figures 5 and 6 present the morphing aileron that was developed by the Italian partners. By preserving the standard functionality as a conventional rigid aileron, morphing enabled an adaptive camber variation through a self-contained kinematics driven by electromechanical actuators. The inner structure consisted of a segmented ‘finger-like’ architecture. Each rib was divided in three blocks connected by hinges and links, enabling relative rotation among the components according to a specific gear ratio. In such a manner, the aerodynamic shapes spanned from a target baseline to morphed configuration in the range of ± 7 degrees through an un-shafted and distributed actuation(Reference Amendola, Dimino, Magnifico and Pecora34).
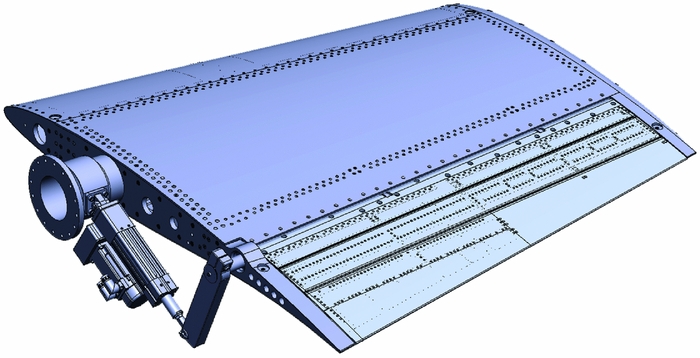
Figure 5. Morphing aileron system.
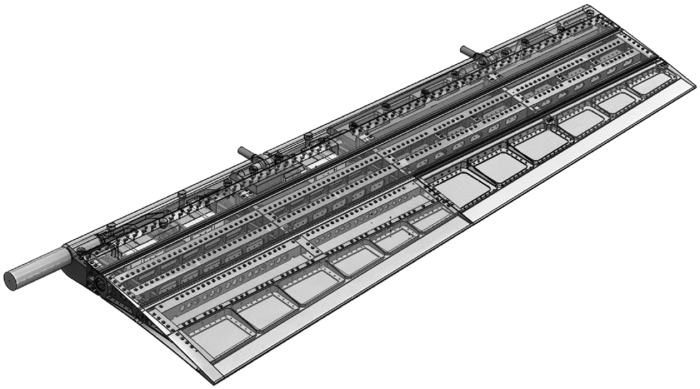
Figure 6. Morphing aileron internal structure.
3.0 SHAPE OPTIMISATION AND AERODYNAMIC ANALYSIS
3.1. Aerodynamic optimisation with genetic algorithm and Xfoil solver
During the wind-tunnel tests, both the upper surface of the wing and the aileron shapes were actively morphed based on the numerical optimisation results. The deformation of the upper surface of the wing was driven by four displacements points, resulted from the optimisation process with Genetic Algorithm. Each set was calculated for a flight condition (combination of speed, Reynolds number, angle-of-attack and aileron deflection). Each set of four numerical displacements correspond to the set of four displacements of the electrical actuators installed in the wing box. For the aileron morphing, the optimisation has provided a guiding shape for each desired deflection, while respecting constraints related to the constant thickness of the aileron, constant slope when aileron was morphing, and established convention for measuring the aileron deflection angle.
It was assumed that the central region of the wing, between the two center ribs on which the actuators were installed, would have a planar shape, thus the flow in this area would have bi-dimensional characteristics. Therefore, the optimisation was conducted on the wing's aerofoil.
All the optimisation, for both morphing upper surface and morphing aileron was performed with an ‘in-house’ developed genetic algorithm optimizer. The genetic algorithm optimizer was coupled with a cubic spline routine for upper surface aerofoil reconstruction, and with the XFoil aerodynamic solver for fast analysis of the optimisation candidates. General schematics of the optimisation software applied to the morphing wing problem are presented in Fig. 7.
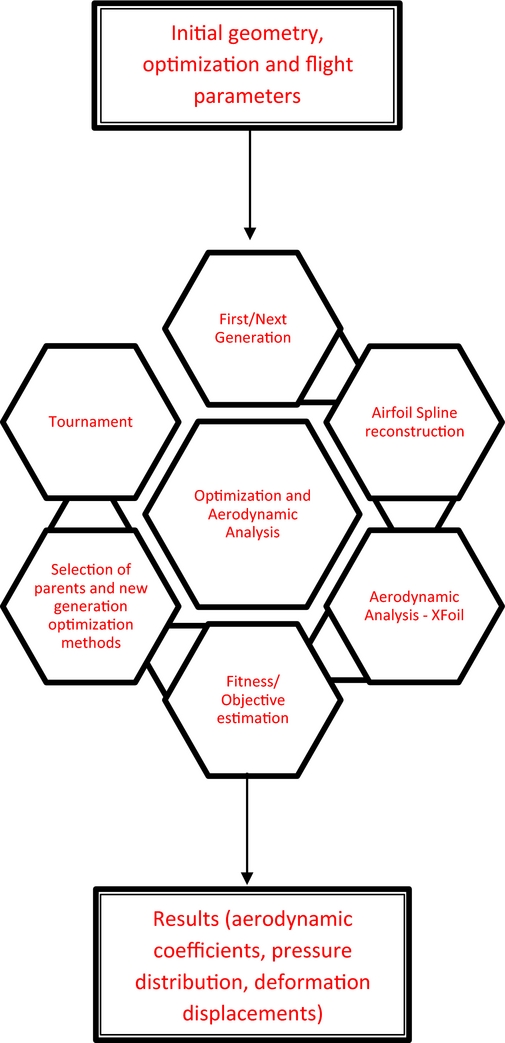
Figure 7. Genetic algorithm optimizer – General schematics.

Figure 8. Chordwise cross-section view of the mesh.
The genetic algorithm optimizer used a tournament process and a two-step cross-over function to speed up its convergence. The optimal mutation parameters, the probability and the amplitude of mutation, were defined based on percentages of the population and on the maximum displacements allowed. The optimizer was set to end the optimisation after a total of 40 generations had passed. The fitness function, Ff, was based on multiple objective functions developed from the aerodynamic parameters that were calculated by XFoil. The aerodynamic parameters are: the lift and drag coefficients, pressure distribution, skin friction coefficient and upper surface transition location.
 $$\begin{eqnarray}
{F_f} & = & {w_1} \cdot {\left( {\frac{{{C_{l\_{\rm{morphed}}}} - {C_{l\_{\rm{original}}}}}}{{{C_{l\_{\rm{original}}}}}}} \right)^{{w_2}}} + {w_3} \cdot \frac{1}{{{C_d}}} + {w_4} \cdot {\left( {\frac{{U{p_{{\rm{Tr\_morphed}}}} - U{p_{{\rm{Tr\_original}}}}}}{{U{p_{{\rm{Tr\_original}}}}}}} \right)^{{w_5}}} \nonumber\\
&& +\, {w_6} \cdot {\left( {\frac{{{{\left( {\frac{{{C_l}}}{{{C_d}}}} \right)}_{{\rm{morphed}}}} - {{\left( {\frac{{{C_l}}}{{{C_d}}}} \right)}_{{\rm{original}}}}}}{{{{\left( {\frac{{{C_l}}}{{{C_d}}}} \right)}_{{\rm{original}}}}}}} \right)^{{w_7}}} + {w_7} \cdot \frac{{U{p_{Tr}}}}{{{C_d}}}
\end{eqnarray}$$
$$\begin{eqnarray}
{F_f} & = & {w_1} \cdot {\left( {\frac{{{C_{l\_{\rm{morphed}}}} - {C_{l\_{\rm{original}}}}}}{{{C_{l\_{\rm{original}}}}}}} \right)^{{w_2}}} + {w_3} \cdot \frac{1}{{{C_d}}} + {w_4} \cdot {\left( {\frac{{U{p_{{\rm{Tr\_morphed}}}} - U{p_{{\rm{Tr\_original}}}}}}{{U{p_{{\rm{Tr\_original}}}}}}} \right)^{{w_5}}} \nonumber\\
&& +\, {w_6} \cdot {\left( {\frac{{{{\left( {\frac{{{C_l}}}{{{C_d}}}} \right)}_{{\rm{morphed}}}} - {{\left( {\frac{{{C_l}}}{{{C_d}}}} \right)}_{{\rm{original}}}}}}{{{{\left( {\frac{{{C_l}}}{{{C_d}}}} \right)}_{{\rm{original}}}}}}} \right)^{{w_7}}} + {w_7} \cdot \frac{{U{p_{Tr}}}}{{{C_d}}}
\end{eqnarray}$$
The results obtained by the optimisation were the actuators’ displacements for the upper surface skin and the morphed shapes for the morphing aileron.
The result obtained by the optimisation algorithm were compared to the results obtained with two other optimizers, the artificial bee colony and the gradient methods, which were validated with experimental results from the CRIAQ MDO 505 wind-tunnel test sessions and from other morphing wing projects(Reference Koreanschi, Sugar-Gabor and Botez35,Reference Sugar Gabor, Koreanschi and Botez36) .
In Koreanschi et al(Reference Koreanschi, Gabor, Acotto, Brianchon, Portier, Botez, Mamou and Mebarki37), the genetic algorithm used for the optimisation of the upper surface of the wing and for the aileron morphing was described in detail, with full parameters choices, fitness function, cross-over, mutation, convergence studies and comparisons with two other optimisation methods – the ABC and the Gradient methods. The optimisation model was found to be robust and reliable and its results were validated using experimental data.
3.2. CFD aerodynamic analysis - Flow equations, turbulence and transition models
CFD simulations were performed to simulate the flow past the wing under the wind-tunnel test flow conditions and setup. The dynamics of fluid flow are governed by the Navier-Stokes equations, which are representative to the fundamental principles of mass, momentum and energy conservation.
The numerical computations were performed with the ANSYS FLUENT solver(Reference Menter38). The steady-state flow equations were solved using a projection method, achieving the constraint of mass conservation by solving the pressure equation, with the pressure-velocity coupling accomplished by using a high-order Rhie-Chow scheme. The cell-face values of the pressure were interpolated using a second-order central differencing scheme, while for all other variables, including the turbulence and transition model equations, a second-order upwind scheme was used. The discrete nonlinear equations were solved in a fully implicit, coupled manner. Convergence acceleration was achieved with a coupled Algebraic Multi-Grid (AMG) approach, using a block-method Incomplete Lower-Upper (ILU) factorization scheme as the linear system smoother.
For turbulent flows, the Reynolds Averaging Navier Stokes (RANS) technique is used to decompose the instantaneous flow variables into their average values and turbulent fluctuations, while the Boussinesq eddy-viscosity hypothesis is used to relate the Reynolds stress tensor and turbulent heat flux terms to the average flow variables.
The turbulent viscosity and the kinetic energy are determined using the k − ω Shear Stress Transport (SST) model(Reference Langtry and Menter39). The SST model represents a combination of the k − ω model, used in the near wall region, and the k − ε model, used for the rest of the flow. Thus, it achieves both accurate boundary-layer representation up to the viscous sub-layer, and insensitivity to boundary conditions at free-stream flow.
In order to include the effects of laminar flow, and to model the laminar-to-turbulent transition process, the γ − Re θt model is used.
The transition onset is controlled by an empirical correlation between Re θc, the critical Reynolds number where the intermittency starts to increase in the boundary layer and ![]() $\overline {R{e_{\theta t}}} $(40). The model contains correction terms to account for laminar separation-induced transition and strong pressure-gradient flows. Coupling of the γ − Re θt transition model with the k − ω SST turbulence model is done by modifying Pk and Dk, which are the turbulent kinetic energy production and the destruction terms, and thus deactivating the turbulence model for the laminar boundary-layer region.
$\overline {R{e_{\theta t}}} $(40). The model contains correction terms to account for laminar separation-induced transition and strong pressure-gradient flows. Coupling of the γ − Re θt transition model with the k − ω SST turbulence model is done by modifying Pk and Dk, which are the turbulent kinetic energy production and the destruction terms, and thus deactivating the turbulence model for the laminar boundary-layer region.
3.3. Grid convergence study
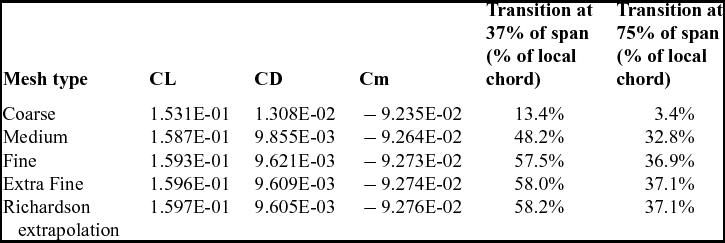
The structured meshes used for the numerical simulation were generated using the ICEM-CFD software. A grid convergence study was performed in order to evaluate the mesh density required to obtain grid-independent aerodynamic coefficients values. Four meshes of increasing cell density were generated, and each one was analysed at a Mach number of 0.15, a Reynolds number of 4.53E+06 (calculated with the wing mean aerodynamic chord) and an angle of attack of 0°. The details regarding the wall cell density for the generated meshes are presented in Table 1.
Table 1 Details about the Four Generated Meshes

The wing aerodynamic coefficients values (lift, drag and pitching moment coefficient about the root section quarter chord point) and the transition point locations on the upper surface, at 37% and 75% of the span stations are presented in Table 2. The transition point locations were determined using the intermittency variable γ distribution calculated with the γ − Re θt model. The table shows that the difference in aerodynamic coefficient values between the Fine mesh level and the Richardson extrapolation of the convergence study is less than 1%, therefore, the Fine mesh provides sufficiently accurate results. It can be observed that the γ − Re θt model requires having a good streamwise mesh refinement level prior achieving the grid convergence or the transition point location (as the grid convergence of the drag coefficient may be affected through the variation of the laminar flow region length).
Table 2 Results obtained for the grid convergence study
The characteristics of the meshes used to perform the simulations were determined based on the results of the grid convergence studies. In order to ensure that the same meshing parameters were used for all the morphed wing cases, an automatic mesh generation procedure was implemented by creating a script to be used for the ICEM-CFD code. The automatic procedure can also handle rigid aileron deflections between ±7°.
The meshes were constructed based on the Fine mesh level created for the convergence study, and include 400 cells around the wing section (200 cells on both the lower and upper surfaces), and 160 cells in the direction of the span (80 cells on both the lower and upper surfaces). The wall normal spacing was set to 3.0E-06 m, refined enough to provide the required γ + <1 condition. Figures 8 and 9 present two cross-section views of the mesh constructed around the unmorphed wing. The results provided for the unmorphed wing were also obtained for the morphed shapes of the wing.

Figure 9. Spanwise cross-section view of the mesh.
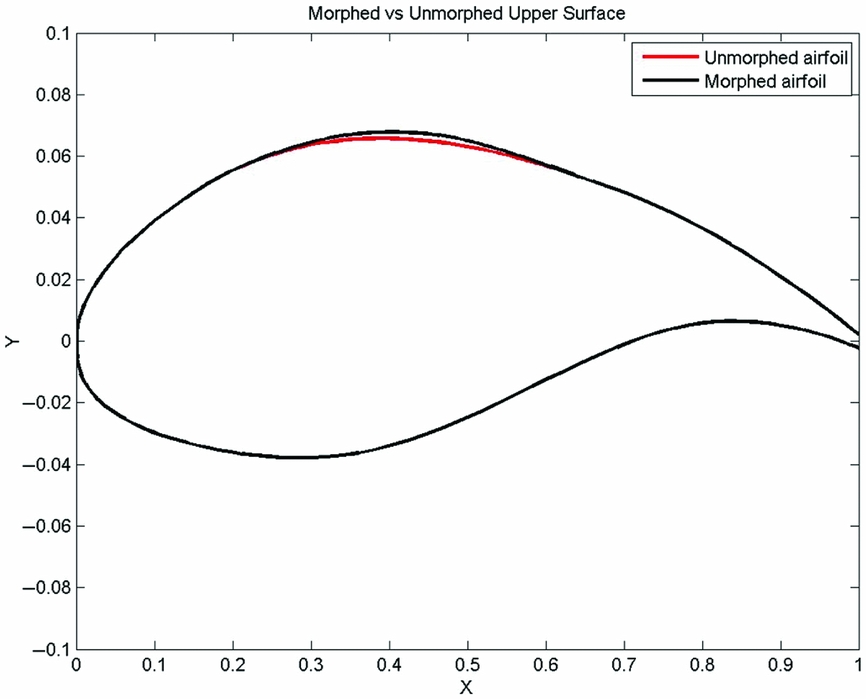
Figure 10. Unmorphed aerofoil versus Morphed aerofoil – Upper surface comparison.
4.0 MORPHED GEOMETRIES
4.1. The theoretical optimised upper surface shapes
The core concept of an active morphing of the wing upper surface is to provide an optimised aerofoil shape for each flight condition. A single-point optimisation must be performed for each combination of Mach number, Reynolds number and angle-of-attack. This procedure increases the aerodynamic performance of the shape-changing aerofoil (with respect to the desired optimisation objective) compared to the multi-point-designed baseline aerofoil.
Aerodynamic optimisations were performed to determine the actuator-driven displacements required to improve the performance of the morphing wing with respect to the original wing. In order to reduce the computational time, the aerodynamic optimisations were performed under two-dimensional flow assumption using the XFOIL solver(Reference Drela41), and an in-house genetic algorithm optimizer, for local flow conditions (local Reynolds number and angle-of-attack) calculated for the mean aerodynamic chord of the wing model(Reference Koreanschi, Sugar Gabor and Botez42).
For the numerical optimisations, the wing upper skin shapes were approximated using cubic splines, as a function of the actuator displacements. This mathematical model was chosen because it enforces the tangency condition with the rigid part of the wing aerofoil (up to the curvature continuity given by the second derivative), it provides an iso-arc-length condition and it shares mathematical properties with a beam bending under an applied load. Figure 10 presents a generic case of the unmorphed aerofoil compared with its morphed upper surface version. Due to constraints related to structural rigidity of the composite skin, the actuator displacements were limited to ±3.5 mm, while the maximum difference between the two displacements was limited to 6 mm.
4.2. Aileron optimisation
The optimisation of the aileron shape was performed using the same genetic algorithm optimizer that was developed for the upper surface morphing concept. The algorithm was applied to a series of nodes along the camber line. Each node was displaced according to the constraints and the desired deflection and the displacement of each node engendered the movement of the next node until the whole aileron shape was deformed.
For the conventional aileron, the main problem resided in the rotation of the entire control surface around its hinge point, which creates a discontinuity of the slope of the aerofoil camber line. The discontinuity is also reflected over the upper and lower surfaces of the wing and aileron articulation. At high deflection angles, the discontinuity can lead to premature boundary-layer separation, and to a loss of efficiency of the control surface.
Consistency between the conventional and the morphed ‘aileron deflection angles’ was a constraint that was taken into account. The overall aileron deflection angle, calculated as the angle between the horizontal (which is defined as the position of the aileron at zero degree deflection) and the tip of the trailing edge of the morphed aileron shape, must remain consistent to the overall deflection angle of a conventional aileron.
Another constraint was related to the ‘camber line’ of the aileron. The curvature of the camber line must maintain a constant slope direction from the articulation point to the tip of the aileron.
The aileron camber line has been divided into several chordwise sections; each defined by a starting and an ending point. The starting point of the first section coincided with the original hinge point, while the ending point of the last section coincided with the tip of the trailing edge. For each point along the camber line, two corresponding points on the upper and lower surfaces were defined based on the local thickness of the aerofoil section. In addition, for each section, the coordinates of the hinge point were calculated, so that the rotation of any section with respect to the previous section preserved the continuity of the camber line.
Using this method, the deflection of any chordwise section, with respect to the section directly upstream of it, preserves both the local thickness of the aerofoil and the length of the segment, since rotation does not modify any other geometrical characteristics. If all segments were rotated in the same direction, the overall deflection of the aileron, as measured at the trailing edge and using the original hinge point as reference, was simply the sum of all segment rotations, where each segment was rotated with reference to the segment immediately upstream of it.
By controlling the number of chordwise segments, as well as the local rotation angles for each individual segment, a great flexibility in the shape changing of the aileron could be obtained, see Fig. 11. All these degrees of freedom could be adjusted to match the technological limitations associated to the fabrication process of such an aileron.
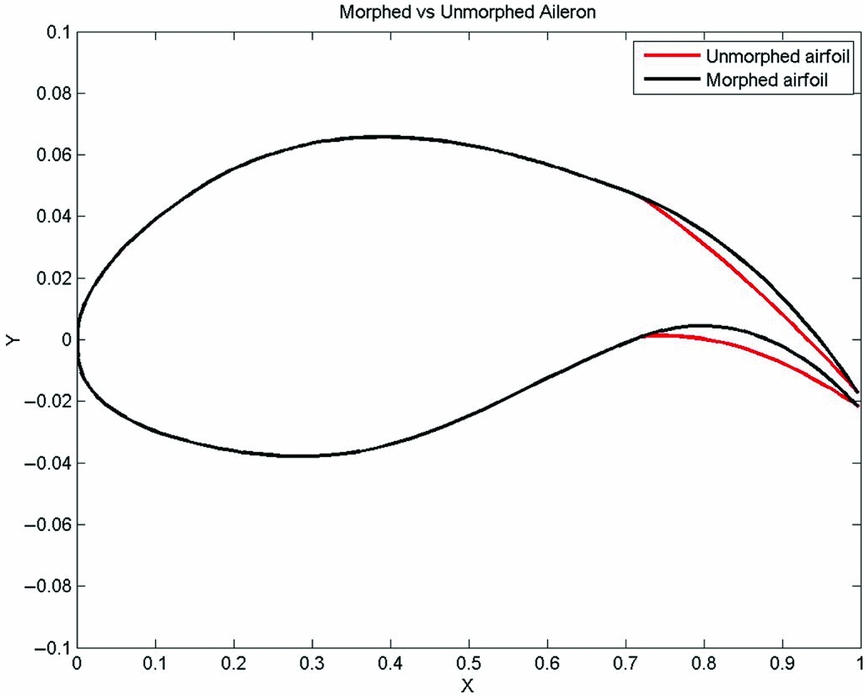
Figure 11. Unmorphed aerofoil versus Morphed aerofoil – Aileron shape comparison.
In Koreanschi et al(Reference Koreanschi, Sugar Gabor and Botez43), details on the morphing techniques used, as well as numerical comparisons, are provided for various flight cases where the wing uses the conventional and the morphing aileron in turn in combination with the upper surface morphing skin. The results have shown improvements in the lift coefficient of up to 19%, using either of the techniques presented in the paper for aileron shape determination, and it has shown the possibility of influencing the behaviour of the boundary layer and perhaps to delay its detachment.
5.0 WIND -TUNNEL TESTING
5.1. Wind-tunnel description
The wind-tunnel tests were performed at the National Research Council Canada at the 2 m × 3 m atmospheric closed-circuit subsonic wind tunnel. The atmospheric wind tunnel can operate at a maximum Mach number of 0.33.
Figure 12 presents the MDO 505 CRIAQ project morphing wing-tip model installed in the tunnel test section, viewed from both the leading edge (Fig. 12a) and the trailing edge (Fig. 12b) of the wing.

Figure 12. CRIAQ MDO 505 Project wing model setup in the wind-tunnel test section.
5.2. Data measurement tools
The upper surface flexible skin of the wing demonstrator was equipped with 32 high-precision Kulite piezoelectric-type transducers, for pressure measurement on the flexible skin. The measured pressures were processed in real time to determine the laminar-to-turbulent transition location. The sensors were installed in two chordwise staggered lines (with 16 Kulite sensors on each line), respectively at spanwise positions of 0.600 m and 0.625 m from the wing root section. In addition to the Kulite piezoelectric sensors, 60 static pressure taps were installed (30 taps on each line), on the wing leading edge, lower surface and aileron, thus providing complete experimental pressure distribution around the wing cross-section at 40% of the wing span. The pressure sensors were installed in a staggered fashion to minimise any interference in between.
Infrared (IR) thermography camera visualisations were performed for capturing the transition region over the entire wing model surface. The wing leading edge, its upper-surface flexible skin and the aileron interface were coated with high-emissivity black paint to improve the quality of the IR photographs. The spanwise stations, where the two pressure sensor lines were installed, were not painted, in order to not influence the pressure reading quality(Reference Mebarki, Mamou and Genest44).
The IR thermography visualisation allowed the identification of the transition region between laminar and turbulent regimes, based on the analysis of the model surface temperature. The turbulent flow regime increases the convective heat transfer between the model and the flow with respect to the laminar boundary layer. As a result, a flow-temperature change, introduced by the wind-tunnel heat exchanger system, will cause different temperature changes over the model, depending on the behaviour of the boundary layer (laminar, transitional and turbulent states).
Figure 13 presents an example of the IR visualisation of the wing model upper-surface transition, for one flight condition (Mach number of 0.15, angle of attack of 1° and no aileron deflection) and for both unmorphed (left figure) and morphed (right figure) skin shapes.
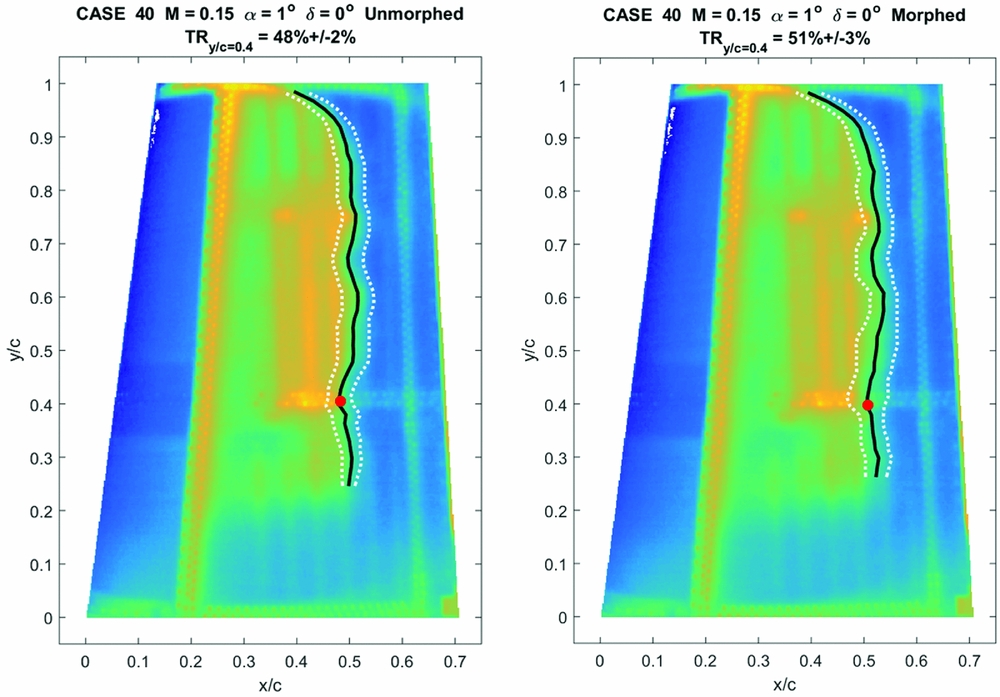
Figure 13. IR visualisation of the laminar-to-turbulent transition region on the upper surface for both unmorphed (left) and morphed (right) skin shapes.
The black line represents the average transition line on the wing upper surface, and its variation as function of the spanwise position can clearly be observed. The two dashed white lines represent the estimated extent of the transition region, determined as function of the chordwise temperature gradient existing between laminar and turbulent regimes. The transition from laminar to turbulent flow occurs over a narrow region and it was automatically detected for the wing upper surface using a MATLAB code that was specifically developed for the IR images post-processing. The red dot corresponds to the estimated transition in the spanwise section situated at 0.612 m from the root section (40% of the model span), that is half-way between the two Kulite piezoelectric pressure sensor lines. The accuracy of the transition detection for this section was estimated to ±2% of the local chord, based on the known Kulite positions and their thermal signatures in the images.
The experimental measurements also included the use of a wake rake pressure acquisition system, to measure the wing profile drag at different spanwise positions, and to use a wind-tunnel balance that had the aim to measure the aerodynamic forces and moments.
To avoid the possibility of damaging the wing-tip model during wind-tunnel testing, and to be able to observe the wing vibration behaviour, three accelerometers were installed. The three accelerometers were installed in the wing box, aileron and wind tunnel balance, respectively, as shown in Fig. 14.
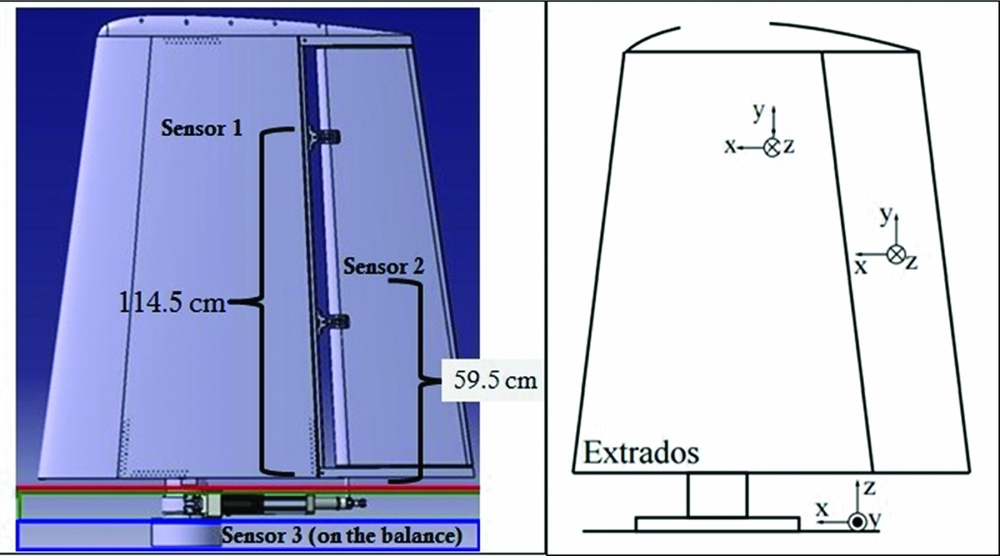
Figure 14. Positions and orientations of the accelerometers on the wing.
At the end of the second wind-tunnel set of tests the upper surface of the wing was measured using high-precision photogrammetry and the results were compared to the expected numerical values. It was expected that the morphed composite skin would reproduce the numerical shape within 0.25 mm of the desired shape along the actuator lines and under 1 mm at the center of the skin.
Figure 15 shows the scan results for the composite upper surface of the wing (the aileron is not included in scan).
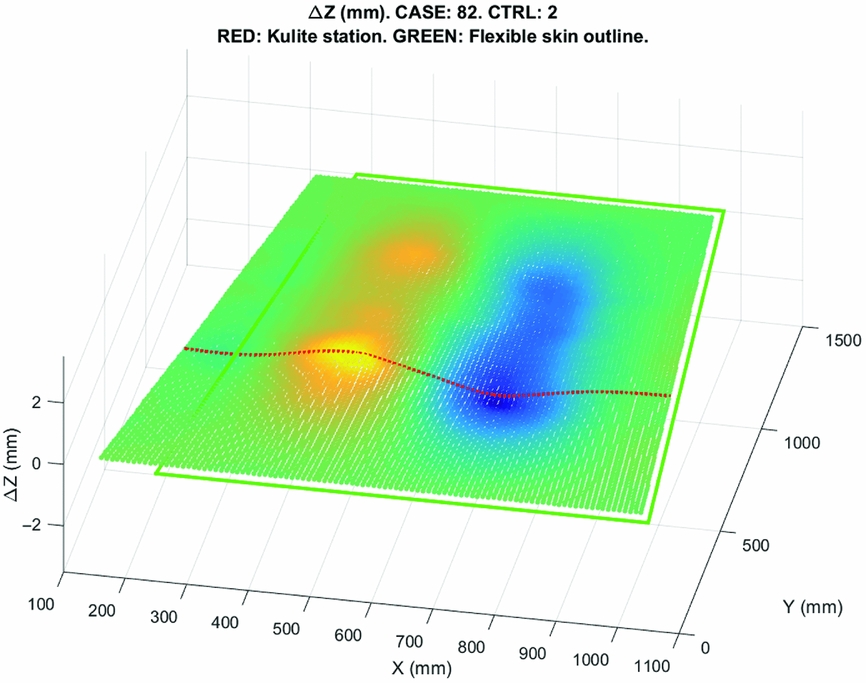
Figure 15. Photogrammetry of the composite upper surface for case 82 (M = 0.2, angle-of-attack = 5°, aileron deflection = −4°).
The deformations presented in Fig. 15 correspond to the actuator displacements presented in Table 3(a) below.
Figures 16(a), 16(b) and 16(c) present the comparison between target and the actual deformation for case 58 and 550-mm, 950-mm and 1150-mm span positions. As can be seen, the target and the real shape overlap, and the deformation was considered successful.
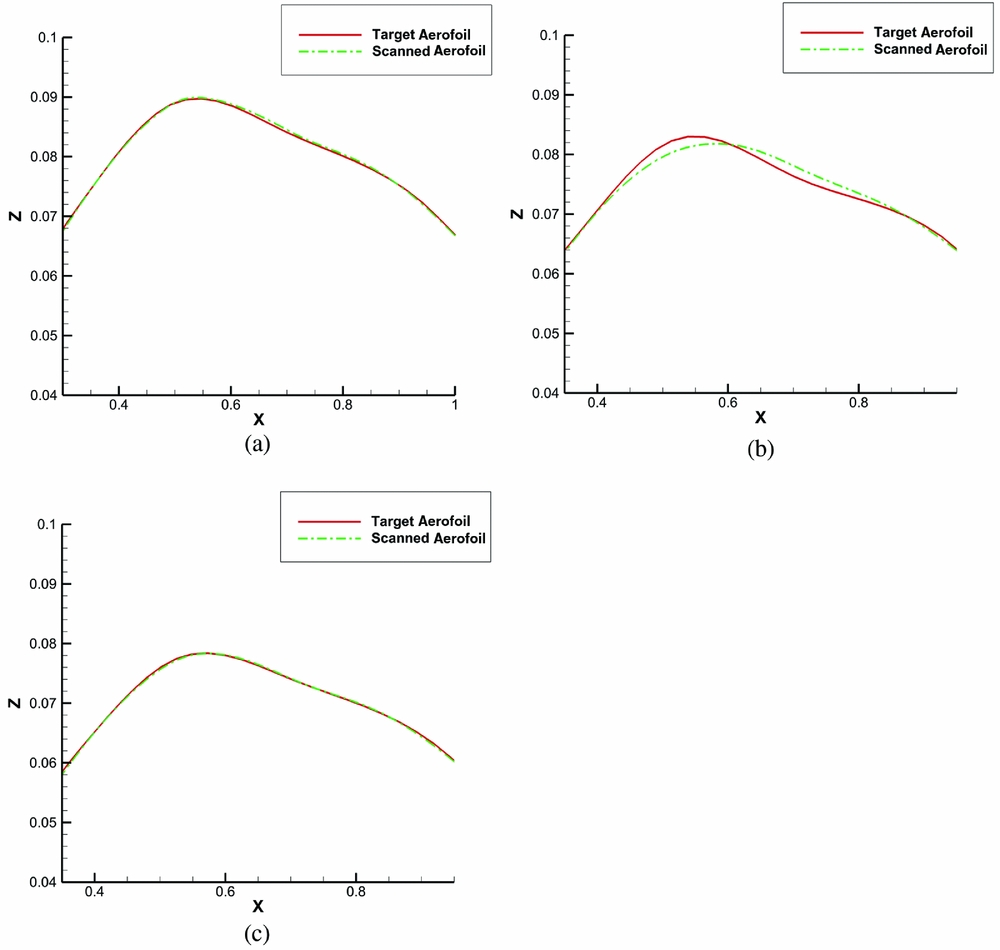
Figure 16. (a) Target versus real wing upper-surface deformation for case 58 at 550-mm span position, (b) Target versus real wing upper-surface deformation for case 58 at 950-mm span position and (c) Target versus real wing upper-surface deformation for case 58 at 1150-mm span position.
The analysis of the measurement data has shown that the composite skin along the actuator lines has reproduced the desired shape within 0.3 mm, while at the center it has less than a 1-mm variation from the desired shape. Overall, the real morphing composite skin managed to reproduce the numerical shape within the expected limits due to the precision of the controllers used and to the specific design of the composite skin.
6.0 RESULTS AND DISCUSSION
The wing demonstrator was tested during three sets of wind-tunnel tests. During the first and second sets of wind-tunnel tests, the wing was equipped with the conventional rigid aileron. During the third set of tests, the wing was equipped with the morphing aileron that was tested in conjunction with the morphing upper surface skin. The results presented in the first part of this section were obtained during the second set of wind-tunnel tests, when the wing demonstrator was equipped with the morphing upper surface and the conventional aileron. The results presented in the second part of this section, were obtained during the third set of wind-tunnel tests, when the wing demonstrator was equipped with the morphing upper surface and the morphing aileron. The first set of wind-tunnel tests, consisted of 32 cases tested for the actuators’ and aileron controllers, as well as for Infrared Imaging calibration.
6.1. Results for the second set of wind-tunnel tests–wing equipped with morphing upper surface skin and conventional aileron
The two-dimensional aerodynamic optimisations that determined the electrical actuators displacements were performed with the objective of controlling the extent of laminar flow on the upper surface of the wing model.
These optimisations were performed for several flight conditions (expressed in terms of Mach number, Reynolds number and angle-of-attack), and several rigid aileron deflection angles. A total of 97 flight cases were tested for the wing equipped with morphing upper surface skin and conventional aileron. The optimisation and testing was carried for a range of angles of attack between −5 and 5 degrees, aileron deflections between −7 and 7 and speed range between Mach 0.15 and Mach 0.25. Due to the large number of tests carried, only 22 of the cases that were optimised, analysed and experimentally tested for laminar flow increase are presented in Table 3. The Reynolds numbers that correspond to the two Mach numbers are 4.28 × 106 and 5.27 × 106. A downwards aileron deflection was considered as positive, while an upwards aileron deflection was considered as negative.
Table 3 Test cases for which the wing-tip aerofoil was optimised for laminar flow improvement
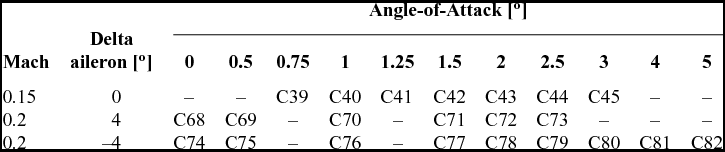
Table 3(a) Actuators’ displacements for the wind-tunnel cases presented in Table 3
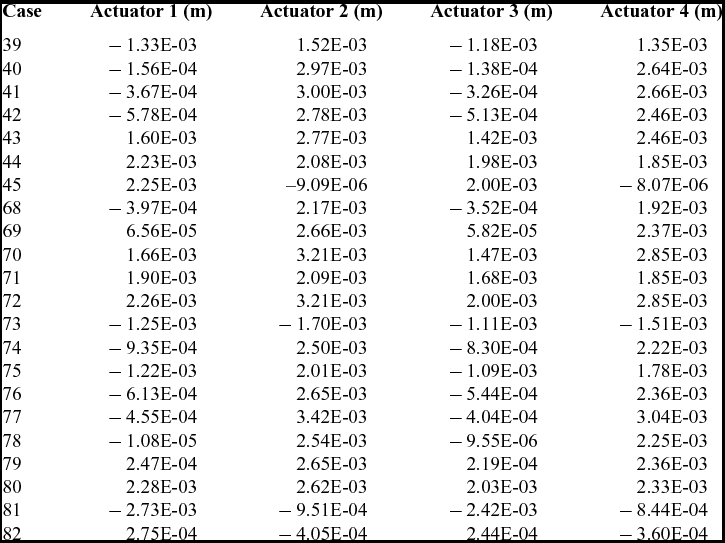
Actuators 1 and 2 are located on the first actuation line at approximately 55 cm from the wing root, and Actuators 3 and 4 correspond to the second actuation line situated at 105 cm from wing root. The order of the actuators on each line is from the leading edge, 32% of the chord, towards trailing edge, 48% of the chord.
For each case, the transition-point location on the pressure sensors line was determined from the numerical simulation, and was further compared to the experimentally measured transition location, determined using the IR thermography. The transition-point location was determined numerically by plotting the turbulence intermittency γ versus the local chord, for the upper- and lower-wing surfaces. In order to consistently extract the transition location, the first derivative of the intermittency plot was used. Since the intermittency is approximately constant for the laminar boundary layer and its value significantly increases across the transition region, the first derivative can be used to identify this high-gradient region. The transition point was considered to be the most upstream point where the derivative becomes non-zero. As an example, Fig. 17 shows the intermittency distribution at the 0.612-m spanwise section, for case C39 original or unmorphed. The laminar-to-turbulent transition corresponds to the high-gradient region.
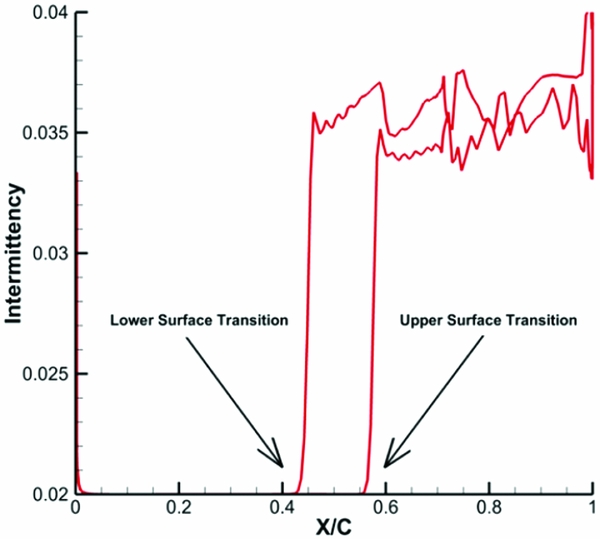
Figure 17. Transition detection for Case 39 unmorphed using the turbulence intermittency distribution.
6.1.1. Upper-surface transition location
In order to evaluate the optimisation success of the wing-tip demonstrator equipped with morphing upper surface, the experimental transition region of the morphed wing-tip demonstrator was compared to the experimental transition of the original (unmorphed) wing-tip demonstrator. The experimental transition region was provided by the infra-red thermography data that was recorded during each of the flight-case wind-tunnel tests.
As such, two parameters were calculated: τ, which represented the difference between the morphed and un-morphed (original) transition region (TR) upper-boundary values and was described by how much of the onset of the fully turbulent flow was modified,
and λ, which represented the difference between the morphed and unmorphed (original) transition region (TR) lower-boundary values and was described by how much of the boundary of the fully laminar flow was modified.
Table 4 presents the values of extension of the laminar region (λ), contraction of the turbulent region (τ), and the average transition extension of the unmorphed (original) and morphed transition region for the seven cases from Table 3.
Table 4 Presentation of (τ) and (λ) parameters for each of the flight cases from Table 3
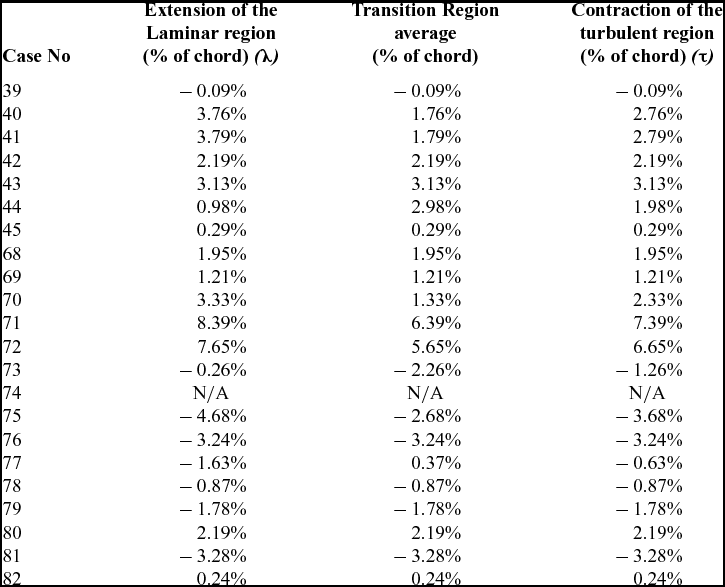
In Table 4, it can be observed that 14 cases out of the 22 presented have obtained both extension of the laminar region and contraction of the turbulent region, having in effect an enlarged transition region. The maximum extension was obtained for case 71, at Mach 0.2, angle-of-attack 1.5° and aileron deflection 4° down, where the laminar extension is 8.39% of the chord and the turbulent region contraction is 6.39% of the chord, closely followed by case 72. The other seven cases, mostly for the wing with the aileron deflection up, have obtained a contraction of the transition region.
In order to better visualise the results presented in Table 4, Figs 18 to 20(a) present the comparison between the experimental unmorphed (original) and morphed transition intervals, while Figs 18 to 20(b) present the comparison between the numerical and experimental unmorphed (original) transition, in order to estimate the degree of accuracy of the numerical analysis. The accuracy level of the numerical values was calculated as an absolute difference between the numerically calculated transition and the closest boundary of the experimental transition interval. It was considered that if the numerical transition was situated inside the experimental transition region, the error would have been 0.
Figure 18(a) shows the unmorphed (original) and morphed transition IR experimental results for cases C39 to C45 (Mach number of 0.15, no aileron deflection and angles of attack between 0.75 and 3°).
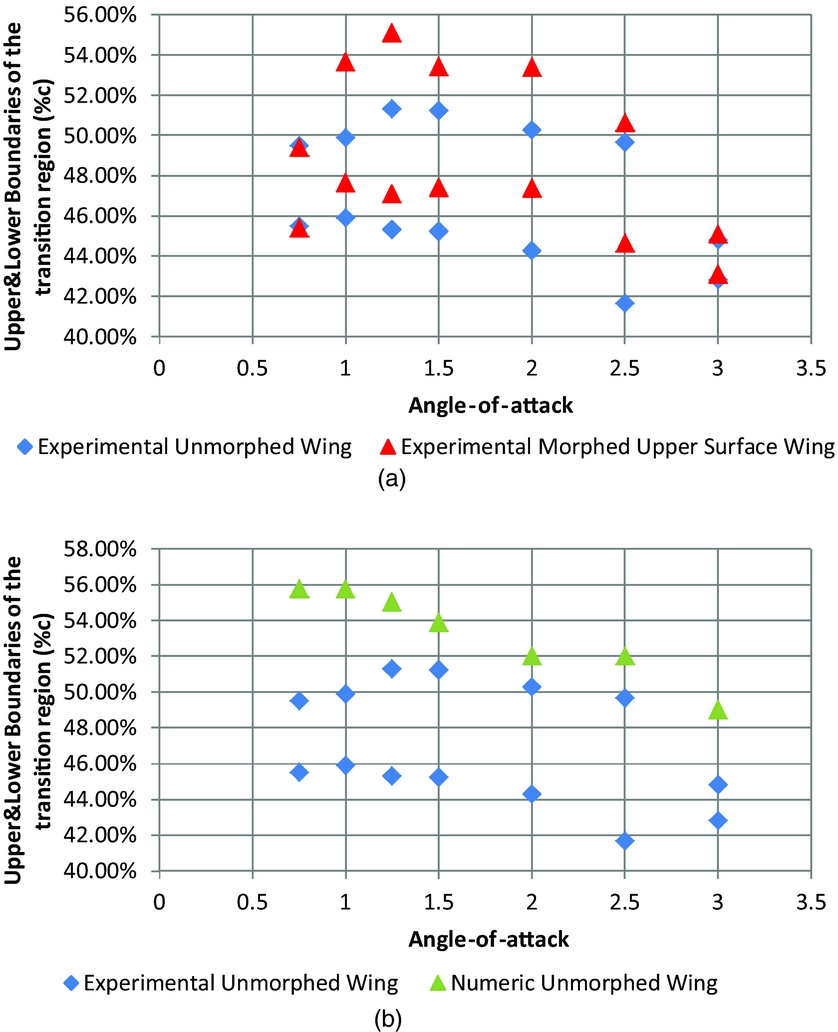
Figure 18. (a) Comparison between unmorphed (original) and morphed IR experimental transition detection for the station located at 40% of the span for cases C39–C45, (b) Comparison between numerical and IR experimental transition detection for the station located at 40% of the span for cases C39–C45–unmorphed (original) state of the wing.
In Fig. 18(b), it can be seen that a reasonable agreement exists between the experimental and the numerically determined transition-point location at the pressure sensors section for the unmorphed (original) wing.
For these cases (C39 to C45, with no aileron deflection), the unmorphed (original) wing error is around 6% of the local chord.
For the morphed geometries results, the agreement between the numerical and IR transition positions is slightly better than for the unmorphed wing, with the average error being approximately 5% of the local chord.
As presented in Table 4, Fig. 18(a) shows that the IR experimental results show a successful improvement of laminar flow for the section of interest. The transition is delayed towards the trailing edge by 3-4% of the chord.
Figure 19(a) shows the unmorphed (original) and morphed transition IR experimental results for cases C68 to C73 (Mach number of 0.20, 4° downwards aileron deflection and angles of attack between 0 and 2.5°).
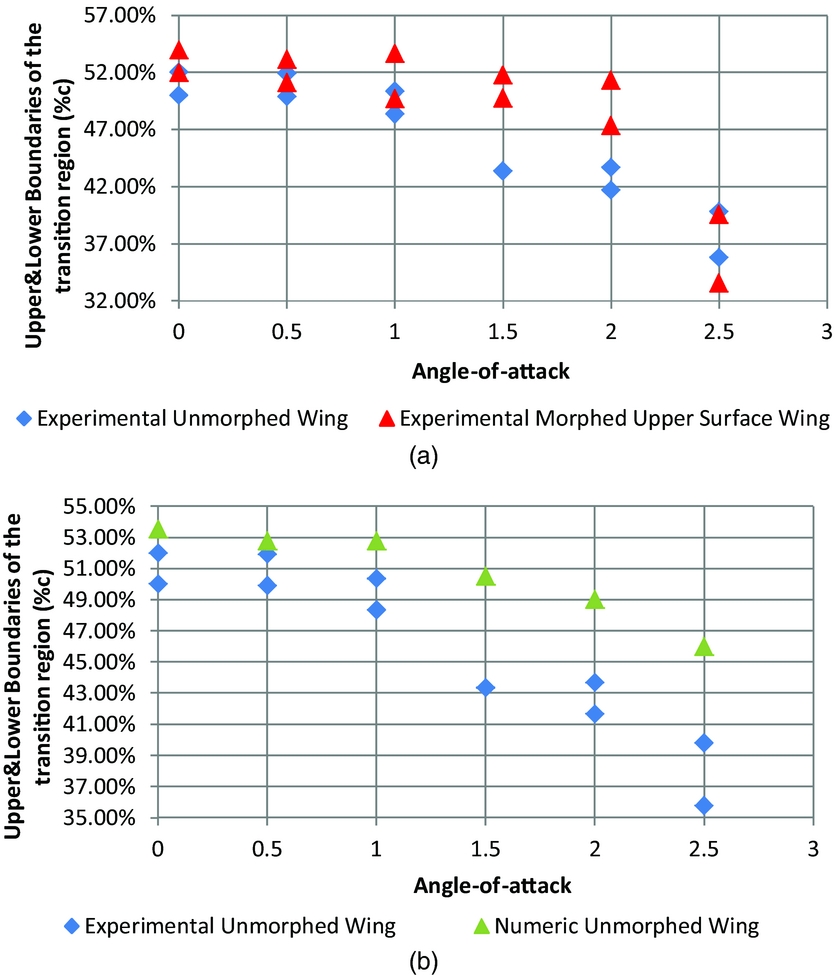
Figure 19. (a) Comparison between unmorphed (original) and morphed IR experimental transition detection for the station located at 40% of the span for cases C68–C73, (b) Comparison between numerical and IR experimental transition detection for the station located at 40% of the span for cases C68–C73–unmorphed (original) state of the wing.
In Fig. 19(b) (cases C68 to C73, with a 4° aileron deflection), for angles of attack smaller than 1°, there is a very good agreement between numerical versus experimental results obtained for the unmorphed (original) wing. The discrepancy is seen to increase for angles of attack higher than 1.5°, as the experimental measurements show an early shift of the transition occurrence towards the wing leading edge. Again, a successful improvement of laminar flow is observed, with delays of approximately 8% of the chord obtained for two angles of attack values (1.5° and 2°). The unmorphed (original) geometries presented in Fig. 19 show a good level of agreement between numerical and IR experimental results, with average errors of 3-4% of the chord. Similar results were obtained for the morphed configurations.
In Fig. 20, the experimental and numerical transition location detection for cases C74 to C82 (Mach number of 0.20, 4° upwards aileron deflection, and angles of attack between 0 and 5°) is presented for both unmorphed (original) and morphed wing geometries. No IR experimental data was available for cases C74 (0° angle-of-attack).
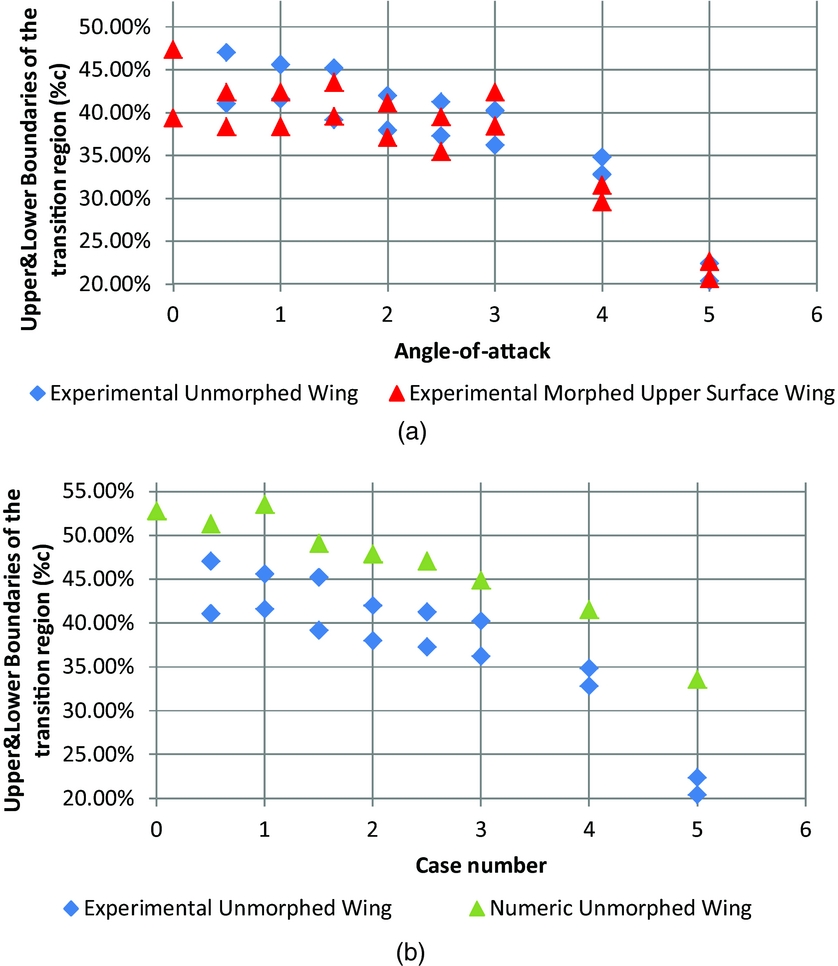
Figure 20. (a) Comparison between unmorphed (original) and morphed IR experimental transition detection for the station located at 40% of the span for cases C74–C82, (b) Comparison between numerical and IR experimental transition detection for the station located at 40% of the span for cases C74–C82 - unmorphed (original) state of the wing.
For cases C74 to C82 (−4° aileron deflection), presented in Fig. 17, there is a good agreement between the IR data and the numerical results for the unmorphed (original) wing (transition position errors of less than 5% of the chord).
With the exception of case 80, the laminar flow delay predicted by the numerical results is not observed in the IR measurements.
6.1.2. Pressure coefficient distribution comparisons
A comparison between the experimental and numerical pressure-coefficient distributions for the section located at 40% of the wing span is presented in Figs 21 to 24, for the following four cases: C40 (Mach number of 0.15, angle-of-attack of 1°, and no aileron deflection), C68 (Mach number of 0.20, angle-of-attack of 0°, and 4° aileron deflection) and for C79 and C82 (Mach number of 0.20, angles of attack of 2.5° and 5°, and −4° aileron deflection).
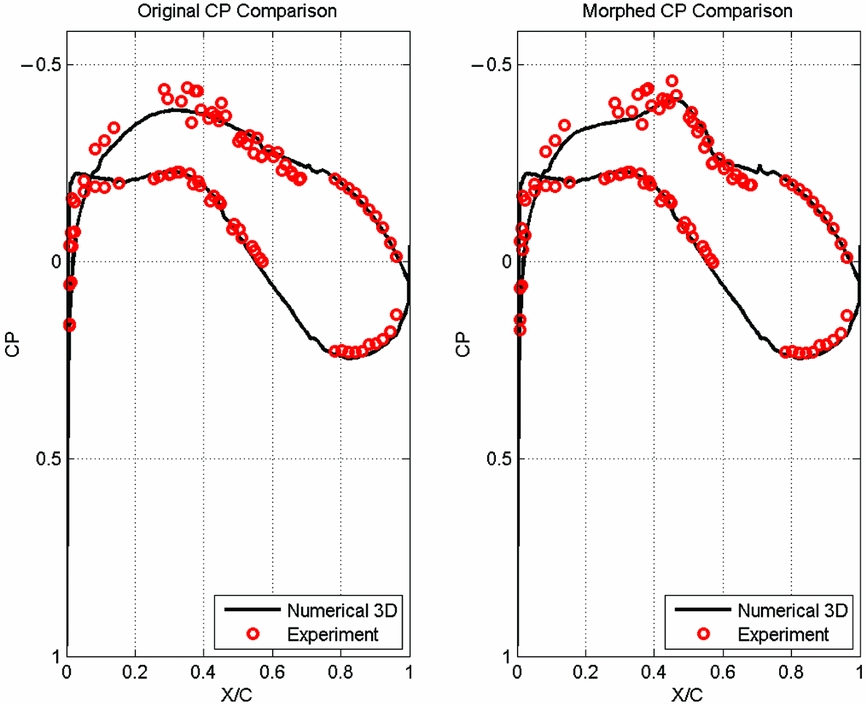
Figure 21. Comparison of experimental versus numerical pressure coefficient distribution for case C40 corresponding to unmorphed/original (left) and morphed (right) wing.
Very good agreement exits between numerical predictions and the wind-tunnel test measurements for the two sets of results given by cases C40 and C 68 (Figs 21 and 22). The influence of the upper skin shape change can be observed from the differences between the unmorphed/original (left) and morphed (right) pressure coefficient distributions, for the chordwise interval between 25% and 60% of the chord. The skin morphing extends the region where the air accelerates over the upper surface, thus creating more favourable conditions for laminar flow, this effect being clearly visible in the two figures.
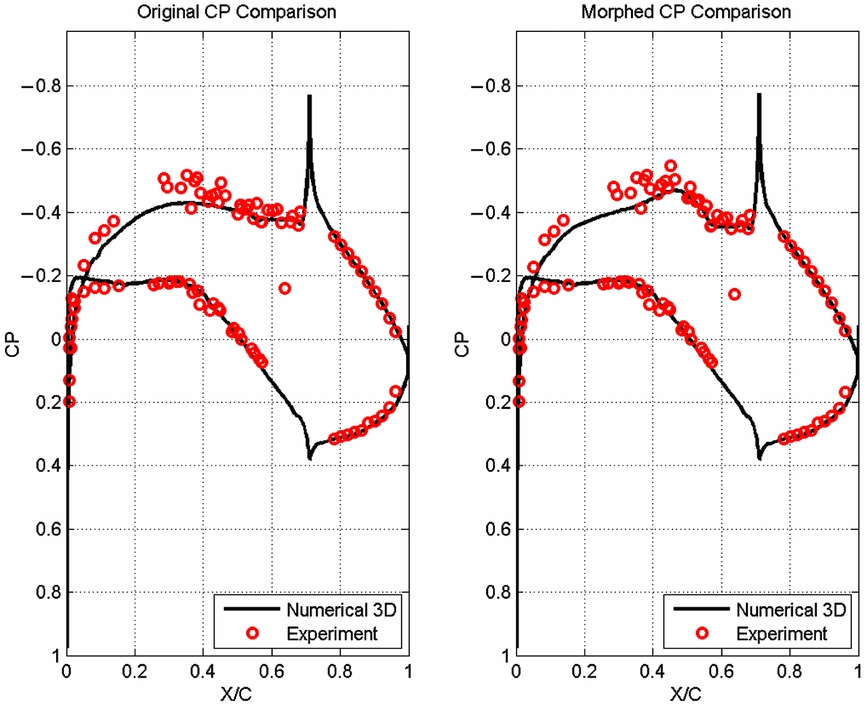
Figure 22. Comparison of experimental versus numerical pressure coefficient distribution for case C68 corresponding to unmorphed/original (left) and morphed (right) wing.
For cases C79 and C82 (shown in Figs 23 and 24), a small difference exists in the upper-surface pressure coefficient up to 50% of the chord, and very good agreement exists between the numerical and experimental results for the aileron, rigid lower skin and the upper surface downstream of 50% of the chord. Once again, the influence of the morphing skin is clearly observable by comparing the left (unmorphed/original) and right (morphed) pressure distributions on both figures.
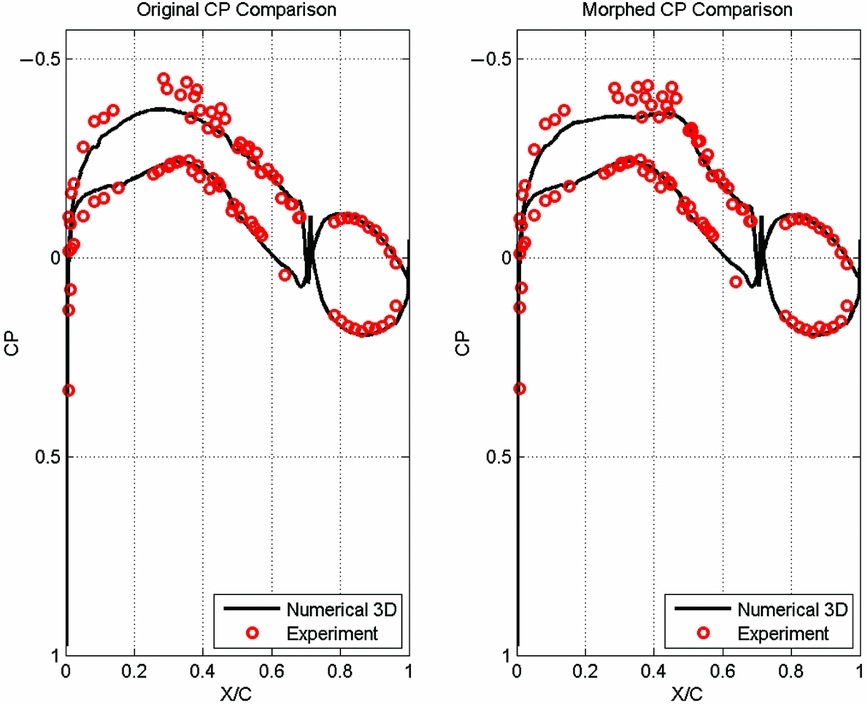
Figure 23. Comparison of experimental versus numerical pressure coefficient distribution for case C79 corresponding to unmorphed/original (left) and morphed (right) wing.
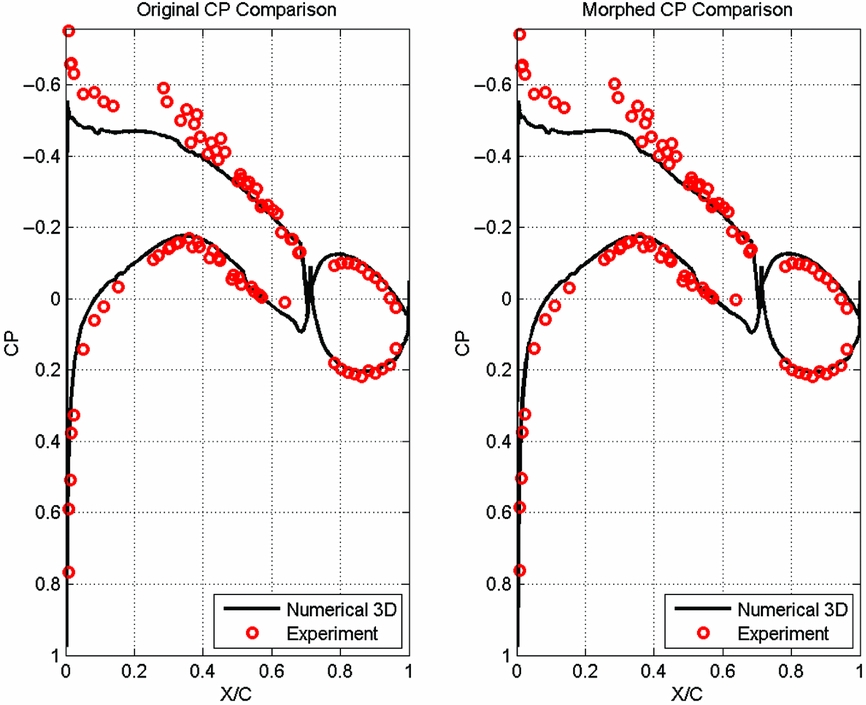
Figure 24. Comparison of experimental versus numerical pressure coefficient distribution for case C82 corresponding to unmorphed/original (left) and morphed (right) wing.
6.2. Results for the third set of wind-tunnel tests–wing equipped with morphing upper surface skin and morphing aileron
During the third set of wind-tunnel tests, 49 flight cases were tested for the wing demonstrator equipped with morphing upper-surface and morphing aileron. For all these flight cases, the optimisation was performed prior to the wind-tunnel tests, and the optimisation objectives were the delay of the flow transition from laminar to turbulent states, and the reduction of the drag coefficient through use of both upper-surface morphing and aileron morphing. Table 5 presents seven of these flight cases, which were tested during the third set of wind-tunnel tests.
Table 5 Flight cases tested during the third set of wind-tunnel tests
Table 5(a) Actuators’ displacements for flight cases presented in Table 5
In order to ensure that the aileron was morphed to the desired shape, the experimental pressure distribution of the wing demonstrator with both its upper surface and aileron actively morphed was compared with the equivalent numerical pressure distribution.
Figures 25 to 28 present the comparison between the numerical and experimental pressure distribution of the wing-tip demonstrator with both upper surface and aileron actively morphing for some of the cases from Table 5. The other cases showed similar level or numerical precision when compared with the experimental data. It can be observed that the two pressure distributions, numerical and experimental, have a very good match, which shows that the aileron had obtained the desired shape during wind-tunnel tests, and that the numerical predictions were close to the experimental results.
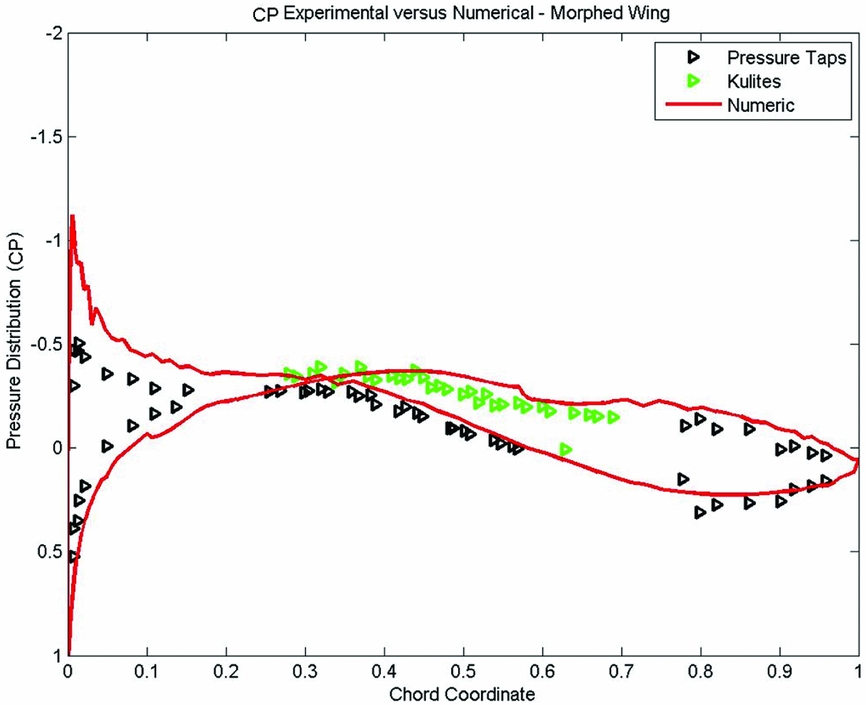
Figure 25. Numerical versus experimental pressure distribution for case 8.
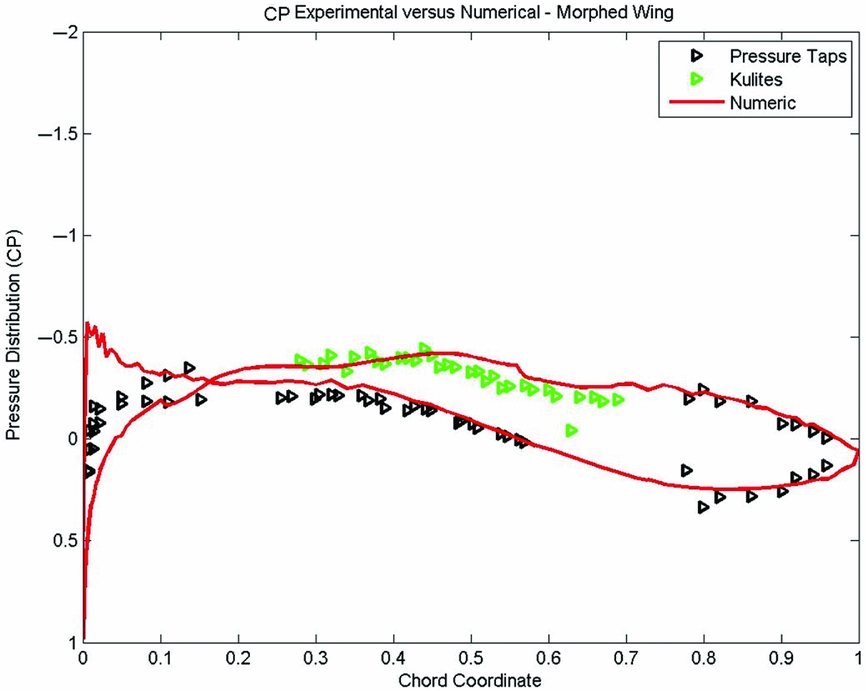
Figure 26. Numerical versus experimental pressure distribution for case 29.
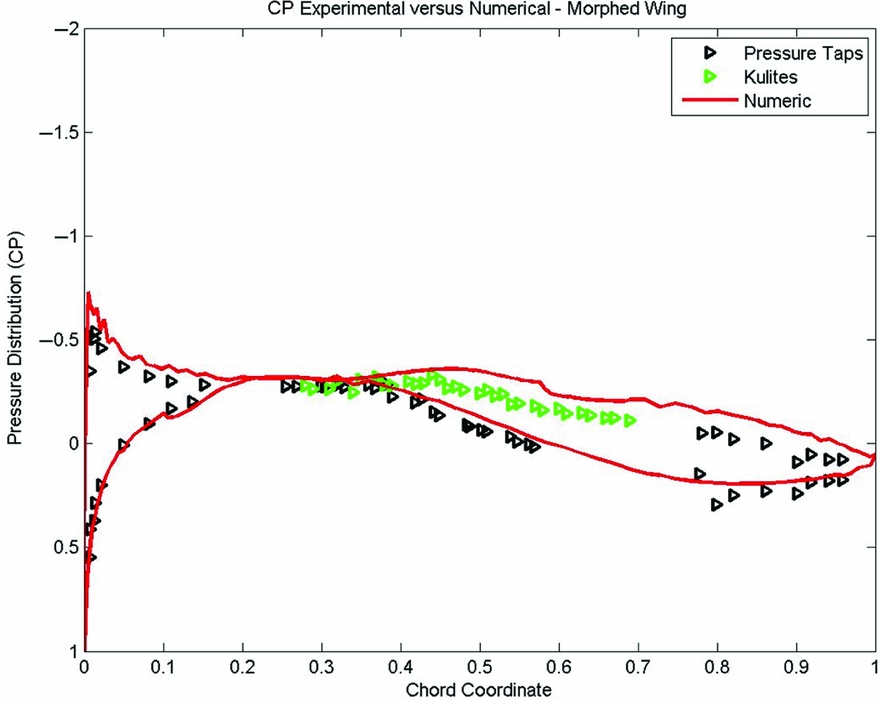
Figure 27. Numerical versus experimental pressure distribution for case 30.
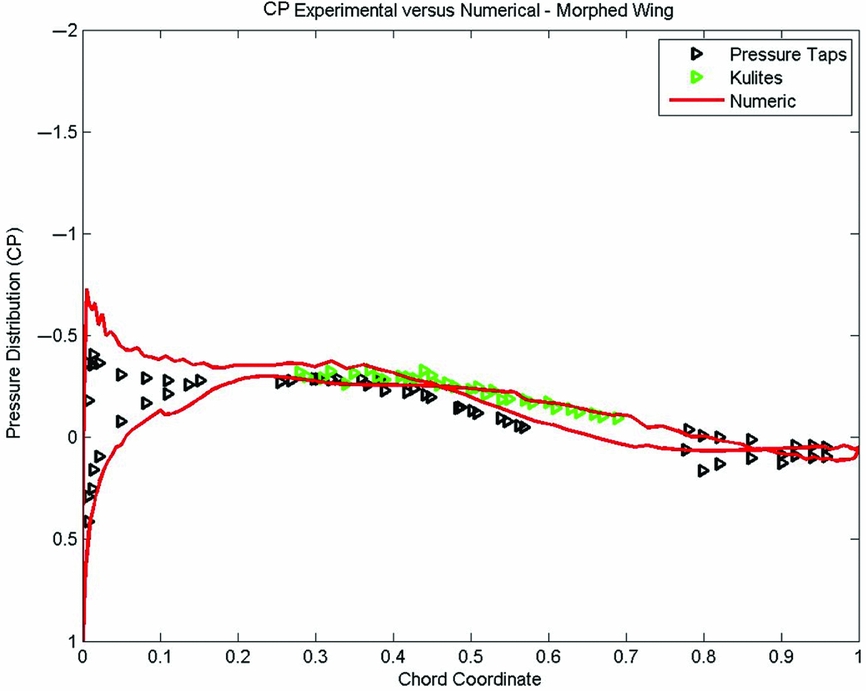
Figure 28. Numerical versus experimental pressure distribution for case 31.
6.2.1. Experimental transition optimisation comparison
In order to evaluate the optimisation success of the wing-tip demonstrator equipped with morphing upper surface and morphing aileron, the experimental transition region of the morphed wing-tip demonstrator (both upper surface and aileron) was compared to the experimental transition of the unmorphed (original) wing-tip demonstrator. The experimental transition region was provided by the infra-red thermography data that was recorded during each of the flight-case wind-tunnel testing.
All the cases presented in Table 5 have obtained a positive extension of the laminar region coupled with a positive contraction of the turbulent region. For their calculation, Equations (2) and (3) were used.
 $$\begin{eqnarray*}
\tau & = & {\rm{MorphedT}}{{\rm{R}}_{{\rm{UB}}}} - {\rm{UnmorphedT}}{{\rm{R}}_{{\rm{UB}}}}\\
&& {\rm{UB}} = {\rm{upper}} \hbox{-} {\rm{boundary}}
\end{eqnarray*}$$
$$\begin{eqnarray*}
\tau & = & {\rm{MorphedT}}{{\rm{R}}_{{\rm{UB}}}} - {\rm{UnmorphedT}}{{\rm{R}}_{{\rm{UB}}}}\\
&& {\rm{UB}} = {\rm{upper}} \hbox{-} {\rm{boundary}}
\end{eqnarray*}$$
 $$\begin{eqnarray*}
\lambda & = & {\rm{MorphedT}}{{\rm{R}}_{{\rm{LB}}}} - {\rm{UnmorphedT}}{{\rm{R}}_{{\rm{LB}}}}\\
&& {\rm{LB}} = {\rm{lower}} \hbox{-} {\rm{boundary}}
\end{eqnarray*}$$
$$\begin{eqnarray*}
\lambda & = & {\rm{MorphedT}}{{\rm{R}}_{{\rm{LB}}}} - {\rm{UnmorphedT}}{{\rm{R}}_{{\rm{LB}}}}\\
&& {\rm{LB}} = {\rm{lower}} \hbox{-} {\rm{boundary}}
\end{eqnarray*}$$
Table 6 presents the values of extension of the laminar region (λ), contraction of the turbulent region (τ), and the average transition extension of the unmorphed (original) and morphed transition region for the seven cases from Table 5.
Table 6 Presentation of (τ) and (λ) parameters for each of the flight cases from Table 5

Flight case 29 gives a small negative contraction of the turbulent region τ that is counterbalanced by almost 2% of the chord of laminar region extension.
The other flight cases gave an extension of the laminar region (λ) of up to 6.5% of the chord, and a contraction of the turbulent region (τ) of up to 5% of the chord.
Figure 29 presents the transition region for the unmorphed (original) and morphed wing for all the cases discussed above. In this figure, a delay of the transition region between unmorphed and morphed states can be observed towards the trailing-edge section of the wing. This transition delay is due to having both the upper surface skin and aileron morphing at the same time.
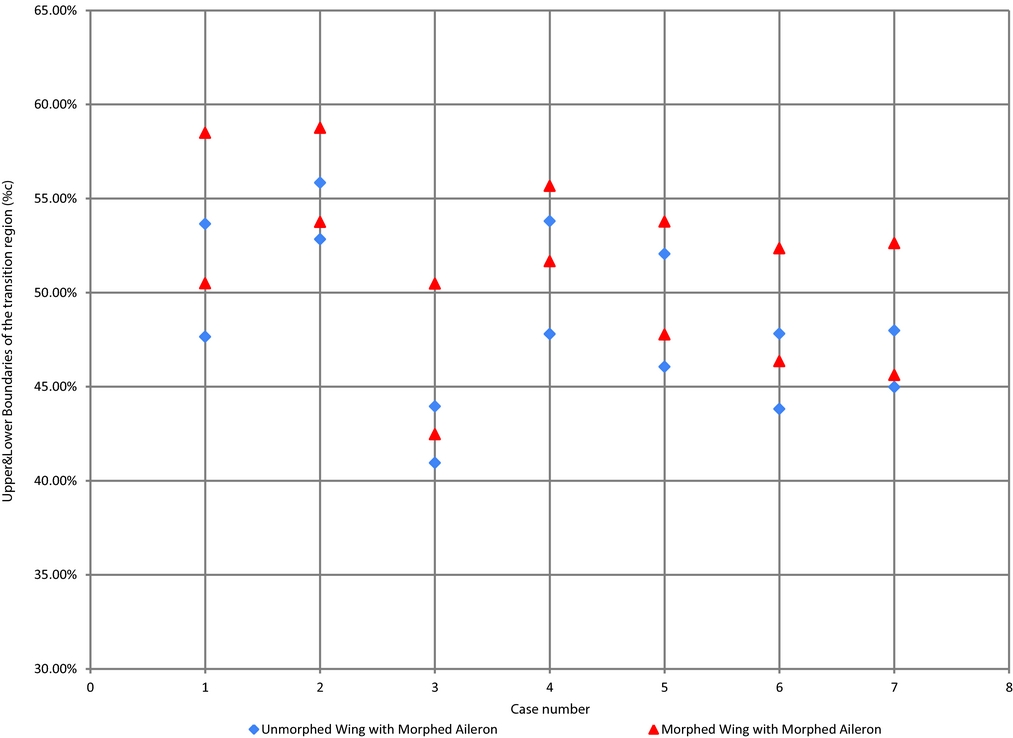
Figure 29. Comparison between unmorphed and morphed states of the wing's upper surface when aileron is morphed – experimental data.
The influence of the morphing aileron and morphing wing upper surface were observed on the behaviour of the boundary layer through extension of the laminar state of the flow, but they also influenced the behaviour of the drag coefficient of the wing. Figure 30 presents the effects that the morphing of the wing upper surface and of the aileron had on the drag, as a comparison between the morphed and unmorphed states of the wing tip. Figure 31 presents the relative difference between the two states of the wing for the drag reduction, while Fig. 32 presents the influence morphing has had on the Lift-Drag relation. All coefficients are presented in counts, where 1 count = 1e−3.
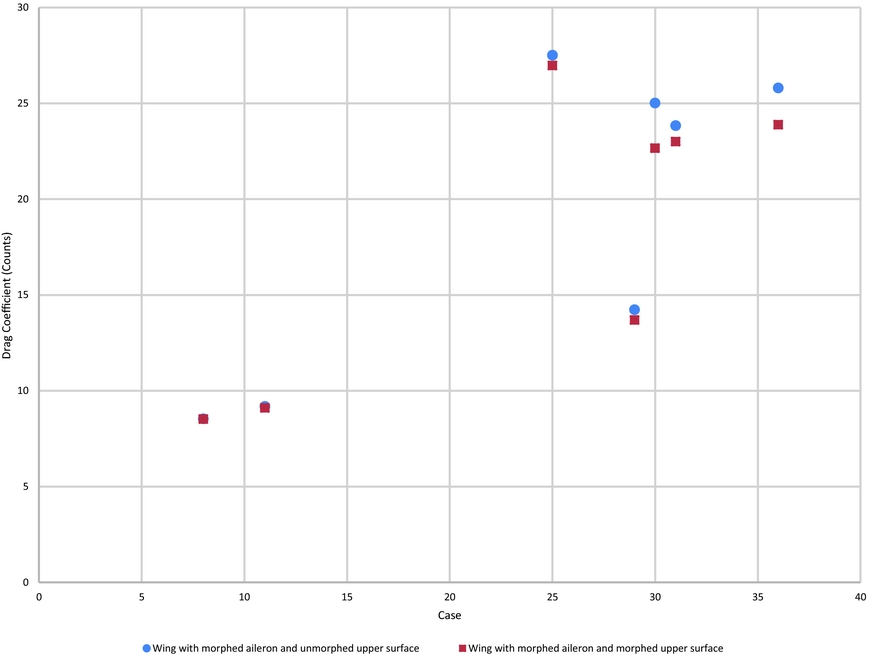
Figure 30. Effect of the morphing upper surface and morphing aileron on the drag coefficient.
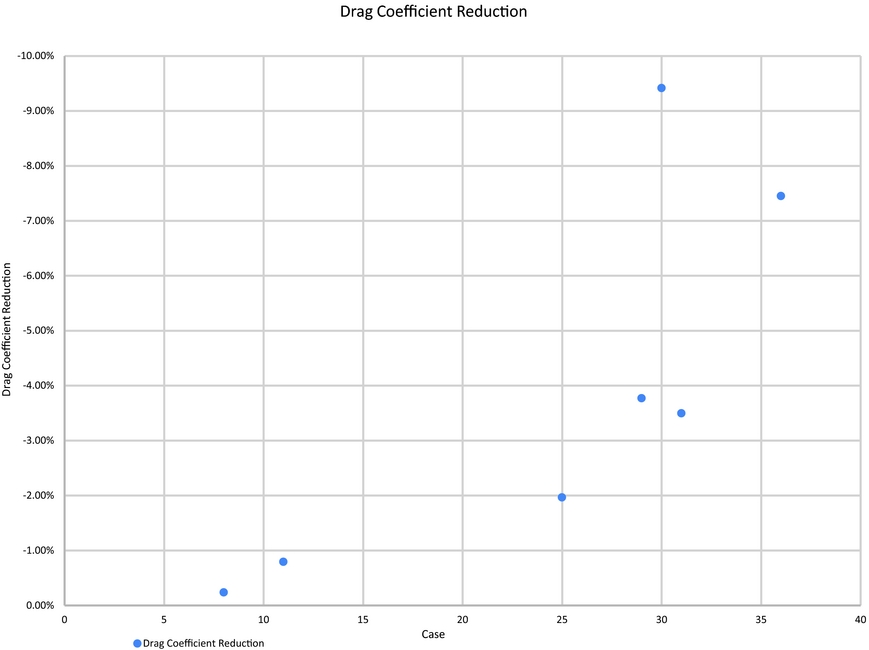
Figure 31. Relative value of the drag coefficient reduction.
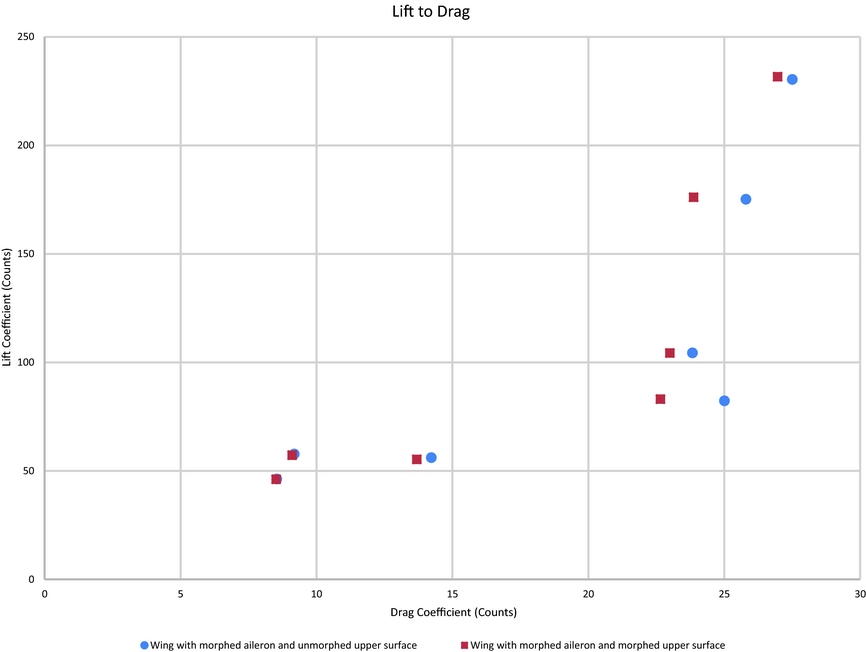
Figure 32. Lift versus drag comparison between morphed and unmorphed states.
The relative drag reduction was calculated as shown in Equation (5):
 $$\begin{equation}
{C_{D\;{\rm{reduction}}}} = \frac{{\left( {{C_{D\;{\rm{morphed}}}} - {C_{D\;{\rm{unmorphed}}}}} \right)}}{{{C_{D\;{\rm{unmorphed}}}}}} \cdot 100
\end{equation}$$
$$\begin{equation}
{C_{D\;{\rm{reduction}}}} = \frac{{\left( {{C_{D\;{\rm{morphed}}}} - {C_{D\;{\rm{unmorphed}}}}} \right)}}{{{C_{D\;{\rm{unmorphed}}}}}} \cdot 100
\end{equation}$$
Based on the experimental results, the coupled morphing of upper-surface and ailerons has achieved a drag-coefficient reduction of up to 9.5%, even when the aileron deflections were small. This fact demonstrates that a smoother slope for the wing camber line, even at small deflections, has a high impact on the wing's performances.
Although, only 7 cases were presented in this paper, from the 49 cases studied during the third set of tests, 32 have obtained both the extension of the flow's laminar state and reduction of the drag coefficient. These results show the promising performances of an intelligent wing with both upper-surface morphing and aileron morphing.
7.0 CONCLUSIONS
In the present paper, the numerical and experimental results of a new wing tip equipped with morphing upper surface, conventional aileron and morphing aileron were presented. The results were obtained during the second and third sets of wind-tunnel tests that took place at the NRC subsonic wind tunnel in Ottawa.
The morphing wing tip was manufactured and fitted with a composite material upper skin. Two-dimensional optimisations were performed with the aim of controlling the extent of the laminar flow region, and the resulting skin shapes were scanned using high-precision photogrammetry. The scanning had the aim to verify that the expected shapes (calculated using the optimisation algorithm) were obtained by manufacturing the wing tip. A grid convergence study was performed to determine the optimal mesh refinement required by the numerical transition model. Subsonic wind-tunnel tests were performed at the NRC 2 m × 2m wind tunnel, and the experimental measurements included Infra-Red thermography, pressure sensors measurements and balance loads measurements.
Three series of wind-tunnel test cases were analysed, each case consisted of a combination of angles of attack, Mach number and aileron deflection angle. Comparisons were made between the unmorphed and morphed upper-skin shapes, for the transition-point location at the station situated at 40% of the wing span, corresponding to the pressure sensors station. Good agreement was obtained between the numerical and IR results, with an average prediction error of approximately 5% of the chord. Both the IR measurements and the numerical results have shown that an increase in the laminar flow region was obtained after the optimisation. The experimental transition delay was between 3 and 9% of the chord, while the numerical improvements in transition delay were smaller.
The experimental results from the third set of wind-tunnel tests have shown that the morphing aileron was capable of obtaining the desired shape, resulting from the pressure distribution comparison. The objective of flow transition delay was achieved for all the flight cases presented in this paper, with the delay of the transition going obtained at 7% of the chord.
The laminarflow extension was obtained for a significant percentage of the upper skin span. Pressure-coefficient comparisons, between numerical and experimental data, were performed at the 40% of the span section, and a good match was obtained.
These results show the success of the numerical optimisation carried at aerofoil level and the possibilities that could be explored with a wing equipped with a morphing upper surface and conventional aileron or for a wing equipped with a morphing upper surface and a morphing aileron wing.
ACKNOWLEDGEMENTS
We would like to thank to Bombardier Aerospace, Thales Canada, The Consortium in Research and Aerospace in Canada (CRIAQ), and to the Natural Sciences and Engineering Research Council of Canada (NSERC) for their financial support. Special thanks are dues to our collaborators and leaders in this project: Dr. Patrick Germain and Dr. Fassi Kafyeke from Bombardier Aerospace, Dr. Philippe Molaret from Thales Canada, Mr. Erik Sherwood and his team from DFS-NRC for the wing model design and fabrication and Dr. Eric Laurendeau from Ecole Polytechnique.










































