NOMENCLATURE
- Dv
-
vertical separation between horizontal wings of box-wing configuration (m)
- Dv/hf + t
-
vertical separation between the wings of a box-wing configuration expressed as a fraction of the height of the fuselage and tailplane
- Dh/lf
-
horizontal separation between the wings of a box-wing configuration expressed as a fraction of the length of the fuselage
- ΔF/FC
-
the percentage change in fuel burn by a box-wing configuration for a particular mission compared to the fuel burn by the conventional configuration designed for that mission
- LD
-
lift-to-drag ratio of the aircraft configuration
- LD/LDC
-
lift-to-drag ratio of the box-wing configuration for a particular mission compared to the lift-to-drag ratio of the conventional configuration designed for that mission
- SLFL
-
landing field length (m)
- RCR
-
cruise range (m)
- W/WC
-
weight of the box-wing configuration for a particular mission compared to the weight of the conventional configuration designed for that mission
1.0 INTRODUCTION
The civil aviation industry faces a number of challenges that need to be addressed in order to ensure its sustainability(Reference Cheze, Chevallier and Gastineau1). An average annual increase of 5% in passenger traffic demand puts pressure on environmental impact and cost and hence the necessity of reducing carbon dioxide emissions to meet reduction targets set by advisory and regulatory bodies is clear(Reference Bows2). Key improvements in technology and operations are required to sustain passenger and cargo mobility growth while reducing emissions, as without them emission levels become uncontrollable(Reference Sgouridis, Bonnefoy and Hansmann3) including new aircraft configurations such as the box-wing and blended wing body. Concurrently, future oil production is forecasted to decrease, leading to a possible shortage in jet fuel supply and increasing prices(Reference Nygren, Akelett and Hook4) in the long term.
The Advisory Council for Aeronautics Research in Europe (ACARE) has set a reduction target of 75% in carbon dioxide emissions per passenger kilometre by 2050, relative to 2005 levels(5). Similarly, the International Air Transport Association (IATA) has set goals of carbon-neutral growth from 2020, and a 50% reduction in carbon dioxide emissions by 2050(6).
Such ambitious goals are difficult to achieve by gradual and evolutionary technology improvements alone. Substantial emission reductions can be achieved by the introduction of new and innovative technologies and design concepts(Reference Lee, Fahey, Forster, Newton, Wit, Lim, Owen and Sausen7,Reference Koch, Lührs, Dahlmann, Linke, Grewe, Litz, Plohr, Nagel, Gollnick and Schumann8) . Quantum-leap improvements in technology need to be allied with new solutions that break away from the current conventional design paradigms(Reference Mistry, Smith and Fielding9). While there are several approaches that are currently the focus of research including laminar flow technology, new engine types with higher bypass ratios and new blade technology, biofuels and multi-stop operations, one design concept that shows promise is the is the box-wing configuration, also known as the PrandtlPlane(Reference Jansen and Perez10). This configuration consists of two horizontal wings joined at the tips by a vertical winglet as shown in Fig. 1.

Figure 1. Box-wing aircraft configuration.
The box-wing configuration is based on the theoretical studies conducted by Prandtl and Munk(Reference Prandtl11,Reference Munk12) in particular, who found that these configurations have improved aerodynamic efficiency over conventional configurations. These findings were confirmed by later studies(Reference Frediani13,Reference Kroo14) , which found a reduction in induced drag for a closed wing system when working within the conditions stipulated by Prandtl and Munk(Reference Prandtl11,Reference Munk12) , such as maintaining equal lift on both wings.
One of the main problems with past design studies on the box-wing is that the aerodynamic and structural aspects were not often considered concurrently to make a trade-off between wing aerodynamic efficiency and structural weight. This paper presents a new methodology for an integrated aerodynamic and structural analysis of a box-wing design configuration. The methodology was applied to the design of a medium-range passenger transport optimised for minimum fuel consumption for a given mission. For the wing system, the following parameters were investigated:
-
• Wing vertical separation
-
• Wing horizontal separation
-
• Wing aspect ratio
In addition, the same mission was used to design an “equivalent” conventional aircraft design for comparative purposes.
2.0 THEORY AND TOOLS
2.1 Aerodynamics
The linear vortex lattice method (VLM) for predicting aerodynamic flow solutions provides a computationally efficient and reasonably accurate solution to wing models and thus is especially helpful for parametric exploration. The Navier-Stokes equations are simplified by assuming steady, attached, incompressible, non-rotational and inviscid flow. Athena Vortex Lattice (AVL) is a freeware, FORTRAN-based linear VLM solver written first by Drela and Youngren at MIT that is widely used for this kind of preliminary analysis(Reference Drela and Youngren15). A modified batch version of this software has been used for this project, and rigorously tested and found to work with a variety of different inputs and conditions without altering the results one would get direct from the original AVL variant, and only serve to speed up and add flexibility to the pre- and post-processing of AVL results.
Taking these on board, an automated program for varying geometric parameters for analysis by AVL has been written for use, and the geometric variation can even be conducted for multiple variables simultaneously, depending how much complexity is desired. AVL has its share of limitations for use in this type of analysis, which constrains its use to a certain set of modelling conditions. Primarily it can only be used to account for the behaviour of subsonic flows, so modelling at Mach numbers higher than 0.8 is to be avoided due to inaccuracies. Similarly, the program does not take into account zero-lift drag coefficient (CD o ), so that must be estimated or calculated separately for accurate analysis. Analysis at higher angles of attack must also not be taken at face value as AVL only models attached flow and not separated flow and hence tends to over-predict aerodynamic values at higher angles of attack, and AVL is meant for best use(Reference Drela and Youngren15) with thin aerofoils at small angles of attack and sideslip, but interpretation of the value of ‘small’ is left up the user – as a linear code, AVL functions accurately within the linear range of the CL − α curve (up to approximately 15° depending on the aerofoil).
However, despite these limitations, AVL has been used in a number of different design studies and experiments, and been verified as reasonably accurate. AVL aerodynamic values were compared with data from wind tunnel testing for non-planar wing configurations and found AVL's theoretical calculations accurate, especially at lower angles of attack(Reference Genco and Altman16). AVL data compared with another computational VLM and existing data found good correlations especially for simple wing geometries(Reference Melin17). It has been used for studies of joined-wing aircraft with reliable results(Reference Mamla and Galinksi18,Reference Landolfo and Altman19) and other design studies have found results computed to be accurate when compared to measured values for stability and control too(Reference Garcia and Becker20).
In this case, it was necessary to link AVL to MATLAB in order to ensure the wing lift distribution was being optimised. A batch version of AVL was linked with a MATLAB tool that was written to vary the twist along the wingspan in order to ensure that the lift distribution along the span of the wing was elliptical. The wing was divided up into eight sections along its span, and each of those sections had a separate twist angle which could be specified individually. Of course, it was necessary to maintain realistic geometric consistency of the wing, and hence the tool was limited to only allow a maximum change in twist of one degree between sections of the wing next to each other. This elliptical lift distribution is especially important for box-wing configurations, as the theory specifically states that maximum drag reduction and hence aerodynamic efficiency can only be achieved when there is equal and elliptical lift distribution on both horizontal wings. This change in the wing geometry was taken into account and implemented when the wing was analysed and sized structurally to ensure consistency of results. The twist optimisation is necessary because the other geometric parameters, such as wing area and aspect ratio, are either going to be fixed for comparison purposes or be part of the parametric sweep, which will necessarily cover values which are not optimal.
The output of the aerodynamic analysis and optimisation, specifically the lift and induced drag, will be necessary for the performance analysis. Furthermore, the aerodynamic loads will be transferred over to the structural analysis tool and serve as the input loads for that link in the toolchain for the design.
2.2 Structures
In order to aid the aircraft designer and analyse a large range of conventional and unconventional wing configurations in a relatively computationally efficient manner, a new tool was developed at the DLR Institute for Air Transportation Systems called WingMASS (Reference Dorbath21)in order to improve the structural design and weight estimation aspect of wing design in the conceptual and preliminary design stage of the process and incorporate an FEA approach into those stages in order to provide a more accurate structural design of the wing planform(Reference Dorbath, Nagel and Gollnick22).
The strength of the WingMASS toolchain is that it allows for relatively large and complex models to be built up and analysed with reasonable speed and efficiency by using the Common Parametric Aircraft Configuration Scheme (CPACS) developed at DLR, which is an XML-based language for several aircraft design tools from various disciplines (including WingMASS) that allows designers to rapidly generate different models. Furthermore, several engineering rules are implemented into the toolchain, minimising the amount of user input required and allowing for a higher level of automation in terms of optimisation and analysis(Reference Dorbath21). The CPACS file is where all the parameters (aircraft geometry, mission, material properties and so forth) are stored, and is used to initial each analysis run.
A basic structural model is generated using quad elements for the basic structural members of the wings, the skin, the spars and the ribs. They are all modelled as shell elements, and where composite materials are used, multi-layer shell elements are created. Stringers are then modelled as a smeared skin, with the equivalent stiffness and materials properties of an explicit stringer model. The spar caps are modelled as beam elements with rectangular cross-sections(Reference Dorbath21). The structural sizing and analysis is done by the Sizing Robot (S_BOT+) element of the WingMASS toolchain, which is implemented in ANSYS Parametric Design Language (APDL). The sizing is done via an iterative sizing loop that initially considers all the loadcases implemented in the CPACS file, sizes accordingly, after which the new material thicknesses are applied to the model and the loop begins again and continues till convergence of material thickness and hence mass.
2.3 Statistical and empirical methods
For the initial design of the conventional aircraft for a given set of mission requirements, a large number of methodologies, historical data and guidelines exist in terms of designing large passenger aircraft of the conventional configuration that could be drawn upon as resourced during this initial part of the process(Reference Raymer23,Reference Roskam24) . These could all be drawn upon and combined where appropriate to initially size the aircraft for the given performance and mission requirements, and estimate the weight and performance of the design.
The weight fractions can be estimated first, according to the chosen mission criteria which then determine the payload masses. The payload and fuel-burn estimates will allow the structural masses of the various components of the aircraft to be estimated, such as the fuselage and tailplane. Such a weight estimation method is presented for standard aircraft types based on statistical and historical data(Reference Roskam25).
Similar equations and calculations also exist for the aircraft sizing. One example would be for the wing sizing, which is based off the wing loading during take-off and landing, with first estimate values for the mass and the maximum lift coefficient. These can be used to estimate the approach speed of the aircraft to the landing field based on statistical data and current design philosophies(Reference Roskam25). The wing loading derived is then used to size the reference wing area of the aircraft, which can then be used to further size the wing, including the aspect ratio, span, chord (arising from the geometric relationship between aspect ratio and area) and other parameters.
The zero-lift drag of the aircraft was also calculated using a component build-up method in order to provide a first-order estimate that could be used for the aerodynamic and performance analysis of the conventional and box-wing configurations, as calculation of the zero-lift drag was not possible with the AVL software(Reference Drela and Youngren15). Instead, the component build-up method(Reference Raymer23) was used to estimate the influence of the skin-friction drag of various aircraft components (such as the fuselage, empennage, wings) as well as the interference drag from how two components joined together that create more drag than the sum of their individual drags. This analysis is only suitable for aircraft in subsonic flow. This method of estimating the zero-lift drag was necessary for the analysis due to the importance of the drag in the aerodynamic performance and fuel burn calculations for the conventional and box-wing aircraft, and to ensure that the additional interference and friction drag effects from the box-wing planform were included in all analyses of that configuration so a better overall picture would emerge of the performance of the box-wing in comparison to the conventional.
3.0 METHODOLOGY
3.1 Overview
The approach for the analysis requires integrating the aerodynamic and structural analysis and optimisation tools into a single toolchain that can then be used to conduct the overall fuel-burn comparison between the box-wing and conventional configurations via a parametric study for a chosen mission.
The aerodynamic analysis requires the geometry and performance characteristics values derived from the mission requirements such as the velocity at the given altitude. This optimisation with the AVL tool leads to outputs which become inputs for the structural analysis using the WingMASS tool. Specifically, the wing twist necessary for the elliptical lift distribution is used to modify the wing geometry and the aerodynamic loads on the wing are used for the structural analysis. The process is outlined in the flowchart in Fig. 2, showing the sequential information flow and how the design for the conventional leads to design for the box-wing, with the geometric parameter variation the next step.

Figure 2. Flowchart overview of analytical approach.
Once the structural analysis is completed for the specified loadcases, the weight breakdown is updated and recalculated using the new weight structure and the flow-on effects on the fuel load. For a given mission, this aero-structural optimisation is conducted for the baseline conventional aircraft configuration, as well as a series of box-wing configurations with different combinations of wing separation and aspect ratio.
The updated MTOW and cruise aerodynamic performance characteristics are inputs for the fuel consumption analysis using Breguet's range equation, which is then compared with the fuel consumption of the equivalent conventional aircraft configuration.
3.2 Case study for a passenger transport for short and medium range
The methodology was applied to the design of a box-wing configuration based on a given mission specification for a short-range, passenger transport for city-hopper type operations:
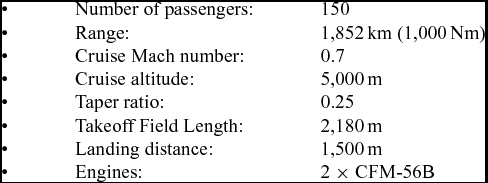
This mission was selected because it provides a promising concept for the box-wing, as it minimises induced drag but can have more zero-lift drag than conventional aircraft configurations due to increased surface area and interference drag(Reference Jansen and Perez10). This leads to a meaningful comparison between the two concepts with respect to fuel consumption for a given mission.
3.3 Conventional design
Multiple load cases inherently complicate the design problem therefore only the cruise phase was chosen for the aerodynamic analysis. The loadcases for the structural design analysis also needed to be chosen. While a wide variety of loadcases could be used, each added would increase the computational time and resources required to complete the analysis. Furthermore, many of the more specialised loadcases depended on design parameters or scenarios that might not become relevant till the more detailed design of the configurations were required. Hence, in this case, two relatively important and straightforward loadcases were chosen for this task, both adhering to the relevant Federal Aviation Regulation (FAR) 25 design criteria for transport aircraft.
In this case, those chosen criteria are for cruise flight, where it is mandated that the sizing of the wing be done for the operating loads with factors of +2.5 g and –1.0 g manoeuvring loads. At the conceptual design stage of the aircraft design study, this is a commonly used set of loadcases for structural design and analysis, and indeed sometimes is simplified further to simply the 2.5 g case(Reference Jemitola, Monterzino and Fielding26). For this investigation, the WingMASS tool was tested and found robust enough and quick enough to handle both loadcases for both the conventional and box-wing configurations and hence both were implemented and used for the structural sizing and optimisation loop when the analysis was conducted. The structural materials used for both conventional and box-wing aircraft will be relevant metal alloys, such aluminium 7075 for the spars and aluminium 2024 for the skin.
Apart from the payload and range requirements specified, further parameters will be required for the ideal conventional design for the mission. The first extra parameters that are considered are the take-off and landing field length restrictions, as these have a large effect on the wing loading and sizing for initial consideration, and are critical in terms of airport usage for aircraft. The maximum distances were chosen based on typical single-aisle aircraft such as the Boeing 737 and Airbus A320.
The design process and methodology for the conventional aircraft is based on historical and statistical data(Reference Roskam24). Once many of the key aerodynamic and structural parameters have been initially sized and estimated, they are then entered into the aircraft design toolchain and methodology developed incorporating AVL and WingMASS. The wing twist was determined to ensure that the wing had the optimum elliptical lift distribution, considering the lift and induced drag coefficients, and then further optimised structurally using the WingMASS tool so a more efficient wing structure was in place and improved the wing's structural weight. Subsequently, the optimised values for wing weight and new MTOW are reiterated again through this process until they converge and lead to a final set of values which are then used for the comparison against the box-wing model with the fuel burn calculations. The final design values for the conventional aircraft configuration are presented in Table 1.
Table 1 Design parameters for conventional configuration

3.4 Box-wing model
In order for there to be an effective comparison between the different configurations, some parameters must be kept the same for both configurations. The most relevant and useful one for this kind of comparison is reference wing area, around which the twin horizontal wings of the box-wing configuration can then be designed. The wing area was used as the reference parameter as it is driven by the wing-loading, hence the take-off distance, and would not be affected by cruise performance. Hence, the initial basic parameter for sizing the box-wing can be the wing area requirement, as the historical and statistical data used in the previous section is not applicable for the design of the box-wing planform.
As well as choosing the reference design parameter, the parameters that are to be varied so the scope of the design space is explored relatively fully must also be chosen. The horizontal and vertical separations between the two wings are two clear choices. The influence of the aspect ratio of the individual wings on the aerodynamic and structural characteristics of the planform must also be investigated – namely is the structural penalty trade-off for aerodynamically superior wings worth more or less when it comes to the box-wing planform than the conventional planform. Necessarily, of course, this involves varying the chords and spans of the individual wings of the box-wing. Aspect ratio uses the span and wing area of a single wing.
Wing twist was determined to ensure an elliptical and equal lift distribution on both wings as required by the Prandtl-Munk theorem(Reference Prandtl11). Each of the two horizontal wings were optimised separately to maintain equal lift distribution by modifying the angle of twist along the span of the wing at different stations, while ensuring that the optimisation angles stayed within realistic bounds and did not vary by more than 1 degree between each station.
However, other variables must be frozen in order to limit the scope of the investigation and allow for effective and efficient computational efforts in terms of the investigation being conducted. For example, aerofoil choice and optimisation is generally considered an important part of the design process for any wing system, let alone an unconventional design such as the box-wing. However, the critical data needed for such an investigation (including computational fluid dynamics meshing and analysis) and the complexity of it would probably demand an entire separate research project of its own. Hence, in this case, the aerofoil for both the conventional and the box-wing was frozen at the same sub-optimal choice. Other geometric parameters such as taper of the wings were also frozen at the value used by the conventional configuration in the interests of simplifying the analysis down to the most vital parameters and isolating their influence on the aerodynamic and structural characteristics of the box-wing configuration.
The fuselage design is also of lesser importance when comparing these two configurations. Unlike other unconventional configurations such as the blended wing body, the box-wing configuration does not require a radical redesign or overhaul of the fuselage when compared to the baseline conventional configuration from which it is based. Instead the same fuselage can be held constant for both aircraft, as the payload and number of passengers that both configurations are being designed for are identical and the structural implications on the fuselage itself from the box-wing configuration at this early stage in the design process are relatively minimal.
Previous box-wing design studies have shown the peculiarities of the box-wing design have a broad impact on the design of the vertical tailplanes. The structural impact comes from the fact that the vertical tail often needs to support and anchor the rear wing, if it is too high to be supported structurally through the fuselage. This can lead to a vertical tailplane that needs to be strengthened and hence made heavier for the box-wing configuration as opposed to the conventional configuration. In terms of stability, the fact that there is a lifting surface at the rear of the aircraft, generating upwards lift can be problematic. In conventional aircraft, the horizontal tailplane actually generates downforce, counterbalancing the lift generated by the wings and ensuring the aircraft is stable and manoeuvrable. In the case of the box-wing, this is not possible as the conditions for aerodynamic efficiency require both wings to generate equal lift. Some studies(Reference Prandtl11,Reference Jemitola, Monterzino and Fielding26) have proposed a V-tail system at the rear for the box-wing, allowing for control devices to be implemented on the vertical tailplanes at the rear to try and overcome this disadvantage.
Once again, the design and study of a complete horizontal and vertical tailplane system and its effect on the overall aircraft design could form a significant research project in its own right. In this case, the size of vertical empennage is held steady as the box-wing configuration is designed and analysed in comparison to the conventional, at least initially. This allows for the focus of the investigation to hold on the wings themselves, the most unique and interesting change in the configuration, and the part that must be modified and optimised first if the box-wing is to have any initial theoretical advantage over the conventional. However, the weight is increased for configurations where the rear wing is attached to the vertical tailplane, to account for the greater structural strength needed to support the rear wing through the structural design, with the weight being proportional to the height of the rear wing attachment to the vertical tailplane as per previous studies on large aircraft with such configurations(Reference Byrnes, Hensleigh and Tolve27).
The integration of the landing gear purely into the fuselage imposes a structural penalty for those designs where it cannot be integrated into the lower surface of the wing. In the case of the box-wing designs, there would be an additional structural penalty from that for certain designs where it would not be possible to integrate the landing gear because of the wing placement changing for aero-structural optimisation reasons. In this study, that weight penalty was not imposed but it must be taken into account when higher-fidelity designs are analysed.
Another part of the box-wing planform that is necessary but challenging to estimate is the coefficient of zero-lift drag. The additional drag components arising for the box-wing, such as the added friction drag and interference drag from the vertical wings, are added to the zero-lift drag already estimated for the conventional. Hence, the overall zero-lift drag for the box-wing planform is greater than that of the conventional planform designed for the same mission, and any analysis comparing them both should attempt to involve both sets of drag values in order to present a more even overall picture of the aerodynamic characteristics of both configurations for comparison. The component build-up drag methodology that was used for is outlined in the previous section.
3.5 Horizontal wing separation
The first set of box-wing planforms kept the vertical wing separation and aspect ratio constant and investigated the influence of the horizontal wing separation on the aerodynamic and structural characteristics. A range of values for the horizontal separation were chosen, as shown in Table 2, with regards to keeping a realistic configuration in mind, and minimising the influence of the wings on each other's airflow via downwash – having the wings too close to each other horizontally led to interference effects which had a large negative influence on the aerodynamic performance of the whole wing planform. Another consideration here was the position of the centre of gravity and the landing gear, which meant the wings could not be too close together, with the front wing shifting backwards as the rear wing had to be placed next to the vertical tailplane. A level of freedom was still included in the design space exploration in order to consider the maxima and minima given purely aero-structural considerations, but the placement range kept realistic thanks to those additional design concerns in order to ensure there was no investigation of truly unfeasible results. The separation was measured as the horizontal distance from the leading edge of the root of the front wing to the leading edge of the root of the rear wing, and as is shown in Fig. 3, was non-dimensionalised by dividing by the length of the fuselage.
Table 2 Horizontal separation values investigated


Figure 3. Horizontal separation and length of fuselage of aircraft concept.
3.6 Vertical wing separation
Vertical wing separation has a theoretically large effect on the aerodynamic and structural efficiency of the box-wing planform(Reference Prandtl11). Here the effect of varying the vertical wing separation was considered, with the aerodynamic advantages to be considered against the structural disadvantages to combine into an overall result of how the geometric parameter affected the design. The separation was measured as the vertical distance from the tip of the root aerofoil to the tip of the root aerofoil, and as is shown in Fig. 4, was non-dimensionalised by dividing by the height of the aircraft from the bottom of the fuselage to the tip of the vertical tailplane, and the values are shown in Table 3.

Figure 4. Vertical separation and height of fuselage and tail of aircraft concept.
Table 3 Vertical separation values investigated

3.7 Aspect ratio
The aspect ratio was varied from a value of 7.87 to 11.87, as per Table 4. Of course, varying the aspect ratio also meant varying the entire geometry of the wing, including the wingspan and the chords. The mean aerodynamic chord was recalculated for each different planform to ensure the aerodynamic analysis was conducted as accurately as possible as well. The maximum value meaning that the wingspan did not extend beyond realistic values for the airports the aircraft might service as it was held at the wingspan of the conventional configuration, while for values lower than the minimum here, an investigation found that the aerodynamic characteristics and performance of the aircraft would not be of an acceptable level.
Table 4 Aspect ratio values investigated for Mission Concept 1

4.0 RESULTS
4.1 Wing geometry effects on fuel burn
Figure 6 shows the effect of wing separation on the difference in fuel burn of the box wing DF relative to that of the conventional aircraft Fc .
Figure 5 shows that ∆F/Fc is minimum at Dh/lf = 0.37, Dv/hf+t = 0.4 and AR = 7.87. Note that this result is specific for the chosen mission. The multi-disciplinary analysis of the box-wing configuration indicated, for the chosen mission, a potential reduction in fuel burn of 5.19% compared to a conventional aircraft configuration. Without considering multi-disciplinary analysis, this result would not have been discovered as the interaction between the structures and aerodynamics is critical. In this particular case, the structural drivers leading to lower weight led to better results, hence the optimum occurring at low values of aspect ratio and vertical separation in particular. If the design had been optimised just for aerodynamic efficiency, the ideal result would have had a high aspect ratio and large vertical wing separation as per Prandtl-Munk Theorem.

Figure 5. Effect of wing separation and aspect ratio on fuel burn difference relative to conventional aircraft.
In contrast, for this mission, the smaller aspect ratio led to a reduction in fuel burn compared to the conventional aircraft, because the box-wing design has a lower weight. For conventional aircraft, reducing the aspect ratio leads to a much higher induced drag as the wingtip vortices increase significantly in terms of size and energy removed from the lifting system. For the box-wing, this effect is much less severe with lower aspect ratios. For the vertical separation, again the structural cost in terms of the longer, slim vertical wing and the additional loads on both it and the attachments to the horizontal wing outweighed the small aerodynamic advantages of increasing the separation. Hence, in this particular case, the structural savings from having shorter wings with a higher aspect ratio were more important than having greater aerodynamic performance, and that would not have been evident without analysing structures and aerodynamics at the same time.
As shown in Fig. 6, the lift-to-drag performance of the box-wing configurations changes only slightly with horizontal wing separation. The slight variations arise from the decrease in interference of the flows of the wings and the downwash on the rear wing. Since the rear wing is above the front wing, there is little effect on it than if the reverse configuration was used.

Figure 6. Box-wing lift-to-drag ratio and MTOW relative to the conventional aircraft configuration.
The aerodynamic efficiency of the configuration increases with vertical wing separation, as shown in Fig. 6, as was hypothesised by theory. The lift-to-drag ratio reduces only slightly as the vertical wing separation is reduced because of the reduction in induced drag and the airflow staying more attached at the lower values of vertical wing separation.
With the aerodynamic characteristics not changing significantly with wing geometry, the structural efficiency of the wing becomes the important factor. Increased horizontal separation leads to increased loads, and the vertical wing has to elongate and become more diagonal, requiring more stiffness and strength to maintain its shape, as shown in Fig. 6. This leads to heavier spars, ribs and skins in the wing primary structure, increasing the overall wing weight and aircraft weight. The increase in wing weight with horizontal wing separation generally cancels any improvement offered in terms of lift-to-drag ratio. Hence, when considering the design space exploration of the box-wing, keeping the horizontal wing separation at a minimum value is recommended, and more focus should be given to other parameters.
The structural efficiency of the box-wing improves as vertical wing separation is reduced. This is due to the fact that the vertical wing is subjected to different loads, especially around the joints to the horizontal wings, and in terms of the magnitude of the butterfly-shaped load along the vertical wing. These additional loads arise due to torsion in the vertical wing, as well as the higher buckling loads that must be resisted by this relatively slender structural member.
Figure 7 shows the Von Mises stresses and pressure differential mapped onto the AVL mesh. Larger vertical wing separation leads to higher stresses and deflection, especially of the vertical wings when the vertical wing separation is highest with the rear wing at the tip of the vertical tail (Dv/hf+t = 1). In contrast, the Fig. 7 shows that for constant horizontal wing separation and aspect ratio, a planform with Dv/hf+t = 0.6 shows 13% lower Von Mises stresses, with much less deflection and bending of the vertical wings. The pressure differential is critical as it illustrates the distribution of loads and bending moments on the vertical wings.

Figure 7. Von Mises stresses and pressure distribution for different vertical wing separation.
This means greater structural support is required at the joints between the vertical and horizontal wings, especially the upper wing, and those loads need to be supported and transferred over that wing too. Hence, the rear, upper wing has to be heavier to resist those loads and moments when the vertical separation is much greater.
This interaction of aerodynamic and structural factors is an important finding, as previous design studies have focused mostly on maximising vertical wing separation. However, the structural impact has rarely been investigated.
Lower aspect ratio wings for the box-wing still perform well enough aerodynamically while offering a weight advantage. High aspect ratio designs are heavier to resist the bending and torsion loads and hence offset any aerodynamic advantage they gain. This outcome is actually quite different and perhaps even counterintuitive when compared to other studies of the box-wing. Previous studies have often concentrated on comparing conventional planforms and their box-wing equivalents by keeping the wingspan the same. This meant that the box-wing had a higher aspect ratio, leading to increased aerodynamic performance but at a great structural weight penalty. However, the true benefit of the box-wing may well lie in a planform that provides a structural benefit and weight saving over the conventional configuration while delivering an aerodynamic performance that is still close to that of the conventional configuration. Conventional wings that have a low aspect ratio and would provide similar weight savings would have higher aerodynamic penalties in terms of induced drag.
This study only considered the effect of wing geometry on wing structural weight and aerodynamics. Obviously, wing separation will also be determined by other factors such as weight and balance, stability and control, etc. This means that the full fuel burn reduction may not be achieved in practice. For example, Fig. 8 shows the optimal aircraft configuration and the same design with a higher horizontal wing separation to achieve weight and balance requirements.

Figure 8. Effect of non-optimal design on fuel burn.
If the horizontal wing separation is increased from Dh/lf = 0.37 to Dh/lf = 0.48 the improvement in fuel burn changes from -5.19% to -3.96%. This is still a significant improvement in the fuel burn compared to the conventional aircraft configuration.
4.2 Validation
Error estimation analysis was conducted for separate components of the toolchain, with the WingMASS structural tool found to be accurate to within 1% of a real aircraft wing structural weight(Reference Dorbath21), while AVL has been analysed by several studies that have found it to be accurate to within 7% for lift and induced drag analysis(Reference Melin17,Reference Garcia and Becker20) . Obviously, comparisons with existing aircraft are only available for the conventional cantilever wing configurations.
Validation of the toolchain and methodology described in this paper was carried out by conducting the analysis for an Airbus A320 aircraft. The mission parameters of the A320 were used to design a conventional aircraft, which was then optimised both aerodynamically and structurally before undergoing the fuel burn analysis. The resulting estimated fuel burn was within 10%, with the difference largely attributable to the focus of the design being on the cruise phase of the mission and the loads experienced during that phase alone.
Furthermore, an additional analysis was carried out with the toolchain on an existing joined-wing model that has been analysed both theoretically and in wind-tunnel tests with NASA. This comparison focused on the aerodynamics of the aircraft, and was done using the model that was designed and tested by Smith and Stonum(Reference Smith and Stonum28). The aerodynamic analysis tool was used to analyse the JW-3 model as specified in that report, and the results found that the model analysed computationally agreed to within 8% of the results found in the wind-tunnel testing.
As the same model was applied to the conventional and box-wing design to ensure a fair comparison, any inaccuracies in the model are consistent for both design configurations. This is a relatively common approach taken for unconventional conceptual design where the preponderance of unknowns and inability to calibrate tools and methods to actual aircraft mean that trends and relative differences are used to measure the improvements offered by the unconventional configuration.
It is clear that the numerical error in the toolchain means that these numbers cannot be relied upon for an absolute empirical judgement of the superiority of the box-wing, but instead they offer a guide as to the optimal geometric configuration on the basis of aero-structural analysis for a given mission. This in turn can be used as a stepping stone for more detailed studies with higher-fidelity models to establish the more detailed designs that offer greater certainty in their calculations.
5.0 CONCLUSION
In 1924, Ludwig Prandtl derived the “best wing system” concept demonstrating that a box-wing system, under proper conditions, provides the minimum induced drag for given lift and wingspan. The box-wing or joined-wing has continued to be the subject of aircraft design research as a potential solution to improving overall efficiency and reducing fuel consumption and emissions. However, this can only be determined if all design aspects are considered, in particular aerodynamics and structures. A methodology and toolchain was developed to conduct a multi-disciplinary analysis of the box-wing configuration. Vortex Lattice Method (AVM) was used for aerodynamic analysis and integrated with a FEM environment, called WingMASS, for structural analysis. This toolchain was applied in a study to compare the fuel burn performance of a box-wing design configuration with that of a conventional aircraft design configuration optimised for a given mission. Semi-empirical methods were included for wing sizing and to compute the aerodynamics and weights for all non-wing components. For the box-wing concept, three geometric parameters were varied: horizontal wing separation, vertical wing separation and aspect ratio. In total, 80 different box-wing designs were analysed based on total fuel required for a given range.
The results show that the box-wing would have a fuel burn reduction of 5% compared to its conventional counterpart for the selected mission. Increasing the horizontal wing separation for weight and balance and stability and control requirements, still leaves a fuel burn reduction of 3%. There is a clear trade-off between aerodynamic efficiency and wing structural weight, which drives these geometric parameters to lower values than those for maximum aerodynamic efficiency (L/D).
Although the actual benefits of the box-wing configuration can only be proven in a detailed design study, the current project shows the potential of fuel burn reduction and the importance of adopting a multi-disciplinary design approach. Future studies will apply the methodology to different mission scenarios to determine if the box-wing is particularly suited for a specific type of mission.
ACKNOWLEDGEMENTS
The help and support of the researchers at the German Aerospace Centre's (DLR) Institute for Air Transport Systems in Hamburg has been incredibly important for this research.














