2.0 THE CONTEXT

A self-contained morphing device, made of links, hinges and joints to alter the inner geometry, is developed with the purpose of providing a standard hinged control surface with an added functionality which may improve aircraft off-design points, such as cruise or climbing. However, similarly to any promising technology to be integrated into aircraft, an estimation of the weight loss or gain is essential with respect to the original configuration, yet not accurate. On the one hand, according to Breguet’s formula, aircraft range strictly depends on aircraft aerodynamic efficiency and the ratio between the maximum take-off weight and the burned fuel weight. On the other hand, it is evident that the benefits associated with morphing in terms of aerodynamic efficiency shall be high enough to compensate for the drawbacks coming from possible structural weight increment. Therefore, in order to gain competitive advantages through morphing devices, it is necessary that, conceptually:

$$\Delta W_{fuel}^E {\rm{ > }}\Delta TOW$$ (1)

where $$\Delta W_{fuel}^E $$ generically indicates the saved fuel weight due to the aerodynamic efficiency (apex E) increment for the effect of the morphing device. ΔTOW is the aircraft maximum take-off weight increment due to the use of the morphing aileron. The herein designed morphing aileron was derived from the previous conventional aerodynamic surface, mounted on a 78-seat aircraft. Its final weight approaches 25 kg. With the aircraft maximum weight around 20 tons, it comes up that the morphing aileron is only 0.13% of the entire aircraft weight. In light of this consideration, the results show that the weight penalty could be easily compensated by the fuel savings ensured by such a morphing technology. During SARISTU project ^{(Reference Carossa, Ricci, De Gaspari, Liauzun, Dumont, Steinbuch, Wölcken and Papadopoulos17)}, it has been demonstrated that the benefit of a morphing flap could be estimated between 3 and 6% for a 20m half-span wing^{(Reference Diodati, Concilio, Ricci, De Gaspari, Huvelin, Dumont and Godard18)}. This benefit can be extrapolated to a rough 0.15–0.3% per m that means, for the referred size, equal to 0.3–0.6%. Furthermore, it should be considered that the analysed region is one of the most effective for the application of these devices. From the manufacturing standpoint, the developed concept consists of many standard pieces and requires careful assembly procedures to support operators. This may affect its industrial applicability. Efforts are currently pursued to simplify the design using topology optimisation methodologies reducing the number of parts.

3.0 AERODYNAMIC LOADS EVALUATION

Three-dimensional in-viscid vortex lattice method^{(Reference Kuethe and Chow19)} was used to calculate pressure coefficient distribution along the wing in correspondence of each considered flight attitude (namely wing angle of attack, flight altitude and speed). Fig. 1 reports the aerodynamic grid used for load computation. The grid represents a wing tip with the morphing aileron positioned at its trailing edge. The mesh is divided in four macro-panels where P1, P2 and P3 represent the wing box (included root and tip), while P4, P5 and P6 are the morphing aileron segments.

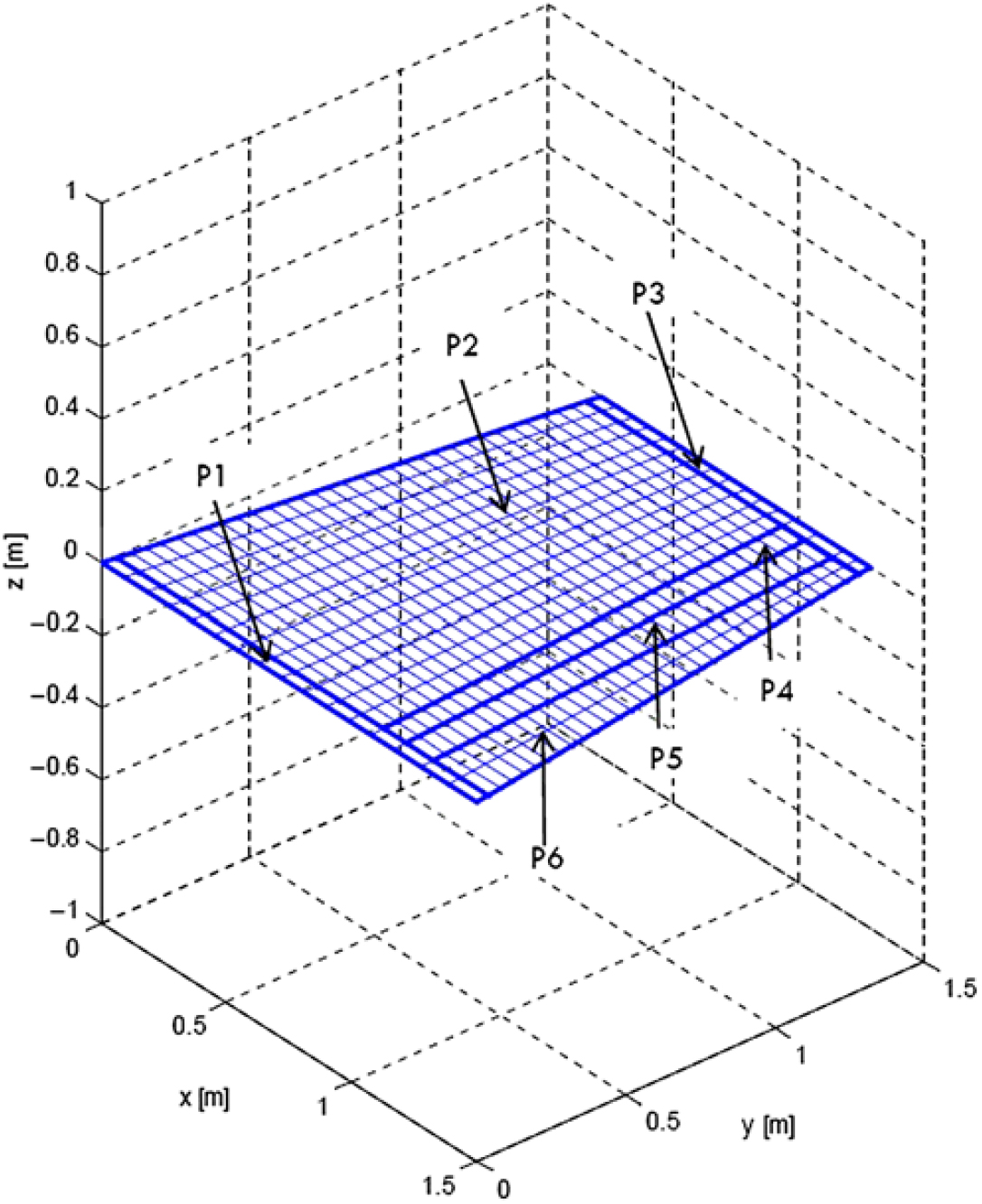
Figure 1. Aerodynamic grid for load computation.

Each panel has been subdivided in several lattice elements that have been reported in detail in the next Table 1, for both spanwise (y direction in Fig. 1) and chordwise (x direction in Fig. 1).

Table 1 VLM Panel Subdivision

For the specific aircraft category, reference operative speeds and wing structural configuration, no loss in aileron effectiveness is expected to occur; aeroelastic effects were consequently considered negligible for the evaluation of the aerodynamic loads and performances of the morphing device. Several cases have been evaluated for different wing angle of attack, rigid aileron deflection around the main hinge axis (namely ε) and angle γ between block B1 with respect to block B2 as shown in the next Fig. 2. The rotation γ is correspondent to the equivalent plain rotation considering the aileron a 1 DOF structure. It has been analysed 15 load cases for various combination of wing angle of attack and aileron deflection as stated in Table 2, showing that the most critical one (24) has been considered for structural sizing and it is widely greater than the maximum load expected in wind tunnel.

Table 2 Load cases considered for aileron structural sizing

Figure 2. Representation of the Aileron Angles ϵ and γ.

3D flat-panel mesh was generated in correspondence to the outer wing segment. For each flight attitude and aileron shape, the lifting pressure (Pi) acting along each box (bi), was calculated according to the following equation:

$$P_i = q_\infty {\rm{(}}P_{0,i} {\kern 1pt} + {\kern 1pt} \alpha P_{\alpha ,i} {\kern 1pt} + {\kern 1pt} \varepsilon P_{\varepsilon ,i} {\kern 1pt} + {\kern 1pt} \gamma P_{\gamma ,i} {\rm{)}} $$(2)

where:

• $$ q = 0.5 \cdot \rho \cdot V_\infty ^2 $$ is the dynamic pressure, ρ the air density at the flight altitude and $$ V_\infty ^2 $$ the airspeed

• α is the wing angle-of-attack

• P _0,i is the pressure arising on b_i due only to unitary dynamic pressure at α and γ equal to zero (airfoil baseline camber effect)

• P _ε,i is the pressure on b_i due only to the unitary ε at unitary dynamic pressure (pressure contribution due to aileron rigid rotation with respect to the wing)

• P _α,i is the pressure on b_i due only to unitary α at unitary dynamic pressure (incidence effect)

• P _γ,i is the pressure on b_i due only to unitary γ at unitary dynamic pressure (morphing effect)

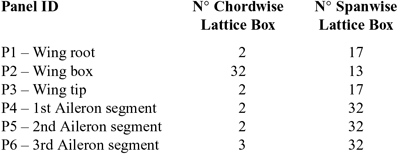
Thanks to Equation (1), P _0,i, P _α,i, P _γ,i where calculated only one time for all the boxes and then combined according to the flight attitude parameters (α, q) and aileron morphed shape (γ) to be investigated under the hypothesis of linearity, i.e. small angles.The combination of α, q, γ leading to the most significant pressure level along aileron segments was then determined and used as design point for structural sizing purpose. The spanwise pressure distribution on the aileron segments at the design point (α = 2°, q = 4425N/m², γ = 7°) are plotted in Fig. 3. This load has been considered as limit load for the design of the aileron structure and actuation system. Fig. 3 reports the pressure distribution along the span and along the three chordwise segments of the aileron. At each spanwise station, you have three values of pressure along the chord: the pressures at the centre of the aerodynamic boxes (Fig. 1) pertinent to the first, second and third segment of the aileron, moreover the pressure contour data on the upper and lower surfaces have been also reported with the resultant global forces.

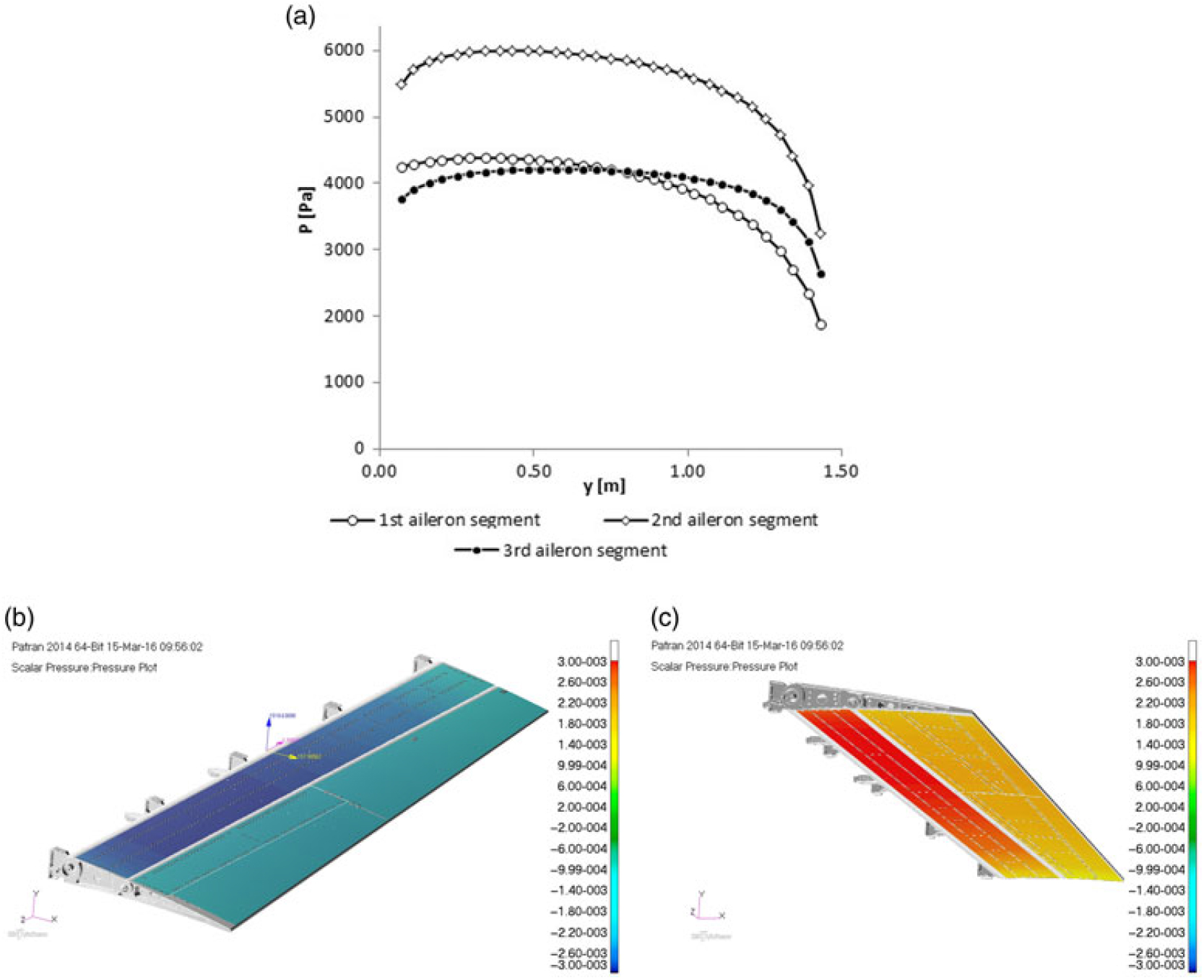
Figure 3. Pressure distribution along aileron span and chord (a) with contour on upper (b) and lower (c) surface. Pressure [MPa].

4.0 THE AILERON STRUCTURE

4.1 The morphing rib

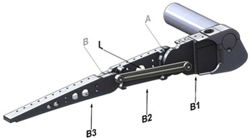
The morphing aileron consists of segmented adaptive ribs based on finger-like segments^{(Reference Pecora, Amoroso, Amendola and Concilio20)} enabling aileron camber morphing upon actuation. Each rib (Fig. 4) is assumed to be segmented into three consecutive blocks (B1, B2, B3) connected to each other by means of two hinges located on the airfoil camber line (A,B). A three-blocks segmentation was considered sufficient in order to meet the desired target shapes. The morphed target shapes have been estimated by means of a 2D aerodynamic optimisation^{(Reference Botez, Koreanschi, Gabor, Mebarki, Mamou, Tondji, Guezguez, Tchatchueng Kammegne, Grigorie, Sandu, Amoroso, Pecora, Lecce, Amendola, Dimino and Concilio21)} with the objective to increase Lift-Drag ratio. Block B1 is rigidly connected to the rest of the wing structure through a torsion tube enabling aileron rotation for roll control. Blocks B2 and B3 are free to rotate around the hinges on the camber line, thus physically turning the camber line into an articulated chain of consecutive segments. A linking rod elements (L) — hinged on not adjacent blocks — forces the camber line segments to rotate according to specific gear ratio.

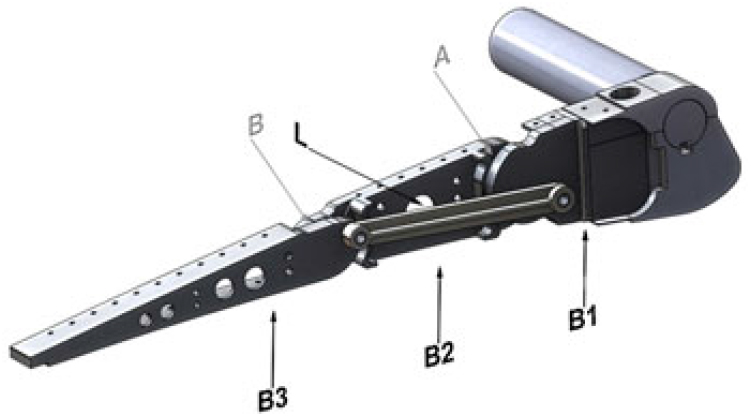
Figure 4. Morphing rib architecture: (a) blocks and links, (b) hinges.

An equivalent representation of the rib mechanism including only the position of the main hinge points is sketched in Fig. 5. In particular, the hinges A and B on the camber line, the hinges L1-1 and L1-2 representing the connection points between the link L and the rib blocks B2 and B3 respectively (see Fig. 4), are depicted. The morphed down configuration (dotted line) is also sketched together with the corresponding kinematic scheme (hinges’ positions in morphed down configuration have been marked with primes). The morphed down configuration was defined as the morphed shape characterised by the same tip displacement (TT’) induced by a rigid rotation of all the aileron around hinge A^{(Reference Amendola, Dimino, Magnifico and Pecora22)}.

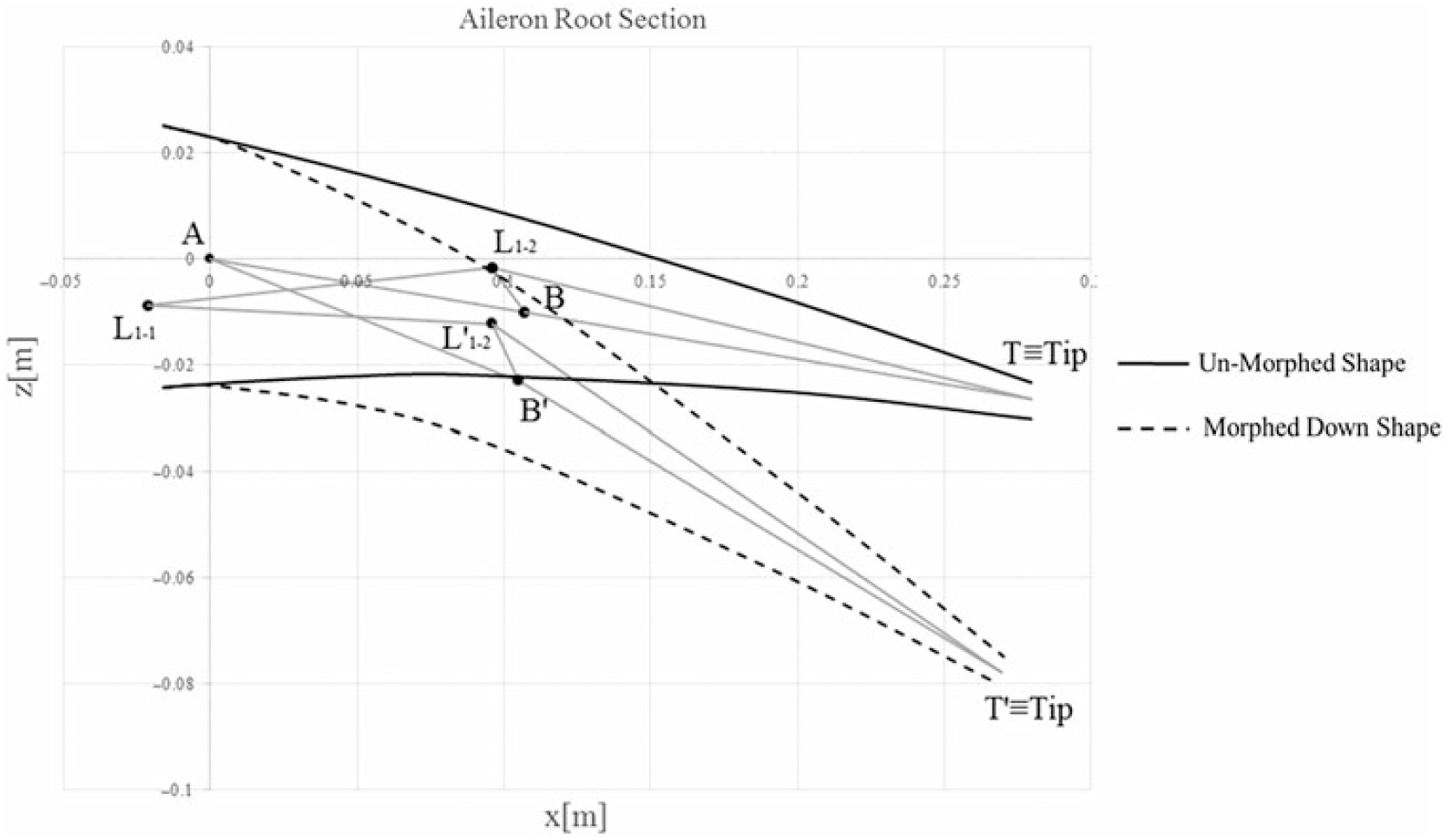
Figure 5. Equivalent representation of the rib mechanism and aileron shapes in un-morphed and morphed patterns.

4.2 The structural skeleton

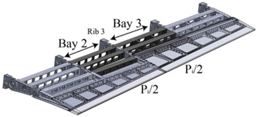
The ribs kinematic is transferred to the overall aileron structure by means of spanwise spars in a multi-box arrangement (Fig. 6). Each box of the structural arrangement is characterised by a single-cell configuration delimited along the span by homologue blocks of consecutive ribs, and along the chord by longitudinal stiffening elements (spars and/or stringers). Upon the actuation of the ribs, all the boxes are put in movement thus changing the external shape of the aileron; if the shape change of each rib is prevented by locking the actuation chain, the multi-box structure is elastically stable under the action of external aerodynamic loads. A four-bay (five-ribs) layout was considered for an overall (true-scale) span of 1.4 meters; AL2024-T351 alloy was used for spars, stringers and rib plates, while C50 steel was used for ribs’ links. Off-the-shelf airworthy components were properly selected for the bearing and bushings at the hinges and coupled to torsional springs to recover any potential free-play. A multi-module skin was considered in conformity to the multi-box segmentation; three aluminium-alloy panels were then adopted, each panel sliding over the consecutive one in an armadillo-like configuration. Airflow leakage at the skin segments interfaces was prevented through low-friction silicone seals. As one might expect, the segmented skin architecture does not significantly affect the aileron torsional stiffness and resulted slightly higher (but on the same order) of a conventional aileron.

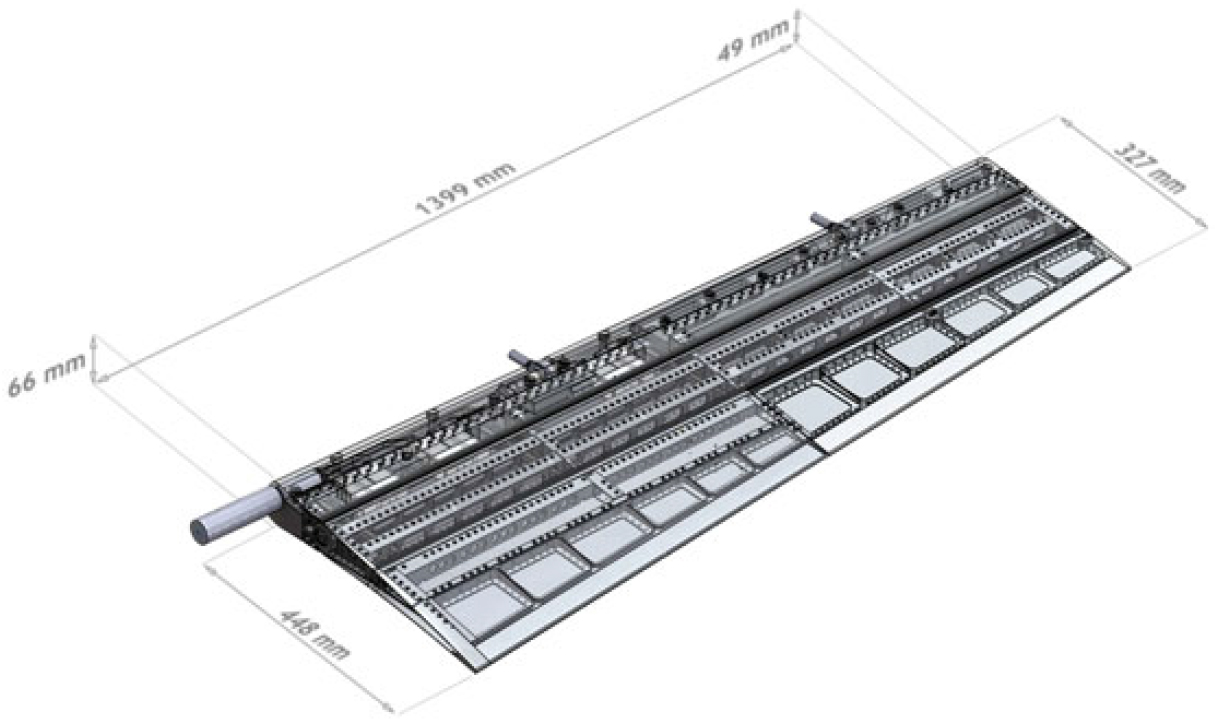
Figure 6. Morphing aileron structure: multi-box arrangement.

4.3 The skin

For typical camber morphing application such as wing trailing edge or aileron, it is important to substitute the conventional skin (rigid and robust) with a flexible one which has to be deformable to allow the structural shape changing and at the same time robust to withstand aerodynamic pressure without yielding. Several design solutions can be found involving innovative materials such as polymeric foam or flexible matrix composites as described by^{(Reference Callister and Rethwisch23,Reference Murray, Gandhi and Vakis24)} . It is important to mention the morphing skin developed inside Saristu Project. It was described by^{(Reference Schorsch, Lühring, Nagel, Pecora and Dimino25)}, and consist of a modular skin composed of flexible segments (foam) and stiff segments (aluminium parts). The entire skin is covered with an adhesive silicone layer to guarantee permanent connection and compactness among deformable foam and aluminium parts. It is evident that the skin design is truly dependent of the current application. This kind of choice, however, presents several drawbacks. The involved materials are not fully tested to the hard environmental conditions, typical of the aircraft operations, and it is expected that some more advance in the material development is necessary before they can safely be installed on-board. For this reason, an intermediate design between conventional and innovative materials was developed. In detail, a segmented skin was adopted, made of several contiguous blocks, sliding over each other. Each box was separately covered by a conventional metallic skin, properly riveted along spars and ribs plates generating an armadillo-like configuration. Rubber sealings were installed to preserve the continuity of the wet surface while covering the gap between the sliding skin panels; each sealing was bonded to only one panel. In this way, one edge resulted free to slide during morphing (Fig. 7), thus not penalising the actuation effort.

Figure 7. Sliding skin and rubber sealings (in black); detail of the sliding skin panels (upper box).

4.4 The kinematic system

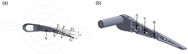
A commercial precision linear guide with recirculating ball carriages was considered (Fig. 8) in order to transmit the actuator torque through the actuation arm. The system is made of a light-weight and compact linear motion rolling guide comprising a U-shaped slip-table and a stainless steel track rail obtained by precision forming. The actuation architecture including the rotary actuator is shown in Fig. 9. The deployment kinematics use a ‘direct-drive’ actuation based on actuation arm that is rigidly connected to the B3 block of Fig. 4. This arm rotates the 1-DOF-based mechanical system and transmits the actuation torque from the actuator to the adaptive rib. The control actions aim at producing small camber variation in the adaptive aileron corresponding to a rigid rotation of a plain control surface comprised between –7° and +7° during flight.

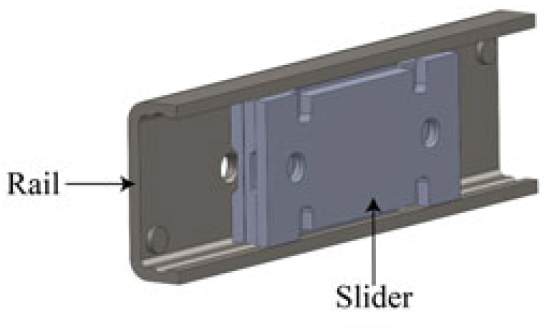
Figure 8. Precision linear guide with recirculating ball carriages⁽²⁶⁾.

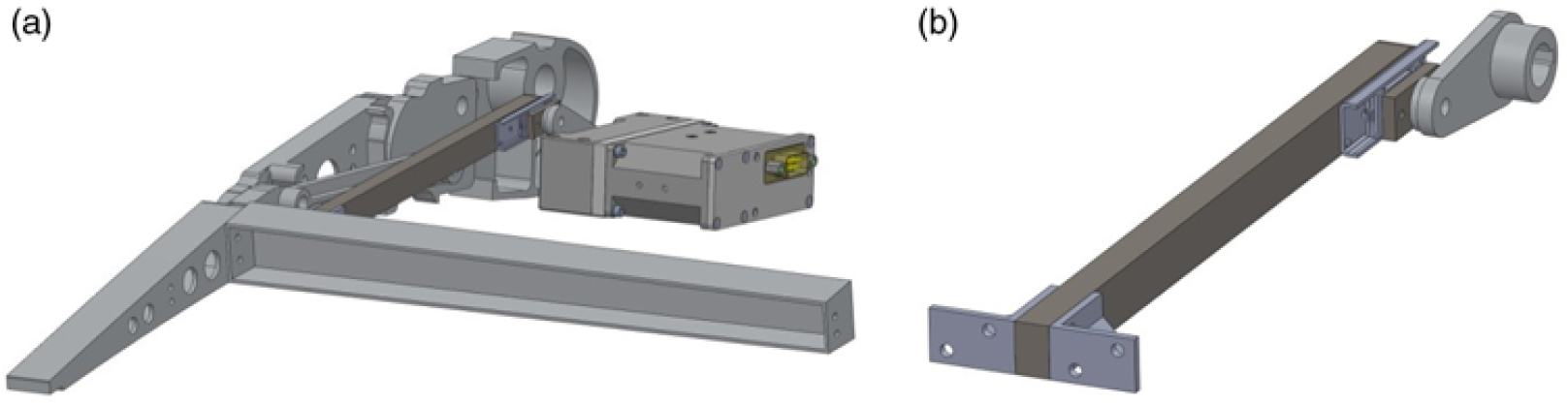
Figure 9. Actuation system using a precision linear guide mechanism.

5.0 ACTUATION SYSTEM

A light-weight and compact leverage was investigated to activate the morphing aileron through electromechanical actuators. An un-shafted distributed servo-electromechanical actuation arrangement is deployed to achieve the aileron shape transition from the baseline configuration to a set of design target shapes in operative conditions. The analytical scheme of the actuation system is based on slider-crank mechanism and its scheme is reported in Fig. 10. The rotational motion of the actuation beam is provided by the crank rotation β which moves the carriage along its guide. A force F is thus generated by the contact between the carriage and the rail. By connecting the actuator shaft to the crank hinge O and the beam to the third rib segment (B3), the actuation torque is transmitted firstly to the crank and secondly to the rib rotating around the hinge V in order to counterbalance the external moment M_rib#3.

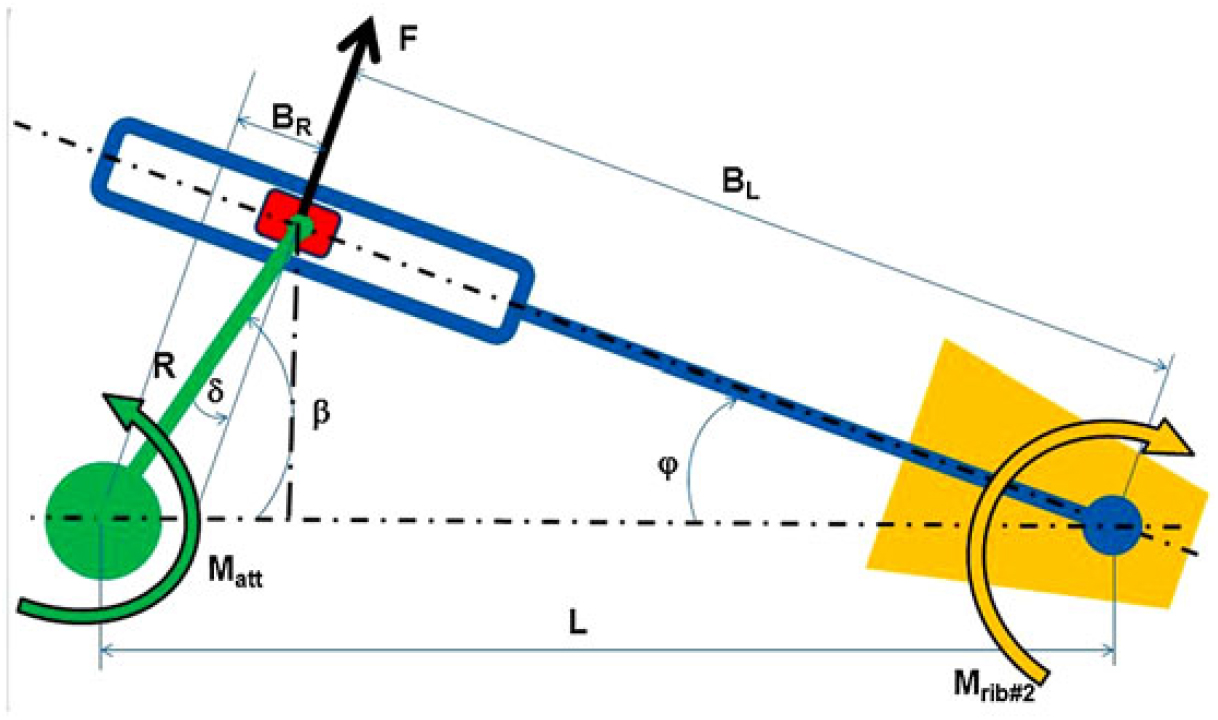
Figure 10. Oscillating glyph connected to the third rib segment of the morphing aileron.

The aileron shape can be, in this way, adaptively controlled to realise small camber variations. The mechanical advantage of the mechanism (indicated as MA) can be written as:

$$ MA = {{LOAD} \over {DRIVER}} = {{M_{rib{\rm{\# }}3} } \over {M_{att} }} = {{FB_L } \over {FB_R }} = {{B_L } \over {B_R }} $$ (3)

where the M_rib#3 is the external moment due to aerodynamic loads estimated with respect to the hinge V, while M_att is the torque provided by the actuator in order to equilibrate the system. F is the force that the crank produces by means of the sliding cursor, B_L is the force arm and B_R is the crank projection along the guide movement direction. Equation (3) shows that the mechanical advantage only depends on the geometrical characteristics of the system, however, combining geometrical terms, it follows that Equation (3) can be written also as function of the angles ϕ and β. It is important to mention that the angle γ, indicated in Fig. 2 as the aileron morphing angle of the blocks 2 and 3 with respect to block 1, correspond to ϕ in the above Fig. 10. The expression of B_L and B_R can be derived:

$$ B_R = R\;\sin \delta \;;\;B_L = L\;\cos \phi - B_R $$ (4)

Substituting then Equation (4) into Equation (3), we obtain:

$$ MA = {{B_L } \over {B_R }} = {{L{\kern 1pt} \cos \phi \;} \over {R{\kern 1pt} \sin \delta \;}} - {\rm{1}} $$ (5)

Another important equation is Equation (8), which allows calculating the actuator shaft rotation (β) needed to achieve a given morphing angle (φ) of the rib block and hence of the entire mechanism. The Equation (8) can be easily obtained thanks to the following mathematical manipulations:

$$ B_L \;\cos \phi {\kern 1pt} = {\kern 1pt} L - R\;\cos \beta \; $$ (6)

$$ B_L \;\sin \phi \; = R\;\sin \beta \; $$ (7)

The ratio between the above equations gives:

$$ \cot \phi = {L \over {R\;\sin \beta \;}} - \cot \beta \; $$ (8)

After estimating MA, it is possible to calculate the actuation torque that the electrical actuator has to supply. Accordingly, the force F should be known in order to verify that the stress arising in the rail carriage does not exceed design allowable levels. The actuation rod is then subjected to the simultaneous action of F and M_rib#3 , both producing bending stress. This indicates that the actuation system design requires a trade-off between the mechanical advantage and the geometrical limits for the actuator shaft rotation and the ratio L/R. The deployment kinematics is based on a direct-drive actuation, moving a beam rigidly connected to the block B3, Fig. 4. The actuation beam transmits the actuation torque to the third rib segment, which then rotates with respect to its original position in a specific plane. All the points rotates around an instantaneous center (IC) of rotation (named V) at a certain time instant. As illustrated in Fig. 11 (a), each point of the third block moves along circles, centered in V. The determination of its coordinates allows estimating the actuation torque, needed to withstand the aerodynamic loads acting on the morphing rib structure.

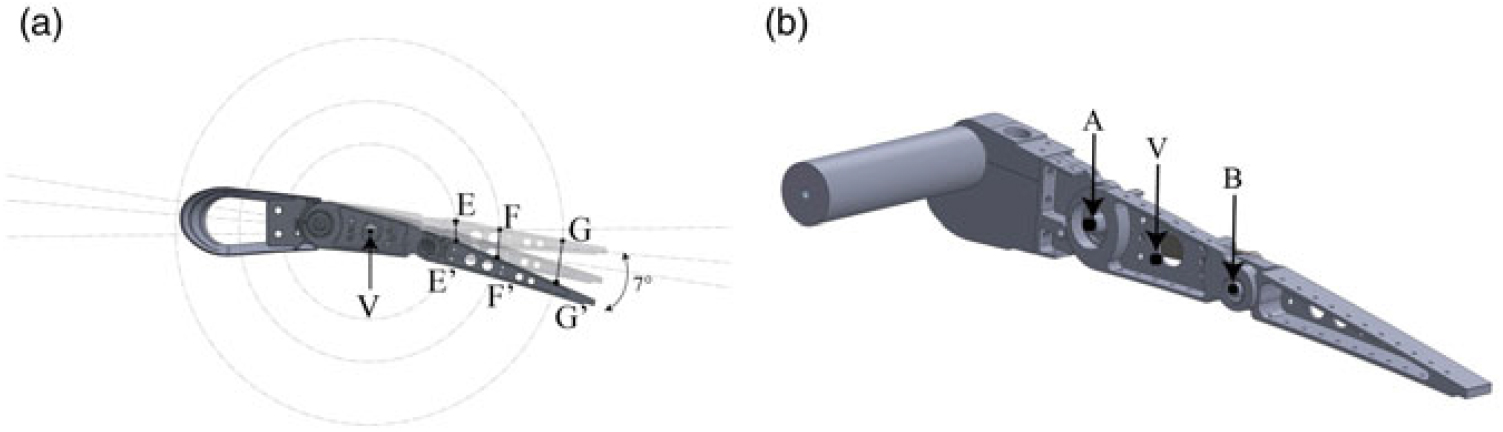
Figure 11. Circular trajectories of sample points (E, F, G) during morphing (a) and hinges position A, V and B (b).

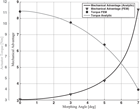
According to such considerations, MA was calculated for different positions of the virtual hinge V. When the rib is morphing down or up, V moves farther or closer to the crank position O, respectively, thus changing the length BL that is directly linked to the MA by Equation (5). It is important to show the graphical trend of the mathematical relation of the MA for different geometrical configurations (distance OV). Several curves are plotted in Fig. 12, where it is noticeable that when the ratio L/R augment (increase the distance of the point V from O), the MA curve (Equation (5)) translates upward toward greater value because the mechanism exhibits a more efficient leverage.

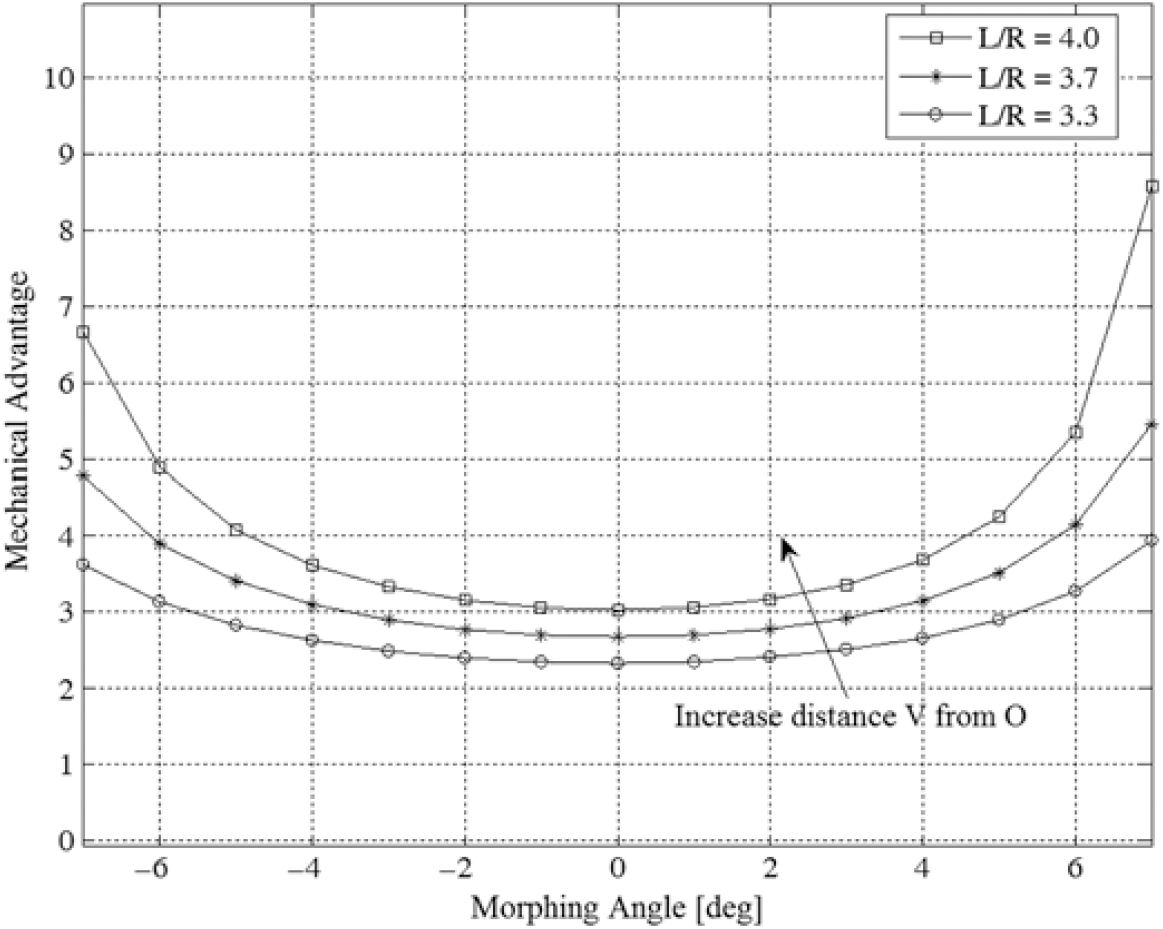
Figure 12. Mechanical Advantage curves with different geometric configurations.

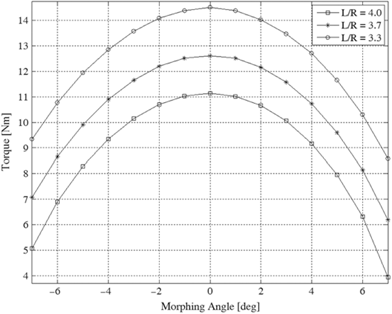
Moreover, the Fig. 13 shows the torque trend with the morphing angle (φ), and it is meaningful to notice that Figs. 12, 13 are interconnected. The torque has been estimated dividing the external moment M_rib#3 by MA in such a manner, the highest curves in Fig. 13, obtained for L/R = 3.3, corresponds to the lowest curve of the MA. There are two contributions to the actuator torque: the external load (maximum in morphed down) and the mechanical advantage. When the aileron is positioned at 0° degree of deflection, the actuator torque is maximum notwithstanding the lower external moment because in this configuration the mechanical advantage reaches its minimum value. Therefore, when the external load increases, the MA increases more than the applied loads resulting in a lower actuator torque. For this reason, in the following Fig. 13, it is visible that at 0 degree the torque become maximum. At this point, for structural sizing, the aerodynamic limit load of paragraph 3 has been applied to the structures at the un-morphed configuration (0 deg) correspondent to the minimum value of the MA (maximum torque).

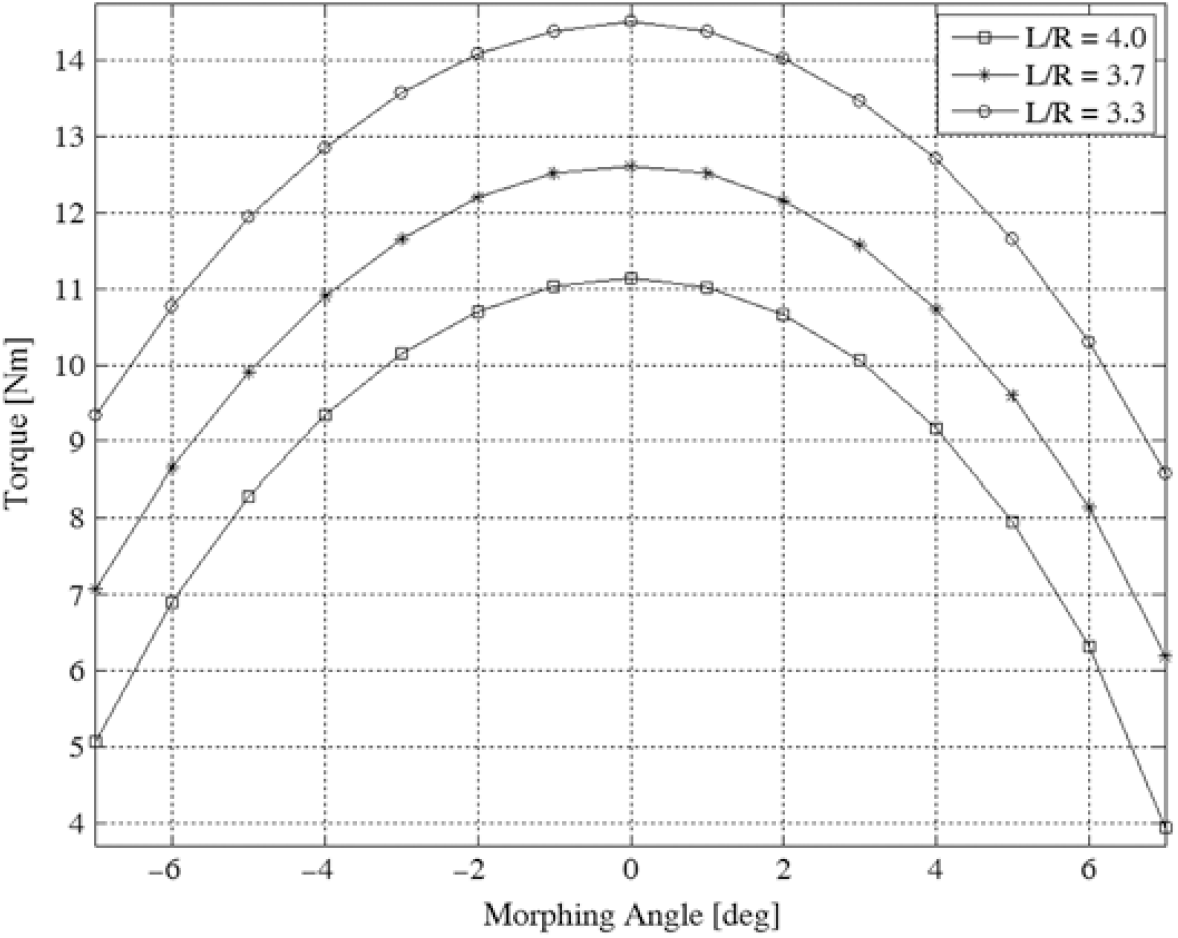
Figure 13. Curves of the actuator torque for several geometric configurations.

In order to preliminarily validate the analytic model, a multi-body simulation, describing the glyph mechanism, has been carried out and the main results are reported in Fig. 14.

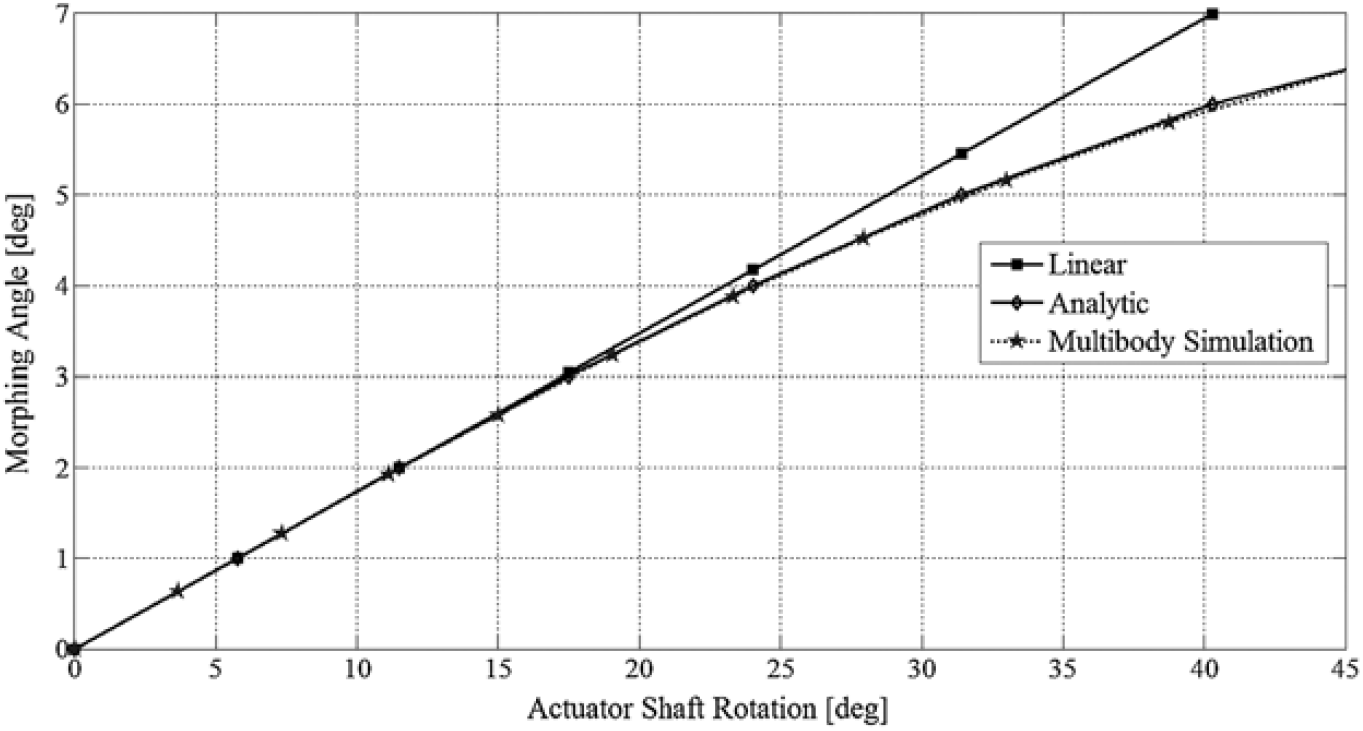
Figure 14. Comparison among linear, analytic and multi-body simulation of the Equation (2).

The diagram shows a good correlation between the results provided by the model described by Equation (8) and the numerical simulations. For small actuator rotations, the functional relationship is practically linear. However, at high values of β, this assumption cannot be hold because it is conspicuous a large deviation from the linear trend.

6.0 NUMERICAL MODELING AND RESULTS ANALYSIS

Pressure distribution calculated by means of vortex lattice method (paragraph 3), was approximated by equivalent lumped loads applied to each aileron rib, according to the scheme shown in Fig. 15 concerning Rib 3 between Bay 2 and 3. In this phase we are interested to compute, for the most loaded rib (Rib number 3), the moment with respect to the instantaneous centre V imposing a constraint to that point. A detailed FE model of the morphing rib was carried out, as reported in Fig. 16 where the rib has been modelled by TET10 elements. Block B1 was considered fixed, and the out-of-plane displacements of B2 and B3 were constrained. The rib block B3 was connected to V through rigid MPC of the RBE2 typology⁽²⁷⁾.

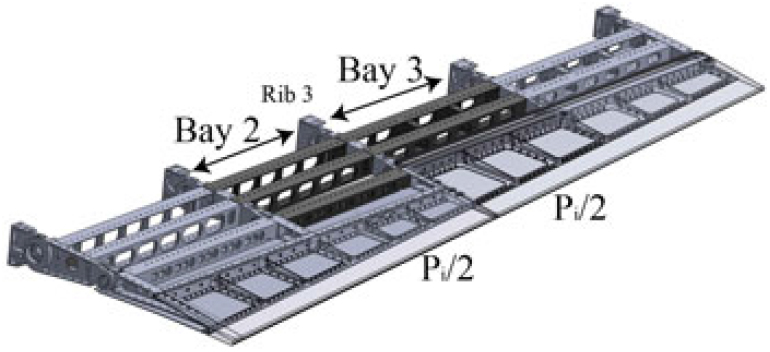
Figure 15. Sketch of the concentrated loads evaluation (hidden skin).

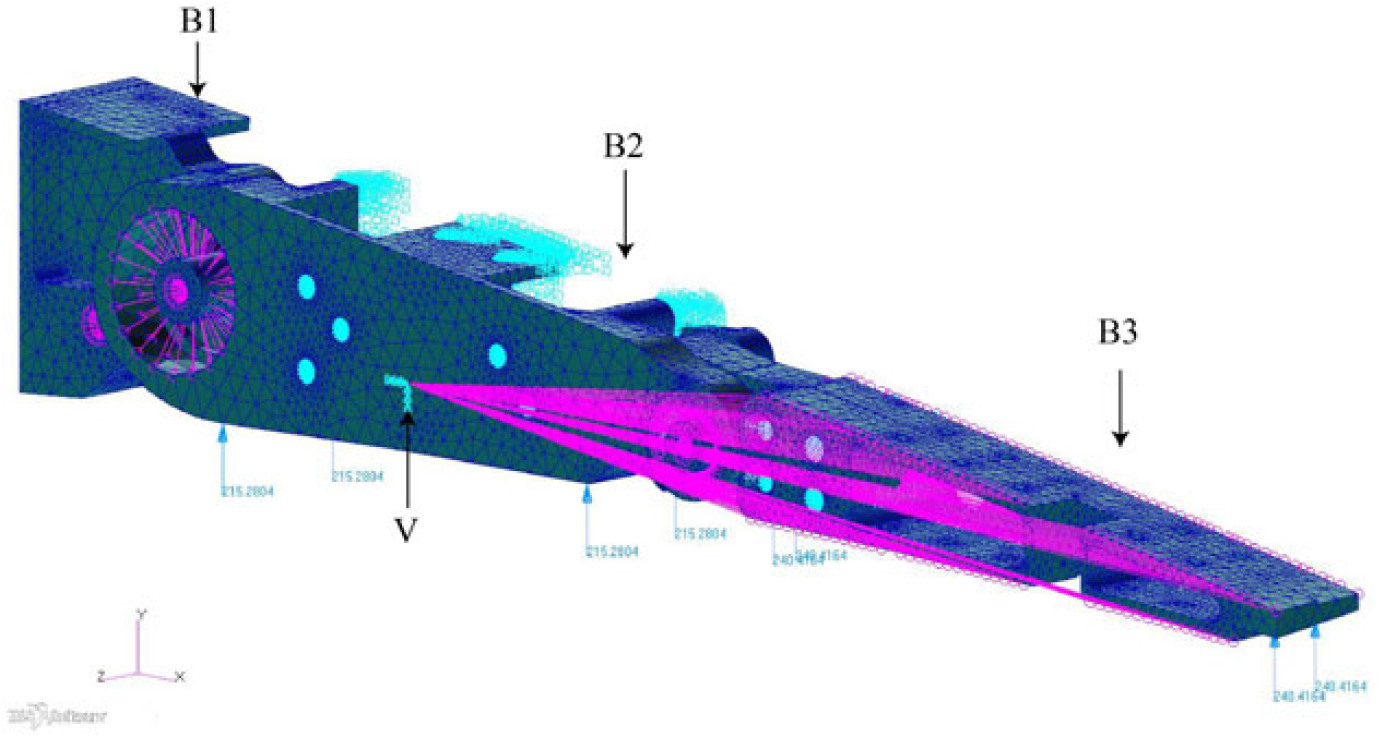
Figure 16. Complete FE model of the aileron rib.

A static analysis was carried out to calculate the operational moment M_rib#3 resulting from the limit load. The aerodynamic moment applied to the rib (indicated as M_rib#3 ) has been divided by the MA in order to predict the actuator torque needed to withstand the operative loads. The main results are recapped in the Table 3.

Table 3 Actuator torque values

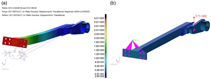
The results indicates that a rotary actuator must provide a torque equal to ~ 4 Nm in order to equilibrate the rib under the external loads. The next step consist of a detailed analysis on the actuation system including the precision linear guide with recirculating ball carriages, the crank and the actuation beam. It is important to mention that the kinematic chain has been integrated into the rib geometry, as previously shown in Fig. 9, so that the geometrical parameters (L/R, B_R and B_L ) are fixed to the design value and for this reason the MA and Torque curves are uniquely defined. The value of L/R is equal to 4 for the kinematic examined. The items of the kinematic chain were then modelled by means of finite elements using TET10 elements and only the results representative of the worst condition are reported (0 deg of morphing). A linear static analysis was, in a first approximation, performed. The aim of the numerical simulation was to verify if the vertical static force acting on the linear guide was below the allowable value prescribed by the producer. In the real operative condition, the linear guide is free to slide along its rail by means of the actuator shaft rotation transmitted by the crank. Being free to move, the guide is not subjected to stress in the direction of motion. Force are transmitted in the vertical (with respect to the guide axis) and, partially, normal direction (with respect to the guide plane). This is its regular way of working. For the current application, the actuator system was sized, referring to the jamming condition, considered as the most critical. In fact, the larger extent of the constraints (additional clamps) is expected to lead to higher stresses, locally (in the contact region) and distributed (overall). When the linear guide is blocked in fact, the actuation beam is simultaneously loaded with the external aerodynamic moment (respect to V), the vertical static force acting on the slider and a horizontal component (linked to the jamming), both producing a pure bending state with a higher stress level rather than the free guide. These considerations are validated by the study conducted by^{(Reference Dimino, Flauto, Diodati, Concilio and Pecora14)} where a non-linear simulation was conducted, showing a low level of structural stress. The hypothesis of a perfect bonding between the rail and slider was formulated and implemented; in such manner, the analyses was then conducted. The kinematic analysis is aimed to estimate the stress and the force acting on the linear guide item. A conservative approach has been assumed where the baseline (un-morphed) structure, whose actuation chain exhibits the lowest mechanical advantage, was loaded by the highest aerodynamic moment (33.81 Nm) associated with the morphed configuration (+7 deg). FEA results are reported in Fig. 17, in terms of total displacements (maximum value: 3.01 mm at beam tip) and load transmitted to the guide (maximum value 371 N).

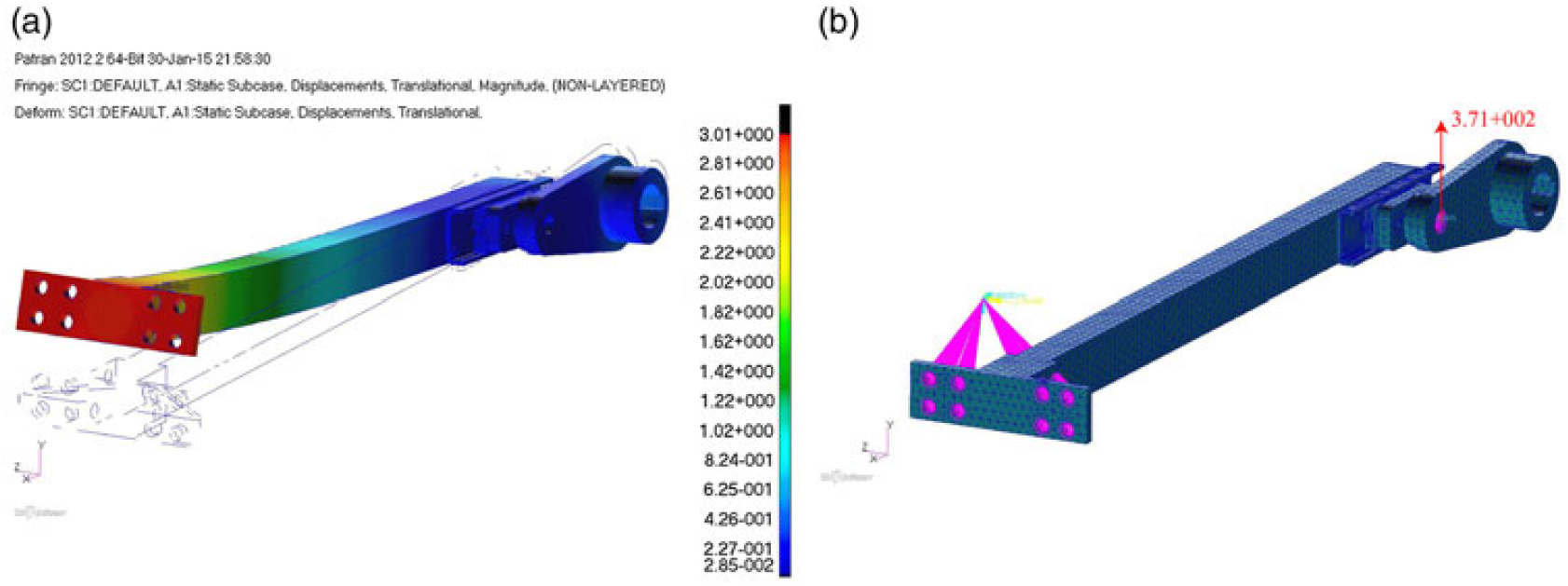
Figure 17. Beam displacement contour (a); guide reaction loads of 371 N (b) at 0° of morphing.

Furthermore, the stress acting on the linear guide are depicted in Fig. 18. It is reported the Von Mises magnitude stress on the left and its component along x direction on the right image. It is noticeable the high stress level in the direction of motion that will become null when the guide slides.

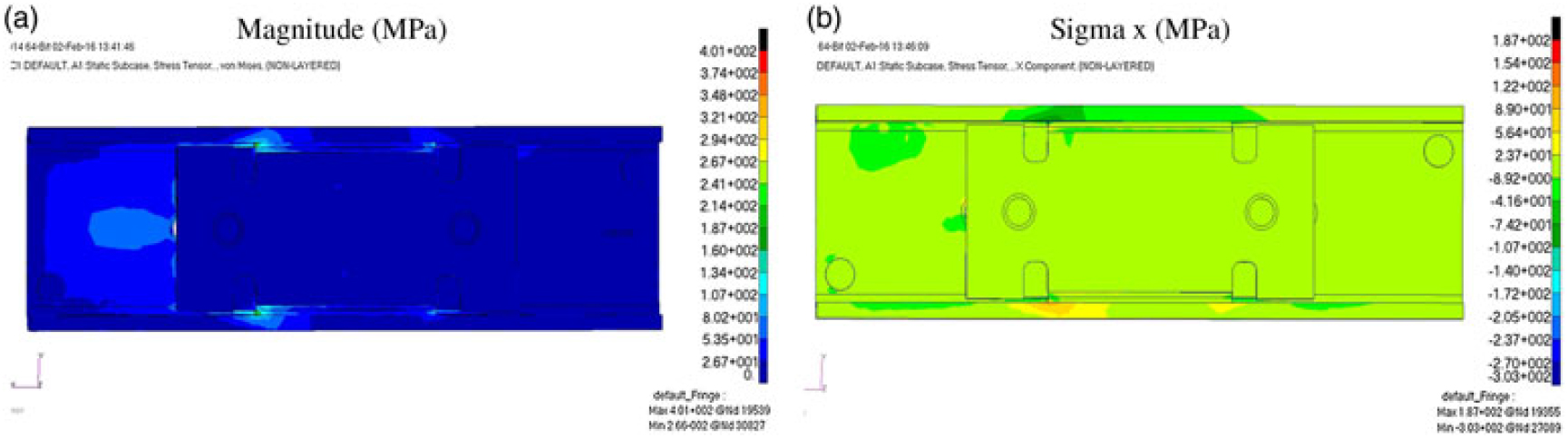
Figure 18. Stress contour on linear guide (slider plus rail), Von Mises a) and X component b).

Moreover, as expected, high local stress in the contact region was found (Fig. 19).

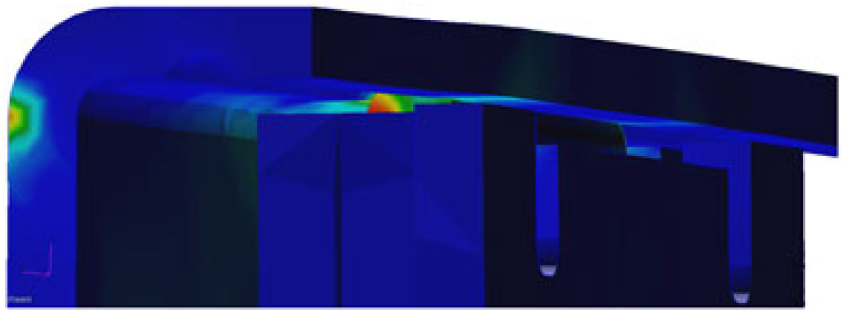
Figure 19. Stress peak in the contact region between slider and rail.

In Fig. 20, it has been reported a comparison between analytical model (Equation 4) and finite element results for the mechanical advantage versus Morphing Angle (ϕ) and finally for the actuator torque during the rib deflection. The graphs in Fig. 20 are estimated for the design value of the distance OV. An excellent agreement between the two curves was achieved.

Figure 20. Comparison between analytical and numerical trend of Actuation torque and Mechanical Advantage versus Morphing Angle (ϕ).

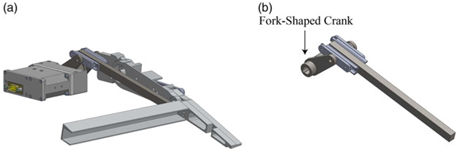
As results of the previous FEM, the maximum static force acting on the linear guide is 371 N. However, being the maximum allowable static force that can be applied to the linear guide limited to 140 N (prescribed by the producers⁽²⁶⁾, it was then demonstrated that single-sided linear guide solution was structurally inadequate. Other designs have been addressed also by^{(Reference Amendola, Dimino, Magnifico and Pecora22)}. As a result, an alternative linear guide-based device based on a non-recirculating ball carriage was investigated, as shown in Fig. 21. This device exhibits substantial benefits, mostly resulting in an increased allowable static force equal to 232N. In addition, in order to mitigate the maximum counterbalancing load acting on the guide to equilibrate the aerodynamic moment, a fork-shaped crank coupled with a double-sided linear guide was also preferred, as shown in Fig. 22. Nevertheless, such a solution resulted in a lower mechanical advantage for the given morphing angle due to the slightly lower BL.

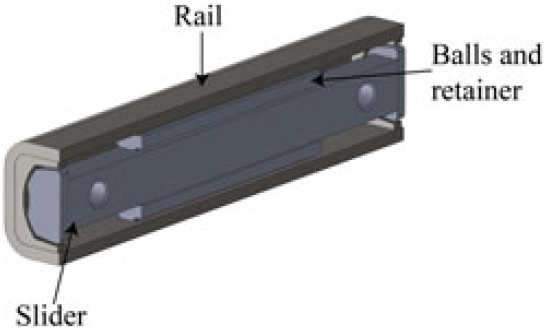
Figure 21. Precision linear slide with non-recirculating ball carriages.

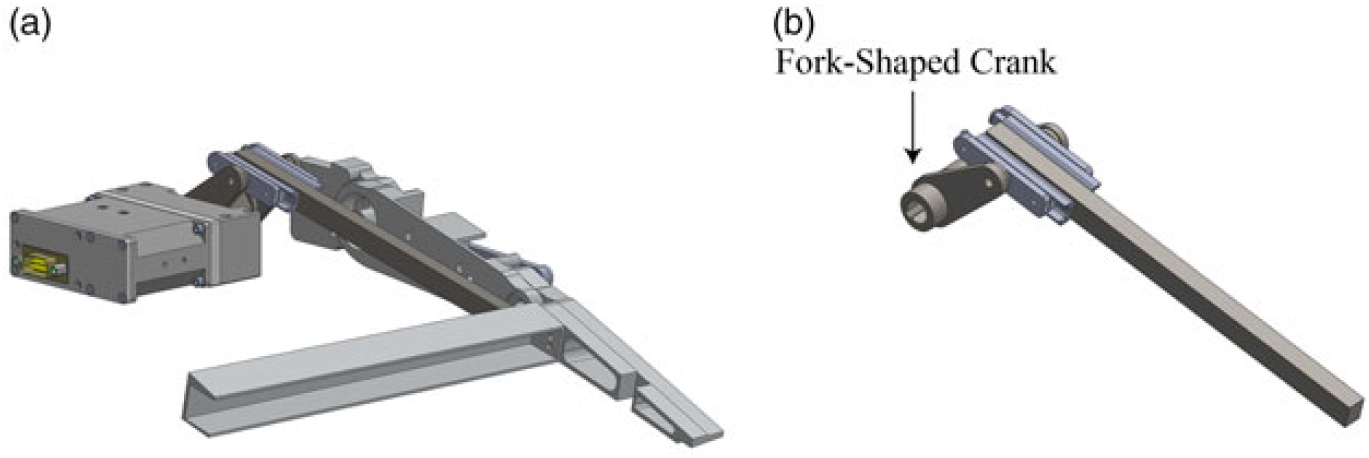
Figure 22. Double sided linear guides-based actuation system driven by a fork-shaped crank.

Figure 23 shows the actuation forces needed to withstand the aerodynamic load arising in the morphed configuration (+7 deg). Moving from a single to a twin guide, it is verified that the MA as a function of the morphing angle, assumes lower values. As a consequence, actuator torque reduces slower than before. Because the effective arm (B_R ) reduces as the morphing angle increase, the actual forces on the crank hinges grow as a function of that rotation. Therefore, the most severe condition in terms of vertical force results the one at max deflection (7 deg). Results are summarised in Table 4. It is clearly noticeable that although in baseline (un-morphed) condition, the actuation chain is subjected to lower pressure loadings, the actuation system shall provide higher torque in order to balance the external aerodynamic moment. Compared to the single guide-based actuation system, the designed architecture reaches a mechanical advantage of just 4.20 at +7 deg.

Table 4 Comparison between analytical and numerical results for the linear guide-based actuation system

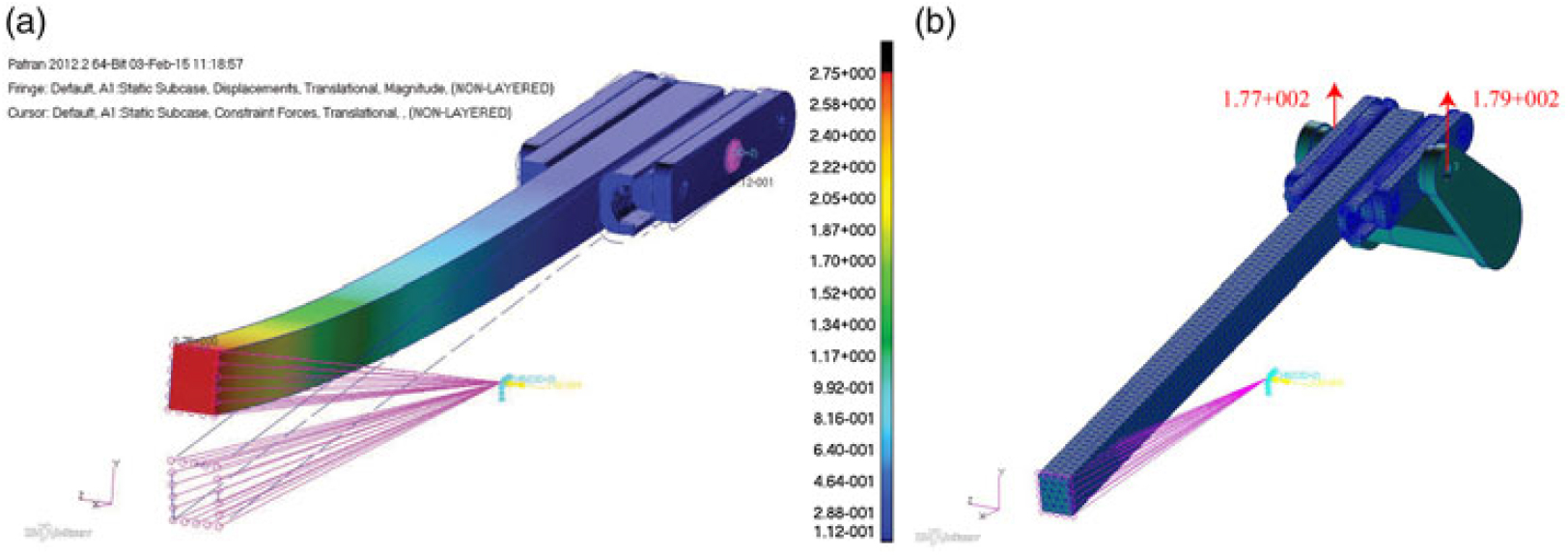
Figure 23. Actuation beam displacement contour (a); guide reaction loads of 177 N and 179 N respectively (b).