NOMENCLATURE
- EI
-
vertical bending stiffness (Nm2)
- F
-
shear force (N)
- h
-
half-length of gust wave (m)
- V
-
equivalent air speed (m/s)
- mg
-
weight distribution along span (N/m)
- M
-
bending moment (Nm)
- n
-
load factor (-)
- S
-
distance along wing semi-span (m)
- z
-
vertical wing-tip deflection (m)
Subscripts
- A
-
manoeuvring conditions
- D
-
design conditions
- g
-
gust
- CS
-
certification specifications
1.0. INTRODUCTION
The wings of high-performance sport sailplanes experience significant deformations in flight. These, in turn, can influence the dynamics of the glider. Bending deflections during manoeuvres and in gusts depend both on the aspect ratio and the structure of the wing. For sailplane wings, the aspect ratio is typically high(Reference Thomas1); depending on the competition class, the wing span can range from 13.5 m (wing aspect ratio of about 20) up to 30 m (wing aspect ratio of 40 and more). The wing spar is usually made from carbon-fibre-reinforced polymer and the relative thickness of the wing near the fuselage rarely exceeds 15% of the chord. At these conditions, wing-tip deflection in sailplanes of the popular 18-metre class can exceed 10% of the wingspan and therefore may significantly affect the dynamic wing loads.
Unmanned aerial vehicles have become very popular recently. Some of them are very flexible and are built with lower safety factors than manned aircrafts. Even though exceeding manoeuvre loads can be avoided by appropriate control, gust loads can be catastrophic for very flexible wings(Reference Noll, Brown, Perez-Davis, Ishmael, Tiffany and Gaier2).
Given the importance of wing deformation, the flight dynamics of and flight loads on flexible wings have been the subject of a number of recent studies( Reference Xiang, Yan and Li 3 - Reference Patil and Hodges 7 ). However, only a few recent publications focus on gust loads of sailplanes. Chudý(Reference Chudý8) analysed the response of a 14-metre sailplane for gusts. He applied continuous turbulence and a discrete gust of the 1-cosine form. The static formulae from the EASA CS-22 document (certification specifications(9) describing load cases for assuring structural integrity at all operating conditions) and dynamic response were applied for the discrete gust. Computational comparison of static formula and dynamic response showed similar results. The dynamic load factor was only 0.66% higher, while bending moment and shear force were respectively 1.18% and 0.24% lower. However, in the analysis, the wing-tip deflection of 14-metre sailplane dive to a gust was negligible. That is why Chudý did not analyse the influence of wing deflection in gust.
Waibel(Reference Waibel10) analysed the possibility of applying EASA CS-22 procedures for very light sailplanes focusing on the gust loads. However, he did not considered influence of flexibility.
Considering that wing-tip deflections exceeding 10% may considerably affect the gust loads, the present paper aims to examine the influence of wing flexibility on gust loads for 18-metre-span sailplanes.
This paper describes how the bending flexibility of sailplane wings affects a ‘1-cosine’ gust loads. The wing experiences bending and torsional deformations. Torsional moments and vertical deformations can be controlled using wing sweep near the wing tip. For that reason, the present article deals with the effect of wing vertical bending on the gust loads. The critical wing section for only the vertical bending moment and vertical shear force is usually at the root of the wing. The bending moment and shear force at the wing root in different critical gust conditions were compared to the bending moment and shear force in the steady straight gliding flight of a rigid sailplane.
2.0 METHOD AND MODEL
Load factors of the manoeuvring envelope and the calculation of the manoeuvring speed, VA , and design speed, VD , are described in CS-22(9). Limit manoeuvring load factors of the utility sailplane category are shown in Table 1.
Table 1 Limit load factors for the utility category(9)

The formula for the gust load factor in(9) is derived for the rigid aircraft, assuming no pitching, for the ‘1-cosine’ gust shape(Reference Flomenhoft11):
 $$\begin{equation}
n = 1 \mp k\left[ {\frac{{{\rho _0}\ U\ V\ a}}{{2\frac{{mg}}{S}}}} \right],
\end{equation}$$
$$\begin{equation}
n = 1 \mp k\left[ {\frac{{{\rho _0}\ U\ V\ a}}{{2\frac{{mg}}{S}}}} \right],
\end{equation}$$
where ρ0 is the density of air at sea level (kg/m2), U is the gust velocity (m/s), V is the equivalent air speed (m/s), a is the slope of the wing curve per radian, m is mass of the sailplane (kg), g is acceleration due to gravity (m/s2), S is the wing area (m2) and k is the gust-alleviation factor.
During flight through the gust, the pitch angle is changing. Bending deflections of the wing shift the centre of gravity vertically in comparison to the centre-of-gravity (c.g.) position of the rigid aircraft. In addition, the bending movement of the wings changes the local angle-of-attack distribution and, consequently, the lift-load distribution along the span(Reference Hoblit12,Reference Wright and Cooper13) .
For modelling sailplane wing-bending flexibility on gust loads, the ASWING software(Reference Drela14) was used. It solves aerodynamic, structural and flight dynamics equations simultaneously. Nonlinear beams model aerodynamic surfaces and the fuselage of the aircraft. The beams are defined by mass, inertial and aerodynamics properties. The aerodynamic model uses a lifting-line method with unsteady effects. Sources plus doublet lines are used to model slender bodies. Such an algorithm allows large deformations of flexible parts.
The ASWING software has been shown to be an effective tool for the preliminary analysis of flexible aircrafts in difficult flight conditions(Reference Drela15,Reference Drela16) .
The sailplane model used for the present analysis describes a typical 18-metresailplane. A three-view generated with ASWING is shown in Fig. 1.

Figure 1. Three projections of our sailplane model as implemented in the ASWING software. Sensor 1: acceleration at the centre of gravity of sailplane; Sensor 2: deflection at the right wing tip.
The dihedral angle of the wing in this model is set to zero for a clearer depiction of the bending deflection. The dihedral angle of real sailplanes is about 3°. Usually, the dihedral angle increases at the wing tip with a transition into winglets.
The main parameters chosen for the model are presented in Table 2.
Table 2 Parameters of the model

The distribution of mass and vertical bending stiffness of the wing is shown in Fig. 2. The torsion stiffness of the wing bending is set to infinity (that is, rigid). Two lines of mass distribution are depicted in Fig. 2. The first line—from wing root to wing -tip—represents the mass distribution in the wing structure, and the second line—from 0.050 to 0.817 of wing semi-span (S/Smax )—represents the mass distribution of the water ballast in the wing.
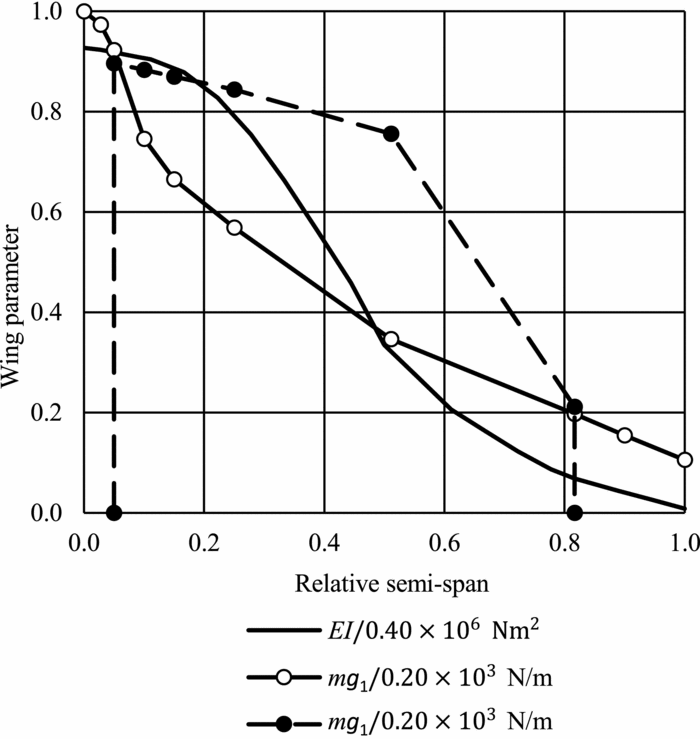
Figure 2. Mass and stiffness distribution of the wing as implemented in the ASWING model.
3.0 RESULTS AND DISCUSSION
The analysis of bending influence is conducted at sea level. According to the formula(9), the gust-load factor for the analysed model at the design gust speed is ngCs = 6.180. Figure 3 shows the bending-moment distribution along the wing semi-span for steady straight glide and for a load factor of 6.180 for a rigid sailplane during stationary load.

Figure 3: Bending-moment distribution along the wing semi-span for steady straight glide and for a load factor of 6.180 for the rigid sailplane.
The maximum bending moment at the wing root for steady straight glide is M 1 = 5.93 kNm. This is the reference value for the comparison of all of the wing-bending moments at the root. The maximum bending moment at the wing root for a load factor of 6.180 is MgCs = 31.11 kNm. The relative bending moment in this case is (MgCs /M 1) = 5.246. The increase of bending moment is not exactly proportional to the load factor increase. This no-proportionality depends on mass distribution between wing and fuselage. The shear forces at the wing root are trended in a similar manner. The maximum shear force at the wing root for steady straight glide is F 1 = 1.325 kN. This is the reference value for comparisons of wing-shear forces at the root. The reference value for the wing-bending deflection is the wing-tip deflection z 1 = 0.484 m for steady straight glide of the flexible sailplane.
For design-load determination, the gust profile is considered to be of a ‘1-Cosine’ shape, with a ‘gradient distance’ of 12.5 chords(Reference Hoblit12). Different wavelengths of gust were analysed.
It is assumed that the design gust speed equals the design manoeuvre speed (see Table 2). EASA CS-22(9) prescribes that a sailplane must safely withstand a vertical gust of ±15 m/s at the design gust speed and a gust of ±7.5 m/s at maximum design speed. Before entering the gust of 15 m/s, the sailplane was trimmed at the design gust speed, and before entering the gust of 7.5 m/s, the sailplane was trimmed at its design maximum speed. The control stick was assumed to be fixed during the flight through the gust. The pitching angle varies according flight dynamics. Figure 4 shows a range of flight parameters versus time when the rigid sailplane flies through vertical gust of 15 m/s and a half-length of h = 15 m. Figure 5 shows the same parameters for the sailplane with flexible wings. Specifically, Figs 4 and 5 show from top to bottom: wing-tip deflection, wing-bending moment at the root, wing shear force at the root and acceleration at the c.g.

Figure 4. Time history of flight parameters from ASWING; rigid wing, gust: 15 m/s, speed before gust: 63.9 m/s, half-length of gust wave: 15 m.

Figure 5. Time history of flight parameters from ASWING; flexible wing, gust: 15 m/s, speed before gust: 63.9 m/s, half-length of gust wave: 15 m.
For the rigid sailplane (see Fig. 4), the wing-tip deflection is zero by definition. For the three other parameters (bending moment, shear force and acceleration), the maximum values appear simultaneously. In contrast, for the flexible wing (see Fig. 5), the maximum values appear at different points in time. The acceleration and shear force reach their maximum first, then the bending moment, and finally the wing-tip deflection.
The maximum values of these parameters depend on the gust wavelength. Figure 6 shows the relative maximum loads versus half-length of the gust wave for the flexible sailplane. (The relative loads are normalised relative to the values at steady straight glide.) Relative loads reach their maximum for gust half-lengths of approximately 15-20 m.

Figure 6. Relative maximum loads on the flexible wing; speed: 63.9 m/s, gust: +15 m/s.
Figure 7 shows the relative shear force versus half-wave length, together with a comparison of the relative maximum shear forces at the wing root of flexible and rigid wings versus half-length. The additional dashed line gives the relative shear force at a manoeuvre load factor of n 1 = 5.3, which does not depend on the gust wave length. The square symbol marks the relative maximum shear force at the root of the rigid wing during stationary load at a gust load factor of n g CS = 6.180 (wave half-length of 12.5 chords). The maximum shear force for the flexible wing does not exceed the one for the manoeuvring load.

Figure 7. Relative shear force at wing root of flexible and rigid wings; speed: 63.9 m/s, gust: +15 m/s.
An analogous comparison of relative maximum bending moments is shown in Fig. 8. The maximum bending moment for the flexible wing does not exceed the one at the manoeuvring load. The shear force acting on the rigid wing and the bending moment of the rigid wing in gust are higher than the corresponding values for the rigid wing at CS-22 gust load. The reason for this may be the no-pitching assumption for the gust-load formula in CS-22.

Figure 8. Relative bending moment at wing root of flexible and rigid wings; speed: 63.9 m/s, gust: +15 m/s.
The load factors at the c.g. of the rigid sailplane are compared to the gust loads with a flexible wing in Fig. 9. The maximum load factor for the flexible wing does not exceed the manoeuvring load factor of n 1 = 5.3.

Figure 9. Relative acceleration (load factor) of flexible and rigid wings; speed: 63.9 m/s, gust: +15 m/s.
In Fig. 10, the maximum shear-force value for the flexible sailplane and the CS-22 values from Fig. 6 for a flight speed of 63.9 m/s and a gust velocity of +15 m/s are compared with other combinations of speed and gust velocity, showing the relative shear force at the wing root when the sailplane flies through the gust. At design gust speed, V = 63.9 m/s, the gust maximum vertical velocity is ± 15 m/s, and at design maximum speed V = 94 m/s, the gust maximum vertical velocity is ± 7.5 m/s. Shear forces are given relative to the shear force during steady straight glide. Positive and negative maximum loads occur at the gust design speed. The positive shear force was explained considering Fig. 7. Here we discuss negative shear force. The value of negative maximum shear force for the flexible wing is lower (74.9%) than the force at CS-22 gust load factor, but higher (120.4%) than the force at CS-22 manoeuvring load factor.

Figure 10. Relative wing shear force at wing root.
Figure 11 shows the relative bending moment at the wing root as the sailplane flies through the gust at the same conditions as considered for the analysis shown in Fig. 10.
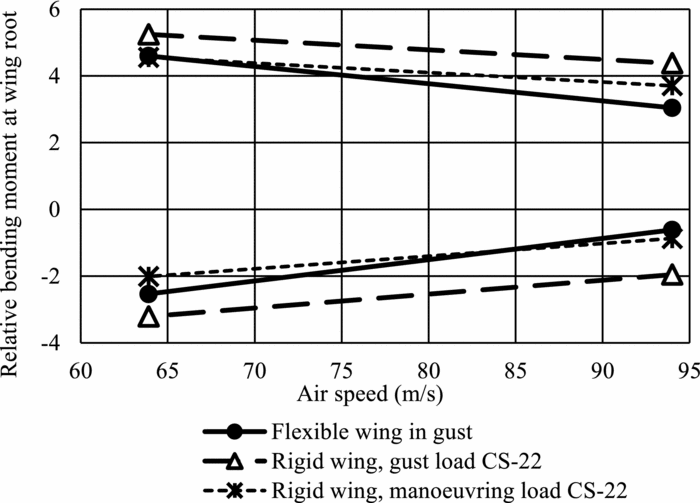
Figure 11. Relative wing-bending moment at wing root.
The bending moments are again given relative to the bending moment during steady straight glide. Also here, positive and negative maximum loads occur at the gust design speed. The positive bending moment was explained considering Fig. 8. Here we discuss negative bending moment. The value of negative maximum bending moment for the flexible wing is lower (78.9%) than the moment at CS-22 gust load factor, but higher (126.0%) than the moment at CS-22 manoeuvring load factor.
4.0 CONCLUSIONS
In contrast to the 14-metre sailplane considered by Chudý(Reference Chudý8), the influence of wing bending flexibility on gust loads is considerably higher for a 18-metre sailplane. The difference of loads for rigid and flexible sailplanes with 14-metre spans is on the order of only 1%, whereas this difference is about 20% for an 18-metre sailplane.
Wing gust loads depend on the gust wave length. Maximum gust loads on bending flexible wings are lower than gust loads on rigid wings, in accordance with the Certification Specifications for Sailplanes and Powered Sailplanes CS-22.
For the typical sailplane with an 18-metre wingspan as analysed here, the maximum positive gust loads do not exceed the manoeuvring loads. Maximum negative gust loads exceed the manoeuvring loads, but not more than 26%, and they are about 21% below the gust loads specified in CS-22.
During cross-country flight, a sailplane needs to extract energy from atmosphere. Usually it gets the energy through circular flight in vertical thermal columns (thermals). While gliding from one thermal to another, the sailplane crosses different thermals, encountering gust loads and energy exchange with atmosphere. Further studies in this area should be on coupling between bending and torsion deformations, as this coupling should reduce gust loads and maximize the energy gain.
The obtained values may not be applied to all sailplane models. Carefully analysis must be performed in each case.















