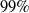Nomenclature
- a
-
action
- A
-
action advantage
- ANN
-
artificial neural network
- BLDC
-
brushless direct current
- CNN
-
convolutional neural network
- D
-
environment emulator
- DQN
-
Deep Q-Network
- DRL
-
deep reinforcement learning
- Et
-
expectation
- ER
-
experience replay
- FFT
-
fast Fourier transform
- FPR
-
false positive rate
- g
-
gradient estimator
- GD
-
gradient descent
- GRU
-
gated recurrent unit neural network
- IMU
-
inertial measurement unit
- K
-
number of classes
- KNN
-
K-nearest neighbours
- L
-
loss function
- MLP
-
multilayer perceptron
- N
-
total number of samples
- PPO
-
proximal policy optimisation
- r
-
reward
- RL
-
reinforcement learning
- s
-
state
- SVM
-
support vector machine
- t
-
step
- T
-
number of time steps
- TFR
-
time frequency representation
- TPR
-
true positive rate
- TRPO
-
trust region policy optimisation
- UAV
-
unmanned aerial vehicle
- V
-
value function
- WPT
-
wavelet packet transform
- x
-
sensor data
- y
-
fault type
Greek symbol
-
$\alpha $
-
learning rate
-
$\pi $
-
policy
-
$\gamma $
-
discount factor
-
$\theta $
-
weight parameters of the ANN
-
$\beta $
-
network parameter
-
$\phi $
-
value function parameter
1.0 Introduction
Actuators, such as motors equipped with propellers, are fundamental components of unmanned aerial vehicles (UAVs), contributing to their control, stability, manoeuverability and versatility. Due to the high levels of vibration and shock experienced during takeoff, landing and flight, as well as the effects of environmental factors and ageing, actuators inevitably suffer damage over time. This damage can include corrosion, wear and cracks, leading to a gradual increase in the risk of faults [Reference Bui, Luu, Nguyen, Loianno and Ho1, Reference Jinquan, Xiaohong, Dawei and Lizhi2]. Some typical actuator faults can lead to a range of consequences, some of which can be critical and pose risks to the vehicle, its mission and potentially to surrounding people and property on the ground. Effective condition monitoring and fault diagnosis techniques play a critical role in enhancing the safety and reliability of UAVs [Reference Duccard3].
Model-based approaches are effective methods for fault diagnosis in UAV systems. Traditional techniques include diagnostic observers, parity space and parameter estimation techniques, which rely heavily on model accuracy [Reference Ding4]. With the rapid development of artificial intelligence and data mining techniques, data-driven machine learning algorithms have emerged as a viable and practical solution for intelligent fault diagnosis [Reference Saied, Attieh, Mazeh, Shraim and Francis5–Reference Saied, Shraim and Francis7]. Machine learning algorithms are primarily concerned with the process of acquiring knowledge and extracting valuable insights from datasets to facilitate predictions and decision-making. Fault diagnosis methods based on machine learning do not rely on the intricacies of fault mechanisms or physics models, which can be challenging to construct or remain unclear, particularly when dealing with complex systems [Reference Lei, Yang, Jiang, Jia, Li and Nandi8]. To construct a machine learning-based fault diagnosis model, the initial steps involve the utilisation of signal processing or statistical techniques to extract data features. Subsequently, a suitable classifier model, such as random forest or support vector machine (SVM), is developed to establish the mapping relationship between these data features and their respective fault labels. An effectively trained model has the capability to automatically deduce the fault type by analysing the new collected sensor data. Many studies use advanced signal processing and machine learning methods for actuators and sensors fault diagnosis in UAV systems, e.g. artificial neural network (ANN) in Refs [Reference Park, Jung and Kim9, Reference Alos and Dahrouj10], K-Nearest neighbours (KNN) [Reference Saied, Attieh, Mazeh, Shraim and Francis5] and SVM [Reference Saied, Lussier, Fantoni, Shraim and Francis11].
In the aforementioned studies, signal analysis methods such as wavelet packet transform (WPT) and fast Fourier transform (FFT) are used for feature extraction at first. In the traditional machine learning diagnostic framework, feature extraction and fault diagnosis procedures are carried out as distinct and separate steps. Typically, during feature extraction, there is an inherent loss of information w.r.t. the original data, information that could potentially aid in fault diagnosis. Consequently, the performance of classic machine learning models is significantly constrained by the level of expertise applied in manual feature extraction. Recent deep learning algorithms such as convolutional neural networks (CNNs), have the capability to directly handle raw data and autonomously extract features through their deep network architecture. Deep learning can consolidate feature extraction and fault diagnosis within a unified end-to-end framework, diminishing the constraints and dependence on manual feature extraction. For example, Ref. [Reference Sadhu, Anjum and Pompili12] proposed a fault diagnosis method architecture based on deep convolutional and long short-term memory neural networks to detect and classify drone misoperations based on real-time sensor data. The authors in Ref. [Reference Benkuan, Xiyuan, Min and Datong13] designed a detection model based on stacked long short-term memory networks where fault detection is achieved by a statistical threshold.
The fault diagnosis methods discussed above rely mainly on supervised learning where labeled samples are needed. Typically, the diagnostic capability of these techniques is constrained by the size and quality of the available samples. A reduction in sample size or the disruption of samples by noise can lead to issues such as like underfitting or overfitting, which in turn lead to model performance degradation [Reference Qian and Liu14]. In practice, UAV systems operate in a normal condition most of the time resulting in a scarcity of accumulated fault samples. Addressing fault diagnosis within the constraints of a limited sample size is then becoming challenging.
Data augmentation [Reference Mumuni and Mumuni15] along with transfer learning [Reference Yao, Kang, Zhou, Rawa and Abusorrah16] emerge as two effective strategies for addressing the challenges associated with learning from limited samples. Data augmentation techniques enhance the sample size by either oversampling or generating synthetic data that closely resemble the existing samples. In the transfer learning approach, the model is initially pre-trained using datasets from a system similar to the target or from other fields. This pre-training equips the model with a foundational diagnostic capability. Subsequently, the model is fine-tuned on the specific small-sample target dataset to adapt it to the particular diagnosis task at hand.
Reinforcement learning (RL) is another branch of artificial intelligence research topic [Reference Nian, Liu and Huang17]. In reinforcement learning, the model acquires knowledge through active interaction with the environment. The RL model dynamically adjusts its actions with the aim of optimising the feedback reward it receives from the environment during the training process. When compared to supervised machine learning algorithms, reinforcement learning is geared towards acquiring an optimal policy. This policy serves as a responsive strategy that aims to maximise rewards, as opposed to the primary task of supervised learning, which is to establish a mapping function between samples and labels. Deep reinforcement learning (DRL) represents a groundbreaking advancement within the field of artificial intelligence. It harnesses the strengths of automatic feature extraction from deep learning and the interactive learning capabilities of reinforcement learning. DRL holds significant promise for tackling intricate real-world challenges. In UAV fields, DRL-based framework was developed for path planning in unknown environment [Reference He, Aouf and Song18], collision avoidance in Ref. [Reference Ouahouah, Bagaa, Prados-Garzon and Taleb19] and wireless data harvesting in Ref. [Reference Bayerlein, Theile, Caccamo and Gesbert20], etc. A review on the application of deep reinforcement learning in UAVs is presented in Ref. [Reference Wang and Xu21].
In recent times, there has been a noticeable increase in the application of deep reinforcement learning to address issues related to fault diagnosis. For example, Ref. [Reference Qian and Liu14] proposed two DRL methods based on CNN and gated recurrent unit neural network (GRU) for bearing and gear fault diagnosis in rotating machinery in nuclear power plants. The authors show that the DRL models have better stability than the deep learning and classic machine learning models after reaching convergence status in both initial sample size and small sample scenarios. The authors in Ref. [Reference Wang, Xu, Sun, Yan and Chen22] introduced an effective fault diagnosis approach for planetary gearboxes using time-frequency representation (TFR) in combination with a CNN-based DRL model. The results demonstrate its robust performance even in diverse operational conditions. The work in Ref. [Reference Li, Wu, Deng, Vu and Shao23] introduced a DRL model that uses a Capsule Neural Network (Cap-net) in combination with an online feature dictionary technique. This model exhibits adaptability to fault diagnosis tasks across varying working conditions. The authors in Ref. [Reference Fan, Zhang and Song24] introduced a DRL-based fault diagnosis technique known as ‘DiagSelect’. This method was specifically designed for scenarios with imbalanced samples. It works by intelligently selecting appropriate samples from the initial training dataset, thus mitigating the issue of sample imbalance and enhancing the overall performance of the model. Other studies that explore fault detection using reinforcement learning can be found in Refs [Reference Rose, McMurray and Hadi25–Reference Wang, Zhuang, Tao, Paszke and Stojanovic27].
As demonstrated by the aforementioned studies, the DRL model has the capability to attain good fault diagnosis performance, even in challenging scenarios characterised by significant noise, varying working conditions and sample imbalances. However, fault diagnosis study of DRL model under small sample scenario is relatively lacking. In addition, to the best of our knowledge, there are no relevant publications discussing the application of DRL-based fault diagnosis method for UAVs.
To address this research gap, this paper introduces two DRL-based fault diagnosis models and compares their performance with existing works. Unlike previous studies, which often focus on larger datasets, this study emphasises scenarios with limited sample sizes. The models training processes and diagnostic accuracy are rigorously examined, demonstrating superior performance and robustness in handling small data conditions, compared to traditional methods found in the literature. This paper highlights how the proposed models outperform those in prior works by maintaining high accuracy even when data is scarce. The primary contributions of this paper can be summarised as follows:
This paper is likely one of the first studies focusing on DRL-based methods for fault diagnosis in UAV systems.
This paper introduces two DRL models designed for diagnosing faults in UAV systems. These models utilide deep Q-network (DQN) and proximal policy optimisation (PPO) architectures, respectively. Furthermore, the paper includes comparative experiments aimed at assessing their performance in comparison to baseline models.
The proposed DRL models demonstrate excellent fault diagnosis capabilities, boasting an accuracy rate exceeding
$99{\rm{\% }}$
. Notably, these models exhibit heightened resilience in scenarios with limited sample sizes compared to the baseline models. Consequently, they emerge as a more fitting choice for fault diagnosis applications within the context of UAV systems.
The rest of this paper are organised as follows: Section 2 introduces the background knowledge of DRL and the proposed fault diagnosis method in this paper. Section 3 describes the actuators fault experimental datasets and the data processing, model parameter setting and evaluating method in detail. Section 4 analyses and discusses the model training process and evaluation results. Section 5 concludes the research of this paper.
2.0 Methodology
Deep reinforcement learning, a very fast-moving field, is the combination of reinforcement learning and deep learning. DRL enables us to use RL in situations approaching real life complexity. Agents occasionally need to create accurate representations of their surroundings from highly detailed sensory inputs in order to apply their prior knowledge to novel circumstances. Because of this, RL agents require ANN to handle these challenging issues. The first developed DRL agent was a deep Q-network (DQN) that employs neural network architecture to predict the Q-value for a given state instead of maintaining a q-map look-up table for each state-action pair and the corresponding value associated with it.
2.1 Deep Q-lg (DQN)
As illustrated in Fig. 1, the RL framework comprises three key components: a learning agent, the environment and their interactions involving states, actions and rewards. The agent, characterised as an intelligent entity, possesses the capability to make decisions and execute actions guided by a specific policy. The environment, on the other hand, serves as the interactive entity for the agent. The term state denoted as
$s$
signifies a particular condition or state within the environment, which is observable and detectable by the agent. The action
$a$
signifies the agent’s behaviour, which exerts a certain impact on the environment. The reward
$r$
embodies the feedback signal originating from the environment, conveying significance to the agent in the form of either a reward or a penalty. The agent’s objective is to acquire knowledge of an optimal policy denoted as
$\pi (a|s)$
through its interaction experiences. This optimal policy dictates the agent’s decision-making process, instructing it on the most suitable action
$a$
to take, given the current observed state
$s$
to maximise the cumulative reward
$r$
obtained from the environment.
Figure 1. Basic components of DRL.
Typically, the function
$Q\!\left( {s,a} \right)$
serves as a representation of the expected reward when selecting action
$a$
within state
$s$
under the policy
$\pi $
, and its value undergoes iterative updates in accordance with the following equation:
\begin{align}Q^{\prime}\!\left( {s,a} \right) = Q\!\left( {s,a} \right) + \alpha \!\left( {r\!\left( {s,a} \right) + \gamma \mathop {{\rm{max}}}\limits_{a^{\prime}} Q\!\left( {s^{\prime},a^{\prime}} \right) - Q\!\left( {s,a} \right)} \right)\end{align}
with
$s^{\prime} = {s_{t + 1}}$
and
$a^{\prime} = {a_{t + 1}}$
. The learning rate
$\alpha $
determines the step size at which the Q-value is updated based on the observed reward and the potential future rewards.
$\gamma $
is the discount factor ranging from
$0$
to
$1$
, it indicates the delay discount reward for the current action.
Artificial neural network (ANN) can serve as a function approximator for estimating the Q function which can be approximated as
$Q\!\left( {s,a;\ \theta } \right)$
, with
$\theta $
representing the weight parameters of the ANN. This type of network is commonly referred to as DQN and was initially introduced in 2015 by Ref. [Reference Mnih28]. The DQN can fully take advantage of the neural network powerful capability to perceive the state of the environment directly from unprocessed sensor data. Currently, different techniques are used in the training of DQN:
$\epsilon $
-greedy exploration mechanism, experience replay (ER) method and network separation.
2.2 Proposed dueling DQN architecture
Fault diagnosis can be considered as a classification decision problem, often comparable to a strategic guessing game. The agent takes on the role of the game player, with the primary objective of accurately guessing the fault type. The environment encompasses an extensive dataset comprising numerous sensor data samples, where each state corresponds to an individual sample. In a fault diagnosis problem involving
$K$
distinct classes, the set of possible guessing actions is denoted as
$\left\{ {0,1, \ldots, K - 1} \right\}$
. Here,
$0$
signifies the absence of a fault (normal condition), while other numerical values, like
$k$
, correspond to specific fault types, such as the
$k$
-th fault category. The agent receives a reward signal upon making a correct guess, while an incorrect guess results in a penalty signal. This reward function will be addressed in details in Section 3.2.
The proposed DQN-based fault diagnosis architecture is based on the dueling DQN framework and is shown in Fig. 2. The environment emulator is built based on a dataset denoted as
$D = \left\{ {{x_i},{y_i}} \right\}$
for
$i = 1{\rm{\;to\;}}N$
, where
$x$
represents sensor data,
$y$
signifies the fault type, and
$N$
indicates the total number of samples. The agent is established employing a multilayer perceptron (MLP) network architecture. This agent’s role is to extract and comprehend the features present in the samples and endeavour to make accurate fault type predictions. The architecture comprises two separate sequences or streams of networks, namely the A-network that outputs the action advantage
$A\!\left( {s,a;\ \theta, \alpha } \right)$
and the V-network that outputs the state value
$V\!\left( {s;\ \theta, \beta } \right)$
, where
$\theta $
denotes the parameters of the network that perform feature processing on the input layer;
$\alpha $
and
$\beta $
are the parameters of the two streams, respectively. These networks are tasked with independently learning the action-advantage function and the state-value function. This architecture effectively separates the value and advantage functions, and then reunites the two streams using a specialised aggregation module to generate an estimate of the state-action value function. The output of the deep Q-network using this dueling network structure is:
\begin{align}Q\!\left( {s,a;\ \theta, \alpha, \beta } \right) = V\!\left( {s;\ \theta, \beta } \right) + A\!\left( {s,a;\ \theta, \alpha } \right)\end{align}
Figure 2. The proposed dueling DQN-based fault diagnosis model.
As the network directly provides Q-values, it doesn’t inherently yield the state value
$V$
or the action advantage
$A$
. To address this issue of identifiability, the action advantage
$A$
is centralised, a step that enhances performance and optimisation stability. In this process,
$a^{\prime}$
represents the set of all possible actions, and
$avgA\!\left( {s,a^{\prime};\ \theta, \alpha } \right)$
corresponds to the average value of the advantage function across all potential actions. The adjusted Q-values are represented by Equation (3]:
\begin{align}Q\!\left( {s,a;\ \theta, \alpha, \beta } \right) = V\!\left( {s;\ \theta, \beta } \right) + \!\left( {A\!\left( {s,a;\ \theta, \alpha } \right) - avgA\!\left( {s,a^{\prime};\ \theta, \alpha } \right)} \right)\end{align}
The uniform random sampling used in the algorithm is not optimal. During interactions with the environment, the system accumulates experience samples, including both successful and unsuccessful attempts or episodes. These experiences are consistently retained in the experience replay unit, and they persist over time. Regularly revisiting these stored experiences allows the agent to grasp the outcomes associated with both correct and incorrect behaviours. Consequently, the agent can continually refine its behaviour based on this accumulated knowledge.
Nevertheless, it is crucial to acknowledge that various experience samples have varying levels of importance. Since the experience replay unit continually receives updates, randomly selecting a limited number of samples for model input using uniform random sampling can lead to a situation where certain high-importance experience samples are not fully leveraged and may even be replaced directly. This scenario can diminish the overall efficiency of model training. To enhance the model’s training efficiency, this architecture adopts a prioritised experience replay approach. This method involves drawing samples from the experience replay unit in a way that increases the likelihood of selecting samples with higher importance.
2.3 Proximal policy optimisation (PPO)
In contrast to value-based methods like Q-learning, policy-based methods optimise the policy
$\pi (a|s;\ \theta )$
(with function approximation) directly and update the parameters
$\theta $
by gradient ascent. Comparing with value-based methods, policy-based methods usually have better convergence properties, are effective in high-dimensional or continuous action spaces, and can learn stochastic policies [Reference Zhang, Zhang, Han and Lu29].
Policy gradient methods work by computing an estimator of the policy gradient and plugging it into a stochastic gradient ascent algorithm. The most commonly used gradient estimator has the form:
\begin{align}\hat g = {E_t}[{{\rm{\Delta }}_\theta }{\rm{log}}{\pi _\theta }({a_t}|{s_t}){\hat A_t}]\end{align}
where
${\pi _\theta }$
is a stochastic policy and
${\hat A_t}$
is an estimator of the advantage function at time step
$t$
. Here, the expectation
${E_t}$
indicates the empirical average over a finite batch of samples, in an algorithm that alternates between sampling and optimisation. Implementations that use automatic differentiation software work by constructing an objective function whose gradient is the policy gradient estimator. By making several approximations to the theoretically justified algorithm, the trust region policy optimisation (TRPO) algorithm [Reference Meng, Zheng, Shi and Pan30] was proposed with the loss function:
\begin{align}{L^{TRPO}}\!\left( \theta \right) = {\hat{E}_t}\left[ \frac{{{\pi _\theta }({a_t}|{s_t})}}{{{\pi _{old}}({a_t}|{s_t})}}.{{\hat A}_t}\right] = {\hat{E}_t} \left[ {r_t}\!\left( \theta \right).{{\hat A}_t} \right] \end{align}
However, there is always the possibility of the action under study could be over 100 times more probable in the current policy than it was in the old policy. However, there is always the possibility that the action being studied could be over 100 times more likely under the current policy than it was under the previous policy. This means that
${r_t}\!\left( \theta \right)$
will end up being too large and hence lead to taking big gradient steps that might ruin the policy. In order to deal with issues like this one, the clipped surrogate objective was designed to improve training stability by limiting the change made to the policy at each step:
\begin{align}{L^{CLIP}} = {\hat{E}_t}\left[ {{{min}}\!\left( {{r_t}\!\left( \theta \right).{{\hat A}_t},{{clip}}\!\left( {{r_t}\!\left( \theta \right),1 - \epsilon, 1 + \epsilon } \right).{{\hat A}_t}} \right)} \right]\end{align}
2.4 Proposed MLP-based actor-critic algorithm architecture
As in the previous section, the fault diagnosis problem is formulated as a classification problem. It is implemented using the actor-critic RL framework shown in Fig. 3. The classical multiperceptron neural network (MLP)-based implementation of this framework optimised with the gradient descent (GD) algorithm is considered.
Figure 3. Actor-critic PPO architecture.
Algorithm 1 PPO with Clipped Surrogate Objective Function
Standard policy-gradient methods frequently encounter slow convergence due to the substantial variances present in gradient estimates. Actor-critic methods are designed to mitigate this issue by incorporating a critic network. The actor network is responsible for selecting actions based on the current state, aiming to improve policy performance over time. The critic network, on the other hand, estimates the value of being in a given state and guides policy updates. By estimating state values, the critic assists the actor in understanding which states are more valuable in the long run. This collaboration between the actor and critic enables more efficient learning of policies. The critic helps the actor to identify areas where the policy is lacking and provides insights into selecting actions that lead to higher rewards. Consequently, the actor-critic architecture enhances the learning process by leveraging value estimates to make informed policy updates. The PPO with clipped surrogate objective function is detailed in Algorithm 1.
3.0 Case study: application to fault diagnosis in a multi-rotor UAV
3.1 Case description
A multirotor system typically employs several types of actuators to control its movement and orientation. The primary actuators include the brushless DC motors (BLDC) and the propellers. These actuators work in coordination with onboard sensors and a flight controller to maintain stability, control orientation and achieve desired flight trajectories. However, for commercial or other considerations, there exist no public actuators fault dataset from multirotors. As an alternative, related works used laboratory datasets to validate their proposed fault diagnosis methods. Therefore, two datasets were collected from a laboratory hexarotor UAV. They contain sensor data under normal and multiple abnormal operating conditions, which are suitable for constructing multi-classification experiments for fault diagnosis. The validation process and results in this paper can provide a valuable reference for further diagnosis applications in UAVs. The collected fault datasets are briefly described in Table 1. The experimental setup is shown in Fig. 4(a). It consists of a stationary ball joint base that gives the multirotor, a hexarotor in this case, unrestricted yaw movement and around
$ \pm {30^ \circ }$
of pitch and roll, while restricting the aircraft to a fixed point in the three-dimensional space. The experiments measured the hexarotor angles and the angular velocities using the mounted inertial measurement unit (IMU), and the motors currents using current sensors connected to the Pixhawk controller by an Arduino board in normal and fault states. The sampling frequency is 50Hz and the operating conditions included healthy actuators, broken propellers (Fig. 4(b)), loss of propeller and motors loss of effectiveness. Each instance (set of input values) corresponds to a time step of the simulation. For each instance, the following input data were used as features:
The measured Euler angles of the hexarotor UAV (roll, pitch and yaw).
The desired roll, pitch and yaw angles.
The measurements given by the 3-axis accelerometer.
The measurements given by the 3 axis-gyroscope.
The measurements given by the 3-axis magnetometer.
The measurements from the current sensors of the six motors.
The vibrations at x, y and z measurements.
Table 1. Detailed information of fault datasets in case study
H= Normal (i.e., health).
PB25–PB100 = Propeller Broken with a percentage of
$25{\rm{\% }},50{\rm{\% }},75{\rm{\% }},100{\rm{\% }}$
.
PL = Propeller loss.
MF30–MF100 = Motor fault with a loss of effectiveness of
$30{\rm{\% }},50{\rm{\% }},75{\rm{\% }},100{\rm{\% }}$
.
Figure 4. Data collection: (a) experimental setup, (b) propeller faults.
3.2 Training setup
In order to implement a DRL approach on this imbalanced multi-class classification problem, the fault diagnosis problem needs to be formulated as an MDP problem. This means that three main components need to be defined:
State space: The state space includes all the possible configurations or conditions that the environment can assume. It encapsulates the essential variables that describe the UAV’s current status, performance and behaviour. Each variable in the state space provides essential data that could potentially help in identifying the presence of faults. This state space is defined by combining the input features into a continuous space represented by a vector of real numbers between 0 and 1. Mathematically, this state space vector can thus be represented as:
(7)where
\begin{align}S = \left[ {{s_1},{s_2}, \ldots, {s_n}} \right]\end{align}
${s_i}$
represents the value of the
$i$
-th feature in the state space. Each
${s_i}$
is a real number between
$0$
and
$1$
, as constrained by the defined observation space. This vector representation captures the multidimensional nature of the state space.
Action space: The action space represents all the possible actions that the agent can take within the environment. An action can be any decision or choice the agent makes to interact with the environment and transition from one state to another. In this case, it is defined as a discrete space representing different classes (actions). The action space size is equal to the number of classes, which, as discussed earlier, is 9, ranging from class 0 to class 8.
(8)where
\begin{align}A = \left\{ {{a_0},{a_1}, \ldots, {a_i}, \ldots, {a_8}} \right\}\end{align}
${a_i}$
represents action
$i$
that can be taken, i.e. the choice of classifying the input as a fault of class
$i$
.
Reward function: Every chosen action will take the system into another state. This change is also accompanied with a reward. The reward should increase the more the agent is able to predict the class correctly, and decrease the more the agent predicts the wrong classification. The reward function is defined below:
(9)
\begin{align}r\!\left( {\hat a,a,w} \right) = \begin{cases} w&{\rm{if\;}}\hat a = a \\ 0&{\rm{otherwise}}\end{cases}\end{align}
In this context,
$\hat a$
represents the predicted action, which corresponds to the class the agent assigns to the input.
$a$
denotes the actual class to which the input belongs.
$w$
is the calculated weight associated with correctly predicting the class. Note that the weights of the classes were calculated in order to take into consideration the fact that the training dataset is imbalanced. This means that each class has a different number of instances than the other, and that could pose an issue for the minority classes as the model will only encounter them far less than majority classes, which could cause inaccuracy and worsen the training of the agent. These weights were calculated as:(10)
\begin{align}{w_i} = \frac{1}{{{n_i}}}\frac{1}{{\mathop \sum \nolimits_{j = 1}^N \frac{1}{{{n_j}}}}}\end{align}
In this equation,
${w_i}$
represents the weight for class
$i$
,
${n_i}$
is the count of samples in class
$i$
, and
$N$
is the total number of classes. In other words, this equation ensures that classes with fewer samples are given higher weights to compensate for their under-representation, while classes with more samples have lower weights. This approach helps to balance the impact of different classes during training and can improve the performance of the machine learning model.
After much trial-and-error, the parameters for the dueling DQN and actor-critic architectures shown in Table 2 were finally selected. The MLP network used in the dueling DQN architecture features two fully connected layers with 64 hidden units, and utilises the hyperbolic tangent (tanh) as the activation function. For the PPO architecture, the policy network and value function network each have two hidden layers, with 64 neurons in each layer. The exploration fraction defines the fraction of total timesteps over which the agent will gradually decrease its exploration. It determines how quickly the exploration rate transitions from high to low. The exploration final epsilon specifies the minimum exploration rate that the agent will use after the exploration fraction period. It ensures a minimum level of exploration even after the exploration rate has decreased. The cliprange hyperparameter is used to limit the update of the policy during optimisation. It prevents the policy from undergoing drastic changes that might lead to instability, and thus determines the acceptable range of policy updates, preventing it from moving too far away from the current policy distribution. The PPO employs a clipped surrogate objective to update the policy in a stable manner. The objective function discourages large policy updates that could destabilise learning. The objective is to maximise the expected reward under the updated policy while controlling the divergence between the new and old policies.
Table 2. Main parameter settings of the proposed DRL models
3.3 Model performance evaluation
To verify that the model can be applied to detecting and classifying faults, we evaluate the model’s performance on a merged dataset consisting of the datasets A and B described previously. During the evaluation process, the final dataset is divided into three sub-datasets: a training set, a validation set and a test set in the sample size ratio of 7:1.5:1.5. For evaluation purposes, since the studied dataset is imbalanced, looking only at the accuracy metric would not give a sufficient result. Even though it is viable to compare all metrics (accuracy, false positive rate (FPR), true positive rate (TPR) precision, recall,…) but it is more convenient to use one metric to compare the performance of different models in an attempt to rank them. The most commonly used metric for such comparisons is the F1 score, as it is a combination between precision and recall, hence proving a suitable metric to use for the choice of best classifier.
Accuracy represents the proportion of instances that are correctly predicted out of the total number of instances:
\begin{align}{\rm{Accurracy}} = \frac{{TP + TN}}{{TP + TN + FP + FN}}\end{align}
with TP, TN, FP and FN being respectively the true positive, true negative, false positive and false negative predictions. The overall precision and recall of the classes are defined as:
\begin{align}\begin{array}{*{20}{l}}{{\rm{Precision}} = \frac{{\mathop \sum \nolimits_{i = 1}^M {\rm{Precision}}\left( i \right)}}{M}}\\[5pt]{{\rm{Recall}} = \frac{{\mathop \sum \nolimits_{i = 1}^M {\rm{Recall}}\left( i \right)}}{M}}\end{array}\end{align}
with
$M$
being the number of classes and Precision(i), Recall(i) or True Positive Rate TPR(i) associated with class
$i$
are calculated as:
\begin{align}\begin{array}{*{20}{l}}{{\rm{Precision}}\!\left( i \right) = \frac{{T{P_i}}}{{T{P_i} + F{P_i}}}}\\[5pt]{{\rm{Recall}}\!\left( i \right) = \frac{{T{P_i}}}{{T{P_i} + F{N_i}}}}\end{array}\end{align}
Then these two terms can be combined together to formulate the F1-score given by the following expression:
\begin{align}{F_1} = \frac{{2\ {\textrm{* Precision*Recall}}}}{{{\rm{Precision}} + {\rm{Recall}}}}\end{align}
The results of the DRL models are compared finally with the well-known techniques applied to solve classification problems such as support vector machines (SVM), decision tree (DT), k-nearest neighbours (kNN), logistic regression (LR), naive Bayes (NB), linear discriminant analysis (LDA) and MLP-based artificial neural network (MLP-ANN). The comparison is grounded in a previous publication [Reference Saied, Attieh, Mazeh, Shraim and Francis5], where the effectiveness of these classical classification techniques was rigorously tested on the same dataset employed in our study. This prior work provides a solid foundation for our analysis, allowing for a direct and meaningful evaluation of how the DRL models perform in relation to these traditional methods.
4.0 Results and discussion
4.1 Analysis of the training process
This section provides a comprehensive analysis of the training process in the applied DRL techniques to assess their effectiveness in the context of fault diagnosis. Specific contents include the analysis of training accuracy curve and average reward.
The number of timesteps is set to 1,000,000 and the training accuracy at each time step is recorded. Training accuracy serves as an indicator of the model’s proficiency in extracting features and recognising patterns within the training dataset. As depicted in Fig. 5, the training accuracy of the neural network model rises faster than the DRL models, ultimately achieving convergence at an earlier stage. This performance can be attributed to the inherent characteristics of supervised learning, which leverages sample labels to guide the parameter updates of the NN model, while the DRL models are being trained using a less robust feedback mechanism, which relies on a scalar reward signal to assess the models’ performance and adjust their parameters in a manner that could potentially maximise the cumulative reward in the interaction. On the other hand, the faster increase in training accuracy of the dueling DQN model compared to the actor-critic DRL model can be attributed to the training dynamics and stochasticity factors, where the actor-critic methods involve stochastic policies, which can introduce randomness into the learning process while the dueling DQN typically uses deterministic policies. Figure 5 shows also that the DRL models exhibit higher training accuracies compared to the simple MLP since they have specialised components for value estimation and policy learning. This added complexity can capture the underlying patterns in the data more effectively. The training accuracies of both DRL models show high similarity after reaching convergence status.
Figure 5. Training accuracy of the neural network, PPO-based DRL and dueling DQN-based DRL models.
Next, we examine the variation characteristics of the average reward values. Figure 6 shows that the PPO-based classifier exhibits a notably faster convergence. This observation aligns with the characteristics of the PPO model that focuses on optimising the policy directly unlike the dueling DQN model that requires a more extended training period to converge. On the other hand, in terms of stability, one can observe that while both techniques exhibit improvements in reward over time, the PPO model tends to provide a smoother and more consistent increase in average reward. This can be attributed to its careful control over policy updates, which prevents drastic policy changes and mitigates the risk of diverging or fluctuating performance. In terms of final performance, the dueling DQN achieves a slightly higher final average reward. This could be considered as an indication that the dueling DQN might be better suited for this specific diagnosis problem where the environment is modeled with discrete action spaces where the agent can choose from a finite set of actions (classes).
Table 3. Models’ performance under initial training sample size
Figure 6. Average reward of PPO-based DRL and dueling DQN-based DRL models.
4.2 Model performance comparison
In this section, we evaluate and compare the results of the various models described previously using the initial sample size according to the evaluation process described in Section 3.3. Table 3 shows the accuracy and F1-Score evaluation results of all models on the test set. The order of model performance superiority on the merged dataset is as follows: dueling DQN
$ \gt $
PPO
$ \gt $
MLP-ANN
$ \gt $
DT
$ \gt $
LDA
$ \gt $
SVM
$ \gt $
KNN
$ \gt $
LR
$ \gt $
NB. The two presented DRL models can achieve very high accuracy of over around
$99{\rm{\% }}$
, showing excellent diagnostic capability. The dueling DQN and PPO models possess interactive learning capabilities, combining the strengths of automated feature extraction inherent in deep learning models. This unique combination empowers the models to delve deeply into the complexities of the environment, particularly when dealing with complex datasets like those related to faults. Consequently, these models excel in their capacities to comprehend and harness the fundamental patterns present in the environment, enabling them to acquire more effective fault diagnosis strategies compared to conventional deep learning models.
4.3 Performance under small samples
In real flights UAVs tend to operate under normal conditions for the majority of their operational time. This poses a challenge when it comes to fault diagnosis, as it often involves working with a limited amount of data, a situation commonly referred to as the ‘small sample problem’. Evaluating a model’s performance in scenarios with limited data is crucial for its relevance in engineering applications. To simulate this scenario, we conduct experiments where only a small portion (ranging from
$0.5{\rm{\% }}$
to
$30{\rm{\% }}$
) of the available training data is used to train the model.
Figure 7 illustrates results across various training sample ratios. It is clear that the two DRL-based models exhibit a lesser degree of accuracy variation as training sample ratios decreases from
$50{\rm{\% }}$
to
$0.5{\rm{\% }}$
. In contrast, the ANN model experiences a more substantial decline in accuracy, indicating its heightened sensitivity to sample reduction. In addition, the dueling DQN-based model slightly outperforms the PPO-based model, boasting a smaller accuracy variation and enhanced stability. Specifically, when training sample ratio stands at
$1{\rm{\% }}$
, dueling DQN achieves an average accuracy of
$95.55{\rm{\% }}$
, while PPO attains an average accuracy of
$93.12{\rm{\% }}$
. These results highlight the exceptional diagnostic accuracy achieved by both models, particularly in scenarios with limited sample sizes.
Figure 7. Test accuracy under small sample scenarios.
4.4 Discussion
While the validation datasets used in this paper are derived from indoor constrained flight settings rather than actual data obtained from real outdoor free flights, it is essential to acknowledge that reaching a consistent
$99{\rm{\% }}$
accuracy rate in real flight scenarios cannot be guaranteed. However, there is a positive perspective to consider. This paper offers a highly specific and effective model architecture, complemented by valuable experimental outcomes related to DRL-based fault diagnosis techniques for actuators faults in rotary UAV systems.
The results presented here provide a relative benchmark for assessing model performance. These findings, while contingent on controlled laboratory data, offer insights into the system’s capabilities to some degree. They serve as a foundation for advancing fault diagnosis methods for UAV systems and offer guidance for the development of more robust, real-world applications. For further applications in this field, there are different aspects which need to be discussed here.
Data source and size: The datasets used in this paper are from indoor flights with less disturbance compared to real outdoor measurements. However, the monitored actuators types, the sensors and the signal acquisition frequency do not differ from real environment which results in the trained model in this paper could be directly applied with further tuning of the models hyperparameters. In addition since UAVs are designed for reliability, actual in-flight faults are relatively rare events. This scarcity of real fault data makes it challenging to collect a sufficiently diverse and representative dataset for training. This makes the implementation of DRL-based model more suitable for fault diagnosis than deep learning models.
Environmental variability: Fault diagnosis techniques should be designed to handle environmental variability and changing conditions during flight. Addressing these challenges in the context of application of DRL for UAVs is still an ongoing research area. It involves designing robust control policies that are resilient to changing conditions. Furthermore, the collection of real-world data under varying conditions is crucial for training DRL models that can reliably operate in complex, dynamic environments.
Model size and complexity: The size and complexity of DRL-based models trained offline may not be suitable for deployment on UAVs, where simplicity and efficiency are often preferred. To address these challenges, a hybrid approach can be considered. Pre-train the DRL model on a server with access to abundant computational resources and then fine-tune the model on the UAV with real data to adapt to the specific UAV environment.
Detection of unknown failures: The current models in this work were primarily designed to identify and classify eight known common failures. While they have proven effective in this context, the models are not explicitly designed to handle unknown or unseen failures. To address this challenge, techniques such as unsupervised learning could be integrated to improve the models’ ability to detect unknown faults.
5.0 Conclusion
In this paper, we propose two DRL-based fault diagnosis techniques using the dueling DQN and PPO actor-critic architectures. The work involves an examination of the model training procedures, an extensive performance evaluation and a comparative analysis with different supervised baseline models. Two experimental imbalanced fault datasets, motors and propellers are selected as case studies. The results show that the DRL-based models outperform neural networks and classical machine learning models in both initial sample size and small sample scenarios. This can be attributed to the enhanced benefits arising from the fusion of robust feature extraction capabilities inherent in deep learning and the interactive learning prowess offered by reinforcement learning. This unique combination serves as a motivational force, enabling the models to acquire a deeper understanding of fundamental features, even in the presence of relatively modest reward feedback signals.
Future investigations will delve deeper into the fault diagnosis capabilities of DRL models, assessing their performance under dynamic operational conditions, including scenarios characterised by high environmental noise and unknown fault scenarios to explore the robustness of DRL in identifying and isolating previously unseen failures.
