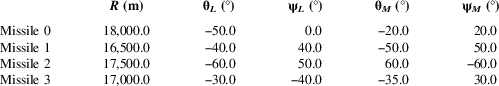NOMENCLATURE
- a y , a z
missile accelerations
- N
navigation constant
- R
relative distance
- s
switching signal of communication topologies
- V M
missile velocity
- (X I , Y I , Z I )
inertial reference co-ordinate system
- (X L , Y L , Z L )
line-of-sight (LOS) co-ordinate system
- (X M , Y M , Z M )
missile body co-ordinate system
- θ M , ψ M
Euler angles from the LOS co-ordinate system to the body co-ordinate system
- θ L , ψ L
LOS angles form the inertial reference co-ordinate system to the LOS co-ordinate system
-
 ${\dot{\rlambda }}_{y} ,\;{\dot{\rlambda }}_{z} $
${\dot{\rlambda }}_{y} ,\;{\dot{\rlambda }}_{z} $
LOS angular velocity components with respect to the LOS co-ordinate system
- σ
heading error
- τ
communication delay
- η i , ξ i , δ i
auxiliary states
-
 ${\mib {\cal A}}$
${\mib {\cal A}}$
adjacency matrix
-
 ${{\rm {\rvarepsilon}}}$
${{\rm {\rvarepsilon}}}$
set of edges
-
 ${{\rm {\cal G}}}$
${{\rm {\cal G}}}$
communication graph
-
 ${\tilde{{\cal G}}}$
${\tilde{{\cal G}}}$
finite set of all possible graphs
-
 $${\mib {\cal L}}$$
$${\mib {\cal L}}$$
Laplacian matrix
-
 $${{\rnu}}$$
$${{\rnu}}$$
set of nodes
1.0 INTRODUCTION
Over the past decades, guidance law design remains a technical of active research for missiles. Due to its simple structure, robustness and optimality, the well-justified proportional navigation guidance (PNG)( Reference Zarchan 1 , Reference Murtaugh and Criel 2 ) law has been widely used as an efficient strategy for almost half a century in missile guidance systems, and also plays an important role on improvements of novel guidance laws( Reference Lu, Doman and Schierman 3 – Reference Cho and Kim 5 ). However, with the development of the modern war, valuable targets are gradually protected by a variety of defence systems against incoming missiles such as surface-to-air missile systems (SAMS) and close-in weapon system (CIWS), which have seriously weakened the efficiency and threat of missiles. Inspired by the facts stated above, co-operative salvo attack of multiple missiles, performing a many-to-one engagement scenario, has been considered as an efficient countermeasure to penetrate the formidable defence systems recently.
Recognising the importance of salvo attack, a variety of guidance schemes have been carried out by many researchers to achieve this objective in recent years. One of the initial efforts in this field is the impact time-based control, in which guidance laws are derived based on a common predesigned impact time for each individual missile respectively to drive missiles to arrive at the target at the same impact time. Authors in Ref. 6 improved the typical PNG law with the feedback of impact time error to realise salvo attack missions, which seems to be the first attempt to utilise the impact time-based control approach. As extensions of Ref. 6, both impact angle and impact time constraints were taken into consideration in Refs 7,8 to achieve salvo attack of multiple missiles. Authors in Ref. 9 further proposed a sliding mode control-based approach to improve the robustness of guidance laws coping with moving target especially. And other impact time-based guidance laws were carried out in Refs. 10 and 11, in which the seeker’s field-of-view constraint and dynamics of autopilot were also considered, respectively. Although the aforementioned formulations were proved to be feasible for salvo attack of multiple missiles, the guidance law based on impact time is designed for individual homing of each missile, which presents an open-loop control approach in essence.
To overcome the inherent drawback of impact time-based guidance laws, co-operative guidance, in which missiles communicate with each other to synchronise the impact time autonomously, has obtained tremendous attention recently. A co-operative PNG law with time-varying navigation gain was proposed in Ref. 12 to adjust the time-to-go variance of missiles, based on which salvo attack can be achieved. Then, authors in Ref. 13 integrated the impact time and impact angle constraints into co-operative guidance law design. Thereafter 2D and 3D co-operative guidance laws were designed in Refs 14, 15, respectively, which are suitable for both stationary and manoeuvring targets. Authors in Refs 16,17 further dealt with finite-time co-operative guidance problem for salvo attack of multiple missiles. Results achieved in Refs 12–17 generally rely on the information on time-to-go, which cannot be measured directly by any on-board devices. Moreover, as pointed in Ref 18 that traditional time-to-go estimation approaches under large initial heading errors may not accurate enough, while precise estimation method arises complexity in nature. To cope with this problem, the properties of the pure proportional navigation (PPN) guidance law are further explored by researchers with the convenient concept that equal path length can provide accurate simultaneous attack without knowing the engagement time. The advantage of this concept lies in the abandoning of the time-to-go estimation, and, thus, it is more suitable for practical applications. Concerning with this framework, authors in Refs 19,20 proposed 2D and 3D co-operative guidance laws without using any information on the time-to-go estimation for stationary targets, respectively, based on the consensus theory, which lay a firm foundation for efficient co-operative guidance law design.
As mentioned above, efficient communication among missiles is the key feature of co-operative guidance. Existing results generally depend on the ideal communications of missiles. However, ceaseless communication brings the huge cost of power resources, which are limited to the battlefield. Moreover, from the view of practical point, communication among missiles may be unreliable due to the existence of communication failure. Hence, it is practical to consider the co-operative guidance problem under switching topologies. Motivated by these observations, authors in Refs 21,22 paid attention to achieve salvo attack of multiple missiles under switching topologies. However, their results suffer from the drawback of relying on the time-to-go estimation, which restricts the application and development of these schemes to some extent. To cope with this problem, distributed co-operative guidance law was proposed based on switching directed topologies in Ref. 23 without any information on time-to-go, and then this result was further extended for distributed group co-operative guidance problem in Ref. 24. Whereas assuming that each possible topology has a directed spanning tree in Refs. 23,24 is very strict and conservative. Furthermore, for co-operative guidance, communication delay between every two missiles is inevitable due to the sensor performance. Authors in Ref. 25 only considered a constant delay case for salvo attack of multiple missiles. Therefore, based on the above analysis, how to achieve co-operative salvo attack of multiple missiles under jointly connected switching topologies subject to time-varying communication delays remains a meaningful but challenging issue.
Inspired by the aforementioned observations, this study considers the distributed 3D co-operative guidance law design problem, which is independent of any information on time-to-go, under jointly connected topologies subject to time-varying communication delays for multiple missiles. Motivated by the creative concept of Refs 20,26, a two-stage guidance scheme is proposed to achieve a simultaneous attack against a stationary target in this study. During the first guidance phase, a distributed co-operative guidance law is derived based on local information from neighbours to achieve consensus on range-to-go and heading error of missiles, which aims to provide favoured initial conditions for the latter stage. Sufficient conditions concerning with jointly connected topologies and time-varying communication delays are obtained to realise this objective in terms of linear matrix inequalities. During the second guidance phase, all missiles are governed by the typical PPN law with the same navigation gain to realise salvo attack eventually. Compared with existing works, the key features of this study are threefold. First, contrary to the results in Refs 23,24, which require that the switching communication network is always connected, the proposed guidance law only requires that communication topologies are jointly connected. Although works in Refs 21,22 also considered the jointly connected network case, they suffered from depending on the estimation of time-to-go. Moreover, guidance laws presented in Refs 21–24 were developed for a 2D engagement, leading to 3D salvo attack a relatively unexploited issue. Second, recognising that the condition of communication delay assumed to be constant in Ref. 25 is some strict and conservative, time-varying communication delays are taken into account in this study to construct the distributed guidance law. The last but not the least, both switching topologies and communication delays are considered simultaneously for 3D co-operative guidance law design in this study, which is rare in salvo attack of multiple missiles to the best of our knowledge.
The remainder of this paper is organised as follows. In Section 2, some preliminaries and problem formulation are described. Section 3 presents the details of the main results achieved by this study. In Section 4, numerical simulation is set up and simulation results are provided. Finally, conclusions are drawn in Section 5.
2.0 PRELIMINARIES
In this section, some preliminaries are provided. The 3D homing engagement geometry of a missile and a target is presented firstly, based on which the typical 3D PPN guidance law is obtained. Then, some useful concepts about the graph theory are introduced to describe the communication network for the multi-missile system, and the problem studied in this paper is stated.
2.1 Formulation of 3D PPN guidance law
In this paper, the 3D homing engagement between missiles and a stationary target is considered, and the following assumptions are required before moving on( Reference Zhao and Zhou 27 ).
Assumption 1. The seeker and autopilot dynamics of a missile are sufficiently fast compared with the guidance loop.
Assumption 2. The missile is point mass and its total velocity is set to the constant value.
Based on the above assumptions, the 3D homing engagement geometry of a missile and a target can be shown in Fig. 1, in which (X I , Y I , Z I ) is the inertial reference co-ordinate system; (X M , Y M , Z M ) denotes the missile body co-ordinate system; (X L , Y L , Z L ) is the line-of-sight (LOS) co-ordinate system; M and T represent the missile and the target, respectively; R denotes the relative range between the missile and the target or the so-called range-to-go; V M is the total velocity of the interceptor missile; the notations θ M and ψ M stand for the Euler angles from the LOS co-ordinate system to the body co-ordinate system of the missile; θ L and ψ L represent the LOS angles in azimuth and elevation directions from the inertial reference co-ordinate system to the LOS co-ordinate system; and the term σ denotes the heading error, which describes the angle between the missile velocity and the LOS.
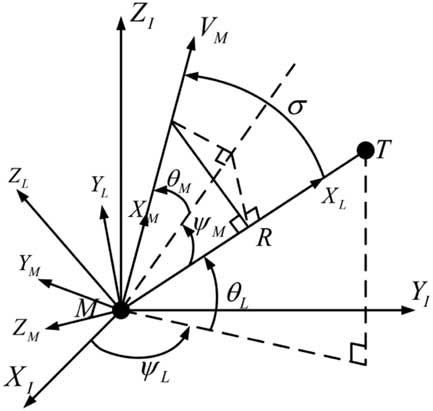
Figure 1 3D homing engagement geometry.
The 3D point-mass equations describing the homing engagement geometry can be given as( Reference Song and Ha 28 )
 $$\left\{ {\matrix{ {\dot{R}{\equals}{\minus}V_{M} \cos {\rm \rtheta }_{M} \cos {\rm \rpsi }_{M} } \hfill \cr {{\dot{\rlambda }}_{y} {\equals}{{V_{M} \sin {\rm \rtheta }_{M} } \over R}} \hfill \cr {{\dot{\rlambda }}_{z} {\equals}{\minus}{{V_{M} \cos {\rm \rtheta }_{M} \sin {\rm \rpsi }_{M} } \over R}} \hfill \cr {{\dot{\rtheta }}_{M} {\equals}{{a_{z} } \over {V_{M} }}{\plus}{{V_{M} } \over R}\cos {\rm \rtheta }_{M} \sin ^{2} {\rm \rpsi }_{M} \tan {\rm \rtheta }_{L} {\plus}{{V_{M} } \over R}\sin {\rm \rtheta }_{M} \cos {\rm \rpsi }_{M} } \hfill \cr \matrix{ {\dot{\rpsi }}_{M} {\equals}{{a_{y} } \over {V_{M} \cos {\rm \rtheta }_{M} }}{\minus}{{V_{M} } \over R}\sin {\rm \rtheta }_{M} \sin {\rm \rpsi }_{M} \cos {\rm \rpsi }_{M} \tan {\rm \rtheta }_{L} \hfill \cr \quad \quad \;{\plus}{{V_{M} } \over {R\cos {\rm \rtheta }_{M} }}\sin ^{2} {\rm \rtheta }_{M} \sin {\rm \rpsi }_{M} {\plus}{{V_{M} } \over R}\cos {\rm \rtheta }_{M} \sin {\rm \rpsi }_{M} \hfill \cr} \hfill \cr } } \right.$$
$$\left\{ {\matrix{ {\dot{R}{\equals}{\minus}V_{M} \cos {\rm \rtheta }_{M} \cos {\rm \rpsi }_{M} } \hfill \cr {{\dot{\rlambda }}_{y} {\equals}{{V_{M} \sin {\rm \rtheta }_{M} } \over R}} \hfill \cr {{\dot{\rlambda }}_{z} {\equals}{\minus}{{V_{M} \cos {\rm \rtheta }_{M} \sin {\rm \rpsi }_{M} } \over R}} \hfill \cr {{\dot{\rtheta }}_{M} {\equals}{{a_{z} } \over {V_{M} }}{\plus}{{V_{M} } \over R}\cos {\rm \rtheta }_{M} \sin ^{2} {\rm \rpsi }_{M} \tan {\rm \rtheta }_{L} {\plus}{{V_{M} } \over R}\sin {\rm \rtheta }_{M} \cos {\rm \rpsi }_{M} } \hfill \cr \matrix{ {\dot{\rpsi }}_{M} {\equals}{{a_{y} } \over {V_{M} \cos {\rm \rtheta }_{M} }}{\minus}{{V_{M} } \over R}\sin {\rm \rtheta }_{M} \sin {\rm \rpsi }_{M} \cos {\rm \rpsi }_{M} \tan {\rm \rtheta }_{L} \hfill \cr \quad \quad \;{\plus}{{V_{M} } \over {R\cos {\rm \rtheta }_{M} }}\sin ^{2} {\rm \rtheta }_{M} \sin {\rm \rpsi }_{M} {\plus}{{V_{M} } \over R}\cos {\rm \rtheta }_{M} \sin {\rm \rpsi }_{M} \hfill \cr} \hfill \cr } } \right.$$
where
![]() ${\dot{\rlambda }}_{y} $
and
${\dot{\rlambda }}_{y} $
and
![]() ${\dot{\rlambda }}_{z} $
are LOS angular velocity components in the LOS co-ordinate system, and a
y
and a
z
denote accelerations of the missile in the missile body co-ordinate system. Then, the heading error σ can be defined from Fig. 1 as
${\dot{\rlambda }}_{z} $
are LOS angular velocity components in the LOS co-ordinate system, and a
y
and a
z
denote accelerations of the missile in the missile body co-ordinate system. Then, the heading error σ can be defined from Fig. 1 as
The typical PPN law in 3D engagement can be given by( Reference Song and Ha 28 )
in which N represents the navigation constant of the missile, and as pointed out in Ref. 20 that selecting N≥2 guarantees the convergence of the heading error.
Submitting (3) into (1) and differentiating (2) yield that
 $$\eqalignno{ {\dot{\rsigma }} & {\equals}{1 \over {\sqrt {1{\minus}\cos ^{2} {\rm \rsigma }} }}\left( {\sin {\rm \rtheta }_{M} \cos {\rm \rpsi }_{M} {\dot{\rtheta }}_{M} {\plus}\cos {\rm \rtheta }_{M} \sin {\rm \rpsi }_{M} {\dot{\rpsi }}_{M} } \right) \cr & {\equals}{{\left( {1{\minus}N} \right)V_{M} } \over {R\sqrt {1{\minus}\cos ^{2} {\rm \rsigma }} }}\sin ^{2} {\rm \rsigma } \cr & {\equals}{\minus}{{\left( {N{\minus}1} \right)V_{M} } \over R}\sin {\rm \rsigma } $$
$$\eqalignno{ {\dot{\rsigma }} & {\equals}{1 \over {\sqrt {1{\minus}\cos ^{2} {\rm \rsigma }} }}\left( {\sin {\rm \rtheta }_{M} \cos {\rm \rpsi }_{M} {\dot{\rtheta }}_{M} {\plus}\cos {\rm \rtheta }_{M} \sin {\rm \rpsi }_{M} {\dot{\rpsi }}_{M} } \right) \cr & {\equals}{{\left( {1{\minus}N} \right)V_{M} } \over {R\sqrt {1{\minus}\cos ^{2} {\rm \rsigma }} }}\sin ^{2} {\rm \rsigma } \cr & {\equals}{\minus}{{\left( {N{\minus}1} \right)V_{M} } \over R}\sin {\rm \rsigma } $$
Then, according to the facts of (1), (2) and (4), one obtains that
Solving the equation presented in (5) in terms of the heading error σ yields that
which indicates that if missiles guided by the typical PPN law are associated with the same initial range-to-go R(0) and initial heading error σ(0), then these missiles have the same flight trajectories. This information is valuable enough to lay a firm foundation for the co-operative guidance law design.
2.2 Problem statement
This study considers the co-operative guidance problem of n + 1 missiles attacking simultaneously a stationary target. In typical scenarios of salvo attack, missiles are usually assumed to be homogeneous, which means that they perform similar aerodynamic properties. Hence, it is necessary and reasonable to regard the same velocity for multiple missiles in a salvo attack mission.
Co-operative salvo attack of multiple missiles depends on the neighbour-to-neighbour communication. Let
 ${{\rm {\cal G}}}$
=(
${{\rm {\cal G}}}$
=(
 $${{\rnu}}$$
,
$${{\rnu}}$$
,
![]() ${{\rm {\rvarepsilon}}}$
) be a directed graph, where
${{\rm {\rvarepsilon}}}$
) be a directed graph, where
![]() $${{\rnu}}$$
={v
0, v
1, … , v
n
} is the set of nodes, and
$${{\rnu}}$$
={v
0, v
1, … , v
n
} is the set of nodes, and
![]() ${{\rm {\rvarepsilon}}}$
⊆
${{\rm {\rvarepsilon}}}$
⊆
![]() $${{\rnu}}$$
×
$${{\rnu}}$$
×
![]() $${{\rnu}}$$
is the set of edges with an ordered pair of nodes. An edge e
i,j
in the directed graph is denoted by the ordered pair of nodes (ν
j
, ν
i
), and e
i,j
∈
$${{\rnu}}$$
is the set of edges with an ordered pair of nodes. An edge e
i,j
in the directed graph is denoted by the ordered pair of nodes (ν
j
, ν
i
), and e
i,j
∈
 ${{\rm {\rvarepsilon}}}$
in the directed graph means that agent i can obtain information from agent j, but not vice versa. Furthermore, self-loops are not allowed, that is e
i,i
∉
${{\rm {\rvarepsilon}}}$
in the directed graph means that agent i can obtain information from agent j, but not vice versa. Furthermore, self-loops are not allowed, that is e
i,i
∉
 ${{\rm {\rvarepsilon}}}$
. A directed path from node ν
i
to ν
j
is a sequence of ordered edges as (ν
i
, ν
k1), (ν
k1, ν
k2), ... , (ν
kl
, ν
j
), with distinct nodes ν
km
, m=1, 2, … , l. A directed graph is called connected if and only if there exists a directed path between any pair of distinct nodes. Moreover, if there is exists a node called the root, and this root has a directed path to every other node of the graph, then the graph is said to contain a directed spanning tree. A nonnegative adjacency matrix
${{\rm {\rvarepsilon}}}$
. A directed path from node ν
i
to ν
j
is a sequence of ordered edges as (ν
i
, ν
k1), (ν
k1, ν
k2), ... , (ν
kl
, ν
j
), with distinct nodes ν
km
, m=1, 2, … , l. A directed graph is called connected if and only if there exists a directed path between any pair of distinct nodes. Moreover, if there is exists a node called the root, and this root has a directed path to every other node of the graph, then the graph is said to contain a directed spanning tree. A nonnegative adjacency matrix
![]() ${\mib {\cal A}}{\equals}\left[ {a_{{i,\,j}} } \right]\in{\mib {\bf R}}^{{\left( {n{\plus}1} \right){\times}\left( {n{\plus}1} \right)}} $
specifies the inter-connection topology of missiles, which can be defined as
${\mib {\cal A}}{\equals}\left[ {a_{{i,\,j}} } \right]\in{\mib {\bf R}}^{{\left( {n{\plus}1} \right){\times}\left( {n{\plus}1} \right)}} $
specifies the inter-connection topology of missiles, which can be defined as
Then, the Laplacian matrix
![]() $${ {\mib {\cal L}}}{\equals}\left[ {l_{{i,j}} } \right]\in{\mib {\Bbb R}}^{{\left( {n{\plus}1} \right){\times}\left( {n{\plus}1} \right)}} $$
of the graph
$${ {\mib {\cal L}}}{\equals}\left[ {l_{{i,j}} } \right]\in{\mib {\Bbb R}}^{{\left( {n{\plus}1} \right){\times}\left( {n{\plus}1} \right)}} $$
of the graph
![]() ${\mib {\cal G}}$
is given as
${\mib {\cal G}}$
is given as
 $$l_{{i,j}} {\equals}\left\{ {\matrix{ {{\minus}a_{{i,j}} } \hfill & {i\,\ne\,j} \hfill \cr {\mathop{\sum}\limits_{k{\equals}0,k\,\ne\,i}^n {a_{{i,k}} } } \hfill & {i{\equals}j} \hfill \cr } } \right.$$
$$l_{{i,j}} {\equals}\left\{ {\matrix{ {{\minus}a_{{i,j}} } \hfill & {i\,\ne\,j} \hfill \cr {\mathop{\sum}\limits_{k{\equals}0,k\,\ne\,i}^n {a_{{i,k}} } } \hfill & {i{\equals}j} \hfill \cr } } \right.$$
The following lemma is satisfied for a connected graph that contains a directed spanning tree.
Lemma 1
(Ref. 29). Zero is a simple eigenvalue of the Laplacian matrix
![]() ${\mib {\cal L}}$
, and all the other eigenvalues are positive if and only if the graph
${\mib {\cal L}}$
, and all the other eigenvalues are positive if and only if the graph
![]() ${\mib {\cal G}}$
is connected.
${\mib {\cal G}}$
is connected.
Suppose that there exists a finite set
![]() $${ \tilde{{\cal G}}}{\equals}\left\{ {{\mib {\cal G}}_{p} \,\colon\,p\in{\cal P}} \right\}$$
of all possible graphs, in which
$${ \tilde{{\cal G}}}{\equals}\left\{ {{\mib {\cal G}}_{p} \,\colon\,p\in{\cal P}} \right\}$$
of all possible graphs, in which
![]() ${\cal P}$
is an index set for all graphs. Then,
${\cal P}$
is an index set for all graphs. Then,
![]() ${\mib {\cal G}}_{{s\left( t \right)}} $
can be utilised to describe the current communication graph at any time t>0, where s(t) : [0, +∞) →
${\mib {\cal G}}_{{s\left( t \right)}} $
can be utilised to describe the current communication graph at any time t>0, where s(t) : [0, +∞) →
![]() ${\cal P}$
represents the switching signal.
${\cal P}$
represents the switching signal.
The control objective of this paper is to design a co-operative guidance law based on information from topology
![]() ${\mib {\cal G}}_{{s\left( t \right)}} $
such that all missiles can reach at a stationary target simultaneously in spite of their variety initial poses and positions.
${\mib {\cal G}}_{{s\left( t \right)}} $
such that all missiles can reach at a stationary target simultaneously in spite of their variety initial poses and positions.
3.0 MAIN RESULTS
Motivated by the property of the typical PPN law, a two-stage co-operative guidance strategy can be considered as a feasible solution for the salvo attack problem of multiple missiles. In the first guidance phase, a co-operative guidance law based on the communication topology is adopted to drive missiles to achieve favoured initial states (i.e. the same range-to-go and the same heading errors) for the second guidance phase. Then, missiles disconnect from each other and the typical PPN guidance law is utilised to drive missiles to accomplish the salvo attack mission.
Before moving on, the following auxiliary states are introduced first
in which R i and σ i , i=0,…, n denote the range-to-go and heading error of the ith missile. Based on (1) and (2), one can obtain from (9) that
in which
Then, the co-operative guidance law design problem can be formulated as a consensus problem of the multi-missile system (10). Moreover, based on (11), the following guidance law can be used to realise favoured conditions of all missiles in the first guidance phase
 $$\left\{ {\matrix{ {a_{{y,i}} {\equals}{\minus}{{V_{M}^{2} } \over {R_{i} }}\sin {\rm \rpsi }_{{M,i}} {\plus}{{u_{i} V_{M} \sqrt {1{\minus}\cos ^{2} {\rm \rsigma }_{i} } } \over {2\sin {\rm \rsigma }_{i} \sin {\rm \rpsi }_{{M,i}} }}} \hfill \cr {a_{{z,i}} {\equals}{\minus}{{V_{M}^{2} } \over {R_{i} }}sin\;{\rm \rtheta }_{{M,i}} \cos {\rm \rpsi }_{{M,i}} {\plus}{{u_{i} V_{M} \sqrt {1{\minus}\cos ^{2} {\rm \rsigma }_{i} } } \over {2\sin {\rm \rsigma }_{i} \sin {\rm \rtheta }_{{M,i}} \cos {\rm \rpsi }_{{M,i}} }}} \hfill \cr } } \right.$$
$$\left\{ {\matrix{ {a_{{y,i}} {\equals}{\minus}{{V_{M}^{2} } \over {R_{i} }}\sin {\rm \rpsi }_{{M,i}} {\plus}{{u_{i} V_{M} \sqrt {1{\minus}\cos ^{2} {\rm \rsigma }_{i} } } \over {2\sin {\rm \rsigma }_{i} \sin {\rm \rpsi }_{{M,i}} }}} \hfill \cr {a_{{z,i}} {\equals}{\minus}{{V_{M}^{2} } \over {R_{i} }}sin\;{\rm \rtheta }_{{M,i}} \cos {\rm \rpsi }_{{M,i}} {\plus}{{u_{i} V_{M} \sqrt {1{\minus}\cos ^{2} {\rm \rsigma }_{i} } } \over {2\sin {\rm \rsigma }_{i} \sin {\rm \rtheta }_{{M,i}} \cos {\rm \rpsi }_{{M,i}} }}} \hfill \cr } } \right.$$
From (12), one can see that σ i =0 or ξ i =−1 is a singular point, which leads to the failure of co-operative guidance. To cope with this problem, the leader-follower strategy with a zero input leader is utilised in this paper. Simply let missile 0 be the selected leader and other missiles are performed as followers. Let δ i =[η i , ξ i ]T, i=0,..., n, then the dynamics of the multi-missile system can be obtained by
in which
![]() ${A}{\equals}\left[ {\matrix{ 0 & 1 \cr 0 & 0 \cr } } \right],{\mib B}{\equals}\left[ {\matrix{ 0 \cr 1 \cr } } \right].$
${A}{\equals}\left[ {\matrix{ 0 & 1 \cr 0 & 0 \cr } } \right],{\mib B}{\equals}\left[ {\matrix{ 0 \cr 1 \cr } } \right].$
Hence, the control objective in the first guidance phase can be concluded as that designing distributed control protocols u i , i=1,…, n such that
is achieved in spite of any initial conditions.
Remark 1. As all missiles are assumed to be associated with the same constant velocity V M , (14) indicates that
Therefore, the control objective achieved in the first guidance phase results in the same range-to-go and the same heading error finally. Moreover, it can be seen from (13) that the leader missile’s input u 0 is set to be 0, which means that the heading error σ0(t) keeps constant in the first guidance phase. Hence, selecting a missile with favoured initial heading error σ0(0) as the leader not only helps to avoid the singularity problem mentioned above but also to obtain favoured conditions for the work of the PNN law in the second guidance phase.
In typical leader-follower co-ordination, it is usually assumed that the leader has no neighbours while the communication network among followers is undirected. Hence, the Laplacian matrix
![]() ${\mib {\cal L}}_{{s\left( t \right)}} $
associated with the graph
${\mib {\cal L}}_{{s\left( t \right)}} $
associated with the graph
![]() ${\mib {\cal G}}_{{s\left( t \right)}} $
has the following form:
${\mib {\cal G}}_{{s\left( t \right)}} $
has the following form:
in which ϕ s(t) ∈ℝ n and H s(t) ∈ℝ n×n is a symmetric positive definite matrix.
To obtain the main results, consider an infinite sequence of nonempty, bounded and contiguous time intervals
![]() $\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right),\;k{\equals}0,1,...$
, with t
0=0 and t
k+1−t
k
≤T for some constant T>0. Suppose that in each interval
$\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right),\;k{\equals}0,1,...$
, with t
0=0 and t
k+1−t
k
≤T for some constant T>0. Suppose that in each interval
![]() $\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right)$
, there exists a sequence of non-overlapping subintervals
$\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right)$
, there exists a sequence of non-overlapping subintervals
![]() $\left[ {t_{k}^{0} ,\;t_{k}^{1} } \right),\,\ldots\,,\left[ {t_{k}^{m} ,\;t_{k}^{{m{\plus}1}} } \right),\,\ldots\,,\left[ {t_{k}^{{m_{k} {\minus}1}} ,\;t_{k}^{{m_{k} }} } \right)$
with
$\left[ {t_{k}^{0} ,\;t_{k}^{1} } \right),\,\ldots\,,\left[ {t_{k}^{m} ,\;t_{k}^{{m{\plus}1}} } \right),\,\ldots\,,\left[ {t_{k}^{{m_{k} {\minus}1}} ,\;t_{k}^{{m_{k} }} } \right)$
with
![]() $t_{k}^{0} {\equals}t_{k} $
and
$t_{k}^{0} {\equals}t_{k} $
and
![]() $t_{k}^{{m_{k} }} {\equals}t_{{k{\plus}1}} $
satisfying
$t_{k}^{{m_{k} }} {\equals}t_{{k{\plus}1}} $
satisfying
![]() $t_{k}^{{m{\plus}1}} {\minus}t_{k}^{m} \geq T_{s} \,\gt\,0,\;0\leq m\leq m_{k} {\minus}1$
. It is assumed that in each subinterval
$t_{k}^{{m{\plus}1}} {\minus}t_{k}^{m} \geq T_{s} \,\gt\,0,\;0\leq m\leq m_{k} {\minus}1$
. It is assumed that in each subinterval
![]() $\left[ {t_{k}^{m} ,\;t_{k}^{{m{\plus}1}} } \right)$
, the communication graph
$\left[ {t_{k}^{m} ,\;t_{k}^{{m{\plus}1}} } \right)$
, the communication graph
![]() ${\mib {\cal G}}_{{s\left( t \right)}} $
is fixed, denoted by
${\mib {\cal G}}_{{s\left( t \right)}} $
is fixed, denoted by
![]() ${\mib {\cal G}}_{{k_{m} }} $
. Then, a mild assumption of communication topologies is introduced.
${\mib {\cal G}}_{{k_{m} }} $
. Then, a mild assumption of communication topologies is introduced.
Assumption 3.
During each subinterval
![]() $\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right)$
, some or all
$\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right)$
, some or all
![]() ${\mib {\cal G}}_{{k_{m} }} ,\;m{\equals}0,1,...,m_{k} $
are permitted to be disconnected; however, it is required that the union graph
${\mib {\cal G}}_{{k_{m} }} ,\;m{\equals}0,1,...,m_{k} $
are permitted to be disconnected; however, it is required that the union graph
![]() $\bigcup\nolimits_{m{\equals}0}^{m_{k} } {{\mib {\cal G}}_{{k_{m} }} } $
is jointly connected (detailed definition is presented in Ref. 30) and contains a directed spanning tree across each interval
$\bigcup\nolimits_{m{\equals}0}^{m_{k} } {{\mib {\cal G}}_{{k_{m} }} } $
is jointly connected (detailed definition is presented in Ref. 30) and contains a directed spanning tree across each interval
![]() $\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right).$
$\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right).$
In the following, for each
![]() $p\in{\mib {\cal P}}$
, eigenvalues of
H
p
can be denoted by
$p\in{\mib {\cal P}}$
, eigenvalues of
H
p
can be denoted by
![]() ${\rm \lambda }_{p}^{i} $
, where i=1,..., n is the index of each follower missile, based on the labelling rule in Ref. 30. Let
${\rm \lambda }_{p}^{i} $
, where i=1,..., n is the index of each follower missile, based on the labelling rule in Ref. 30. Let
![]() $\ell \left( p \right){\equals}\left\{ {i\,\colon\,\lambda _{p}^{i} \,\ne\,0,i{\equals}1,...,n} \right\}$
, then the following lemma can be used to obtain the relation between jointly connected graphs and eigenvalues of Laplacian matrices.
$\ell \left( p \right){\equals}\left\{ {i\,\colon\,\lambda _{p}^{i} \,\ne\,0,i{\equals}1,...,n} \right\}$
, then the following lemma can be used to obtain the relation between jointly connected graphs and eigenvalues of Laplacian matrices.
Lemma 2
(Ref. 30). Graphs
![]() $\left\{ {{\mib {\cal G}}_{{s\left( t \right)}} \,\colon\,s\left( t \right)\to{\mib {\cal P}}} \right\}$
are jointly connected across each interval
$\left\{ {{\mib {\cal G}}_{{s\left( t \right)}} \,\colon\,s\left( t \right)\to{\mib {\cal P}}} \right\}$
are jointly connected across each interval
![]() $\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right)$
if and only if
$\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right)$
if and only if
Remark 2.
Lemma 2 gives the relation between jointly connected graphs and the non-zero eigenvalues, which lays a firm foundation for the co-operative guidance law design and stability analysis. Additionally, it also guarantees that the union graph across each interval
![]() $\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right)$
contains a directed spanning tree
$\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right)$
contains a directed spanning tree
Based on the communication topology
![]() ${\mib {\cal G}}_{{s\left( t \right)}} $
, the consensus protocol is designed as
${\mib {\cal G}}_{{s\left( t \right)}} $
, the consensus protocol is designed as
 $$\eqalignno{ u_{i} \left( t \right) & {\equals}{\minus}{\mib B}^{{\rm T}} {\mib P}\mathop{\sum}\limits_{j{\equals}1,j\,\ne\,i}^n {a_{{i,j}} \left( t \right)\left( {{\bf \rdelta }_{i} \left( {t{\minus}{\rm \tau }\left( t \right)} \right){\minus}{\bf \rdelta }_{j} \left( {t{\minus}{\rm \tau }\left( t \right)} \right)} \right)} \cr & {\minus}{\mib B}^{{\rm T}} {\mib P}a_{{i,0}} \left( t \right)\left( {{\bf \rdelta }_{i} \left( {t{\minus}{\rm \tau }\left( t \right)} \right){\minus}{\bf \rdelta }_{0} \left( {t{\minus}{\rm \tau }\left( t \right)} \right)} \right) $$
$$\eqalignno{ u_{i} \left( t \right) & {\equals}{\minus}{\mib B}^{{\rm T}} {\mib P}\mathop{\sum}\limits_{j{\equals}1,j\,\ne\,i}^n {a_{{i,j}} \left( t \right)\left( {{\bf \rdelta }_{i} \left( {t{\minus}{\rm \tau }\left( t \right)} \right){\minus}{\bf \rdelta }_{j} \left( {t{\minus}{\rm \tau }\left( t \right)} \right)} \right)} \cr & {\minus}{\mib B}^{{\rm T}} {\mib P}a_{{i,0}} \left( t \right)\left( {{\bf \rdelta }_{i} \left( {t{\minus}{\rm \tau }\left( t \right)} \right){\minus}{\bf \rdelta }_{0} \left( {t{\minus}{\rm \tau }\left( t \right)} \right)} \right) $$
where P ∈ℝ2×2 is a positive definite matrix, and τ(t) is a uniform time-varying communication delay satisfying the following assumption.
Assumption 4.
There exist constants
![]() ${\rm \tau }_{m} \,\gt\,0$
and
${\rm \tau }_{m} \,\gt\,0$
and
![]() $0\,\lt\,{\rm \tau }_{{dm}} \,\lt\,1$
such that
$0\,\lt\,{\rm \tau }_{{dm}} \,\lt\,1$
such that
![]() $0\leq {\rm \tau }\left( t \right)\leq {\rm \tau }_{m} $
and
$0\leq {\rm \tau }\left( t \right)\leq {\rm \tau }_{m} $
and
![]() $\left| {{\dot{\tau }}\left( t \right)} \right|\leq {\rm \tau }_{{dm}} $
are achieved.
$\left| {{\dot{\tau }}\left( t \right)} \right|\leq {\rm \tau }_{{dm}} $
are achieved.
To analyse the leader–follower consensus of the multi-missile system (13), let
![]() ${\tilde{\delta}_{i}} {\equals}{\bf \rdelta }_{i} {\minus}{\bf \rdelta }_{0} ,i{\equals}1,...,n$
be the state error of the ith missile. Then, the dynamics of
${\tilde{\delta}_{i}} {\equals}{\bf \rdelta }_{i} {\minus}{\bf \rdelta }_{0} ,i{\equals}1,...,n$
be the state error of the ith missile. Then, the dynamics of
![]() $\tilde{\delta}_{i}$
can be obtained based on (18) as
$\tilde{\delta}_{i}$
can be obtained based on (18) as
Let
![]() $${\tilde{\rdelta }}{\equals}\left[ {{\tilde{\rdelta }}_{1}^{{\rm T}} ,...,{\tilde{\rdelta }}_{n}^{{\rm T}} } \right]^{{\rm T}} $$
, then the network dynamics can be rewritten in the compact form as
$${\tilde{\rdelta }}{\equals}\left[ {{\tilde{\rdelta }}_{1}^{{\rm T}} ,...,{\tilde{\rdelta }}_{n}^{{\rm T}} } \right]^{{\rm T}} $$
, then the network dynamics can be rewritten in the compact form as
The following theorem presents sufficient conditions to guarantee the consensus of the multi-missile system (13) based on the control law in (18).
Theorem 1. Suppose that Assumptions 1–4 hold. Then, the consensus problem for the multi-missile system (13) can be achieved by the control protocol (18) if there exists matrix P >0 such that the following linear matrix inequalities (LMIs)
are satisfied, where
![]() ${\rm \lambda }_{{\min }} $
and
${\rm \lambda }_{{\min }} $
and
![]() ${\rm \lambda }_{{\max }} $
are the smallest non-zero and the biggest eigenvalues associated with all possible communication topologies.
${\rm \lambda }_{{\max }} $
are the smallest non-zero and the biggest eigenvalues associated with all possible communication topologies.
Proof.
To start the consensus analysis, consider the following Lyapunov–Krasovskii function:
with
 $$\left\{ {\matrix{ {V_{1} \left( t \right){\equals}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( t \right)} \hfill \cr {V_{2} \left( t \right){\equals}{\int}_{t{\minus}\tau \left( t \right)}^t {{\tilde{\rdelta }}^{{\rm T}} \left( {\rm \romega } \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( {\rm \romega } \right){\rm d\romega }} {\plus}{\int}_{{\minus}\tau _{m} }^0 {{\int}_{t{\plus}\rrho }^t {{\dot{\tilde{\rdelta }}}^{{\rm T}} \left( {\rm \romega } \right){\dot{\tilde{\rdelta }}}\left( {\rm \romega } \right){\rm d\romega d\rrho }} } } \hfill \cr } } \right.$$
$$\left\{ {\matrix{ {V_{1} \left( t \right){\equals}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( t \right)} \hfill \cr {V_{2} \left( t \right){\equals}{\int}_{t{\minus}\tau \left( t \right)}^t {{\tilde{\rdelta }}^{{\rm T}} \left( {\rm \romega } \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( {\rm \romega } \right){\rm d\romega }} {\plus}{\int}_{{\minus}\tau _{m} }^0 {{\int}_{t{\plus}\rrho }^t {{\dot{\tilde{\rdelta }}}^{{\rm T}} \left( {\rm \romega } \right){\dot{\tilde{\rdelta }}}\left( {\rm \romega } \right){\rm d\romega d\rrho }} } } \hfill \cr } } \right.$$
From (25), it can be seen that V(t) is continuously differentiable at any time except for the switching time. Then, at any non-switching time t, the time derivative of V 1(t) and V 2(t) along the trajectory of system (20) can be given by
 $$\eqalignno{ \dot{V}_{1} \left( t \right) & {\equals}2{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\dot{\tilde{\rdelta }}}\left( t \right) \cr & {\equals}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,\left( {{\mib PA}{\plus}{\mib A}^{{\rm T}} {\mib P}} \right)} \right){\tilde{\rdelta }}\left( t \right){\minus}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( {t{\minus}{\rm \tau }\left( t \right)} \right) \cr & {\equals}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,\left( {{\mib PA}{\plus}{\mib A}^{{\rm T}} {\mib P}} \right)} \right){\tilde{\rdelta }}\left( t \right){\minus}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right) \cr & {\plus}{\int}_{t{\minus}\tau \left( t \right)}^t {{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\dot{\tilde{\rdelta }}}\left( {\rm \romega } \right){\rm d\romega }} \cr & \leq {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,\left( {{\mib PA}{\plus}{\mib A}^{{\rm T}} {\mib P}} \right)} \right){\tilde{\rdelta }}\left( t \right){\minus}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right) \cr & {\plus}{\int}_{t{\minus}\tau \left( t \right)}^t {{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}}^{{\rm T}} {\mib H}_{{s\left( t \right)}} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib PPBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right){\rm {\plus}}{\dot{\tilde{\rdelta }}}^{{^{{\rm T}} }} \left( {\rm \romega } \right){\dot{\tilde{\rdelta }}}\left( {\rm \romega } \right){\rm d\romega }} \cr & \leq {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,\left( {{\mib PA}{\plus}{\mib A}^{{\rm T}} {\mib P}} \right)} \right){\tilde{\rdelta }}\left( t \right){\minus}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right) \cr & {\plus}{\rm \tau }_{m} {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}}^{{\rm T}} {\mib H}_{{s\left( t \right)}} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib PPBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right){\plus}{\int}_{t{\minus}\tau _{m} }^t {{\dot{\tilde{\rdelta }}}^{{^{{\rm T}} }} \left( {\rm \romega } \right){\dot{\tilde{\rdelta }}}\left( {\rm \romega } \right){\rm d\romega }} $$
$$\eqalignno{ \dot{V}_{1} \left( t \right) & {\equals}2{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\dot{\tilde{\rdelta }}}\left( t \right) \cr & {\equals}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,\left( {{\mib PA}{\plus}{\mib A}^{{\rm T}} {\mib P}} \right)} \right){\tilde{\rdelta }}\left( t \right){\minus}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( {t{\minus}{\rm \tau }\left( t \right)} \right) \cr & {\equals}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,\left( {{\mib PA}{\plus}{\mib A}^{{\rm T}} {\mib P}} \right)} \right){\tilde{\rdelta }}\left( t \right){\minus}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right) \cr & {\plus}{\int}_{t{\minus}\tau \left( t \right)}^t {{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\dot{\tilde{\rdelta }}}\left( {\rm \romega } \right){\rm d\romega }} \cr & \leq {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,\left( {{\mib PA}{\plus}{\mib A}^{{\rm T}} {\mib P}} \right)} \right){\tilde{\rdelta }}\left( t \right){\minus}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right) \cr & {\plus}{\int}_{t{\minus}\tau \left( t \right)}^t {{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}}^{{\rm T}} {\mib H}_{{s\left( t \right)}} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib PPBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right){\rm {\plus}}{\dot{\tilde{\rdelta }}}^{{^{{\rm T}} }} \left( {\rm \romega } \right){\dot{\tilde{\rdelta }}}\left( {\rm \romega } \right){\rm d\romega }} \cr & \leq {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,\left( {{\mib PA}{\plus}{\mib A}^{{\rm T}} {\mib P}} \right)} \right){\tilde{\rdelta }}\left( t \right){\minus}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right) \cr & {\plus}{\rm \tau }_{m} {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}}^{{\rm T}} {\mib H}_{{s\left( t \right)}} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib PPBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right){\plus}{\int}_{t{\minus}\tau _{m} }^t {{\dot{\tilde{\rdelta }}}^{{^{{\rm T}} }} \left( {\rm \romega } \right){\dot{\tilde{\rdelta }}}\left( {\rm \romega } \right){\rm d\romega }} $$
and
 $$\eqalignno{ \dot{V}_{2} \left( t \right) & {\equals}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( t \right){\minus}\left( {1{\minus}{\dot{\rtau }}\left( t \right)} \right){\tilde{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) \cr & {\plus}{\rm \rtau }_{m} {\dot{\tilde{\rdelta }}}^{{\rm T}} \left( t \right){\dot{\tilde{\rdelta }}}\left( t \right){\minus}{\int}_{t{\minus}\rtau _{m} }^t {{\dot{\tilde{\rdelta }}}^{{\rm T}} \left( {\rm \romega } \right){\dot{\tilde{\rdelta }}}\left( {\rm \romega } \right){\rm d\romega }} \cr & \:\leq {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( t \right){\minus}\left( {1{\minus}{\rm \rtau }_{{dm}} } \right){\tilde{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) \cr & {\plus}2{\rm \rtau }_{m} {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,{\mib A}^{{\rm T}} {\mib A}} \right){\tilde{\rdelta }}\left( t \right){\minus}{\int}_{t{\minus}\rtau _{m} }^t {{\dot{\tilde{\rdelta }}}^{{\rm T}} \left( {\rm \romega } \right){\dot{\tilde{\rdelta }}}\left( {\rm \romega } \right){\rm d\romega }} \cr & {\plus}2{\rm \rtau }_{m} {\tilde{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\mib H}_{{s\left( t \right)}}^{{\rm T}} {\mib H}_{{s\left( t \right)}} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib BB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) $$
$$\eqalignno{ \dot{V}_{2} \left( t \right) & {\equals}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( t \right){\minus}\left( {1{\minus}{\dot{\rtau }}\left( t \right)} \right){\tilde{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) \cr & {\plus}{\rm \rtau }_{m} {\dot{\tilde{\rdelta }}}^{{\rm T}} \left( t \right){\dot{\tilde{\rdelta }}}\left( t \right){\minus}{\int}_{t{\minus}\rtau _{m} }^t {{\dot{\tilde{\rdelta }}}^{{\rm T}} \left( {\rm \romega } \right){\dot{\tilde{\rdelta }}}\left( {\rm \romega } \right){\rm d\romega }} \cr & \:\leq {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( t \right){\minus}\left( {1{\minus}{\rm \rtau }_{{dm}} } \right){\tilde{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) \cr & {\plus}2{\rm \rtau }_{m} {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,{\mib A}^{{\rm T}} {\mib A}} \right){\tilde{\rdelta }}\left( t \right){\minus}{\int}_{t{\minus}\rtau _{m} }^t {{\dot{\tilde{\rdelta }}}^{{\rm T}} \left( {\rm \romega } \right){\dot{\tilde{\rdelta }}}\left( {\rm \romega } \right){\rm d\romega }} \cr & {\plus}2{\rm \rtau }_{m} {\tilde{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\mib H}_{{s\left( t \right)}}^{{\rm T}} {\mib H}_{{s\left( t \right)}} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib BB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) $$
Therefore, based on (26) and (27), one has
 $$\eqalignno{ \dot{V}\left( t \right) & {\equals}\dot{V}_{1} \left( t \right){\plus}\dot{V}_{2} \left( t \right) \cr & \leq {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,\left( {{\mib PA}{\plus}{\mib A}^{{\rm T}} {\mib P}{\plus}{\mib P}{\plus}2\rtau _{m} {\mib A}^{{\rm T}} {\mib A}} \right)} \right){\tilde{\rdelta }}\left( t \right) \cr & {\minus}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right) \cr & {\plus}{\rm \rtau }_{m} {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}}^{{\rm T}} {\mib H}_{{s\left( t \right)}} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib PPBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right) \cr & {\minus}\left( {1{\minus}{\rm \rtau }_{{dm}} } \right){\tilde{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) \cr & {\plus}2{\rm \rtau }_{m} {\tilde{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\mib H}_{{s\left( t \right)}}^{{\rm T}} {\mib H}_{{s\left( t \right)}} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib BB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) $$
$$\eqalignno{ \dot{V}\left( t \right) & {\equals}\dot{V}_{1} \left( t \right){\plus}\dot{V}_{2} \left( t \right) \cr & \leq {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,\left( {{\mib PA}{\plus}{\mib A}^{{\rm T}} {\mib P}{\plus}{\mib P}{\plus}2\rtau _{m} {\mib A}^{{\rm T}} {\mib A}} \right)} \right){\tilde{\rdelta }}\left( t \right) \cr & {\minus}{\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right) \cr & {\plus}{\rm \rtau }_{m} {\tilde{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib H}_{{s\left( t \right)}}^{{\rm T}} {\mib H}_{{s\left( t \right)}} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib PPBB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( t \right) \cr & {\minus}\left( {1{\minus}{\rm \rtau }_{{dm}} } \right){\tilde{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\tilde{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) \cr & {\plus}2{\rm \rtau }_{m} {\tilde{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\mib H}_{{s\left( t \right)}}^{{\rm T}} {\mib H}_{{s\left( t \right)}} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib BB}^{{\rm T}} {\mib P}} \right){\tilde{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) $$
Noting that
H
s(t) is symmetric, hence there exists an orthogonal matrix
W
s(t) such that
![]() ${\mib W}_{{s\left( t \right)}} {\mib H}_{{s\left( t \right)}} {\mib W}_{{s\left( t \right)}}^{{\rm T}} {\equals}{\bf \Lambda } _{{s\left( t \right)}} \,\colon\,{\equals}{\rm diag}\left\{ {\lambda _{{s\left( t \right)}}^{1} ,...,\lambda _{{s\left( t \right)}}^{n} } \right\}$
. Let
${\mib W}_{{s\left( t \right)}} {\mib H}_{{s\left( t \right)}} {\mib W}_{{s\left( t \right)}}^{{\rm T}} {\equals}{\bf \Lambda } _{{s\left( t \right)}} \,\colon\,{\equals}{\rm diag}\left\{ {\lambda _{{s\left( t \right)}}^{1} ,...,\lambda _{{s\left( t \right)}}^{n} } \right\}$
. Let
![]() ${\bf \bar{\rdelta }}\left( t \right){\equals}\left( {{\mib W}_{{s\left( t \right)}} \,\otimes\,{\mib I}_{2} } \right){\tilde{\rdelta }}\left( t \right)$
, and it follows from (28) that
${\bf \bar{\rdelta }}\left( t \right){\equals}\left( {{\mib W}_{{s\left( t \right)}} \,\otimes\,{\mib I}_{2} } \right){\tilde{\rdelta }}\left( t \right)$
, and it follows from (28) that
 $$\eqalignno{ \dot{V}\left( t \right)\leq & {\bf \bar{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,\left( {{\mib PA}{\plus}{\mib A}^{{\rm T}} {\mib P}{\plus}{\mib P}{\plus}2{\rm \rtau }_{m} {\mib A}^{{\rm T}} {\mib A}} \right)} \right){\bf \bar{\rdelta }}\left( t \right) \cr {\minus} & {\bf \bar{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\bf \Lambda } _{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\bf \bar{\rdelta }}\left( t \right) \cr {\plus} & {\rm \rtau }_{m} {\bf \bar{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\bf \Lambda } _{{s\left( t \right)}}^{2} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib PPBB}^{{\rm T}} {\mib P}} \right){\bf \bar{\rdelta }}\left( t \right) \cr {\minus} & \left( {1{\minus}{\rm \rtau }_{{dm}} } \right){\bf \bar{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\bf \bar{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) \cr {\plus} & 2{\rm \rtau }_{m} {\bf \bar{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\bf \Lambda } _{{s\left( t \right)}}^{2} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib BB}^{{\rm T}} {\mib P}} \right){\bf \bar{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) \cr \leq & \mathop{\sum}\limits_{i\in\ell \left( {s\left( t \right)} \right)} {{\bf \bar{\rdelta }}_{i}^{{\rm T}} \left( t \right)\left( {{\minus}2{\rm \lambda }_{{\min }} {\mib PBB}^{{\rm T}} {\mib P}{\plus}{\rm \rtau }_{m} {\rm \lambda }_{{\max }}^{2} {\mib PBB}^{{\rm T}} {\mib PPBB}^{{\rm T}} {\mib P}} \right){\bf \bar{\rdelta }}_{i} \left( t \right)} \cr {\plus} & \mathop{\sum}\limits_{i\in\ell \left( {s\left( t \right)} \right)} {{\bf \bar{\rdelta }}_{i}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\minus}\left( {1{\minus}{\rm \rtau }_{{dm}} } \right){\mib P}{\plus}2{\rm \rtau }_{m} \lambda _{{\max }}^{2} {\mib PBB}^{{\rm T}} {\mib BB}^{{\rm T}} {\mib P}} \right){\bf \bar{\rdelta }}_{i} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)} $$
$$\eqalignno{ \dot{V}\left( t \right)\leq & {\bf \bar{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\mib I}_{n} \,\otimes\,\left( {{\mib PA}{\plus}{\mib A}^{{\rm T}} {\mib P}{\plus}{\mib P}{\plus}2{\rm \rtau }_{m} {\mib A}^{{\rm T}} {\mib A}} \right)} \right){\bf \bar{\rdelta }}\left( t \right) \cr {\minus} & {\bf \bar{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\bf \Lambda } _{{s\left( t \right)}} \,\otimes\,2{\mib PBB}^{{\rm T}} {\mib P}} \right){\bf \bar{\rdelta }}\left( t \right) \cr {\plus} & {\rm \rtau }_{m} {\bf \bar{\rdelta }}^{{\rm T}} \left( t \right)\left( {{\bf \Lambda } _{{s\left( t \right)}}^{2} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib PPBB}^{{\rm T}} {\mib P}} \right){\bf \bar{\rdelta }}\left( t \right) \cr {\minus} & \left( {1{\minus}{\rm \rtau }_{{dm}} } \right){\bf \bar{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\mib I}_{n} \,\otimes\,{\mib P}} \right){\bf \bar{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) \cr {\plus} & 2{\rm \rtau }_{m} {\bf \bar{\rdelta }}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\bf \Lambda } _{{s\left( t \right)}}^{2} \,\otimes\,{\mib PBB}^{{\rm T}} {\mib BB}^{{\rm T}} {\mib P}} \right){\bf \bar{\rdelta }}\left( {t{\minus}{\rm \rtau }\left( t \right)} \right) \cr \leq & \mathop{\sum}\limits_{i\in\ell \left( {s\left( t \right)} \right)} {{\bf \bar{\rdelta }}_{i}^{{\rm T}} \left( t \right)\left( {{\minus}2{\rm \lambda }_{{\min }} {\mib PBB}^{{\rm T}} {\mib P}{\plus}{\rm \rtau }_{m} {\rm \lambda }_{{\max }}^{2} {\mib PBB}^{{\rm T}} {\mib PPBB}^{{\rm T}} {\mib P}} \right){\bf \bar{\rdelta }}_{i} \left( t \right)} \cr {\plus} & \mathop{\sum}\limits_{i\in\ell \left( {s\left( t \right)} \right)} {{\bf \bar{\rdelta }}_{i}^{{\rm T}} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)\left( {{\minus}\left( {1{\minus}{\rm \rtau }_{{dm}} } \right){\mib P}{\plus}2{\rm \rtau }_{m} \lambda _{{\max }}^{2} {\mib PBB}^{{\rm T}} {\mib BB}^{{\rm T}} {\mib P}} \right){\bf \bar{\rdelta }}_{i} \left( {t{\minus}{\rm \rtau }\left( t \right)} \right)} $$
where the fact of (21) is utilised to obtain the above inequality. From (29), it concludes based on (22) and (23) that there exists a constant κ>0 such that
is achieved. Hence,
![]() $\mathop{{\lim }}\limits_{{t\to{\plus}\infty}} V\left( t \right)$
exists.
$\mathop{{\lim }}\limits_{{t\to{\plus}\infty}} V\left( t \right)$
exists.
Considering the infinite sequences V(t k ), k=0,1,... and using Cauchy’s convergence criteria, one has for any α>0, there exists a positive number k α such that
For each integral, one obtains
 $$\eqalignno{ & \quad {\int}_{t_{k}^{j} }^{t_{k}^{{j{\plus}1}} } {{\minus}\dot{V}\left( {\rm \romega } \right){\rm d\romega }} \cr & \geq {\rm \kappa }{\int}_{t_{k}^{j} }^{t_{k}^{{j{\plus}1}} } {\mathop{\sum}\limits_{i\in\ell \left( {s\left( {t_{k}^{j} } \right)} \right)} {\left( {{\bf \bar{\rdelta }}_{i}^{{\rm T}} \left( {\rm \romega } \right){\bf \bar{\rdelta }}_{i} \left( {\rm \romega } \right){\plus}{\bf \bar{\rdelta }}_{i}^{{\rm T}} \left( {{\rm \romega }{\minus}{\rm \rtau }\left( {\rm \romega } \right)} \right){\bf \bar{\rdelta }}_{i} \left( {{\rm \romega }{\minus}{\rm \rtau }\left( {\rm \romega } \right)} \right)} \right)} {\rm d\romega }} \cr & \geq {\rm \kappa }{\int}_{t_{k}^{j} }^{t_{k}^{j} {\plus}T_{s} } {\mathop{\sum}\limits_{i\in\ell \left( {s\left( {t_{k}^{j} } \right)} \right)} {\left( {{\bf \bar{\rdelta }}_{i}^{{\rm T}} \left( {\rm \romega } \right){\bf \bar{\rdelta }}_{i} \left( {\rm \romega } \right){\plus}{\bf \bar{\rdelta }}_{i}^{{\rm T}} \left( {{\rm \romega }{\minus}{\rm \rtau }\left( {\rm \romega } \right)} \right){\bf \bar{\rdelta }}_{i} \left( {{\rm \romega }{\minus}{\rm \rtau }\left( {\rm \romega } \right)} \right)} \right)} {\rm d\romega }} $$
$$\eqalignno{ & \quad {\int}_{t_{k}^{j} }^{t_{k}^{{j{\plus}1}} } {{\minus}\dot{V}\left( {\rm \romega } \right){\rm d\romega }} \cr & \geq {\rm \kappa }{\int}_{t_{k}^{j} }^{t_{k}^{{j{\plus}1}} } {\mathop{\sum}\limits_{i\in\ell \left( {s\left( {t_{k}^{j} } \right)} \right)} {\left( {{\bf \bar{\rdelta }}_{i}^{{\rm T}} \left( {\rm \romega } \right){\bf \bar{\rdelta }}_{i} \left( {\rm \romega } \right){\plus}{\bf \bar{\rdelta }}_{i}^{{\rm T}} \left( {{\rm \romega }{\minus}{\rm \rtau }\left( {\rm \romega } \right)} \right){\bf \bar{\rdelta }}_{i} \left( {{\rm \romega }{\minus}{\rm \rtau }\left( {\rm \romega } \right)} \right)} \right)} {\rm d\romega }} \cr & \geq {\rm \kappa }{\int}_{t_{k}^{j} }^{t_{k}^{j} {\plus}T_{s} } {\mathop{\sum}\limits_{i\in\ell \left( {s\left( {t_{k}^{j} } \right)} \right)} {\left( {{\bf \bar{\rdelta }}_{i}^{{\rm T}} \left( {\rm \romega } \right){\bf \bar{\rdelta }}_{i} \left( {\rm \romega } \right){\plus}{\bf \bar{\rdelta }}_{i}^{{\rm T}} \left( {{\rm \romega }{\minus}{\rm \rtau }\left( {\rm \romega } \right)} \right){\bf \bar{\rdelta }}_{i} \left( {{\rm \romega }{\minus}{\rm \rtau }\left( {\rm \romega } \right)} \right)} \right)} {\rm d\romega }} $$
Hence, it follows from (32) that
As switches in the interval
![]() $\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right)$
are finite, therefore, one has for ∀k≥k
α
$\left[ {t_{k} ,\;t_{{k{\plus}1}} } \right)$
are finite, therefore, one has for ∀k≥k
α
Based on Lemma 2 and Assumption 3, it follows from (34) that there exist some positive integers β1,...,β n such that
The fact
![]() $\dot{V}\left( t \right)\leq 0$
implies that
$\dot{V}\left( t \right)\leq 0$
implies that
![]() $${\bf \bar{\rdelta }}\left( t \right)$$
and
$${\bf \bar{\rdelta }}\left( t \right)$$
and
![]() $${\tilde{\rdelta }}\left( t \right)$$
are bounded. Invoking Barbalat’s lemma, one can obtain from (35) that
$${\tilde{\rdelta }}\left( t \right)$$
are bounded. Invoking Barbalat’s lemma, one can obtain from (35) that
![]() $\mathop{{\lim }}\limits_{{t\to{\plus}\infty}} {\tilde{\rdelta }}\left( t \right){\equals}\mathop{{\lim }}\limits_{{t\to{\plus}\infty}} {\bf \bar{\rdelta }}\left( t \right){\equals}0$
. This completes the proof of Theorem 1.
$\mathop{{\lim }}\limits_{{t\to{\plus}\infty}} {\tilde{\rdelta }}\left( t \right){\equals}\mathop{{\lim }}\limits_{{t\to{\plus}\infty}} {\bf \bar{\rdelta }}\left( t \right){\equals}0$
. This completes the proof of Theorem 1.
Remark 3. According to Assumption 4 that 1−τ dm >0 holds, therefore, there always exists a feasible solution matrix P such that LMIs (21)–(23) holds. Additionally, as mentioned in Ref. 31 that, unlike the time-delayed multi-agent systems with fixed communication topologies, where necessary and sufficient conditions for the stability of such systems can be determined by analysing the positions of the roots of the characteristic equations, for the multi-agent systems with switching communication topology, only sufficient conditions for the stability can be obtained through the Lyapunov stability analysis.
In general, the missile guidance is a finite-time control problem. However, due to the asymptotical convergence of the control law (18), the first guidance phase is expressed in terms of infinite-time form in this study. Considering this observation, a terminal condition should be prescribed to terminate the first guidance phase. Hence, an implementable version of the proposed guidance law can be summarised as
 $$\matrix{ {\left\{ {\matrix{ {a_{{y,i}} {\equals}{\minus}NV_{M} {\dot{\rlambda }}_{{y,i}} \sin {\rm \rtheta }_{{M,i}} \sin {\rm \rpsi }_{{M,i}} {\plus}NV_{M} {\dot{\rlambda }}_{{z,i}} \cos {\rm \rtheta }_{{M.i}} } \hfill \cr {a_{{z,i}} {\equals}{\minus}NV_{M} {\dot{\rlambda }}_{{y,i}} \cos {\rm \rpsi }_{{M,i}} } \hfill \cr } } \right.} \hfill & {{\rm if}\;\left\{ {\matrix{ {\left| {{\rm \eta }_{i} {\minus}{\rm \eta }_{j} } \right|\leq {\rm {\rvarepsilon}}_{1} } \hfill \cr {\left| {{\rm \rxi }_{i} {\minus}{\rm \rxi }_{j} } \right|\leq {\rm {\rvarepsilon}}_{2} } \hfill \cr } } \right.} \hfill \cr {\left\{ {\matrix{ {a_{{y,i}} {\equals}{\minus}{{V_{M}^{2} } \over {R_{i} }}\sin {\rm \rpsi }_{{M,i}} {\plus}{{u_{i} V_{M} \sqrt {1{\minus}\cos ^{2} {\rm \rsigma }_{i} } } \over {2\sin {\rm \rsigma }_{i} \sin {\rm \rpsi }_{{M,i}} }}} \hfill \cr {a_{{z,i}} {\equals}{\minus}{{V_{M}^{2} } \over {R_{i} }}sin\;{\rm \rtheta }_{{M,i}} \cos {\rm \rpsi }_{{M,i}} {\plus}{{u_{i} V_{M} \sqrt {1{\minus}\cos ^{2} {\rm \rsigma }_{i} } } \over {2\sin {\rm \rsigma }_{i} \sin {\rm \rtheta }_{{M,i}} \cos {\rm \rpsi }_{{M,i}} }}} \hfill \cr } } \right.} \hfill & {{\rm otherwise}} \hfill \cr } $$
$$\matrix{ {\left\{ {\matrix{ {a_{{y,i}} {\equals}{\minus}NV_{M} {\dot{\rlambda }}_{{y,i}} \sin {\rm \rtheta }_{{M,i}} \sin {\rm \rpsi }_{{M,i}} {\plus}NV_{M} {\dot{\rlambda }}_{{z,i}} \cos {\rm \rtheta }_{{M.i}} } \hfill \cr {a_{{z,i}} {\equals}{\minus}NV_{M} {\dot{\rlambda }}_{{y,i}} \cos {\rm \rpsi }_{{M,i}} } \hfill \cr } } \right.} \hfill & {{\rm if}\;\left\{ {\matrix{ {\left| {{\rm \eta }_{i} {\minus}{\rm \eta }_{j} } \right|\leq {\rm {\rvarepsilon}}_{1} } \hfill \cr {\left| {{\rm \rxi }_{i} {\minus}{\rm \rxi }_{j} } \right|\leq {\rm {\rvarepsilon}}_{2} } \hfill \cr } } \right.} \hfill \cr {\left\{ {\matrix{ {a_{{y,i}} {\equals}{\minus}{{V_{M}^{2} } \over {R_{i} }}\sin {\rm \rpsi }_{{M,i}} {\plus}{{u_{i} V_{M} \sqrt {1{\minus}\cos ^{2} {\rm \rsigma }_{i} } } \over {2\sin {\rm \rsigma }_{i} \sin {\rm \rpsi }_{{M,i}} }}} \hfill \cr {a_{{z,i}} {\equals}{\minus}{{V_{M}^{2} } \over {R_{i} }}sin\;{\rm \rtheta }_{{M,i}} \cos {\rm \rpsi }_{{M,i}} {\plus}{{u_{i} V_{M} \sqrt {1{\minus}\cos ^{2} {\rm \rsigma }_{i} } } \over {2\sin {\rm \rsigma }_{i} \sin {\rm \rtheta }_{{M,i}} \cos {\rm \rpsi }_{{M,i}} }}} \hfill \cr } } \right.} \hfill & {{\rm otherwise}} \hfill \cr } $$
in which ε1 and ε2 are two small enough positive constants. It can be seen from (36) that the consensus-based guidance law is utilised to realise agreement of the heading error and range-to-go among all missiles in the first guidance phase. When the terminal condition is touched off, all missiles will be guided by the PPN law to achieve salvo attack.
According to the property of the typical PPN law, if ε1 and ε2 are small enough, the impact time errors among missiles can be neglected in nature. However, one should be noted that if ε1 and ε2 are too small, the initial range-to-go for the terminal guidance phase will be very short or even become zero before |η
i
−η
j
|≤ε1 and |ξ
i
−ξ
j
|≤ε2 are satisfied, which may also lead to the failure of salve attack. To address this problem and guarantee successful salvo attack,
![]() $$\left\Vert {\mib P} \right\Vert$$
should be selected appropriately according to the limitation of the bounded manoeuvrability of missiles to obtain a favoured initial range-to-go for the terminal guidance phase, based on which one can decrease the values of ε1 and ε2 to obtain more precise salvo attack.
$$\left\Vert {\mib P} \right\Vert$$
should be selected appropriately according to the limitation of the bounded manoeuvrability of missiles to obtain a favoured initial range-to-go for the terminal guidance phase, based on which one can decrease the values of ε1 and ε2 to obtain more precise salvo attack.
Remark 4. Note that the communication topology in this study can be jointly connected. This result is meaningful on the battlefield, where the communication topology can be cut-off due to channel failures and rearrangements of multiple missiles during the first guidance phase. Communication topology in Refs 20,25 is restricted to be fixed, which requires vast communication cost and may not be suitable for practical applications due to sensor limitations. Although guidance laws presented in Refs 23,24 concerned with the switching topology condition, they required the switching topology contains a directed spanning tree during each time interval. These requirements in Refs 20,23–25 are more restrictive than those in the current paper.
Remark 5. The communication delay considered in Ref. 25 is restricted to be fixed, which is somewhat stringent from the view of practice. To relax the constraint on the communication delay, this study further considers the bounded time-varying communication delays in the co-operative guidance law design, which is significantly different from the existing work achieved in Ref. 25.
4.0 SIMULATIONS AND RESULTS
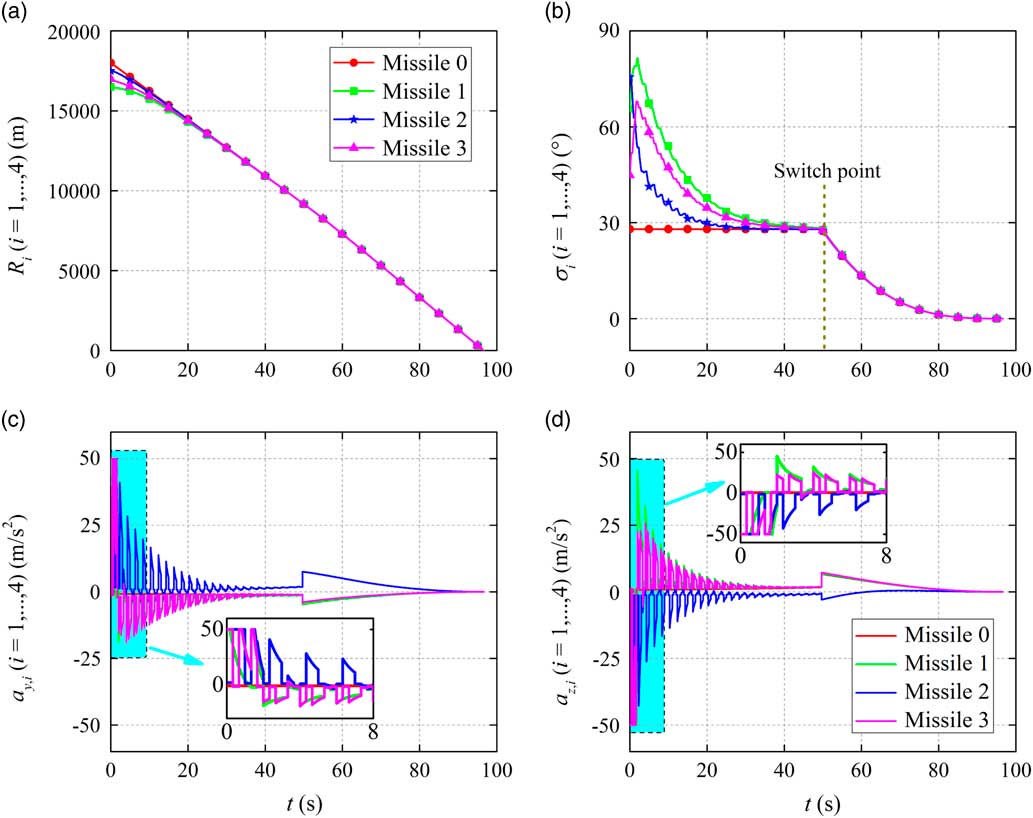
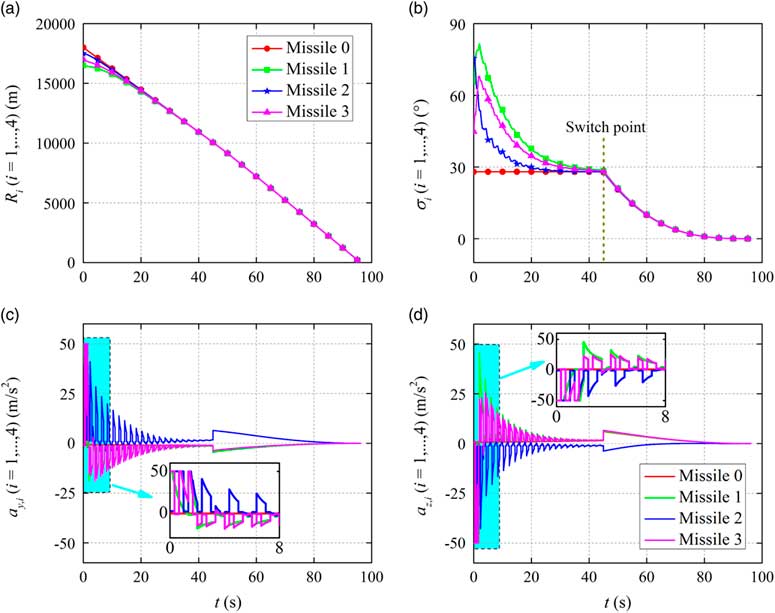
In this section, numerical simulations are carried out to demonstrate the effectiveness of the proposed co-operative law. We consider an engagement scenario in which four missiles are expected to simultaneously attack a stationary target located at (0, 0, 0) m, and missile 0 is selected as the leader in this scenario. It is presumed that the missile’s velocity is 200 m/s. The navigation gain utilised in the second guidance phase is chosen as N=4. The limitations of missile’s accelerations are |a y,i |≤50 m/s2 and |a z,i |≤50 m/s2. The numerical simulations are performed with respect to various terminal conditions for the first guidance phase: case 1: ε2=0.001; case 2: ε2=0.003; case 3: ε2=0.005. Moreover, the other terminal condition is selected as ε1=0.05.
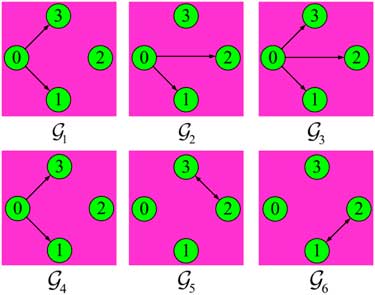
The initial conditions of multiple missiles are shown in Table 1. The communication topologies among these missiles are presented in Fig. 2. It can be obviously seen from Fig. 2 that the union graphs
![]() $${\mib {\cal G}}_{1} \bigcup {{\mib {\cal G}}_{2} } \bigcup {{\mib {\cal G}}_{3} } $$
and
$${\mib {\cal G}}_{1} \bigcup {{\mib {\cal G}}_{2} } \bigcup {{\mib {\cal G}}_{3} } $$
and
![]() $${\mib {\cal G}}_{4} \bigcup {{\mib {\cal G}}_{5} } \bigcup {{\mib {\cal G}}_{6} } $$
are both jointly connected. Hence, the switching signal s(t) can be formulated as
$${\mib {\cal G}}_{4} \bigcup {{\mib {\cal G}}_{5} } \bigcup {{\mib {\cal G}}_{6} } $$
are both jointly connected. Hence, the switching signal s(t) can be formulated as
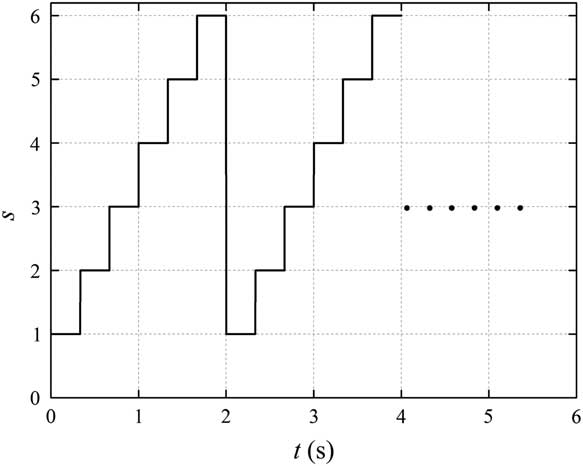
 $$s\left( t \right){\equals}\left\{ {\matrix{ 1 \hfill & {k\leq t\,\lt\,k{\plus}{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}} \hfill \cr 2 \hfill & {k{\plus}{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}\leq t\,\lt\,k{\plus}{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}} \hfill \cr 3 \hfill & {k{\plus}{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}\leq t\,\lt\,k{\plus}1} \hfill \cr 4 \hfill & {k{\plus}1\leq t\,\lt\,\left( {k{\plus}1} \right){\plus}{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}} \hfill \cr 5 \hfill & {\left( {k{\plus}1} \right){\plus}{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}\leq t\,\lt\,\left( {k{\plus}1} \right){\plus}{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}} \hfill \cr 6 \hfill & {\left( {k{\plus}1} \right){\plus}{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}\leq t\,\lt\,\left( {k{\plus}1} \right){\plus}1} \hfill \cr } k{\equals}0,1,2,...} \right.$$
$$s\left( t \right){\equals}\left\{ {\matrix{ 1 \hfill & {k\leq t\,\lt\,k{\plus}{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}} \hfill \cr 2 \hfill & {k{\plus}{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}\leq t\,\lt\,k{\plus}{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}} \hfill \cr 3 \hfill & {k{\plus}{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}\leq t\,\lt\,k{\plus}1} \hfill \cr 4 \hfill & {k{\plus}1\leq t\,\lt\,\left( {k{\plus}1} \right){\plus}{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}} \hfill \cr 5 \hfill & {\left( {k{\plus}1} \right){\plus}{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}\leq t\,\lt\,\left( {k{\plus}1} \right){\plus}{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}} \hfill \cr 6 \hfill & {\left( {k{\plus}1} \right){\plus}{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$3$}}\leq t\,\lt\,\left( {k{\plus}1} \right){\plus}1} \hfill \cr } k{\equals}0,1,2,...} \right.$$
which is shown in Fig. 3. Additionally, it can be obtained that
![]() ${\rm \lambda }_{{\max }} {\equals}2.0$
and
${\rm \lambda }_{{\max }} {\equals}2.0$
and
![]() ${\rm \lambda }_{{\min }} {\equals}1.0$
. The time delay is set to be τ(t)=0.09 + 0.01 cos(t/10), hence τ
m
=0.1 and τ
dm
=0.01. Solving LMIs (21)–(23) yields that
${\rm \lambda }_{{\min }} {\equals}1.0$
. The time delay is set to be τ(t)=0.09 + 0.01 cos(t/10), hence τ
m
=0.1 and τ
dm
=0.01. Solving LMIs (21)–(23) yields that
Table 1 Initial conditions of multiple missiles


Figure 2 Communication topologies.

Figure 3 Time history of the switching signal.
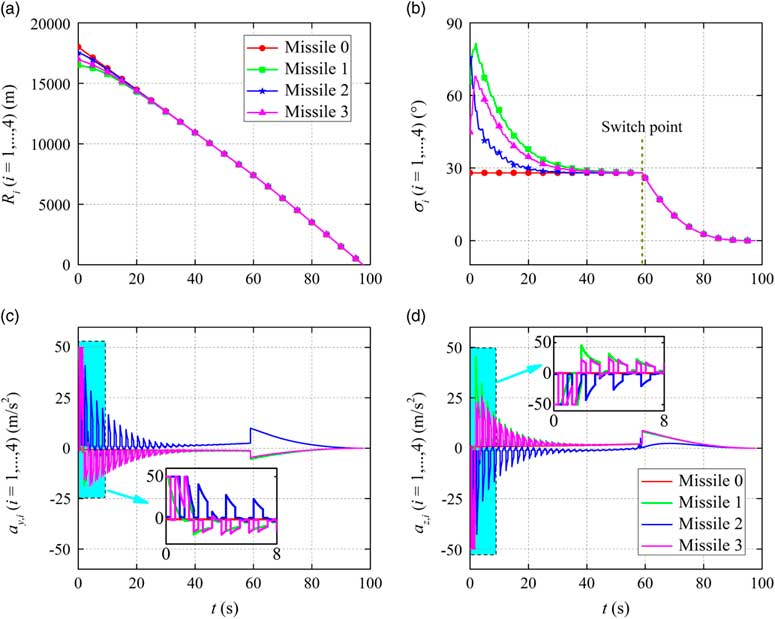
The simulation results for different cases are given in Figs 4–6, where the time histories of the relative range, the heading error and the missile achieved accelerations are presented in detail. It can be seen from these figures that based on the proposed co-operative guidance law the salvo attack can be achieved in spite of various terminal conditions of the first guidance phase. During the first guidance phase, the consensus of the multi-missile system is realised for different cases, resulting in the same relative range and heading error achieved by all missiles. Then, the typical PPN law takes charge of all missiles to accomplish the salvo attack mission, eventually. Moreover, it can be seen from the time histories of the missile accelerations that the missile accelerations achieved in the first guidance phase change as the communication topology switches and large amplitude of the missile accelerations are required at the beginning of the co-operative guidance to regulate the states of missiles. Then, owing to the typical PPN law, all accelerations converge to zero in the second guidance phase.
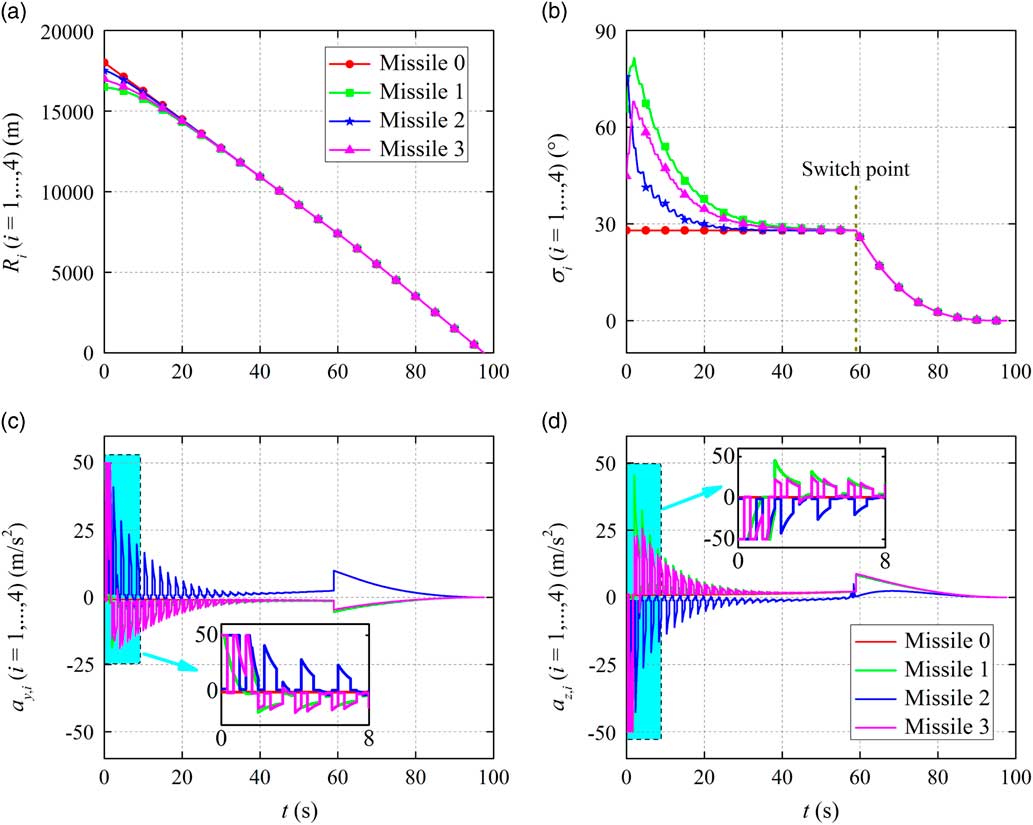
Figure 4 Simulation results for Case 1.
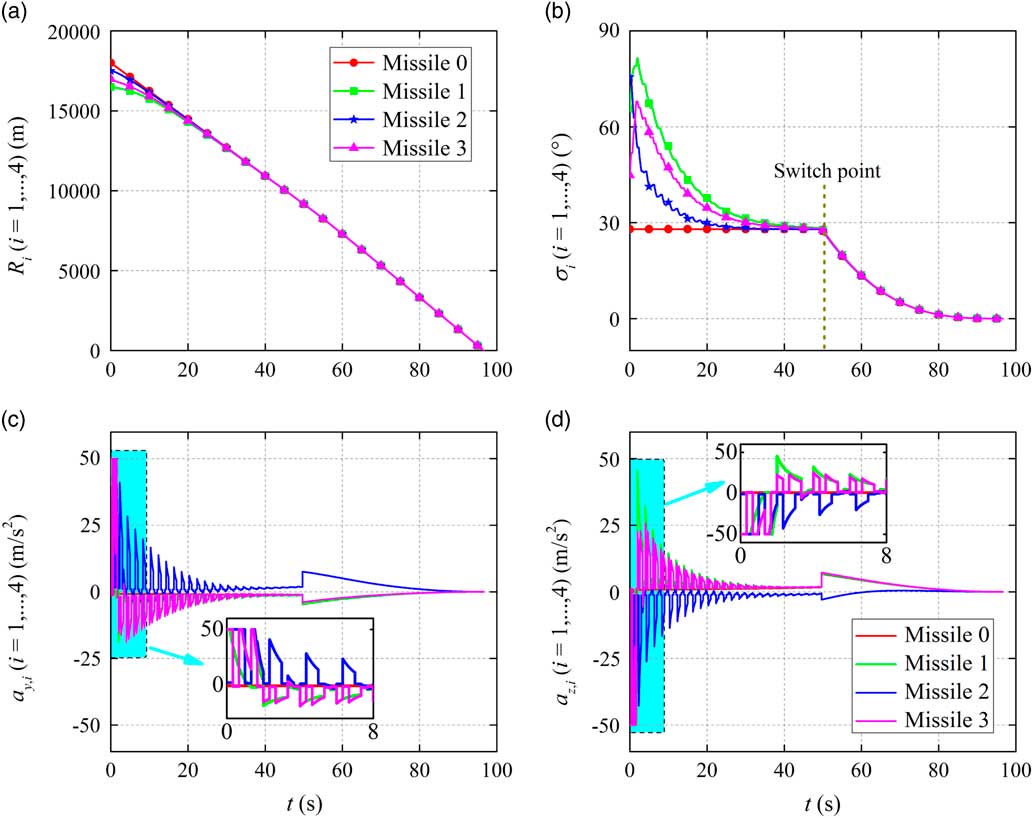
Figure 5 Simulation results for Case 2.
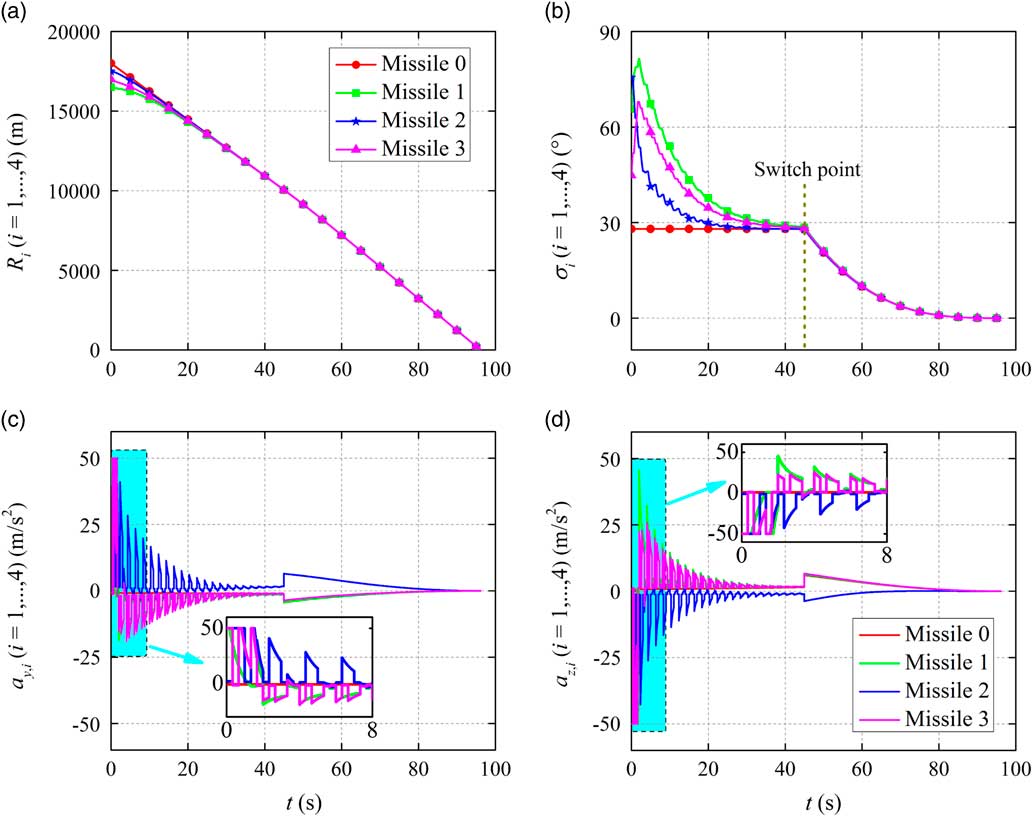
Figure 6 Simulation results for Case 3.
To further explore the effect of various terminal conditions on the whole guidance phase, the quantitative analysis regarding the switching time of the two guidance phase, the impact time and the consensus precision are summarised in Table 2, where the consensus precision is defined as
![]() $\mathop{\sum}\limits_{i{\equals}1}^3 {\left| {{\rm \rsigma }_{i} \left( {t_{s} } \right){\minus}{\rm \rsigma }_{0} \left( {t_{s} } \right)} \right|} $
with t
s
being the switching time. From the simulation results, it is evidently shown that decreasing the value of ε2 can increase the consensus precision, resulting in the increased impact time in turn. This is mainly due to that lower the value of ε2 requires more time to regulate the states of missiles to satisfy the terminal condition for the first guidance phase.
$\mathop{\sum}\limits_{i{\equals}1}^3 {\left| {{\rm \rsigma }_{i} \left( {t_{s} } \right){\minus}{\rm \rsigma }_{0} \left( {t_{s} } \right)} \right|} $
with t
s
being the switching time. From the simulation results, it is evidently shown that decreasing the value of ε2 can increase the consensus precision, resulting in the increased impact time in turn. This is mainly due to that lower the value of ε2 requires more time to regulate the states of missiles to satisfy the terminal condition for the first guidance phase.
Table 2 Summary of the quantitative results

5.0 CONCLUSIONS
In this paper, the co-operative salvo attack problem of multiple missiles against a stationary target is investigated. By sufficiently exploring the property of the typical PPN law, a two-stage guidance scheme is proposed to achieve this goal. During the first guidance phase, a consensus-based co-operative guidance law is proposed under jointly connected switching topologies to generate favoured initial conditions for the latter guidance phase, where uniform time-varying communication delays are taken into consideration to make the guidance law be more suitable for practical applications. Stability analysis is carried out based on a Lyapunov–Krasovskii function to theoretically demonstrate that the consensus on the range-to-go and the heading error of multiple missiles can be achieved during the first guidance phase. Then, missiles are governed by the typical PPN law to realise salvo attack eventually in the second guidance phase. The key feature of the proposed guidance law lies in that it does not rely on the time-to-go or its estimation. Numerical simulations fully demonstrate the effectiveness of the presented formulation of this study. Based on these results, it is of interest to further investigate co-operative finite-time guidance problem subject to non-uniform communication delays.
Acknowledgements
The authors would like to thank the editor and all the anonymous reviewers for their valuable comments and suggestions.