1. Introduction
1.1. The model
Suppose that we are given a finite connected multigraph with strictly positive real-valued edge lengths. We introduce a model for the destruction of such a network by fire. The edges are flammable. First, a point is picked uniformly (i.e. according to the normalised Lebesgue measure) and set alight. (With probability 1, this point will lie in the interior of an edge.) The fire passes at speed 1 along the edge (in both directions) until it reaches a node. A node of degree d ≥ 3 will pass the fire onto all of its other neighbouring edges with probability ![]() ${\textstyle{1 \over 2}}$ or stop the fire with probability
${\textstyle{1 \over 2}}$ or stop the fire with probability ![]() ${\textstyle{1 \over 2}}$. If it stops the fire, it becomes a vertex of degree d −1. A vertex of degree 2 necessarily passes a fire arriving from along one of its neighbouring edges onto the other edge. The fire spreads until it either goes out or has burnt the whole network. If it goes out before the whole network is burnt, a new uniform point is picked and set alight, and the process continues as before. We are interested in two aspects of this process.
${\textstyle{1 \over 2}}$. If it stops the fire, it becomes a vertex of degree d −1. A vertex of degree 2 necessarily passes a fire arriving from along one of its neighbouring edges onto the other edge. The fire spreads until it either goes out or has burnt the whole network. If it goes out before the whole network is burnt, a new uniform point is picked and set alight, and the process continues as before. We are interested in two aspects of this process.
• How many new fires must be set in order to burn the whole network?
• How many times does it happen that a point is burnt from two different directions? We refer to the second phenomenon as a clash.
Let α : ℕ → ℕ be a function such that α(n)/n → 0 as n → ∞. We will study these questions in the setting where the base network is a random multigraph with n vertices of degree 3 and α(n) vertices of degree 4, sampled according to the configuration model (see below for a description). Throughout this paper, we will implicitly assume n to be even. We take the edge lengths to be independent and identically distributed standard exponential random variables.
Let Fn be the number of fires we must set in order to burn the whole network. Let Cn be the number of clashes. We will study the limiting behaviour of these quantities as n → ∞. It turns out that both scale as ![]() ${\sqrt{n}}$ as long as
${\sqrt{n}}$ as long as ![]() $\alpha(n) = O{(\sqrt{n})}$ and as α(n) if
$\alpha(n) = O{(\sqrt{n})}$ and as α(n) if ![]() $\alpha(n) \gg {\sqrt{n}}$. In order to state our results more precisely, we introduce an auxiliary stochastic process.
$\alpha(n) \gg {\sqrt{n}}$. In order to state our results more precisely, we introduce an auxiliary stochastic process.
Let (B t)t≥0 be a standard Brownian motion and, for a ≥ 0, let ![]() ${(X_t^a,L_t^a)_{0 \le t \le 1}}$ be the unique solution to the stochastic differential equation (SDE) with reflection determined by
${(X_t^a,L_t^a)_{0 \le t \le 1}}$ be the unique solution to the stochastic differential equation (SDE) with reflection determined by
where ![]() ${(L_t^a)_{0 \le t < 1}}$ is the local time process of Xa at level 0. We construct the solution explicitly below, and show that both of these quantities have finite almost-sure limits as t → 1, which we call
${(L_t^a)_{0 \le t < 1}}$ is the local time process of Xa at level 0. We construct the solution explicitly below, and show that both of these quantities have finite almost-sure limits as t → 1, which we call ![]() $L_1^a$ and
$L_1^a$ and ![]() $X_1^a$.
$X_1^a$.
Theorem 1.1
(i) Suppose that
 $\alpha(n)/{\sqrt{n}} \to a$ as n → ∞, where a ≥ 0. Then, as n → ∞,
$\alpha(n)/{\sqrt{n}} \to a$ as n → ∞, where a ≥ 0. Then, as n → ∞,
 $\frac{1}{\sqrt{n}\,} (F^n, C^n) \underrightarrow{\rm D} \bigg(\frac{1}{2}L^a_1, \int_0^1
\frac{X^a_s}{3(1-s)} {\text{d}} s \bigg),$
$\frac{1}{\sqrt{n}\,} (F^n, C^n) \underrightarrow{\rm D} \bigg(\frac{1}{2}L^a_1, \int_0^1
\frac{X^a_s}{3(1-s)} {\text{d}} s \bigg),$
where the limiting random variables are almost surely finite.
(ii) Suppose that
 $\alpha(n) \gg\sqrt{n}$. Then, as n→ ∞,
$\alpha(n) \gg\sqrt{n}$. Then, as n→ ∞,
 $\frac{1}{\alpha(n)} F^n \underrightarrow{\rm P} 0, \quad\quad \frac{1}{\alpha(n)} C^n \underrightarrow{\rm P}
\frac{1}{4}.$
$\frac{1}{\alpha(n)} F^n \underrightarrow{\rm P} 0, \quad\quad \frac{1}{\alpha(n)} C^n \underrightarrow{\rm P}
\frac{1}{4}.$
1.2. Motivation: the Karp–Sipser algorithm on a random graph
The Karp–Sipser algorithm, introduced in [Reference Karp and Sipser12], is a greedy algorithm for finding a matching in a fixed graph. The algorithm works as follows. Call a vertex of degree 1 a pendant vertex. If there is at least one pendant vertex in the graph, choose one uniformly at random and include the edge incident to it in the matching. Remove this edge, the two vertices that form it, and any other edges incident to them. If, on the other hand, there are no pendant vertices in the graph, choose one of the existing edges uniformly at random, and include it in the matching. Remove the chosen edge together with the two vertices that form it, as well as any other edges incident to those vertices. Now repeat the procedure on the resulting graph, until there are no edges remaining.
A key observation is that whenever there exists a pendant vertex in a graph, that vertex and its neighbour are included in some maximum matching. So the Karp–Sipser algorithm never makes a ‘mistake’ in including such an edge in its matching. On the other hand, in the other type of move (picking a uniform edge and including it in the matching) it is possible that it includes an edge which would not be in any maximum matching.
The Karp–Sipser algorithm turns out to be very successful at finding a near-maximum matching in certain classes of (sparse) random graphs [Reference Aronson, Frieze and Pittel1], [Reference Bohman and Frieze6], [Reference Karp and Sipser12]. Suppose that we take the graph to be the Erdős–Rényi random graph G(N, M), with N vertices and M edges, where M = ⌊cN/2⌋ and c > 0 is a constant. Let D N be the difference between the size of a maximum matching on G(N, M) and the matching produced by the Karp–Sipser algorithm. Let A N be the number of vertices remaining in the graph at the point of the first uniform random choice which are left unmatched by the Karp–Sipser algorithm. Then D N ≤ A N/2. Aronson et al. [Reference Aronson, Frieze and Pittel1] proved the following theorem.
Theorem 1.2
(i) If c < e then
 $\mathbb {P}{D_N = 0} \to 1$ as N → ∞.
$\mathbb {P}{D_N = 0} \to 1$ as N → ∞.(ii) If c > e, there exist constants C 1, C 2 > 0 such that
 $\frac{C_1 N^{1/5}}{(\log N)^{75/2}} \le \mathbb {E}{A_N} \le C_2 N^{1/5} (\log
N)^{12}.$
$\frac{C_1 N^{1/5}}{(\log N)^{75/2}} \le \mathbb {E}{A_N} \le C_2 N^{1/5} (\log
N)^{12}.$
Aronson et al. [Reference Aronson, Frieze and Pittel1] conjectured that, in fact, ![]() $N^{-1/5} \mathbb {E}{A_N}$ converges as N → ∞; indeed, one might also reasonably conjecture that N −1/5A N possesses a limit in distribution as N → ∞. One of our aims in this paper is to make progress towards understanding how such a limit in distribution might arise.
$N^{-1/5} \mathbb {E}{A_N}$ converges as N → ∞; indeed, one might also reasonably conjecture that N −1/5A N possesses a limit in distribution as N → ∞. One of our aims in this paper is to make progress towards understanding how such a limit in distribution might arise.
The Karp–Sipser algorithm proceeds in two phases. In the first phase (phase I), the algorithm recursively attacks the pendant subtrees in the graph, matching as it goes. Phase II starts the first time that the algorithm is forced to pick a uniform edge. At the start of phase II, the graph necessarily contains only vertices of degree 2 or more. It will, in general, have several components, of which some may consist of isolated cycles. In these cycle components, the Karp–Sipser algorithm necessarily yields a maximum matching. So the source of the ‘mistakes’ is the complex components of the graph present at the start of phase II. Our original motivation for introducing the model studied in this paper is to understand the behaviour of the Karp–Sipser algorithm on the type of complex components appearing in phase II.
For c < e, phase I is essentially the whole story, apart from a few isolated cycles (which cannot cause ‘mistakes’). On the other hand, for c > e, a nontrivial graph remains at the end of phase I. The work of Aronson et al. [Reference Aronson, Frieze and Pittel1] suggests that, for c > e, the part of the Karp–Sipser process which gives the dominant contribution to A N arises close to the end of phase II. Their analysis indicates the following heuristic picture for the structure of the graph at this point: ignoring log-corrections, it is approximately a uniform random graph with Θp(N 3/5) vertices of degree 2, Θ p(N 2/5) vertices of degree 3, and Θp(N 1/5) vertices of degree 4. We will shortly describe the structure of this graph.
Before going any further, it will be useful to introduce the configuration model [Reference Bender and Canfield3], [Reference Bollobás7], [Reference Wormald18], [Reference Wormald19], [Reference Wormald20]. Fix n and a sequence d = (d 1, d 2, …, d n), where d i ≥ 0 is the degree of vertex i and ![]() ${\sum_{i=1}^{n}}d_i$ is even. First assign vertex i a number d i of half-edges. Then choose a uniform random pairing of the half-edges. This generates a random multigraph CM(d). In particular, assuming that there exists at least one simple graph with degrees d, conditionally on the event that CM(d) is simple, it is uniformly distributed on the set of simple graphs with those degrees. (See the account in Chapter 7 of [Reference van der Hofstad16] for proofs of these results.)
${\sum_{i=1}^{n}}d_i$ is even. First assign vertex i a number d i of half-edges. Then choose a uniform random pairing of the half-edges. This generates a random multigraph CM(d). In particular, assuming that there exists at least one simple graph with degrees d, conditionally on the event that CM(d) is simple, it is uniformly distributed on the set of simple graphs with those degrees. (See the account in Chapter 7 of [Reference van der Hofstad16] for proofs of these results.)
For a fixed k ≥ 2, we will write Dirichletk(1, 1, …, 1) for the uniform distribution on the simplex {x=(x 1, x 2, …, x k) : x 1, x 2, …, x k ≥ 0, ![]() $\mathop \sum \limits_{i = 1}^k {x_i} = 1\}$ (which is the simplest of the family of Dirichlet distributions). We will omit the subscript k when the number of coordinates is clear from the context.
$\mathop \sum \limits_{i = 1}^k {x_i} = 1\}$ (which is the simplest of the family of Dirichlet distributions). We will omit the subscript k when the number of coordinates is clear from the context.
Now fix t, u > 0 and v ≥ 0, and suppose that we start from a degree sequence with ˪tN 3/5˩ vertices of degree 2, ˪uN 2/5˩ vertices of degree 3, and ˪vN 1/5˩ vertices of degree 4. Let G N be a uniform random graph with these degrees. Let K N be the kernel of G N, that is, the multigraph obtained by contracting paths of vertices of degree 2. It is straightforward to see that K N is distributed according to the configuration model with ˪uN 2/5˩ vertices of degree 3 and ˪vN 1/5˩ vertices of degree 4. With probability tending to 1 as N → ∞, G N possesses a giant complex component C N, containing all of the vertices of degrees 3 and 4 (i.e. the kernel), as well as some random number ![]() $t'_N$ of the vertices of degree 2, where
$t'_N$ of the vertices of degree 2, where ![]() $t'_N/N^{3/5} \underrightarrow{\rm P} t$ as n → ∞. On this event of high probability, C N is a uniform connected graph with its degree sequence. Outside the giant, there is a collection of O p(log N) disjoint cycles, containing the remaining vertices of degree 2. (We have not found a good reference for these statements, which are folklore in the random graphs literature; statements in a similar spirit may be found, for example, in [Reference Joos, Perarnau, Rautenbach and Reed10]. Theorem 2 of [Reference Joos, Perarnau, Rautenbach and Reed10] implies that G N contains a giant component with high probability. By Theorem 3.15 of [Reference van der Hofstad17], K N is connected with high probability. That the giant component of G N contains K N and a proportion 1 of all vertices of degree 2 comes down to the fact that the number of ways of generating a random two-regular graph is negligible compared to the number of ways of generating a graph with kernel K N. Finally, a random two-regular graph on n vertices has O p(log n) components; see [Reference Arratia, Barbour and Tavaré2].)
$t'_N/N^{3/5} \underrightarrow{\rm P} t$ as n → ∞. On this event of high probability, C N is a uniform connected graph with its degree sequence. Outside the giant, there is a collection of O p(log N) disjoint cycles, containing the remaining vertices of degree 2. (We have not found a good reference for these statements, which are folklore in the random graphs literature; statements in a similar spirit may be found, for example, in [Reference Joos, Perarnau, Rautenbach and Reed10]. Theorem 2 of [Reference Joos, Perarnau, Rautenbach and Reed10] implies that G N contains a giant component with high probability. By Theorem 3.15 of [Reference van der Hofstad17], K N is connected with high probability. That the giant component of G N contains K N and a proportion 1 of all vertices of degree 2 comes down to the fact that the number of ways of generating a random two-regular graph is negligible compared to the number of ways of generating a graph with kernel K N. Finally, a random two-regular graph on n vertices has O p(log n) components; see [Reference Arratia, Barbour and Tavaré2].)
Now consider the following way of constructing a complex component which we claim has approximately the same distribution as C N. First generate the kernel K N according to the configuration model with ˪uN 2/5˩ vertices of degree 3 and ˪vN 1/5˩ vertices of degree 4. Then, one-by-one, allocate ![]() $t_N'$ vertices of degree 2 to the edges of K N: at each step, an edge of the current structure is chosen uniformly at random, split into two edges in series, and the vertex is inserted into the middle. Thus, the lengths of the paths of degree-2 vertices we insert between neighbouring vertices in K N evolve according to a multicolour Pólya’s urn with
$t_N'$ vertices of degree 2 to the edges of K N: at each step, an edge of the current structure is chosen uniformly at random, split into two edges in series, and the vertex is inserted into the middle. Thus, the lengths of the paths of degree-2 vertices we insert between neighbouring vertices in K N evolve according to a multicolour Pólya’s urn with ![]() ${\textstyle{1 \over 2}}(3\left\lfloor {u{N^{2/5}}} \right\rfloor + 4{\rm{ }}\left\lfloor {v{N^{1/5}}} \right\rfloor)$ colours and a single ball of each colour to start. (By Proposition 7.13 of [Reference van der Hofstad16], K N possesses constant-order numbers of self-loops and multiple edges; in the urn process, there is negligible probability that we fail to allocate any vertices of degree 2 to the self-loops or to at least two of a set of edges between the same two vertices.) Then, for large N, the proportions of the
${\textstyle{1 \over 2}}(3\left\lfloor {u{N^{2/5}}} \right\rfloor + 4{\rm{ }}\left\lfloor {v{N^{1/5}}} \right\rfloor)$ colours and a single ball of each colour to start. (By Proposition 7.13 of [Reference van der Hofstad16], K N possesses constant-order numbers of self-loops and multiple edges; in the urn process, there is negligible probability that we fail to allocate any vertices of degree 2 to the self-loops or to at least two of a set of edges between the same two vertices.) Then, for large N, the proportions of the ![]() $t_N'$ vertices of degree 2 which get allocated to each of the edges of K N look approximately like a Dirichlet(1, 1, …, 1) vector, with
$t_N'$ vertices of degree 2 which get allocated to each of the edges of K N look approximately like a Dirichlet(1, 1, …, 1) vector, with ![]() ${\textstyle{1 \over 2}}(3\left\lfloor {u{N^{2/5}}} \right\rfloor + 4{\rm{ }}\left\lfloor {v{N^{1/5}}} \right\rfloor)$ coordinates.
${\textstyle{1 \over 2}}(3\left\lfloor {u{N^{2/5}}} \right\rfloor + 4{\rm{ }}\left\lfloor {v{N^{1/5}}} \right\rfloor)$ coordinates.
Let us now consider how the Karp–Sipser algorithm behaves on G N. We may neglect the cycle components, as they can give rise to at most O(log N) unmatched vertices. The algorithm first picks a uniform edge, matches its endpoints, and then removes the neighbouring edges. Typically, we matched two vertices somewhere inside a long path of degree-2 vertices, and so we are now left with two pendant vertices, each at the end of a path of degree-2 vertices with a higher-degree vertex at its end. If such a path is of odd length, the Karp–Sipser algorithm will ‘consume’ the degree-2 vertices but leave the higher-degree vertex untouched (except to reduce its degree by 1). If, on the other hand, the path is of even length, the higher-degree vertex gets matched and removed, causing its neighbours to become pendant vertices. Thus, in this case, the algorithm eats further away into the graph. If ever a particular path gets eaten away at from both ends (which can happen since the graph has cycles), there is a chance that some vertex in the path will remain unmatched. Again, whether this in fact happens or not depends on the parity of the path of degree-2 vertices. For large enough N, we expect that such paths will be of odd and even lengths with approximately equal probability. So we expect that paths which get burnt from both ends will give rise to an unmatched vertex with probability ![]() ${\textstyle{1 \over 2}}$.
${\textstyle{1 \over 2}}$.
As we have already argued, since the number of edges in the multigraph is much smaller than the number of degree-2 vertices, the proportions of degree-2 vertices assigned to each edge of the multigraph will be, for large N, close to Dirichlet(1, 1, …, 1). For fixed k ≥ 2, a vector (D 1, D 2, …, D k) with Dirichletk(1, 1, …, 1) distribution may be obtained by sampling E 1, E 2, …, E k, independent and identically distributed standard exponential random variables and setting
The right-hand side is independent of the random variable ![]() ${\sum_{i=1}^k E_i}$. Once we have accounted for parity, the lengths of the paths of degree-2 vertices play a role only when we pick a new uniform edge to match, which we do with probability proportional to length. So only relative lengths matter, and we can equivalently think of E 1, …, E k as the ‘lengths’ of the paths of degree-2 vertices in our approximate model. (In what follows, we will primarily use Dirichlet(1, 1, …, 1) edge lengths, but it is convenient to be able to move back and forth between these two points of view.)
${\sum_{i=1}^k E_i}$. Once we have accounted for parity, the lengths of the paths of degree-2 vertices play a role only when we pick a new uniform edge to match, which we do with probability proportional to length. So only relative lengths matter, and we can equivalently think of E 1, …, E k as the ‘lengths’ of the paths of degree-2 vertices in our approximate model. (In what follows, we will primarily use Dirichlet(1, 1, …, 1) edge lengths, but it is convenient to be able to move back and forth between these two points of view.)
In summary, letting n be the number of vertices of degree 3 and α(n) be the number of vertices of degree 4, we obtain the model described in Section 1.1 as an approximation. We do not attempt here to assess the quality of this approximation (and we only make rigorous statements about the model described in Section 1.1). Rather our interest is in the mechanism by which the distribution of the number of vertices which remain unmatched at the end of the Karp–Sipser algorithm arises. With the scaling suggested by Aronson et al. [Reference Aronson, Frieze and Pittel1] we would have n = Θ(N 2/5) and α(n) = Θ(N 1/5), i.e. ![]() $\alpha(n) = \Theta(\sqrt{n})$. So we should be in regime (i) of Theorem 1.1, which supports the conjecture that N −1/5A N possesses a limit in distribution.
$\alpha(n) = \Theta(\sqrt{n})$. So we should be in regime (i) of Theorem 1.1, which supports the conjecture that N −1/5A N possesses a limit in distribution.
1.3. Our analysis
Our model has two convenient features which make it amenable to analysis: the distributional properties of the edge lengths and the fact that we may sample the multigraph edge by edge at the same time as we burn it. Let us first address the edge lengths. We will make use of the following result, which follows from standard properties of exponential random variables via the relationship (1.2).
Proposition 1.1
(Proposition 1 of [Reference Bertoin and Goldschmidt4].) (i) Suppose that (D 1, D 2, …, D k) ∼ Dirichletk(1, 1, …, 1), and let I be a random index from {1, 2, …, k} with conditional distribution ![]() $\mathbb {P}(I = i\mid D_1, \ldots, D_k) = D_i,$, 1 ≤ i ≤ k. Let U be independent of everything else with uniform distribution on [0, 1]. Then defining
$\mathbb {P}(I = i\mid D_1, \ldots, D_k) = D_i,$, 1 ≤ i ≤ k. Let U be independent of everything else with uniform distribution on [0, 1]. Then defining
it follows that ![]() $({D'_1},{D'_2}, \ldots ,{D'_{k + 1}})$ has Dirichletk+1(1, 1, …, 1) distribution.
$({D'_1},{D'_2}, \ldots ,{D'_{k + 1}})$ has Dirichletk+1(1, 1, …, 1) distribution.
(ii) Suppose that ![]() $(D'_1, D'_2, \ldots, D'_{k+1})$ ∼ Dirichletk+1(1, 1, …, 1) and that J is chosen independently and uniformly at random from {1, 2, …, k}. Then defining
$(D'_1, D'_2, \ldots, D'_{k+1})$ ∼ Dirichletk+1(1, 1, …, 1) and that J is chosen independently and uniformly at random from {1, 2, …, k}. Then defining
it follows that (D 1, D 2, …, D k) ∼ Dirichletk(1, 1, …, 1).
Using part (i) of this proposition, we see that if we start from Dirichlet(1, 1, …, 1) edge lengths and pick a point uniformly from the length measure, then splitting it yields distances from the sampled point to the adjacent vertices of degree at least 3 either side of it, which are again part of a Dirichlet(1, 1, …, 1) vector (with one more coordinate). We will see in what follows that the property that (given the number of edges in the multigraph) the relative edge lengths are Dirichlet(1, 1, …, 1) is preserved. Consider the process at an instant when the fire has just reached a vertex, or when a point has just been set alight. In general, there are several edges burning, and using the memoryless property of the exponential distribution, their relative distances to the adjacent vertices are still standard exponential divided by the sum of those exponentials. In particular, whenever there are multiple edges burning, the next to reach its vertex is chosen uniformly from among all those present. Since we are not interested in how long the whole process takes, but rather in the number of times we must set light to the network and how many clashes we observe, we perform our analysis in discrete time: that is, we consider the multigraph without edge lengths, always set fire to a uniformly chosen edge (which has the effect of splitting it into two edges, both alight), and we choose which edge next finishes burning uniformly from among those currently alight.
Recall the description of the configuration model from the previous section. We may generate the pairing of the half-edges in any order we like, which makes the configuration model particularly amenable to an exploration-process-type analysis. In particular, given that we have revealed the pairings of a particular collection of half-edges, assuming we keep track of the degree sequence of the rest of the graph, the rest of the graph is again a configuration model with that degree sequence. We exploit this property below. Observe that we have n vertices of degree 3 and α(n) vertices of degree 4 in our configuration model. Our process starts by picking a uniform edge, splitting it in two and setting each resulting edge alight. (Let us refer to this as the beginning of a wave, with a new wave beginning every time we set light to a point in the multigraph.) A uniform one of these two edges reaches its vertex next. It samples its vertex from among those of degree 3 with probability 3n/(3n + 4α(n)) and from those of degree 4 with probability 4α(n)/(3n + 4α(n)). Thereafter, we may think of edges which are alight as the first half-edge of a pair, whose second half-edge we have yet to sample.
Suppose that we currently have x edges burning, and that there are u vertices with three unattached half-edges and v vertices with four unattached half-edges. We pick the next half-edge to process uniformly from those currently burning, and pick its pair uniformly at random from among those available, including any which are themselves burning. The pair half-edge is already burning with probability (x − 1)/(3u + 4v + x − 1), in which case we form an edge which is burning from both ends and generate a clash. Otherwise, if we connect to a vertex of degree 3, which occurs with probability 3u/(3u + 4v + x − 1), the fire is either passed to the two other half-edges (with probability ![]() ${\textstyle{1 \over 2}}$) or stopped. If it is stopped, the vertex of degree 3 becomes a vertex of degree 2. There are two different things that might happen to this vertex of degree 2. With probability 1/(3u + 4v + x − 3), its two half-edges are in fact connected to each other to form an isolated cycle. (As observed above, this is a rare event: there are only O(1) self-loops in the whole multigraph.) Any such isolated cycle necessarily yields a clash. With the complementary probability, the two remaining half-edges are not connected to each other but rather to other half-edges. Since vertices of degree 2 cannot stop fires, in this case we may simply remove the vertex and contract the path of length 2 in which it sat to a single edge. (Using Proposition 1.1(ii), this results in the relative lengths of the edges in the unseen parts of the multigraph still being Dirichlet(1, 1, …, 1) distributed.) In either case, the remaining unseen part of the multigraph (after deletion of the loop, or contraction of a path of length 2) is still distributed according to the configuration model with the updated degree distribution. Finally, if we connect to a vertex of degree 4, which occurs with probability 4v/(3u + 4v + x − 1), then either the fire is passed to all three other neighbours (with probability
${\textstyle{1 \over 2}}$) or stopped. If it is stopped, the vertex of degree 3 becomes a vertex of degree 2. There are two different things that might happen to this vertex of degree 2. With probability 1/(3u + 4v + x − 3), its two half-edges are in fact connected to each other to form an isolated cycle. (As observed above, this is a rare event: there are only O(1) self-loops in the whole multigraph.) Any such isolated cycle necessarily yields a clash. With the complementary probability, the two remaining half-edges are not connected to each other but rather to other half-edges. Since vertices of degree 2 cannot stop fires, in this case we may simply remove the vertex and contract the path of length 2 in which it sat to a single edge. (Using Proposition 1.1(ii), this results in the relative lengths of the edges in the unseen parts of the multigraph still being Dirichlet(1, 1, …, 1) distributed.) In either case, the remaining unseen part of the multigraph (after deletion of the loop, or contraction of a path of length 2) is still distributed according to the configuration model with the updated degree distribution. Finally, if we connect to a vertex of degree 4, which occurs with probability 4v/(3u + 4v + x − 1), then either the fire is passed to all three other neighbours (with probability ![]() ${\textstyle{1 \over 2}}$) or to none of them, in which case the result is that we obtain another vertex of degree 3.
${\textstyle{1 \over 2}}$) or to none of them, in which case the result is that we obtain another vertex of degree 3.
Note that we must treat the very first edge of a wave differently: although we start with two burning half-edges, they cannot be paired to each other (since otherwise there would be an edge in the original graph with no vertex, which is impossible). So let us treat the first step of a wave as consisting of picking a uniform edge, splitting it in two, sampling the vertex to which one of the resulting burning edges is attached and seeing whether it passes the fire on or not. So, if at some step, there are no burning half-edges, on the next step there will be either 1, 3, or 4 burning half-edges, corresponding to the events that the first of the two fires was stopped, that it was passed on through a vertex of degree 3, or that it was passed on through a vertex of degree 4.
In this way, we see that at each step of the procedure, we either process one vertex or generate a clash. A vertex of degree 3 is processed precisely once; a vertex of degree 4 is processed once or twice, depending on whether it stops the first fire it encounters or not. If we track the number of vertices of degrees 3 and 4 and the number of currently burning half-edges, we have a Markovian evolution, which we may hope to analyse using the tools of stochastic process theory. In particular, in what follows we make extensive use of martingales.
The rest of the paper is organized as follows. In Section 2 we write down explicitly the transition probabilities of our Markov chain, and give some first estimates relevant for the forthcoming analysis. In particular, we identify a coupling which facilitates our analysis of the end of the process. In Section 3 we prove fluid limits for the suitably rescaled number of nodes of degrees 3 and 4; that is, we show that these processes remain close to deterministic functions on a time interval which is bounded away from the end of the process (this is an application of the so-called differential equations method [Reference Darling and Norris8], [Reference Wormald21]). In Section 4 we analyse the ![]() $\alpha(n)\gg\sqrt{n}$ case, and prove a fluid limit result for the (suitably rescaled) numbers of fires and clashes we observe, as long as we are bounded away from the end of the process. In Section 5 we deal with the limiting properties of the number of fires and the number of clashes we observe, again as long as we bounded away from the end of the process, for
$\alpha(n)\gg\sqrt{n}$ case, and prove a fluid limit result for the (suitably rescaled) numbers of fires and clashes we observe, as long as we are bounded away from the end of the process. In Section 5 we deal with the limiting properties of the number of fires and the number of clashes we observe, again as long as we bounded away from the end of the process, for ![]() $\alpha(n)=O(\sqrt{n})$. In this case, the limiting process for the number of fires is a reflected diffusion, and the proof is based on an invariance principle for reflecting Markov chains (in the spirit of [Reference Ethier and Kurtz9], [Reference Kang and Williams11], and [Reference Stroock and Varadhan15]). Finally, in Section 6 we prove that the end of the process does not contribute significantly to any of these quantities, and so the convergence results can be extended into that range also.
$\alpha(n)=O(\sqrt{n})$. In this case, the limiting process for the number of fires is a reflected diffusion, and the proof is based on an invariance principle for reflecting Markov chains (in the spirit of [Reference Ethier and Kurtz9], [Reference Kang and Williams11], and [Reference Stroock and Varadhan15]). Finally, in Section 6 we prove that the end of the process does not contribute significantly to any of these quantities, and so the convergence results can be extended into that range also.
2. The Markov chain
For i ≥ 0, let Un(i) and Vn(i) represent the number of nodes of degrees 3 and 4, respectively, after i steps of the burning procedure. Let Xn(i) be the number of burning half-edges after i steps. Let Nn(i) be the counting process of the number of clashes observed up to step i. Set Un(0) = n, Vn(0)=α(n), Xn(0)=0, and Nn(0) = 0. We have already argued that the process (Un(i), Vn(i), Xn(i), Nn(i))i≥0 evolves in a Markovian manner until time ζ n = inf{i ≥ 0: Un(i)+Vn(i)+Xn(i) = 0}, when it stops. Write ![]() ${L^n}(k) = 2{\sum\nolimits_{i = 0}^{k - 1} {\bf 1} _{\{ {X^n}(i) = 0\} }}$ (we will think of this quantity as a local time). Then
${L^n}(k) = 2{\sum\nolimits_{i = 0}^{k - 1} {\bf 1} _{\{ {X^n}(i) = 0\} }}$ (we will think of this quantity as a local time). Then ![]() ${F^n} = {\textstyle{1 \over 2}}{L^n}({\zeta _n})$ and Cn = Nn(ζ n). We will find it convenient to rescale time by n (essentially because we start with n+α(n) vertices and a typical step involves the removal of a vertex of degree 3).
${F^n} = {\textstyle{1 \over 2}}{L^n}({\zeta _n})$ and Cn = Nn(ζ n). We will find it convenient to rescale time by n (essentially because we start with n+α(n) vertices and a typical step involves the removal of a vertex of degree 3).
Recall the definition of the process Xa from (1.1). We also let x: [0, 1] → ℝ+ be the (deterministic) function x(t) = (1−t)2/3 −(1−t)4/3. For 0 ≤ t ≤ 1, let
Let 𝔻(ℝ+, ℝ) denote the space of càdlàg functions from ℝ+ to ℝ, equipped with the Skorokhod topology. (In fact, since our limit processes will always be continuous, we will rather obtain convergence with respect to the uniform norm.) The crux of our argument is the following scaling limit theorem which straightforwardly implies Theorem 1.1.
Theorem 2.1
(i) Suppose that
 $\alpha(n)/\sqrt{n} \to a$ as n → ∞ for a ≥ 0. Then, uniformly as n → ∞
$\alpha(n)/\sqrt{n} \to a$ as n → ∞ for a ≥ 0. Then, uniformly as n → ∞
 ${1 \over {\sqrt n {\mkern 1mu} }}({X^n}(\left\lfloor {nt} \right\rfloor),{L^n}(\left\lfloor {nt} \right\rfloor),{N^n}(\left\lfloor {nt} \right\rfloor),{\mkern 1mu} 0 \le t \le {{{\zeta _n}} \over n})\underrightarrow{\rm D}(X_t^a,L_t^a,N_t^a,{\mkern 1mu} 0 \le t \le 1).$
${1 \over {\sqrt n {\mkern 1mu} }}({X^n}(\left\lfloor {nt} \right\rfloor),{L^n}(\left\lfloor {nt} \right\rfloor),{N^n}(\left\lfloor {nt} \right\rfloor),{\mkern 1mu} 0 \le t \le {{{\zeta _n}} \over n})\underrightarrow{\rm D}(X_t^a,L_t^a,N_t^a,{\mkern 1mu} 0 \le t \le 1).$
(ii) Suppose that
 $\alpha(n)\gg\sqrt{n}$. Then, uniformly as n → ∞,
$\alpha(n)\gg\sqrt{n}$. Then, uniformly as n → ∞,
 ${1 \over {\alpha (n)}}({X^n}(\left\lfloor {nt} \right\rfloor),{L^n}(\left\lfloor {nt} \right\rfloor),{N^n}(\left\lfloor {nt} \right\rfloor),{\mkern 1mu} 0 \le t \le {{{\zeta _n}} \over n}){\rm{ }}\underrightarrow{\rm D}(x(t),0,m(t),{\mkern 1mu} 0 \le t \le 1).$
${1 \over {\alpha (n)}}({X^n}(\left\lfloor {nt} \right\rfloor),{L^n}(\left\lfloor {nt} \right\rfloor),{N^n}(\left\lfloor {nt} \right\rfloor),{\mkern 1mu} 0 \le t \le {{{\zeta _n}} \over n}){\rm{ }}\underrightarrow{\rm D}(x(t),0,m(t),{\mkern 1mu} 0 \le t \le 1).$
2.1. Transition probabilities
We have already described the possible transitions of our four-dimensional Markov chain in the introduction. Let us be a little more explicit about the transition probabilities.
Suppose that (Un(i), Vn(i), Xn(i), ![]() $N^n(i)) = (u,v,x,m) \in \mathbb {Z}_+^4$. If x = 0 but u + v > 0, then
$N^n(i)) = (u,v,x,m) \in \mathbb {Z}_+^4$. If x = 0 but u + v > 0, then
 \begin{align}
& (U^n(i+1), V^n(i+1), X^n(i+1), N^n(i+1)) \\
& \quad\quad = \begin{cases}
(u-1, v, 1, m+1) & \text{with probability $\dfrac{3u}{2(3u + 4v)(3u+4v-2)}$,}
\\
(u-1, v, 1, m) & \text{with probability $\dfrac{3u(3u+4v-3)}{2(3u + 4v)(3u+4v-2)}$,}
\\
(u-1, v, 3, m) & \text{with probability $\dfrac{3u}{2(3u+4v)}$,}
\\
(u+1, v-1, 1, m) & \text{with probability $\dfrac{4v}{2(3u+4v)}$,}
\\
(u, v-1, 4, m) & \text{with probability $\dfrac{4v}{2(3u+4v)}$}.
\end{cases}
\end{align}
\begin{align}
& (U^n(i+1), V^n(i+1), X^n(i+1), N^n(i+1)) \\
& \quad\quad = \begin{cases}
(u-1, v, 1, m+1) & \text{with probability $\dfrac{3u}{2(3u + 4v)(3u+4v-2)}$,}
\\
(u-1, v, 1, m) & \text{with probability $\dfrac{3u(3u+4v-3)}{2(3u + 4v)(3u+4v-2)}$,}
\\
(u-1, v, 3, m) & \text{with probability $\dfrac{3u}{2(3u+4v)}$,}
\\
(u+1, v-1, 1, m) & \text{with probability $\dfrac{4v}{2(3u+4v)}$,}
\\
(u, v-1, 4, m) & \text{with probability $\dfrac{4v}{2(3u+4v)}$}.
\end{cases}
\end{align}
If x > 0 then
 \begin{align}
& (U^n(i+1), V^n(i+1), X^n(i+1), N^n(i+1)) \\
& \quad\quad =
\begin{cases}
(u-1, v, x-1, m+1) & \text{with probability $\dfrac{3u}{2(3u+4v + x-1)(3u + 4v + x-3)}$,}
\\
(u-1, v, x-1, m) & \text{with probability $\dfrac{3u(3u+4v+x-4)}{2(3u+4v+x-1)(3u+4v+x-3)}$,}
\\
(u-1, v, x+1, m) & \text{with probability $\dfrac{3u}{2(3u+4v+x-1)}$,}
\\
(u+1, v-1, x-1, m) & \text{with probability $\dfrac{4v}{2(3u+4v+x-1)}$,}
\\
(u, v-1, x+2, m) & \text{with probability $\dfrac{4v}{2(3u+4v+x-1)}$,}
\\
(u, v, x-2, m+1) & \text{with probability $\dfrac{x-1}{(3u+4v+x-1)}$}.
\end{cases}
\end{align}
\begin{align}
& (U^n(i+1), V^n(i+1), X^n(i+1), N^n(i+1)) \\
& \quad\quad =
\begin{cases}
(u-1, v, x-1, m+1) & \text{with probability $\dfrac{3u}{2(3u+4v + x-1)(3u + 4v + x-3)}$,}
\\
(u-1, v, x-1, m) & \text{with probability $\dfrac{3u(3u+4v+x-4)}{2(3u+4v+x-1)(3u+4v+x-3)}$,}
\\
(u-1, v, x+1, m) & \text{with probability $\dfrac{3u}{2(3u+4v+x-1)}$,}
\\
(u+1, v-1, x-1, m) & \text{with probability $\dfrac{4v}{2(3u+4v+x-1)}$,}
\\
(u, v-1, x+2, m) & \text{with probability $\dfrac{4v}{2(3u+4v+x-1)}$,}
\\
(u, v, x-2, m+1) & \text{with probability $\dfrac{x-1}{(3u+4v+x-1)}$}.
\end{cases}
\end{align}
Writing ![]() ${({\cal F}_i^n)_{i \ge 0}}$ for the natural filtration of the four-dimensional process, we have
${({\cal F}_i^n)_{i \ge 0}}$ for the natural filtration of the four-dimensional process, we have
 \begin{gather}
\begin{aligned}
\mathbb {E}{U^n(i+1) - U^n(i) \mid \mathcal {F}^n_i} & = \frac{2V^n(i) - 3
U^n(i)}{3 U^n(i) + 4 V^n(i) + X^n(i) - {\bf 1} _{\{ {X^n}(i) > 0\} } },
\\
\mathbb {E}{V^n(i+1) - V^n(i) \mid \mathcal {F}^n_i} & = \frac{-4V^n(i)}{3 U^n(i) +
4 V^n(i) + X^n(i) - {\bf 1} _{\{ {X^n}(i) > 0\} }},
\end{aligned}
\\
\begin{aligned}
\mathbb {E}{X^n(i+1) - X^n(i) \mid \mathcal {F}^n_i} & = 2 {\bf 1} _{\{ {X^n}(i) = 0\} } +
\frac{2V^n(i) -2X^n(i) + 2 {\bf 1} _{\{ {X^n}(i) > 0\} }}{3U^n(i) + 4 V^n(i) + X^n(i) -
{\bf 1} _{\{ {X^n}(i) > 0\} }}, \label{eq exp changes X}
\end{aligned}
\end{gather}
\begin{gather}
\begin{aligned}
\mathbb {E}{U^n(i+1) - U^n(i) \mid \mathcal {F}^n_i} & = \frac{2V^n(i) - 3
U^n(i)}{3 U^n(i) + 4 V^n(i) + X^n(i) - {\bf 1} _{\{ {X^n}(i) > 0\} } },
\\
\mathbb {E}{V^n(i+1) - V^n(i) \mid \mathcal {F}^n_i} & = \frac{-4V^n(i)}{3 U^n(i) +
4 V^n(i) + X^n(i) - {\bf 1} _{\{ {X^n}(i) > 0\} }},
\end{aligned}
\\
\begin{aligned}
\mathbb {E}{X^n(i+1) - X^n(i) \mid \mathcal {F}^n_i} & = 2 {\bf 1} _{\{ {X^n}(i) = 0\} } +
\frac{2V^n(i) -2X^n(i) + 2 {\bf 1} _{\{ {X^n}(i) > 0\} }}{3U^n(i) + 4 V^n(i) + X^n(i) -
{\bf 1} _{\{ {X^n}(i) > 0\} }}, \label{eq exp changes X}
\end{aligned}
\end{gather}
 \begin{gather}\begin{aligned}
\mathbb {E}[{N^n(i+1) - N^n(i) \mid \mathcal {F}^n_i}]
\end{aligned}
\\
\begin{aligned}
&\quad\quad{\begin{gathered}= \frac{3U^n(i) + 2(X^n(i) - {\bf 1} _{\{ {X^n}(i) > 0\} })(3U^n(i) + 4V^n(i) + X^n(i) - 3)}{2(3U^n(i) + 4V^n(i) + X^n(i)
-{\bf 1} _{\{ {X^n}(i) > 0\} })(3U^n(i) + 4V^n(i) + X^n(i) -{\bf 1} _{\{ {X^n}(i) > 0\} } -
2)}\end{gathered}}. \label{eq exp changes N}\end{aligned}
\end{gather}
\begin{gather}\begin{aligned}
\mathbb {E}[{N^n(i+1) - N^n(i) \mid \mathcal {F}^n_i}]
\end{aligned}
\\
\begin{aligned}
&\quad\quad{\begin{gathered}= \frac{3U^n(i) + 2(X^n(i) - {\bf 1} _{\{ {X^n}(i) > 0\} })(3U^n(i) + 4V^n(i) + X^n(i) - 3)}{2(3U^n(i) + 4V^n(i) + X^n(i)
-{\bf 1} _{\{ {X^n}(i) > 0\} })(3U^n(i) + 4V^n(i) + X^n(i) -{\bf 1} _{\{ {X^n}(i) > 0\} } -
2)}\end{gathered}}. \label{eq exp changes N}\end{aligned}
\end{gather}
We will also need the following conditional second moments:
 \begin{align}
\mathbb {E}{[(U^n(i+1) - U^n(i))^2 \mid \mathcal {F}^n_i}] & = \frac{3U^n(i) + 2
V^n(i)}{3U^n(i) + 4V^n(i) + X^n(i) - {\bf 1} _{\{ {X^n}(i) > 0\} }}, \notag
\\
\mathbb {E}{[(V^n(i+1) - V^n(i))^2 \mid \mathcal {F}^n_i}] & =
\frac{4V^n(i)}{3U^n(i) + 4V^n(i) + X^n(i) - {\bf 1} _{\{ {X^n}(i) > 0\} }}, \notag
\\
\mathbb {E}{[(X^n(i+1) - X^n(i))^2 \mid \mathcal {F}^n_i}] & =
\begin{cases} 5 +
\frac{14V^n(i)}{3U^n(i) + 4V^n(i)} & \text{if $X^n(i) = 0$,}
\\
1 + \frac{6V^n(i) + 3X^n(i) -3}{3U^n(i) + 4V^n(i) + X^n(i) - 1} &
\text{if $X^n(i) > 0$},
\end{cases} \label{eqn:squareincrX}
\\
\mathbb {E}{[(N^n(i+1) - N^n(i))^{2} \mid \mathcal {F}^n_i} & = \mathbb {E}[{N^n(i+1) -
N^n(i) \mid \mathcal {F}^n_i}]. \notag
\end{align}
\begin{align}
\mathbb {E}{[(U^n(i+1) - U^n(i))^2 \mid \mathcal {F}^n_i}] & = \frac{3U^n(i) + 2
V^n(i)}{3U^n(i) + 4V^n(i) + X^n(i) - {\bf 1} _{\{ {X^n}(i) > 0\} }}, \notag
\\
\mathbb {E}{[(V^n(i+1) - V^n(i))^2 \mid \mathcal {F}^n_i}] & =
\frac{4V^n(i)}{3U^n(i) + 4V^n(i) + X^n(i) - {\bf 1} _{\{ {X^n}(i) > 0\} }}, \notag
\\
\mathbb {E}{[(X^n(i+1) - X^n(i))^2 \mid \mathcal {F}^n_i}] & =
\begin{cases} 5 +
\frac{14V^n(i)}{3U^n(i) + 4V^n(i)} & \text{if $X^n(i) = 0$,}
\\
1 + \frac{6V^n(i) + 3X^n(i) -3}{3U^n(i) + 4V^n(i) + X^n(i) - 1} &
\text{if $X^n(i) > 0$},
\end{cases} \label{eqn:squareincrX}
\\
\mathbb {E}{[(N^n(i+1) - N^n(i))^{2} \mid \mathcal {F}^n_i} & = \mathbb {E}[{N^n(i+1) -
N^n(i) \mid \mathcal {F}^n_i}]. \notag
\end{align}
2.2. A coupling and some first estimates
The process runs for ζ n steps. At each step, we process a whole edge of the multigraph, except at the start of a wave, when we possibly need two steps to process an edge. There are ![]() $\tfrac12(3n+4\alpha(n))$ edges in total and so ζ n ≤ 3n + 4α(n).
$\tfrac12(3n+4\alpha(n))$ edges in total and so ζ n ≤ 3n + 4α(n).
In the sequel, and particularly in Section 6, we will make extensive use of a coupling of a modified version of Xn and a reflecting simple symmetric random walk, which we now introduce. First, we divide the burning half-edges into two stacks, of sizes ![]() $X^n_1(i)$ and
$X^n_1(i)$ and ![]() $X^n_2(i)$, such that
$X^n_2(i)$, such that ![]() $X^n(i) = X^n_1(i) + X^n_2(i)$ for all 0 ≤ i ≤ ζ n. We may give these subprocesses whatever dynamics we choose, as long as their sum behaves as (Xn(i))i≥0. We proceed as follows.
$X^n(i) = X^n_1(i) + X^n_2(i)$ for all 0 ≤ i ≤ ζ n. We may give these subprocesses whatever dynamics we choose, as long as their sum behaves as (Xn(i))i≥0. We proceed as follows.
Whenever ![]() $X^n_1(i) > 0$, we select the next half-edge to process from the first stack. If the fire is absorbed,
$X^n_1(i) > 0$, we select the next half-edge to process from the first stack. If the fire is absorbed, ![]() $X^n_1$ is simply reduced by 1. If we connect to a vertex of degree 3 and pass the fire on,
$X^n_1$ is simply reduced by 1. If we connect to a vertex of degree 3 and pass the fire on, ![]() $X^n_1$ increases by 1. If we connect to a vertex of degree 4 and pass the fire on, we let each of
$X^n_1$ increases by 1. If we connect to a vertex of degree 4 and pass the fire on, we let each of ![]() $X^n_1$ and
$X^n_1$ and ![]() $X^n_2$ increase by 1. If we create a clash with a half-edge from the first stack,
$X^n_2$ increase by 1. If we create a clash with a half-edge from the first stack, ![]() $X^n_1$ is reduced by 2. We may also create a clash with a vertex from the second stack, in which case
$X^n_1$ is reduced by 2. We may also create a clash with a vertex from the second stack, in which case ![]() $X^n_1$ and
$X^n_1$ and ![]() $X^n_2$ are both reduced by 1.
$X^n_2$ are both reduced by 1.
If ![]() $X^n_1(i) = 0$ but
$X^n_1(i) = 0$ but ![]() $X^n_2(i) > 0$, then we select the half-edge to process from the second stack, add any new half-edges arising from passing the fire on to a vertex of degree 3 to
$X^n_2(i) > 0$, then we select the half-edge to process from the second stack, add any new half-edges arising from passing the fire on to a vertex of degree 3 to ![]() $X_1^n$ and add 2 of the three burning half-edges arising from passing the fire on to a vertex of degree 4 to
$X_1^n$ and add 2 of the three burning half-edges arising from passing the fire on to a vertex of degree 4 to ![]() $X_1^n$ and the last one to
$X_1^n$ and the last one to ![]() $X^n_2$. Finally, if
$X^n_2$. Finally, if ![]() $X^n_1(i) = X^n_2(i) = 0$, then we allocate all new half-edges to the first stack, except if we connect to a vertex of degree 4 and pass on the fire, in which case
$X^n_1(i) = X^n_2(i) = 0$, then we allocate all new half-edges to the first stack, except if we connect to a vertex of degree 4 and pass on the fire, in which case ![]() $X^n_1$ jumps to 3 and
$X^n_1$ jumps to 3 and ![]() $X^n_2$ jumps to 1.
$X^n_2$ jumps to 1.
We will also track the clashes and split them according to whether they involve a half-edge from the second stack or not, yielding ![]() $N^n(i) = N_1^n(i) + N_2^n(i)$ for i ≥ 0.
$N^n(i) = N_1^n(i) + N_2^n(i)$ for i ≥ 0.
We will describe the transition probabilities of this process in detail below. Our aim is to couple ![]() $X_1^n$ with a process Yn in such a way that
$X_1^n$ with a process Yn in such a way that ![]() $X_1^n(i) \le {Y^n}(i)$ for all i ≥ 0 and Yn is a simple symmetric random walk (SSRW), reflected at 2. In order to keep the notation to a reasonable level, we will describe the transitions of
$X_1^n(i) \le {Y^n}(i)$ for all i ≥ 0 and Yn is a simple symmetric random walk (SSRW), reflected at 2. In order to keep the notation to a reasonable level, we will describe the transitions of ![]() ${(X_1^n(i),X_2^n(i),{Y^n}(i),N_1^n(i),N_2^n(i))_{i \ge 0}}$, leaving those of (Un(i), Vn(i))i≥0 implicit.
${(X_1^n(i),X_2^n(i),{Y^n}(i),N_1^n(i),N_2^n(i))_{i \ge 0}}$, leaving those of (Un(i), Vn(i))i≥0 implicit.
Conditional on ![]() $X_1^n(i) = x_1 > 0, X_2^n(i) = x_2 \ge 0$, Yn(i) = y ≥ 3, Un(i) = u, Vn(i) = v, with x = x 1 + x 2,
$X_1^n(i) = x_1 > 0, X_2^n(i) = x_2 \ge 0$, Yn(i) = y ≥ 3, Un(i) = u, Vn(i) = v, with x = x 1 + x 2,
 \begin{align}
& (X_1^n(i+1) - X_1^n(i), X_2^n(i+1) - X_2(i), Y^n(i+1) - Y^n(i),
N^n_1(i+1) -N^n_1(i),
\\
&N^n_2(i+1) -N^n_2(i))
\\
& \quad\quad =
\begin{cases}
({-}2, 0, -1, +1, 0) & \text{with probability $\dfrac{x_1-1}{2(3u+4v+x-1)}$},
\\
({-}2,0, +1, +1, 0) & \text{with probability $\dfrac{x_1-1}{2(3u+4v+x-1)}$},
\\
({-}1, -1, -1, 0, +1) & \text{with probability $\dfrac{x_2}{2(3u+4v+x-1)}$},
\\
({-}1,-1, +1, 0, +1) & \text{with probability $\dfrac{x_2}{2(3u+4v+x-1)}$},
\\
({-}1, 0, -1, +1, 0) & \text{with probability $\dfrac{3u}{2(3u+4v + x-1)(3u + 4v +
x-3)}$},
\\
({-}1,0, -1, 0, 0) & \text{with probability}\ \dfrac{4v}{2(3u+4v+x-1)}\\
&\quad\quad\quad\quad\quad\quad\ + \dfrac{3u(3u+4v+x-4)}{2(3u+4v + x-1)(3u + 4v +
x-3)},
\\
({+}1,0, +1, 0, 0) & \text{with probability $\dfrac{3u}{2(3u+4v+x-1)}$},
\\
({+}1,+1,+1, 0, 0) & \text{with probability $\dfrac{4v}{2(3u+4v+x-1)}$}.
\end{cases}
\end{align}
\begin{align}
& (X_1^n(i+1) - X_1^n(i), X_2^n(i+1) - X_2(i), Y^n(i+1) - Y^n(i),
N^n_1(i+1) -N^n_1(i),
\\
&N^n_2(i+1) -N^n_2(i))
\\
& \quad\quad =
\begin{cases}
({-}2, 0, -1, +1, 0) & \text{with probability $\dfrac{x_1-1}{2(3u+4v+x-1)}$},
\\
({-}2,0, +1, +1, 0) & \text{with probability $\dfrac{x_1-1}{2(3u+4v+x-1)}$},
\\
({-}1, -1, -1, 0, +1) & \text{with probability $\dfrac{x_2}{2(3u+4v+x-1)}$},
\\
({-}1,-1, +1, 0, +1) & \text{with probability $\dfrac{x_2}{2(3u+4v+x-1)}$},
\\
({-}1, 0, -1, +1, 0) & \text{with probability $\dfrac{3u}{2(3u+4v + x-1)(3u + 4v +
x-3)}$},
\\
({-}1,0, -1, 0, 0) & \text{with probability}\ \dfrac{4v}{2(3u+4v+x-1)}\\
&\quad\quad\quad\quad\quad\quad\ + \dfrac{3u(3u+4v+x-4)}{2(3u+4v + x-1)(3u + 4v +
x-3)},
\\
({+}1,0, +1, 0, 0) & \text{with probability $\dfrac{3u}{2(3u+4v+x-1)}$},
\\
({+}1,+1,+1, 0, 0) & \text{with probability $\dfrac{4v}{2(3u+4v+x-1)}$}.
\end{cases}
\end{align}
Conditional on ![]() $X_1^n(i) = x_1 > 0$,
$X_1^n(i) = x_1 > 0$, ![]() $X_2^n(i) = x_2 \ge 0$ Yn(i) = y = 2, Un(i) = u, Vn(i) = v, with x = x 1 + x 2,
$X_2^n(i) = x_2 \ge 0$ Yn(i) = y = 2, Un(i) = u, Vn(i) = v, with x = x 1 + x 2,
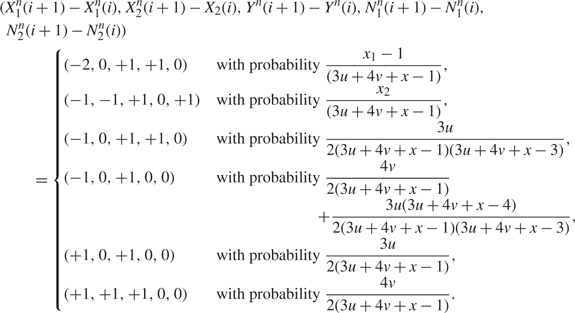 \begin{align}
& (X_1^n(i+1) - X_1^n(i), X_2^n(i+1) - X_2(i), Y^n(i+1) - Y^n(i),
N^n_1(i+1) -N^n_1(i),
\\
&N^n_2(i+1) -N^n_2(i))
\\
&\quad\quad =
\begin{cases}
({-}2, 0, +1, +1, 0) & \text{with probability $\dfrac{x_1-1}{(3u+4v+x-1)}$},
\\
({-}1, -1, +1, 0, +1) & \text{with probability $\dfrac{x_2}{(3u+4v+x-1)}$},
\\
({-}1, 0, +1, +1, 0) & \text{with probability $\dfrac{3u}{2(3u+4v + x-1)(3u
+ 4v + x-3)}$},
\\
({-}1,0, +1, 0, 0) & \text{with probability}\ \dfrac{4v}{2(3u+4v+x-1)}\\
&\quad\quad\quad\quad\quad\quad\ + \dfrac{3u(3u+4v+x-4)}{2(3u+4v + x-1)(3u + 4v + x-3)},
\\
({+}1,0, +1, 0, 0) & \text{with probability $\dfrac{3u}{2(3u+4v+x-1)}$},
\\
({+}1,+1,+1, 0, 0) & \text{with probability $\dfrac{4v}{2(3u+4v+x-1)}$}.
\end{cases}
\end{align}
\begin{align}
& (X_1^n(i+1) - X_1^n(i), X_2^n(i+1) - X_2(i), Y^n(i+1) - Y^n(i),
N^n_1(i+1) -N^n_1(i),
\\
&N^n_2(i+1) -N^n_2(i))
\\
&\quad\quad =
\begin{cases}
({-}2, 0, +1, +1, 0) & \text{with probability $\dfrac{x_1-1}{(3u+4v+x-1)}$},
\\
({-}1, -1, +1, 0, +1) & \text{with probability $\dfrac{x_2}{(3u+4v+x-1)}$},
\\
({-}1, 0, +1, +1, 0) & \text{with probability $\dfrac{3u}{2(3u+4v + x-1)(3u
+ 4v + x-3)}$},
\\
({-}1,0, +1, 0, 0) & \text{with probability}\ \dfrac{4v}{2(3u+4v+x-1)}\\
&\quad\quad\quad\quad\quad\quad\ + \dfrac{3u(3u+4v+x-4)}{2(3u+4v + x-1)(3u + 4v + x-3)},
\\
({+}1,0, +1, 0, 0) & \text{with probability $\dfrac{3u}{2(3u+4v+x-1)}$},
\\
({+}1,+1,+1, 0, 0) & \text{with probability $\dfrac{4v}{2(3u+4v+x-1)}$}.
\end{cases}
\end{align}
Conditional on ![]() $X_1^n(i) = 0$,
$X_1^n(i) = 0$, ![]() $X_2^n(i) = x_2 > 0$, Yn(i) = y ≥ 3, Un(i) = u, Vn(i) = v,
$X_2^n(i) = x_2 > 0$, Yn(i) = y ≥ 3, Un(i) = u, Vn(i) = v,
 \begin{align}
& (X_1^n(i+1) - X_1^n(i), X_2^n(i+1) - X_2(i), Y^n(i+1) - Y^n(i),
N^n_1(i+1) -N^n_1(i),
\\
&N^n_2(i+1) -N^n_2(i))
\\
&\quad\quad =
\begin{cases}
(0, -2, -1, 0, +1) & \text{with probability
$\dfrac{x_2-1}{2(3u+4v+x_2-1)}$},
\\
(0,-2, +1, 0, +1) & \text{with probability
$\dfrac{x_2-1}{2(3u+4v+x_2-1)}$},
\\
(0, -1, -1, +1, 0) & \text{with probability $\dfrac{3u}{2(3u+4v + x_2-1)(3u + 4v +
x_2-3)}$},
\\
(0,-1, -1, 0, 0) & \text{with probability}\ \dfrac{4v}{2(3u+4v+x_2-1)}\\
&\quad\quad\quad\quad\quad\quad\ + \dfrac{3u(3u+4v+x_2-4)}{2(3u+4v + x_2-1)(3u + 4v +
x_2-3)},
\\
({+}2,-1, +1, 0, 0) & \text{with probability $\dfrac{3u}{2(3u+4v+x_2-1)}$},
\\
({+}2,0,+1,0, 0) & \text{with probability $\dfrac{4v}{2(3u+4v+x_2-1)}$}.
\end{cases}
\end{align}
\begin{align}
& (X_1^n(i+1) - X_1^n(i), X_2^n(i+1) - X_2(i), Y^n(i+1) - Y^n(i),
N^n_1(i+1) -N^n_1(i),
\\
&N^n_2(i+1) -N^n_2(i))
\\
&\quad\quad =
\begin{cases}
(0, -2, -1, 0, +1) & \text{with probability
$\dfrac{x_2-1}{2(3u+4v+x_2-1)}$},
\\
(0,-2, +1, 0, +1) & \text{with probability
$\dfrac{x_2-1}{2(3u+4v+x_2-1)}$},
\\
(0, -1, -1, +1, 0) & \text{with probability $\dfrac{3u}{2(3u+4v + x_2-1)(3u + 4v +
x_2-3)}$},
\\
(0,-1, -1, 0, 0) & \text{with probability}\ \dfrac{4v}{2(3u+4v+x_2-1)}\\
&\quad\quad\quad\quad\quad\quad\ + \dfrac{3u(3u+4v+x_2-4)}{2(3u+4v + x_2-1)(3u + 4v +
x_2-3)},
\\
({+}2,-1, +1, 0, 0) & \text{with probability $\dfrac{3u}{2(3u+4v+x_2-1)}$},
\\
({+}2,0,+1,0, 0) & \text{with probability $\dfrac{4v}{2(3u+4v+x_2-1)}$}.
\end{cases}
\end{align}
Conditional on ![]() $X_1^n(i) = 0$,
$X_1^n(i) = 0$, ![]() $X_2^n(i) = x_2 > 0$, Yn(i) = y = 2, Un(i) = u, Vn(i) = v,
$X_2^n(i) = x_2 > 0$, Yn(i) = y = 2, Un(i) = u, Vn(i) = v,
 \begin{align}
& (X_1^n(i+1) - X_1^n(i), \ X_2^n(i+1) - X_2(i), \ Y^n(i+1) - Y^n(i),
N^n_1(i+1) -N^n_1(i),
\\
&N^n_2(i+1) -N^n_2(i))
\\
&\quad\quad =
\begin{cases}
(0,-2, +1, 0, +1) & \text{with probability
$\dfrac{x_2-1}{(3u+4v+x_2-1)}$},
\\
(0, -1, +1, +1, 0) & \text{with probability $\dfrac{3u}{2(3u+4v +
x_2-1)(3u + 4v + x_2-3)}$},
\\
(0,-1, +1, 0, 0) & \text{with probability}\ \dfrac{4v}{2(3u+4v+x_2-1)}\\
&\quad\quad\quad\quad\quad\quad\ + \dfrac{3u(3u+4v+x_2-4)}{2(3u+4v + x_2-1)(3u + 4v + x_2-3)},
\\
({+}2,-1, +1, 0, 0) & \text{with probability $\dfrac{3u}{2(3u+4v+x_2-1)}$},
\\
({+}2,0,+1,0, 0) & \text{with probability $\dfrac{4v}{2(3u+4v+x_2-1)}$}.
\end{cases}
\end{align}
\begin{align}
& (X_1^n(i+1) - X_1^n(i), \ X_2^n(i+1) - X_2(i), \ Y^n(i+1) - Y^n(i),
N^n_1(i+1) -N^n_1(i),
\\
&N^n_2(i+1) -N^n_2(i))
\\
&\quad\quad =
\begin{cases}
(0,-2, +1, 0, +1) & \text{with probability
$\dfrac{x_2-1}{(3u+4v+x_2-1)}$},
\\
(0, -1, +1, +1, 0) & \text{with probability $\dfrac{3u}{2(3u+4v +
x_2-1)(3u + 4v + x_2-3)}$},
\\
(0,-1, +1, 0, 0) & \text{with probability}\ \dfrac{4v}{2(3u+4v+x_2-1)}\\
&\quad\quad\quad\quad\quad\quad\ + \dfrac{3u(3u+4v+x_2-4)}{2(3u+4v + x_2-1)(3u + 4v + x_2-3)},
\\
({+}2,-1, +1, 0, 0) & \text{with probability $\dfrac{3u}{2(3u+4v+x_2-1)}$},
\\
({+}2,0,+1,0, 0) & \text{with probability $\dfrac{4v}{2(3u+4v+x_2-1)}$}.
\end{cases}
\end{align}
Conditional on ![]() $X_1^n(i) = 0$,
$X_1^n(i) = 0$, ![]() $X_2^n(i) = 0$, Yn(i) = y ≥ 3, Un(i) = u, Vn(i) = v,
$X_2^n(i) = 0$, Yn(i) = y ≥ 3, Un(i) = u, Vn(i) = v,
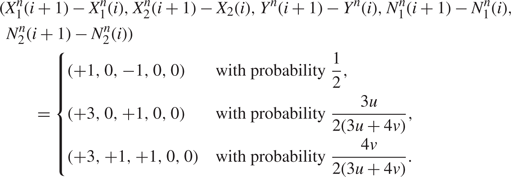 \begin{align}
& (X_1^n(i+1) - X_1^n(i), X_2^n(i+1) - X_2(i), Y^n(i+1) - Y^n(i),
N^n_1(i+1) -N^n_1(i),
\\
&N^n_2(i+1) -N^n_2(i))
\\
&\quad\quad =
\begin{cases}
({+}1,0, -1,0,0) & \text{with probability $\dfrac{1}{2}$},
\\
({+}3,0, +1,0,0) & \text{with probability $\dfrac{3u}{2(3u+4v)}$},
\\
({+}3,+1,+1,0,0) & \text{with probability $\dfrac{4v}{2(3u+4v)}$}.
\end{cases}
\end{align}
\begin{align}
& (X_1^n(i+1) - X_1^n(i), X_2^n(i+1) - X_2(i), Y^n(i+1) - Y^n(i),
N^n_1(i+1) -N^n_1(i),
\\
&N^n_2(i+1) -N^n_2(i))
\\
&\quad\quad =
\begin{cases}
({+}1,0, -1,0,0) & \text{with probability $\dfrac{1}{2}$},
\\
({+}3,0, +1,0,0) & \text{with probability $\dfrac{3u}{2(3u+4v)}$},
\\
({+}3,+1,+1,0,0) & \text{with probability $\dfrac{4v}{2(3u+4v)}$}.
\end{cases}
\end{align}
Finally, conditional on ![]() $X_1^n(i) = 0$,
$X_1^n(i) = 0$, ![]() $X_2^n(i) = 0$, Yn(i) = y = 2, Un(i) = u, Vn(i) = v,
$X_2^n(i) = 0$, Yn(i) = y = 2, Un(i) = u, Vn(i) = v,
 \begin{align}
& (X_1^n(i+1) - X_1^n(i), X_2^n(i+1) - X_2(i), Y^n(i+1) - Y^n(i),
N^n_1(i+1) -N^n_1(i),
\\
&N^n_2(i+1) -N^n_2(i))
\\
&\quad\quad =
\begin{cases}
({+}1,0, +1,0,0) & \text{with probability $\dfrac{1}{2}$},
\\
({+}3,0, +1,0,0) & \text{with probability $\dfrac{3u}{2(3u+4v)}$},
\\
({+}3,+1,+1,0,0) & \text{with probability $\dfrac{4v}{2(3u+4v)}$}.
\end{cases}
\end{align}
\begin{align}
& (X_1^n(i+1) - X_1^n(i), X_2^n(i+1) - X_2(i), Y^n(i+1) - Y^n(i),
N^n_1(i+1) -N^n_1(i),
\\
&N^n_2(i+1) -N^n_2(i))
\\
&\quad\quad =
\begin{cases}
({+}1,0, +1,0,0) & \text{with probability $\dfrac{1}{2}$},
\\
({+}3,0, +1,0,0) & \text{with probability $\dfrac{3u}{2(3u+4v)}$},
\\
({+}3,+1,+1,0,0) & \text{with probability $\dfrac{4v}{2(3u+4v)}$}.
\end{cases}
\end{align}
By construction, Yn performs an SSRW with upward reflection at 2. For fixed i ≥ 0, as long as ![]() $Y^n(i) \ge 2$ and
$Y^n(i) \ge 2$ and ![]() $X_1^n(i) \le Y^n(i)$, we obtain
$X_1^n(i) \le Y^n(i)$, we obtain ![]() $X_1^n(j) \le Y^n(j)$ for all j ≥ i.
$X_1^n(j) \le Y^n(j)$ for all j ≥ i.
Finally, we observe that, since a vertex of degree 4 contributes to the size of the second stack at most once, ![]() $X_2^n(i) \le V^n(0) - V^n(i)$ for all i ≥ 0. Similarly, the number of clashes involving at least one half-edge from the second stack is bounded above by the number of vertices of degree 4 processed so far,
$X_2^n(i) \le V^n(0) - V^n(i)$ for all i ≥ 0. Similarly, the number of clashes involving at least one half-edge from the second stack is bounded above by the number of vertices of degree 4 processed so far, ![]() $N_2^n(i) \le V^n(0) - V^n(i)$.
$N_2^n(i) \le V^n(0) - V^n(i)$.
Henceforth, we will use the notation ![]() $(\mathcal {F}_i^n)_{i \ge 0}$ for the natural filtration of the process
$(\mathcal {F}_i^n)_{i \ge 0}$ for the natural filtration of the process
For future reference, we note that
 \begin{align}
\!\!\!\!\mathbb {E}[{X_1^n(i+1) - X_1^n(i) \mid \mathcal {F}^n_i}] & = {\bf 1} _{\{ {X_1^n}(i) = 0, X_2^n(i)> 0\}} + 2 {\bf 1}_{\{X_1^n(i) = 0, X^n_2(i) = 0\}}
\\
&- \frac{2(X_1^n(i) - {\bf 1} _{\{ {X^n}(i) > 0\} }) + (X_2^n(i) - {\bf 1} _{\{ {X_1^n}(i) = 0, X_2^n(i) > 0\}})}{3U^n(i) + 4 V^n(i) + X^n(i) - {\bf 1}_{\{X^n(i) >
0\}}}\label{eqn:X_1}
\end{align}
\begin{align}
\!\!\!\!\mathbb {E}[{X_1^n(i+1) - X_1^n(i) \mid \mathcal {F}^n_i}] & = {\bf 1} _{\{ {X_1^n}(i) = 0, X_2^n(i)> 0\}} + 2 {\bf 1}_{\{X_1^n(i) = 0, X^n_2(i) = 0\}}
\\
&- \frac{2(X_1^n(i) - {\bf 1} _{\{ {X^n}(i) > 0\} }) + (X_2^n(i) - {\bf 1} _{\{ {X_1^n}(i) = 0, X_2^n(i) > 0\}})}{3U^n(i) + 4 V^n(i) + X^n(i) - {\bf 1}_{\{X^n(i) >
0\}}}\label{eqn:X_1}
\end{align}
and
 \begin{align}
& \mathbb {E}[{N_1^n(i+1) - N_1^n(i) \mid \mathcal {F}^n_i}]
\\
& \quad\quad {\begin{gathered}= \frac{3U^n(i) + 2(X_1^n(i) -
{\bf 1}_{\{X_1^n(i) > 0\}})(3U^n(i) + 4V^n(i) + X^n(i) - 3)}{2(3U^n(i) + 4V^n(i) +
X^n(i) -{\bf 1}_{\{X^n(i) > 0\}})(3U^n(i) + 4V^n(i) + X^n(i) -{\bf 1}_{\{X^n(i) > 0\}} -
2)}.\end{gathered}}\label{eqn:N_1}
\end{align}
\begin{align}
& \mathbb {E}[{N_1^n(i+1) - N_1^n(i) \mid \mathcal {F}^n_i}]
\\
& \quad\quad {\begin{gathered}= \frac{3U^n(i) + 2(X_1^n(i) -
{\bf 1}_{\{X_1^n(i) > 0\}})(3U^n(i) + 4V^n(i) + X^n(i) - 3)}{2(3U^n(i) + 4V^n(i) +
X^n(i) -{\bf 1}_{\{X^n(i) > 0\}})(3U^n(i) + 4V^n(i) + X^n(i) -{\bf 1}_{\{X^n(i) > 0\}} -
2)}.\end{gathered}}\label{eqn:N_1}
\end{align}
As a first consequence of our coupling, we show that Xn varies on a smaller scale than n.
Lemma 2.1
It holds that ![]() $({1}/{(\alpha(n) \vee \sqrt{n})}) \sup_{0 \le i \le \zeta_n} X^{n}(i)$ is bounded in L 4. In particular, (1/n) sup0≤i≤ζn Xn(i) converges in probability to 0 as n → ∞.
$({1}/{(\alpha(n) \vee \sqrt{n})}) \sup_{0 \le i \le \zeta_n} X^{n}(i)$ is bounded in L 4. In particular, (1/n) sup0≤i≤ζn Xn(i) converges in probability to 0 as n → ∞.
Proof. We have Xn(0) = 0; let Yn(0) = 2. Then, by the coupling, we have
Now let Z be a standard SSRW, and note that Z is a martingale. Then Yn has the same law as (2 + |Z(i)|)i≥0. Bearing in mind that, for i ≥ 1, we have ![]() $\mathbb {E}{(Z(i))^4}=i(3i-2) \le 3i^2$, by Doob’s L 4 inequality,
$\mathbb {E}{(Z(i))^4}=i(3i-2) \le 3i^2$, by Doob’s L 4 inequality,
Hence,
 \begin{align}
\mathbb {E} \Big[{ \Big(\ \sup_{0 \le i \le \zeta_n} X^n(i) \Big)^4}\Big] & \le
\mathbb {E}\Big[{\Big(\alpha(n) + 2 + \sup_{0 \le i \le 3n + 4\alpha(n)} |Z(i)|
\Big)^4}\Big]
\\
& \le 16\Bigl[(\alpha(n)+2)^4 + \tfrac{256}{27}(3n+4\alpha(n))^2\Bigr].
\end{align}
\begin{align}
\mathbb {E} \Big[{ \Big(\ \sup_{0 \le i \le \zeta_n} X^n(i) \Big)^4}\Big] & \le
\mathbb {E}\Big[{\Big(\alpha(n) + 2 + \sup_{0 \le i \le 3n + 4\alpha(n)} |Z(i)|
\Big)^4}\Big]
\\
& \le 16\Bigl[(\alpha(n)+2)^4 + \tfrac{256}{27}(3n+4\alpha(n))^2\Bigr].
\end{align}
Thus, there exists a constant C > 0 such that, for all n≥ 1,
and since α(n)/n → 0, we may deduce the claimed convergence in probability.
3. Fluid limit approximations for the auxiliary processes
In this section we prove that Un and Vn, after appropriate rescaling, remain concentrated around their expected trajectories. To this end, we employ the differential equations method [Reference Darling and Norris8], [Reference Wormald21]. Here we briefly recall the main idea, closely following Darling and Norris [Reference Darling and Norris8], although our presentation is for discrete-time rather than continuous-time processes and is in a somewhat simplified setting. Suppose that we are given a stochastic process Pn evolving in discrete time with finite state space 𝒮n ⊆ ℤ. We assume that Pn is either itself Markov or is a coordinate of some higher-dimensional Markov process Pn. Let the natural filtration of Pn be denoted by ![]() $(\mathcal {F}^n_P(i))_{i \ge 0}$. For each i ≥ 0, the process
$(\mathcal {F}^n_P(i))_{i \ge 0}$. For each i ≥ 0, the process ![]() $(M^n_P(i))_{i \ge 0}$, defined by
$(M^n_P(i))_{i \ge 0}$, defined by
 \begin{equation}
M^{n}_{P}(i)=P^{n}(i) -P^{n}(0)
-\sum_{j=0}^{i-1}\mathbb {E}[{P^{n}(j+1)-P^{n}(j)\mid {\mathcal {F}^{n}_{{P}}(j)}}],
\end{equation}
\begin{equation}
M^{n}_{P}(i)=P^{n}(i) -P^{n}(0)
-\sum_{j=0}^{i-1}\mathbb {E}[{P^{n}(j+1)-P^{n}(j)\mid {\mathcal {F}^{n}_{{P}}(j)}}],
\end{equation}
is a martingale. We will use this notation throughout the paper, and will refer to ![]() $M_P^n$ as the standard martingale associated with the process Pn. Then, for each fixed t > 0, we have
$M_P^n$ as the standard martingale associated with the process Pn. Then, for each fixed t > 0, we have
 \begin{equation}
\frac{P^{n}{(\left\lfloor {nt} \right\rfloor)}}{n}=\frac{P^{n}(0)}{n}+\frac{M^{n}_{P}
{(\left\lfloor {nt} \right\rfloor)}}{n}+\sum_{j=0}^{{\left\lfloor {nt} \right\rfloor }-1}{\frac{\mathbb {E}[{P^{n}(j+1)-P^{n}(j) \mid{{\mathcal {F}^{n}_{{P}}(j)]}}}}{n}}.
\end{equation}
\begin{equation}
\frac{P^{n}{(\left\lfloor {nt} \right\rfloor)}}{n}=\frac{P^{n}(0)}{n}+\frac{M^{n}_{P}
{(\left\lfloor {nt} \right\rfloor)}}{n}+\sum_{j=0}^{{\left\lfloor {nt} \right\rfloor }-1}{\frac{\mathbb {E}[{P^{n}(j+1)-P^{n}(j) \mid{{\mathcal {F}^{n}_{{P}}(j)]}}}}{n}}.
\end{equation}
Fix t 0 > 0, and let ![]() $\mathcal {U} \subseteq \mathbb {R}$. We will make four assumptions.
$\mathcal {U} \subseteq \mathbb {R}$. We will make four assumptions.
(i) For some constant
 $p(0) \in \mathcal {U}$, we have
$p(0) \in \mathcal {U}$, we have  $\left\vert{P^{n}(0)/n-p(0)}\right\vert \underrightarrow{\rm P} {0}$.
$\left\vert{P^{n}(0)/n-p(0)}\right\vert \underrightarrow{\rm P} {0}$.(ii) Suppose that
 $\nu\colon [0,t_0] \times \mathcal {U} \to{\mathbb {R}}$ is a bi-Lipschitz function with Lipschitz constant K. Suppose that p, the unique solution to the differential equation dp(t)/dt = ν(t, p(t)) with initial condition p(0), is such that, for some ε > 0, p(t) lies at a distance greater than ε from
$\nu\colon [0,t_0] \times \mathcal {U} \to{\mathbb {R}}$ is a bi-Lipschitz function with Lipschitz constant K. Suppose that p, the unique solution to the differential equation dp(t)/dt = ν(t, p(t)) with initial condition p(0), is such that, for some ε > 0, p(t) lies at a distance greater than ε from  $\mathcal {U}^c$ for all 0 ≤ t ≤ t 0.
$\mathcal {U}^c$ for all 0 ≤ t ≤ t 0.(iii) Let
 $T_n = \inf\{t \ge 0\colon P^n({\left\lfloor {nt} \right\rfloor })/n \notin \mathcal {U}\}$. We assume that
$T_n = \inf\{t \ge 0\colon P^n({\left\lfloor {nt} \right\rfloor })/n \notin \mathcal {U}\}$. We assume that
 \begin{align}
\sup_{0 \le t \le t_0 \wedge T_n}
\left\vert\sum_{j=0}^{{\left\lfloor {nt} \right\rfloor }-1}{\frac{\mathbb {E}[{P^{n}(j+1)-P^{n}(j)\mid
{{\mathcal {F}^{n}_{P}(j)]}}}}{n}-\int_{0}^{t}{\nu \biggl(s,
\frac{P^{n}({\left\lfloor {ns} \right\rfloor })}{n}\biggr)}{\text{d}} s}\right\vert \underrightarrow{\rm P} 0.
\end{align}
\begin{align}
\sup_{0 \le t \le t_0 \wedge T_n}
\left\vert\sum_{j=0}^{{\left\lfloor {nt} \right\rfloor }-1}{\frac{\mathbb {E}[{P^{n}(j+1)-P^{n}(j)\mid
{{\mathcal {F}^{n}_{P}(j)]}}}}{n}-\int_{0}^{t}{\nu \biggl(s,
\frac{P^{n}({\left\lfloor {ns} \right\rfloor })}{n}\biggr)}{\text{d}} s}\right\vert \underrightarrow{\rm P} 0.
\end{align}
(iv) We have
 $\mathbb {E} {[M_P^n{(\left\lfloor {n({t_0} \wedge {T_n})} \right\rfloor)^2}]/{n^2} \to 0}$ as n → ∞.
$\mathbb {E} {[M_P^n{(\left\lfloor {n({t_0} \wedge {T_n})} \right\rfloor)^2}]/{n^2} \to 0}$ as n → ∞.
Assumption (i) tells us that the initial condition is well concentrated on the scale of n. It follows from Assumption (iii) that, conditionally on Pn being in state nx at time ns, the size of the expected increment of Pn is close to ν(s, x). It is then natural to compare Pn/n to the solution to the differential equation in (ii), as long as Pn/n remains within the set ![]() $\mathcal {U}$.
$\mathcal {U}$.
Proposition 3.1
Under assumptions (i)–(iv), we have
Proof. Since p solves the given differential equation, we may write it in integral form as ![]() $p(t) = p(0) + \int_0^t \nu(s, p(s)) {\text{d}} s$. Hence,
$p(t) = p(0) + \int_0^t \nu(s, p(s)) {\text{d}} s$. Hence,
 \begin{align}
\frac{P^n({\left\lfloor {nt} \right\rfloor })}{n} - p(t) & = \frac{P^{n}(0)}{n} - p(0)
+\frac{M^{n}_{P}({\left\lfloor {nt} \right\rfloor })}{n}\\
& + \sum_{j=0}^{{\left\lfloor {nt} \right\rfloor }-1}
{\frac{\mathbb {E}[{P^{n}(j+1)-P^{n}(j)\mid {{\mathcal {F}^{n}_{P}(j)]}}}}{n}}- \int_0^t \nu(s,p(s)) {\text{d}} s.
\end{align}
\begin{align}
\frac{P^n({\left\lfloor {nt} \right\rfloor })}{n} - p(t) & = \frac{P^{n}(0)}{n} - p(0)
+\frac{M^{n}_{P}({\left\lfloor {nt} \right\rfloor })}{n}\\
& + \sum_{j=0}^{{\left\lfloor {nt} \right\rfloor }-1}
{\frac{\mathbb {E}[{P^{n}(j+1)-P^{n}(j)\mid {{\mathcal {F}^{n}_{P}(j)]}}}}{n}}- \int_0^t \nu(s,p(s)) {\text{d}} s.
\end{align}
By Doob’s L 2 inequality, assumption (iv) implies that ![]() $\sup_{0 \le t_0 \wedge T_n}(|M^{n}_{P}(i)|/n)\underrightarrow{\rm P} 0$ as n → ∞. Fix δ > 0, and let
$\sup_{0 \le t_0 \wedge T_n}(|M^{n}_{P}(i)|/n)\underrightarrow{\rm P} 0$ as n → ∞. Fix δ > 0, and let
 \begin{align}
\Omega_{n,\delta} & = \left\{ \left\vert{\frac{P^{n}(0)}{n}-p(0)}
\right\vert \le \frac{\delta \text {e}^{-Kt_0}}{3} \right\} \cap \left\{
\sup_{0\le t \le t_0 \wedge T_n} \frac{|M^{n}_{P}({\left\lfloor {nt} \right\rfloor })|}{n} \le
\frac{\delta \text {e}^{-Kt_0}}{3} \right\}
\\
& \cap\biggl\{\sup_{0 \le t \le t_0 \wedge T_n}\!
\left\vert\sum_{j=0}^{{\left\lfloor {nt} \right\rfloor }-1}{\frac{\mathbb {E}[{P^{n}(j+1)-P^{n}(j)\mid
{{\mathcal {F}^{n}_{P}(j)]}}}}{n}-\int_{0}^{t}{\! \nu \biggl(s,
\frac{P^{n}({\left\lfloor {ns} \right\rfloor })}{n}\biggr)}{\text{d}} s}\right\vert
\\
&\le \frac{\delta \text {e}^{-Kt_0}}{3}\! \biggr\}.
\end{align}
\begin{align}
\Omega_{n,\delta} & = \left\{ \left\vert{\frac{P^{n}(0)}{n}-p(0)}
\right\vert \le \frac{\delta \text {e}^{-Kt_0}}{3} \right\} \cap \left\{
\sup_{0\le t \le t_0 \wedge T_n} \frac{|M^{n}_{P}({\left\lfloor {nt} \right\rfloor })|}{n} \le
\frac{\delta \text {e}^{-Kt_0}}{3} \right\}
\\
& \cap\biggl\{\sup_{0 \le t \le t_0 \wedge T_n}\!
\left\vert\sum_{j=0}^{{\left\lfloor {nt} \right\rfloor }-1}{\frac{\mathbb {E}[{P^{n}(j+1)-P^{n}(j)\mid
{{\mathcal {F}^{n}_{P}(j)]}}}}{n}-\int_{0}^{t}{\! \nu \biggl(s,
\frac{P^{n}({\left\lfloor {ns} \right\rfloor })}{n}\biggr)}{\text{d}} s}\right\vert
\\
&\le \frac{\delta \text {e}^{-Kt_0}}{3}\! \biggr\}.
\end{align}
By the assumptions, we have ![]() $\mathbb {P}(\Omega_{n,\delta}^c) \to 0$ as n → ∞. On the event Ωn,δ, we have, for 0 ≤ t ≤ t 0 ^ T n,
$\mathbb {P}(\Omega_{n,\delta}^c) \to 0$ as n → ∞. On the event Ωn,δ, we have, for 0 ≤ t ≤ t 0 ^ T n,
 \begin{align}
\left| \frac{P^{n}({\left\lfloor {nt} \right\rfloor })}{n}-p(t) \right| & \le \delta \text {e}^{-Kt_0} +
\int_0^t \left| \nu \biggl(s, \frac{P^{n}({\left\lfloor {ns} \right\rfloor })}{n}\biggr) {\text{d}} s -
\nu(s, p(s))\right| {\text{d}} s
\\
& \leq \delta \text {e}^{-Kt_0} + K \int_{0}^{t} \left|\frac{P^{n}({\left\lfloor {ns} \right\rfloor })}
{n}-p(s)\right| {\text{d}} s ,
\end{align}
\begin{align}
\left| \frac{P^{n}({\left\lfloor {nt} \right\rfloor })}{n}-p(t) \right| & \le \delta \text {e}^{-Kt_0} +
\int_0^t \left| \nu \biggl(s, \frac{P^{n}({\left\lfloor {ns} \right\rfloor })}{n}\biggr) {\text{d}} s -
\nu(s, p(s))\right| {\text{d}} s
\\
& \leq \delta \text {e}^{-Kt_0} + K \int_{0}^{t} \left|\frac{P^{n}({\left\lfloor {ns} \right\rfloor })}
{n}-p(s)\right| {\text{d}} s ,
\end{align}
by the Lipschitz property of ν on ![]() $\mathcal {U}$. Hence, by Gronwall’s lemma, on the event Ωn,δ, sup0≤t≤t0^Tn ⌊Pn(nt)/n − p(t)⌋ ≤ δ. The result follows.
$\mathcal {U}$. Hence, by Gronwall’s lemma, on the event Ωn,δ, sup0≤t≤t0^Tn ⌊Pn(nt)/n − p(t)⌋ ≤ δ. The result follows.
We begin with a preparatory lemma.
Lemma 3.1
For t < 1 and 0 ≤ i ≤ ⌊nt⌋, we have
where ![]() ${\sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}|E_{U,1}^n(i)|}, {\sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}|E_{U,2}^n(i)|}$, and
${\sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}|E_{U,1}^n(i)|}, {\sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}|E_{U,2}^n(i)|}$, and ![]() ${({n}/{\alpha(n)}) \sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}|E_{V}^{n}(i)|}$ all converge to 0 in L 2 as n → ∞.
${({n}/{\alpha(n)}) \sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}|E_{V}^{n}(i)|}$ all converge to 0 in L 2 as n → ∞.
Proof. Let us note that
Having in mind that in each step we remove at most one vertex, for 0 ≤ i ≤ ⌊nt⌋, we have Un(i) ≥ n − i, and so
which converges to 0 in L 2 as n → ∞ by Lemma 2.1. A very similar argument shows that ![]() ${\sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}|E_{U,2}^n(i)|}$ converges to 0 in L 2 as n → ∞.
${\sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}|E_{U,2}^n(i)|}$ converges to 0 in L 2 as n → ∞.
Turning now to Vn, we see that
Letting
we have
and so Lemma 2.1 implies that ![]() $\sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}({n}/{\alpha(n)})|E_{V}^n(i)| \to 0$ in L 2 as n → ∞.
$\sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}({n}/{\alpha(n)})|E_{V}^n(i)| \to 0$ in L 2 as n → ∞.
Lemma 3.2
Let t < 1. Then, as n → ∞, we have
If, in addition, we assume that α(n) → ∞ as n → ∞, then
 \begin{equation}
\sup _{0 \leq i \leq\lfloor n t\rfloor}\left|\frac{V^{n}(i)}{\alpha(n)}-\left(1-\frac{i}{n}\right)^{4 / 3}\right| \stackrel{\mathrm{p}}{\rightarrow} 0.
\end{equation}
\begin{equation}
\sup _{0 \leq i \leq\lfloor n t\rfloor}\left|\frac{V^{n}(i)}{\alpha(n)}-\left(1-\frac{i}{n}\right)^{4 / 3}\right| \stackrel{\mathrm{p}}{\rightarrow} 0.
\end{equation}
Proof. Having in mind the size of expected increments given by Lemma 3.1, and Un(0) = n and Vn(0) = α(n), the candidate for the fluid limit is the solution to the system of differential equations given by
and the initial condition u(0) = 1, v(0) = 1. The solution is given by u(s) = 1 − s, v(s) = (1 − s)4/3. We observe that u(s) and v(s) remain bounded away from 0 for all 0 ≤ s ≤ t.
Let ![]() $T^n_{U} = \inf\{s \ge 0\colon U^n({\left\lfloor {ns} \right\rfloor }) = 0\}$. Since Un(i) ≥ n − i, it is clear that
$T^n_{U} = \inf\{s \ge 0\colon U^n({\left\lfloor {ns} \right\rfloor }) = 0\}$. Since Un(i) ≥ n − i, it is clear that ![]() $T^n_U \ge 1$ for all n and so, in particular,
$T^n_U \ge 1$ for all n and so, in particular, ![]() $T_U^n > t$. For i ≥ 0, let
$T_U^n > t$. For i ≥ 0, let ![]() ${(M_U^n(i))_{i \ge 0}}$ be the standard martingale associated with Un. By Lemma 3.1, we have, for 0
${(M_U^n(i))_{i \ge 0}}$ be the standard martingale associated with Un. By Lemma 3.1, we have, for 0
 $\left| \sum_{j=0}^{{\left\lfloor {ns} \right\rfloor }-1} \frac{\mathbb {E}[{U^n(j+1)-U^n(j) \mid
\mathcal {F}_j^n}}{n}] + \int_0^s {\text{d}} u \right| \le
\sup_{0\leq{s}\leq{t}}\left| \frac{{\left\lfloor {ns} \right\rfloor }}{n}- s \right| + t \sup_{0 \le
i \le {\left\lfloor {nt} \right\rfloor }} |E^n_{U,1}(i)|,$
$\left| \sum_{j=0}^{{\left\lfloor {ns} \right\rfloor }-1} \frac{\mathbb {E}[{U^n(j+1)-U^n(j) \mid
\mathcal {F}_j^n}}{n}] + \int_0^s {\text{d}} u \right| \le
\sup_{0\leq{s}\leq{t}}\left| \frac{{\left\lfloor {ns} \right\rfloor }}{n}- s \right| + t \sup_{0 \le
i \le {\left\lfloor {nt} \right\rfloor }} |E^n_{U,1}(i)|,$
which converges in probability to 0 as n → ∞. Moreover,
 $\mathbb {E}{M_U^n(i)^2} = \mathbb {E}\Biggl[\sum_{j=0}^{i-1} \mathrm{var}\;(U^n(j+1) - U^n(j) \mid
\mathcal {F}_j^n)\Biggr] \le i \Big(1 + \mathbb {E}\Big[{\sup_{0 \le j \le i}
|E_{U,2}^n(j)|}\Big]\Big),$
$\mathbb {E}{M_U^n(i)^2} = \mathbb {E}\Biggl[\sum_{j=0}^{i-1} \mathrm{var}\;(U^n(j+1) - U^n(j) \mid
\mathcal {F}_j^n)\Biggr] \le i \Big(1 + \mathbb {E}\Big[{\sup_{0 \le j \le i}
|E_{U,2}^n(j)|}\Big]\Big),$
and so, by Lemma 3.1, we have
Hence, by Proposition 3.1, ![]() $\sup_{0 \le s \le t} |{U^n(\left\lfloor {nt} \right\rfloor)}/{n} - u(s)| \underrightarrow{\rm P} 0$. We now turn to Vn. Let us first deal with the second moment of the standard martingale
$\sup_{0 \le s \le t} |{U^n(\left\lfloor {nt} \right\rfloor)}/{n} - u(s)| \underrightarrow{\rm P} 0$. We now turn to Vn. Let us first deal with the second moment of the standard martingale ![]() $M_V^n$. We have
$M_V^n$. We have
 \begin{align}
\mathbb {E}[{M_V^n(i)^2}] & = \mathbb {E}\Biggl[{\sum_{j=0}^{i-1} \mathrm{var}\;({V^n(j+1) - V^n(j)
\mid \mathcal {F}_j^n})}\Biggr]
\\
& \le i \,
\mathbb {E}\Biggl[{\sup_{0\leq{j}\leq{i}}{\biggl({\left|{\frac{4V^{n}(j)}
{3U^{n}(j)}} \right|+|{E^{n}_{V}(j)}|}\biggr)}}\Biggr].
\end{align}
\begin{align}
\mathbb {E}[{M_V^n(i)^2}] & = \mathbb {E}\Biggl[{\sum_{j=0}^{i-1} \mathrm{var}\;({V^n(j+1) - V^n(j)
\mid \mathcal {F}_j^n})}\Biggr]
\\
& \le i \,
\mathbb {E}\Biggl[{\sup_{0\leq{j}\leq{i}}{\biggl({\left|{\frac{4V^{n}(j)}
{3U^{n}(j)}} \right|+|{E^{n}_{V}(j)}|}\biggr)}}\Biggr].
\end{align}
Since ![]() ${4V^{n}(j)}/{(3U^{n}(j))}\leq{{4\alpha(n)}/{(3(n-j))}}$, Lemma 3.1 gives
${4V^{n}(j)}/{(3U^{n}(j))}\leq{{4\alpha(n)}/{(3(n-j))}}$, Lemma 3.1 gives ![]() $\mathbb {E}{M_V^n({\left\lfloor {nt} \right\rfloor })^2}/\alpha(n)^2\to 0$. Turning now to the drift, we have
$\mathbb {E}{M_V^n({\left\lfloor {nt} \right\rfloor })^2}/\alpha(n)^2\to 0$. Turning now to the drift, we have
 \begin{align}
&\sup_{0\leq{s}\leq{t}}\left| \sum_{j=0}^{\left\lfloor {ns} \right\rfloor - 1}
\frac{\mathbb {E}[{V^{n}(j+1)-V^{n}(j) \mid \mathcal {F}^{n}_j}]}{\alpha(n)}+
\int_0^s \frac{4v(r)}{3u(r)} {\text{d}} r \right|\\
&\quad\quad \le \sup_{0\leq{s}\leq{t}}\left| \int_{0}^{\left\lfloor {ns} \right\rfloor/n} \bigg(
\frac{4V^{n}(\left\lfloor {nr} \right\rfloor)/\alpha(n)}{3U^{n}(\left\lfloor {nr} \right\rfloor)/n} - \frac{4v(r)}{3u(r)}
\bigg) {\text{d}} r \right| + \sup_{0 \le s \le t} \left|
\int_{\left\lfloor {ns} \right\rfloor/n}^s{\frac{4v(r)}{3u(r)}}{\text{d}} r \right|
\\
& \quad\quad + \frac{nt}{\alpha(n)} \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} |E_V^n(i)|.
\end{align}
\begin{align}
&\sup_{0\leq{s}\leq{t}}\left| \sum_{j=0}^{\left\lfloor {ns} \right\rfloor - 1}
\frac{\mathbb {E}[{V^{n}(j+1)-V^{n}(j) \mid \mathcal {F}^{n}_j}]}{\alpha(n)}+
\int_0^s \frac{4v(r)}{3u(r)} {\text{d}} r \right|\\
&\quad\quad \le \sup_{0\leq{s}\leq{t}}\left| \int_{0}^{\left\lfloor {ns} \right\rfloor/n} \bigg(
\frac{4V^{n}(\left\lfloor {nr} \right\rfloor)/\alpha(n)}{3U^{n}(\left\lfloor {nr} \right\rfloor)/n} - \frac{4v(r)}{3u(r)}
\bigg) {\text{d}} r \right| + \sup_{0 \le s \le t} \left|
\int_{\left\lfloor {ns} \right\rfloor/n}^s{\frac{4v(r)}{3u(r)}}{\text{d}} r \right|
\\
& \quad\quad + \frac{nt}{\alpha(n)} \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} |E_V^n(i)|.
\end{align}
The penultimate term on the right-hand side clearly tends to 0, and the last term converges to 0 in probability by Lemma 3.1. We have
 \begin{align}
& \sup_{0\leq{s}\leq{t}}\left| \int_{0}^{\left\lfloor {ns} \right\rfloor/n} \bigg(
\frac{4V^{n}(\left\lfloor {nr} \right\rfloor)/\alpha(n)}{3U^{n}(\left\lfloor {nr} \right\rfloor)/n} - \frac{4v(r)}{3u(r)}
\bigg) {\text{d}} r \right|\\
&\quad\quad \le \int_{0}^{{\left\lfloor {nt} \right\rfloor }/n} \! \frac{4V^{n}(\left\lfloor {ns} \right\rfloor)/\alpha(n)}{3u(s)}
{\Bigg|{\frac{u(s)}{U^{n}(\left\lfloor {ns} \right\rfloor)/n}}-1\Bigg|}{\text{d}} s + \int_{0}^{{\left\lfloor {nt} \right\rfloor }/n} \frac{4}{3u(s)}
\Bigg|{\frac{V^{n}(\left\lfloor {ns} \right\rfloor)}{\alpha(n)}-v(s)}\Bigg|{\text{d}} s
\\
&\quad\quad \le \frac{4}{3(1-t)} \sup_{0 \le s \le t} \left|
\frac{u(s)}{U^n(\left\lfloor {ns} \right\rfloor)/n} - 1 \right| + \frac{4}{3(1-t)} \int_0^t
\left| {\frac{V^{n}(\left\lfloor {ns} \right\rfloor)}{\alpha(n)}-v(s)}\right|{\text{d}} s.
\end{align}
\begin{align}
& \sup_{0\leq{s}\leq{t}}\left| \int_{0}^{\left\lfloor {ns} \right\rfloor/n} \bigg(
\frac{4V^{n}(\left\lfloor {nr} \right\rfloor)/\alpha(n)}{3U^{n}(\left\lfloor {nr} \right\rfloor)/n} - \frac{4v(r)}{3u(r)}
\bigg) {\text{d}} r \right|\\
&\quad\quad \le \int_{0}^{{\left\lfloor {nt} \right\rfloor }/n} \! \frac{4V^{n}(\left\lfloor {ns} \right\rfloor)/\alpha(n)}{3u(s)}
{\Bigg|{\frac{u(s)}{U^{n}(\left\lfloor {ns} \right\rfloor)/n}}-1\Bigg|}{\text{d}} s + \int_{0}^{{\left\lfloor {nt} \right\rfloor }/n} \frac{4}{3u(s)}
\Bigg|{\frac{V^{n}(\left\lfloor {ns} \right\rfloor)}{\alpha(n)}-v(s)}\Bigg|{\text{d}} s
\\
&\quad\quad \le \frac{4}{3(1-t)} \sup_{0 \le s \le t} \left|
\frac{u(s)}{U^n(\left\lfloor {ns} \right\rfloor)/n} - 1 \right| + \frac{4}{3(1-t)} \int_0^t
\left| {\frac{V^{n}(\left\lfloor {ns} \right\rfloor)}{\alpha(n)}-v(s)}\right|{\text{d}} s.
\end{align}
The first term on the right-hand side converges to 0 in probability. So following the argument in the proof of Proposition 3.1, we easily obtain ![]() $\sup_{0\leq{s}\leq{t}}|{{V^{n}(\left\lfloor {ns} \right\rfloor)}/{\alpha(n)}-v(s)}| \underrightarrow{\rm P} 0$.
$\sup_{0\leq{s}\leq{t}}|{{V^{n}(\left\lfloor {ns} \right\rfloor)}/{\alpha(n)}-v(s)}| \underrightarrow{\rm P} 0$.
4. Fluid limit for  $\alpha(n) \gg \sqrt{n}$
$\alpha(n) \gg \sqrt{n}$
In the case where ![]() $\alpha(n) \gg \sqrt{n}$, we will also prove fluid limits for Xn and Nn.
$\alpha(n) \gg \sqrt{n}$, we will also prove fluid limits for Xn and Nn.
Theorem 4.1
Fix t ∈ (0, 1). For ![]() $\alpha(n)\gg\sqrt{n}$, as n→ ∞, we have
$\alpha(n)\gg\sqrt{n}$, as n→ ∞, we have
To this end, we again study the expected increments.
Lemma 4.1
For t < 1 and 0 ≤ i ≤ ⌊nt⌋, we have
 \begin{gather}
\mathbb {E}[{X^n(i+1) - X^n(i) \mid \mathcal {F}^n_i}] =
2{{\bf 1}_{\{X^n(i)=0\}}}+\frac{2\alpha(n)(1-i/n)^{4/3}-2X^n(i)}
{3(n-i)}+E_{X,1}^{n}(i),\\
\mathbb {E}[{(X^n(i+1) - X^n(i))^2 \mid \mathcal {F}^n_i}] =
4{{\bf 1}_{\{X^n(i)=0\}}}+1+E_{X,2}^n(i),\\
\mathbb {E}[{N^n(i+1) - N^n(i) \mid \mathcal {F}^n_i}]=\mathbb {E}[{(N^n(i+1) - N^n(i))^2 \mid
\mathcal {F}^n_i}]= \frac{X^n(i)}{3(n-i)}+E_N^{n}(i),
\end{gather}
\begin{gather}
\mathbb {E}[{X^n(i+1) - X^n(i) \mid \mathcal {F}^n_i}] =
2{{\bf 1}_{\{X^n(i)=0\}}}+\frac{2\alpha(n)(1-i/n)^{4/3}-2X^n(i)}
{3(n-i)}+E_{X,1}^{n}(i),\\
\mathbb {E}[{(X^n(i+1) - X^n(i))^2 \mid \mathcal {F}^n_i}] =
4{{\bf 1}_{\{X^n(i)=0\}}}+1+E_{X,2}^n(i),\\
\mathbb {E}[{N^n(i+1) - N^n(i) \mid \mathcal {F}^n_i}]=\mathbb {E}[{(N^n(i+1) - N^n(i))^2 \mid
\mathcal {F}^n_i}]= \frac{X^n(i)}{3(n-i)}+E_N^{n}(i),
\end{gather}
where ![]() $ ({n}/{(\alpha(n) \vee \sqrt{n})}) {\sup_{0\leq{i}\leq{\left\lfloor {nt} \right\rfloor}}}|E_{X,1}^{n}(i)| {\underrightarrow {\rm P}} {0} $,
$ ({n}/{(\alpha(n) \vee \sqrt{n})}) {\sup_{0\leq{i}\leq{\left\lfloor {nt} \right\rfloor}}}|E_{X,1}^{n}(i)| {\underrightarrow {\rm P}} {0} $, ![]() ${\sup_{0\leq{i}\leq{\left\lfloor {nt} \right\rfloor}}}|E_{X,2}^{n}(i)| \to {0}$ in L 2, and
${\sup_{0\leq{i}\leq{\left\lfloor {nt} \right\rfloor}}}|E_{X,2}^{n}(i)| \to {0}$ in L 2, and ![]() $ ({n}/{(\alpha(n) \vee \sqrt{n})}) {\sup_{0\leq{i}\leq{\left\lfloor {nt} \right\rfloor}}}|E_N^{n}(i)| \to 0 $ in L 2 as n→∞.
$ ({n}/{(\alpha(n) \vee \sqrt{n})}) {\sup_{0\leq{i}\leq{\left\lfloor {nt} \right\rfloor}}}|E_N^{n}(i)| \to 0 $ in L 2 as n→∞.
Proof. By (2.1), we have
 \begin{align}
&\mathbb {E}[{X^n(i+1) - X^n(i) \mid \mathcal {F}_i^n}]
\\
&\quad\quad = 2{{\bf 1}_{\{X^n(i)=0\}}}+\frac{2\alpha(n)(1-i/n)^{4/3}-2X^n(i)}{3(n-i)}
\\
&\quad\quad +\frac{2V^n(i)-2\alpha(n)(1-i/n)^{4/3}+ 2{{\bf 1}_{\{X^n(i)>0\}}}}{3(n-i)}
\\
&\quad\quad
+\frac{2V^n(i)-2X^n(i)+2{{\bf 1}_{\{X^n(i)>0\}}}}{3(n-i)}\end{align}
\begin{align}
&\mathbb {E}[{X^n(i+1) - X^n(i) \mid \mathcal {F}_i^n}]
\\
&\quad\quad = 2{{\bf 1}_{\{X^n(i)=0\}}}+\frac{2\alpha(n)(1-i/n)^{4/3}-2X^n(i)}{3(n-i)}
\\
&\quad\quad +\frac{2V^n(i)-2\alpha(n)(1-i/n)^{4/3}+ 2{{\bf 1}_{\{X^n(i)>0\}}}}{3(n-i)}
\\
&\quad\quad
+\frac{2V^n(i)-2X^n(i)+2{{\bf 1}_{\{X^n(i)>0\}}}}{3(n-i)}\end{align}
 \begin{align}\quad\quad\times{\Biggl(
\biggl({1+\frac{3U^n(i)-3(n-i)+4V^n(i)+X^n(i)-
{{\bf 1}_{\{X^n(i)>0\}}}}{3(n-i)}}\biggr)^{-1} - 1\Biggr)}
\\
=:\,2{{\bf 1}_{\{X^n(i)=0\}}}+\frac{2\alpha(n)(1-i/n)^{4/3}-2X^n(i)}{3(n-i)}+
E_{X,1}^{n}(i).
\end{align}
\begin{align}\quad\quad\times{\Biggl(
\biggl({1+\frac{3U^n(i)-3(n-i)+4V^n(i)+X^n(i)-
{{\bf 1}_{\{X^n(i)>0\}}}}{3(n-i)}}\biggr)^{-1} - 1\Biggr)}
\\
=:\,2{{\bf 1}_{\{X^n(i)=0\}}}+\frac{2\alpha(n)(1-i/n)^{4/3}-2X^n(i)}{3(n-i)}+
E_{X,1}^{n}(i).
\end{align}
By the fluid limit for Vn in Lemma 3.2, we have
 $\frac{n}{\alpha(n)} \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} \left|
\frac{2V^n(i)-2\alpha(n)(1-i/n)^{4/3}+ 2{{\bf 1}_{\{X^n(i)>0\}}}}{3(n-i)} \right|
\underrightarrow {\rm P} 0.$
$\frac{n}{\alpha(n)} \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} \left|
\frac{2V^n(i)-2\alpha(n)(1-i/n)^{4/3}+ 2{{\bf 1}_{\{X^n(i)>0\}}}}{3(n-i)} \right|
\underrightarrow {\rm P} 0.$
Since (1 + x)−1 ≥ 1− x for x > 0, and Un(i) ≥ n−i, we have
 \begin{align}
\Delta^n &\ := \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} \left|{\biggl({1+\frac{3U^n(i)
-3(n-i)+4V^n(i)+X^n(i)-{{\bf 1}_{\{X^n(i)>0\}}}}{3(n-i)}}\biggr)^{-1}-1}\right|
\\
&\, \le \frac{1}{3(1-t)} \biggl(3\sup_{0\le i \le {\left\lfloor {nt} \right\rfloor }}
\left|{\frac{U^n(i)}{n}- \biggl(1-\frac{i}{n} \biggr)
}\right|+\frac{4\alpha(n)}{n}+{{\frac{1+ \sup_{0\le i \le
t}{X^n({i})}}{n}}} \biggr).\end{align}
\begin{align}
\Delta^n &\ := \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} \left|{\biggl({1+\frac{3U^n(i)
-3(n-i)+4V^n(i)+X^n(i)-{{\bf 1}_{\{X^n(i)>0\}}}}{3(n-i)}}\biggr)^{-1}-1}\right|
\\
&\, \le \frac{1}{3(1-t)} \biggl(3\sup_{0\le i \le {\left\lfloor {nt} \right\rfloor }}
\left|{\frac{U^n(i)}{n}- \biggl(1-\frac{i}{n} \biggr)
}\right|+\frac{4\alpha(n)}{n}+{{\frac{1+ \sup_{0\le i \le
t}{X^n({i})}}{n}}} \biggr).\end{align}
The quantity on the right-hand side is bounded above by 4/(1 − t). Using Lemma 2.1 (which states that Xn is of smaller order than n) and the fluid limit for Un from Lemma 3.2, we see that Δn converges to 0 in probability and, since it is bounded, also in L 4.
By Lemma 2.1, ![]() $ ({1}/{(\alpha(n) \vee \sqrt{n})}) \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} (X^n(i) + V^n(i)) $ is tight in n. It follows that
$ ({1}/{(\alpha(n) \vee \sqrt{n})}) \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} (X^n(i) + V^n(i)) $ is tight in n. It follows that ![]() $ ({n}/{(\alpha(n) \vee \sqrt{n})}) \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} {(2V^n(i) - 2X^n(i) + 2 {{\bf 1}_{\{X^n(i) > 0\}}})}/{(3(n-i))} $ is also tight, and so
$ ({n}/{(\alpha(n) \vee \sqrt{n})}) \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} {(2V^n(i) - 2X^n(i) + 2 {{\bf 1}_{\{X^n(i) > 0\}}})}/{(3(n-i))} $ is also tight, and so ![]() ${({n}/{(\alpha(n) \vee \sqrt{n})}) \sup_{0 \le i \le \left\lfloor {nt} \right\rfloor{\left\lfloor {nt} \right\rfloor }} |E_{X,1}^n(i)|\underrightarrow{\rm P}} 0$.
${({n}/{(\alpha(n) \vee \sqrt{n})}) \sup_{0 \le i \le \left\lfloor {nt} \right\rfloor{\left\lfloor {nt} \right\rfloor }} |E_{X,1}^n(i)|\underrightarrow{\rm P}} 0$.
For the second moment, rewriting (2.3), we have
 \begin{align}
& \mathbb {E}[{(X^n(i+1) - X^n(i))^2 \mid \mathcal {F}^n_i}]
\\
&\quad\quad = 4{{\bf 1}_{\{X^n(i)=0\}}}+1+\frac{6V^n(i)+8V^n(i){{\bf 1}_{\{X^n(i)=0\}}}+
3X^n(i)-3{{\bf 1}_{\{X^n(i)>0}}}{3U^n(i)+4V^n(i)+X^n(i)-{{\bf 1}_{\{X^n(i)>0\}}}}
\\
& \quad\quad =\!:\,4{{\bf 1}_{\{X^n(i)=0\}}}+1 + E_{X,2}^n(i).
\end{align}
\begin{align}
& \mathbb {E}[{(X^n(i+1) - X^n(i))^2 \mid \mathcal {F}^n_i}]
\\
&\quad\quad = 4{{\bf 1}_{\{X^n(i)=0\}}}+1+\frac{6V^n(i)+8V^n(i){{\bf 1}_{\{X^n(i)=0\}}}+
3X^n(i)-3{{\bf 1}_{\{X^n(i)>0}}}{3U^n(i)+4V^n(i)+X^n(i)-{{\bf 1}_{\{X^n(i)>0\}}}}
\\
& \quad\quad =\!:\,4{{\bf 1}_{\{X^n(i)=0\}}}+1 + E_{X,2}^n(i).
\end{align}
But then ![]() $\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} |E_{X,2}^n(i)| \leq{{(14\alpha(n)+ 3\sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}X^n(i))}/{(3n(1-t))}}$, which converges to 0 in probability and in L 4, by Lemma 2.1. Turning now to the increments of Nn, we have
$\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} |E_{X,2}^n(i)| \leq{{(14\alpha(n)+ 3\sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}X^n(i))}/{(3n(1-t))}}$, which converges to 0 in probability and in L 4, by Lemma 2.1. Turning now to the increments of Nn, we have
 \begin{align}
& \mathbb {E}[{N^n(i+1) - N^n(i) \mid \mathcal {F}^n_i}]
\\
&\quad\quad{\begin{gathered} =
\frac{X^n(i)}{3(n-i)}+\frac{X^n(i)}{3(n-i)}\biggl({{\biggl({1+
\frac{3U^n(i)-3(n-i)+4V^n(i)+X^n(i)-{{\bf 1}_{\{X^n(i)>0\}}} }{3(n-i)}}\biggr)^{-1}}
-1}\biggr)\end{gathered}}
\\
&\quad\quad{\begin{gathered} +\frac{3U^{n}(i)-2{{\bf 1}_{\{X^{n}(i)>0\}}}
(3U^{n}(i)+4V^{n}(i)+X^{n}(i)-3)} {2(3U^{n}(i)+4V^{n}(i)+X^{n}(i)
-{{\bf 1}_{\{X^{n}(i)>0\}}})(3U^{n}(i)+4V^{n}(i)+X^{n}(i) - {{\bf 1}_{\{X^{n}(i)>0\}}} -
2)}\end{gathered}}
\\
&\quad\quad =\!: \frac{X^n(i)}{3(n-i)} + E_N^{n}(i).
\end{align}
\begin{align}
& \mathbb {E}[{N^n(i+1) - N^n(i) \mid \mathcal {F}^n_i}]
\\
&\quad\quad{\begin{gathered} =
\frac{X^n(i)}{3(n-i)}+\frac{X^n(i)}{3(n-i)}\biggl({{\biggl({1+
\frac{3U^n(i)-3(n-i)+4V^n(i)+X^n(i)-{{\bf 1}_{\{X^n(i)>0\}}} }{3(n-i)}}\biggr)^{-1}}
-1}\biggr)\end{gathered}}
\\
&\quad\quad{\begin{gathered} +\frac{3U^{n}(i)-2{{\bf 1}_{\{X^{n}(i)>0\}}}
(3U^{n}(i)+4V^{n}(i)+X^{n}(i)-3)} {2(3U^{n}(i)+4V^{n}(i)+X^{n}(i)
-{{\bf 1}_{\{X^{n}(i)>0\}}})(3U^{n}(i)+4V^{n}(i)+X^{n}(i) - {{\bf 1}_{\{X^{n}(i)>0\}}} -
2)}\end{gathered}}
\\
&\quad\quad =\!: \frac{X^n(i)}{3(n-i)} + E_N^{n}(i).
\end{align}
For 0 ≤ i ≤ ⌊nt⌋, we have
 \begin{align}
&\left|{\frac{3U^{n}(i)-2{{\bf 1}_{\{X^{n}(i)>0\}}}(3U^{n}(i)+4V^{n}(i)+X^{n}(i)
-3)}{2(3U^{n}(i)+4V^{n}(i)+X^{n}(i)-{{\bf 1}_{\{X^{n}(i)>0\}}})(3U^{n}(i)+
4V^{n}(i)+X^{n}(i)-{{\bf 1}_{\{X^{n}(i)>0\}}}-2)}}\right|
\\
&\quad\quad\le {\frac{3}{2n(1-t)}}.
\end{align}
\begin{align}
&\left|{\frac{3U^{n}(i)-2{{\bf 1}_{\{X^{n}(i)>0\}}}(3U^{n}(i)+4V^{n}(i)+X^{n}(i)
-3)}{2(3U^{n}(i)+4V^{n}(i)+X^{n}(i)-{{\bf 1}_{\{X^{n}(i)>0\}}})(3U^{n}(i)+
4V^{n}(i)+X^{n}(i)-{{\bf 1}_{\{X^{n}(i)>0\}}}-2)}}\right|
\\
&\quad\quad\le {\frac{3}{2n(1-t)}}.
\end{align}
Hence,
We have Δn→ 0 in L 4. Moreover, ![]() $ ({1}/{(\alpha(n) \vee \sqrt{n})}) \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} X^n(i) $ is bounded in L 4, and so, by the Cauchy–Schwarz inequality, we obtain
$ ({1}/{(\alpha(n) \vee \sqrt{n})}) \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} X^n(i) $ is bounded in L 4, and so, by the Cauchy–Schwarz inequality, we obtain ![]() $ ({n}/{(\alpha(n) \vee \sqrt{n})}) \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} |E_N^n(i)| \to 0 $ in L 2, as desired.
$ ({n}/{(\alpha(n) \vee \sqrt{n})}) \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} |E_N^n(i)| \to 0 $ in L 2, as desired.
Before we can proceed to the proof of Theorem 4.1, we need some technical lemmas to deal with the fact that Xn reflects off 0. Let γ n = inf{i ≥ 0: Xn(i) ≥ Vn(i)}.
Lemma 4.2
Fix ![]() $t \in(\tfrac12, 1)$. Then there exists t 0 ∈ (0, t) sufficiently small that
$t \in(\tfrac12, 1)$. Then there exists t 0 ∈ (0, t) sufficiently small that ![]() $\mathcal {P}(\gamma^n < t_0 n) \to 0$ as n → ∞.
$\mathcal {P}(\gamma^n < t_0 n) \to 0$ as n → ∞.
Proof. Let γ̃ n = inf{i ≥ 0: Xn(i) ≥ 3α(n)/8}. Observe that Vn is decreasing and that if s 0 = 1 − 2−3/4 ≈ 0.405 then ![]() $ (1-s_0)^{4/3} = {\tfrac12} > {\tfrac38} $. Then, by Lemma 3.2, we have ℙ(Vn(⌊ns 0⌋ > 3α(n)/8)) → 1 as n → ∞. So if we can show that there exists s 1 ∈ (0, t) such that ℙ(ỹn < ns 1) → 1 as n → ∞ then, setting t 0 = s 0 ∧ s 1, we obtain ℙ(yn < nt 0) → 0. So it remains to prove that there exists such an s 1.
$ (1-s_0)^{4/3} = {\tfrac12} > {\tfrac38} $. Then, by Lemma 3.2, we have ℙ(Vn(⌊ns 0⌋ > 3α(n)/8)) → 1 as n → ∞. So if we can show that there exists s 1 ∈ (0, t) such that ℙ(ỹn < ns 1) → 1 as n → ∞ then, setting t 0 = s 0 ∧ s 1, we obtain ℙ(yn < nt 0) → 0. So it remains to prove that there exists such an s 1.
The time inhomogeneity of the process Xn makes explicit calculations awkward. We instead couple Xn with a simpler process An. If An(i) = 0 then An(i + 1) = 1. If An(i) > 0 then
 $A^n(i+1) - A^n(i) =
\begin{cases}
-1 & \text{ with probability } \dfrac{1}{2},
\\
+1 & \text{ with probability } \dfrac{1}{2} - \dfrac{4 \alpha(n)}{3n(1-t)},
\\
+2 & \text{ with probability } \dfrac{4\alpha(n)}{3n(1-t)}.
\end{cases}$
$A^n(i+1) - A^n(i) =
\begin{cases}
-1 & \text{ with probability } \dfrac{1}{2},
\\
+1 & \text{ with probability } \dfrac{1}{2} - \dfrac{4 \alpha(n)}{3n(1-t)},
\\
+2 & \text{ with probability } \dfrac{4\alpha(n)}{3n(1-t)}.
\end{cases}$
(We implicitly take n sufficiently large that ![]() $4 \alpha(n)/(3n(1-t)) < \tfrac12$.) We set An(0) = 0. It is straightforward to see that we may couple Xn and An in such a way that Xn(i) ≤ 3+ An(i) for all 0 ≤ i ≤ ⌊nt⌋. Let λ n = inf{i ≥ 0: An(i) ≥ 3α(n)/8 − 3}. Then we certainly have λ n ≤ γ̃ n. So we will find an s 1 ∈ (0, t) such that ℙ(λn < ns 1) → 0. For simplicity, write b = ˪3α(n)/8˩ − 3 for the upper barrier and d = 4α(n)/(3n(1 − t)) for the drift. The quantity
$4 \alpha(n)/(3n(1-t)) < \tfrac12$.) We set An(0) = 0. It is straightforward to see that we may couple Xn and An in such a way that Xn(i) ≤ 3+ An(i) for all 0 ≤ i ≤ ⌊nt⌋. Let λ n = inf{i ≥ 0: An(i) ≥ 3α(n)/8 − 3}. Then we certainly have λ n ≤ γ̃ n. So we will find an s 1 ∈ (0, t) such that ℙ(λn < ns 1) → 0. For simplicity, write b = ˪3α(n)/8˩ − 3 for the upper barrier and d = 4α(n)/(3n(1 − t)) for the drift. The quantity
is calculated via a standard calculation in Lemma A.1 in Appendix A. Substituting the given values of b and d in the (lengthy) expression there, we obtain 1 − h 1 ∼ 8α(n)/(3n(1 − t)) as n → ∞. By the strong Markov property, the random walk An visits 0 a Geometric(1 − h 1) number of times before going above 3α(n)/8 − 3, and so
 $\frac{1}{\alpha(n)} \mathbb {E}\Biggl[{\sum_{i=0}^{\lambda_n-1}{{\bf 1}_{\{A^n(i) = 0\}}}}\Biggr] \sim \frac{3n(1-t)}{8 \alpha(n)^2} \to 0,$
$\frac{1}{\alpha(n)} \mathbb {E}\Biggl[{\sum_{i=0}^{\lambda_n-1}{{\bf 1}_{\{A^n(i) = 0\}}}}\Biggr] \sim \frac{3n(1-t)}{8 \alpha(n)^2} \to 0,$
since ![]() $\alpha(n) \gg \sqrt{n}$.
$\alpha(n) \gg \sqrt{n}$.
Now note that the standard martingale for An is
 $M^n_{A}(i) = A^n(i) -\frac{4 \alpha(n) i}{3n(1-t)} - \sum_{j=0}^{i-1} \bigg(1 - \frac{4 \alpha(n)}{3n(1-t)} \bigg) {{\bf 1}_{\{A^n(j) = 0\}}}.$
$M^n_{A}(i) = A^n(i) -\frac{4 \alpha(n) i}{3n(1-t)} - \sum_{j=0}^{i-1} \bigg(1 - \frac{4 \alpha(n)}{3n(1-t)} \bigg) {{\bf 1}_{\{A^n(j) = 0\}}}.$
Let ![]() $\mathcal {F}^{n}_A(j)$ be the natural filtration of An. We have
$\mathcal {F}^{n}_A(j)$ be the natural filtration of An. We have
and so
for sufficiently large n. For any s > 0, then
 $\sup_{0 \le i \le \lambda_n \wedge \left\lfloor {ns} \right\rfloor} \left| \frac{A^n(i)}{\alpha(n)} - \frac{4 i}{3n(1-t)} \right| \le \frac{\sup_{0 \le i \le \left\lfloor {ns} \right\rfloor} |M^n_{A}(i)|}{\alpha(n)} + \frac{1}{\alpha(n)} \sum_{j=0}^{\lambda_n-1} {{\bf 1}_{\{A^n(i) = 0\}}}.$
$\sup_{0 \le i \le \lambda_n \wedge \left\lfloor {ns} \right\rfloor} \left| \frac{A^n(i)}{\alpha(n)} - \frac{4 i}{3n(1-t)} \right| \le \frac{\sup_{0 \le i \le \left\lfloor {ns} \right\rfloor} |M^n_{A}(i)|}{\alpha(n)} + \frac{1}{\alpha(n)} \sum_{j=0}^{\lambda_n-1} {{\bf 1}_{\{A^n(i) = 0\}}}.$
For any δ > 0, it then follows by using Doob’s L 2 inequality that
 \begin{align}
\mathbb {P}\biggl({\sup_{0 \le i \le \lambda_n \wedge \left\lfloor {ns} \right\rfloor} \bigg|
\frac{A^n(i)}{\alpha(n)} - \frac{4 i}{3n(1-t)} \bigg| > \delta}\biggr) &
\le 4 \frac{\mathbb {E}[M_{A}^n(\left\lfloor {ns} \right\rfloor)^2]}{\delta^2 \alpha(n)^2} +
\frac{1}{\delta \alpha(n)} \mathbb {E}\biggl[{\sum_{j=0}^{\lambda_n-1} {{\bf 1}_{\{A^n(i) =
0\}}}}\biggr]
\\
& \le \frac{8 \left\lfloor {ns} \right\rfloor}{\delta^2 \alpha(n)^2} + \frac{1}{\delta \alpha(n)}
\mathbb {E}\biggl[{\sum_{j=0}^{\lambda_n-1} {{\bf 1}_{\{A^n(i) = 0\}}}}\biggr]
\\
&\to 0 \quad\text{as} n \to \infty.
\end{align}
\begin{align}
\mathbb {P}\biggl({\sup_{0 \le i \le \lambda_n \wedge \left\lfloor {ns} \right\rfloor} \bigg|
\frac{A^n(i)}{\alpha(n)} - \frac{4 i}{3n(1-t)} \bigg| > \delta}\biggr) &
\le 4 \frac{\mathbb {E}[M_{A}^n(\left\lfloor {ns} \right\rfloor)^2]}{\delta^2 \alpha(n)^2} +
\frac{1}{\delta \alpha(n)} \mathbb {E}\biggl[{\sum_{j=0}^{\lambda_n-1} {{\bf 1}_{\{A^n(i) =
0\}}}}\biggr]
\\
& \le \frac{8 \left\lfloor {ns} \right\rfloor}{\delta^2 \alpha(n)^2} + \frac{1}{\delta \alpha(n)}
\mathbb {E}\biggl[{\sum_{j=0}^{\lambda_n-1} {{\bf 1}_{\{A^n(i) = 0\}}}}\biggr]
\\
&\to 0 \quad\text{as} n \to \infty.
\end{align}
Finally, if we take s 1 = 3(1 − t)/16 then ![]() $4{\rm{ }}\left\lfloor {n{s_1}} \right\rfloor /(3n(1 - t)) \le {\textstyle{1 \over 4}} < {\textstyle{3 \over 8}}$. Then, for
$4{\rm{ }}\left\lfloor {n{s_1}} \right\rfloor /(3n(1 - t)) \le {\textstyle{1 \over 4}} < {\textstyle{3 \over 8}}$. Then, for ![]() $\delta \in (0, \tfrac18)$,
$\delta \in (0, \tfrac18)$,
The result follows.
Proposition 4.1
For the t 0 ∈ (0, t) from Lemma 4.2, ![]() ${L^n(\left\lfloor{nt_0}\right\rfloor)}/{\alpha(n)}\underrightarrow{\rm P} 0$ as n → ∞.
${L^n(\left\lfloor{nt_0}\right\rfloor)}/{\alpha(n)}\underrightarrow{\rm P} 0$ as n → ∞.
Proof. We again make use of a coupling, this time to produce a lower bound: we define a process Dn such that Dn(i) ≤ Xn(i) for i ≤ γn − 1.
Conditionally on (Un(i), Vn(i), Xn(i), Dn(i)) = (u, v, x, d) with Dn(i) = d > 1, we let
 $D^n(i+1) - D^n(i) =
\begin{cases}
+2 & \text{ with probability } \dfrac{4(x-1){{\bf 1}_{\{x >
0\}}}}{2(3u+4v+(x-1){{\bf 1}_{\{x >
0\}}})},\\
+1 & \text{ with probability } \dfrac{3u + 4v - 4(x-1){{\bf 1}_{\{x > 0\}}}}
{2(3u+4v+(x-1){{\bf 1}_{\{x >
0\}}})},
\\
-1 & \text{ with probability } \dfrac{3u + 4v}{2(3u+4v+(x-1){{\bf 1}_{\{x > 0\}}})},
\\
-2 & \text{ with probability } \dfrac{2(x-1){{\bf 1}_{\{x >
0\}}}}{2(3u+4v+(x-1){{\bf 1}_{\{x > 0\}}})}.
\end{cases}$
$D^n(i+1) - D^n(i) =
\begin{cases}
+2 & \text{ with probability } \dfrac{4(x-1){{\bf 1}_{\{x >
0\}}}}{2(3u+4v+(x-1){{\bf 1}_{\{x >
0\}}})},\\
+1 & \text{ with probability } \dfrac{3u + 4v - 4(x-1){{\bf 1}_{\{x > 0\}}}}
{2(3u+4v+(x-1){{\bf 1}_{\{x >
0\}}})},
\\
-1 & \text{ with probability } \dfrac{3u + 4v}{2(3u+4v+(x-1){{\bf 1}_{\{x > 0\}}})},
\\
-2 & \text{ with probability } \dfrac{2(x-1){{\bf 1}_{\{x >
0\}}}}{2(3u+4v+(x-1){{\bf 1}_{\{x > 0\}}})}.
\end{cases}$
Conditionally on (Un(i), Vn(i), Xn(i), Dn(i)) = (u, v, x, d) with Dn(i) = d = 1, we let
 $D^n(i+1) - D^n(i) =
\begin{cases}
+2 & \text{ with probability } \dfrac{2(x-1)}{2(3u+4v+(x-1){{\bf 1}_{\{x > 0\}}})},
\\
+1 & \text{ with probability } \dfrac{3u + 4v - 2(x-1){{\bf 1}_{\{x >
0\}}}}{2(3u+4v+(x-1){{\bf 1}_{\{x > 0\}}})},
\\
-1 & \text{ with probability } \dfrac{3u + 4v+ 2(x-1){{\bf 1}_{\{x >
0\}}}}{2(3u+4v+(x-1){{\bf 1}_{\{x > 0\}}})}.
\end{cases}
$D^n(i+1) - D^n(i) =
\begin{cases}
+2 & \text{ with probability } \dfrac{2(x-1)}{2(3u+4v+(x-1){{\bf 1}_{\{x > 0\}}})},
\\
+1 & \text{ with probability } \dfrac{3u + 4v - 2(x-1){{\bf 1}_{\{x >
0\}}}}{2(3u+4v+(x-1){{\bf 1}_{\{x > 0\}}})},
\\
-1 & \text{ with probability } \dfrac{3u + 4v+ 2(x-1){{\bf 1}_{\{x >
0\}}}}{2(3u+4v+(x-1){{\bf 1}_{\{x > 0\}}})}.
\end{cases}
Conditionally on (Un(i), Vn(i), Xn(i), Dn(i)) = (u, v, x, d) with Dn(i) = d = 0, we let Dn(i + 1) = 1. Since we assume that i ≤ γ n − 1, it is straightforward to see that we may produce a coupling such that Dn(i) ≤ Xn(i).
Let ![]() $\tilde{L}^n(i) = 2 {\sum_{j=0}^{i-1}} {{\bf 1}_{\{D^n(j) = 0\}}}$, and observe that we have L̃n(γn ∧ ⌊nt 0⌋) ≥ Ln(γn ∧ ⌊nt 0⌋). But then, for any δ > 0,
$\tilde{L}^n(i) = 2 {\sum_{j=0}^{i-1}} {{\bf 1}_{\{D^n(j) = 0\}}}$, and observe that we have L̃n(γn ∧ ⌊nt 0⌋) ≥ Ln(γn ∧ ⌊nt 0⌋). But then, for any δ > 0,
By Lemma 4.2, we have ℙ (γn < ⌊nt 0⌋) → 0 and so it suffices to prove that the first term tends to 0.
We have
where (![]() $ (\mathcal {F}_D^n(i))_{i \ge 0} $ denotes the natural filtration of (Un, Vn, Xn, Dn). Also,
$ (\mathcal {F}_D^n(i))_{i \ge 0} $ denotes the natural filtration of (Un, Vn, Xn, Dn). Also,
 \begin{align}
\mathrm{var}\;(D^n(i+1) - D^n(i) \mid \mathcal {F}_D^n(i)) & \le 1 +
\frac{9\;(X^n(i) - {{\bf 1}_{\{X^n(i) > 0\}}}){{\bf 1}_{\{D^n(i) \ge 1\}}}}{3U^n(i) +
4V^n(i) + X^n(i) - {{\bf 1}_{\{X^n(i) > 0\}}}}
\\
& \le 1 + \frac{3 \alpha(n)}{n(1-s)}
\end{align}
\begin{align}
\mathrm{var}\;(D^n(i+1) - D^n(i) \mid \mathcal {F}_D^n(i)) & \le 1 +
\frac{9\;(X^n(i) - {{\bf 1}_{\{X^n(i) > 0\}}}){{\bf 1}_{\{D^n(i) \ge 1\}}}}{3U^n(i) +
4V^n(i) + X^n(i) - {{\bf 1}_{\{X^n(i) > 0\}}}}
\\
& \le 1 + \frac{3 \alpha(n)}{n(1-s)}
\end{align}
for i ≤ γn ∧ ⌊ns⌋. Hence, ![]() $\big(D^n(i) - {\sum_{j=0}^{i-1}}{{\bf 1}_{\{D^n(j)=0\}}} \big)_{i \ge 0}$ is a mean 0 martingale, with bounded steps and
$\big(D^n(i) - {\sum_{j=0}^{i-1}}{{\bf 1}_{\{D^n(j)=0\}}} \big)_{i \ge 0}$ is a mean 0 martingale, with bounded steps and
 $\sum_{j=0}^{i-1} \mathbb {E}\,[{(D^n(j+1) - D^n(j) - {{\bf 1}_{\{D^n(j) = 0\}}})^2
\mid \mathcal {F}^n_D(j)}] = i + E^{n}_{D}(i)$
$\sum_{j=0}^{i-1} \mathbb {E}\,[{(D^n(j+1) - D^n(j) - {{\bf 1}_{\{D^n(j) = 0\}}})^2
\mid \mathcal {F}^n_D(j)}] = i + E^{n}_{D}(i)$
for i ≤ γ n ∧ ⌊nt 0⌋, where ![]() ${\sup_{i \le \gamma^n \wedge \left\lfloor{nt_0}\right\rfloor}}({n}/{\alpha(n)}){\left\vert{E^{n}_{D}(i)}\right\vert}$ is bounded with high probability. By the martingale functional central limit theorem (see Theorem 1.4 of [Reference Ethier and Kurtz9, Section 7.1]), we then have, on the event {γ n ≥ ⌊nt 0⌋},
${\sup_{i \le \gamma^n \wedge \left\lfloor{nt_0}\right\rfloor}}({n}/{\alpha(n)}){\left\vert{E^{n}_{D}(i)}\right\vert}$ is bounded with high probability. By the martingale functional central limit theorem (see Theorem 1.4 of [Reference Ethier and Kurtz9, Section 7.1]), we then have, on the event {γ n ≥ ⌊nt 0⌋},
 $\frac{1}{\sqrt{n}\,} \Biggl(D^n(\left\lfloor{nu}\right\rfloor) -
\sum_{j=0}^{\left\lfloor{nu}-1\right\rfloor}{{\bf 1}_{\{D^n(j)=0\}}} \Biggr)_{0 \le u \le t_0} \underrightarrow {\rm D}
(W_u)_{0 \le u \le t_0},$
$\frac{1}{\sqrt{n}\,} \Biggl(D^n(\left\lfloor{nu}\right\rfloor) -
\sum_{j=0}^{\left\lfloor{nu}-1\right\rfloor}{{\bf 1}_{\{D^n(j)=0\}}} \Biggr)_{0 \le u \le t_0} \underrightarrow {\rm D}
(W_u)_{0 \le u \le t_0},$
where W is a standard Brownian motion. But we also have
 $\frac{1}{\sqrt{n}\,} \sum_{j=0}^{\left\lfloor{nt_0}\right\rfloor - 1} {{\bf 1}_{\{D^n(j) = 0\}}} = -
\inf_{0 \le i \le \left\lfloor{nt_0}\right\rfloor}\frac{1}{\sqrt{n}\,} \Biggl(D^n(i) -
\sum_{j=0}^{i-1}{{\bf 1}_{\{D^n(j)=0\}}} \Biggr),$
$\frac{1}{\sqrt{n}\,} \sum_{j=0}^{\left\lfloor{nt_0}\right\rfloor - 1} {{\bf 1}_{\{D^n(j) = 0\}}} = -
\inf_{0 \le i \le \left\lfloor{nt_0}\right\rfloor}\frac{1}{\sqrt{n}\,} \Biggl(D^n(i) -
\sum_{j=0}^{i-1}{{\bf 1}_{\{D^n(j)=0\}}} \Biggr),$
and so, by the continuous mapping theorem, we deduce that, on {γ n ≥ ⌊nt 0⌋},
 $\frac{\tilde{L}^n(\left\lfloor{nt_0}\right\rfloor)}{\sqrt{n}} = \frac{2}{\sqrt{n}\,}
\sum_{j=0}^{\left\lfloor{nt_0}\right\rfloor -1} {{\bf 1}_{\{D^n(j) = 0\}}} \underrightarrow {\rm D} - 2 \inf_{0 \le u \le
t_0} W_u.$
$\frac{\tilde{L}^n(\left\lfloor{nt_0}\right\rfloor)}{\sqrt{n}} = \frac{2}{\sqrt{n}\,}
\sum_{j=0}^{\left\lfloor{nt_0}\right\rfloor -1} {{\bf 1}_{\{D^n(j) = 0\}}} \underrightarrow {\rm D} - 2 \inf_{0 \le u \le
t_0} W_u.$
The result then follows since ![]() $\alpha(n) \gg \sqrt{n}$.
$\alpha(n) \gg \sqrt{n}$.
We now turn to the proof of the main theorem in this section.
Proof of Theorem 4.1. It follows from Lemma 4.1 that the expected increments of Xn and Nn are
This suggests that, as long as Xn does not hit 0 too often, the candidate for the fluid limit should be the solution to
with initial conditions x(0) = 0 and m(0) = 0. The unique solution to this system of differential equations is given by x(s) = (1 − s)2/3 − (1 − s)4/3 and ![]() $m(s)=\tfrac{1}{4}-\tfrac{1}{2}(1-s)^{2/3}+\tfrac{1}{4}(1-s)^{4/3}$ for s ∈ [0, 1]. We will use Proposition 4.1 to help control the local time at the start, and then prove the fluid limit result in the standard manner.
$m(s)=\tfrac{1}{4}-\tfrac{1}{2}(1-s)^{2/3}+\tfrac{1}{4}(1-s)^{4/3}$ for s ∈ [0, 1]. We will use Proposition 4.1 to help control the local time at the start, and then prove the fluid limit result in the standard manner.
Let Tn = inf{s ≥ t 0 : Xn(⌊ns⌋) = 0}. Then, for t ≥ t 0, we have Ln(⌊n(t ∧ Tn)⌋) = Ln(⌊nt 0⌋), since we may only accumulate local time at 0. We have
 $\mathbb {E}[{M_X^n(i)^2}] = \mathbb {E}\,\Biggl[{\sum_{j=0}^{i-1} \text {var}{X^n(j+1) - X^n(j) \mid
\mathcal {F}_j^n}}\Biggr] \le i \Big(5 + \mathbb {E}\,\Big[{\sup_{0 \le j \le i}
\big|E_{X,2}^n(j)\big|}\Big]\Big),$
$\mathbb {E}[{M_X^n(i)^2}] = \mathbb {E}\,\Biggl[{\sum_{j=0}^{i-1} \text {var}{X^n(j+1) - X^n(j) \mid
\mathcal {F}_j^n}}\Biggr] \le i \Big(5 + \mathbb {E}\,\Big[{\sup_{0 \le j \le i}
\big|E_{X,2}^n(j)\big|}\Big]\Big),$
and so ![]() ${\mathbb {E}{M_X^n({\left\lfloor {nt} \right\rfloor })^2}}/{\alpha(n)^2}\to 0$ by Lemma 4.1 and the fact that
${\mathbb {E}{M_X^n({\left\lfloor {nt} \right\rfloor })^2}}/{\alpha(n)^2}\to 0$ by Lemma 4.1 and the fact that ![]() $\alpha(n) \gg \sqrt{n}$. It follows as usual that
$\alpha(n) \gg \sqrt{n}$. It follows as usual that
Then
 \begin{align}
& \sup_{0 \le s \le t \wedge T^n}\Bigl| \sum_{j=0}^{\left\lfloor {ns} \right\rfloor -1}
\frac{\mathbb {E}{X^n(j+1) - X^n(j) \mid \mathcal {F}_j^n}}{\alpha(n)} - \int_0^s
\left(\frac{2}{3} (1-u)^{1/3} - \frac{2x(s)}{3(1-s)} \right) {\text{d}} u \Bigr|\\
&\quad\quad \le \sup_{0 \le s \le t } \Bigl| \frac{1}{n} \sum_{j=0}^{\left\lfloor {ns} \right\rfloor-1}
\frac{2}{3} (1-j/n)^{1/3} - \int_0^s \frac{2}{3} (1-u)^{1/3} {\text{d}} u \Bigr|
+ \sup_{0 \le s \le t \wedge T^n} \sum_{j=0}^{\left\lfloor {ns} \right\rfloor
-1}\frac{2{{\bf 1}_{\{X^n(i) = 0\}}}}{\alpha(n)}\\
&\quad\quad\quad + \sup_{0 \le s \le t \wedge T^n}\Bigl| \frac{1}{n}
\sum_{j=0}^{\left\lfloor {ns} \right\rfloor -1} \frac{2}{3(1-j/n)} \frac{X^n(j)}{\alpha(n)} -
\int_0^s \frac{2x(u)}{3(1-u)}{\text{d}} u \Bigr|\\
&\quad\quad\quad + \frac{{\left\lfloor {nt} \right\rfloor }}{\alpha(n)} \sup_{0 \le i \le \left\lfloor{n(t\wedge
T^n)}\right\rfloor} |E^n_{X,1}(i)|.
\end{align}
\begin{align}
& \sup_{0 \le s \le t \wedge T^n}\Bigl| \sum_{j=0}^{\left\lfloor {ns} \right\rfloor -1}
\frac{\mathbb {E}{X^n(j+1) - X^n(j) \mid \mathcal {F}_j^n}}{\alpha(n)} - \int_0^s
\left(\frac{2}{3} (1-u)^{1/3} - \frac{2x(s)}{3(1-s)} \right) {\text{d}} u \Bigr|\\
&\quad\quad \le \sup_{0 \le s \le t } \Bigl| \frac{1}{n} \sum_{j=0}^{\left\lfloor {ns} \right\rfloor-1}
\frac{2}{3} (1-j/n)^{1/3} - \int_0^s \frac{2}{3} (1-u)^{1/3} {\text{d}} u \Bigr|
+ \sup_{0 \le s \le t \wedge T^n} \sum_{j=0}^{\left\lfloor {ns} \right\rfloor
-1}\frac{2{{\bf 1}_{\{X^n(i) = 0\}}}}{\alpha(n)}\\
&\quad\quad\quad + \sup_{0 \le s \le t \wedge T^n}\Bigl| \frac{1}{n}
\sum_{j=0}^{\left\lfloor {ns} \right\rfloor -1} \frac{2}{3(1-j/n)} \frac{X^n(j)}{\alpha(n)} -
\int_0^s \frac{2x(u)}{3(1-u)}{\text{d}} u \Bigr|\\
&\quad\quad\quad + \frac{{\left\lfloor {nt} \right\rfloor }}{\alpha(n)} \sup_{0 \le i \le \left\lfloor{n(t\wedge
T^n)}\right\rfloor} |E^n_{X,1}(i)|.
\end{align}
The first term is clearly the difference between a Riemann approximation to an integral and that integral, and tends to 0. As we have Ln(⌊n(t ∧ Tn)⌋) = Ln(⌊nt 0⌋), the second term converges in probability to 0 by Proposition 4.1. The fourth term converges in probability to 0 by Lemma 4.1. The third term is bounded above by
 \begin{align}
& \frac{2}{3(1-t)} \int_0^{\left\lfloor {n(t \wedge {T^n})} \right\rfloor
/n} \Bigl|
\frac{X^n(\left\lfloor {nu} \right\rfloor)}{\alpha(n)} - x(u) \Bigr| {\text{d}} u\\
& \quad + \int_0^t
\Bigl|\frac{2}{3(1-u)} - \frac{2}{3(1-\left\lfloor {nu} \right\rfloor/u)} \Bigr| x(u) {\text{d}} u + \sup_{0 \le s \le t} \int_{\left\lfloor {ns} \right\rfloor/n}^s \frac{2x(u)}{3(1-u)}
{\text{d}} u,
\end{align}
\begin{align}
& \frac{2}{3(1-t)} \int_0^{\left\lfloor {n(t \wedge {T^n})} \right\rfloor
/n} \Bigl|
\frac{X^n(\left\lfloor {nu} \right\rfloor)}{\alpha(n)} - x(u) \Bigr| {\text{d}} u\\
& \quad + \int_0^t
\Bigl|\frac{2}{3(1-u)} - \frac{2}{3(1-\left\lfloor {nu} \right\rfloor/u)} \Bigr| x(u) {\text{d}} u + \sup_{0 \le s \le t} \int_{\left\lfloor {ns} \right\rfloor/n}^s \frac{2x(u)}{3(1-u)}
{\text{d}} u,
\end{align}
where the second and third terms clearly tend to 0 as n → ∞. The rest of the argument then goes through as in the proof of Proposition 3.1 to show that ![]() ${\sup_{0 \le s \le t\wedge T^n}} |{X^n(\left\lfloor {ns} \right\rfloor)}/{\alpha(n)} - x(s)| \underrightarrow{\rm P} 0$. Now observe that for fixed t > t 0, inft0≤s≤t x(s) > 0. So, for sufficiently small δ > 0, sup0≤s≤t∧Tn |Xn(⌊ns⌋)/α(n) − x(s)| ≤ δ implies that Tn > t and Ln(⌊nt⌋) = Ln(⌊nt 0⌋). Hence,
${\sup_{0 \le s \le t\wedge T^n}} |{X^n(\left\lfloor {ns} \right\rfloor)}/{\alpha(n)} - x(s)| \underrightarrow{\rm P} 0$. Now observe that for fixed t > t 0, inft0≤s≤t x(s) > 0. So, for sufficiently small δ > 0, sup0≤s≤t∧Tn |Xn(⌊ns⌋)/α(n) − x(s)| ≤ δ implies that Tn > t and Ln(⌊nt⌋) = Ln(⌊nt 0⌋). Hence,
Finally, to get the result for Nn, note that
 $\mathbb {E}\,[{M^n_N(i)^2}] \le \mathbb {E}\Biggl[\sum_{j=0}^{i-1} \mathbb {E}\,\big[{N^n(j+1)-N^n(j) \mid
\mathcal {F}_j^n}\big]\Biggr],$
$\mathbb {E}\,[{M^n_N(i)^2}] \le \mathbb {E}\Biggl[\sum_{j=0}^{i-1} \mathbb {E}\,\big[{N^n(j+1)-N^n(j) \mid
\mathcal {F}_j^n}\big]\Biggr],$
and so
 \begin{align}
\frac{\mathbb {E}[{M^n_N({\left\lfloor {nt} \right\rfloor })^2}]}{\alpha(n)^2} & \le \frac{1}{n\alpha(n)} \mathbb {E}{
\Biggl[\sum_{i=0}^{{\left\lfloor {nt} \right\rfloor }-1} \frac{X^n(i)/\alpha(n)}{3(1-i/n)}}\Biggr] +
\frac{nt}{\alpha(n)^2}\mathbb {E}\Big[\kern1.5pt{\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} E_N^n(i)}\Big]
\\
& \le \frac{t}{3(1-t)\alpha(n)^2}\mathbb {E}\Big[\kern1.5pt{\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }}X^n(i)}\Big] +
\frac{nt}{\alpha(n)^2}\mathbb {E}\Big[\kern1.5pt{\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} E_N^n(i)}\Big]\\
& \to 0,
\end{align}
\begin{align}
\frac{\mathbb {E}[{M^n_N({\left\lfloor {nt} \right\rfloor })^2}]}{\alpha(n)^2} & \le \frac{1}{n\alpha(n)} \mathbb {E}{
\Biggl[\sum_{i=0}^{{\left\lfloor {nt} \right\rfloor }-1} \frac{X^n(i)/\alpha(n)}{3(1-i/n)}}\Biggr] +
\frac{nt}{\alpha(n)^2}\mathbb {E}\Big[\kern1.5pt{\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} E_N^n(i)}\Big]
\\
& \le \frac{t}{3(1-t)\alpha(n)^2}\mathbb {E}\Big[\kern1.5pt{\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }}X^n(i)}\Big] +
\frac{nt}{\alpha(n)^2}\mathbb {E}\Big[\kern1.5pt{\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} E_N^n(i)}\Big]\\
& \to 0,
\end{align}
 \begin{align}
\sup_{0 \le s \le t} \Bigl|\frac{N^n(\left\lfloor {ns} \right\rfloor)}{\alpha(n)} - m(s) \Bigr|
& \le \frac{\sup_{0 \le s \le t} |M_N^n(\left\lfloor {ns} \right\rfloor)|}{\alpha(n)} +
\frac{\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} |E_N^n(i)|}{\alpha(n)}
\\
& + \sup_{0 \le s \le t} \Bigl| \frac{1}{n} \sum_{j=0}^{\left\lfloor {ns} \right\rfloor-1}
\frac{1}{3(1-j/n)} \frac{X^n(j)}{\alpha(n)} - \int_0^s
\frac{x(s)}{3(1-s)} {\text{d}} s \Bigr|,
\end{align}
\begin{align}
\sup_{0 \le s \le t} \Bigl|\frac{N^n(\left\lfloor {ns} \right\rfloor)}{\alpha(n)} - m(s) \Bigr|
& \le \frac{\sup_{0 \le s \le t} |M_N^n(\left\lfloor {ns} \right\rfloor)|}{\alpha(n)} +
\frac{\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} |E_N^n(i)|}{\alpha(n)}
\\
& + \sup_{0 \le s \le t} \Bigl| \frac{1}{n} \sum_{j=0}^{\left\lfloor {ns} \right\rfloor-1}
\frac{1}{3(1-j/n)} \frac{X^n(j)}{\alpha(n)} - \int_0^s
\frac{x(s)}{3(1-s)} {\text{d}} s \Bigr|,
\end{align}
and the usual argument allows us to complete the proof.
5. Diffusion limit for  ${\alpha(n)=O({\sqrt{n}})}$}
${\alpha(n)=O({\sqrt{n}})}$}
5.1. The limiting process
Proposition 5.1
Let a ≥ 0, and let (Bt 0 ≤ t ≤ 1) be a Brownian motion. There is a unique solution (Xa, La) to the SDE with reflection at 0 given by
for 0 ≤ t < 1 with initial condition ![]() $X^a_0=0$,
$X^a_0=0$, ![]() $L_a^0=0$, satisfying the conditions
$L_a^0=0$, satisfying the conditions
•
 $X^a_{t}\geq{0}$ for 0 ≤ t < 1,
$X^a_{t}\geq{0}$ for 0 ≤ t < 1,•
 $L_{t}^a$ is nondecreasing, and
$L_{t}^a$ is nondecreasing, and•
 $\int_{0}^{t}{{{\bf 1}_{\{{{X^a_s > 0\}}}}}}{{\text{d}} L^a_{s}}=0$ for 0 ≤ t < 1.
$\int_{0}^{t}{{{\bf 1}_{\{{{X^a_s > 0\}}}}}}{{\text{d}} L^a_{s}}=0$ for 0 ≤ t < 1.
Indeed, let
Then the solution to (5.1) is given explicitly for 0 ≤ t < 1 by
 \begin{gather}
L_t^a = \int_0^t (1-s)^{2/3} {\text{d}} K_s^a,
\\
X_t^a = a(1-t)^{2/3} - a(1-t)^{4/3} + (1 - t)^{2/3} \int_0^t \frac{{\text{d}}
B_u}{(1-u)^{2/3}} + (1-t)^{2/3} K_t^a.
\end{gather}
\begin{gather}
L_t^a = \int_0^t (1-s)^{2/3} {\text{d}} K_s^a,
\\
X_t^a = a(1-t)^{2/3} - a(1-t)^{4/3} + (1 - t)^{2/3} \int_0^t \frac{{\text{d}}
B_u}{(1-u)^{2/3}} + (1-t)^{2/3} K_t^a.
\end{gather}
Moreover, the following statements are true almost surely:
Finally, for a ≥ 0 and r ≥ a + 1, we have
Proof. Theorem 2.1.1 from [Reference Pilipenko13] guarantees the existence of a unique solution to the reflected SDE on the time interval [0, t] for any fixed t < 1, since the diffusion and drift coefficients satisfy the appropriate Lipschitz and linear growth conditions.
For 0 ≤ t < 1, define
Then we straightforwardly have ![]() ${\text{d}} Y^a_t = \tfrac{2}{3}a(1-t)^{-1/3}{\text{d}} t + (1-t)^{-2/3} {\text{d}} B_t + {\text{d}} K_t^a$ and, by Skorokhod’s lemma (see, for example, Lemma 2.1 of [Reference Revuz and Yor14, Chapter VI]), Ka is the local time at 0 of Ya.
${\text{d}} Y^a_t = \tfrac{2}{3}a(1-t)^{-1/3}{\text{d}} t + (1-t)^{-2/3} {\text{d}} B_t + {\text{d}} K_t^a$ and, by Skorokhod’s lemma (see, for example, Lemma 2.1 of [Reference Revuz and Yor14, Chapter VI]), Ka is the local time at 0 of Ya.
Now let ![]() $X^a_t = (1-t)^{2/3} Y_t^a$ and
$X^a_t = (1-t)^{2/3} Y_t^a$ and ![]() $L^a_t = \int_0^t (1-s)^{2/3} {\text{d}} K_s^a$. Then, by construction,
$L^a_t = \int_0^t (1-s)^{2/3} {\text{d}} K_s^a$. Then, by construction, ![]() $Y_t^a \ge 0$ for 0 ≤ t < 1 and so
$Y_t^a \ge 0$ for 0 ≤ t < 1 and so ![]() $X_t^a \ge 0$ for 0 ≤ t < 1. Furthermore,
$X_t^a \ge 0$ for 0 ≤ t < 1. Furthermore,
Clearly ![]() $L_0^a = 0$ and
$L_0^a = 0$ and ![]() $L_t^a$ is nondecreasing. Let us show that the local time at 0 of Xa is La. By Tanaka’s formula, the local time is given by
$L_t^a$ is nondecreasing. Let us show that the local time at 0 of Xa is La. By Tanaka’s formula, the local time is given by
 \begin{align}
& |X_t^a| - \int_0^t \mathrm{sgn}(X_s^a) {\text{d}} X_s^a
\\
&\quad\quad = (1-t)^{2/3} |Y_t^a| + \frac{2}{3} \int_0^t \mathrm{sgn}(Y_s^a)
Y_s^a (1-s)^{-1/3} {\text{d}} s - \int_0^t (1-s)^{2/3} \mathrm{sgn}(Y_s^a) {\text{d}}
Y_s^a
\\
&\quad\quad = \int_0^t (1-s)^{2/3} {\text{d}}|Y_s^a| - \int_0^t (1-s)^{2/3}
\mathrm{sgn}(Y_s^a) {\text{d}} Y_s^a,
\end{align}
\begin{align}
& |X_t^a| - \int_0^t \mathrm{sgn}(X_s^a) {\text{d}} X_s^a
\\
&\quad\quad = (1-t)^{2/3} |Y_t^a| + \frac{2}{3} \int_0^t \mathrm{sgn}(Y_s^a)
Y_s^a (1-s)^{-1/3} {\text{d}} s - \int_0^t (1-s)^{2/3} \mathrm{sgn}(Y_s^a) {\text{d}}
Y_s^a
\\
&\quad\quad = \int_0^t (1-s)^{2/3} {\text{d}}|Y_s^a| - \int_0^t (1-s)^{2/3}
\mathrm{sgn}(Y_s^a) {\text{d}} Y_s^a,
\end{align}
by integration by parts. But we also have ![]() $K_t^a = |Y_t^a| - \int_0^t \mathrm{sgn}(Y_s^a) {\text{d}} Y_s^a$ and so the last line is equal to
$K_t^a = |Y_t^a| - \int_0^t \mathrm{sgn}(Y_s^a) {\text{d}} Y_s^a$ and so the last line is equal to ![]() $\int_0^t (1-s)^{2/3} {\text{d}} K_s^a$, which is
$\int_0^t (1-s)^{2/3} {\text{d}} K_s^a$, which is ![]() $L_t^a$. It follows that
$L_t^a$. It follows that ![]() $\int_0^t {{1_{\{ X_s^a > 0\} }}} {\rm{d}}L_s^a = 0$. Hence, (Xa, La) solves the reflected SDE.
$\int_0^t {{1_{\{ X_s^a > 0\} }}} {\rm{d}}L_s^a = 0$. Hence, (Xa, La) solves the reflected SDE.
For a = 0, we have
and so (by Exercise 1.3.1 of [Reference Pilipenko13]) we have
Let us first show that ![]() $\lim_{t\to{1}}X^0_t=0$. By the Dubins–Schwarz theorem, we have
$\lim_{t\to{1}}X^0_t=0$. By the Dubins–Schwarz theorem, we have
where f(t) = 3(1 − t)−1/3 − 3 is the quadratic variation of the process on the left-hand side of (5.2). Let us recall that ![]() $ (B_t,\, t \ge 0) {\underline {\rm{D}}
} (t B_{{1}/{t}},\, t \ge 0) $. Thus, we have
$ (B_t,\, t \ge 0) {\underline {\rm{D}}
} (t B_{{1}/{t}},\, t \ge 0) $. Thus, we have
Then we have
almost surely as t → 1. It follows that ![]() $\lim_{t \to 1} X_t^0 = 0$ almost surely. Moreover,
$\lim_{t \to 1} X_t^0 = 0$ almost surely. Moreover,
By the change of variables u = f (t), this is in turn equal to 9 ![]() $\int_{0}^{\infty} \vert{B_u}\vert (u+3)^{-3} {\text{d}} u$. Since
$\int_{0}^{\infty} \vert{B_u}\vert (u+3)^{-3} {\text{d}} u$. Since ![]() ${B_u\underline{\underline {\rm{D}}}
{\sqrt{u}B_1}}$ and
${B_u\underline{\underline {\rm{D}}}
{\sqrt{u}B_1}}$ and ![]() ${\mathbb {E}{\vert{B_u}\vert}=\sqrt{2u/\pi}}$, we have
${\mathbb {E}{\vert{B_u}\vert}=\sqrt{2u/\pi}}$, we have
and so ![]() $\int_{0}^{1}{({X_t^0}/{(3(1-t))}){\text{d}} t} < \infty$ almost surely. Since we have
$\int_{0}^{1}{({X_t^0}/{(3(1-t))}){\text{d}} t} < \infty$ almost surely. Since we have
and ![]() $X_t^0$,
$X_t^0$, ![]() ${\int_{0}^{t}{({X_s^0}/{(3(1-s))}){\text{d}} t}}$ dt and B t all possess finite almost-sure limits as t → 1, the same must also be true of
${\int_{0}^{t}{({X_s^0}/{(3(1-s))}){\text{d}} t}}$ dt and B t all possess finite almost-sure limits as t → 1, the same must also be true of ![]() $L_t^0$.
$L_t^0$.
To obtain the almost-sure finiteness statements for a general a ≥ 0, note that if we build X 0 and Xa from the same Brownian motion then
It follows that ![]() $\lim_{t \to 1} X_t^a = 0$ almost surely. We also obtain
$\lim_{t \to 1} X_t^a = 0$ almost surely. We also obtain
Finally, by the same argument as in the a = 0 case, we must then also have ![]() $L_1^a\ :\!= {\lim_{t \to 1}} L_t^a < \infty$ almost surely.
$L_1^a\ :\!= {\lim_{t \to 1}} L_t^a < \infty$ almost surely.
We now turn to the final statement. By (5.3), it is sufficient to show the result for a = 0. For any 0 ≤ t < 1, we have
by standard Gaussian tail bounds.
5.2. The invariance principle
It follows from Theorem 4.1 that, for ![]() $\alpha(n)\gg\sqrt{n}$, the number of fires rescaled by α(n) possesses a fluid limit. This arises because the dominant contribution to the number of fires comes from connecting to nodes of degree 4. If we had no vertices of degree 4, we would connect only to vertices of degree 3, and the number of fires would make jumps of +1 or −1 only, each with probability
$\alpha(n)\gg\sqrt{n}$, the number of fires rescaled by α(n) possesses a fluid limit. This arises because the dominant contribution to the number of fires comes from connecting to nodes of degree 4. If we had no vertices of degree 4, we would connect only to vertices of degree 3, and the number of fires would make jumps of +1 or −1 only, each with probability ![]() ${\textstyle{1 \over 2}}$. This suggests that Xn should behave like a simple symmetric random walk. If
${\textstyle{1 \over 2}}$. This suggests that Xn should behave like a simple symmetric random walk. If ![]() $\alpha(n) \sim a\sqrt{n}$, a > 0, this random walk acquires a positive drift.
$\alpha(n) \sim a\sqrt{n}$, a > 0, this random walk acquires a positive drift.
Recall that, for 0 ≤ i ≤ ζn, we have ![]() $L^{n}(i)=2 \sum_{j=0}^{i-1}{{{\bf 1}_{\{X^{n}(j)=0\}}}}$. We will prove the following scaling limit.
$L^{n}(i)=2 \sum_{j=0}^{i-1}{{{\bf 1}_{\{X^{n}(j)=0\}}}}$. We will prove the following scaling limit.
Theorem 5.1
Fix t < 1, and suppose that ![]() $\alpha(n)/\sqrt{n}\to{a}$ for a ≥ 0. Then
$\alpha(n)/\sqrt{n}\to{a}$ for a ≥ 0. Then
uniformly, where (![]() $X^{a}_s$,
$X^{a}_s$, ![]() $L^{a}_s$, 0 ≤ s ≤ 1) is the process from Proposition 5.1.
$L^{a}_s$, 0 ≤ s ≤ 1) is the process from Proposition 5.1.
We will deduce Theorem 5.1 from the following general invariance principle for reflected diffusions. Such invariance principles go back to [Reference Stroock and Varadhan15], and we do not believe that this result is novel. But since we could not find a version in the existing literature adapted to our particular setting, we give a proof in Appendix A, using ideas from [Reference Ethier and Kurtz9] and [Reference Kang and Williams11].
Theorem 5.2
Let q: ℝ+ × ℝ+ → ℝ+, and b: ℝ+ × ℝ+ → ℝ satisfy the following conditions.
• Lipschitz condition: there exists K > 0 for all t ≥ 0 and all y 1, y 2 ∈ ℝ+ such that
 \begin{equation}
\vert{q(t,y_{1})-q(t,y_{2})}\vert+\vert{b(t,y_{1})-b(t,y_{2})}
\vert\leq{K\vert{y_{1}-y_{2}}\vert}.
\end{equation}
\begin{equation}
\vert{q(t,y_{1})-q(t,y_{2})}\vert+\vert{b(t,y_{1})-b(t,y_{2})}
\vert\leq{K\vert{y_{1}-y_{2}}\vert}.
\end{equation}
• Linear growth condition: there exists C > 0 for all t ≥ 0 and all x ∈ ℝ+ such that
 \begin{equation}
\vert{q(t,y)}\vert+\vert{b(t,y)}\vert\leq{C(1+\vert{y}\vert)}.
\end{equation}
\begin{equation}
\vert{q(t,y)}\vert+\vert{b(t,y)}\vert\leq{C(1+\vert{y}\vert)}.
\end{equation}
Let Yn and Bn be 𝔻(ℝ+, ℝ)-valued stochastic processes, and let Qn and Ln be increasing 𝔻(ℝ+, ℝ)-valued stochastic processes. Let ![]() $\mathcal {F}_t^n = \sigma(Y^n(s)$, Ln(s), Qn(s), Bn(s): s ≤ t), and let τn(r) = inf{t ≥ 0: |Yn(t)| ≥ r or |Yn(t −)| ≥ r}. Suppose that
$\mathcal {F}_t^n = \sigma(Y^n(s)$, Ln(s), Qn(s), Bn(s): s ≤ t), and let τn(r) = inf{t ≥ 0: |Yn(t)| ≥ r or |Yn(t −)| ≥ r}. Suppose that
(a) Mn = Yn − Bn is an (
 $ (\mathcal {F}^n_t) $)-local martingale;
$ (\mathcal {F}^n_t) $)-local martingale;(b) (Mn)2 − Qn is an (
 $ (\mathcal {F}^n_t) $)-local martingale;
$ (\mathcal {F}^n_t) $)-local martingale;and that, for all r > 0 and T > 0,
(c) limn→∞ 𝔼 [supt≤T∧τn(r) |Yn(t) – Yn(t –)|2] = 0;
(d) limn→∞ 𝔼[supt≤T∧τn(r) |Bn(t) – Bn(t –)|2] = 0;
(e) limn→∞ 𝔼[supt≤T∧τn(r) |Qn(t) – Qn(t –)|] = 0;
(f)
 $\sup_{t \le T \wedge \tau^n(r)} | B^n(t) - L^n(t) - \int_0^t b(s,Y^n(s)) {\text{d}} s | \underrightarrow{\rm P} 0$ as $n \to \infty$;
$\sup_{t \le T \wedge \tau^n(r)} | B^n(t) - L^n(t) - \int_0^t b(s,Y^n(s)) {\text{d}} s | \underrightarrow{\rm P} 0$ as $n \to \infty$;(g)
 $\sup_{t \le T \wedge \tau^n(r)} | Q^n(t) - \int_0^t q(s,Y^n(s)) {\text{d}} s | \underrightarrow{\rm P} 0$ as $n \to \infty$;
$\sup_{t \le T \wedge \tau^n(r)} | Q^n(t) - \int_0^t q(s,Y^n(s)) {\text{d}} s | \underrightarrow{\rm P} 0$ as $n \to \infty$;(h)
 $Y^n(0) \underrightarrow{\rm P} 0$ as $n \to \infty$;
$Y^n(0) \underrightarrow{\rm P} 0$ as $n \to \infty$;(i) there exists a sequence (δ n)n≥1 of constants with δ n → 0 such that Ln(0) = 0, Ln(t) − Ln(t − ) ≤ δ n, and
 $L^n(t) = \int_0^t {{\bf 1}_{\{Y^n(s) \le \delta_n\}}} {\text{d}} L^n(s)$.
$L^n(t) = \int_0^t {{\bf 1}_{\{Y^n(s) \le \delta_n\}}} {\text{d}} L^n(s)$.
Then ![]() $ (Y^n, L^n) {\underrightarrow {\rm D}} (Y,L) $ in the Skorokhod topology as n → ∞, where (Y, L) is the unique solution to the reflected SDE specified by Y 0 = L 0 = 0, L is nondecreasing, and
$ (Y^n, L^n) {\underrightarrow {\rm D}} (Y,L) $ in the Skorokhod topology as n → ∞, where (Y, L) is the unique solution to the reflected SDE specified by Y 0 = L 0 = 0, L is nondecreasing, and
where ![]() ${\int_0^t} {{\bf 1}_{\{Y_s > 0\}}} {\text{d}} L_s=0$, W is a standard Brownian motion, and
${\int_0^t} {{\bf 1}_{\{Y_s > 0\}}} {\text{d}} L_s=0$, W is a standard Brownian motion, and ![]() $\sigma(t,y) = \sqrt{q(t,y)}$.
$\sigma(t,y) = \sqrt{q(t,y)}$.
Proof of Theorem 5.1. Define ![]() $\tilde{X}^{n}(s)={{X}^{n}(\lfloor{ns}\rfloor)}/{\sqrt{n}}$ and
$\tilde{X}^{n}(s)={{X}^{n}(\lfloor{ns}\rfloor)}/{\sqrt{n}}$ and ![]() $\tilde{L}^{n}(s) ={{L}^{n}(\lfloor{ns}\rfloor)}/{\sqrt{n}}$. Recall from Proposition 5.1 that (
$\tilde{L}^{n}(s) ={{L}^{n}(\lfloor{ns}\rfloor)}/{\sqrt{n}}$. Recall from Proposition 5.1 that (![]() $X^{a}_s$,
$X^{a}_s$, ![]() $L^{a}_s$, 0 ≤ s ≤ t) is the solution to the reflected SDE
$L^{a}_s$, 0 ≤ s ≤ t) is the solution to the reflected SDE
For 0 ≤ s ≤ t and x ≥ 0, let q(s, x) = 1 and ![]() $b(s,x)=-\tfrac{2}{3}{{x}/{(1-s)}}+\tfrac{2}{3}a(1-s)^{1/3}$. It follows straightforwardly that, for 0 ≤ s ≤ t, the functions q and b satisfy the Lipschitz and linear growth conditions given in Theorem 5.2.
$b(s,x)=-\tfrac{2}{3}{{x}/{(1-s)}}+\tfrac{2}{3}a(1-s)^{1/3}$. It follows straightforwardly that, for 0 ≤ s ≤ t, the functions q and b satisfy the Lipschitz and linear growth conditions given in Theorem 5.2.
For i ≤ ⌊nt⌋, let
 ${B}^{n}(i) = \sum_{j=0}^{i-1} \mathbb {E}\,[{X^n(j+1) - X^n(j) \mid \mathcal {F}^n_j}],$
${B}^{n}(i) = \sum_{j=0}^{i-1} \mathbb {E}\,[{X^n(j+1) - X^n(j) \mid \mathcal {F}^n_j}],$
so that ![]() $M^n_{X}(i) = X^n(i) - B^n(i)$, as well as
$M^n_{X}(i) = X^n(i) - B^n(i)$, as well as
 \begin{align}
Q^{n}(i) & = \sum_{j=0}^{i-1} \mathbb {E}[{M_X^n(j+1)^2 - M_X^n(j)^2 \mid
\mathcal {F}^n_j}]
\\
&= \sum_{j=0}^{i-1} \mathbb {E}[{({{M}_X^{n}(j+1)}-M_X^n(j))^{2}\mid
{\mathcal {F}^{n}_{j}}}]
\\
&= \sum_{j=0}^{i-1} (\mathbb {E}[{({X}^{n}(j+1)-{{X}^{n}(j)})^{2}\mid
{{\mathcal {F}^{n}_{i}}}}] -\mathbb {E}[{{X}^{n}(j+1)-X^{n}(j)\mid
{{\mathcal {F}^{n}_{j}}}}]^{2}).
\end{align}
\begin{align}
Q^{n}(i) & = \sum_{j=0}^{i-1} \mathbb {E}[{M_X^n(j+1)^2 - M_X^n(j)^2 \mid
\mathcal {F}^n_j}]
\\
&= \sum_{j=0}^{i-1} \mathbb {E}[{({{M}_X^{n}(j+1)}-M_X^n(j))^{2}\mid
{\mathcal {F}^{n}_{j}}}]
\\
&= \sum_{j=0}^{i-1} (\mathbb {E}[{({X}^{n}(j+1)-{{X}^{n}(j)})^{2}\mid
{{\mathcal {F}^{n}_{i}}}}] -\mathbb {E}[{{X}^{n}(j+1)-X^{n}(j)\mid
{{\mathcal {F}^{n}_{j}}}}]^{2}).
\end{align}
Since everything is bounded, ![]() $M_X^n$ and
$M_X^n$ and ![]() $ (M_X^n)^2 - Q^n $ are both (
$ (M_X^n)^2 - Q^n $ are both (![]() $ (\mathcal {F}_i^n) $)-martingales. Let
$ (\mathcal {F}_i^n) $)-martingales. Let
be the appropriately rescaled versions of these quantities. Then (a) and (b) hold by construction and the main task facing us is to check that conditions (f) and (g) of Theorem 5.2 are fulfilled for M̃n and (M̃n)2 − Q̃n.
By Lemma 4.1,
 \begin{equation}
\begin{aligned}
B^n(i) & =2 \sum_{j=0}^{i-1} {{\bf 1}_{\{X^n(j)=0\}}} + \sum_{j=0}^{i-1} \frac{2\alpha(n)(1-j/n)^{4/3}-2X^n(j)}{3(n-j)}+ \sum_{j=0}^{i-1} E_{X,1}^{n}(j) \\
& = L^n(i) + \sum_{j=0}^{i-1} \frac{2\alpha(n)(1-j/n)^{4/3}-2X^n(j)}{3(n-j)}+ \sum_{j=0}^{i-1} E_{X,1}^{n}(j).
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
B^n(i) & =2 \sum_{j=0}^{i-1} {{\bf 1}_{\{X^n(j)=0\}}} + \sum_{j=0}^{i-1} \frac{2\alpha(n)(1-j/n)^{4/3}-2X^n(j)}{3(n-j)}+ \sum_{j=0}^{i-1} E_{X,1}^{n}(j) \\
& = L^n(i) + \sum_{j=0}^{i-1} \frac{2\alpha(n)(1-j/n)^{4/3}-2X^n(j)}{3(n-j)}+ \sum_{j=0}^{i-1} E_{X,1}^{n}(j).
\end{aligned}
\end{equation}
Then
 \begin{align}
& \sup_{0\leq s \le t}\Big| \tilde{B}^{n}(s)-\tilde{L}^{n}(s)-
\int_{0}^{s}\bigg(\frac{2a}{3}(1-u)^{1/3} -
\frac{2\tilde{X}^{n}(u)}{(1-u)} \bigg){\text{d}} u \Big|
\\
&\quad\quad \le \sup_{0\le s \le t}\Big| \sum_{j=0}^{\left\lfloor {ns} \right\rfloor -1} \frac{1}{n}
\bigg(\frac{2\alpha(n)}{3\sqrt{n}}(1 - j/n)^{1/3} -
\frac{2\tilde{X}^{n}(j/n)}{3(1-j/n)}\bigg)
\\
&-\int_{0}^{s}\bigg(\frac{2a}{3}(1-u)^{1/3} -
\frac{2\tilde{X}^{n}(u)}{3(1-u)} \bigg) {\text{d}} u\Big| + \sup_{0\le i \le
{\left\lfloor {nt} \right\rfloor }}\sqrt{n} |E_{X,1}^{n}(i)|,
\end{align}
\begin{align}
& \sup_{0\leq s \le t}\Big| \tilde{B}^{n}(s)-\tilde{L}^{n}(s)-
\int_{0}^{s}\bigg(\frac{2a}{3}(1-u)^{1/3} -
\frac{2\tilde{X}^{n}(u)}{(1-u)} \bigg){\text{d}} u \Big|
\\
&\quad\quad \le \sup_{0\le s \le t}\Big| \sum_{j=0}^{\left\lfloor {ns} \right\rfloor -1} \frac{1}{n}
\bigg(\frac{2\alpha(n)}{3\sqrt{n}}(1 - j/n)^{1/3} -
\frac{2\tilde{X}^{n}(j/n)}{3(1-j/n)}\bigg)
\\
&-\int_{0}^{s}\bigg(\frac{2a}{3}(1-u)^{1/3} -
\frac{2\tilde{X}^{n}(u)}{3(1-u)} \bigg) {\text{d}} u\Big| + \sup_{0\le i \le
{\left\lfloor {nt} \right\rfloor }}\sqrt{n} |E_{X,1}^{n}(i)|,
\end{align}
which converges to 0 in probability as n → ∞ by Lemma 4.1. Hence, condition (f) holds.
By Lemma 4.1,
 \begin{align}
Q^n(i) & = \sum_{j=0}^{i-1} \Biggl(1+E_{X,2}^{n}(j) -4{{\bf 1}_{\{X^n(j)=0\}}}
\bigg(\frac{2\alpha(n)(1-j/n)^{4/3}-2X^{n}(j)}{3(n-j)}+E_{X,1}^{n}(j)
\bigg)
\\
&
-\left(\frac{2\alpha(n)(1-j/n)^{4/3}-2X^{n}(j)}{3(n-j)}+E_{X,1}^{n}(j)
\right)^{2} \Biggr).
\end{align}
\begin{align}
Q^n(i) & = \sum_{j=0}^{i-1} \Biggl(1+E_{X,2}^{n}(j) -4{{\bf 1}_{\{X^n(j)=0\}}}
\bigg(\frac{2\alpha(n)(1-j/n)^{4/3}-2X^{n}(j)}{3(n-j)}+E_{X,1}^{n}(j)
\bigg)
\\
&
-\left(\frac{2\alpha(n)(1-j/n)^{4/3}-2X^{n}(j)}{3(n-j)}+E_{X,1}^{n}(j)
\right)^{2} \Biggr).
\end{align}
Then
 \begin{align}
&\sup_{0\leq s \leq t} | \tilde{Q}^{n}(s)-s |\\
&\ \ \ =\sup_{0\leq s \leq t} \!\Big| \frac{\left\lfloor {ns} \right\rfloor}{n}-s +\!\sum_{j=0}^{\left\lfloor {ns} \right\rfloor-1} \Biggl(\frac{E_{X,2}^{n}(j)}{n} -
\!\biggl(\frac{2(\alpha(n)/\sqrt{n})(1-j/n)^{4/3}-2\tilde{X}(j/n)}{3(n-j)}
+\frac{E_{X,1}^{n}(j)}{\sqrt{n}}\biggr)^{\!2}\\
&\quad\quad-\frac{4}{\sqrt{n}\,} {{\bf 1}_{\{\tilde{X}^{n}(j/n)=0\}}} \biggl(
\frac{2(\alpha(n)/\sqrt{n})(1-j/n)^{4/3}-2\tilde{X}(j/n)}{3(n-j)}
+\frac{E_{X,1}^{n}(j)}{\sqrt{n}}\biggr) \Biggr)\Big|.
\end{align}
\begin{align}
&\sup_{0\leq s \leq t} | \tilde{Q}^{n}(s)-s |\\
&\ \ \ =\sup_{0\leq s \leq t} \!\Big| \frac{\left\lfloor {ns} \right\rfloor}{n}-s +\!\sum_{j=0}^{\left\lfloor {ns} \right\rfloor-1} \Biggl(\frac{E_{X,2}^{n}(j)}{n} -
\!\biggl(\frac{2(\alpha(n)/\sqrt{n})(1-j/n)^{4/3}-2\tilde{X}(j/n)}{3(n-j)}
+\frac{E_{X,1}^{n}(j)}{\sqrt{n}}\biggr)^{\!2}\\
&\quad\quad-\frac{4}{\sqrt{n}\,} {{\bf 1}_{\{\tilde{X}^{n}(j/n)=0\}}} \biggl(
\frac{2(\alpha(n)/\sqrt{n})(1-j/n)^{4/3}-2\tilde{X}(j/n)}{3(n-j)}
+\frac{E_{X,1}^{n}(j)}{\sqrt{n}}\biggr) \Biggr)\Big|.
\end{align}
Now, for large enough n, we have
 \begin{aligned}
& \Bigl| \frac{2(\alpha(n)/\sqrt{n})(1-j/n)^{4/3}-2\tilde{X}(j/n)}{3(n-j)}+\frac{E_{X,1}^{n}(j)}{\sqrt{n}} \Bigr| \\
& \quad\quad \le \frac{1}{n} \frac{4a}{3(1-t)^{1/3}} + \frac{1}{n} \frac{2}{3(1-t)} \sup_{0 \le s \le t} \tilde{X}^n(s) + \frac{\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} |E_{X,1}^n(i)|}{\sqrt{n}}.
\end{aligned}
\begin{aligned}
& \Bigl| \frac{2(\alpha(n)/\sqrt{n})(1-j/n)^{4/3}-2\tilde{X}(j/n)}{3(n-j)}+\frac{E_{X,1}^{n}(j)}{\sqrt{n}} \Bigr| \\
& \quad\quad \le \frac{1}{n} \frac{4a}{3(1-t)^{1/3}} + \frac{1}{n} \frac{2}{3(1-t)} \sup_{0 \le s \le t} \tilde{X}^n(s) + \frac{\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} |E_{X,1}^n(i)|}{\sqrt{n}}.
\end{aligned}
Since ![]() ${\sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}{|E_{X,2}^{n}(i)|}\underrightarrow{\rm P} {0}}$,
${\sup_{0\leq{i}\leq{\lfloor{nt}\rfloor}}{|E_{X,2}^{n}(i)|}\underrightarrow{\rm P} {0}}$, ![]() ${\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} |E_{X,1}^n(i)| \underrightarrow{\rm P} 0}$, and sup0≤s≤t X̃n(s) is tight, it follows that
${\sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} |E_{X,1}^n(i)| \underrightarrow{\rm P} 0}$, and sup0≤s≤t X̃n(s) is tight, it follows that ![]() $\sup_{0\leq s \leq t} | \tilde{Q}^{n}(s)-s | \underrightarrow{\rm P} 0$ as n → ∞, and so condition (g) of Theorem 5.2 is fulfilled.
$\sup_{0\leq s \leq t} | \tilde{Q}^{n}(s)-s | \underrightarrow{\rm P} 0$ as n → ∞, and so condition (g) of Theorem 5.2 is fulfilled.
Since the increments of Xn are bounded, conditions (c)–(e) of Theorem 5.2 are trivially satisfied. As X̃n(0) = 0, condition (h) is satisfied. Finally, note that condition (i) is fulfilled if we take ![]() $\delta_n = 2/\sqrt{n}$, since
$\delta_n = 2/\sqrt{n}$, since ![]() $\tilde{L}^n(s) - \tilde{L}^n(s-) \le 2/\sqrt{n}$ and
$\tilde{L}^n(s) - \tilde{L}^n(s-) \le 2/\sqrt{n}$ and
 $\int_0^s {{\bf 1}_{\{\tilde{X}^n(u) \le {2}/{\sqrt{n}\}}}} {\text{d}} L^n(u) = 2
\sum_{i=0}^{\left\lfloor {ns} \right\rfloor-1} {{\bf 1}_{\{\tilde{X}^n(i) = 0\}}} = L^n(s).$
$\int_0^s {{\bf 1}_{\{\tilde{X}^n(u) \le {2}/{\sqrt{n}\}}}} {\text{d}} L^n(u) = 2
\sum_{i=0}^{\left\lfloor {ns} \right\rfloor-1} {{\bf 1}_{\{\tilde{X}^n(i) = 0\}}} = L^n(s).$
Applying Theorem 5.2 completes the proof.
Finally, we are ready to prove the convergence of the suitably rescaled number of clashes we encounter up to a fixed time t < 1.
Lemma 5.1
For fixed 0 < t < 1, we have ![]() $\big({N^{n}(\lfloor{ns}\rfloor)}/{\sqrt{n}},\, 0\leq s \leq t \big) \underrightarrow {\rm D} \left(N_s^a,\, 0\leq s \leq t \right)$ uniformly as n → ∞.
$\big({N^{n}(\lfloor{ns}\rfloor)}/{\sqrt{n}},\, 0\leq s \leq t \big) \underrightarrow {\rm D} \left(N_s^a,\, 0\leq s \leq t \right)$ uniformly as n → ∞.
Proof. The argument is standard, since Nn is a counting process which is bounded by (3n + 4α(n))/2. We have
 \begin{align}
\mathbb {E}[{M^n_N(k)^2}] & \le \mathbb {E}\,\Bigg[{\sum_{i=0}^{k-1} \mathbb {E}\,[{N^n(i+1) - N^n(i) \mid
\mathcal {F}_i^n}]}\Bigg] = \mathbb {E}[{N^n(k)]}\,,
\end{align}
\begin{align}
\mathbb {E}[{M^n_N(k)^2}] & \le \mathbb {E}\,\Bigg[{\sum_{i=0}^{k-1} \mathbb {E}\,[{N^n(i+1) - N^n(i) \mid
\mathcal {F}_i^n}]}\Bigg] = \mathbb {E}[{N^n(k)]}\,,
\end{align}
where the inequality holds since Nn(i + 1) − Nn(i) ∈ {0, 1}. Now,
 \begin{align}
\frac{1}{\sqrt{n}\,} \mathbb {E}{N^n({\left\lfloor {nt} \right\rfloor })} & \le \frac{1}{\sqrt{n}\,}
\sum_{i=1}^{{\left\lfloor {nt} \right\rfloor }-1} \mathbb {E}\, \biggl[{ \frac{3n + 2 X^n(i) (3n + 4 \alpha(n) + 2
X^n(i))}{2(3n(1-t) - 1) (3n(1-t) - 3)}}\biggr]
\\
& \le \frac{\sqrt{n} t \left(3n + 2 \mathbb {E}[{\sup_{0 \le i \le \zeta_n} X^n(i)]}
(3n + 4 \alpha(n) + 2n + 2 \alpha(n))\right)}{2(3n(1-t) -1) (3n(1-t) -
3)}
\\
&\le C\label{eqn:NnUI}
\end{align}
\begin{align}
\frac{1}{\sqrt{n}\,} \mathbb {E}{N^n({\left\lfloor {nt} \right\rfloor })} & \le \frac{1}{\sqrt{n}\,}
\sum_{i=1}^{{\left\lfloor {nt} \right\rfloor }-1} \mathbb {E}\, \biggl[{ \frac{3n + 2 X^n(i) (3n + 4 \alpha(n) + 2
X^n(i))}{2(3n(1-t) - 1) (3n(1-t) - 3)}}\biggr]
\\
& \le \frac{\sqrt{n} t \left(3n + 2 \mathbb {E}[{\sup_{0 \le i \le \zeta_n} X^n(i)]}
(3n + 4 \alpha(n) + 2n + 2 \alpha(n))\right)}{2(3n(1-t) -1) (3n(1-t) -
3)}
\\
&\le C\label{eqn:NnUI}
\end{align}
for some constant C, uniformly in n. In particular, 𝔼[Nn(⌊nt⌋)],n → ∞. Fix δ > 0. Using Markov’s inequality, we obtain ![]() $M_N^n({\left\lfloor {nt} \right\rfloor })/{\sqrt{n} \underrightarrow{\rm P}} 0$ as n → ∞.
$M_N^n({\left\lfloor {nt} \right\rfloor })/{\sqrt{n} \underrightarrow{\rm P}} 0$ as n → ∞.
Now, by Lemma 4.1, we have ![]() $\sqrt{n} \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} \big| \mathbb {E}{N^n(i+1) - N^n(i) \mid \mathcal {F}^n_i} - {X^n(i)}/{(3(n-i))} \big| \underrightarrow{\rm P} 0$, and so
$\sqrt{n} \sup_{0 \le i \le {\left\lfloor {nt} \right\rfloor }} \big| \mathbb {E}{N^n(i+1) - N^n(i) \mid \mathcal {F}^n_i} - {X^n(i)}/{(3(n-i))} \big| \underrightarrow{\rm P} 0$, and so
 $\sup_{0\leq s \leq t}\frac{1}{\sqrt{n}\,} \Bigl| \sum_{i=1}^{\left\lfloor {ns} \right\rfloor-1}
\mathbb {E}{N^n(i+1) - N^n(i) \mid \mathcal {F}_i^n} - \sum_{i=0}^{\left\lfloor {ns} \right\rfloor - 1}
\frac{X^n(i)}{3(n-i)} \Bigr| \underrightarrow{\rm P} 0.$
$\sup_{0\leq s \leq t}\frac{1}{\sqrt{n}\,} \Bigl| \sum_{i=1}^{\left\lfloor {ns} \right\rfloor-1}
\mathbb {E}{N^n(i+1) - N^n(i) \mid \mathcal {F}_i^n} - \sum_{i=0}^{\left\lfloor {ns} \right\rfloor - 1}
\frac{X^n(i)}{3(n-i)} \Bigr| \underrightarrow{\rm P} 0.$
Finally, we have
 $\frac{1}{\sqrt{n}\,} \sum_{i=0}^{\left\lfloor {ns} \right\rfloor - 1} \frac{X^n(i)}{3(n-i)} =
\frac{1}{\sqrt{n}\,} \int_0^{\left\lfloor {ns} \right\rfloor/n} \frac{X^n(\left\lfloor {nu} \right\rfloor)}{3\left(1 -
{\left\lfloor {nu} \right\rfloor}/{n}\right)} {\text{d}} u.$
$\frac{1}{\sqrt{n}\,} \sum_{i=0}^{\left\lfloor {ns} \right\rfloor - 1} \frac{X^n(i)}{3(n-i)} =
\frac{1}{\sqrt{n}\,} \int_0^{\left\lfloor {ns} \right\rfloor/n} \frac{X^n(\left\lfloor {nu} \right\rfloor)}{3\left(1 -
{\left\lfloor {nu} \right\rfloor}/{n}\right)} {\text{d}} u.$
But then, using Theorem 5.1 and the continuous mapping theorem, we obtain
uniformly for 0 ≤ s ≤ t. Hence, ![]() $N^n(\left\lfloor {ns} \right\rfloor)/{\sqrt{n} \underrightarrow {\rm D}} N_s^a$ as n → ∞, uniformly for 0 ≤ s ≤ t, as desired.
$N^n(\left\lfloor {ns} \right\rfloor)/{\sqrt{n} \underrightarrow {\rm D}} N_s^a$ as n → ∞, uniformly for 0 ≤ s ≤ t, as desired.
6. The end of the process
We now understand the scaling behaviour of the process (Xn(i), Ln(i), Nn(i))i≥0 on the time interval [0, ⌊n(1 − ε) ⌋] for any ε > 0. It remains to get from ⌊n(1 − ε)⌋ to ζ n.
We first show that Vn(n) is small and that Xn(⌊n(1 − ε)⌋), Ln(⌊n(1 − ε)⌋), Nn(⌊n(1 − ε)⌋) are, for small ε, good approximations of Xn(n), Ln(n), Nn(n), by careful use of the coupling from Section 2.2.
Proposition 6.1
For any δ > 0,
(a) if α(n) → ∞ then
 $V^n(n)/\alpha(n) \underrightarrow{\rm P} 0$ as n → ∞;
$V^n(n)/\alpha(n) \underrightarrow{\rm P} 0$ as n → ∞;(b)
 $\lim_{\varepsilon \to 0} \limsup_{n \to \infty} \mathbb {P}\,({ (N^n(n) - N^n(\left\lfloor{n(1 - \varepsilon)}\right\rfloor))/{(\alpha(n) \vee \sqrt{n})}> \delta}) = 0$;
$\lim_{\varepsilon \to 0} \limsup_{n \to \infty} \mathbb {P}\,({ (N^n(n) - N^n(\left\lfloor{n(1 - \varepsilon)}\right\rfloor))/{(\alpha(n) \vee \sqrt{n})}> \delta}) = 0$;(c)
 $\lim_{\varepsilon \to 0} \limsup_{n \to \infty} \mathbb {P}\,({ ({1}/{(\alpha(n) \vee \sqrt{n})}) \sup_{\left\lfloor{n(1-\varepsilon)}\right\rfloor \le i \le n} X^n(i) > \delta}) = 0$;
$\lim_{\varepsilon \to 0} \limsup_{n \to \infty} \mathbb {P}\,({ ({1}/{(\alpha(n) \vee \sqrt{n})}) \sup_{\left\lfloor{n(1-\varepsilon)}\right\rfloor \le i \le n} X^n(i) > \delta}) = 0$;(d)
 $\lim_{\varepsilon \to 0} \limsup_{n \to \infty} \mathbb {P}\,({ (L^n(n) - L^n(\left\lfloor{n(1 - \varepsilon)}\right\rfloor))/{(\alpha(n) \vee \sqrt{n})} > \delta}) = 0$.
$\lim_{\varepsilon \to 0} \limsup_{n \to \infty} \mathbb {P}\,({ (L^n(n) - L^n(\left\lfloor{n(1 - \varepsilon)}\right\rfloor))/{(\alpha(n) \vee \sqrt{n})} > \delta}) = 0$.
Proof. (a) We have
and, by Lemma 3.2, ℙ (Vn(⌊(1 − ε)n⌋) > 2ε 4/3α(n)) → 0 as n → ∞. But Vn is decreasing and so
Since Vn(n) ≥ 0 and this inequality holds for any ε > 0, it must follow that the left-hand side is, in fact, equal to 0. Markov’s inequality then gives ![]() $V^n(n)/\alpha(n) \underrightarrow{\rm P} 0$.
$V^n(n)/\alpha(n) \underrightarrow{\rm P} 0$.
(b) Recall the coupling and notation from Section 2.2. First note that
 \begin{align}
& \mathbb {E}[{N^n(n) - N^n(\left\lfloor{n(1-\varepsilon)]}\right\rfloor)}
\\
& \quad\quad = \mathbb {E}[{N_1^n(n) - N_1^n(\left\lfloor{n(1-\varepsilon)]}\right\rfloor)} + \mathbb {E}[{N_2^n(n) -
N_2^n(\left\lfloor{n(1-\varepsilon)]}\right\rfloor)}
\\
& \quad\quad \le \mathbb {E}[{N_1^n(n) - N_1^n(\left\lfloor{n(1-\varepsilon)]}\right\rfloor)} +
\mathbb {E}[{V^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)]}.\label{eqn:N=N_1+N_2}
\end{align}
\begin{align}
& \mathbb {E}[{N^n(n) - N^n(\left\lfloor{n(1-\varepsilon)]}\right\rfloor)}
\\
& \quad\quad = \mathbb {E}[{N_1^n(n) - N_1^n(\left\lfloor{n(1-\varepsilon)]}\right\rfloor)} + \mathbb {E}[{N_2^n(n) -
N_2^n(\left\lfloor{n(1-\varepsilon)]}\right\rfloor)}
\\
& \quad\quad \le \mathbb {E}[{N_1^n(n) - N_1^n(\left\lfloor{n(1-\varepsilon)]}\right\rfloor)} +
\mathbb {E}[{V^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)]}.\label{eqn:N=N_1+N_2}
\end{align}
From (2.5), the process
is the standard martingale. Hence,
 \begin{align}
& \mathbb {E}\,[{N_1^n(n) - N_1^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)}] \notag
\\
&\quad =
{\mathbb {E}\,\bigg[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1}
\frac{3U^n(i) + 2(X_1^n(i) - {{\bf 1}_{\{X_1^n(i) > 0\}}})(3U^n(i) + 4V^n(i) + X^n(i)
- 3)}{2(3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}})(3U^n(i) + 4V^n(i) +
X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}} - 2)}}\bigg]} \notag\end{align}
\begin{align}
& \mathbb {E}\,[{N_1^n(n) - N_1^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)}] \notag
\\
&\quad =
{\mathbb {E}\,\bigg[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1}
\frac{3U^n(i) + 2(X_1^n(i) - {{\bf 1}_{\{X_1^n(i) > 0\}}})(3U^n(i) + 4V^n(i) + X^n(i)
- 3)}{2(3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}})(3U^n(i) + 4V^n(i) +
X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}} - 2)}}\bigg]} \notag\end{align}
 \begin{align}
&\quad \le \frac{1}{6} \sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1}
\frac{1}{(n-i)} + \mathbb {E}\,\bigg[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1} \frac{X_1^n(i)
- {{\bf 1}_{\{X_1^n(i) > 0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\bigg]
\\
&\quad \le \frac{1}{6}(\log(\left\lceil {n\varepsilon } \right\rceil
) + 1) +
\mathbb {E}\,\bigg[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) >
0\}}}}{3U^n(i) + 4 V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\bigg]. \label{eqn:nbound}
\end{align}
\begin{align}
&\quad \le \frac{1}{6} \sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1}
\frac{1}{(n-i)} + \mathbb {E}\,\bigg[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1} \frac{X_1^n(i)
- {{\bf 1}_{\{X_1^n(i) > 0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\bigg]
\\
&\quad \le \frac{1}{6}(\log(\left\lceil {n\varepsilon } \right\rceil
) + 1) +
\mathbb {E}\,\bigg[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) >
0\}}}}{3U^n(i) + 4 V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\bigg]. \label{eqn:nbound}
\end{align}
Let us fix C > 6 and define a sequence of stopping times in the following way. Let ![]() $T_0 = \inf\{k \ge \left\lfloor{n(1-\varepsilon)}\right\rfloor\colon X_1^n(k) \ge \left\lfloor{C \sqrt{n-k}}\right\rfloor\}$, and, inductively, for i ≥ 1, let
$T_0 = \inf\{k \ge \left\lfloor{n(1-\varepsilon)}\right\rfloor\colon X_1^n(k) \ge \left\lfloor{C \sqrt{n-k}}\right\rfloor\}$, and, inductively, for i ≥ 1, let
Then, since Un(i) ≥ n − i,
 \begin{align}
& \mathbb {E}\Biggl[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) >
0\}}}}{3U^n(i) + 4 V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\Biggr]\\
&\quad\quad \le \mathbb {E}\Biggl[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{T_0-1} \frac{X_1^n(i) -
{{\bf 1}_{\{X_1^n(i) > 0\}}}}{3(n-i)}}\Biggr] + \mathbb {E}\Biggl[{\sum_{k=1}^{n} \sum_{i=S_k}^{T_k-1}
\frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) > 0\}}}}{3(n-i)}}\Biggr]\\
&\quad\quad + \mathbb {E}\Biggl[{\sum_{k=1}^{n} \sum_{i=T_{k-1}}^{S_k-1} \frac{X_1^n(i) -
{{\bf 1}_{\{X_1^n(i) > 0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\Biggr].
\end{align}
\begin{align}
& \mathbb {E}\Biggl[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) >
0\}}}}{3U^n(i) + 4 V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\Biggr]\\
&\quad\quad \le \mathbb {E}\Biggl[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{T_0-1} \frac{X_1^n(i) -
{{\bf 1}_{\{X_1^n(i) > 0\}}}}{3(n-i)}}\Biggr] + \mathbb {E}\Biggl[{\sum_{k=1}^{n} \sum_{i=S_k}^{T_k-1}
\frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) > 0\}}}}{3(n-i)}}\Biggr]\\
&\quad\quad + \mathbb {E}\Biggl[{\sum_{k=1}^{n} \sum_{i=T_{k-1}}^{S_k-1} \frac{X_1^n(i) -
{{\bf 1}_{\{X_1^n(i) > 0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\Biggr].
\end{align}
Either we have T 0 = ⌊n(1 − ε)⌋ (in which case the first sum is empty) or, on the time interval [⌊n(1 − ε)⌋, T 0 − 1], we have ![]() $X_1^n(i) -1 \le C \sqrt{n-i}$. Likewise, on the interval [S k, T k − 1], we have
$X_1^n(i) -1 \le C \sqrt{n-i}$. Likewise, on the interval [S k, T k − 1], we have ![]() $X_1^n(i) -1 \le C \sqrt{n-i}$. So
$X_1^n(i) -1 \le C \sqrt{n-i}$. So
 \begin{align}
& \mathbb {E} \Biggl[\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{T_0-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i)
> 0\}}}}{3(n-i)}\Biggr]\!+ \mathbb {E}\Biggl[\sum_{k=1}^{n} \sum_{i=S_k}^{T_k-1} \frac{X_1^n(i) -
{{\bf 1}_{\{X_1^n(i) > 0\}}}}{3(n-i)}\Biggr]\! \le \frac{C}{3} \sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1}
\frac{1}{\sqrt{n-i}\,}.
\end{align}
\begin{align}
& \mathbb {E} \Biggl[\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{T_0-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i)
> 0\}}}}{3(n-i)}\Biggr]\!+ \mathbb {E}\Biggl[\sum_{k=1}^{n} \sum_{i=S_k}^{T_k-1} \frac{X_1^n(i) -
{{\bf 1}_{\{X_1^n(i) > 0\}}}}{3(n-i)}\Biggr]\! \le \frac{C}{3} \sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1}
\frac{1}{\sqrt{n-i}\,}.
\end{align}
Since ![]() $\sum_{i=1}^{\left\lceil {n\varepsilon } \right\rceil} i^{-1/2} \le \int_0^{\left\lceil {n\varepsilon } \right\rceil} x^{-1/2} {\text{d}} x \le 2 \sqrt{n\varepsilon +1}$, we obtain
$\sum_{i=1}^{\left\lceil {n\varepsilon } \right\rceil} i^{-1/2} \le \int_0^{\left\lceil {n\varepsilon } \right\rceil} x^{-1/2} {\text{d}} x \le 2 \sqrt{n\varepsilon +1}$, we obtain
 \begin{equation} \label{eqn:rootn}
\mathbb {E}\Biggl[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{T_0-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) >
0\}}}}{3(n-i)}}\Biggr]+ \mathbb {E}\Biggl[{\sum_{k=1}^{n} \sum_{i=S_k}^{T_k-1} \frac{X_1^n(i) -
{{\bf 1}_{\{X_1^n(i) > 0\}}}}{3(n-i)}}\Biggr] \le \frac{2C}{3}\sqrt{n \varepsilon +1}.
\end{equation}
\begin{equation} \label{eqn:rootn}
\mathbb {E}\Biggl[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{T_0-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) >
0\}}}}{3(n-i)}}\Biggr]+ \mathbb {E}\Biggl[{\sum_{k=1}^{n} \sum_{i=S_k}^{T_k-1} \frac{X_1^n(i) -
{{\bf 1}_{\{X_1^n(i) > 0\}}}}{3(n-i)}}\Biggr] \le \frac{2C}{3}\sqrt{n \varepsilon +1}.
\end{equation}
It therefore remains to deal with the term
 $\mathbb {E}\Biggl[{\sum_{k=1}^{n} \sum_{i=T_{k-1}}^{S_k-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) >
0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\Biggr].$
$\mathbb {E}\Biggl[{\sum_{k=1}^{n} \sum_{i=T_{k-1}}^{S_k-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) >
0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\Biggr].$
Now note from (2.4) that
 \begin{align}
&\bigg(X_1^n(k) + \sum_{i=0}^{k-1}\frac{2X_1^n(i) - 2{{\bf 1}_{\{X_1^n(i) > 0\}}} +
X^n_2(i) - {{\bf 1}_{\{X_1^n(i) = 0, X_2^n(i) > 0\}}}}{3U^n(i) + 4 V^n(i) + X^n(i) -
{{\bf 1}_{\{X^n(i) > 0\}}}}\\
&\quad - \sum_{i=0}^{k-1} {{\bf 1}_{\{X_1^n(i) = 0, X_2^n(i)
> 0\}}} - 2\sum_{i=0}^{k-1} {{\bf 1}_{\{X_1^n(i) = X_2^n(i) = 0\}}} , \, k \ge 0\bigg)
\end{align}
\begin{align}
&\bigg(X_1^n(k) + \sum_{i=0}^{k-1}\frac{2X_1^n(i) - 2{{\bf 1}_{\{X_1^n(i) > 0\}}} +
X^n_2(i) - {{\bf 1}_{\{X_1^n(i) = 0, X_2^n(i) > 0\}}}}{3U^n(i) + 4 V^n(i) + X^n(i) -
{{\bf 1}_{\{X^n(i) > 0\}}}}\\
&\quad - \sum_{i=0}^{k-1} {{\bf 1}_{\{X_1^n(i) = 0, X_2^n(i)
> 0\}}} - 2\sum_{i=0}^{k-1} {{\bf 1}_{\{X_1^n(i) = X_2^n(i) = 0\}}} , \, k \ge 0\bigg)
\end{align}
is a martingale. Since ![]() $X_1^n$ does not touch 0 on the time interval [T k−1, S k − 1], we have, by the optional stopping theorem,
$X_1^n$ does not touch 0 on the time interval [T k−1, S k − 1], we have, by the optional stopping theorem,
 \begin{align}
& \mathbb {E}\,\bigg[{\sum_{i=T_{k-1}}^{S_k-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) > 0\}}}}{3U^n(i)
+ 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\bigg]
\\
&\quad\quad = \frac{1}{2} \mathbb {E}{X_1^n(T_{k-1}) - X_1^n(S_{k})} -
\frac{1}{2}\mathbb {E}\,\bigg[{\sum_{i=T_{k-1}}^{S_k-1} \frac{X^n_2(i) -{{\bf 1}_{\{X_1^n(i) = 0,
X_2^n(i) > 0\}}}}{3U^n(i) + 4 V^n(i) + X^n(i) - {{\bf 1}_{\{X^n(i)
> 0\}}}} }\bigg]
\\
&\quad\quad \le \tfrac{1}{2} \mathbb {E}{X_1^n(T_{k-1})}\\
&\quad\quad\le \frac{C \mathbb {E}{\sqrt{n-T_{k-1}}}}{2}
\\
&\quad\quad\le \frac{C \sqrt{n - \mathbb {E}{T_{k-1}}}}{2},
\end{align}
\begin{align}
& \mathbb {E}\,\bigg[{\sum_{i=T_{k-1}}^{S_k-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) > 0\}}}}{3U^n(i)
+ 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\bigg]
\\
&\quad\quad = \frac{1}{2} \mathbb {E}{X_1^n(T_{k-1}) - X_1^n(S_{k})} -
\frac{1}{2}\mathbb {E}\,\bigg[{\sum_{i=T_{k-1}}^{S_k-1} \frac{X^n_2(i) -{{\bf 1}_{\{X_1^n(i) = 0,
X_2^n(i) > 0\}}}}{3U^n(i) + 4 V^n(i) + X^n(i) - {{\bf 1}_{\{X^n(i)
> 0\}}}} }\bigg]
\\
&\quad\quad \le \tfrac{1}{2} \mathbb {E}{X_1^n(T_{k-1})}\\
&\quad\quad\le \frac{C \mathbb {E}{\sqrt{n-T_{k-1}}}}{2}
\\
&\quad\quad\le \frac{C \sqrt{n - \mathbb {E}{T_{k-1}}}}{2},
\end{align}
where the last inequality follows using Jensen’s inequality. So we have
 \begin{equation} \label{eqn:sum}
\begin{aligned}
& \mathbb {E}\,\bigg[{\sum_{k=1}^{n} \sum_{i=T_{k-1}}^{S_k-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) > 0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\bigg] \le \frac{C}{2} \sum_{k=0}^n \sqrt{n - \mathbb {E}{T_{k}}}.
\end{aligned}
\end{equation}
\begin{equation} \label{eqn:sum}
\begin{aligned}
& \mathbb {E}\,\bigg[{\sum_{k=1}^{n} \sum_{i=T_{k-1}}^{S_k-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) > 0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\bigg] \le \frac{C}{2} \sum_{k=0}^n \sqrt{n - \mathbb {E}{T_{k}}}.
\end{aligned}
\end{equation}
We thus need a lower bound on ![]() $\mathbb {E}{T_k}$ for any k. Let us assume that at some time ⌊n(1−ε)⌋ ≤ ℓ < n, we have
$\mathbb {E}{T_k}$ for any k. Let us assume that at some time ⌊n(1−ε)⌋ ≤ ℓ < n, we have ![]() $X_1^n(\ell) = 0$. In order to find such a lower bound, we use the coupling from Section 2.2, which yields an SSRW reflected above 2, Yn, such that Yn(ℓ) = 2 and
$X_1^n(\ell) = 0$. In order to find such a lower bound, we use the coupling from Section 2.2, which yields an SSRW reflected above 2, Yn, such that Yn(ℓ) = 2 and ![]() $X_1^n(i) \le Y^n(i)$ for all i ≥ ℓ. Recall that
$X_1^n(i) \le Y^n(i)$ for all i ≥ ℓ. Recall that ![]() $ (Y^n(i))_{i \ge \ell} {\underline {\rm{D}}
} (2 + |Z(i)|)_{i \ge \ell} $, where Z is an SSRW with Z(ℓ) = 0. Then if
$ (Y^n(i))_{i \ge \ell} {\underline {\rm{D}}
} (2 + |Z(i)|)_{i \ge \ell} $, where Z is an SSRW with Z(ℓ) = 0. Then if ![]() $\sigma =
\inf\{i \ge \ell\colon 2+|Z(i)| = \left\lfloor{C \sqrt{n-i}}\right\rfloor\}$, we have σ stochastically smaller than T k conditioned on S k = ℓ. Now, (Z(i)2 − i)i≥ℓ is a martingale, and so 𝔼[Z(σ)2 – σ] = –ℓ. But
$\sigma =
\inf\{i \ge \ell\colon 2+|Z(i)| = \left\lfloor{C \sqrt{n-i}}\right\rfloor\}$, we have σ stochastically smaller than T k conditioned on S k = ℓ. Now, (Z(i)2 − i)i≥ℓ is a martingale, and so 𝔼[Z(σ)2 – σ] = –ℓ. But
 \begin{align}
\mathbb {E}\,[{Z(\sigma)^2}] &= \mathbb {E}\,[{(\left\lfloor{C\sqrt{n-\sigma}}\right\rfloor - 2)^2}]
\\
& \ge \mathbb {E}\,[{(C \sqrt{n-\sigma} - 3)^2}]
\\
& \ge C^2 (n - \mathbb {E}{\sigma}) - 6 C \mathbb {E}\,[{\sqrt{n - \sigma}}\ ].
\end{align}
\begin{align}
\mathbb {E}\,[{Z(\sigma)^2}] &= \mathbb {E}\,[{(\left\lfloor{C\sqrt{n-\sigma}}\right\rfloor - 2)^2}]
\\
& \ge \mathbb {E}\,[{(C \sqrt{n-\sigma} - 3)^2}]
\\
& \ge C^2 (n - \mathbb {E}{\sigma}) - 6 C \mathbb {E}\,[{\sqrt{n - \sigma}}\ ].
\end{align}
Since n − σ ∈ ℤ, we have the very crude bound ![]() $\sqrt{n-\sigma} \le n-\sigma$. Hence,
$\sqrt{n-\sigma} \le n-\sigma$. Hence,
Then 𝔼[σ] ≥ ((C 2 – 6C)n + ℓ)/(C 2 – 6C + 1). By the stochastic domination, for k ≥ 1 we obtain 𝔼[Tk] ≥ ((C 2 – 6C)n + 𝔼[Sk])/(C 2 – 6C + 1). Since S k ≥ T k−1, we obtain 𝔼[Tk] ≥ ((C 2 – 6C)n + 𝔼[T k–1])/(C 2 – 6C + 1), and so n – 𝔼[Tk] ≤ (n–𝔼[T k–1])/(C 2 – 6C + 1). By induction,
since T 0 ≥ ⌊n(1 − ε)⌋. It follows from (6.5) that
 \begin{aligned}
\mathbb {E}\,\bigg[{\sum_{k=1}^{n} \sum_{i=T_{k-1}}^{S_k-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) >
0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\bigg] & \le \frac{C\sqrt{C^2 -
6C+1}\sqrt{n \varepsilon + 1}}{2(\sqrt{C^2 - 6C+1} - 1)} .
\end{aligned}
\begin{aligned}
\mathbb {E}\,\bigg[{\sum_{k=1}^{n} \sum_{i=T_{k-1}}^{S_k-1} \frac{X_1^n(i) - {{\bf 1}_{\{X_1^n(i) >
0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\bigg] & \le \frac{C\sqrt{C^2 -
6C+1}\sqrt{n \varepsilon + 1}}{2(\sqrt{C^2 - 6C+1} - 1)} .
\end{aligned}
Putting this together with (6.2), (6.3), and (6.4), we obtain
 \begin{align}
\mathbb {E}{N^n(n) - N^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)} & \le \frac{1}{6}(\log(\left\lceil {n\varepsilon } \right\rceil) + 1) + C \sqrt{n
\varepsilon+1} \\
&\quad + \frac{C\sqrt{C^2 - 6C+1}\sqrt{n \varepsilon +
1}}{2(\sqrt{C^2 - 6C+1} - 1)} + \mathbb {E}{V^n(\left\lfloor{(1-\varepsilon)n}\right\rfloor)}\,.
\end{align}
\begin{align}
\mathbb {E}{N^n(n) - N^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)} & \le \frac{1}{6}(\log(\left\lceil {n\varepsilon } \right\rceil) + 1) + C \sqrt{n
\varepsilon+1} \\
&\quad + \frac{C\sqrt{C^2 - 6C+1}\sqrt{n \varepsilon +
1}}{2(\sqrt{C^2 - 6C+1} - 1)} + \mathbb {E}{V^n(\left\lfloor{(1-\varepsilon)n}\right\rfloor)}\,.
\end{align}
Using (6.1), we have lim supn–∞ 𝔼[Vn(⌊n(1 – ɛ)⌋)]/α(n) ≤ 2ɛ 4/3. Hence,
 \begin{align}
&\limsup_{n \to \infty} \frac{1}{\alpha(n) \vee \sqrt{n}\,} \mathbb {E}[{N^n(n) -
N^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)]}
\\
&\quad\quad\le \left(C + \frac{C\sqrt{C^2 - 6C+1}}{2(\sqrt{C^2 - 6C+1} - 1)}
\right) \sqrt{\varepsilon} + 2 \varepsilon^{4/3}.\label{eqn:Nnbound}
\end{align}
\begin{align}
&\limsup_{n \to \infty} \frac{1}{\alpha(n) \vee \sqrt{n}\,} \mathbb {E}[{N^n(n) -
N^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)]}
\\
&\quad\quad\le \left(C + \frac{C\sqrt{C^2 - 6C+1}}{2(\sqrt{C^2 - 6C+1} - 1)}
\right) \sqrt{\varepsilon} + 2 \varepsilon^{4/3}.\label{eqn:Nnbound}
\end{align}
Applying Markov’s inequality and taking ε → 0 then yields, for δ > 0,
(c) We will show that ![]() $ \mathbb {E}{\sup_{\left\lfloor{n(1-\varepsilon)}\right\rfloor \le i \le n} X^n(i)}/{(\alpha(n) \vee \sqrt{n})}$ is small. We again use the coupling of
$ \mathbb {E}{\sup_{\left\lfloor{n(1-\varepsilon)}\right\rfloor \le i \le n} X^n(i)}/{(\alpha(n) \vee \sqrt{n})}$ is small. We again use the coupling of ![]() $X^n_1$ with Yn, but started now with
$X^n_1$ with Yn, but started now with ![]() $Y^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor) = X_1^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)+2$. This gives
$Y^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor) = X_1^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)+2$. This gives
Since ![]() $X^n(i) = X_1^n(i) + X_2^n(i)$ with
$X^n(i) = X_1^n(i) + X_2^n(i)$ with ![]() $X_2^n(i) \le V^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)$ for i ≥ ⌊n(1 − ε)⌋, we have
$X_2^n(i) \le V^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)$ for i ≥ ⌊n(1 − ε)⌋, we have
and so we obtain
 \begin{align}
& \frac{1}{\alpha(n) \vee \sqrt{n}\,}\mathbb {E}\,\Big[{\sup_{\left\lfloor{n(1-\varepsilon)}\right\rfloor \le i
\le n} X^n(i)}\Big]
\\
& \quad\quad \le \frac{2+ \mathbb {E}[{V^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)]} +
\mathbb {E}[{X_1^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)]}}{\alpha(n) \vee \sqrt{n}} +
\frac{1}{\sqrt{n}\,} \mathbb {E}\,\Big[{\sup_{0 \le i \le \left\lceil {n\varepsilon } \right\rceil} |Z(i)|}\Big]
\\
& \quad\quad \le \frac{2+\mathbb {E}[{V^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)]}+
\mathbb {E}[{X_1^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)]} }{\alpha(n)\vee \sqrt{n}} + 2
\sqrt{\varepsilon},
\end{align}
\begin{align}
& \frac{1}{\alpha(n) \vee \sqrt{n}\,}\mathbb {E}\,\Big[{\sup_{\left\lfloor{n(1-\varepsilon)}\right\rfloor \le i
\le n} X^n(i)}\Big]
\\
& \quad\quad \le \frac{2+ \mathbb {E}[{V^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)]} +
\mathbb {E}[{X_1^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)]}}{\alpha(n) \vee \sqrt{n}} +
\frac{1}{\sqrt{n}\,} \mathbb {E}\,\Big[{\sup_{0 \le i \le \left\lceil {n\varepsilon } \right\rceil} |Z(i)|}\Big]
\\
& \quad\quad \le \frac{2+\mathbb {E}[{V^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)]}+
\mathbb {E}[{X_1^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)]} }{\alpha(n)\vee \sqrt{n}} + 2
\sqrt{\varepsilon},
\end{align}
by Doob’s L 2 inequality. We have already shown that ![]() $\lim_{\varepsilon \to 0} \limsup_{n \to \infty} \mathbb {E}\,[V^n(\left\lfloor{n(1{-}\varepsilon)}\right\rfloor)]{(\alpha(n) \vee \sqrt{n})} = 0$. For
$\lim_{\varepsilon \to 0} \limsup_{n \to \infty} \mathbb {E}\,[V^n(\left\lfloor{n(1{-}\varepsilon)}\right\rfloor)]{(\alpha(n) \vee \sqrt{n})} = 0$. For ![]() $\alpha(n)/\sqrt{n} \to a$, we have
$\alpha(n)/\sqrt{n} \to a$, we have ![]() $X^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)/{\sqrt{n} \underrightarrow {\rm D} X^a_{1-\varepsilon}}$ as n → ∞. By Lemma 2.1,
$X^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)/{\sqrt{n} \underrightarrow {\rm D} X^a_{1-\varepsilon}}$ as n → ∞. By Lemma 2.1, ![]() $ (X^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)/\sqrt{n}) $ is a uniformly integrable sequence of random variables, and so we obtain
$ (X^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)/\sqrt{n}) $ is a uniformly integrable sequence of random variables, and so we obtain ![]() $\mathbb {E}{X^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)/\sqrt{n}} \to \mathbb {E}{X^a_{1-\varepsilon}}$ as n → ∞. Hence,
$\mathbb {E}{X^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)/\sqrt{n}} \to \mathbb {E}{X^a_{1-\varepsilon}}$ as n → ∞. Hence,
By the final statement of Proposition 5.1, we have ![]() $\mathbb {P}{X_{1-\varepsilon}^a > r \sqrt{\varepsilon}} \le \text {e}^{-(r-a)^2/6}$ for r > a and it follows, in particular, that
$\mathbb {P}{X_{1-\varepsilon}^a > r \sqrt{\varepsilon}} \le \text {e}^{-(r-a)^2/6}$ for r > a and it follows, in particular, that ![]() $\mathbb {E}{X_{1-\varepsilon}^a} \le C \sqrt{\varepsilon}$ for some constant C > 0.
$\mathbb {E}{X_{1-\varepsilon}^a} \le C \sqrt{\varepsilon}$ for some constant C > 0.
For ![]() $\alpha(n) \gg \sqrt{n}$, we have
$\alpha(n) \gg \sqrt{n}$, we have ![]() $X^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)/\alpha(n) \underrightarrow{\rm P} \varepsilon^{2/3} - \varepsilon^{4/3}$. Again, using the uniform integrability from Lemma 2.1, we obtain 𝔼[Xn(⌊n(1 – ε)⌋)]/α(n) → ε 2/3 – ε 4/3 and so we have lim supn→∞ (𝔼 [sup⌊n(1–ε)⌋≤i≤n Xn(i)]/α(n)) ≤ 2ε 4/3 + ε 2/3 – ε 4/3. Hence, for any α(n),
$X^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)/\alpha(n) \underrightarrow{\rm P} \varepsilon^{2/3} - \varepsilon^{4/3}$. Again, using the uniform integrability from Lemma 2.1, we obtain 𝔼[Xn(⌊n(1 – ε)⌋)]/α(n) → ε 2/3 – ε 4/3 and so we have lim supn→∞ (𝔼 [sup⌊n(1–ε)⌋≤i≤n Xn(i)]/α(n)) ≤ 2ε 4/3 + ε 2/3 – ε 4/3. Hence, for any α(n),
and another application of Markov’s inequality gives
(d) Recall that the standard martingale associated with Xn is
 \begin{equation}M_X^n(k) = X^n(k) +\frac{1}{2}V^n(k) - L^n(k) + \sum_{i=0}^{k-1}
\frac{2X^n(i) - 2 {{\bf 1}_{\{X^n(i) > 0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) - {{\bf 1}_{\{X^n(i)
> 0\}}}}.
\end{equation}
\begin{equation}M_X^n(k) = X^n(k) +\frac{1}{2}V^n(k) - L^n(k) + \sum_{i=0}^{k-1}
\frac{2X^n(i) - 2 {{\bf 1}_{\{X^n(i) > 0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) - {{\bf 1}_{\{X^n(i)
> 0\}}}}.
\end{equation}
It follows that
 \begin{align}
\mathbb {E}[{X^n(n) - X^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor}] & = \mathbb {E}[{L^n(n) - L^n(\left\lfloor{n(1 - \varepsilon)}\right\rfloor)}] + \tfrac{1}{2}
\mathbb {E}[{V^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor) - V^n(n)}]\\
&\quad- \mathbb {E}\Biggl[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1}\frac{2X^n(i) - 2
{{\bf 1}_{\{X^n(i)
> 0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) - {{\bf 1}_{\{X^n(i) > 0\}}}}}\Biggr].
\end{align}
\begin{align}
\mathbb {E}[{X^n(n) - X^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor}] & = \mathbb {E}[{L^n(n) - L^n(\left\lfloor{n(1 - \varepsilon)}\right\rfloor)}] + \tfrac{1}{2}
\mathbb {E}[{V^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor) - V^n(n)}]\\
&\quad- \mathbb {E}\Biggl[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1}\frac{2X^n(i) - 2
{{\bf 1}_{\{X^n(i)
> 0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) - {{\bf 1}_{\{X^n(i) > 0\}}}}}\Biggr].
\end{align}
Now, from (2.2) we have
 $\mathbb {E}{N^n(n) - N^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)} \ge
\mathbb {E}\Biggl[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1} \frac{X^n(i) - {{\bf 1}_{\{X^n(i) >
0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\Biggr].$
$\mathbb {E}{N^n(n) - N^n(\left\lfloor{n(1-\varepsilon)}\right\rfloor)} \ge
\mathbb {E}\Biggl[{\sum_{i=\left\lfloor{n(1-\varepsilon)}\right\rfloor}^{n-1} \frac{X^n(i) - {{\bf 1}_{\{X^n(i) >
0\}}}}{3U^n(i) + 4V^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}}}}\Biggr].$
Hence,
Applying Markov’s inequality and using (6.6) and (6.7), we obtain, for any δ > 0,
Lemma 6.1
We have Un(n) ≤ Nn(n) + 3Vn(0).
Proof. At each step we either connect to a node of degree 3 or 4, or there is a clash. Each node of degree 3 is removed after we connect to it, and each node of degree 4 can be visited at most twice before being removed. Thus, during the first n steps, a node of degree 3 is removed at least n − Nn(n) − 2Vn(0) times. Moreover, at most Vn(0) nodes of degree 4 become nodes of degree 3. Hence, Un(n) ≤ Un(0) − (n − Nn(n) − 2Vn(0)) + Vn(0) = Nn(n) + 3Vn(0).
We finally turn to the behaviour of our processes on the time interval [n, ζ n].
Proposition 6.2
As n → ∞,
(a)
 $\zeta_n/n \underrightarrow{\rm P} 1$;
$\zeta_n/n \underrightarrow{\rm P} 1$;(b)
 $ ({1}/{\alpha(n) \vee \sqrt{n}}) \sup_{n \le i \le \zeta_n} X^n(i) \underrightarrow{\rm P} 0 $;
$ ({1}/{\alpha(n) \vee \sqrt{n}}) \sup_{n \le i \le \zeta_n} X^n(i) \underrightarrow{\rm P} 0 $;(c)
 $ (N^n(\zeta_n) - N^n(n))/{(\alpha(n) \vee \sqrt{n})} \underrightarrow{\rm P} 0$;
$ (N^n(\zeta_n) - N^n(n))/{(\alpha(n) \vee \sqrt{n})} \underrightarrow{\rm P} 0$;(d)
 $ (L^n(\zeta_n) - L^n(n))/{(\alpha(n) \vee \sqrt{n})} \underrightarrow{\rm P} 0$.
$ (L^n(\zeta_n) - L^n(n))/{(\alpha(n) \vee \sqrt{n})} \underrightarrow{\rm P} 0$.
Proof. Write ![]() $\bar{\alpha}(n) = \alpha(n) \vee \sqrt{n}$.
$\bar{\alpha}(n) = \alpha(n) \vee \sqrt{n}$.
(a) As in each step we remove at least two half-edges, by the same argument as gave us the bound ζ n ≤ 3n + 4α(n) in Section 2.2, we have ζ n − n ≤ 3Un(n) + 4Vn(n) ≤ 3Un(n) + 4α(n). So Lemma 6.1 implies that
If ![]() $\alpha(n)/{\sqrt{n}} \to a$ then
$\alpha(n)/{\sqrt{n}} \to a$ then ![]() $N^n(n)/{\sqrt{n} \underrightarrow {\rm D}} N_1^a$, and it follows that
$N^n(n)/{\sqrt{n} \underrightarrow {\rm D}} N_1^a$, and it follows that ![]() $\zeta_n/n \underrightarrow{\rm P} 1$ and, indeed, that
$\zeta_n/n \underrightarrow{\rm P} 1$ and, indeed, that ![]() $ (\zeta_n - n)/{\sqrt{n}} $ is a tight sequence of random variables. If, on the other hand,
$ (\zeta_n - n)/{\sqrt{n}} $ is a tight sequence of random variables. If, on the other hand, ![]() $\alpha(n) \gg {\sqrt{n}}$, we have
$\alpha(n) \gg {\sqrt{n}}$, we have ![]() $N^n(n)/\alpha(n) \underrightarrow{\rm P} \tfrac14$, and again we obtain
$N^n(n)/\alpha(n) \underrightarrow{\rm P} \tfrac14$, and again we obtain ![]() $\zeta_n/n \underrightarrow{\rm P} 1$ with (ζ n − n)/α(n) a tight sequence of random variables.
$\zeta_n/n \underrightarrow{\rm P} 1$ with (ζ n − n)/α(n) a tight sequence of random variables.
(b) By the usual coupling with Yn, we have
where ![]() $ (Y^n(n+i))_{0 \le i \le \zeta_n-n} {\underline {\rm{D}}
} (2 + |X_1^n(n) + Z(i)|)_{0 \le i \le \zeta_n - n} $. Fix δ > 0. Then, for any C > 13, since
$ (Y^n(n+i))_{0 \le i \le \zeta_n-n} {\underline {\rm{D}}
} (2 + |X_1^n(n) + Z(i)|)_{0 \le i \le \zeta_n - n} $. Fix δ > 0. Then, for any C > 13, since ![]() $\sup_{0 \le i \le C\bar{\alpha}(n)} |Z(i)|/\sqrt{\bar{\alpha}(n)}$ is bounded in L 2, we have
$\sup_{0 \le i \le C\bar{\alpha}(n)} |Z(i)|/\sqrt{\bar{\alpha}(n)}$ is bounded in L 2, we have
 \begin{align}
& \limsup_{n \to \infty} \mathbb {P}\,\bigg({\frac{\sup_{0 \le i \le \zeta_n-n}
|Z(i)|}{\bar{\alpha}(n)} > \frac{\delta}{2}}\bigg)
\\
& \quad\quad \le \limsup_{n \to \infty} \mathbb {P}\,\bigg({\frac{\sup_{0 \le i \le
C\bar{\alpha}(n)} |Z(i)|}{\bar{\alpha}(n)} > \frac{\delta}{2}}\bigg) +
\limsup_{n \to \infty} \mathbb {P}({\zeta_n - n > C \bar{\alpha}(n))}
\\
& \quad\quad \le \mathbb {P}\,\bigg({N_1 > \frac{C -13}{3}}\bigg),
\end{align}
\begin{align}
& \limsup_{n \to \infty} \mathbb {P}\,\bigg({\frac{\sup_{0 \le i \le \zeta_n-n}
|Z(i)|}{\bar{\alpha}(n)} > \frac{\delta}{2}}\bigg)
\\
& \quad\quad \le \limsup_{n \to \infty} \mathbb {P}\,\bigg({\frac{\sup_{0 \le i \le
C\bar{\alpha}(n)} |Z(i)|}{\bar{\alpha}(n)} > \frac{\delta}{2}}\bigg) +
\limsup_{n \to \infty} \mathbb {P}({\zeta_n - n > C \bar{\alpha}(n))}
\\
& \quad\quad \le \mathbb {P}\,\bigg({N_1 > \frac{C -13}{3}}\bigg),
\end{align}
where, for the last inequality, we recall (6.9). We have ![]() $V^n(n)/\bar{\alpha}(n) \underrightarrow{\rm P} 0$ by Proposition 6.1(a) and
$V^n(n)/\bar{\alpha}(n) \underrightarrow{\rm P} 0$ by Proposition 6.1(a) and ![]() $X^n(n)/\bar{\alpha}(n) \underrightarrow{\rm P} 0$, so, since C > 13 was arbitrary, we obtain
$X^n(n)/\bar{\alpha}(n) \underrightarrow{\rm P} 0$, so, since C > 13 was arbitrary, we obtain ![]() $ ({1}/{\bar{\alpha}(n)})
\sup_{n \le i \le \zeta_n} X^n(i) \underrightarrow{\rm P} 0 $.
$ ({1}/{\bar{\alpha}(n)})
\sup_{n \le i \le \zeta_n} X^n(i) \underrightarrow{\rm P} 0 $.
(c) We have
 \begin{align}\label{eqn:split}
& \mathbb {P}\Bigg({\frac{1}{\bar{\alpha}(n)} (N^n(\zeta_n) - N^n(n)) > \delta}\Bigg)
\\
& \quad\quad \le \mathbb {P}\,\bigg({\frac{1}{\bar{\alpha}(n)}(N^n(\zeta_n) - N^n(n)) >
\delta, \frac{N^n(n)}{\bar{\alpha}(n)} \le \frac{1}{\varepsilon} }\bigg) +
\mathbb {P}\,\bigg({\frac{N^n(n)}{\bar{\alpha}(n)} > \frac{1}{\varepsilon}}\bigg)
\\
& \quad\quad \le \frac{1}{\delta \bar{\alpha}(n)}\mathbb {E}\,[{(N^n(\zeta_n) - N^n(n))
{{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le {1}/{\varepsilon\}}}} }] + \varepsilon
\frac{\mathbb {E}[{N^n(n)}]}{\bar{\alpha}(n)}.
\end{align}
\begin{align}\label{eqn:split}
& \mathbb {P}\Bigg({\frac{1}{\bar{\alpha}(n)} (N^n(\zeta_n) - N^n(n)) > \delta}\Bigg)
\\
& \quad\quad \le \mathbb {P}\,\bigg({\frac{1}{\bar{\alpha}(n)}(N^n(\zeta_n) - N^n(n)) >
\delta, \frac{N^n(n)}{\bar{\alpha}(n)} \le \frac{1}{\varepsilon} }\bigg) +
\mathbb {P}\,\bigg({\frac{N^n(n)}{\bar{\alpha}(n)} > \frac{1}{\varepsilon}}\bigg)
\\
& \quad\quad \le \frac{1}{\delta \bar{\alpha}(n)}\mathbb {E}\,[{(N^n(\zeta_n) - N^n(n))
{{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le {1}/{\varepsilon\}}}} }] + \varepsilon
\frac{\mathbb {E}[{N^n(n)}]}{\bar{\alpha}(n)}.
\end{align}
Let η n = inf{i ≥ n: Un(i) ≤ ε ᾱ(n)}. We have ζ n − η n ≤ 3Un(η n) + 4Vn(n) ≤ 3ε ᾱ(n) and ζ n − n ≤ 3Nn(n). Now
 \begin{align}
& \mathbb {E}\,[{(N^n(\zeta_n) - N^n(n)) {{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le
{1}/{\varepsilon\}}}}}]
\\
&\quad\quad {\begin{gathered}\le \mathbb {E} \biggl[
\sum_{i=n}^{\zeta_n - 1} \frac{3U^n(i) + 2(X^n(i) - {{\bf 1}_{\{X^n(i) >
0\}}})(3U^n(i) + 4V^n(i) + X^n(i) - 3)} {2(3U^n(i) + 4V^n(i) + X^n(i)
-{{\bf 1}_{\{X^n(i) > 0\}}})(3U^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}} - 2)}\end{gathered}}\\
& \phantom{\sum_{i=n}^{\zeta_n - 1}}\times {{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le
{1}/{\varepsilon\}}}} \biggr]
\\
&\quad\quad \le \mathbb {E}\Biggl[{\sum_{i=n}^{\zeta_n - 1} \left(\frac{X^n(i) + 1}{3 U^n(i)}
\wedge 1\right) {{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le {1}/{\varepsilon\}}}}}\Biggr]
\\
&\quad\quad \le \mathbb {E}\Biggl[{\sum_{i=n}^{\eta_n} \left(\frac{X^n(i) + 1}{3 \varepsilon
\bar{\alpha}(n)}\wedge 1\right) {{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le
{1}/{\varepsilon\}}}}}\Biggr] + 3 \varepsilon \bar{\alpha}(n)
\\
&\quad\quad \le \frac{1}{\varepsilon^2} \mathbb {E}\,\Biggl[{ \bigg(\bigg(1+\sup_{n \le i \le
\zeta_n} X^n(i) \bigg) \wedge 3 \varepsilon \bar{\alpha}(n) \bigg)
{{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le {1}/{\varepsilon\}}}}}\Biggr] + 3 \varepsilon
\bar{\alpha}(n).
\end{align}
\begin{align}
& \mathbb {E}\,[{(N^n(\zeta_n) - N^n(n)) {{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le
{1}/{\varepsilon\}}}}}]
\\
&\quad\quad {\begin{gathered}\le \mathbb {E} \biggl[
\sum_{i=n}^{\zeta_n - 1} \frac{3U^n(i) + 2(X^n(i) - {{\bf 1}_{\{X^n(i) >
0\}}})(3U^n(i) + 4V^n(i) + X^n(i) - 3)} {2(3U^n(i) + 4V^n(i) + X^n(i)
-{{\bf 1}_{\{X^n(i) > 0\}}})(3U^n(i) + X^n(i) -{{\bf 1}_{\{X^n(i) > 0\}}} - 2)}\end{gathered}}\\
& \phantom{\sum_{i=n}^{\zeta_n - 1}}\times {{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le
{1}/{\varepsilon\}}}} \biggr]
\\
&\quad\quad \le \mathbb {E}\Biggl[{\sum_{i=n}^{\zeta_n - 1} \left(\frac{X^n(i) + 1}{3 U^n(i)}
\wedge 1\right) {{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le {1}/{\varepsilon\}}}}}\Biggr]
\\
&\quad\quad \le \mathbb {E}\Biggl[{\sum_{i=n}^{\eta_n} \left(\frac{X^n(i) + 1}{3 \varepsilon
\bar{\alpha}(n)}\wedge 1\right) {{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le
{1}/{\varepsilon\}}}}}\Biggr] + 3 \varepsilon \bar{\alpha}(n)
\\
&\quad\quad \le \frac{1}{\varepsilon^2} \mathbb {E}\,\Biggl[{ \bigg(\bigg(1+\sup_{n \le i \le
\zeta_n} X^n(i) \bigg) \wedge 3 \varepsilon \bar{\alpha}(n) \bigg)
{{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le {1}/{\varepsilon\}}}}}\Biggr] + 3 \varepsilon
\bar{\alpha}(n).
\end{align}
By the coupling, the expectation is bounded by
Now
is a bounded random variable which converges to 0 in probability, and so we obtain
Now note that, combining Theorem 4.1, (5.4), and (6.6), there exists a constant C > 0 such that ![]() $\sup_{n \ge 1} (\mathbb {E}{N^n(n)}/\bar{\alpha}(n)) < C$ and so, using (6.10), we obtain
$\sup_{n \ge 1} (\mathbb {E}{N^n(n)}/\bar{\alpha}(n)) < C$ and so, using (6.10), we obtain
Since ε > 0 was arbitrary, we get ![]() $ (N^n(\zeta_n) - N^n(n))/\bar{\alpha}(n) \underrightarrow{\rm P} 0$.
$ (N^n(\zeta_n) - N^n(n))/\bar{\alpha}(n) \underrightarrow{\rm P} 0$.
Finally, we observe that, using the martingale ![]() $M_X^n$ defined in (6.8) and the optional stopping theorem, we have
$M_X^n$ defined in (6.8) and the optional stopping theorem, we have ![]() $0 \le \mathbb {E}{(L^n(\zeta_n) - L^n(n)) {{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le {1}/{\varepsilon\}}}}}$ and
$0 \le \mathbb {E}{(L^n(\zeta_n) - L^n(n)) {{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le {1}/{\varepsilon\}}}}}$ and
 \begin{align}
& \mathbb {E}{(L^n(\zeta_n) - L^n(n)) {{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le
{1}/{\varepsilon\}}}}}
\\
& \quad\quad \le \mathbb {E}{(X^n(\zeta_n) - X^n(n)){{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le
{1}/{\varepsilon\}}}}} + 2 \mathbb {E}{(N^n(\zeta_n) - N^n(n))
{{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le {1}/{\varepsilon\}}}}}
\\
& \quad\quad \le 2 \mathbb {E}{(N^n(\zeta^n) - N^n(n)){{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)}
\le {1}/{\varepsilon\}}}}}\,,
\end{align}
\begin{align}
& \mathbb {E}{(L^n(\zeta_n) - L^n(n)) {{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le
{1}/{\varepsilon\}}}}}
\\
& \quad\quad \le \mathbb {E}{(X^n(\zeta_n) - X^n(n)){{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le
{1}/{\varepsilon\}}}}} + 2 \mathbb {E}{(N^n(\zeta_n) - N^n(n))
{{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le {1}/{\varepsilon\}}}}}
\\
& \quad\quad \le 2 \mathbb {E}{(N^n(\zeta^n) - N^n(n)){{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)}
\le {1}/{\varepsilon\}}}}}\,,
\end{align}
since Xn(ζ n) = 0 and Xn(n) ≥ 0. So then
 \begin{align}
& \mathbb {P}\,\bigg({ \frac{1}{\bar{\alpha}(n)} \left(L^n(\zeta_n) - L^n(n) \right) >
\delta}\bigg)
\\
& \quad\quad \le \mathbb {P}\,\bigg({\frac{1}{\bar{\alpha}(n)}(L^n(\zeta_n) - L^n(n)) >
\delta, \frac{N^n(n)}{\bar{\alpha}(n)} \le \frac{1}{\varepsilon} }\bigg) +
\mathbb {P}\,\bigg({\frac{N^n(n)}{\bar{\alpha}(n)} > \frac{1}{\varepsilon}}\bigg)
\\
& \quad\quad \le \frac{2}{\delta \bar{\alpha}(n)}\mathbb {E}{(N^n(\zeta_n) - N^n(n))
{{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le {1}/{\varepsilon\}}}} } + \varepsilon
\frac{\mathbb {E}{N^n(n)}}{\bar{\alpha}(n)},
\end{align}
\begin{align}
& \mathbb {P}\,\bigg({ \frac{1}{\bar{\alpha}(n)} \left(L^n(\zeta_n) - L^n(n) \right) >
\delta}\bigg)
\\
& \quad\quad \le \mathbb {P}\,\bigg({\frac{1}{\bar{\alpha}(n)}(L^n(\zeta_n) - L^n(n)) >
\delta, \frac{N^n(n)}{\bar{\alpha}(n)} \le \frac{1}{\varepsilon} }\bigg) +
\mathbb {P}\,\bigg({\frac{N^n(n)}{\bar{\alpha}(n)} > \frac{1}{\varepsilon}}\bigg)
\\
& \quad\quad \le \frac{2}{\delta \bar{\alpha}(n)}\mathbb {E}{(N^n(\zeta_n) - N^n(n))
{{\bf 1}_{\{{N^n(n)}/{\bar{\alpha}(n)} \le {1}/{\varepsilon\}}}} } + \varepsilon
\frac{\mathbb {E}{N^n(n)}}{\bar{\alpha}(n)},
\end{align}
and the rest of the argument goes through as before.
We now have all the elements needed to prove Theorem 2.1.
Proof of Theorem 2.1
(i) From Theorem 5.1 and Lemma 5.1, for any ε > 0 we have
By Proposition 5.1, we have (X 1−ε, L 1−ε, N 1−ε) → (0, L 1, N 1) almost surely as ε → 0. By the principle of accompanying laws (see Theorem 3.2 of [Reference Billingsley5]) the statement of Proposition 6.1 is exactly what we need in order to deduce that
Proposition 6.2 then allows us to conclude that
as desired.
(ii) From Theorem 4.1, for any ε > 0, we have
It is straightforward that x(1 − ε) → 0 and that ![]() $m(1-\varepsilon) \to \tfrac14$ as ε → 0. By another application of the principle of accompanying laws, and Propositions 6.1 and 6.2, we may then conclude that
$m(1-\varepsilon) \to \tfrac14$ as ε → 0. By another application of the principle of accompanying laws, and Propositions 6.1 and 6.2, we may then conclude that
as desired.
Appendix A
A.1. Proof of the invariance principle
Proof of Theorem 5.2
Let ![]() ${\theta}^n(r) = \inf\{t \ge 0\colon Q^n(t) >{\int_0^t \sup_{|y| \le r}} q(s,y) {\text {d}} s {+} 1 \}$. Set
${\theta}^n(r) = \inf\{t \ge 0\colon Q^n(t) >{\int_0^t \sup_{|y| \le r}} q(s,y) {\text {d}} s {+} 1 \}$. Set ![]() $\tilde{M}^n_r := M^n({\cdot}\wedge \theta^n(r) \wedge \tau^n(r))$. Relative compactness of
$\tilde{M}^n_r := M^n({\cdot}\wedge \theta^n(r) \wedge \tau^n(r))$. Relative compactness of ![]() $\{\tilde{M}^n_r\}_{n \ge 1}$ follows as in Theorem 4.1 of [Reference Ethier and Kurtz9, Chapter 7]. Conditions (c) and (d) imply that any subsequential weak limit has sample paths in ℂ(ℝ+, ℝ) almost surely. Then all of the conditions in Assumption 4.1 of [Reference Kang and Williams11] hold for the processes stopped at τn(r). It follows by Theorem 4.2 of [Reference Kang and Williams11] that the sequence of processes {(Yn, Mn, Ln)}n≥1 is tight and such that any subsequential weak limit almost surely has continuous sample paths.
$\{\tilde{M}^n_r\}_{n \ge 1}$ follows as in Theorem 4.1 of [Reference Ethier and Kurtz9, Chapter 7]. Conditions (c) and (d) imply that any subsequential weak limit has sample paths in ℂ(ℝ+, ℝ) almost surely. Then all of the conditions in Assumption 4.1 of [Reference Kang and Williams11] hold for the processes stopped at τn(r). It follows by Theorem 4.2 of [Reference Kang and Williams11] that the sequence of processes {(Yn, Mn, Ln)}n≥1 is tight and such that any subsequential weak limit almost surely has continuous sample paths.
Now fix r 0 > 0 and let {Ynk(· ∧ τnk(r 0)), Mnk(· ∧ τnk(r 0)), Lnk(· ∧ τnk(r 0))}k≥1 be a convergent subsequence with limit Y r0, M r0, L r0. Let τ r0(r) = inf{t ≥ 0: |Y r0(t)| ≥ r}. Then, for all but countably many r < r 0 (i.e. those such that ℙ (lims→r τ r0(s) = τ r0(r)) = 1), we have
 \begin{align}
& (Y^{n_k}({\cdot} \wedge \tau^{n_k}(r)), M^{n_k}({\cdot} \wedge
\tau^{n_k}(r)), L^{n_k}({\cdot} \wedge \tau^{n_k}(r)), \tau^{n_k}(r)) \\
&\quad\underrightarrow {\rm D} (Y_{r_0}({\cdot} \wedge \tau_{r_0}(r)), M_{r_0}(\cdot \wedge
\tau_{r_0}(r)), L_{r_0}({\cdot} \wedge \tau_{r_0}(r)), \tau_{r_0}(r)).
\end{align}
\begin{align}
& (Y^{n_k}({\cdot} \wedge \tau^{n_k}(r)), M^{n_k}({\cdot} \wedge
\tau^{n_k}(r)), L^{n_k}({\cdot} \wedge \tau^{n_k}(r)), \tau^{n_k}(r)) \\
&\quad\underrightarrow {\rm D} (Y_{r_0}({\cdot} \wedge \tau_{r_0}(r)), M_{r_0}(\cdot \wedge
\tau_{r_0}(r)), L_{r_0}({\cdot} \wedge \tau_{r_0}(r)), \tau_{r_0}(r)).
\end{align}
Conditions (f), (c), and (d) guarantee that Mnk (· ∧ τnk(r 0)) is a uniformly integrable martingale. Conditions (b), (g), and (e) guarantee that
is a uniformly integrable martingale. Thus, by Problem 7 of [Reference Ethier and Kurtz9, Chapter 7], as in the proof of Theorem 1.4(b) therein, it must follow that
and ![]() $M_{r_0}(t \wedge \tau_{r_0}(r))^2 - \int_0^{t \wedge \tau_{r_0}(r)} q(s, Y_{r_0}(s)){\text{d}} s$ are continuous martingales. It then follows that
$M_{r_0}(t \wedge \tau_{r_0}(r))^2 - \int_0^{t \wedge \tau_{r_0}(r)} q(s, Y_{r_0}(s)){\text{d}} s$ are continuous martingales. It then follows that ![]() $M_{r_0}(t \wedge \tau_{r_0}(r)) = \int_0^{t \wedge \tau_{r_0}(r)} \sigma(s, Y_{r_0}(s)) {\text{d}} W(s)$ for some Brownian motion W. But then we have
$M_{r_0}(t \wedge \tau_{r_0}(r)) = \int_0^{t \wedge \tau_{r_0}(r)} \sigma(s, Y_{r_0}(s)) {\text{d}} W(s)$ for some Brownian motion W. But then we have
Moreover, by (i), L r 0(0) = 0, L r 0 is nondecreasing, and ![]() ${\int_0^{t \wedge \tau_{r_0}(r)}} {{\bf 1}_{\{Y_{r_0}(s) > 0\}}} {\text{d}} L_{r_0}(s) = 0$ So (Y r 0, L r 0) solves a stopped version of the reflected SDE. But if (Y, L) is the unique solution of the reflected SDE with Brownian motion W then (Y(· ∧ τ(r)), L(· ∧ τ(r))) is the unique solution of the stopped version, where τ(r) t = inf{t ≥ 0: |Y(s)| ≥ r}. Consequently,
${\int_0^{t \wedge \tau_{r_0}(r)}} {{\bf 1}_{\{Y_{r_0}(s) > 0\}}} {\text{d}} L_{r_0}(s) = 0$ So (Y r 0, L r 0) solves a stopped version of the reflected SDE. But if (Y, L) is the unique solution of the reflected SDE with Brownian motion W then (Y(· ∧ τ(r)), L(· ∧ τ(r))) is the unique solution of the stopped version, where τ(r) t = inf{t ≥ 0: |Y(s)| ≥ r}. Consequently, ![]() $ (Y^n({\cdot} \wedge \tau^n(r)), L^n({\cdot} \wedge \tau^n(r))) {\underrightarrow {\rm D}} (Y({\cdot} \wedge \tau(r)), L({\cdot} \wedge \tau(r)) $ for any r such that ℙ(lims→r τ(s) = τ(r)) = 1. But τ(r) → ∞ as r → ∞, since Y has continuous sample paths. Hence,
$ (Y^n({\cdot} \wedge \tau^n(r)), L^n({\cdot} \wedge \tau^n(r))) {\underrightarrow {\rm D}} (Y({\cdot} \wedge \tau(r)), L({\cdot} \wedge \tau(r)) $ for any r such that ℙ(lims→r τ(s) = τ(r)) = 1. But τ(r) → ∞ as r → ∞, since Y has continuous sample paths. Hence, ![]() $ (Y^n, L^n) {\underrightarrow {\rm D}} (Y,L) $.
$ (Y^n, L^n) {\underrightarrow {\rm D}} (Y,L) $.
A.2. A hitting probability calculation
Fix ![]() $d \in (0,\tfrac12)$ and an integer b ≥ 1. Suppose that A is a random walk which makes steps of size −1 with probability
$d \in (0,\tfrac12)$ and an integer b ≥ 1. Suppose that A is a random walk which makes steps of size −1 with probability ![]() ${\textstyle{1 \over 2}}$, +1 with probability
${\textstyle{1 \over 2}}$, +1 with probability ![]() $\tfrac12 - d$, and +2 with probability d.
$\tfrac12 - d$, and +2 with probability d.
Lemma A.1
The probability, started from 1, that A hits 0 before {b, b + 1} is given by
Proof. For 0 ≤ k ≤ b + 1, let h k = ℙ (A hits 0 before {b, b + 1} | A(0) = k). Then, for 1 ≤ k ≤ b − 1, we have ![]() $h_k = \tfrac{1}{2} h_{k-1} + (\tfrac{1}{2} - d) h_{k+1} + d h_{k+2}$ and elementary calculations yield
$h_k = \tfrac{1}{2} h_{k-1} + (\tfrac{1}{2} - d) h_{k+1} + d h_{k+2}$ and elementary calculations yield ![]() $h_k = \varphi + \beta \lambda_{-}^k + \gamma \lambda_+^k$ for 0 ≤ k ≤ b + 1, where
$h_k = \varphi + \beta \lambda_{-}^k + \gamma \lambda_+^k$ for 0 ≤ k ≤ b + 1, where ![]() $\lambda_{\pm} = {(-1 \pm {\sqrt{1+8d}})}/{(4d)}$. The boundary conditions are h 0 = 1 and h b = h b+1 = 0. Solving for the constants gives
$\lambda_{\pm} = {(-1 \pm {\sqrt{1+8d}})}/{(4d)}$. The boundary conditions are h 0 = 1 and h b = h b+1 = 0. Solving for the constants gives
 \begin{gather}
\varphi = \frac{\lambda_{-}^{b+1} \lambda_{+}^b - \lambda_{-}^b
\lambda_{+}^{b+1}}{\lambda_{-}^{b+1} \lambda_+^b - \lambda_{-}^b
\lambda_{+}^{b+1} - \lambda_{-}^{b+1} + \lambda_{-}^b - \lambda_+^{b+1} +
\lambda_{+}^b},
\\
\beta = \frac{\lambda_{+}^b - \lambda_{+}^{b+1}}{\lambda_{-}^{b+1}
\lambda_+^b - \lambda_{-}^b \lambda_{+}^{b+1} - \lambda_{-}^{b+1} +
\lambda_{-}^b - \lambda_+^{b+1} + \lambda_{+}^b},
\\
\gamma = \frac{\lambda_{-}^b - \lambda_{-}^{b+1}}{\lambda_{-}^{b+1}
\lambda_+^b - \lambda_{-}^b \lambda_{+}^{b+1} - \lambda_{-}^{b+1} +
\lambda_{-}^b - \lambda_+^{b+1} + \lambda_{+}^b},
\end{gather}
\begin{gather}
\varphi = \frac{\lambda_{-}^{b+1} \lambda_{+}^b - \lambda_{-}^b
\lambda_{+}^{b+1}}{\lambda_{-}^{b+1} \lambda_+^b - \lambda_{-}^b
\lambda_{+}^{b+1} - \lambda_{-}^{b+1} + \lambda_{-}^b - \lambda_+^{b+1} +
\lambda_{+}^b},
\\
\beta = \frac{\lambda_{+}^b - \lambda_{+}^{b+1}}{\lambda_{-}^{b+1}
\lambda_+^b - \lambda_{-}^b \lambda_{+}^{b+1} - \lambda_{-}^{b+1} +
\lambda_{-}^b - \lambda_+^{b+1} + \lambda_{+}^b},
\\
\gamma = \frac{\lambda_{-}^b - \lambda_{-}^{b+1}}{\lambda_{-}^{b+1}
\lambda_+^b - \lambda_{-}^b \lambda_{+}^{b+1} - \lambda_{-}^{b+1} +
\lambda_{-}^b - \lambda_+^{b+1} + \lambda_{+}^b},
\end{gather}
and simplifying the expression for h 1 gives the claimed result.
Acknowledgements
We are very grateful to James Martin for valuable discussions. We would like to thank Ruth Williams for directing us to her paper [Reference Kang and Williams11] which very much facilitated our proof of the invariance principle. CG’s research was supported by EPSRC Fellowship EP/N004833/1. We are grateful to the referee for reading the paper carefully and for comments which led to several improvements.