2. Optimal stopping for random walks

In this section we use n ∈ ℤ+ (instead of t) to denote the discrete-time parameter. Let ξ, ξ ₁, ξ ₂, … be a sequence of real-valued independent and identically distributed (i.i.d.) random variables. To avoid trivial cases, assume that ℙ(ξ > 0) > 0. For X ₀ = x ∈ ℝ, let X _n+1 = X _n + ξ _n+1 for n = 0, 1, …, so that {X _n}_n≥0 is a random walk with initial state x. For y ∈ ℝ ∪ {− ∞}, define τ _y := inf{n ≥ 0: X _n ≥ y} (a threshold-type stopping time) and Ty := inf{n ≥ 1: X _n ≥ y} (which is different from τ _y if X ₀ ≥ y). Consider a nonnegative reward function g: ℝ → [0, ∞) which is nonconstant, increasing (i.e. g(x) ≤ g(y) for x < y), and logconcave (i.e. g(θx + (1 − θ)y) ≥ (g(x))^θ (g(y)) ^1−θ for all x, y and 0 < θ < 1). Letting log 0 := − ∞, the function h(x) : = log g(x) is increasing and concave, so that the left-hand derivative h′(x−) is well defined (possibly + ∞) at every x with h(x) > − ∞. Letting h′(x −) : = + ∞ if h(x) = − ∞, then h′(x −) is decreasing (and nonnegative) in x ∈ ℝ. Define

(2.1)$$\beta :=\underset{x\to \infty }{\mathop{\lim }}\,{h}'(x\,\,-),$$

(2.2)$$u:=\inf \{x\in \mathbb{R}:\frac{{\mathbb {E}_{x}}\left( {{e}^{-q{{T}_{x}}}}g\left( {{X}_{{{T}_{x}}}} \right){{\mathbf{1}}_{\left\{ {{T}_{x}}<\infty \right\}}} \right)}{g(x)}\le 1\}\quad \left( \frac{a}{0}:=\infty \text{ for }a\ge 0 \right), $$

(2.3)$$W:=\underset{y\in \mathbb{R}}{\mathop{\sup }}\,{{\mathbb {E}}_{0}}({{\text{e}}^{-q{{\tau }_{y}}}}g({{X}_{{{\tau }_{y}}}}){{\mathbf{1}}_{\left\{ {{\tau }_{y}}<\infty \right\}}})=\underset{y\in \mathbb{R}}{\mathop{\sup }}\,\,\,\,\,E({{\text{e}}^{-q{{\tau }_{y}}}}g({{X}_{{{\tau }_{y}}}}){{\mathbf{1}}_{\left\{ {{\tau }_{y}}<\infty \right\}}}),$$

(2.4)$$V(x):=\underset{\tau \in \mathcal{M}}{\mathop{\sup }}\,{{\mathbb {E}}_{x}}\left( {{\text{e}}^{-q\tau }}g({{X}_{\tau }}){{\mathbf{1}}_{\left\{ \tau <\infty \right\}}} \right)\text{ }x\in \mathbb{R}.$$

(While the subscript x in 𝔼_x refers to the initial state X ₀ = x, in the x = 0 case, we write 𝔼 = 𝔼₀ for simplicity, as in (2.3).)

Remark 2.1

A nonnegative, nonconstant, increasing, and logconcave function g is continuous everywhere except possibly at

(2.5)$$\begin{equation}\label{v1} x_0\,{:\!=}\,\inf\{s\in\mathbb{R}\colon g(s)>0\}. \end{equation}$$

Note that − ∞ ≤ x ₀ < ∞. Moreover, since g is nonconstant, g is not identically 0 while lim_x→−∞ g(x) = 0. In Theorem 2.1 below, g is assumed to be right continuous, which implies that g(x ₀) = g(x ₀ +) if x ₀ > −∞.

Remark 2.2

Note that $\mathcal{L}(T_x,X_{T_x}\mathbf{1}_{\{T_x<\infty\}}{\mid} X_0\ {=}\ x)\ {=}\ \mathcal{L}(T_0,(x\ {+}\ X_{T_0})\mathbf{1}_{\{T_0<\infty\}}{\mid} X_0\ {=}\ 0)$, where $\mathcal{L}(Z)$ denotes the law of a random vector Z. Since, by logconcavity, g(x + δ)/g(x) is decreasing in x for δ ≥ 0, it follows that

(2.6)$$\frac{{{\mathbb {E}}_{x}}({{\text{e}}^{-q{{T}_{x}}}}g({{X}_{{{T}_{x}}}}){{\mathbf{1}}_{\{{{T}_{x}}<\infty \}}})}{g(x)}=\frac{E({{e}^{-q{{T}_{0}}}}g(x+{{X}_{{{T}_{0}}}}){{\mathbf{1}}_{\{{{T}_{0}}<\infty \}}})}{g(x)}\quad \text{is decreasing in }x.$$

It can be argued that if G(x) := 𝔼_x(e^{–qT _x}g (X_Tx)1_{{T x < ∞}}) = ∞ for some x then G(x) = ∞ for all x ∈ ℝ, in which case we have u = ∞. Thus, if u < ∞ then G(x) < ∞ is continuous and increasing in x > x ₀, so that

$${{{{\rm\mathbb {E}}_x}({{\rm{e}}^{ - q{T_x}}}g({X_{{T_x}}}){{\bf{1}}_{\{ {T_x} < \infty \} }})} \over {g(x)}}\quad ( = {{G(x)} \over {g(x)}})\quad {\rm{is\,\,\, continuous }}({\rm{and\,\,\, decreasing}}){\rm{in\,\,\, x}} > {{\rm{x}}_{\rm{0}}},$$

where x ₀ is given in (2.5). It follows that

(2.7)$${{\rm\mathbb {E}}_u}\left( {{{\rm{e}}^{ - q{T_u}}}g\left( {{X_{{T_u}}}} \right){{\bf{1}}_{\left\{ {{T_u} < \infty } \right\}}}} \right) = g(u)\quad {\rm{provided\,\,\, }}{x_0} < u < \infty .$$

Remark 2.3

By Corollary 2.1, u = inf{x: V(x) = g(x)} = sup{x: V(x) > g(x)}. By Theorem 2.1, (− ∞, u) and [u, ∞) are the (optimal) continuation and stopping regions, respectively. If u = −∞, there is no continuation region, so stopping immediately is optimal. If u = ∞, the stopping region is empty and there is no optimal stopping time in the sense that, for any initial state x and for any stopping time τ, we can always find another stopping time τ′ ^′ such that ℙ_x(τ′ ≥ τ) = 1 and

$${{\rm\mathbb {E}}_x}[{e^{ - q\tau '}}g({X_{\tau '}})\mid {{\cal F}_\tau }] > {\,^{ - q\tau }}g({X_\tau })\quad {\rm{a}}.{\rm{s}}.\;{\rm{on}}\{ \tau < \infty \} .$$

Remark 2.4

Novikov and Shiryaev [Reference Novikov and Shiryaev18] solved (1.1) for g(x) = (x ⁺)^ν with ν > 0, and found that the optimal threshold is the positive root of the associated Appell function, which generalizes an earlier result of Darling et al. [Reference Darling, Liggett and Taylor8] for ν = 1. It can be shown that their optimal threshold agrees with (2.2). As an illustration, consider g(x) = x ⁺ and q = 0, for which Darling et al. [Reference Darling, Liggett and Taylor8] showed that if 𝔼(ξ) < 0 then τ _𝔼(M) is optimal where M := sup{0, ξ ₁, ξ ₁ + ξ ₂, … }. For 𝔼(ξ) < 0, the value of u defined in (2.2) satisfies (cf. (2.7))

$$0 < u = g(u) = {{\rm\mathbb {E}}_u}\left( {g({X_{{T_u}}}){{\bf{1}}_{\{ {T_u} < \infty \} }}} \right) = {{\rm\mathbb {E}}_u}\left( {{X_{{T_u}}}{{\bf{1}}_{\{ {T_u} < \infty \} }}} \right) = {\rm\mathbb {E}}\left( {(u + {X_{{T_0}}}){{\bf{1}}_{\{ {T_0} < \infty \} }}} \right),$$

yielding

$$\begin{equation} u=\frac{\mathbb {E}\left(X_{T_0}\mathbf{1}_{\{T_0<\infty\}}\right)} {\mathbb {p}(T_0=\infty)}=\mathbb {E}(M),\end{equation}$$

where the second equality follows from the fact that $\mathcal{L}(M)=\mathcal{L}\left((X_{T_0}+M')\mathbf{1}_{\{T_0<\infty\}} \mid X_0=0\right),$, with M′ being an independent copy of M. When 𝔼(ξ) ≥ 0 or 𝔼(ξ) is undefined (i.e. 𝔼(max{ξ, 0}) = ∞ = 𝔼(max{– ξ, 0})), it is readily shown that u = ∞ = 𝔼(M). Thus, the value of u defined in (2.2) equals 𝔼(M) regardless of whether 𝔼(ξ) < 0.

Remark 2.5

For g(x) > 0, it can be shown that 𝔼_x(e^{–qT _x}g (X_Tx)1_{{T x < ∞}})/g(x) ≤ 1 if and only if 𝔼_x(e^{–qτ _x+}g (X_τx+)1_{{τ x+ < ∞}})/g(x) ≤ 1, where τ _x+ := inf{n ≥ 0: X _n > x}. It follows that the definition of u in (2.2) is equivalent to

$$u = \inf \{ x \in :{{{{\rm\mathbb {E}}_x}\left( {{{\rm{e}}^{ - q{\tau _{x + }}}}g\left( {{X_{{\tau _{x + }}}}} \right){{\bf{1}}_{\left\{ {{\tau _{x + }} < \infty } \right\}}}} \right)} \over {g(x)}} \le 1\} .$$

If x ₀ < u < ∞, it follows from (2.7) that

$$g(u) = {{\rm\mathbb {E}}_u}\left( {{{\rm{e}}^{ - q{T_u}}}g({X_{{T_u}}}){{\bf{1}}_{\{ {T_u} < \infty \} }}} \right) = {{\rm\mathbb {E}}_u}\left( {{{\rm{e}}^{ - q{\tau _{u + }}}}g({X_{{\tau _{u + }}}}){{\bf{1}}_{\{ {\tau _{u + }} < \infty \} }}} \right),$$

which together with the optimality of τ _u implies that τ _u+ is also optimal. However, τ _u+ may not be optimal if u = x ₀ > − ∞. As an example, consider the (logconcave) function g(x) = 1_[0,∞)(x) for which u = x ₀ = 0. While τ ₀ is optimal, we have g(0) = 1 > 𝔼₀(e^{–qτ ₀₊}g (X_τ0+)1_{{τ 0+ < ∞}}) if q > 0 or 𝔼(ξ) < 0.

To prove Theorem 2.1, we need the following lemmas.

Lemma 2.3

Assume that ℙ(ξ > 0) > 0. Let g: ℝ → [0, ∞) be nonconstant, increasing, and logconcave. Suppose that

$${{\mathbb{E}}_{y}}({{\text{e}}^{-q{{T}_{y}}}}g({{X}_{{{T}_{y}}}}){{\mathbf{1}}_{\left\{ {{T}_{y}}<\infty \right\}}})\text{ }g(y)\text{ }\ge 1\quad \text{for some}y>{{x}_{0}}:=\inf \{s:g(s)>0\}.$$

Then the following statements hold:

1. (i) 𝔼_x(e^{–qT _a}g (X_Ta)1_{{T a < ∞}}) ≤ 𝔼_x(e^{–qT _y}g (X_Ty)1_{{T y < ∞}}) for x ∈ ℝ and a ∈ [ − ∞, y);

2. (ii) g(x) ≤ 𝔼_x(e^{–qτ _y}g (X_τy)1_{{τ y < ∞}}) for x ∈ ( − ∞, y).

Lemma 2.4

Assume that ℙ(ξ > 0) > 0. Let g: ℝ → [0, ∞) be nonconstant, increasing and logconcave. Suppose that

$${{{{\rm\mathbb {E}}_y}({{\rm{e}}^{ - q{T_y}}}g({X_{{T_y}}}){{\bf{1}}_{\left\{ {{T_y} < \infty } \right\}}})} \over {g(y)}} \ge 1\quad {\rm{for\,\, some\,\,\, }}y > {x_0}{\mkern 1mu} : = {\mkern 1mu} \inf \{ s:g(s) > 0\} .$$

Then the following statements hold:

1. (i) 𝔼_x(e^{–qT _y}g (X_Ty)1_{{T y < ∞}}) ≥ 𝔼_x(e^{–qT _a}g (X_Ta)1_{{T a < ∞}}) for x ∈ ℝ and a ∈ (y, ∞);

2. (ii) g(y) ≥ 𝔼_y(e^{–qτ _a}g (X_τa)1_{{τ a < ∞}}) for a ∈ (y,∞).

Lemma 2.6

Assume that ℙ(ξ > 0) > 0. Let g: ℝ → [0, ∞) be nonconstant, increasing, logconcave, and right continuous. Define u as in (2.2). Suppose that there exist x′ ∈ ℝ and c > 0 such that g(x) = c for x ≥ x′. Then u ≤ x′ and τ_u is optimal. Moreover, the value function V(x) satisfies V(x) > g(x) for x < u and V(x) = g(x) for x ≥ u.

Lemma 2.1 follows easily by conditioning on X ₁ = x + ξ. Lemma 2.2 is a standard result (see [Reference Novikov and Shiryaev17, Lemma 5]). The proofs of Lemmas 2.3–2.6 are relegated to Appendix A. We are now ready to prove Theorem 2.1.

Proof of Theorem 2.1(i). Let {b _k}_k≥1 be an increasing sequence such that b ₁ > x ₀ and lim_k→∞ b _k = ∞. For each k ≥ 1, let g _k(x) := g(x ∧ b _k) := g( min{x, b _k}) for x ∈ ℝ, and let

(2.8)$$\begin{equation}\label{e13} V_k(x)\,{:\!=}\,\sup_{\tau\in\mathcal{M}}\mathbb {E}_x(e^{-q\tau}g_k(X_\tau)\mathbf{1}_{\{\tau<\infty\}}). \end{equation}$$

Then, for k ≥ 1, g _k(x) is nonconstant, increasing, logconcave, and right continuous. Since g _k(x) is increasing in k, so is V _k(x). Note that g _k(x)=g(b _k)>0 for x ≥ b _k and g _k(x) = g(x) for x < b _k. We have V _k(x) ≤ g(b _k) for x ∈ ℝ, and, by Lemma 2.6, it follows that τ _{u k} is optimal for the optimal stopping problem (2.8) with reward function g _k, where

(2.9)$$\begin{equation}\label{v2} u_k\,{:\!=}\,\inf\Biggl\{x\in\mathbb{R}\colon \frac{\mathbb {E}_x(e^{-qT_x}g_k(X_{T_x})\mathbf{1}_{\{T_x<\infty\}})}{g_k(x)} \le1\Biggr\}\le b_k<\infty. \end{equation}$$

We claim that u _k is increasing in k. If u _k+1 ≥ b _k then u _k+1 ≥ u _k clearly. In the u _k+1 < b _k case, we have V _k(u _k+1) ≤ V _k+1(u _k+1) = g _k+1(u _k+1) = g(u _k+1) = g _k(u _k+1), implying that u _k+1 ≥ u _k.

Let u _∞ : = lim_k→∞ u _k and V _∞(x) := lim_k→∞ V _k(x). For any $\tau\in\mathcal{M}$, we have, by the monotone convergence theorem,

$$\begin{equation} \mathbb {E}_x(e^{-q\tau}g(X_{\tau})\mathbf{1}_{\{\tau<\infty\}})= \lim_{k\to\infty}\mathbb {E}_x(e^{-q\tau}g_{k}(X_{\tau})\mathbf{1}_{\{\tau<\infty\}})\le\nonumber V_{\infty}(x), \end{equation}$$

implying that V(x) = V _∞(x) for all x. Now we prove in three steps that τ _u is optimal if −∞ ≤ u < ∞. We show in step 1 that u _∞ ≤ u ( < ∞), in step 2 that τ _{u ∞} is optimal, and in step 3 that u _∞ ≥ u.

Step 1. To prove that u _∞ ≤ u, suppose to the contrary that u < u _∞. Choose an x and a (large) k such that u < x < u _k and b _k ≥ x. We have, by (2.2),

$$\begin{equation} g_k(x)=g(x)\ge \mathbb {E}_x\left(e^{-qT_x}g\big(X_{T_x}\big)\mathbf{1}_{\left\{T_x< \infty\right\}}\right)\ge \mathbb {E}_x\left(e^{-qT_x}g_k\left(X_{T_x}\right)\mathbf{1}_{\left\{T_x< \infty\right\}}\right),\end{equation}$$

which together with (2.9) implies that x ≥ u _k, a contradiction. This proves that u _∞ ≤ u.

Step 2. To prove that τ _{u ∞} is optimal, it suffices to show that

(2.10)$$\begin{equation}\label{e14} \mathbb {E}_x\left(e^{-q\tau_{u_\infty}}g(X_{\tau_{u_\infty}}) \mathbf{1}_{\{\tau_{u_\infty}<\infty\}}\right)\ge \sup_{k}V_k(x)\ (=V_\infty(x)=V(x))\quad\text{for all }x. \end{equation}$$

If u _∞ = −∞ then u _∞ = u _k = −∞ for all k, implying that, for all x,

$$\begin{equation} V_k(x)=g_k(x)\le g(x)=\mathbb {E}_x\left(e^{-q\tau_{u_\infty}}g(X_{\tau_{u_\infty}}) \mathbf{1}_{\{\tau_{u_\infty}<\infty\}}\right)\quad\text{for all }k,\end{equation}$$

establishing (2.10) for the u _∞ = −∞ case.

Suppose that −∞ < u _∞ ( ≤ u < ∞). Since u _∞ ≥ u _k for all k, we have, for x ≥ u _∞,

$$\begin{equation} \mathbb {E}_x\left(e^{-q\tau_{u_\infty}}g(X_{\tau_{u_\infty}})\mathbf{1}_{\{\tau_{u_\infty}<\infty\}}\right)=g(x)\ge g_k(x)=V_k(x)\quad\text{for all }k.\end{equation}$$

It remains to prove (2.10) for x < u _∞. Note that u _∞ ≥ u _k ≥ x ₀ for all k. If u _∞ = x ₀ then u _k = u _∞ = x ₀ for all k, so that

$$\begin{equation} V_k(x)=\mathbb {E}_x\left(e^{-q\tau_{u_\infty}}g_k(X_{\tau_{u_\infty}}) \mathbf{1}_{\{\tau_{u_\infty}<\infty\}}\right)\le \mathbb {E}_x\left(e^{-q\tau_{u_\infty}}g(X_{\tau_{u_\infty}}) \mathbf{1}_{\{\tau_{u_\infty}<\infty\}}\right)\quad\text{for all }k,\end{equation}$$

proving (2.10).

Now suppose that u _∞ > x ₀. To prove (2.10) for x < u _∞, let k ₀ be so large that x < u _{k 0}, 2u _{k 0} − u _∞ > x ₀, and b _{k 0} > u _∞. Thus, for all k ≥ k ₀, we have x < u _k, 2u _k − u _∞ > x ₀ and b _k > u _∞. For k ≥ k ₀, let ε _k := u _∞ − u _k ( ≥ 0),

$${U_k}(x){\mkern 1mu} : = {\mkern 1mu} {_x}\left( {{e^{ - q{\tau _{{u_\infty }}}}}{g_k}({X_{{\tau _{{u_\infty }}}}}){{\bf{1}}_{\{ {\tau _{{u_\infty }}} < \infty \} }}} \right),\,\,\tau '{\mkern 1mu} : = {\mkern 1mu} {\tau _{{u_k} - {\varepsilon _k}}}{\mkern 1mu} : = {\mkern 1mu} \inf \{ n \ge 0:{X_n} \ge {u_k} - {\varepsilon _k}\} ,$$

and

$$\begin{equation} \tilde{V}_k(y)\,{:\!=}\,\mathbb {E}_y\big(e^{-q\tau'}g_k(X_{\tau'}) \mathbf{1}_{\{\tau'<\infty\}}\big)\, (\le V_k(y))\quad\text{for } y\in\mathbb{R}.\end{equation}$$

Since $\mathcal{L}(\tau_{u_\infty},X_{\tau_{u_\infty}} \mathbf{1}_{\{\tau_{u_\infty}<\infty\}}\mid X_0=x)=\mathcal{L}(\tau_{u_k},(\varepsilon_k+X_{\tau_{u_k}}) \mathbf{1}_{\{\tau_{u_k}<\infty\}}\mid X_0=x-\varepsilon_k)$, we have

(2.11)$$\begin{align} U_k(x)&=\mathbb {E}_{x-\varepsilon_k}\big(e^{-q\tau_{u_k}}g_k(\varepsilon_k+X_{\tau_{u_k}})\mathbf{1}_{\{\tau_{u_k}<\infty\}}\big) \\ &\ge \mathbb {E}_{x-\varepsilon_k}\big(e^{-q\tau_{u_k}} g_k(X_{\tau_{u_k}})\mathbf{1}_{\{\tau_{u_k}<\infty\}}\big) \\& =V_k(x-\varepsilon_k)\ge {V}_k(x-\varepsilon_k).\label{e2.13} \end{align}$$

Let τ ^″:= τ _{u k−x} := inf{n ≥ 0: X _n ≥ u _k − x}. On {τ ^″< ∞}, we have

$$\begin{equation} g_k(x-\varepsilon_k+X_{\tau''})\ge g_k(u_k-\varepsilon_k)= g_k(2u_k-u_\infty)=g((2u_k-u_\infty)\wedge b_k)=g(2u_k-u_\infty)>0.\end{equation}$$

Since $\mathcal{L}(\tau_{u_\infty},X_{\tau_{u_\infty}} \mathbf{1}_{\{\tau_{u_\infty}<\infty\}}\mid X_0=x)=\mathcal{L}(\tau_{u_k},(\varepsilon_k+X_{\tau_{u_k}}) \mathbf{1}_{\{\tau_{u_k}<\infty\}}\mid X_0=x-\varepsilon_k)$, we have

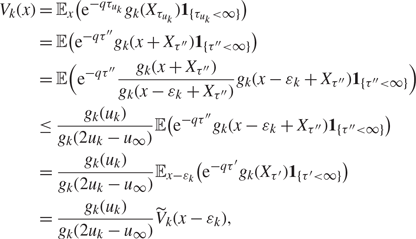(2.12)$$\begin{align} V_k(x)&=\mathbb {E}_x\big(e^{-q\tau_{u_k}}g_k(X_{\tau_{u_k}})\mathbf{1}_{\{\tau_{u_k}<\infty\}}\big) \\ &=\mathbb {E}\big(e^{-q\tau''}g_k(x+X_{\tau''})\mathbf{1}_{\{\tau''<\infty\}}\big) \\ &=\mathbb {E}\Bigl(e^{-q\tau''}\frac{g_k(x+X_{\tau''})}{g_k(x-\varepsilon_k+X_{\tau''})}g_k(x-\varepsilon_k+X_{\tau''})\mathbf{1}_{\{\tau''<\infty\}}\Bigr) \\ &\le\frac{g_k(u_k)}{g_k(2u_k-u_\infty)}\mathbb {E}\big(e^{-q\tau''}g_k(x-\varepsilon_k+X_{\tau''})\mathbf{1}_{\{\tau''<\infty\}}\big) \\ &=\frac{g_k(u_k)}{g_k(2u_k-u_\infty)}\mathbb {E}_{x-\varepsilon_k} \big(e^{-q\tau'}g_k(X_{\tau'})\mathbf{1}_{\{\tau'<\infty\}}\big) \\&=\frac{g_k(u_k)}{g_k(2u_k-u_\infty)} {V}_k(x-\varepsilon_k),\label{e2.14} \end{align}$$

where the inequality is due to the logconcavity of g _k. By (2.11) and (2.12), we have

(2.13)$$\begin{equation}\label{v3} U_k(x)\ge\frac{g_k(2u_k-u_\infty)}{g_k(u_k)}V_k(x)= \frac{g(2u_k-u_\infty)}{g(u_k)}V_k(x)\quad\text{for }k\ge k_0. \end{equation}$$

Letting k → ∞, the right- and left-hand sides of (2.13) tend, respectively, to V _∞(x) and 𝔼_x(e^{–qτ _{u ∞}} g(X_{τu ∞})1_{{τ u ∞ < ∞}}), yielding (2.10).

Step 3. We now prove that u _∞ ≥ u. Suppose to the contrary that u > u _∞ ( ≥ x ₀). Then it follows from (2.2) that 𝔼_{u ∞}(e^{–qT _{u ∞}} g(X_{Tu ∞})1_{{T u ∞ < ∞}})/g(u _∞) > 1, which implies by the optimality of τ _{u ∞} (established in step 2) that

$$\begin{equation} g(u_\infty)<\mathbb {E}_{u_\infty}\bigl(e^{-qT_{u_\infty}}g\left(X_{T_{u_\infty}}\right)\mathbf{1}_{\left\{T_{u_\infty}<\infty\right\}}\bigr)\le V(u_\infty)=g(u_\infty),\end{equation}$$

a contradiction. Thus, u ≤ u _∞. The proof is complete.

Proof of Theorem 2.1(ii). Let Q _y(x) :=𝔼_x(e^{–qτ _y} g(X_τy)1_{{τ y < ∞}}), x, y ∈ ℝ. Claim that

(2.14)$$\begin{equation}\label{u3} Q_{y}(x)\text{ is increasing in }y\in\mathbb{R}. \end{equation}$$

For any given x, y and y′ with y < y′, we have ℙ_x(τ _y ≤ τ _y′) = 1. On {τ _y < ∞}, define

$$\begin{equation} H\,{:\!=}\,\mathbb {E}_{x}\bigl(e^{-q(\tau_{y'}-\tau_{y})}g(X_{\tau_{y'}}) \mathbf{1}_{\{\tau_{y'}<\infty\}}\mid\mathcal{F}_{\tau_{y}}\bigr),\end{equation}$$

so that Q _y′(x) = 𝔼_x(e^{–qτ _y} H 1_{{τ y < ∞}}). If y < y′ ≤ x ₀, we have H ≥ g(X _{τ y}) = 0 on {τ _y < ∞, X _{τ y} < x ₀} and H = g(X _{τ y}) on {τ _y < ∞, X _{τ y} ≥ x ₀}. If y′ > x ₀, we have 𝔼_y′(e^{–qT _y′} g(X_{T y′})1_{T y′<∞}})/g(y′) > 1 (since u = ∞). By Lemma 2.3(ii), H ≥ g(X _{τ y}) on {τ _y < ∞, X _{τ y} < y′} and H = g(X _{τ y}) on {τ _y < ∞, X _{τ y} ≥ y′}. Thus, we have shown that H ≥ g(X _{τ y}) on {τ _y < ∞}, implying that

$$\begin{equation} Q_{y'}(x)=\mathbb {E}_{x}\left(e^{-q\tau_{y}}H\mathbf{1}_{\{\tau_{y}<\infty\}}\right)\ge \mathbb {E}_x\left(e^{-q\tau_y}g(X_{\tau_y})\mathbf{1}_{\{\tau_y<\infty\}}\right)=Q_{y}(x),\end{equation}$$

establishing (2.14). Let

$$\begin{equation} \label{u4} Q(x)\,{:\!=}\,\sup_{y}Q_{y}(x)=\lim_{y\to\infty}Q_{y}(x) \quad\text{and}\quad Q(0)=W.\end{equation}$$

To show that

(2.15)$$\begin{equation}\label{u5} V(x)=Q(x)=\lim_{y\to\infty}Q_{y}(x), \end{equation}$$

consider an increasing sequence {b _k}_k≥1 with b ₁ > x ₀ and lim_k→∞ b _k = ∞. Let g _k(x) := g(x ∧ b _k), and let V _k(x) and u _k be defined as in (2.8) and (2.9), respectively. Observing that V(x) = lim_k→∞ V _k(x) = sup_k V _k(x), we have

$$\begin{align&#x002A;} V(x)=\sup_{k}V_{k}(x)&=\sup_{k}\mathbb {E}_{x}\bigl(e^{-q\tau_{u_k}}g_{k} (X_{\tau_{u_k}})\mathbf{1}_{\{\tau_{u_k}<\infty\}}\bigr)\\ &\le\sup_{k}\mathbb {E}_{x}\bigl(e^{-q\tau_{u_k}}g(X_{\tau_{u_k}}) \mathbf{1}_{\{\tau_{u_k}<\infty\}}\bigr) \\ &=\sup_{k}Q_{u_k}(x)\\&\le Q(x)\\&\le V(x), \end{align&#x002A;}$$

where the second equality is due to the optimality of the threshold u _k for the reward function g _k. This proves (2.15).

Since $\mathcal{L}(\tau_y,X_{\tau_y}\mathbf{1}_{\{\tau_y<\infty\}} \mid X_0=x)=\mathcal{L}(\tau_{y-x},(x+X_{\tau_{y-x}})\mathbf{1}_{\{\tau_{y-x}<\infty\}}\mid X_0=0)$, we have

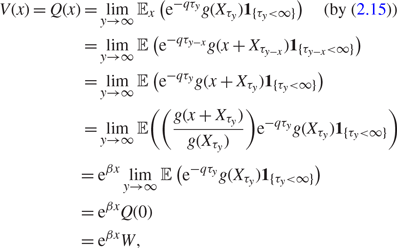(2.16)$$\begin{align} V(x)=Q(x)&=\lim_{y\to\infty}\mathbb {E}_{x}\left(e^{-q\tau_{y}}g(X_{\tau_{y}}) \mathbf{1}_{\{\tau_{y}<\infty\}}\right)\quad\text{(by (ef{u5}))} \\ &=\lim_{y\to\infty}\mathbb {E}\left(e^{-q\tau_{y-x}}g(x+X_{\tau_{y-x}}) \mathbf{1}_{\{\tau_{y-x}<\infty\}}\right) \\ &=\lim_{y\to\infty}\mathbb {E}\left(e^{-q\tau_{y}}g(x+X_{\tau_{y}}) \mathbf{1}_{\{\tau_{y}<\infty\}}\right) \\ &=\lim_{y\to\infty}\mathbb {E}\Bigg(\Bigg(\frac{g(x+X_{\tau_y})} {g(X_{\tau_y})}\Bigg)e^{-q\tau_{y}}g(X_{\tau_{y}}) \mathbf{1}_{\{\tau_{y}<\infty\}}\Bigg) \\ &=e^{\beta x}\lim_{y\to\infty}\mathbb {E}\left(e^{-q\tau_{y}}g(X_{\tau_{y}}) \mathbf{1}_{\{\tau_{y}<\infty\}}\right) \\&=e^{\beta x}Q(0) \\&=e^{\beta x}W,\label{v7} \end{align}$$

where we have used the facts that, on {τ _y < ∞}, X _{τ y} ≥ y and

$$\begin{equation} \inf_{z\ge y}\frac{g(x+z)}{g(z)}\le \frac{g(x+X_{\tau_y})}{g(X_{\tau_y})}\le\sup_{z\ge y}\frac{g(x+z)}{g(z)}.\end{equation}$$

Note that

$$\begin{equation} \inf_{z\ge y}\frac{g(x+z)}{g(z)}=\inf_{z\ge y}e^{h(x+z)-h(z)}\ge\inf_{z\ge y}e^{h'((x+z)\mathbb {E}rn1.5pt{-})x}=\min\big\{e^{h'((x+y)\mathbb {E}rn1.5pt{-})x},e^{\beta x}\big\}\to e^{\beta x}\end{equation}$$

as y → ∞, and that

$$\begin{equation} \sup_{z\ge y}\frac{g(x+z)}{g(z)}=\sup_{z\ge y}e^{h(x+z)-h(z)}\le\sup_{z\ge y}e^{h'(z\mathbb {E}rn1.5pt{-})x}=\max\big\{e^{h'(y\mathbb {E}rn1.5pt{-})x},e^{\beta x}\big\}\to e^{\beta x}\end{equation}$$

as y → ∞. Suppose that W = ∞. By (2.16), V(x) = e^βxW = ∞. In view of Q _y(x) → ∞ as y → ∞, let y _k, k = 1, 2, …, be such that

$$\begin{equation} Q_{y_k}(x)=\mathbb {E}_{x}\bigl(e^{-q\tau_{y_k}}g(X_{\tau_{y_k}})\mathbf{1}_{\{\tau_{y_k}<\infty\}}\bigr)>2^k.\end{equation}$$

Let τ be a randomized stopping time of threshold type which chooses the threshold y _k with probability 2^−k, k = 1, 2, …. Then we have 𝔼_x(e^–qτ g(X_τ)1_{{τ < ∞}}) = ∞.

Now suppose that W <∞. To prove that there is no optimal stopping time, it suffices to show for x ∈ ℝ and any stopping time τ with ℙx(τ <∞) > 0 that

(2.17)$$\begin{equation}\label{u6} V(x)>\mathbb {E}_x\left(e^{-q\tau}g(X_{\tau})\mathbf{1}_{\{\tau<\infty\}}\right). \end{equation}$$

Consider an increasing sequence of stopping times $\tau'_{k}\,{:\!=}\,\inf\{n\ge\tau\colon X_{n}\ge k\}\ge\tau$, k =1,2, .... We have

$$\begin{align&#x002A;} V(x)\ge&\mathbb {E}_x\bigl(e^{-q\tau'_{k}}g(X_{\tau'_{k}})\mathbf{1}_{\{\tau'_{k}<\infty\}}\bigr)\\ =&\mathbb {E}_x\bigl(e^{-q\tau}\mathbf{1}_{\{\tau<\infty\}} \mathbb {E}_{x}\bigl(e^{-q(\tau'_{k}-\tau)}g(X_{\tau'_{k}}) \mathbf{1}_{\{\tau'_{k}<\infty\}}\mid\mathcal{F}_{\tau}\bigr)\bigr)\\ =&\mathbb {E}_x\left(e^{-q\tau}Q_{k}(X_{\tau})\mathbf{1}_{\{\tau<\infty\}}\right), \end{align&#x002A;}$$

which, by (2.15), increases to 𝔼_x(e^–qτ V (X_τ)1_{{τ < ∞}}) as K → ∞. Since V(y) > g(y) for all y and ℙ_x(τ < ∞) > 0, we have V(x) ≥ 𝔼_x(e^–qτ V (X_τ)1_{{τ < ∞}}) > 𝔼_x(e^–qτ g(X_τ)1_{{τ < ∞}}), establishing (2.17). The proof is complete.

3. Optimal stopping for Lévy processes

Let X = {X _t}_t≥0 be a Lévy process with initial state X ₀ = x ∈ ℝ. For a comprehensive discussion of Lévy processes, see [Reference Bertoin2], [Reference Kyprianou12], and [Reference Sato20]. As in Section 2, assume that ℙ(X ₁ > 0) > 0 since the ℙ(X ₁ ≤ 0) = 1 case is trivial. For q ≥ 0 and g: ℝ → [0, ∞), let

(3.1)$$\begin{equation}\label{e3.1} V(x)\,{:\!=}\,\sup_{\tau\in\mathcal{M}}\mathbb {E}_x\left(e^{-q\tau}g(X_\tau)\mathbf{1}_{\{\tau<\infty\}}\right), \end{equation}$$

where $\mathcal{M}$ is the class of all stopping times τ taking values in [0, ∞] with respect to the filtration $\{\mathcal{F}_t\}_{t\ge0}$, $\mathcal{F}_t$ being the natural enlargement of σ{X _s, 0 ≤ s ≤ t}.

To apply Theorem 2.1 to the problem (3.1), we introduce a sequence of optimal stopping problems in discrete time (cf. [Reference Shiryaev22, Chapter 3]). For ℓ = 1,2, ...., let $\mathcal{M}^{(\ell)}$ denote the class of all stopping times in $\mathcal{M}$ taking values in {n2^−ℓ: n = 0, 1, …, ∞} and

(3.2)$$\begin{equation}\label{e3.2} V^{(\ell)}(x)\,{:\!=}\,\sup_{\tau\in\mathcal{M}^{(\ell)}}\mathbb {E}_x \left(e^{-q\tau}g(X_\tau)\mathbf{1}_{\{\tau<\infty\}}\right), x\in\mathbb{R}. \end{equation}$$

Note that, by the Markov property of X, V ^(ℓ)(x) equals the supremum of 𝔼_x(e^–qτg (X_τ)1_{{τ x < ∞}}) over the (smaller) class of all stopping times τ taking values in {n2^−ℓ : n = 0, 1, …, ∞} such that $\{\tau=n2^{-\ell}\}\in\sigma\{X_{i2^{-\ell}},\, i=0,1,\dots,n\}\subset\mathcal{F}_{n2^{-\ell}}$. So we can apply Theorem 2.1 to (3.2).

Let u ^(ℓ) be defined as in (2.2) with T _x replaced by $T_x^{(\ell)}\,{:\!=}\,2^{-\ell}\inf\{n\ge1\colon X_{n{2}^{-\ell}}\ge x\}$, i.e.

$$\begin{equation} \label{b1} u^{(\ell)}\,{:\!=}\,\inf\Bigg\{x\in\mathbb{R}\colon \frac{\mathbb {E}_x\left(e^{-qT_x^{(\ell)}}g(X_{T_x^{(\ell)}}) \mathbf{1}_{\{T_x^{(\ell)}<\infty\}}\right)}{g(x)}\le1\Bigg\}.\end{equation}$$

For y ∈ ℝ ∪{–∞}, let $\tau_y\,{:\!=}\,\inf\{t\ge0\colon X_t\ge y\}\in\mathcal{M}$ and

$$\begin{equation} \tau_y^{(\ell)}=\tau^{(\ell)}(y)\,{:\!=}\,2^{-\ell}\inf\{n\ge0\colon X_{n2^{-\ell}}\ge y\}\in\mathcal{M}^{(\ell)}.\end{equation}$$

By Theorem 2.1, if u ^(ℓ) < ∞ then $\tau_{u^{(\ell)}}^{(\ell)}=\tau^{(\ell)}(u^{(\ell)})$ is optimal for (3.2), i.e.

$$\begin{equation} \label{e3.3} V^{(\ell)}(x)=\mathbb {E}_x\big(e^{-q\tau^{(\ell)}(u^{(\ell)})}g \big(X_{\tau^{(\ell)}(u^{(\ell)})}\big)\mathbf{1}_{\{\tau^{(\ell)} (u^{(\ell)})<\infty\}}\big), x\in\mathbb{R}.\end{equation}$$

By Lemma 3.1 below, u ^(ℓ) is increasing in ℓ. Let

(3.3)$$\begin{equation}\label{b2} u\,{:\!=}\,\lim_{\ell\to\infty}u^{(\ell)} \quad\text{and}\quad W\,{:\!=}\,\sup_{y\in\mathbb{R}}\mathbb {E}\left(e^{-q\tau_y}g(X_{\tau_y}) \mathbf{1}_{\{\tau_y<\infty\}}\right). \end{equation}$$

Lemma 3.1

For x ∈ ℝ and ℓ = 1, 2, …, we have V ^(ℓ+1)(x) ≥ V ^(ℓ)(x) > 0 and u ^(ℓ+1) ≥ u ^(ℓ) ≥ x ₀, where x ₀ := inf{s: g(s) > 0}.

Proof. Since $\mathcal{M}^{(\ell)}\subset\mathcal{M}^{(\ell+1)}$, we have 0 < V ^(ℓ)(x) ≤ V ^(ℓ+1)(x). To show that u ^(ℓ+1) ≥ u ^(ℓ), it suffices to consider the case u ^(ℓ+1) < ∞ (possibly u ^(ℓ+1) = −∞). By Corollary 2.1(i),

$$\begin{equation} g(x)=V^{(\ell+1)}(x)\ge V^{(\ell)}(x)\ge g(x)\quad\text{for } x\ge u^{(\ell+1)},\end{equation}$$

implying that V ^(ℓ)(x) = g(x) for x ≥ u ^(ℓ+1). By Corollary 2.1(i) again, u ^(ℓ+1) ≥ u ^(ℓ).

Lemma 3.2

Suppose that g(x) > 0 for all x ∈ ℝ. Then

1. (i) V ^(∞)(x) := lim_ℓ→∞ V ^(ℓ)(x) = V(x) for x ∈ ℝ;

2. (ii) V(x) > g(x) for x < u and V(x) = g(x) for x ≥ u;

3. (iii) V(x)/g(x) is decreasing in x.

Proof. Since g is logconcave, g(x) > 0, for all x ∈ ℝ, implies that g is continuous.

(i) Since V(x) ≥ V ^(ℓ)(x), we have V(x) ≥ V ^(∞)(x). To show that V(x) ≤ V ^(∞)(x), let $\tau\in\mathcal{M}$ be any stopping time. For ℓ = 1, 2, …, define τ ^(ℓ) := 2^−ℓ(⌊2^ℓτ⌋+ 1), where ⌊x⌋ denotes the largest integer not exceeding x with ⌊∞⌋:= ∞. Clearly, $\tau^{(\ell)}\in\mathcal{M}^{(\ell)}$ and τ ^(ℓ) ↘ τ as ℓ → ∞. It follows from the right continuity of {X _t} and the continuity of g that

$$\begin{equation} e^{-q\tau^{(\ell)}}g(X_{\tau^{(\ell)}})\to e^{-q\tau}g(X_\tau) \quad\text{a.s.\ on} \{\tau<\infty\}.\end{equation}$$

We have, by Fatou’s lemma,

$$\begin{align&#x002A;} V^{(\infty)}(x) =\sup_{\ell}V^{(\ell)}(x)\ge \sup_{\ell}\mathbb {E}_x\big(e^{-q\tau^{(\ell)}}g(X_{\tau^{(\ell)}}) \mathbf{1}_{\{\tau^{(\ell)}<\infty\}}\big)\ge \mathbb {E}_x\left(e^{-q\tau}g(X_\tau)\mathbf{1}_{\{\tau<\infty\}}\right). \end{align&#x002A;}$$

Since $\tau\in\mathcal{M}$ is arbitrary, we have V(x) ≤ V ^(∞)(x).

(ii) For x < u, choose a (large) ℓ with x < u ^(ℓ) ≤ u. It follows from Corollary 2.1(i) that g(x) < V ^(ℓ)(x) ≤ V ^(∞)(x) = V(x). For x ≥ u, since u ^(ℓ) ≤ u ≤ x, we have, by Corollary 2.1(i), g(x) = V ^(ℓ)(x) for all ℓ, implying that g(x) = V ^(∞)(x) = V(x).

(iii) By Corollary 2.1(ii), V ^(ℓ)(x)/g(x) is decreasing in x. Since V ^ℓ(x) ↗ V(x) as ℓ → ∞, it follows that V(x)/g(x) is decreasing in x.

Lemma 3.3

If −∞ < u < ∞ then V(x) = g(x) for x ≥ u.

Proof. Let h(x) := log g(x). Fix an x > u ( ≥ x ₀ := inf{s: g(s) > 0}). If h′(x −) = 0 then g(x) = sup{g(y): y ∈ ℝ} ≥ V(x), implying that V(x) = g(x). Suppose that h′(x −) > 0. Let

$$\tilde{h}(y):=\left\{ \begin{array}{&#x002A;{35}{l}} h(x)+{h}'(xrn1.5pt-)(y-x) & \text{if }y\,<x, \\ h(y) & \text{otherwise}\text{.} \\ \end{array} \right.$$

Let g̃(y) := e^h̃(y) > 0 for all y ∈ ℝ, which is larger than or equal to g(y), nonconstant, increasing, logconcave and continuous. Define

$$\begin{equation} \tilde{u}^{(\ell)}\,{:\!=}\,\inf\Bigg\{y\in\mathbb{R}\colon \frac{\mathbb {E}_y\left(e^{-qT^{(\ell)}_{y}}\tilde{g}(X_{T^{(\ell)}_y}) \mathbf{1}_{\{T^{(\ell)}_y<\infty\}}\right)}{\tilde{g}(y)}\le1\Bigg\}.\end{equation}$$

Since g̃(y) = g(y) for all y ≥ x and u ^(ℓ) ≤ u < x, we have ũ ^(ℓ) ≤ x. Let ũ := lim_ℓ→∞ ũ ^(ℓ) ≤ x. By Lemma 3.2(ii) applied to g̃,

$$\begin{equation} g(x)=\tilde{g}(x)=\tilde{V}(x)\,{:\!=}\,\sup_{\tau\in\mathcal{M}} \mathbb {E}_x\left(e^{-q\tau}\tilde{g}(X_\tau)\mathbf{1}_{\{\tau<\infty\}}\right)\ge V(x),\end{equation}$$

so V(x) = g(x). We have shown that V(x) = g(x) for all x > u. Finally, V(u) = g(u) follows from the monotonicity of g and V and the right continuity of g.

Lemma 3.4

Suppose that −∞ < u < ∞. For x < u and $\tau\in\mathcal{M}$ with ℙ_x(τ ≥ τ _u) = 1, we have

$$\begin{equation} \mathbb {E}_x\left(e^{-q\tau}g(X_\tau)\mathbf{1}_{\{\tau<\infty\}}\right)\le \mathbb {E}_x\left(e^{-q\tau_{u}}g(X_{\tau_{u}})\mathbf{1}_{\{\tau_{u}<\infty\}}\right).\end{equation}$$

Proof. Since, on {τ _u < ∞}, X _{τ u+s} − X _{τ u} (s ≥ 0) is independent of $\mathcal{F}_{\tau_u}$ and has the same law as X _s − X ₀, we have, on {τ _u < ∞},

$$\begin{align&#x002A;} \mathbb {E}_x\big(e^{-q(\tau-\tau_u)}g(X_{\tau_u}+(X_\tau-X_{\tau_u})) \mathbf{1}_{\{\tau<\infty\}}\mid\mathcal{F}_{\tau_u}\big)&\le V(X_{\tau_u})=g(X_{\tau_u})\quad\mbox{a.s.}, \end{align&#x002A;}$$

where the equality follows from Lemma 3.3 (noting that X _{τ u} ≥ u on {τ _u < ∞}). Hence, 𝔼_x(e^−qτg(X_τ)1_{{τ < ∞}}) ≤ 𝔼_x(e^{−qτ _u}g(X_τu)1_{{τ u < ∞}}), completing the proof.

Lemma 3.5

Suppose that −∞ < u < ∞. For x < u,

$$\begin{equation} V^{(\ell)}(x-u+u^{(\ell)})\le \mathbb {E}_x\left(e^{-q\tau_u}g(X_{\tau_u})\mathbf{1}_{\{\tau_u<\infty\}}\right).\end{equation}$$

Proof. For ease of notation, write v := u^{(ℓ )} and δ := u − u ^(ℓ) ≥ 0. Noting that, for x < u,

$$\begin{equation} \mathcal{L}(\tau^{(\ell)}_u,X_{\tau^{(\ell)}_u} \mathbf{1}_{\{\tau^{(\ell)}_u<\infty\}}\mid X_0=x)=\mathcal{L}(\tau^{(\ell)}_v,(\delta+X_{\tau^{(\ell)}_v}) \mathbf{1}_{\{\tau^{(\ell)}_v<\infty\}}\mid X_0=x-\delta),\end{equation}$$

we have

$$\begin{align&#x002A;} V^{(\ell)}(x-\delta)&=\mathbb {E}_{x-\delta}\big(e^{-q\tau^{(\ell)}_v}g(X_{\tau^{(\ell)}_v})\mathbf{1}_{\{\tau^{(\ell)}_v<\infty\}}\big)\\ &=\mathbb {E}_{x}\big(e^{-q\tau^{(\ell)}_u}g(X_{\tau^{(\ell)}_u}-\delta) \mathbf{1}_{\{\tau^{(\ell)}_u<\infty\}}\big)\\ &\le \mathbb {E}_{x}\big(e^{-q\tau^{(\ell)}_u}g(X_{\tau^{(\ell)}_u})\mathbf{1}_{\{\tau^{(\ell)}_u<\infty\}}\big)\\ &\le \mathbb {E}_{x}\big(e^{-q\tau_u}g(X_{\tau_u})\mathbf{1}_{\{\tau_u<\infty\}}\big), \end{align&#x002A;}$$

where the last inequality follows from Lemma 3.4 and the fact that $\mathbb {P}_x(\tau^{(\ell)}_u\ge\tau_u)=1$.

Lemma 3.6

Suppose that x ₀ < u < ∞. Then V(x) is continuous everywhere and τ_u is optimal.

Proof. Fix v ∈ (x ₀, u). Let h(x) := log g(x), and

$$\tilde{h}(x):=\left\{ \begin{array}{&#x002A;{35}{l}} h(v)+{h}'(vrn1.5pt-)(x-v) & if\,x<v \\ h(x) & \text{otherwise}, \\ \end{array} \right.$$

and g̃(x) := e^h̃(x) > 0, so that g̃(x) ≥ g(x) for x ∈ ℝ. Clearly, g̃(x) is nonconstant, increasing, logconcave, and continuous. Define ũ ^(ℓ), ũ, Ṽ ^(ℓ)(x), and Ṽ(x) in terms of g̃ in exactly the same way that u ^(ℓ), u, V ^(ℓ)(x), and V(x) are in terms of g. For (large) ℓ with v < u ^(ℓ), the fact that g̃(x) = g(x) for all x ≥ v yields ũ ^(ℓ) = u ^(ℓ), implying that ũ := lim_ℓ→∞ ũ ^(ℓ) = lim_ℓ→∞ u ^(ℓ) = u. Moreover, ũ ^(ℓ) = u ^(ℓ) > v and g̃(x) = g(x) for all x ≥ v implies that Ṽ ^(ℓ)(x) = V ^(ℓ)(x) for x ∈ ℝ, which in turn implies that V(x) = Ṽ(x) for x ∈ ℝ, since

$$\begin{equation} V(x)\le\tilde{V}(x)=\lim_{\ell\to\infty}\tilde{V}^{(\ell)}(x)=\lim_{\ell\to\infty}V^{(\ell)}(x)\le V(x),\end{equation}$$

where the first equality is due to Lemma 3.2(i) applied to g̃

By Lemma 3.2(iii) (applied to g̃), Ṽ(x)/g̃(x) is decreasing in x, which implies that Ṽ(x−)/g̃(x−), ≥ Ṽ(x +)/g̃(x +), x ∈ ℝ. Since g̃(x) = g̃(x −) = g̃(x +) > 0, we have Ṽ(x −) ≥ Ṽ(x +), so Ṽ(x −) = Ṽ(x +). Thus, Ṽ(x) ( = V(x)) is a continuous function.

To show the optimality of τ _u, we need to prove

(3.4)$$\begin{equation}\label{d1} V(x)=\mathbb {E}_x\left(e^{-q\tau_u}g(X_{\tau_u})\mathbf{1}_{\{\tau_u<\infty\}} \right)\quad\mbox{for }x\in\mathbb{R}. \end{equation}$$

By Lemma 3.3, V(x) = g(x) for x ≥ u, so that (3.4) holds for x ≥ u. For x < u( = ũ), we have, by Lemma 3.5 (applied to g̃),

$$\begin{equation} \mathbb {E}_x\left(e^{-q\tau_u}g(X_{\tau_u})\mathbf{1}_{\{\tau_u<\infty\}} \right)=\mathbb {E}_x\left(e^{-q\tau_u}\tilde{g}(X_{\tau_u})\mathbf{1}_{\{\tau_u<\infty\}}\right)\ge \tilde{V}^{(\ell)}(x-u+\tilde{u}^{(\ell)}).\end{equation}$$

It follows that

$$\begin{align&#x002A;} \mathbb {E}_x\left(e^{-q\tau_u}g(X_{\tau_u})\mathbf{1}_{\{\tau_u<\infty\}}\right)&\ge\sup_{\ell}\tilde{V}^{(\ell)}(x-u+\tilde{u}^{(\ell)})\\ &\ge\lim_{\varepsilon\downarrow0}\lim_{\ell\to\infty} \tilde{V}^{(\ell)}(x-\varepsilon)\\&=\tilde{V}(x\mathbb {E}rn1.5pt{-})\\&=\tilde{V}(x)\\&=V(x), \end{align&#x002A;}$$

where the first equality is due to Lemma 3.2(i) applied to g̃. This proves (3.4).

Lemma 3.7

Suppose that −∞ < u < ∞ and τ_u is optimal. Then

1. (i) g(x) ≤ 𝔼_x(e^{−qτ _y}g(X_τy)1_{{τ y < ∞}}) for x < y ≤ u;

2. (ii) 𝔼_x(e^{−qτ _y}g(X_τy)1_{{τ y < ∞}}) ≤ 𝔼_x(e^{−qτ _z}g(X_τz)1_{{τ z < ∞}}) for x ≤ y < z ≤ u.

Proof. (i) The desired inequality holds trivially if g(x) = 0. Suppose that g(x) > 0. Since $\mathcal{L}(\tau_y,(u-y+X_{\tau_y})\mathbf{1}_{\{\tau_y<\infty\}}\mid X_0=x)=\mathcal{L}(\tau_u,X_{\tau_u}\mathbf{1}_{\{\tau_u<\infty\}}\mid X_0=x+u-y)$, we have

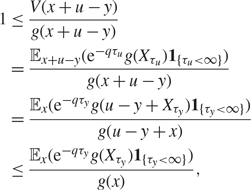$$\begin{align&#x002A;} 1&\le \frac{V(x+u-y)}{g(x+u-y)} \\ &=\frac{\mathbb {E}_{x+u-y}(e^{-q\tau_u}g(X_{\tau_u})\mathbf{1}_{\{\tau_u<\infty\}} )}{g(x+u-y)} \\ &=\frac{\mathbb {E}_{x}(e^{-q\tau_y}g(u-y+X_{\tau_y})\mathbf{1}_{\{\tau_y<\infty\}} )}{g(u-y+x)} \\ &\le \frac{\mathbb {E}_{x}(e^{-q\tau_y}g(X_{\tau_y})\mathbf{1}_{\{\tau_y<\infty\}} )}{g(x)}, \end{align&#x002A;}$$

where the last inequality follows from the logconcavity of g.

(ii) Noting that τ _z ≥ τ _y a.s., on {τ _y < τ _z} = {τ _y < ∞, X _{τ y} < z}, by (i) we have

$$\begin{equation} \mathbb {E}_x\big(e^{-q(\tau_z-\tau_y)}g(X_{\tau_z}) \mathbf{1}_{\{\tau_z<\infty\}}\mid\mathcal{F}_{\tau_y}\big)\ge g(X_{\tau_y})\quad\mbox{a.s.,}\end{equation}$$

from which the desired inequality in (ii) follows.

Proof of Theorem 3.1(i). If u = −∞ then u^{(ℓ )} = −∞ for ℓ= 1, 2, …, implying that 0 < V ^(ℓ)(x) = g(x) for all x ∈ℝ and ℓ = 1, 2, …. It follows from Lemma 3.2(i) that

$$\begin{equation} V(x)=\lim_{\ell\to\infty}V^{(\ell)}(x)=g(x)\quad\text{for }x\in\mathbb{R},\end{equation}$$

proving that τ _u = τ _−∞ is optimal.

If x ₀ < u < ∞, τ _u is optimal by Lemma 3.6. It remains to show that, for u = x ₀ > −∞,

(3.5)$$\begin{equation}\label{b4} V(x)=\mathbb {E}_x\left(e^{-q\tau_u}g(X_{\tau_u}) \mathbf{1}_{\{\tau_u<\infty\}}\right)\quad\text{for }x\in\mathbb{R}. \end{equation}$$

By Lemma 3.3, V(x) = g(x) for x ≥ u = x ₀, so that (3.5) holds for x ≥ u = x ₀. For x < u = x ₀ and any stopping time $\tau\in\mathcal{M}$, we have X _{τ x 0} ≥ x ₀ = u a.s. on {τ _{x 0} < τ}, so that, on {τ _{x 0} < τ},

(3.6)$$\begin{equation}\label{d2} g(X_{\tau_{x_0}})=V(X_{\tau_{x_0}})\ge \mathbb {E}_x\big(e^{-q(\tau-\tau_{x_0})}g\left(X_{\tau}\right) \mathbf{1}_{\{\tau_{x_0}<\tau<\infty\}}\mid\mathcal{F}_{\tau_{x_0}}\big) \quad\mbox{a.s.} \end{equation}$$

It follows from (3.6) that

$$\begin{equation} \mathbb {E}_x\big(e^{-q\tau_{x_0}}g(X_{\tau_{x_0}})\mathbf{1}_{\{\tau_{x_0}<\tau\}}\big)\ge \mathbb {E}_x\big(e^{-q\tau}g(X_\tau)\mathbf{1}_{\{\tau_{x_0}<\tau<\infty\}}\big),\end{equation}$$

which together with g(X _τ ) = 0 a.s. on {τ < τ _{x 0}} implies that

$$\begin{equation} \mathbb {E}_x\big(e^{-q\tau_{x_0}}g(X_{\tau_{x_0}})\mathbf{1}_{\{\tau_{x_0}<\infty\}}\big)\ge \mathbb {E}_x\big(e^{-q\tau}g(X_\tau)\mathbf{1}_{\{\tau<\infty\}}\big).\end{equation}$$

Since $\tau\in\mathcal{M}$ is arbitrary, (3.5) follows. The proof is complete.

Proof of Theorem 3.1(ii). Assume that u = ∞. We claim that, for x ∈ℝ,

(3.7)$$\begin{equation}\label{b5} Q_{y}(x)\,{:\!=}\,\mathbb {E}_x\left(e^{-q\tau_y}g(X_{\tau_y}) \mathbf{1}_{\{\tau_y<\infty\}}\right)\quad\mbox{is increasing in }y. \end{equation}$$

Consider an increasing sequence {b _k} satisfying b ₁ > x ₀ and lim_k→∞ b _k = ∞. Let g _k(x) := g(x ∧ b _k), which is nonconstant, increasing, logconcave, and right continuous. For ℓ ≥ 1, let

$$\begin{equation} u_k^{(\ell)}\,{:\!=}\,\inf\Biggl\{x\in\mathbb{R}\colon \frac{\mathbb {E}_x\left(e^{-qT_x^{(\ell)}}g_k(X_{T_x^{(\ell)}}) \mathbf{1}_{\{T_x^{(\ell)}<\infty\}}\right)}{g_k(x)}\le1\Biggr\}\le b_k.\end{equation}$$

Let $u_k\,{:\!=}\,\lim_{\ell\to\infty}u_{k}^{(\ell)}\le b_k<\infty$. In other words, u _k is defined in terms of g _k in exactly the same way that u is defined in terms of g. Since u _k < ∞, we have, by Theorem 3.1(i),

(3.8)$$\begin{equation}\label{b6} V_k(x)\,{:\!=}\,\sup_{\tau\in\mathcal{M}}\mathbb {E}_x\left(e^{-q\tau}g_k(X_{\tau}) \mathbf{1}_{\{\tau<\infty\}}\right)=\mathbb {E}_x\big(e^{-q\tau_{u_k}} g_k(X_{\tau_{u_k}})\mathbf{1}_{\{\tau_{u_k}<\infty\}}\big). \end{equation}$$

Thus, V _k(x) = g _k(x) for x ≥ u _k and V _k(x) > g _k(x) for x < u _k. Since g _k is increasing in k, it is easily shown that both V _k and u _k are increasing. Let V _∞(x) := lim_k→∞ V _k(x) and u _∞ := lim_k→∞ u _k. Clearly V _∞(x) = V(x). Since $u^{(\ell)}_k\nearrow u^{(\ell)}$ as k → ∞ and $u^{(\ell)}_k\nearrow u_k$ as ℓ → ∞, it follows that u := lim _ℓ→∞ u ^(ℓ) = ∞ implies that u _∞ := lim_k→∞ u _k = ∞. Incidentally, since V(x) ≥ V _k(x) > g _k(x) = g(x) for x < u _k ≤ b _k, we have

$$\begin{equation} \label{d5} V(x)>g(x)\quad\mbox{for all }x\in\mathbb{R}.\end{equation}$$

To prove (3.7), it suffices to show for x ≤ y ₁ < y ₂,

(3.9)$$\begin{equation}\label{b7} \mathbb {E}_x\big(e^{-q\tau_{y_1}}g(X_{\tau_{y_1}})\mathbf{1}_{\{\tau_{y_1}<\infty\}}\big)\le \mathbb {E}_x\big(e^{-q\tau_{y_2}}g(X_{\tau_{y_2}})\mathbf{1}_{\{\tau_{y_2}<\infty\}}\big). \end{equation}$$

For large k with u _k > y ₂, applying Lemma 3.7 to g _k yields

(3.10)$$\begin{equation}\label{b8} \mathbb {E}_x\big(e^{-q\tau_{y_1}}g_k(X_{\tau_{y_1}})\mathbf{1}_{\{\tau_{y_1}<\infty\}}\big)\le \mathbb {E}_x\big(e^{-q\tau_{y_2}}g_k(X_{\tau_{y_2}})\mathbf{1}_{\{\tau_{y_2}<\infty\}}\big). \end{equation}$$

By the monotone convergence theorem, the two sides of (3.10) converge to the corresponding sides of (3.9), respectively. This proves (3.9) and establishes the claim (3.7).

By (3.7), W := sup_y∈ℝ 𝔼(e^{−qτ _y}g(X_τy)1_{{τ y < ∞}}) = lim_y→∞ 𝔼(e^{−qτ _y}g(X_τy)1_{{τ y < ∞}}). Following the argument for (2.16) in the proof of Theorem 2.1(ii), we can show that

(3.11)$$\begin{equation}\label{d3} Q(x)\,{:\!=}\,\sup_{y\in\mathbb{R}}Q_{y}(x)=\lim_{y\to\infty}Q_{y}(x)=e^{\beta x}W. \end{equation}$$

Furthermore, we have

$$\begin{align&#x002A;} V(x)&=V_\infty(x)\\&=\lim_{k\to\infty}V_k(x)\\ &=\lim_{k\to\infty}\mathbb {E}_x\big(e^{-q\tau_{u_k}}g_k(X_{\tau_{u_k}})\mathbf{1}_{\{\tau_{u_k}<\infty\}}\big)\;\;\;\mbox{(by (ef{b6}))}\\ &\le\sup_{k}\mathbb {E}_x\big(e^{-q\tau_{u_k}}g(X_{\tau_{u_k}}) \mathbf{1}_{\{\tau_{u_k}<\infty\}}\big)\\&\le Q(x)\\&\le V(x), \end{align&#x002A;}$$

implying by (3.11) that

$$\begin{equation} \label{d4} V(x)=Q(x)=e^{\beta x}W\quad\text{for }x\in\mathbb{R}.\end{equation}$$

If W = ∞, it is readily seen that there are randomized stopping times that yield an infinite expected (discounted) reward. Suppose that W < ∞. Following the argument for (2.17) in the proof of Theorem 2.1(ii), we can show that there is no optimal stopping time. The proof is complete.

4. On the principle of smooth fit for Lévy processes

In this section we investigate the principle of smooth fit for Lévy processes. Let X = {X _t}_t≥0 be a Lévy process with initial state X ₀ = x ∈ ℝ, and assume that ℙ(X ₁ > 0) > 0. For y ∈ ℝ, let τ _y := inf{t ≥ 0: X _t ≥ y} and τ _y+ := inf{t ≥ 0: X _t > y}.

Theorem 4.1

Let g: ℝ → [0, ∞) be nonconstant, increasing, logconcave, and right continuous. Define V(x) and u as in (3.1) and (3.3). Suppose that −∞ ≤ x ₀ < u < ∞ and g is differentiable at u (i.e. g′(u −) = g′(u +) = g′(u)). If 0 is regular for (0, ∞) for X then V is differentiable at u, i.e. V′(u −) = V′(u +) ( = g′(u)).

Proof. Since V(u − ε) > g(u − ε) for ε > 0 and V(u) = g(u), we have

(4.1)$$\begin{equation}\label{d11} \overline{\lim_{\varepsilon\downarrow0}}\;\varepsilon^{-1}\left[V(u)-V(u-\varepsilon)\right]\le\overline{\lim_{\varepsilon\downarrow0}}\;\varepsilon^{-1}\left[g(u)-g(u-\varepsilon)\right]=g'(u\mathbb {E}rn1.5pt{-})=g'(u). \end{equation}$$

Since

$$\begin{gather&#x002A;} \mathcal{L}(\tau_{u+\varepsilon}, X_{\tau_{u+\varepsilon}}\mathbf{1}_{\{\tau_{u+\varepsilon}<\infty\}}\mid X_0=u)=\mathcal{L}(\tau_{\varepsilon},(u+X_{\tau_{\varepsilon}})\mathbf{1}_{\{\tau_{\varepsilon}<\infty\}}\mid X_0=0) \\ \text{and}\quad \mathcal{L}(\tau_{u},X_{\tau_{u}}\mathbf{1}_{\{\tau_{u}<\infty\}}\mid X_0=u-\varepsilon)=\mathcal{L}(\tau_{\varepsilon},(u-\varepsilon+X_{\tau_{\varepsilon}})\mathbf{1}_{\{\tau_{\varepsilon}<\infty\}}\mid X_0=0), \end{gather&#x002A;}$$

we have

(4.2)$$\begin{align} &\varepsilon^{-1}\left[V(u)-V(u-\varepsilon)\right] \\ & \ge\varepsilon^{-1} \left[\mathbb {E}_u\left(e^{-q\tau_{u+\varepsilon}}g(X_{\tau_{u+\varepsilon}}) \mathbf{1}_{\{\tau_{u+\varepsilon}<\infty\}}\right)-\mathbb {E}_{u-\varepsilon} \left(e^{-q\tau_{u}}g(X_{\tau_{u}})\mathbf{1}_{\{\tau_{u}<\infty\}}\right) \right] \\ & =\varepsilon^{-1}\left[\mathbb {E}\left(e^{-q\tau_{\varepsilon}}g(u+ X_{\tau_{\varepsilon}})\mathbf{1}_{\{\tau_{\varepsilon}<\infty\}}\right) -\mathbb {E}\left(e^{-q\tau_{\varepsilon}}g(u-\varepsilon+X_{\tau_{\varepsilon}}) \mathbf{1}_{\{\tau_{\varepsilon}<\infty\}}\right)\right] \\ & =\varepsilon^{-1}\mathbb {E}\left(e^{-q\tau_{\varepsilon}}\left(g(u+ X_{\tau_{\varepsilon}})-g(u-\varepsilon+X_{\tau_{\varepsilon}})\right) \mathbf{1}_{\{\tau_{\varepsilon}<\infty\}}\right)\label{d12}. \end{align}$$

By the concavity of h(x) : = log g(x), we have, on {τ _ε < ∞},

(4.3)$$\begin{align} g(u+X_{\tau_{\varepsilon}})-g(u-\varepsilon+X_{\tau_{\varepsilon}})&=e^{h(u-\varepsilon+X_{\tau_{\varepsilon}})}\big[e^{h(u+X_{\tau_{\varepsilon}})-h(u-\varepsilon+X_{\tau_{\varepsilon}})}-1\big] \\ &\ge e^{h(u-\varepsilon+X_{\tau_{\varepsilon}})}\big[e^{\varepsilon h'((u+X_{\tau_{\varepsilon}})\mathbb {E}rn1.5pt{+})}-1\big] \\ &=e^{h(u-\varepsilon+X_{\tau_{\varepsilon}})}e^{\theta\varepsilon h'((u+X_{\tau_{\varepsilon}})\mathbb {E}rn1.5pt{+})}\varepsilon h'((u+X_{\tau_{\varepsilon}})\mathbb {E}rn1.5pt{+})\label{d13} \end{align}$$

for some θ ∈ (0, 1) by the mean value theorem. It follows from (4.2) and (4.3) that

(4.4)$$\begin{align} &\mathop{\underline{\lim}}_{\varepsilon\downarrow0}\varepsilon^{-1} [V(u)-V(u-\varepsilon)] \\ & \ge\mathop {\underline{\lim}}_{\varepsilon\downarrow0}\mathbb {E}\big(e^{- q\tau_{\varepsilon}+h(u-\varepsilon+X_{\tau_{\varepsilon}})+\theta \varepsilon h'((u+X_{\tau_{\varepsilon}})\mathbb {E}rn1.5pt{+})}h'((u+X_{\tau_{\varepsilon}})\mathbb {E}rn1.5pt{+}) \mathbf{1}_{\{\tau_{\varepsilon}<\infty\}}\big) \\ & \ge \mathbb {E}\Big(\mathop{\underline{\lim}}_{\varepsilon\downarrow0}e^{- q\tau_{\varepsilon}+h(u-\varepsilon+X_{\tau_{\varepsilon}})+\theta \varepsilon h'((u+X_{\tau_{\varepsilon}})\mathbb {E}rn1.5pt{+})}h'((u+X_{\tau_{\varepsilon}})\mathbb {E}rn1.5pt{+}) \mathbf{1}_{\{\tau_{\varepsilon}<\infty\}}\Big) \\ & =\mathbb {E}\big(e^{-q\tau_{0+}}e^{h(u+X_{\tau_{0+}})}h'((u+X_{\tau_{0+}})\mathbb {E}rn1.5pt{+}) \mathbf{1}_{\{\tau_{0+}<\infty\}}\big) \\ & =e^{h(u)}h'(u\mathbb {E}rn1.5pt{+})\label{d14}, \end{align}$$

where the second-to-last equality follows from the fact that τ _ε ↓ τ ₀₊ as ε ↓ 0 together with the right continuity of {X _t} and the concavity of h, and the last equality follows from ℙ(τ ₀₊ = 0) = 1 (since 0 is regular for (0, ∞)). Combining (4.1) and (4.4) together with e^h(u)h′(u +) = g′(u +) = g′(u) yields V′(u −) = g′(u) = V′(u +). The proof is complete.

Lemma 4.1

Let g: ℝ → [0, ∞) be nonconstant, increasing, logconcave, and right continuous. Suppose that 0 is irregular for (0, ∞) for X and

(4.6)$$\begin{equation}\label{d24} \frac{\mathbb {E}_x\left(e^{-q\tau_{x+}}g(X_{\tau_{x+}}) \mathbf{1}_{\left\{\tau_{x+}<\infty\right\}}\right)}{g(x)}\le1 \quad\mbox{for some }x>x_0. \end{equation}$$

Then

$$\begin{equation} g(x)\ge \mathbb {E}_x\big(e^{-q\tau_{y}}g(X_{\tau_{y}}) \mathbf{1}_{\left\{\tau_{y}<\infty\right\}}\big)\quad\mbox{for all } y>x.\end{equation}$$

Proof. The following proof is similar to those of Lemmas 2.3 and 2.4. Note that

$$\begin{equation} \frac{\mathbb {E}_z\left(e^{-q\tau_{z+}}g(X_{\tau_{z+}}) \mathbf{1}_{\left\{\tau_{z+}<\infty\right\}}\right)}{g(z)} =\frac{\mathbb {E}\big(e^{-q\tau_{0+}}g(z+X_{\tau_{0+}}) \mathbf{1}_{\left\{\tau_{0+}<\infty\right\}}\big)}{g(z)}\end{equation}$$

is decreasing in z ∈ (x ₀, ∞), implying by (4.6) that

(4.7)$$\begin{equation}\label{d25} \mathbb {E}_z\left(e^{-q\tau_{z+}}g(X_{\tau_{z+}})\mathbf{1}_{\left\{\tau_{z+}<\infty\right\}}\right)\le g(z)\quad\text{for }z>x. \end{equation}$$

Let J ₀ := τ _x+ and, for n ≥ 1,

$$\begin{equation} J_n\,{:\!=}\, \begin{cases} \inf\{t>J_{n-1}\colon X_t>X_{J_{n-1}}\} &\mbox{if }J_{n-1}<\infty,\\ \infty & \mbox{otherwise.} \end{cases}\end{equation}$$

Note that $\mathcal{L}(J_{n+1}-J_n\mid X_0=x,J_n<\infty)=\mathcal{L}(\tau_{0+}\mid X_0=0)$ and that ℙ(τ ₀₊ > 0) = 1. It follows that J _n → ∞ a.s. Fix y > x. Since the Lévy process X either satisfies $\overline{\lim}_{t\to\infty}X_t=+\infty$ a.s. or lim_t→∞ X _t = −∞ a.s., we have J _n = τ _y < ∞ for some n in the former case and J _n = ∞ for large n in the latter case. In either case, L _n := min{J _n, τ _y} = τ _y for large n. As a consequence, e^{−qL _n}g(X _{L n})1_{{L n<∞}} → e^{−qτ _y}g(X _{τ y})1_{{τ y<∞}} a.s., so that, by Fatou’s lemma,

(4.8)$$\begin{equation}\label{d26} \mathop{\underline{\lim}}_{n\to\infty}\mathbb {E}_x\left(e^{-qL_n}g(X_{L_n})\mathbf{1}_{\{L_n<\infty\}}\right)\ge \mathbb {E}_x\left(e^{-q\tau_y}g(X_{\tau_y})\mathbf{1}_{\{\tau_y<\infty\}}\right). \end{equation}$$

By (4.7), it is readily shown that 𝔼_x (e^{−qL _n}g(X _{L n})1_{{L n<∞}}) is decreasing in n, which together with (4.8) implies that 𝔼_x (e^{−qτ _y}g(X _{τ y})1_{{τ y<∞}}) ≤ 𝔼_x (e^{−qL ₀}g(X _{L 0})1_{{L 0<∞}}) ≤ g(x). The proof is complete.

Let

(4.9)$$\begin{equation}\label{d16} u'\,{:\!=}\,\inf\Bigg\{x\in\mathbb{R}\colon \frac{\mathbb {E}_x\left(e^{-q\tau_{x+}}g(X_{\tau_{x+}}) \mathbf{1}_{\{\tau_{x+}<\infty\}}\right)}{g(x)}\le1\Bigg\}. \end{equation}$$

Lemma 4.2

Let g: ℝ → [0, ∞) be nonconstant, increasing, logconcave, and right continuous. Define u and u′ as in (3.3) and (4.9). If 0 is irregular for (0, ∞) for X then u′= u.

Proof. We first show that u ≥ u′. It suffices to consider the u < ∞ case. By Theorem 3.1, we have 𝔼_x (e^{−qτ _x}g(X _{τ x+})1_{{τ x+<∞}}) ≤ V(x+) for all x ≥ u, implying by (4.9) that u′≤ u. To show u ≤ u′, suppose to the contrary that u > u′. Let x be such that u > x > u′( ≥ x ₀). If u < ∞, it follows from (4.9) and Lemma 4.1 that

$$g(x)\ge {{}_{x}}\left( {{e}^{-q{{\tau }_{u}}}}g({{X}_{{{\tau }_{u}}}}){{\mathbf{1}}_{\{{{\tau }_{u}}<\infty \}}} \right)\text{ }\begin{matrix} =V(x)\quad (byTheoremeft3.1(i)) \\ >g(x)\quad (since\,x<u), \\ \end{matrix}$$

a contradiction. If u = ∞, it follows from (4.9) and Lemma 4.1 that

$$\begin{equation} g(x)\ge \mathbb {E}_x\left(e^{-q\tau_{y}}g(X_{\tau_{y}}) \mathbf{1}_{\{\tau_{y}<\infty\}}\right)\quad\mbox{for all }y>x,\end{equation}$$

which implies that, by Theorem 3.1(ii),

$$\begin{equation} g(x)\ge \lim_{y\to\infty}\mathbb {E}_x\left(e^{-q\tau_{y}}g(X_{\tau_{y}}) \mathbf{1}_{\{\tau_{y}<\infty\}}\right)=V(x)>g(x),\end{equation}$$

a contradiction. This proves u ≤ u′ and completes the proof.

Proof of Theorem 4.2. (i) We have

(4.10)$$\begin{align} \mathbb {E}_u\left(e^{-q\tau_{u+}}g(X_{\tau_{u+}})\mathbf{1}_{\{\tau_{u+}<\infty\}}\right)\le V(u)=g(u),\label{a2}\\ \end{align} $$

(4.11)$$\begin{array}{&#x002A;{35}{l}} {{\mathbb {E}}_{x}}\left( {{e}^{-q{{\tau }_{x+}}}}g({{X}_{{{\tau }_{x+}}}}){{\mathbf{1}}_{\{{{\tau }_{x+}}<\infty \}}} \right)>g(x)\quad \text{for }{{\text{x}}_{\text{0}}} & <x & <u, \\ \end{array}$$

where (4.11) is due to the definition of u′and u′= u (by Lemma 4.2). Since both g(x) and 𝔼_x (e^{−qτ _x}g(X _{τ x+})1_{{τ x+<∞}}) (= 𝔼 (e^{−qτ ₀₊}g(X _{τ 0+})1_{{τ 0+<∞}}) are continuously increasing in x > x ₀, (4.10) and (4.11) together imply that

(4.12)$$\begin{equation}\label{a4} V(u)=g(u)=\mathbb {E}_u\left(e^{-q\tau_{u+}}g(X_{\tau_{u+}}) \mathbf{1}_{\{\tau_{u+}<\infty\}}\right)=\mathbb {E}\left(e^{-q\tau_{0+}}g(u+X_{\tau_{0+}})\mathbf{1}_{\{\tau_{0+}<\infty\}}\right), \end{equation}$$

which in turn implies that both τ _u and τ _u+ are optimal stopping times.

For x < u,

$$\begin{equation} V(x)=\mathbb {E}_x\left(e^{-q\tau_{u+}}g(X_{\tau_{u+}}) \mathbf{1}_{\{\tau_{u+}<\infty\}}\right)= \mathbb {E}_x\left(\mathbb {E}_x\left(e^{-q\tau_{u+}}g(X_{\tau_{u+}}) \mathbf{1}_{\{\tau_{u+}<\infty\}}\mid\mathcal{F}_{\tau_{x+}}\right) \right).\end{equation}$$

On {τ _x+ < ∞}, since X _{s+τ x+} − X _{τ x+} is independent of $\mathcal{F}_{\tau_{x+}}$ and has the same law as X _s − X ₀, and since τ _u+ is optimal, we have

$$\begin{equation} \mathbb {E}_x\big(e^{-q(\tau_{u+}-\tau_{x+})}g(X_{\tau_{u+}}) \mathbf{1}_{\{\tau_{u+}<\infty\}}\mid\mathcal{F}_{\tau_{x+}}\big) =V(X_{\tau_{x+}})\quad\mbox{a.s.}\end{equation}$$

It follows that

$$\begin{equation} V(x)=\mathbb {E}_x\left(e^{-q\tau_{x+}}V(X_{\tau_{x+}}) \mathbf{1}_{\{\tau_{x+}<\infty\}}\right)= \mathbb {E}\left(e^{-q\tau_{0+}}V(x+X_{\tau_{0+}})\mathbf{1}_{\{\tau_{0+} <\infty\}}\right).\end{equation}$$

Taking x = u − ε for ε > 0 yields

(4.13)$$\begin{align} V(u-\varepsilon)&=\mathbb {E}\left(e^{-q\tau_{0+}}V(u-\varepsilon+X_{\tau_{0+}})\mathbf{1}_{\{\tau_{0+}<\infty\}}\right).\label{a5} \end{align}$$

By (4.12) and (4.13),

$$\begin{align&#x002A;} \varepsilon^{-1}[V(u)-V(u-\varepsilon)]&=\varepsilon^{-1}\mathbb {E} (e^{-q\tau_{0+}}(g(u+X_{\tau_{0+}})-V(u-\varepsilon+ X_{\tau_{0+}}))\mathbf{1}_{\{\tau_{0+}<\infty\}}) \\ &=A(\varepsilon) -B(\varepsilon), \end{align&#x002A;}$$

where

$$\begin{align&#x002A;} A(\varepsilon)&\,{:\!=}\,\varepsilon^{-1}\mathbb {E}\left(e^{-q\tau_{0+}}\left(g(u+X_{\tau_{0+}})-g(u-\varepsilon+X_{\tau_{0+}})\right)\mathbf{1}_{\{\tau_{0+}<\infty\}}\right),\\ B(\varepsilon)&\,{:\!=}\,\varepsilon^{-1}\mathbb {E}\left(e^{-q\tau_{0+}}\left(V(u-\varepsilon+X_{\tau_{0+}})-g(u-\varepsilon+X_{\tau_{0+}})\right)\mathbf{1}_{\{\tau_{0+}<\infty\}}\right). \end{align&#x002A;}$$

To show that

(4.14)$$\begin{equation}\label{a6} \lim_{\varepsilon\downarrow0}A(\varepsilon)=\mathbb {E}\left(e^{-q\tau_{0+}}g'((u+X_{\tau_{0+}})\mathbb {E}rn1.5pt{-})\mathbf{1}_{\{\tau_{0+}<\infty\}}\right), \end{equation}$$

we have

(4.15)$$\begin{align} & \le g(u+{{X}_{{{\tau }_{0+}}}})-g(u-\varepsilon +{{X}_{{{\tau }_{0+}}}}) \\ & =g(u-\varepsilon +{{X}_{{{\tau }_{0+}}}})[{{e}^{h(u+{{X}_{{{\tau }_{0+}}}})-h(u-\varepsilon +{{X}_{{{\tau }_{0+}}}})}}-1] \\ & \le g(u-\varepsilon +{{X}_{{{\tau }_{0+}}}})[{{e}^{\varepsilon {h}'((u-\varepsilon +{{X}_{{{\tau }_{0+}}}})\mathbb{E}rn1.5pt+)}}-1] \\ & =g(u-\varepsilon +{{X}_{{{\tau }_{0+}}}}){{e}^{\theta \varepsilon {h}'((u-\varepsilon +{{X}_{{{\tau }_{0+}}}})\mathbb{E}rn1.5pt+)}}\varepsilon {h}'((u-\varepsilon +{{X}_{{{\tau }_{0+}}}})\mathbb{E}rn1.5pt+) \\ \end{align}$$

for some θ ∈ (0, 1), where the inequality is due to the concavity of h(x) := log g(x) and the last equality follows from the mean value theorem applied to the function e^x. So, for any (fixed) v ∈ (x ₀, u) and for 0 < ε < u − v, on {τ ₀₊ < ∞},

$$\begin{align&#x002A;} &\varepsilon^{-1}\big[g(u+X_{\tau_{0+}})-g(u-\varepsilon+X_{\tau_{0+}}) \big] \\ & \le g(u-\varepsilon+X_{\tau_{0+}})e^{\theta\varepsilon h'((u-\varepsilon+X_{\tau_{0+}})\mathbb {E}rn1.5pt{+})}h'((u-\varepsilon+X_{\tau_{0+}})\mathbb {E}rn1.5pt{+}) \\ & \le g(u+X_{\tau_{0+}})e^{\varepsilon h'(v\mathbb {E}rn1.5pt{+})}h'((u-\varepsilon+X_{\tau_{0+}})\mathbb {E}rn1.5pt{+}) \\ & \le g(u+X_{\tau_{0+}})e^{(u-v)h'(v\mathbb {E}rn1.5pt{+})}h'(v\mathbb {E}rn1.5pt{+}). \end{align&#x002A;}$$

Since on {τ ₀₊ < ∞}

$$\begin{equation} \lim_{\varepsilon\downarrow0}g(u+X_{\tau_{0+}})e^{\varepsilon h'(v\mathbb {E}rn1.5pt{+})}h'((u-\!\varepsilon\!+X_{\tau_{0+}})\mathbb {E}rn1.5pt{+})=g(u+X_{\tau_{0+}}\!)h'((u+X_{\tau_{0+}})-\!)=g'((u+X_{\tau_{0+}})\mathbb {E}rn1.5pt{-}),\end{equation}$$

we have

(4.16)$$\begin{align} \overline{\lim_{\varepsilon\downarrow0}}A(\varepsilon)&\le \lim_{\varepsilon\downarrow0}\mathbb {E}\big(e^{-q\tau_{0+}}g(u+X_{\tau_{0+}}) e^{\varepsilon h'(v\mathbb {E}rn1.5pt{+})}h'((u-\varepsilon+X_{\tau_{0+}})\mathbb {E}rn1.5pt{+})\mathbf{1}_{\{\tau_{0+} <\infty\}}\big) \\ &=\mathbb {E}\left(e^{-q\tau_{0+}}g'((u+X_{\tau_{0+}})\mathbb {E}rn1.5pt{-}) \mathbf{1}_{\{\tau_{0+}<\infty\}}\right),\label{a7} \end{align}$$

by the dominated convergence theorem together with the fact (cf. (4.12)) that 𝔼 (e^{−qτ ₀₊}g(X _{τ 0+})1_{{τ 0+<∞}}. Instead of the upper bound in (4.15), we can use the lower bound

$$\begin{equation} g(u+X_{\tau_{0+}})-g(u-\varepsilon+X_{\tau_{0+}})\ge g(u-\varepsilon+X_{\tau_{0+}})\big[e^{\varepsilon h'((u+X_{\tau_{0+}})\mathbb {E}rn1.5pt{-})}-1\big]\end{equation}$$

to derive in a similar way

$$\begin{equation} \mathop{\underline{\lim}}_{\varepsilon\downarrow0}A(\varepsilon)\ge \mathbb {E}\left(e^{-q\tau_{0+}}g'((u+X_{\tau_{0+}})\mathbb {E}rn1.5pt{-}) \mathbf{1}_{\{\tau_{0+}<\infty\}}\right),\end{equation}$$

which together with (4.16) establishes (4.14).

To show that lim_ε↓0 B(ε) = 0, note that V(x) = g(x) for x ≥ u and g(x) < V(x) ≤ g(u) for x < u. So

$$\begin{align&#x002A;} B(\varepsilon)&=\varepsilon^{-1}\mathbb {E}\big(e^{-q\tau_{0+}}\left(V(u-\varepsilon+X_{\tau_{0+}})-g(u-\varepsilon+X_{\tau_{0+}})\right)\mathbf{1}_{\{\tau_{0+}<\infty,\;X_{\tau_{0+}}<\varepsilon\}}\big)\\ &\le\varepsilon^{-1}\mathbb {E}\big((g(u)-g(u-\varepsilon))\mathbf{1}_{\{\tau_{0+}<\infty,\;X_{\tau_{0+}}<\varepsilon\}}\big)\\ &=\varepsilon^{-1}\left(g(u)-g(u-\varepsilon)\right)\mathbb {p}(\tau_{0+}<\infty,X_{\tau_{0+}}<\varepsilon), \end{align&#x002A;}$$

implying that

(4.17)$$\begin{equation}\label{a9} \overline{\lim_{\varepsilon\downarrow0}}\,B(\varepsilon)\le g'(u\mathbb {E}rn1.5pt{-})\mathbb {p}(\tau_{0+}<\infty,\,X_{\tau_{0+}}=0)=0 \end{equation}$$

(since 0 is irregular for (0, ∞) and X does not creep upwards). Combining (4.14) and (4.17) yields

$$\begin{equation} V'(u\mathbb {E}rn1.5pt{-})=\lim_{\varepsilon\downarrow0}\varepsilon^{-1} \left[V(u)-V(u-\varepsilon)\right]=\mathbb {E}\left(e^{-q\tau_{0+}} g'((u+X_{\tau_{0+}})\mathbb {E}rn1.5pt{-})\mathbf{1}_{\{\tau_{0+}<\infty\}}\right).\end{equation}$$

(ii) We have, by (i),

$$\begin{align&#x002A;} V'(u\mathbb {E}rn1.5pt{-})&=\mathbb {E}\left(e^{-q\tau_{0+}}h'((u+X_{\tau_{0+}})\mathbb {E}rn1.5pt{-}) g(u+X_{\tau_{0+}})\mathbf{1}_{\{\tau_{0+}<\infty\}}\right)\\ &\le \mathbb {E}\left(e^{-q\tau_{0+}}h'(u\mathbb {E}rn1.5pt{+})g(u+X_{\tau_{0+}}) \mathbf{1}_{\{\tau_{0+}<\infty\}}\right)\\ &=h'(u\mathbb {E}rn1.5pt{+})g(u)\\&=g'(u\mathbb {E}rn1.5pt{+})\\&=V'(u\mathbb {E}rn1.5pt{+}), \end{align&#x002A;}$$

where the inequality is due to the concavity of h(x). This inequality is an equality if and only if ℙ(h′((u + X _{τ 0+}) −) = h′(u +) | τ ₀₊ < ∞) = 1 or, equivalently, h′ ((u + ζ) −) = h′(u +).

(iii) Condition (4.5) implies that h′(x −) = h′(x +) = h′(u +) for u < x < u + ζ, which in turn implies that

(4.18)$$\begin{equation}\label{a10} g(x)=g(u)e^{h'(u\mathbb {E}rn1.5pt{+})(x-u)}\quad\text{for }u\le x\le u+\zeta. \end{equation}$$

By (4.12) and (4.18),

(4.19)$$\begin{align} g(u)&=\mathbb {E}\left(e^{-q\tau_{0+}}g(u+X_{\tau_{0+}}) \mathbf{1}_{\{\tau_{0+}<\infty\}}\right)=g(u)\mathbb {E}\big(e^{-q\tau_{0+}}e^{h'(u\mathbb {E}rn1.5pt{+})X_{\tau_{0+}}}\mathbf{1}_{\{\tau_{0+}<\infty\}}\big).\label{a11} \end{align}$$

Let g̃ (x) := g(u)e^{h′(u +)(x−u)} for x ∈ ℝ, so that

(4.20)$$\begin{equation}\label{a12} \tilde {g}(x)=g(x)\quad\text{for }u\le x\le u+\zeta. \end{equation}$$

Note that, for all y ∈ ℝ,

(4.21)$$\begin{align}\label{a13} \mathbb {E}_y\left(e^{-q\tau_{y+}} \tilde{g}(X_{\tau_{y+}}) \mathbf{1}_{\{\tau_{y+}<\infty\}}\right)&=\mathbb {E}\big(e^{-q\tau_{0+}} \tilde{g}(y+X_{\tau_{0+}})\mathbf{1}_{\{\tau_{0+}<\infty\}}\big) \\ &=g(u)e^{h'(u\mathbb {E}rn1.5pt{+})(y-u)}\mathbb {E}\big(e^{-q\tau_{0+}}e^{h'(u\mathbb {E}rn1.5pt{+}) X_{\tau_{0+}}}\mathbf{1}_{\{\tau_{0+}<\infty\}}\big) \\ &=g(u)e^{h'(u\mathbb {E}rn1.5pt{+})(y-u)} \\&= {g}(y), \end{align}$$

where the third equality follows from (4.19). To show that

(4.22)$$V(x)=\tildeg(x)= {g}(u){{e}^{{h}'(u+)(x-u)}}\quad \text{for }x<u,$$

we treat the two cases h′(u +) = 0 and h′(u +) > 0 separately. If h′(u +) = 0 then g(u) = max{g(x): x ∈ ℝ}. In order for (4.12) to hold, necessarily q = 0 and ℙ(τ ₀₊ < ∞) = 1, which implies that V(x) = g(u) for all x, proving (4.22). Now assume that h′(u +) > 0. Note that g̃ is nonconstant, continuous, increasing, and logconcave. It is readily shown by (4.21) that

$$\begin{equation} \tilde {V}(x)\,{:\!=}\,\sup_{\tau\in\mathcal{M}} \mathbb {E}_x\left(e^{-q\tau}\tilde {g}(X_{\tau}) \mathbf{1}_{\{\tau<\infty\}}\right)= {g}(x)\quad\mbox{for all } x\in\mathbb{R},\end{equation}$$

and that, for any a ∈ [ − ∞, ∞), τ _a is optimal for the reward function g̃. So we have, for x < u,

$$\begin{equation} {\tilde g}(x)=\mathbb {E}_x\left(e^{-q\tau_{u}}\tilde {g}(X_{\tau_{u}}) \mathbf{1}_{\{\tau_{u}<\infty\}}\right)=\mathbb {E}_x\left(e^{-q\tau_{u}}g(X_{\tau_{u}})\mathbf{1}_{\{\tau_{u}<\infty\}}\right)=V(x),\end{equation}$$

where the second equality is due to (4.20). The proof is complete.

Remark 4.3

When smooth fit fails, it is of interest to find conditions under which the principle of continuous fit holds. Again suppose that g is increasing and logconcave. If the optimal threshold satisfies ∞ > u > x ₀ := inf{s: g(s) > 0} then, by Lemma 3.6, the value function V(x) is continuous everywhere, so that there is continuous fit at u. Suppose that u = x ₀ and g is discontinuous at x ₀, i.e. g(x ₀ −) = 0 < g(x ₀) = g(x ₀ +). For a Lévy process X for which 0 is regular for (0, ∞), it is clear that V is continuous at u ( = x ₀), i.e. V(x ₀ −) = V(x ₀) = g(x ₀). We now consider a Lévy process X for which 0 is irregular for (0, ∞). Since u = x ₀, we have, by Lemma 4.2 and (4.9),

(4.23)$$\begin{equation}\label{u1} g(x_0)\ge \mathbb {E}(e^{-q\tau_{0+}}g(x_0+X_{\tau_{0+}})\mathbf{1}_{\{\tau_{0+}<\infty\}}). \end{equation}$$

It follows from u = x ₀ that V(x ₀)=g(x ₀) and V(x ₀-) = 𝔼 (e^{−qτ ₀₊}g(x ₀ + X _{τ 0+})1_{{τ 0+<∞}}. This proves that there is continuous fit (i.e. V(x ₀) = V(x ₀ −)) if and only if the inequality in (4.23) is an equality.

5. Concluding remarks

The optimal stopping problem (1.1) involves the reward function g and the underlying process {X _t} as well as the discount rate q ≥ 0. Motivated by well-known results in the literature, we explored the close connection between increasing and logconcave reward functions and optimal stopping times of threshold type. Specifically, in this paper, g is assumed to be nonnegative, nonconstant, increasing, logconcave, and right continuous, while {X _t} is either a random walk in discrete time or a Lévy process in continuous time. We showed that there exists a unique threshold u ∈ [ − ∞, ∞] such that

• • the value function V(x) > g(x) for x < u and V(x) = g(x) for x ≥ u;

• • if −∞ ≤ u < ∞ then τ _u = inf{t ≥ 0: X _t ≥ u} is optimal;

• • if u = ∞, the stopping region {x: V(x) = g(x)} = [u, ∞) =∅ and no optimal stopping time exists in the sense that for any initial state x and for any stopping time τ, one can always find another stopping time τ′ such that P _x(τ′ ≥ τ) = 1 and

  $$\begin{equation} \mathbb {E}_x\big(e^{-q\tau'}g(X_{\tau'})\mid\mathcal{F}_{\tau}\big)> e^{-q\tau}g(X_{\tau})\quad\mbox{a.s.\ on }\{\tau<\infty\}.\end{equation}$$

The work of Alili and Kyprianou [Reference Alili and Kyprianou1] made use of a fluctuation identity to give insight into the importance of the role played by the regularity of the paths of {X _t} in the solution for the American put optimal stopping problem. Building on it, we investigated the principle of smooth fit more generally when g is increasing and logconcave. We obtained necessary and sufficient conditions for the smooth fit principle to hold. We also briefly discussed the principle of continuous fit when smooth fit fails.

After the present paper had been submitted, a referee brought to our attention the article by Christensen and Irle [Reference Christensen and Irle5]. (Note that both [Reference Christensen and Irle5] and the original version [Reference Lin and Yao14] of the present paper were posted on arxiv in October 2017.) The authors proposed a general method for finding the optimal threshold for discrete-time optimal stopping problems with general underlying Markov processes {X _n}_n≥0. By considering an auxiliary problem involving the associated ascending ladder process, they introduced a threshold α ^∗ as a natural candidate for the optimal threshold. Assuming that the optimal threshold is greater than x ₀ := inf{s: g(s) > 0} and that, for every x ∈ ℝ,

(5.1)$$\begin{equation}\label{u2} \mathbb {E}_x\big(\!\sup_{n}e^{-qn}g(X_n)\big)<\infty \quad \mbox{and}\quad e^{-qn}g(X_n)\to0\quad\mbox{a.s.\ as }n\to\infty, \end{equation}$$

they obtained a sufficient condition for α ^∗ to be optimal. Furthermore, they showed that the sufficient condition is satisfied when g is increasing and logconcave and {X _n}_n≥0 is a random walk, in which case α ^∗ coincides with u in (2.2). They also showed that the sufficient condition is satisfied in some well-known problems beyond the random walk setting. On the other hand, in the present paper, for the discrete-time case, we considered a general random walk {X _n}_n≥0 without imposing condition (5.1) or any other condition. Theorem 2.1 completely characterizes the solution of (1.1) in terms of u, where the full range of u is −∞ ≤ x ₀ ≤ u ≤ ∞. The two extreme cases u = x ₀ and u = ∞ required careful analysis especially when g is discontinuous at x ₀. Furthermore, we treated the continuous-time case in some detail with a thorough discussion of the principle of smooth fit. When {X _t}_t≥0 is a Lévy process with 0 irregular for (0, ∞), the optimal threshold given in (4.9) is the continuous-time counterpart of u in (2.2), which is of independent interest.